Parameter Identification of a Nonlinear Two Mass System Using Prior Knowledge

Abstract

This article presents a new method for system identification based on dynamic neural networks using prior knowledge. A discrete chart is derived from a given signal flow chart. This discrete chart is implemented in a dynamic neural network model. The weights of the model correspond to physical parameters of the real system. Nonlinear parts of the signal flow chart are represented by nonlinear subparts of the neural network. An optimization algorithm trains the weights of the dynamic neural network model. The proposed identification approach is tested with a nonlinear two mass system.

1 Introduction

If the system is unknown and no prior knowledge is available the identification process can start with an oversized neural network. To find a model of the system as simple as possible a pruning algorithm deletes unnecessary parts of the network. This approach reduces the complexity of the network. As shown in [2, 3] this identification approach is able to remove weights from an oversized general dynamic neural networks (short GDNN, in GDNNs the layers have feedback connections with time delays, see Fig. 1).

The approach presented in this article is completely different. The assumption is that prior knowledge is available in form of a continuous signal flow chart. The model is derived in two steps. First the structure is altered in such a way, that all backward paths contain integrator blocks. In the second step the integrator blocks are discretized by Implicit and Explicit Euler approximation. In this article the parameters are trained with the powerful Levenberg–Marquardt (LM) algorithm [5]. Real time recurrent learning (RTRL) is used to calculate the necessary Jacobian matrix.

In [6, 7] a so called structured recurrent neural network is used for identifying dynamic systems. On a first glance the structured recurrent network seems to be similar to the approach in this article. However, the approach presented in this article does neither depend on a state observer nor on system-dependent derivative calculations. No matter what model is used for the identification process, the derivative calculations are conducted for the GDNN-model in general [9–11].

The second section presents the general dynamic network (GDNN). For implementing a special model structure administration matrices are introduced. Section 3 explains the optimization method used to train the network parameters throughout this article. Section 4 describes the mechatronic system to be identified. The structured GDNN is constructed in Section 5. In Section 6 the identification approach is tested with a nonlinear dynamic system. Finally, Section 7 summarizes the results.

2 General Dynamic Neural Network

Figure 1 shows an example of a three-layer GDNN with feedback connections. De Jesus described the GDNN-model in his doctoral thesis [10]. The sophisticated formulations and notations of the GDNN-model allow an efficient computation of the Jacobian matrix using real time recurrent learning (RTRL) [4, 9, 11, 16]. In this article we follow these conventions suggested by De Jesus. The simulation equation for layer m is calculated by

$$\begin{array}{rll}{\underline{n}}^{m}(t) = \sum\limits_{l\,\in\, {L}_{m}^{f}} \sum\limits _{d\,\in\, D{L}^{m,l}}{\mathop{LW}\limits_{\sim}}^{m,l}(d) \cdot {\underline{a}}^{l}(t - d)+ \sum\limits_{l\in {I}_{m}} \sum\limits_{d\in D{I}^{m,l}}{\mathop{LW}\limits_{\sim} }^{m,l}(d) \cdot {\underline{p}}^{l}(t - d) +{ \underline{b}}^{m}, \end{array}$$

(1)

where ${\underline{n}^m}(t)$ is the summation output of layer $m,{\underline{p}}^{l}(t)$ is the l-th input to the network, ${\mathop{IW}\limits_{{\sim}}}^{m, l}$ is the input weight matrix between input l and layer m, ${\mathop{LW}\limits_{{\sim}}}^{m, l}$ is the layer weight matrix between layer l and layer m, $\underline{b}^m$ is the bias vector of layer m, DL ^m,l is the set of all delays in the tapped delay line between layer l and layer m, DI ^m,l is the set of all input delays in the tapped delay line between input l and layer m, I _m is the set of indices of input vectors that connect to layer m and $L^f_m$ is the set of indices of layers that directly connect forward to layer m. The output of layer m is

$${ \underline{a}}^{m}(t) ={ \underline{f}}^{m}({\underline{n}}^{m}(t)),$$

(2)

where $\underline{f}^m(\cdot)$ are either nonlinear tanh- or linear activation functions. At each point in time the Eqs. 1 and 2 are iterated forward through the layers. Time is incremented from t = 1 to t = Q. (See [10] for a full description of the notation used here.) In order to construct a flexible model-structure, it is necessary that only particular weights in the weight matrices do exist. This is realized by the introduction of administration matrices.

Fig. 1

Example of a three-layer GDNN with feedback connections in all layers – the output of a tapped delay line (TDL) is a vector containing delayed values of the TDL input. Below the matrix-boxes and below the arrows the dimensions are shown. R ^m and S ^m respectively indicate the dimension of the input and the number of neurons in layer m. ${\underline{\hat{y}}}$ is the output of the GDNN

2.1 Administration Matrices

For each weight matrix there exists one weight administration matrix to mark which weights are used in the GDNN-model. The layer weight administration matrices ${{\mathop{\mathcal{A}L}\limits_{{\sim}}}}^{m,l}(d)$ have the same dimensions as the layer weight matrices ${\mathop{LW}\limits_{{\sim}}}^{m, l} (d)$, the input weight administration matrices ${\mathop{\mathcal{A}I}\limits_{{\sim}}}^{m,l}(d)$ have the same dimensions as the input weight matrices ${\mathop{IW}\limits_{{\sim}}}^{m,l}(d)$ and the bias weight administration vectors $\underline{\mathcal{A}b}^{m}$ have the same dimensions as the bias weight vectors $\underline{b}$ ^m. The elements of the administration matrices can have the boolean values 0 or 1, indicating if a weight is valid or not. If e.g. the layer weight ${\mathop{lw}\limits_{\sim}}_{k,i}^{m, l}(d) =[{{\mathop{LW}_{{\sim}}}^{m, l}(d)}]_{k, i}$ from neuron i of layer l to neuron k of layer m with a dth-order time-delay is valid, then ${\big [{{\mathop{\mathcal{A}L}\limits_{{\sim}}}}^{m,l}(d)\big ]}_{k,i} = \alpha {l}_{k,i}^{\,m,l}(d) = 1$. If the element in the administration matrice equals to zero, the corresponding weight has no influence on the GDNN. With these definitions the kth output of layer m can be computed by

$$\begin{array}{rll}{ n}_{k}^{m}(t)& = \sum\limits_{l\in {L}_{m}^{f}}\sum\limits_{d\in D{L}^{m,l}}\left (\sum\limits_{i=1}^{{S}^{l} }l{w}_{k,i}^{m,l}(d) \cdot \alpha {l}_{ k,i}^{\,m,l}(d) \cdot {a}_{ i}^{l}(t - d)\right ) \\&\quad\quad +\sum\limits_{l\in {I}_{m}} \sum\limits_{d\in D{I}^{m,l}}\left (\sum\limits_{i=1}^{{R}^{l} }i{w}_{k,i}^{m,l}(d) \cdot \alpha {i}_{ k,i}^{m,l}(d) \cdot {p}_{ i}^{l}(t - d)\right ) + {b}_{ k}^{m} \cdot \alpha {b}_{ k}^{m}, \\& \\{a}_{k}^{m}(t)& = {f}_{ k}^{m}({n}_{ k}^{m}(t)), \end{array}$$

(3)

where S ^l is the number of neurons in layer l and R ^l is the dimension of the lth input. By setting certain entries of the administration matrices to one a certain GDNN-structure is generated. As this model uses structural knowledge from the system, it is called Structured Dynamic Neural Network (SDNN).

2.2 Implementation

For the simulations throughout this paper the graphical programming language Simulink (Matlab) is used. SDNN and the optimization algorithm are implemented as S-function in C++.

3 Parameter Optimization

First of all a quantitative measure of the network performance has to be defined. In the following we use the squared error

$$\begin{array}{rll}E({\underline{w}}_{k})& = \frac{1} {2} \cdot \sum\limits_{q=1}^{Q}{({\underline{y}}_{q} -{\underline{\hat{y}}}_{q}({\underline{w}}_{k}))}^{T} \cdot ({\underline{y}}_{q} -{\underline{\hat{y}}}_{q}({\underline{w}}_{k})) \\& = \frac{1} {2} \cdot \sum\limits_{q=1}^{Q}{\underline{e}}_{q}^{T}({\underline{w}}_{k}) \cdot {\underline{e}}_{q}({\underline{w}}_{k}),\\\end{array}$$

(4)

where q denotes one pattern in the training set, $\underline{y}_q$ and ${\underline{\hat{y}}}$ _q ${{(\underline{w}_k)}}$are the desired target and the actual model output of the q-th pattern respectively. The vector ${\underline{w}}$ _k is composed of all weights in the SDNN. The cost function E ${{(\underline{w}_k)}}$ is small if the training process performs well and large if it performs poorly. The cost function forms an error surface in a (N + 1)-dimensional space, where N is equal to the number of weights in the SDNN. In the next step this space has to be searched in order to reduce the cost function.

3.1 Levenberg–Marquardt Algorithm

All Newton methods are based on the second-order Taylor series expansion about the old weight vector ${\underline{w}}$ _k :

$$\begin{array}{rll}E({\underline{w}}_{k+1})& = E({\underline{w}}_{k} + \Delta {\underline{w}}_{k})\\& = E({\underline{w}}_{k}) +{ \underline{g}}_{k}^{T} \cdot \Delta {\underline{w}}_{ k} + \frac{1} {2} \cdot \Delta {\underline{w}}_{k}^{T} \cdot {\mathop{H}\limits_{\sim}}{}_{k} \cdot \Delta {\underline{w}}_{k}.\end{array}$$

(5)

If a minimum on the error surface is found, the gradient of the expansion Eq. 2 with respect to Δ ${\underline{w}}$ _k is zero:

$$\begin{array}{rll}\nabla E({\underline{w}}_{k+1})& ={ \underline{g}}_{k} +{\mathop{H}\limits_{\sim}}{}_{k} \cdot \Delta {\underline{w}}_{k} = 0.\end{array}$$

(6)

Solving Eq. 6 for Δ ${\underline{w}}$ _k results in the Newton method

$$\begin{array}{rll}\Delta {\underline{w}}_{k}& = -{\mathop{H}\limits_{\sim}}{}_{k}^{-1} \cdot {\underline{g}}_{ k}^{T}, \\{\underline{w}}_{k+1}& ={ \underline{w}}_{k} -{ \mathop{H}\limits_{\sim} }{}_{k}^{-1} \cdot {\underline{g}}_{ k}.\end{array}$$

(7)

The vector $-{\mathop{H}\limits_{\sim}}{}_{k}^{-1}\cdot {\underline{g}}_k^T$ is known as the Newton direction, which is a descent direction, if the Hessian matrix ${\mathop{H}\limits_{\sim}}{}_{k}$ is positive definite. The LM approach approximates the Hessian matrix by [5]

$${ \mathop{H}\limits_{\sim}}{}_{k} \approx { \mathop{J}\limits_{\sim} }^{T}({\underline{w}}_{ k}) \cdot \stackrel{ \mathop{J}\limits_{\sim}} ({\underline{w}}_{k})$$

(8)

and it can be shown that

$${ \underline{g}}_{k} ={ \mathop{J}\limits_{\sim} }^{T}(\underline{w}_{ k}) \cdot \underline{e}({\underline{w}}_{k}),$$

(9)

where $\mathop{J}\limits_{\sim}({\underline{w}}_k)$ is the Jacobian matrix:

$$\mathop{J}\limits_{\sim}({\underline{w}}_{k}) = \left [\begin{array}{rllll}\displaystyle\frac{\partial {e}_{1}({\underline{w}}_{k})} {\partial {w}_{1}} & \displaystyle\frac{\partial {e}_{1}({\underline{w}}_{k})} {\partial {w}_{2}} & \cdots & \frac{\partial {e}_{1}({\underline{w}}_{k})} {\partial {w}_{N}}\\ \displaystyle\frac{\partial {e}_{2}({\underline{w}}_{k})} {\partial {w}_{1}} & \displaystyle\frac{\partial {e}_{2}({\underline{w}}_{k})} {\partial {w}_{2}} & \cdots & \displaystyle\frac{\partial {e}_{2}({\underline{w}}_{k})} {\partial {w}_{N}}\\\vdots & \vdots & \ddots & \vdots \\\displaystyle\frac{\partial {e}_{Q}({\underline{w}}_{k})} {\partial {w}_{1}} & \displaystyle\frac{\partial {e}_{Q}({\underline{w}}_{k})} {\partial {w}_{2}} & \cdots &\displaystyle\frac{\partial {e}_{Q}({\underline{w}}_{k})} {\partial {w}_{N}}\\\end{array} \right ]$$

(10)

The Jacobian matrix includes first derivatives only. N is the number of all weights in the neural network and Q is the number of evaluated time steps. With Eqs. 4, 5 and 6 the LM method can be expressed with the scaling factor μ _k

$${ \underline{w}}_{k+1} ={ \underline{w}}_{k} -{\left [{\mathop{J}\limits_{\sim}}^{T}({\underline{w}}_{ k}) \cdot \mathop{J}\limits_{\sim} ({\underline{w}}_{k}) + {\mu }_{k} \cdot \mathop{I}\limits_{\sim} \right ]}^{-1} \cdot { \mathop{J}\limits_{\sim} }^{T}({\underline{w}}_{ k}) \cdot \underline{e}({\underline{w}}_{k}),$$

(11)

where $\mathop{I}\limits_{\sim}$ is the identity matrix. As the LM algorithm is the best optimization method for small and moderate networks (up to a few hundred weights), this algorithm is used for all simulations in this paper.

LM optimization is usually carried out offline. In this paper we use a sliding time window that includes the information of the last Q time steps. With the last Q errors the Jacobian matrix $\mathop{J}\limits_{\sim}({\underline{w}}_k)$ from Eq. 10 is calculated quasi-online. In every time step the oldest training pattern drops out of the time window and a new one (from the current time step) is added – just like a first in first out (FIFO) buffer. If the time window is large enough, it can be assumed that the information content of the training data is constant. With this simple method we are able to implement the LM algorithm quasi-online. For the simulations in this paper the window size is set to Q = 25000 using a sampling time of 1ms.

3.2 Jacobian Calculations

To create the Jacobian matrix, the derivatives of the errors have to be computed, see Eq. 10. The GDNN has feedback elements and internal delays, so that the Jacobian cannot be calculated by the standard backpropagation algorithm. There are two general approaches to calculate the Jacobian matrix for dynamic systems: By backpropagation through time (BPTT) [15] or by real time recurrent learning (RTRL) [16]. For Jacobian calculations the RTRL algorithm is more efficient than the BPTT algorithm [11]. According to this the RTRL algorithm is used in this paper. The interested reader is referred to [2, 8, 11] for further details.

Fig. 2

Laboratory setup of the TMS

4 Two-Mass-System

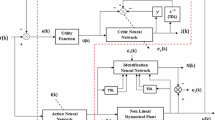
The considered plant (shown in Fig. 2) is a nonlinear two-mass flexible servo system (TMS), which is a common example for an electrical drive connected to a work machine via flexible shaft. Figure 3 displays the signal flow chart of the TMS, where the spring constant c and the damping d model the shaft between the two machines [14]. $\dot{\varphi}_1$ and $\dot{\varphi}_2$ denote the rotation speed of the main engine and the work machine respectively. The torque of inertia of the machines are depicted by J ₁ and J ₂. The motor torque is M ₁ and the torque at the work machine is M ₂. M _B1 and M _B2 are the acceleration torques of the main engine and the work machine respectively. The difference of the rotation speeds is denoted by $\Delta \dot{\varphi}$ and Δ ϕ is the difference of the angles. The torque of the spring and the damping torque are depicted by M _C and M _D respectively. The friction torques of the engine and the working machine are M _R1 and M _R2 respectively. The objective in this paper is to identify the linear TMS-parameters and the characteristics of the two friction torques.

Fig. 3

Signal flow chart of the TMS with friction

5 Structured Dynamic Neural Networks

To construct a structured network with the help of GDNNs it is necessary to redraw the signal flow chart from Fig. 3 because the implementation of algebraic loops is not feasible [1]. All feedback connections must contain at least one time delay, otherwise the signals cannot be propagated through the network correctly. This goal is accomplished by inserting integrator blocks in the feedback loops. Figure 4 displays the redrawn version of Fig. 3. By using the Euler approximation it is possible to discretize the redrawn signal flow chart. The Implicit Euler approximation y(t) = y(t − 1) + x(t)⋅T replaces all integrator blocks in the forward paths and the Explicit Euler approximation y(t) = y(t − 1) + x(t − 1)⋅T replaces all integrator blocks in the feedback paths. This approach ensures that all feedback connections contain the necessary time delays. The resulting discrete signal flow chart, which can be implemented as a SDNN, is displayed in Fig. 5. z ^{− 1} denotes a first order time delay and T is the sampling time. All other denotations are the same as in Fig. 3. In total the SDNN consists of 16 layers. The summing junctions depict the neurons of the network. Every summing junction is marked with a number, which denotes the layer of the neuron and its position within the layer. For instance, 15. 1 marks the first neuron of the 15th layer. The friction of the engine and the work machine can be modeled by an optional number of neurons in the 5th layer and in the 11th layer respectively. These are the only neurons with tanh-transfer functions. All other neurons have linear transfer functions. The connections in Fig. 5 which do neither belong to a linear parameter (depicted as box) nor to a friction-subpart are initialized with 1 or –1. The optimization algorithm is able to tune the parameters corresponding to the spring constant c, the damping d and the torque of inertia J ₂ and the friction weights of the work machine. As it is not possible to identify the two torques of inertia as well as the two characteristic curves of the TMS simultaneously, the engine parameters are determined in a first no-load-identification which is conducted in idle running, see Section 6.

Fig. 4

Redrawn signal flow chart of the TMS from Fig. 3

Fig. 5

Structured recurrent network of a nonlinear TMS

6 Identification

6.1 Excitation Signal

The system is excited by an APRBS-signal (Amplitude Modulated Pseudo Random Binary Sequence [13]) combined with a bias produced by a relay. The APRBS-signal has an amplitude range between –7 and 7 Nm and an amplitude interval between 10 and 250 ms. The relay output switches to –4 Nm if the rotation speed of the TMS is greater than $10\frac{{\rm rad}}{{\rm s}}$ and it switches to 4 Nm if the rotation speed is smaller than $\hbox{--}10\frac{{\rm rad}} {{\rm s} }$. The suggested excitation signal ensures that the TMS, which is globally integrating, remains in a well defined range for which the SDNN is able to learn the friction. Moreover, the output of the relay is multiplied by 0.2 for a rotation speed in the range of $\hbox{--}2\,{\rm to}\,2\frac{{\rm rad}} {{\rm s}}$. Thus, the SDNN receives more information about the friction in the region of the very important zero crossing. The resulting output of the TMS can be regarded in upper panel of Fig. 8. This excitation signal is used in all the following identification processes.

6.2 Engine Parameters

For a successful TMS-identification it is necessary to identify the engine parameters in idle mode first. The obtained values are used as fix parameters in the identification of the whole TMS in Chapter 6. The upper left drawing of Fig. 6 displays the signal flow chart of the nonlinear engine, where M ₁ is the torque, $\dot{\varphi}_1$ is the rotation speed, and J ₁ denotes the torque of inertia. In order to be able to discretize the signal flow chart, we insert the integrator block in the backward path. The resulting signal flow chart is shown in the upper right drawing of Fig. 6.

As explained above, for discretizing the signal flow chart the Implicit Euler approximation has to replace the integrator in the forward path, whereas the Explicit Euler approximation replaces the integrator in the backward path. The sampling time T is incorporated in the gain corresponding to the torque of inertia J ₁. The lower drawing of Fig. 6 displays the resulting discrete signal flow chart, which can be implemented as a SDNN in which all the summing junctions are regarded as neurons. The neurons in layer 5 model the friction of the engine.

Fig. 6

Signal flow chart of the engine (upper left side), redrawn signal flow chart of the engine (upper right side) and resulting SDNN (lower drawing)

For the identification process the engine is excited with the signal explained in Section 6. The quasi-online calculated cost function E(${\underline{w}}$ _k ) Eq. 4 with Q = 25000 is minimized by the LM optimization algorithm Eq. 11. The sampling time is set to T = 1ms and the identification process starts after 5 s, seen in the upper panel of Fig. 7. The SDNN-model of Fig. 6 has three neurons in the fifth layer with six weights to model the friction. These weights are initialized randomly between –0.5 and 0.5. Table 1 shows two different initial values for the torque of inertia J ₁ and the corresponding results. The calculated results are mean values between the last 25, 000 optimization steps. Figure 7 displays the characteristic curve of the friction at t = 100 s identified by the SDNN. We observe that the network is able to model the jump due to the static friction with just three neurons. The following identification of the whole TMS uses this friction curve from Fig. 7 and the result J ₁ = 0. 1912 from Table 1 for the torque of inertia.

Fig. 7

Identification of the engine parameters – Torque of inertia and friction curve identified by the nonlinear subpart in the 5th layer

Table 1 Initial values and final values of the torque of inertia of the engine J ₁

6.3 TMS Parameters

To identify the parameters of the whole TMS we excite the plant with the torque signal described in Section 6 and use the SDNN-model constructed in Chapter 5. The torque of inertia of the engine J ₁ and its friction are initialized according to the results of Section 6. These weights remain unchanged during the whole identification process, whereas the weights corresponding to the torque of inertia of the work machine J ₂, the spring constant c, the damping d and the work machine friction are trained. The work machine friction is modeled by three neurons with tanh functions in the 11th layer, see Fig. 5. The six weights of this nonlinear subpart are initialized randomly between –0.5 and 0.5. The upper panel of Fig. 8 displays the outputs of the TMS and the SDNN-model during the identification process for the first set of initial values of Table 2. The lower panel of this figure shows only 5 s for a detailed view. The identification process starts after 5 s. The sampling time is set to T = 1 ms. The quasi-online calculated cost function E ${{(\underline{w}_k)}}$ Eq. 4 with Q = 25000 is minimized by the LM optimization algorithm Eq. 11 and is depicted in the middle panel of Fig. 8. Due to the quasi-online approach the cost function value increases until t = 25 s, until the training data window is completely filled up. The results in Table 2 are mean values of the last 25000 optimization steps.

Fig. 8

Output signals of the SDNN model $\hat{\dot{\varphi}}_2$ and the real TMS $\dot{\varphi}_2$ with resulting cost function

Figure 9 displays the developing of the damping, the spring constant and the torque of inertia during the identification process for the first initialization of Table 2. Figure 10 shows the characteristic curve of the work machine friction identified by the SDNN after 100 s. In addition to that Table 2 shows the results of a second identification run with another initialization. The resulting torque of inertia and spring constant are almost equal. Only the damping shows different final values. The higher mean error (compared to the first identification) implies that the second optimization process ended in a local minimum.

Fig. 9

Linear parameter signals during the identification

Fig. 10

Friction curve identified by the nonlinear subpart in the 11th layer

Table 2 Initial values and final values for the identification of the TMS

7 Conclusion

The system identification approach in this article is based on a given continuous signal flow chart. Before discretizing the signal flow chart, integrator blocks are inserted in all feedback loops. The Implicit Euler approximation replaces all integrator blocks in the forward paths, whereas the Explicit Euler approximation is used to replace the integrator blocks in the feedback paths. Since the resulting discrete flow chart contains time delays in all feedback connections it can be implemented as a SDNN without algebraic loops. Physical parameters of the system are represented by certain weights of the SDNN. Nonlinear subparts of the network model nonlinearities of the system. The suggested identification approach is tested with a nonlinear TMS. The results verify that the suggested approach enables us to identify the torques of inertia, the spring constant, the damping and the two friction curves of the TMS. Problems may occur if the optimization algorithm gets stuck in a local minimum. In this case the identification process has to be restarted with a different set of initial values. With the help of the mean error the success of the identification process can be validated.