A Meshfree Framework for Ideal Magnetohydrodynamics

Abstract

A meshfree framework for numerical simulations of magnetohydrodynamic flows is proposed. The framework is based on the Least-Squares-Based Upwind Finite Difference method (LSFD-U) and is capable of handling arbitrary point distributions. The approach is based on the least-squares method of error minimisation to compute the inviscid flux derivatives. The flux derivatives at every point require the fluxes at the point as well as those in fictitious interfaces in a neighbourhood around it. The fluxes at the fictitious interfaces are computed by using any numerical flux formula of interest that incorporates upwinding and consequently a global rather than the one-sided stencil may be chosen for computation. The meshfree framework is implemented through AUSM scheme, using a first-order accurate spatial and temporal discretisation. Studies on the one-dimensional MHD shock tube problems demonstrate the efficacy of the algorithm. The effect of non-uniform point distributions on the performance of the meshfree framework particularly with regard to conservation has also been studied. On the non-uniform grid the solutions of meshfree framework are not in agreement with the solutions of the finite volume framework unlike on uniform meshes. The finite volume formulation is known to be conservative and therefore it is very clear that meshfree formulation has conservation issues particularly as the grid becomes more non-uniform. It is therefore desirable to have a formulation for meshfree framework that preserves conservation at a discrete level like the finite volume method. Attempts have been made to develop a conservative meshfree framework using weighted least-squares technique for a particular case of one-dimensional non-uniform point distribution.

1 Introduction

In recent decades, advancements in computing technology and hardware have enabled the use of numerical simulations to tackle problems with complexity and scale larger than ever before. While the algorithms of mesh-based methods (like FDM, FEM and FVM) are being nurtured day by day, mesh or grid generation for complex real life configuration and sophisticated problems has become a bottleneck for computational science. To address this issue a class of methods called ‘‘Meshless’’ (also known as ‘‘Meshfree’’ or ‘‘Gridfree’’) methods have been developed. These methods require the information at a set of grid points around a node to approximate the derivatives at that node. Though the use of arbitrary point distributions increases the computational effort compared to the mesh-based methods, the advancement of computing technology has made these techniques realistic.

In this work a meshfree framework for numerical simulations of magnetohydrodynamic (MHD) flows is proposed. MHD investigates the flow of electrically conducting fluids in the presence of magnetic fields. In other words, the magnetic field influences the fluid motion, and at the same time the fluid motion changes the magnetic field. Thus, the governing equations are inherently coupled in terms of the fluid velocity and the induced magnetic field. The MHD equations are non-strictly hyperbolic and nonconvex [1]. As a result, the wave structure is more involved than the wave structure of the Euler equations. Till date, a number of researchers have investigated many flow problems of MHD owing to its important applications in the fields like astrophysics, geology, geophysics, metallurgy, power generation, thermo-nuclear reactors, liquid metals cooling systems, biofluids and drug delivery.

Although, the application of meshfree methods for solving different hydrodynamical problems is not uncommon, very limited application of meshfree techniques is observed in solving MHD flow problems. Out of the different meshfree methods, most of the authors have previously used smoothed particle hydrodynamics (SPH) in their MHD simulations. Namely, Brackbill [2] extended the Fluid-Implicit-Particle Method (FLIP) (combination of particle-in-cell (PIC) and SPH) to MHD and Jiang et al. [3] applied SPH simulations to show that a magnetic field applied in the streamwise direction can restrain the turbulence fluctuations in the transverse plane of fluid flow. Element-Free Galerkin (EFG) method was also used by several authors in [4–7] for solving MHD flow problems. Among other meshfree approaches, Bourantas et al. [8] used the meshless point collocation method (MPCM); Dehghan and Mirzaei used the local boundary integral equation (LBIE) meshless method [9], and the meshless local Petrov-Galerkin (MLPG) method [10] to obtain the numerical solution for MHD flows. Recently, Deghan and Salehi [11] used a meshfree weak-strong (MWS) form method to solve MHD flow problems.

The meshfree framework developed in this work is based on the Least-Squares-Based Upwind Finite Difference method (LSFD-U) introduced by Sridar and Balakrishnan [12]. The least squares method of error minimisation is used to compute the inviscid flux derivatives. The fluxes at the fictitious interfaces are computed by using any numerical flux formula of interest that incorporates upwinding and consequently a global rather than one-sided stencil may be chosen for computation. Although LSFD-U has many positive properties, however like all other meshless methods, it also lacks conservation at the discrete level owing to its local nature. Most importantly, when sharp discontinuities exist, non-conservative numerical methods under- or overestimate shock speeds, as a result of which numerical shocks increasingly lag or lead the true shocks. To deal with this issue, Chiu et al. [13] made an attempt to present a novel conservative meshfree method by careful construction of discrete derivative operators. In the present work, we attempt to enforce discrete conservation in LSFD-U for a particular case of one-dimensional non-uniform point distribution.

The organization of the rest of this paper is as follows: In Sect. 2, the governing equations of ideal MHD are defined. In Sect. 3, a general discussion on the least-squares-based update procedure is presented. An introduction to LSFD-U procedure is given in Sect. 4. Discussions on conservation issues related to meshfree methods and the procedure to obtain a conservative meshfree method is given in Sect. 5. Results and discussions are presented in Sect. 6. Finally in Sect. 7, concluding remarks are given.

2 Ideal MHD Equations

The magnetohydrodynamics (MHD) equations characterise the flow of electrically conducting fluids in the presence of magnetic fields. The coupling of fluid dynamics equations with Maxwell’s equations of electrodynamics results into the governing equations of MHD. Ideal MHD equations can be obtained by neglecting electrostatic forces, displacement current, effects of viscosity, electrical resistivity and heat conduction. They can be written as:

$$ \frac{\partial \rho }{\partial t} + \nabla \cdot (\rho \varvec{V}) = 0 $$

(1)

$$ \frac{{\partial (\rho \varvec{V})}}{\partial t} + \nabla \cdot (\rho \varvec{VV} + \varvec{I}P_{t} - \varvec{BB}) = 0 $$

(2)

$$ \frac{{\partial \varvec{B}}}{\partial t} + \nabla \cdot (\varvec{VB} - \varvec{BV}) = 0 $$

(3)

$$ \frac{\partial E}{\partial t} + \nabla \cdot \{ (E + P_{t} )\varvec{V} - \varvec{B}(\varvec{B} \cdot \varvec{V})\} = 0 $$

(4)

with the constraint $\nabla \cdot \varvec{B} = 0$. In the above equations $\rho$ denotes density, $\varvec{V}$ the velocity field, $\varvec{B}$ the magnetic field, $P_{t}$ the full pressure, and $E$ denotes the total energy. The full pressure and total energy are defined by

$$ P_{t} = P + \frac{1}{2}(B_{x}^{2} + B_{y}^{2} + B_{z}^{2} ) $$

$$ E = \frac{1}{2}\rho (u^{2} + v^{2} + w^{2} ) + \frac{P}{(\gamma - 1)} + \frac{1}{2}(B_{x}^{2} + B_{y}^{2} + B_{z}^{2} ) $$

where $P$ is the static pressure; $u$, $v$, and $w$ are the components of the velocity field $\varvec{V}$ and $B_{x}$, $B_{y}$ and $B_{z}$ are the components of the magnetic field $\varvec{B}$ in the $x$, $y$ and $z$ directions, respectively. The ideal MHD equations are non-strictly hyperbolic and nonconvex in nature [1], since there are some fields which are neither linearly degenerate nor genuinely nonlinear.

When the variables change only with respect to $x$ and $t$ and $B_{x}$ remains as a constant, we can obtain the one-dimensional ideal MHD equations from system (1–4). The resulting equations in the conservative form can be written as:

$$ \frac{{\partial \varvec{U}}}{\partial t} + \frac{{\partial \varvec{F}}}{\partial x} = 0 $$

(5)

where,

$$ U = \left[ {\begin{array}{*{20}c} \rho \\ {\rho u} \\ {\rho v} \\ {\rho w} \\ {B_{y} } \\ {B_{z} } \\ E \\ \end{array} } \right];\quad F = \left[ {\begin{array}{*{20}c} {\rho u} \\ {\rho u^{2} + P_{t} - B_{x}^{2} } \\ {\rho uv - B_{x} B_{y} } \\ {\rho uw - B_{x} B_{z} } \\ {uB_{y} - vB_{x} } \\ {uB_{z} - wB_{x} } \\ {(E + P_{t} )u - B_{x} (uB_{x} + vB_{y} + wB_{z} )} \\ \end{array} } \right] $$

3 Least-Squares Based Update Procedure for One-Dimensional Problems

To describe the least-squares method we consider the one-dimensional point distribution presented in Fig. 1. An arbitrary function $\phi$(x) is introduced to approximate the derivative at point ‘o’. Truncated Taylor series is used to estimate functional value at the neighbouring point of ‘o’ (say at point ‘$i$’). Taylor series expansion for $\phi_{i}$ around point ‘o’ is given by:

Fig. 1

Typical 1D point distribution

$$ \phi_{i} = \phi_{o} + \left. {\frac{\partial \phi }{\partial x}} \right|_{o} \varDelta x_{i} + \left. {\frac{{\partial^{2} \phi }}{{\partial x^{2} }}} \right|_{o} \frac{{(\varDelta x_{i} )^{2} }}{2!} + \left. {\frac{{\partial^{3} \phi }}{{\partial x^{3} }}} \right|_{o} \frac{{(\varDelta x_{i} )^{3} }}{3!} + \; \cdots $$

(6)

with $\varDelta ( \cdot )_{i} = ( \cdot )_{i} - ( \cdot )_{o}$. The $i$th element of the error vector $E$ is defined as:

$$ E_{i} = \varDelta \phi_{i} - \left. {\frac{\partial \phi }{\partial x}} \right|_{o} \varDelta x_{i} - \left. {\frac{{\partial^{2} \phi }}{{\partial x^{2} }}} \right|_{o} \frac{{(\varDelta x_{i} )^{2} }}{2!} - \left. {\frac{{\partial^{3} \phi }}{{\partial x^{3} }}} \right|_{o} \frac{{(\varDelta x_{i} )^{3} }}{3!} - {\kern 1pt} \; \cdots $$

(7)

Let ‘$m$‘represent the number of neighbours of ‘o’. For linear least-squares (LLSQ) fit we include terms up to first order derivative for defining the error vector. Then the derivative at point ‘o’ is determined by minimizing the sum of all the squared residuals i.e., the error vector for all neighbouring points of ‘o’ under consideration (known as neighbouring points) w.r.t $\left. {\frac{\partial \phi }{\partial x}} \right|_{o}$. The sum of all the squared residuals can be written as:

$$ \sum\limits_{i = 1}^{m} E_{i}^{2} = \sum\limits_{i = 1}^{m} \left[ {\varDelta \phi_{i} - \left. {\frac{\partial \phi }{\partial x}} \right|_{o} \varDelta x_{i} } \right]^{2} $$

(8)

After minimizing w.r.t $\left. {\frac{\partial \phi }{\partial x}} \right|_{o}$ we get the gradient at point ‘o’:

$$ \left. {\frac{\partial \phi }{\partial x}} \right|_{o} = \frac{{\sum\nolimits_{i = 1}^{m} {(w_{i} \varDelta \phi_{i} \varDelta x_{i} )} }}{{\sum\nolimits_{i = 1}^{m} {w_{i} (\varDelta x_{i} )^{2} } }} $$

(9)

where, $w_{i}$ is a monotonically decreasing weight function which can be written as

$$ \begin{array}{*{20}l} {w_{i} = \frac{1}{{r_{i}^{p} }}} \hfill \\ \end{array} $$

(10)

with ‘$r_{i}$‘as the distance between point ‘o’ and its neighbouring points ` $i$’ and $p \ge 1$. The weights give preference to neighbouring information which is closer to point ‘o’ than those are far away. When the weights are chosen to be identically unity then the approach is referred to as unweighted least-squares approach or simply least-squares approach. The gradient becomes

$$ \left. {\frac{\partial \phi }{\partial x}} \right|_{o} = \frac{{\sum\nolimits_{i = 1}^{m} {(\varDelta \phi_{i} \varDelta x_{i} )} }}{{\sum\nolimits_{i = 1}^{m} {(\varDelta x_{i} )^{2} } }} $$

(11)

4 Upwind Least-Squares Finite Difference Method

In this work we use upwind least-squares finite difference method (LSFD-U) proposed by Sridar and Balakrishnan [12]. To understand the method we consider the one-dimensional point distribution presented in Fig. 2. In LSFD-U, the upwind flux is calculated at a fictitious interface $I$ associated with the neighbouring point $i$. This flux is then used in the least-squares formula. As stated in Eq. (9), the linear least-squares approximation for flux gradient at point ‘o’ can be written as:

Fig. 2

Use of fictitious interface to enforce upwinding in 1D problem

$$ \left. {\frac{\partial F}{\partial x}} \right|_{o} = \frac{{\sum\nolimits_{I = 1}^{m} {w_{I} (\varDelta F_{I} \varDelta x_{I} )} }}{{\sum\nolimits_{I = 1}^{m} {w_{I} (\varDelta x_{I} )^{2} } }} $$

(12)

with $\varDelta ( \cdot )_{I} = ( \cdot )_{I} - ( \cdot )_{o}$. In the above equation $F_{I}$ indicates the upwind flux calculated at the fictitious interface $I$ corresponding to the neighbouring point $i$. The appealing property of this method is that, the flux $F_{I}$ at the fictitious interface can be determined by using any numerical flux formula of interest. Additionally, a global stencil of grid points can be used in this method instead of a one-sided upwind stencil resulting in lesser computational effort and greater accuracy. As this method does not use one-sided stencil of grid points, the difficulty of locating physically relevant neighbours near the boundaries of the computational domain can be avoided.

5 Enforcing Conservation in LSFD-U

Like all other meshless methods, LSFD-U also faces a fundamental challenge i.e., the lack of discrete conservation. Owing to the local nature of the scheme, it does not preserve conservation at the discrete level except with a uniform point distribution. Compared to mesh-based approaches non-conservative numerical methods consistently under- or overestimate shock speeds when sharp discontinuities exist, and therefore the numerical shocks increasingly lag or lead the true shocks as time progresses. The effects of non-conservation on accuracy and stability of meshfree algorithms, as compared to their mesh-based counterparts is often a cause of concern in terms of the utility of these techniques.

In this section, we attempt to enforce discrete conservation within the meshfree framework for a very specific one-dimensional case. A non-uniform point distribution as shown in Fig. 3 is considered, where every point has a neighbourhood stencil consisting of one left and one right neighbour. Studies are performed using both unweighted and weighted LSFD-U, to study the impact of weights on non-uniform point distribution. We have considered a weight function $w_{I} = 1/r_{I}^{p}$ with $p = 1$.

Fig. 3

1D non-uniform point distribution

6 Results and Discussions

We have tested our algorithm on two MHD shock tube problems to check the consistency and robustness of our method under different conditions on the physical variables. Our suite of one-dimensional problems include the Brio and Wu problem and the Dai and Woodward problem (also known as Ryu and Jones problem).

6.1 Test Case 1: Brio and Wu Problem

Brio and Wu problem is an MHD analogue of the Sod shock tube problem. It is a coplanar Riemann problem for MHD, with two initial constant states $U_{l}$ and $U_{r}$ which were suggested by Brio and Wu in [1]. Even though, the Brio and Wu test problem is non-physical and cannot be realised in a laboratory environment, it is regarded as a benchmark problem to test numerical schemes for local linear degeneracy and lack of strict hyperbolicity in one-dimensional ideal MHD. As in [1] we choose (ρ, u, v, w, $B_{y}$, $B_{z}$, p) _l  = (1, 0, 0, 0, 1, 0, 1); (ρ, u, v, w, $B_{y}$, $B_{z}$, p) _r  = (1/8, 0, 0, 0, −1, 0, 1/10); $B_{x}$ = 0.75 and $\gamma$ = 1.4, with the initial discontinuity at the middle of the tube.

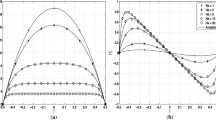
Numerical solutions obtained for 800 grid points with length of the tube = 800 m and $\varDelta t = 0.2$ s (CFL ~ 0.8) are shown at $t = 80$ s. Figure 4 shows the solutions for this test obtained through unweighted LSFD-U, weighted LSFD-U and simple finite volume method using AUSM [14] flux vector splitting formula on the same non-uniform point distribution.

Fig. 4

Solutions for Brio Wu shock tube problem

Five waves are generated in the solution. A fast rarefaction wave (FR), and a slow compound wave (SM) (compound wave is a combination of a shock and rarefaction wave of the same family attached with each other) move towards the left, and a contact discontinuity (C), a slow shock (SS), and a fast rarefaction wave (FR) move towards the right. This numerical example is important, since it demonstrates one of the typical characteristics of the solutions of the MHD system i.e., a compound wave. The existence of the compound wave in the solution is correlated with the non-convex character of the MHD system by Brio and Wu in [1].

6.2 Test Case 2: Dai and Woodward Problem

This MHD shock tube problem was first suggested by Dai and Woodward [15] and later solved by Ryu and Jones [16], which involves three-dimensional field and velocity structure where the magnetic field plane rotates. Initial left and right values are: (ρ, u, v, w, $B_{y}$, $B_{z}$, p) _l  = (1.08, 1.2, 0.01, 0.5, 3.6/$\surd (4\pi )$, 2.0/$\surd (4\pi$), 0.95) and, (ρ, u, v, w, $B_{y}$, $B_{z}$, p) _r  = (1.0, 0.0, 0.0, 0.0, 4.0/$\surd (4\pi )$, 2.0/$\surd (4\pi )$, 1.0). With, $B_{x}$ = 2.0/$\surd (4\pi )$ and $\gamma$ = 5/3. Numerical solutions obtained for 512 grid points at $t$ = 0.2 s with length of the tube = 1 m and $\varDelta t = 10^{ - 5}$ s are plotted in Fig. 5. Two fast shocks (FS), two slow shocks (SS), two rotational discontinuities (RD) and a contact discontinuity (C) are generated in the solution. This is an important test case since we can check the ability of the scheme to capture all the seven waves in MHD with a single test. For a fast shock the magnitude of each transverse component of magnetic field increases from its pre-shock state to its post-shock state while it is vice versa for a slow shock. A rotational discontinuity propagates at the Alfven speed and there are jumps in transverse components of flow velocity, but no jumps in density, static pressure and longitudinal component of flow velocity. Importantly, across a rotational discontinuity, the transverse part of magnetic field undergoes a rotation around the normal of the surface, but the magnitude remains unchanged.

Fig. 5

Solutions for Dai Woodward shock tube problem

The results demonstrate the efficacy of our algorithm. On the non-uniform grid the solutions of the unweighted LSFD-U are not in agreement with the solutions of the finite volume framework, however, there are no discernible differences between the solutions of weighted LSFD-U and the solutions of the finite volume framework. This suggests that the weighting has been successful in eliminating conservation issues related with LSFD-U and it preserves conservation at a discrete level like the finite volume method. However, the behaviour of weights on asymmetric neighbourhood stencils has not been studied for now and is a matter of ongoing investigation.

7 Conclusions

In this paper we have proposed a meshfree framework for numerical simulations of ideal magnetohydrodynamic flows. The framework is based on the Least-Squares-Based Upwind Finite Difference method (LSFD-U), which employs a global stencil on any arbitrary point distribution. Any upwind numerical flux formula of interest (we have used AUSM) can be used to compute the fluxes at the fictitious interfaces. The ability of LSFD-U has been demonstrated by solving two different MHD shock tube problems and the importance of weighting on LSFD-U in enforcing discrete conservation has been highlighted over its unweighted counterpart. Efforts to develop a conservative meshfree framework on non-uniform point distributions with asymmetric neighbourhood stencil is currently under progress.