Keywords

AMS Subject Classification:

1 Introduction

Experimentally, it has been observed that below a critical temperature, ferromagnetic materials have a tendency to split up into a small uniformly magnetized regions called domains separated by a thin transition layer known as domain walls. Over the period of time, study of formation and motions of domain walls gained a lot of attention and became one of the most fascinating topic among researchers. It is due to the fact that the ferromagnetic materials are used on a wide scale in magnetic storage industry. In particular, ferromagnetic nanowires play a very dominant role in nanoelectronic devices in which the information is encoded as magnetic domains separated by domain walls along the wire. For example, in case of racetrack memory, we obtain a three-dimensional storage device by using U-shaped nanowires normal to the plane of silicon wafer (see [1]). For the rigorous treatment of domains and its characteristics, we refer the reader to [2] and the references therein.

The model used to describe the magnetic behavior of ferromagnetic material is called micromagnetism and was introduced by Brown [3]. The evolution of magnetization inside the ferromagnetic medium is triggered by the Landau–Lifschitz equation which is parabolic and nonlinear. The relevant configurations of magnetization are minimizers of an energy functional, consisting of several components. We shall see that these relevant configurations of magnetization coincide with the steady-states of Landau–Lifschitz equation.

The general framework of the ferromagnetism is as follows. We consider a finite homogeneous ferromagnetic material which occupies a domain \(\varOmega \subset \mathbb R^{3}\). The time-varying magnetic moment u of a ferromagnetic material is a solution of the Landau–Lifschitz equation (LLE)

$$\begin{aligned} \dfrac{\partial u}{\partial t}=-u \times \mathscr {H}_{eff}-u \times \left( u \times \mathscr {H}_{eff} \right) , \end{aligned}$$
(1)

with the physical saturation constraint

$$\begin{aligned} |u(t,.)|=1 ~ \text{ for }~ \left( t,. \right) \in \mathbb R^{+} \times \mathbb R^{3} ~ a.e., \end{aligned}$$
(2)

where the abbreviation a.e. stands for almost everywhere. The total effective field \(\mathscr {H}_{eff}=-\nabla \mathscr {E} \) is derived from the micromagnetism energy \(\mathscr {E}\) given by

$$\begin{aligned} \mathscr {E}(u)=\dfrac{A}{2} \displaystyle \underset{\varOmega }{\int } | \nabla u | ^{2} +\dfrac{1}{2}\displaystyle \underset{\mathbb R^{3}}{\int } |\mathscr {H}_{d}(u)|^{2}-\displaystyle \underset{\varOmega }{\int } \mathscr {H}_{a}\cdot u, \end{aligned}$$
(3)

where the term represents the exchange, stray field and external energy contribution respectively. The constant \(A>0\) is called the exchange constant. Also, \(\mathscr {H}_{a}\) denotes an applied magnetic field and \( \mathscr {H}_{d}(u) \) is the stray field which is characterized by the Maxwell equations:

\({\left\{ \begin{array}{ll} ~~\text {curl } \mathscr {H}_{d}(u)=0 ~~\text {in}~ \mathbb R^{3} ,\\ ~~\text {div } (\mathscr {H}_{d}(u)+\bar{u})=0~~\text {in}~ \mathbb R^{3}, \\ ~~H_{d}(u)~ \text {vanishes at infinity}. \end{array}\right. }\)

where \(\bar{u}\) is the extension of u in \(\mathbb R^{3}\) by 0 outside of \(\varOmega \). We obtain that,

$$\begin{aligned} \mathscr {H}_{eff}= \Delta u + \mathscr {H}_{d}(u)+\mathscr {H}_{a}. \end{aligned}$$

We take the scalar product of (1) with \(\mathscr {H}_{eff}\) and integrate in time (assuming time invariant applied field). Using \(\mathscr {H}_{eff}=-\nabla \mathscr {E}\), we obtain (see [4, 5])

$$\begin{aligned} \dfrac{d}{dt}\mathscr {E}(u(t))=-\displaystyle \underset{\varOmega }{\int }|\mathscr {H}_{eff}(u)-\left( \mathscr {H}_{eff}(u)) \cdot u \right) u|^{2}, \end{aligned}$$
(4)

this denotes the dissipation of energy which is mainly due to the second term appears on the right hand side of (1). Furthermore, steady-states of (1) satisfy \(u \times \mathscr {H}_{eff}=0\) in domain \(\varOmega \), which is exactly the Euler–Lagrange equations of the minimization problem for (3). Therefore, minimizers of (3), i.e., relevant physical configurations of the magnetization are nothing but the steady-state solutions of (1) under the constraint (2).

Existence results of weak solutions for the Landau–Lifschitz equation have been discussed in [6–8], whereas the strong solutions are considered in [9, 10] and known to exist locally in time. Numerical aspects of ferromagnetic materials have been investigated in [11, 12] and the references therein. Stability and controllability results related with ferromagnetic nanowires are studied in [5, 13, 14]. Higher dimensional models and network models of such materials can be found in [15, 16].

In the present article, we consider a two-dimensional finite network model of ferromagnetic nanowires of semi-infinite length. We assume the relevant configuration of the magnetization of the network is of the form \(u^{*}=\mu \mathbf {e}_{1}\) where \(\mu =(\mu _{i})_{i \in I}\) with \(\mu _{i}=\left\{ -1,+1 \right\} \). We prove that these relevant configurations are asymptotically stable in a long time behavior under certain condition on the distance between the consecutive nanowires. The organization of this article is as follows:

In Sect. 2, we present the schematics of the considered model and introduce the problem related to the stability of the steady-states in the absence of external magnetic field. In Sect. 3, we give the statement of the main result and establish some preliminary estimates to derive the Theorem.

2 Modeling of a Network Model

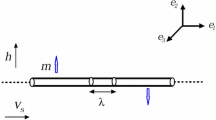
In this section, we present a schematics and modeling of a network model under consideration. We consider a two-dimensional finite network model of ferromagnetic nanowires of semi-infinite length. In which nanowires are supposed to have homogeneous geometry and to be placed on the plane \(( \mathbf {e}_{1}, \mathbf {e}_{2})\), where \((\mathbf {e}_{1}, \mathbf {e}_{2}, \mathbf {e}_{3})\) is the canonical basis of \(\mathbb R^{3}\). We represent the distance between the two consecutive nanowires by \(\ell > 0\). Since, we consider the finite framework of a network model therefore the index i takes it values in the finite set \( I=\left\{ 0,1,2,\ldots ,N \right\} \). We denote the coordinates of a point on the ith nanowire by \( (x_{i}, i \ell ) \), where \(0\le x_{i} < \infty \) with \(i \in I\) (see Fig. 1). We use the following notations:

\({\left\{ \begin{array}{ll} \left( \mathbb R^{3} \right) ^{I} = \left\{ u=(u_{i})_{i \in I}, \text{ such } \text{ that } \forall ~ i \in I, u_{i} \in \mathbb R^{3} \right\} ,\\ \\ \left( \mathbb S^{2} \right) ^{I}= \left\{ u=(u_{i})_{i \in I} \in (\mathbb R^{3})^{I}, \text{ such } \text{ that } \forall ~ i \in I, |u_{i}|=1 \right\} , \\ \\ \Vert u\Vert = \underset{i}{\text {sup}} |u_{i}| , {\text {where}}\,i \in {\text {I}} {\text {and}} |\cdot | {\text {is the euclidean norm in}} \mathbb R^{3}. \end{array}\right. }\)

where \(\mathbb S^{2}\) represents the unit sphere in \(\mathbb R^{3}\).

Fig. 1
figure 1

Schema of network model

Full size image

We assume that the magnetization on each nanowire is constant in the space variable, i.e., we deal with the ordinary differential model of micromagnetism. This can be justified by the assumption that the radius of the nanowires are very small as compared to \(\ell \). We denote \(u_{i}=u_{i}(t)\) the magnetization at any point on the ith nanowire. Therefore, the unknown \(u=(u_{0},\ldots ,u_{N})\) is defined as \( u{:}\,\mathbb R^{+} \rightarrow (\mathbb S^{2})^{I} \), i.e., \( u= u(t)=(u_{i}(t))_{i \in I} \). Exchange field vanishes due to the aforementioned assumption renders the only contribution of demagnetizing (stray) field in total effective field.

We recall that the stray energy is connected with the magnetic field generated by the medium itself. We calculate the stray field for the entire network in the following fashion. On a fixed nanowire say \(j_{0}\), we represent its stray field as \(\mathscr {H}_{d}(u)(j_{0})\) which consist of two parts: the stray field generated on \(j_{0}\)th nanowire by its own magnetization, i.e., by \(u_{j_{0}}\), denoted by \(\mathscr {H}_{d}^{int}(u)(j_{0})\), and the field generated by the magnetization of other nanowires, denoted by \(\mathscr {H}_{d}^{ext}(u)(j_{0})\). We write the stray field as:

$$\begin{aligned} \mathscr {H}_{d}(u)(j_{0})=\mathscr {H}_{d}^{int}(u)(j_{0})+\mathscr {H}_{d}^{ext}(u)(j_{0}). \end{aligned}$$

The demagnetizing field on \(j_{0}\)th nanowire due to its own magnetization is given by (see [13, 17])

$$\begin{aligned} \mathscr {H}_{d}^{int}(u)(j_{0})=-u_{j_{0}}^{2}\mathbf {e}_{2}-u_{j_{0}}^{3}\mathbf {e}_{3}. \end{aligned}$$
(5)

The stray field generated by the \(i_{0}\)th nanowire on the \(j_{0}\)th nanowire is given by (see [18])

$$\begin{aligned} \mathscr {H}_{i_{0},j_{0}}(u_{i_{0}})(\zeta )=-\dfrac{1}{4\pi } \displaystyle \int _{0}^{\infty } \dfrac{u_{i_{0}}}{|\zeta -\eta |^{3}}dy + \dfrac{3}{4\pi } \displaystyle \int _{0}^{\infty } \dfrac{(\zeta -\eta )}{|\zeta -\eta |^{5}}u_{i_{0}} \cdot (\zeta -\eta )dy. \end{aligned}$$

with \(\zeta =(x,j_{0} \ell ) \) and \(\eta =(y,i_{0} \ell ) \), where x and y belongs to \([0,\infty )\).

On calculating the values of these integrals, we obtain:

$$\begin{aligned} \mathscr {H}_{i_{0},j_{0}}(u_{i_{0}})(\zeta )= (\mathscr {H}_{i_{0},j_{0}}^{1}, \mathscr {H}_{i_{0},j_{0}}^{2}, \mathscr {H}_{i_{0},j_{0}}^{3}), \end{aligned}$$

where,

$$\begin{aligned} \mathscr {H}_{i_{0},j_{0}}^{1}=\dfrac{1}{4 \pi \ell ^{2}|i_{0}-j_{0}|^{2}} \left[ -\dfrac{x\ell ^{2}|i_{0}-j_{0}|^{2}}{(x^{2}+\ell ^{2}|i_{0}-j_{0}|^{2})^{3/2}} u_{i_{0}}^{1}+ \dfrac{\ell ^{3}|i_{0}-j_{0}|^{3}}{(x^{2}+\ell ^{2}|i_{0}-j_{0}|^{2})^{3/2}} u_{i_{0}}^{2} \right] . \end{aligned}$$
$$\begin{aligned} \mathscr {H}_{i_{0},j_{0}}^{2}=\dfrac{1}{4 \pi \ell ^{2}|i_{0}-j_{0}|^{2}}&\left[ \dfrac{\ell ^{3}|i_{0}-j_{0}|^{3}}{(x^{2}+\ell ^{2}|i_{0}-j_{0}|^{2})^{3/2}} u_{i_{0}}^{1}\right. \\&+\left. \left\{ 1+\dfrac{x}{(x^{2}+\ell ^{2}|i_{0}-j_{0}|^{2})^{3/2}}(x^{2}+2\ell ^{2}|i_{0}-j_{0}|^{2})\right\} u_{i_{0}}^{2} \right] . \end{aligned}$$
$$\begin{aligned} \mathscr {H}_{i_{0},j_{0}}^{3}=-\dfrac{1}{4 \pi \ell ^{2}|i_{0}-j_{0}|^{2}} \left[ 1+\dfrac{x}{(x^{2}+\ell ^{2}|i_{0}-j_{0}|^{2})^{1/2}} \right] u_{i_{0}}^{3}. \end{aligned}$$

Therefore, the total network exterior field at the \(j_{0}\)th nanowire is given by:

$$\begin{aligned} \mathscr {H}_{d}^{ext}(u)(j_{0})=\displaystyle \sum \limits _{i_{0} \ne j_{0}}\mathscr {H}_{i_{0},j_{0}}(u(i_{0}))= \left( \begin{array}{c} \varPsi ^{1} (u^{1})(j_{0})+\varPsi ^{2} (u^{2})(j_{0}) \\ \varPsi ^{2} (u^{1})(j_{0})+\varPsi ^{3} (u^{2})(j_{0}) \\ \varPsi ^{4} (u^{3})(j_{0}) \end{array} \right) , \end{aligned}$$
(6)

where \((u^{1},u^{2},u^{3})\) are the coordinates of u and for \( k=\left\{ 1,\ldots ,4 \right\} \), the linear operators \( \varPsi ^{k}{:}\, (\mathbb R^{3})^{I} \rightarrow (\mathbb R^{3})^{I} \) is defined as, for all \( u=(u_{i})_{i \in I} \) in \( (\mathbb R^{3})^{I}\),

$$\begin{aligned} \varPsi ^{1} (u)(j_{0})(\zeta )= & {} -\dfrac{1}{4 \pi \ell ^{2}} \displaystyle \sum \limits _{j \ne j_{0}} \dfrac{1}{|j-j_{0}|^{2}}\left[ \dfrac{x\ell ^{2}|j-j_{0}|^{2}}{(x^{2}+\ell ^{2}|j-j_{0}|^{2})^{3/2}} \right] u(j),\\ \varPsi ^{2} (u)(j_{0})(\zeta )= & {} \dfrac{1}{4 \pi \ell ^{2}} \displaystyle \sum \limits _{j \ne j_{0}} \dfrac{1}{|j-j_{0}|^{2}}\left[ \dfrac{\ell ^{3}|j-j_{0}|^{3}}{(x^{2}+\ell ^{2}|j-j_{0}|^{2})^{3/2}} \right] u(j),\\ \varPsi ^{3} (u)(j_{0})(\zeta )= & {} \dfrac{1}{4 \pi \ell ^{2}} \displaystyle \sum \limits _{j \ne j_{0}} \dfrac{1}{|j-j_{0}|^{2}}\left[ 1+\dfrac{x}{(x^{2}+\ell ^{2}|j-j_{0}|^{2})^{3/2}}(x^{2}+2\ell ^{2}|j-j_{0}|^{2}) \right] u(j),\\ \varPsi ^{4} (u)(j_{0})(\zeta )= & {} -\dfrac{1}{4 \pi \ell ^{2}} \displaystyle \sum \limits _{j \ne j_{0}} \dfrac{1}{|j-j_{0}|^{2}}\left[ 1+\dfrac{x}{(x^{2}+\ell ^{2}|j-j_{0}|^{2})^{1/2}} \right] u(j). \end{aligned}$$

Hence, we study the following system:

$$\begin{aligned}&\dfrac{du_{i}}{dt}=-u_{i} \times (\mathscr {H}_{eff}(u))(i)-u_{i}\times (u_{i} \times (\mathscr {H}_{eff}(u))(i)) \\&\mathscr {H}_{eff}(u))(i)=\mathscr {H}_{d}^{int}(u)(i)+\mathscr {H}_{d}^{ext}(u)(i) \nonumber \end{aligned}$$
(7)

for \(i \in I\) and \(t \in \mathbb R^{+}\) with \( u_{i}: \mathbb R^{+} \rightarrow \mathbb S^{2} \).

We assume the relevant steady-states configurations of the magnetization distribution as:

$$\begin{aligned} u_{i}^{*}=\mu _{i}\mathbf {e}_{1}~~ \text{ with }~~ \mu _{i}=\left\{ -1, +1 \right\} , ~~ \forall ~ i \in I. \end{aligned}$$
(8)

Experimentally, we relate these relevant configurations to the memory state in a magnetic storage device, where \( \mu _{i} =1\) corresponds to a bit 1 and \( \mu _{i} =-1\) corresponds to a bit 0. Next, we introduce the problem related to stability of the relevant configurations under consideration.

Asymptotic stability of any relevant configuration.

In the absence of an external applied field, for any initial conditions in a vicinity of a given relevant configuration, the solution of the Landau–Lifschitz equation (7) converges to the relevant configuration.

We give the mathematical statement of the result in the following section:

3 Main Result

In order to state the result, we need to introduce the following notations. We observe that for \( \rho \in \mathbb S^{2} \), if \(0<\rho _{1}<1\) (resp. \(-1<\rho _{1}<0 \)), the quantity \( \rho _{2}^{2}+ \rho _{3}^{2} \) exhibits the distance between \( \rho \) and \( +\mathbf {e_{1}} \) (resp. \( -\mathbf {e_{1}}\)). We have:

$$\begin{aligned} \dfrac{1}{2}|\rho - \mathbf {e_{1}} |^{2} ~\le ~ \rho _{2}^{2}+ \rho _{3}^{2} ~\le ~ |\rho - \mathbf {e_{1}} |^{2}. \end{aligned}$$

For \( \alpha > 0 \) sufficiently small, we define \( \mathscr {D}_{+1}(\alpha ) \) and \( \mathscr {D}_{-1}(\alpha ) \) by

$$\begin{aligned} \mathscr {D}_{+1}(\alpha )= & {} \left\{ \rho \in \mathbb S^{2}, ~\rho _{1}>0 ~~\text {and}~~ \rho _{2}^{2}+ \rho _{3}^{2} < \alpha ^{2} \right\} , \\ \mathscr {D}_{-1}(\alpha )= & {} \left\{ \rho \in \mathbb S^{2}, ~\rho _{1}<0 ~~\text {and}~~ \rho _{2}^{2}+ \rho _{3}^{2} < \alpha ^{2} \right\} . \end{aligned}$$

For \( \mu =(\mu _{i})_{i \in I} \) with \( \mu _{i} \in \left\{ -1, +1 \right\} \), we denote, for \( \alpha > 0 \),

$$\begin{aligned} \mathscr {D}_{\mu }(\alpha )=\left\{ u \in (\mathbb S^{2})^{I},~~ \forall ~ i \in I ,~~ u_{i} \in \mathscr {D}_{\mu _{i}}(\alpha ) \right\} . \end{aligned}$$
(9)

Our main result about the asymptotic stability of any relevant position is the following:

Theorem 1

Suppose u is the solution of the Landau–Lifschitz equation (7) with initial condition \( u(0)=u^{init} \), where \( u^{init} \) satisfies the saturation condition (2). There exists \(\beta \), a positive constant independent of the size of the network such that if

$$\begin{aligned} \dfrac{1}{\ell ^{2}} \le \beta , \end{aligned}$$
(10)

then there exist \(\alpha _{0}>0\) and \(\kappa > 0\), such that for all relevant configurations \(u^{*}\) \((i.e., ~u_{i}^{*}=\mu _{i}\mathbf {e}_{1}\) for all \(i \in I )\), for all \( u^{init} \in \mathscr {D}_{\mu }(\alpha _{0}) \), u satisfies:

$$\begin{aligned} \Vert u(t)-u^{*}\Vert \rightarrow 0 ~ ~\text{ as }~~ t \rightarrow \infty . \end{aligned}$$

Proof

We derive the stability result of a relevant configuration for the Landau–Lifschitz equation without an external magnetic source. For this we analyze the following system with unknown u defined as \(u{:}\,\mathbb R^{+} \rightarrow (\mathbb S^{2})^{I} \),

$$\begin{aligned}&\dfrac{du}{dt}=-u \times \mathscr {H}_{eff}(u)- u \times (u\times \mathscr {H}_{eff}(u)) \\\nonumber&\mathscr {H}_{eff}(u)=\mathscr {H}_{d}^{int}(u)+\mathscr {H}_{d}^{ext}(u) \end{aligned}$$
(11)

The existence and uniqueness of a solution of (11) for any initial condition follows from the Cauchy–Lipschitz theorem. We assume that \(u^{*}\) be a fixed relevant configuration satisfies the saturation constraint (2), i.e, \( u^{*} \in (\mathbb S^{2})^{I} \) such that

$$\begin{aligned} u_{i}^{*}=\mu _{i}\mathbf {e}_{1}, ~~\text{ with }~~ \mu _{i} \in \left\{ -1, +1 \right\} , ~~ \forall ~ i \in I. \end{aligned}$$

Because of the physical saturation constraint (2), we only deal with perturbations u of \(u^{*}\) satisfying:

$$\begin{aligned} |u_{i}(t)|=1, ~~\forall ~ i \in I ~~\text {and}~~\forall ~ t\ge 0. \end{aligned}$$

We consider u as a small perturbation of \(u^{*}\) and describe it as:

$$\begin{aligned} u_{i}=\mu _{i}\mathbf {e}_{1}+\gamma (\omega _{i})\mu _{i}\mathbf {e}_{1}+\omega _{i}^{2}\mathbf {e}_{2}+\omega _{i}^{3}\mathbf {e}_{3}, ~~ \forall ~ i \in I \end{aligned}$$
(12)

with \( \omega _{i}=\left( \omega _{i}^{2}, \omega _{i}^{3} \right) \) and \( \gamma : (\mathbb R^{2})^{I} \rightarrow (\mathbb R)^{I} \) is a smooth map defined as \( \gamma (\omega _{i})=\sqrt{1-|\omega _{i}|^{2}}-1 \).

To obtain the transformed system of (11) in new variable \( \omega \in C^{1}\left( \mathbb R^{+}; (\mathbb R^{2})^{I} \right) \), we use the perturbation (12) of \(u^{*}\). We substitute (12) in (11) and take the projection of the obtained expression along the direction of \(\mathbf {e}_{2} \) and \(\mathbf {e}_{3} \).

After a lengthy algebraic computations, it yields that u given by (12) satisfies (11) if and only if \(\omega =(\omega ^{2}, \omega ^{3}) \) verifies the following system:

$$\begin{aligned} \dfrac{d\omega }{dt}=\left( \begin{array}{cc} -1 &{} -\mu \\ \mu &{} -1 \end{array} \right) \omega +\mathscr {A}(\mu ) + \mathscr {B}(\omega ) + \mathscr {C}(\omega ), \end{aligned}$$
(13)

where

$$\begin{aligned} \mathscr {A}(\mu )=\left( \begin{array}{c} \varPsi ^{2}(\mu ) \\ -\mu \varPsi ^{2}(\mu ) \end{array} \right) , \end{aligned}$$

The linear term \( \mathscr {B}(\omega ) \) is given by:

$$\begin{aligned} \mathscr {B}(\omega )=\left( \begin{array}{c} -(\omega ^{3}+\mu \omega ^{2})\varPsi ^{1}(\mu )+\varPsi ^{2}(\mu \gamma )\\ +\varPsi ^{3}(\omega ^{2})+\mu \varPsi ^{4}(\omega ^{3}) \\ \\ (\omega ^{2}-\mu \omega ^{3})\varPsi ^{1}(\mu )-\mu \varPsi ^{2}(\mu \gamma )\\ -\mu \gamma \varPsi ^{2}(\mu )-\mu \varPsi ^{3}(\omega ^{2})+\varPsi ^{4}(\omega ^{3}) \end{array} \right) , \end{aligned}$$

The nonlinear term \(\mathscr {C}(\omega )\) is given by:

$$\begin{aligned} \mathscr {C}(\omega )=\left( \begin{array}{c} -\mu \gamma \omega ^{3}-(\omega ^{3}+\mu \omega ^{2}+\mu \gamma \omega ^{2})\varPsi ^{1}(\mu \gamma )\\ -\mu \gamma \omega ^{2} \varPsi ^{1}(\mu ) -(\omega ^{3}+\mu \omega ^{2}+\mu \gamma \omega ^{2})\varPsi ^{2}(\omega ^{2})\\ -(\varPsi ^{2}(\mu )+\varPsi ^{2}(\mu \gamma ))(\omega ^{2})^{2} -(\omega ^{2})^{2}\varPsi ^{3}(\omega ^{2})\\ +(\mu \gamma -\omega ^{2}\omega ^{3})\varPsi ^{4}(\omega ^{3})+((\omega ^{2})^{2}+(\omega ^{3})^{2})\omega ^{2} \\ \\ \mu \gamma \omega ^{2}+(\omega ^{2}-\mu \omega ^{3}-\mu \gamma \omega ^{3})\varPsi ^{1}(\mu \gamma )\\ -\mu \gamma \omega ^{3} \varPsi ^{1}(\mu )+(\omega ^{2}-\mu \omega ^{3}-\mu \gamma \omega ^{3})\varPsi ^{2}(\omega ^{2})\\ -(\varPsi ^{2}(\mu )+\varPsi ^{2}(\mu \gamma ))\omega ^{2}\omega ^{3}-\mu \gamma \varPsi ^{2}(\mu \gamma )\\ -(\mu \gamma +\omega ^{2}\omega ^{3})\varPsi ^{3}(\omega ^{2})-(\omega ^{3})^{2}\varPsi ^{4}(\omega ^{3})\\ +((\omega ^{2})^{2}+(\omega ^{3})^{2})\omega ^{3} \end{array} \right) . \end{aligned}$$

Our objective is to analyze the stability behavior of a relevant configuration \(u^{*}\) for LLE (11). Evidently, both the forms of Landau–Lifschitz equation, (11) and (13) are equivalent and the stability of zero solution for (13) renders the stability of \(u^{*}\) for (11). We state this in the following Proposition.

Proposition 1

Let \(u \in C^{1}\left( \mathbb R^{+}; (\mathbb S^{2})^{I} \right) \) with \(|u|=1 \) and verifies (11). Let \( \omega \in C^{1}\left( \mathbb R^{+}; (\mathbb R^{2})^{I} \right) \) defined by:

$$\begin{aligned} u=\mu \mathbf {e}_{1}+\gamma (\omega )\mu \mathbf {e}_{1}+\omega ^{2}\mathbf {e}_{2}+\omega ^{3}\mathbf {e}_{3} \end{aligned}$$

Then u is a solution to Landau–Lifschitz equation (11) if and only if \(\omega \) is a solution to (13). Moreover, \(u^{*}\) is asymptotically stable for (11) if and only if 0 is asymptotically stable for (13).

Proof

We follow the similar technique used in partial differential equation framework in [13–15]. It is apparent that by taking the projection on both \( \mathbf {e}_{2} \) and \( \mathbf {e}_{3} \) axis, if u satisfies (11) then \(\omega \) verifies (13). For the converse part, we write (11) on the form

$$\begin{aligned} \dfrac{du}{dt}=\mathscr {F}(u). \end{aligned}$$

Furthermore \( u \cdot \mathscr {F}(u)=0 \). Since \(\omega \) satisfies (13), we have

$$\begin{aligned} \left( \dfrac{du}{dt}-\mathscr {F}(u) \right) \cdot \mathbf {e}_{k}=0, ~~~~ \forall ~ k \in \left\{ 2,3 \right\} . \end{aligned}$$

Using the constraint \(|u|=1\), which renders \( u \cdot \dfrac{du}{dt}=0 \). we obtain

$$\begin{aligned} \mu \left( 1+\gamma \right) \left( \dfrac{du}{dt}-\mathscr {F}(u) \right) \cdot \mathbf {e_{1}}=0, \end{aligned}$$

with \( \mu \ne 0 \) and \( \gamma \ne -1 \), implies that u satisfies (11). This completes the proof of Proposition 1.

Now we study the stability of zero solution for the transformed Landau–Lifschitz equation (13). First, we establish some preliminary estimates. We estimate the linear operators \( \varPsi ^{k}{:}\,(\mathbb R^{3})^{I} \rightarrow (\mathbb R^{3})^{I} \) in the following fashion, we obtain for all \( k=\left\{ 1,\ldots ,4 \right\} \)

$$\begin{aligned} \Vert \varPsi ^{k}(u)\Vert ~ \le ~\dfrac{K_{1}}{\pi \ell ^{2}} \left( \displaystyle \sum \limits _{ j \ne 0}\dfrac{1}{|j|^{2}}\right) \Vert u\Vert ,~~ \forall ~ u=(u_{i})_{i \in I} \in (\mathbb R^{3})^{I}. \end{aligned}$$
(14)

Using (14), the operators \( \mathscr {A}, \mathscr {B} \) and \(\mathscr {C}\) appear on the right hand side of (13) are estimated with straightforward arguments in the following lemmas.

Lemma 1

There exists a constant \( K_{2} \) such that, for all \( \omega \in (\mathbb R^{3})^{I} \) with \( \Vert \omega \Vert < 1 \), we have

$$\begin{aligned} \Vert \mathscr {B}(\omega )\Vert ~ \le ~ \dfrac{K_{2}}{\ell ^{2}}\Vert \omega \Vert . \end{aligned}$$

Lemma 2

We assume that \( \dfrac{1}{\ell ^{2}} \le 1 \). There exist constants \( K_{3} \) and \( K_{4} \) such that, for all \( \omega \in (\mathbb R^{3})^{I} \) with \( \Vert \omega \Vert < 1 \), we have

$$\begin{aligned} \Vert \mathscr {A}(\mu )\Vert ~ \le ~ K_{3} ~~ \text{ and }~~ \Vert \mathscr {C}(\omega )\Vert \le K_{4}\Vert \omega \Vert ^{2}. \end{aligned}$$

It is worth to mention that the constants \(K_{2}, K_{3}\) and \( K_{4} \) neither depend on \(\ell \) nor on the size of the network. We notice that \(\Vert \gamma (\omega )\Vert \le \Vert \omega \Vert \) whenever \(\Vert \omega \Vert < 1\).

We have \( \omega \in C^{1}\left( \mathbb R^{+};(\mathbb R^{2})^{I} \right) \) with,

$$\begin{aligned} |\omega _{i}(t)|=\left( (\omega _{i}^{2}(t))^{2}+(\omega _{i}^{3}(t))^{2}\right) ^{\frac{1}{2}} \end{aligned}$$

We notice that \(u \in \mathscr {D}_{\mu }(\alpha )\) if and only if \(|\omega | < \alpha \) (see (9)).

Taking the inner product of (13) with \( \left( \omega _{i}^{2}, \omega _{i}^{3} \right) \), we obtain, for all \(i \in I\),

$$\begin{aligned} \left( \omega _{i}^{2}\dfrac{d}{dt}\omega _{i}^{2}+\omega _{i}^{3}\dfrac{d}{dt}\omega _{i}^{3} \right) + \left( (\omega _{i}^{2})^{2}+(\omega _{i}^{3})^{2} \right)&=\left( (\mathscr {A}(\mu ))_{i}+(\mathscr {B}(\omega ))_{i}\right. \\&\quad \left. +\,(\mathscr {C}(\omega ))_{i} \right) \cdot \left( \omega _{i}^{2}, \omega _{i}^{3} \right) , \end{aligned}$$

Using Lemmas 1 and 2, we have,

$$\begin{aligned} \dfrac{1}{2}\dfrac{d}{dt}\left( |\omega _{i} |^{2} \right) + |\omega _{i}|^{2} ~\le ~ K_{3}\Vert \omega \Vert + \dfrac{K_{2}}{\ell ^{2}}\Vert \omega \Vert ^{2}+K_{4}\Vert \omega \Vert ^{3}. \end{aligned}$$
(15)

We define \(\beta \) by,

$$\begin{aligned} \beta = \dfrac{1}{K_{2}} \end{aligned}$$
(16)

Our goal is to show that zero solution is asymptotically stable for (13). We set the distance between the nanowires in such a way so that \(\dfrac{1}{\ell ^{2}}\) remains less than \(\beta \).

Multiplying (15) by \(e^{2t}\) and integrate from 0 to t. We get, for all \(i \in I \),

$$\begin{aligned} \left( |\omega _{i}(t)|^{2} \right) e^{2t}~ \le ~ \Vert \omega (0)\Vert ^{2}\,+\,&2K_{3}\displaystyle \int _{0}^{t} \Vert \omega (\textit{v})\Vert e^{2\textit{v}}d\textit{v}\\&+ 2\dfrac{K_{2}}{\ell ^{2}}\displaystyle \int _{0}^{t}\Vert \omega (\textit{v})\Vert ^{2}e^{2\textit{v}}d\textit{v}+2 K_{4}\displaystyle \int _{0}^{t}\Vert \omega (\textit{v})\Vert ^{3}e^{2\textit{v}}d\textit{v}\end{aligned}$$

We take the supremum on \(i \in I \) and obtain that

$$\begin{aligned} \Vert \omega (t)\Vert ^{2} e^{2t}~ \le ~ \Vert \omega (0)\Vert ^{2}+&2K_{3}\displaystyle \int _{0}^{t} \Vert \omega (\textit{v})\Vert e^{2\textit{v}}d\textit{v}\\&+ 2\dfrac{K_{2}}{\ell ^{2}}\displaystyle \int _{0}^{t}\Vert \omega (\textit{v})\Vert ^{2}e^{2\textit{v}}d\textit{v}+2 K_{4}\displaystyle \int _{0}^{t}\Vert \omega (\textit{v})\Vert ^{3}e^{2\textit{v}}d\textit{v}\end{aligned}$$

We denote \( \kappa =1-\dfrac{K_{2}}{\ell ^{2}} \). Equation (16) together with condition \( \dfrac{1}{\ell ^{2}}< \beta \) implies \(\kappa > 0\). Now while \( \Vert \omega (\textit{v})\Vert \le \dfrac{\kappa }{2K_{4}}e^{-2\textit{v}} \le \dfrac{\kappa }{2K_{4}} \), we have

$$\begin{aligned} \Vert \omega (t)\Vert ^{2}e^{2t}~\le ~\Vert \omega (0)\Vert ^{2}+\dfrac{K_{3}}{K_{4}}\kappa t +\left( 2-\kappa \right) \displaystyle \int _{0}^{t}\Vert \omega (\textit{v})\Vert ^{2}e^{2\textit{v}}d\textit{v}, ~~ \forall ~ t \ge 0. \end{aligned}$$

Using Gronwall lemma, while \( \Vert \omega (\textit{v})\Vert \le \dfrac{\kappa }{2K_{4}} \), we obtain

$$\begin{aligned} {\begin{matrix} \Vert \omega (t)\Vert ^{2}~&\le ~ \left[ \Vert \omega (0)\Vert ^{2}+\dfrac{K_{3}}{K_{4}}\kappa t \right] e^{-\kappa t} \end{matrix}} \end{aligned}$$

It is evident that the term \(te^{-\kappa t} \rightarrow 0 \) as \(t \rightarrow \infty \). Therefore, whenever \( \Vert \omega (0)\Vert \le \dfrac{\kappa }{2K_{4}} \), we obtain

$$\begin{aligned} \Vert \omega (t)-0\Vert \rightarrow 0 ~~ \text{ as }~~ t \rightarrow \infty . \end{aligned}$$

We set \( \alpha _{0}=\dfrac{\kappa }{2K_{4}} \), and it shows that zero solution is asymptotically stable for the perturbed LLE (13) which in turn reflect the asymptotic behavior of relevant configurations for LLE (11). This completes the proof of Theorem 1.