Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Electronic and photonic properties of semiconductor quantum structures have attracted the interest of both theoretical and experimental researchers in the last few years, precisely due to the rapid growth of fabrication procedure of lower dimension devices. Quantum well, wire and dot are the prime candidates among nanostructures, where carrier motion can be confined along one, two or three dimensions, leading to quantized energy states. Different geometrical shapes [1, 2] and material compositions [3, 4] are already implemented to design semiconductor quantum heterostructures for various applications like resonant tunneling diode [5], quantum cascade laser [6], transistor [7], optical emitter [8, 9], optical detector [10], resonator [11], memory element [12] etc. Application-specific use of nanostructures requires precise computation of energy states, and thus choice of numerical method plays a key role to evaluate eigen energies for different devices [13, 14]. Recently, core-shell structure becomes an important candidate due to its inherent advantage of wider tuning range of emission/absorption spectra [15], higher absorption cross-section [16]. These structures have also improved oscillator strength compared to conventional quantum dot structures [17], which determines the probability of optical transitions between any two subbands [18]. Hence investigation of oscillator strength and absorption cross-section becomes very important for use of the heterostructure in photonic applications.

Oscillator strength of T-shaped quantum wire is computed for different material parameters [19], and also for self-assembly quantum dots [20] in presence of electric field. It is also computed for cylindrical quantum wire for field induced transition [21], and different potential configuration [22] Holovatsky [23] calculated it for elliptic nanotube and spherical dot [24]. In the present paper, authors computed oscillator strength for core-shell quantum wire of triangular geometry for the optical transition between ground and first excited states, and corresponding absorption cross-section is evaluated. InAs/Ga0.47In0.53As is the material composition considered for simulation along with the incorporation of first-order band nonparabolicity of Kane-type, and simulated result is compared with that obtained for parabolic dispersion relation with similar geometrical dimensions and material composition. The parabolic assumption is nothing but an oversimplified mathematical consideration. Structural parameters are varied to observe the change of the parameters along with a wider range of incident radiation, and peak of the cross-section is also measured. Results are important to understand the probability of optical transitions in the structure, which plays key role in determining its candidature for optical transmitter/detector application.

2 Mathematical Modeling

We consider the schematic structure of triangular core-shell quantum wire as shown in Fig. 78.1, where electrons are confined in z and y directions.

Fig. 78.1
figure 1

Schematic structure of triangular core-shell quantum wire with Cartesian coordinate

Full size image

The time-independent Schrödinger equation considering Kane-type nonparabolicity of first-order for wavefunction ψ in y–z plane in Cartesian system can be written as

$$ \begin{aligned} & - \frac{{\hbar^{2} }}{2}\left\{ {\frac{\partial }{\partial y}\left[ {\frac{1}{{m^{*} }}\frac{\partial }{\partial y}\psi } \right] + \frac{\partial }{\partial z}\left[ {\frac{1}{{m^{*} }}\frac{\partial }{\partial z}\psi } \right]} \right\} \\ & - \gamma \frac{{\hbar^{4} }}{4}\left\{ {\frac{\partial }{\partial y}\left[ {\frac{1}{{m^{*} }}\frac{\partial }{\partial y}\psi } \right] + \frac{\partial }{\partial z}\left[ {\frac{1}{{m^{*} }}\frac{\partial }{\partial z}\psi } \right]} \right\}^{2}\,+\,V(y,z)\psi = E\psi \\ \end{aligned} $$
(78.1)

where γ is the coefficient of band nonparabolicity . Introducing finite difference technique, (78.1) can be written as

$$ \begin{aligned} & - \frac{{\hbar^{4} \gamma }}{{4m^{*2} \left( {\Delta z} \right)^{4} }}\left[ {\psi (i + 2,j) + \psi (i - 2,j) - 4\psi (i + 1,j) - 4\psi (i - 1,j) + 6\psi (i,j)} \right] \\ & - \frac{{\hbar^{4} \gamma }}{{4m^{*2} \left( {\Delta y} \right)^{4} }}\left[ {\psi (i,j + 2) + \psi (i,j - 2) - 4\psi (i,j + 1) - 4\psi (i,j - 1) + 6\psi (i,j)} \right] \\ & - \frac{{\hbar^{4} \gamma }}{{4m^{*2} \left( {\Delta z} \right)^{2} \left( {\Delta y} \right)^{2} }}\left[ {\psi (i + 1,j) + \psi (i - 1,j) - 2\psi (i,j)} \right]\cdot \left[ {\psi (i,j + 1) + \psi (i,j - 1) - 2\psi (i,j)} \right] \\ & - \frac{{\hbar^{2} }}{{2m^{*} \left( {\Delta z} \right)^{2} }}\left[ {\psi (i + 1,j) + \psi (i - 1,j) - 2\psi (i,j)} \right] \\ & - \frac{{\hbar^{2} }}{{2m^{*} \left( {\Delta y} \right)^{2} }}\left[ {\psi (i,j + 1) + \psi (i,j - 1) - 2\psi (i,j)} \right] + V\psi \left( {i,j} \right) = E\psi \left( {i,j} \right) \\ \end{aligned} $$
(78.2)

where i(j) is the no. of points along z(y) axis, and Δz(Δy) is dimension of the smallest grid along z(y) direction. Solution of (78.2) gives eigenstates, from which intersubband energies (ΔE j,i , which denotes the intersubband transition energy form ith state to jth state) can be estimated. The efficiency of transition is determined by the parameter oscillator strength, which is given by

$$ f_{ji} = \frac{{2m^{*}\Delta E_{j,i} }}{{\hbar^{2} }}\left| {\left\langle {j\left| z \right|\left. i \right\rangle } \right.} \right|^{2} $$
(78.3)

where we assume the transition form quantum level ‘i’ to quantum level ‘j’. Absorption cross-section can be computed from the knowledge of oscillator strength as

$$ \sigma_{ji} = \frac{{q^{2} T}}{{2\varepsilon_{0} m^{*} nc}}f_{ji} \left[ {1 + T^{2} \left( {\frac{{E -\Delta E_{j,i} }}{\hbar }} \right)^{2} } \right]^{ - 1} $$
(78.4)

where ‘n’ is the refractive index of the core material, and ‘T’ is the relaxation time. Peak absorption cross-section si given by

$$ \sigma_{ji} = \frac{{q^{2} T}}{{2\varepsilon_{0} m^{*} nc}}f_{ji} $$
(78.5)

3 Results and Discussions

Using (78.3), oscillator strength of the structure is computed and plotted with width and length of the core region for the optical transition between ground state (E111) and next higher excited state (E112). In Fig. 78.2, it is observed that with increase of dimension for core layer, oscillator strength monotonically decreases, whereas the rate is almost negligible when parabolic dispersion relation is considered. This is due to the fact that for nonparabolic band structure, the dipole matrix element decreases rapidly whereas for parabolic band, transition energy decreases at a faster rate. But the matrix element is related with oscillator strength with square form, and hence the rate of change for the former is comparatively higher. Also with increase of core layer width, quantum confinement decreases, which causes reduction of eigenenergies, hence oscillator strength decreases.

Fig. 78.2
figure 2

Oscillator strength with a width of the core region for nonparabolic and parabolic band structures; b height of core region for nonparabolic and parabolic band structures

Full size image

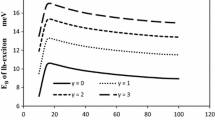
In Fig. 78.3, absorption cross-section is plotted with incident radiation for two different core layer dimensions considering both types of dispersion relations. From the plot, it may be observed that with increase of dimension of either core width or height, cross-section peak appears at lower magnitude of incident radiation. The shift of peak position is larger for parabolic band compared to the nonparabolic one. As cross-section attains the peak corresponding to the transition energy between the two quantum levels, so the peak appears at the higher transition energy for lower width (/height) and goes to the lower value with increase of thickness. Again, since the transition energy increases due to nonparabolicity, so the peak appears at lower magnitude of incident radiation. But the shift of transition energy is very small with change of layer thickness in either of the quantized direction, so the shift of cross-section is almost negligible when nonparabolic dispersion relation is taking into account.

Fig. 78.3
figure 3

Absorption cross-section with incident radiation for a two different core widths considering parabolic and nonparabolic band structures; b two different core heights considering parabolic and nonparabolic band structures

Full size image

In Fig. 78.4, peak position of absorption cross-section is plotted with core layer dimensions. From the plot, it may be observed that with increase of width (/height), cross-section peak decreases. This is because higher core dimension decreases quantum confinement, which reduces energy. This effectively reduces oscillator strength . Since peak of the cross-section is directly proportional to oscillator strength, so peak magnitude reduces in a similar fashion to the oscillator strength. The rate is higher for nonparabolic band structure, and is almost negligible for parabolic overestimation.

Fig. 78.4
figure 4

a Absorption cross-section peak with width of core region for nonparabolic and parabolic band structures; b Absorption cross-section peak with width of core region for nonparabolic and parabolic band structures

Full size image

4 Conclusion

Oscillator strength and absorption cross-section of core-shell triangular quantum wire is computed as function of structural parameters and with incident radiation. Band nonparabolicity of first order is considered for near accurate result. Computation reveals that oscillator strength rapidly decreases with dimension of the wire for nonparabolic semiconductor, whereas it remains almost constant when simplified parabolic band structure is considered. Hence it significantly depends on the bandgap of the material. Peak of absorption cross-section appears when incident radiation numerically equals to the intersubband transition energy, and magnitude of peak decreases with increasing dimension. Peak magnitude is higher for nonparabolic band structure. Result suggests that absorption is highly selective in core-shell structure as the cross-section profile may nearly be approximated to the Dirac-delta function.