Keywords

1 Introduction

With the rise and emergence of the Internet, the transmission of huge scale of image data over communication media such as cell phones, facsimile, television, computer networks, satellites etc. has increased [1]. These digital data are easily accessible to others creating opportunities for pernicious parties to defile the confidential information and making commercial copies of the copyrighted content without permission of the original owner.

Image encryption has emerged out to be a potential solution to this problem of protecting intellectual property and ensuring righteousness to the digital data. Image Encryption works by locking an image file with a ‘key’ and providing that key only to its authorized user. This provides a high degree of security enhancing its robustness [2]. Once the encrypted file is opened, it becomes vulnerable to any form of dissemination without any further form of control.

In the color image encryption we have three planes RGB (Red, Green, Blue). Each of these three planes is quantized separately. The pixels of the original image are scrambled and mingled through random sequence which is chaotic in nature. The original image can be recovered after several iterations depending on initial conditions. The scrambling takes place by arranging pixels and taking each bit of image and XORed with random sequence that is generated [3]. The features like non-deterministic, randomness, periodicity of chaotic maps make the digital image data more secure.

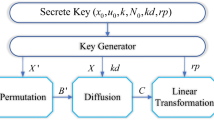
2 Image Encryption Using 2D Chaotic Map

The several disadvantages of 1D logistic map led to the introduction of various 2D chaotic maps which makes the digital image data more secure. Figure 1 shows the 2D chaotic maps that we analyzed upon.

Fig. 1
figure 1

2D chaotic map classification

Full size image

2.1 2D Logistic Map

The 2D logistic map came into picture to encounter the disadvantages of 1D logistic map. The increased number of control parameters and key spaces makes it a bit tough to predict the secret content for the pernicious parties [4]. The color image is first broken down into 3 planes (Red, Blue, Green). For each plane we generate 2 chaotic sequences with chaotic behavior defined as:

$$ Z\left( {X,Y} \right) = \left\{ {\begin{array}{*{20}l} {X_{i + 1} = \mu_{1} *X_{i} \left( {1 - X_{i} } \right) + \beta_{1} \left( {Y_{i} } \right)^{2} } \hfill \\ {Y_{i + 1} = \mu_{2} *Y_{i} \left( {1 - Y_{i} } \right) + \beta_{2} (\left( {X_{i} } \right)^{2} + X_{i} *Y_{i} )} \hfill \\ \end{array} } \right. $$
(1)

where, \( i = 0, \, 1, \, 2, \ldots \mu_{1} ,\beta_{1} ,\mu_{2} ,\beta_{2} \) are the system control parameters. X 0 and Y 0 are the initial conditions. The range of the control parameters are: \( 2.75 < \mu_{1} \le 3.4 \), \( 0.15 < \beta_{1} \le 0.21 \), \( 2.70 < \mu_{2} \le 3.45 \), \( 0.13 < \beta_{2} \le 0.15 \), \( 0 < X_{i} ,Y_{i} \le 1 \).

Let us take one M × M color image which is broken down into 3 planes (Red, Green and Blue). For each of the three planes, we generate the random sequence by using the above equation. The 1D matrix, Y is transposed and multiplied with X to generate a 2D matrix of size M × M, called K. The elements of the matrix K are quantized to binary format using the following equation:

$$ P\left( x \right) = \left\{ {\begin{array}{*{20}l} {0, } \hfill & {if \;0 < K(i,j) \le 0.5} \hfill \\ {1, } \hfill & {if\;K\left( {i,j} \right) > 0.5} \hfill \\ \end{array} } \right. $$
(2)

Each element of the quantized matrix is then XORed with the respective bit of every pixel of the M × M color image. This is done with the bits of all the three planes individually. The three planes are then concatenated to form a single plane and thus an encrypted image is produced.

The original image can be recovered by providing the appropriate key along with the correct value of the initial condition. For ‘lena64’ image, the encrypted image using 2D logistic map is shown in Fig. 2. Here, we have taken \( \mu_{1} = 2.93 \), \( \beta_{1} = 0.17 \), \( \mu_{2} = 3.26 \), \( \beta_{2} = 0.14 \), \( X_{0} = 0.895 \;{\text{and}}\;Y_{0} = 0.923. \) The decryption will be done by taking the same arguments.

Fig. 2
figure 2

Results for image encryption using 2D logistic map

Full size image

2.2 Henon Map

Henon map was proposed by Michel Henon in 1976 which is a discrete time dynamical and 2D invertible map represented with an attractor. This map generates a random sequence which is used to encrypt the shuffled pixels of the M × M original image. The sequence is generated by the formula defined as [5, 6].

$$ Z\left( {X,Y} \right) = \left\{ {\begin{array}{*{20}l} {X_{i + 1} = 1 - a*\left( {X_{i} } \right)^{2} + Y_{i} } \hfill \\ {Y_{i + 1} = b*Y_{i} } \hfill \\ \end{array} } \right. $$
(3)

where, i = 0, 1, 2… a and b are control parameters. We take one M × M color image and is broken down into 3 planes (RGB).

For each plane, 2 chaotic sequences are generated using the above equation and taking a = 1.4 and b = 0.3 as the control parameters. The 1D matrices X and Y are reconstructed as row and column matrices respectively. These matrices are multiplied together to generate a matrix K of size M × M. This matrix is quantized to a binary format using Eq. (2).

Each element of the quantized matrix P(x) is XORed with each bit of every pixel of M × M color image to produce an encrypted image for each plane. All the 3 encrypted images are concatenated to a single plane. The original image can be recovered by providing appropriate system keys and initial conditions. Figure 3 shows the result of image encryption using Henon map.

Fig. 3
figure 3

Results for image encryption using Henon map

Full size image

2.3 Baker Map

Baker Map is a 2D chaotic map from unit square M × M into itself which is again a discrete time dynamical system. It is an extension of 1D Tent map exhibiting deterministic chaos feature. The parameters are the encryption key for the encryption of the chaotic function. There are two alternative definitions of the Baker map. One definition folds over or rotates one of the sliced halves before joining and the other definition doesn’t. The folded baker map [7] is generated as:

$$ Z\left( {X,Y} \right) = \left\{ {\begin{array}{*{20}l} {\left[ {X_{i + 1} ,Y_{i + 1} } \right] = \left[ {2X_{i} ,\frac{{Y_{i} }}{2}} \right], } \hfill & {if\;0 \le X_{i} < 0.5} \hfill \\ {\left[ {X_{i + 1} ,Y_{i + 1} } \right] = \left[ {2\left( {1 - X_{i} } \right), 1 - \frac{{Y_{i} }}{2}} \right],} \hfill & { if\;0.5 \le X_{i} < 1} \hfill \\ \end{array} } \right. $$
(4)

where, X0 and Y0 are the initial conditions. Here, Xi is expanded twice horizontally and Yi is contracted to half vertically. This matrix is quantized to a binary format using Eq. (2). The quantized sequence is XORed with each bit of every pixel of M × M color image. Thus, producing an encrypted image for all the 3 planes separately. The encrypted results of all the 3 planes are concatenated to form a single plane, producing an encrypted image of the original image. The original image can be recovered by providing the appropriate initial values of X0 and Y0. Image encryption using Baker map is shown in Fig. 4.

Fig. 4
figure 4

Results for image encryption using Baker map

Full size image

2.4 Arnold Cat Map

Arnold cat map is a chaotic map from the torus into itself, named after Vladimir Arnold, who demonstrated its effect using cat’s image in 1960s [8]. This chaotic map transforms the image by shuffling the pixels through several iterations. The image returns to its original state after a number of iterations of transformations, known as Arnold’s period. A M × M color image is taken and broken down into 3 planes (RGB). Equation for 2D Arnold cat map is given as [9]:

$$ Z\left( {X,Y} \right) = \left\{ {\begin{array}{*{20}l} {X_{i + 1} = \left( {X_{i} + aY_{j} } \right)mod\;N} \hfill \\ {Y_{j + 1} = \left( {bX_{i} + \left( {ab + 1} \right)Y_{j} } \right)mod\;N} \hfill \\ \end{array} } \right. $$
(5)

where, a and b are the control parameters of the system. The above equation is applied on the original pixel co-ordinates (X i , Y j ) to form a new pixel co-ordinates (X i+1, Y j+1). The iteration continues by replacing the old pixel positions. The results of the 3 planes are concatenated together to a single plane. The original image can be recovered by iterating the pixels till Arnold’s period. The 2D Arnold cat map holds chaotic behavior along with diffusion, randomness and enhanced security; thus making it more robust and dynamic than 1D chaotic map.

Figure 5 shows the result of color image encryption using Arnold cat map. Here, we have taken the parameters as: a = 2, b = 3 and Arnold’s period = 17.

Fig. 5
figure 5

Results for image encryption using Arnold cat map

Full size image

2.5 Cross Chaos Map

Cross chaos map is a chaotic map which is used for randomization purpose. The two chaotic sequences are generated as [10, 11]:

$$ Z\left( {X,Y} \right) = \left\{ {\begin{array}{*{20}l} {X_{i + 1} = 1 - \mu * \left( {Y_{i} } \right)^{2} } \hfill \\ {Y_{i + 1} = { \cos }(k * { \cos }^{ - 1} X_{i} )} \hfill \\ \end{array} ;\quad X,Y \in \left[ { - 1,1} \right]} \right. $$
(6)

where, \( \mu , k \) are the control parameters of the system. X 0 and Y 0 are the initial conditions. The M × M color image is broken down into 3 planes (RGB). For each plane, two chaotic sequences are generated. The system works better for μ = 2 and k = 6 [10, 11]. The 1D sequences X and Y are reconstructed to form row and column matrices respectively, which are multiplied together to generate K, one M × M matrix. Finally, this matrix is quantized using the same quantization function discussed in earlier. The encrypted result from all the 3 planes are concatenated to form a single encrypted image for one plane.

The original image can be recovered by providing the appropriate system parameters and initial conditions. Here, we have taken μ = 2, k = 6, X 0 = 0.64 and Y 0 = 0.76. The detail of image encryption using cross chaos map is shown in Fig. 6.

Fig. 6
figure 6

Results for image encryption using cross chaos map

Full size image

3 Comparative Analysis of Security

The security level of the above implemented 2D chaotic maps need to be checked. We do this comparative analysis by calculating 2 parameters: NPCR (number of pixel change rate) and UACI (unified average change intensity). Differential attack analysis shows relationship between original image and encrypted image. NPCR is used to check how a change in single pixel in original image brings about a significant change in the encrypted image [12]. Let’s take two images, P and Q with a difference of only one pixel. We define another matrix, K such as:

$$ K\left( {i,j} \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {if\;P\left( {i,j} \right) = Q(i,j)} \hfill \\ {1,} \hfill & { if\;P\left( {i,j} \right) \ne Q(i,j)} \hfill \\ \end{array} } \right. $$
(7)

NPCR can be calculated as:

$$ NPCR = \frac{{\mathop \sum \nolimits_{i,j} K(i,j)}}{a \times b} \times 100\;\% $$
(8)

where, a and b are the height and width of both images P and Q. UACI calculates the percentage of different pixels in both the images [12]. This can be calculated as:

$$ UACI = \frac{{\mathop \sum \nolimits_{i,j} \frac{{|P\left( {i,j} \right) - Q\left( {i,j} \right)|}}{255}}}{a \times b} \times 100\;\% $$
(9)

Table 1 shows the values obtained after the simulation of NPCR and UACI together calculated using Eqs. (8) and (9).

Table 1 NPCR and UACI values
Full size table

The result shows that the value of NPCR is around 99 % and UACI is around 33 %. The higher the average value of NPCR and UACI, the better is the chaotic map.

$$ Average = \frac{NPCR + UACI}{2} $$
(10)

Table 2 shows average values of NPCR and UACI for each of the chaotic maps using the values from Table 1. The result shows that Arnold 2D Cat map is better than other maps.

Table 2 Average of NPCR and UACI
Full size table

4 Conclusion

In this paper, we have used different version of 2D chaotic maps to encrypt the color images. The involvement of several control parameters in 2D chaotic maps makes them more robust and thus provides higher security than 1D chaotic map. NPCR and UACI values assure the security nature of these maps. Though cryptography has some limitations, still it is growing up at a very good pace. Every now and then, we are introduced to a new, secure and fast chaotic algorithm. Although we can’t say that this kind of cryptography is best and will stand up to all the real attacks, still we consider that 2D chaotic cryptography. In future, will solve the security and copyright issues over transmission of digital images. These encryption methods will be applicable for watermarking techniques soon in near future. These maps can also be enhanced in higher dimension to increase the efficiency; thus, making transmission of digital images via various communication media more secure.