Keywords

1 Introduction

Digital image processing is a rapidly growing discipline with a broad range of applications in medicine, environmental sciences, and in many other fields. The field of digital image processing refers to processing two-dimensional pictures by a digital computer.

Rosenfeld [2, 3] represented a digital image by a graph whose nodes are pixels and whose edges are linking adjacent pixels to each other. He named the resultant graph as the neighborhood graph. But this representation contains two paradoxes, namely connectivity and boundary paradoxes. Kovalevsky [4] introduced the notion of abstract cellular complexes to study the structure of digital images and introduced axiomatic digital topology [8], which has no paradoxes. Moreover, he showed that every finite topological space with separation property is isomorphic to an abstract cellular complex. Further, Kovalevsky [5, 6] introduced the notions of a half plane, a digital line segment, etc., while using the notions of open sets, closed sets, closure, and interior.

The concepts of semi-open set and semi-continuity were introduced by Levine [10]. The half-open intervals \( \left( {a,\left. b \right]} \right. \) and \( \left[ {a,\left. b \right)} \right. \) are characterized as semi-open subsets of the real line. Though the collections of semi-open sets do not form a classical topology on R, it satisfies the condition of a basis in R, and hence, both half-open intervals of the form \( \left[ {a,\left. b \right)} \right. \) and \( \left( {a,\left. b \right]} \right. \) generate two special topologies, namely lower limit topology and upper limit topology, respectively, on R. This motivates us to study the notion of semi-open complex in abstract cellular complex. In this paper, we introduced the basic concepts of semi-open subcomplex in abstract cellular complex and studied some of their basic properties, which enable us to study the structure of digital images through semi-open subcomplexes.

In this paper, the concept of a semi-open subcomplex is introduced and some of its properties in abstract cellular complexes are studied. Further, the semi-open subcomplex is characterized by introducing the notions of semi-frontier, semi-interior, and semi-closure. Further, the relationship between a semi-open subcomplex and a homogeneously n-dimensional subcomplex is studied, and the notions of quasi-solid, semi-region are introduced. Finally, the algorithm to tracing the semi-frontier of an image using Kovalevsky’s chain code is presented.

2 Preliminaries

In this section, some basic definitions are recalled.

Definition 2.1 [4]

An abstract cellular complex (ACC) C = (E, B, dim) is a set E of abstract elements provided with an antisymmetric, irreflexive, and transitive binary relation B ⊂ E × E called the bounding relation, and with a dimension function dim: E → I from E into the set I of non-negative integers such that dim(e′) < dim(e″) for all pairs (e′, e″) ∈ B.

Definition 2.2 [4]

A subcomplex S = (E′, B′) of a given K-complex C = (E, B) is a k-complex whose set E′ is the subset of E and the relation B′ is an intersection of B with E′ × E′.

Definition 2.3 [4]

A subcomplex S of C is called open in C if for every element e′ of S all elements of C which are bounded by e′ are also in S.

Definition 2.4 [4]

The smallest subset of a set S which contains a given cell c ∈ S and is open in S is called smallest neighborhood of c relative to S and is denoted by SON(c, S).

Definition 2.5 [4]

The smallest subset of a set \( S \) which contains a given cell c ∈ S and is closed in S is called the closure of c relative to S and is denoted by Cl(c, S).

Definition 2.6 [4]

The frontier of a subcomplex S of an abstract cellular complex C relative to C is the subcomplex Fr(S, C) containing of all cells c of C such that the SON(c) contains cells both of S and of its complement C–S.

Definition 2.7 [9]

Let t and T be subsets of the space S such that t ⊆ T ⊆ S. The set t-Fr (t, T) is called the interior of t in T, and it is denoted by Int(t, T).

3 Semi-open Subcomplexes in Abstract Cellular Complex

Definition 3.1

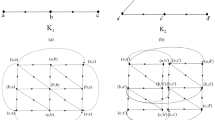
A subcomplex S in an abstract cellular complex C is called semi-open subcomplex if there exist an open subcomplex O such that O ⊆ S ⊆ Cl(O), where Cl denotes the closure operator in C (Fig. 1).

Fig. 1
figure 1

Semi-open subcomplex in 2D

Full size image

Remark 3.1

It follows from the Definition 3.1 that an example of a semi-open subcomplex can be a pixel with at least one element of its frontier.

Theorem 3.1

A subcomplex S of an abstract cellular complex C is semi-open subcomplex if and only if \( S \subseteq {\text{Cl}}\left( {{\text{Int}}\left( S \right)} \right). \)

Proof

Suppose \( S \not\subset {\text{Cl}}\left( {{\text{Int}}\left( S \right)} \right), \) then there exist a cell x ∈ S such that x ∉ Cl(Int(S)). This implies that x ∉ Int(S) and x ∉ Fr(Int(S)). X ∉ Int(S) implies that there exist no open subcomplex O containing x such that O ⊆ S, and x ∉ Fr(Int(S)) implies that there exists no open subcomplex O contained in S such that x ∈ Fr(O). Hence, there exists no open subcomplex O such that O ⊆ S ⊆ Int(O) ∪ Fr(O) = Cl(O). This is a contradiction to the assumption that S is a semi-open subcomplex in C. Converse part is obvious from the definition of Int(S), while Int(S) is an open subcomplex contained in S.

Theorem 3.2

Every open subcomplex is a semi-open subcomplex.

Proof

Proof follows directly from Theorem 3.1.

Remark 3.2

The converse of the above Theorem 3.2 need not be true.

Lemma 3.1

If S is a subcomplex of an abstract cellular complex C then the following equations hold:

  1. i

    C–Int(S) = Cl(C–S)

  2. ii

    C–Cl(S) = Int(C–S)

Definition 3.2

A subcomplex S of an abstract cellular complex C is called semi-closed if C–S is semi-open.

Theorem 3.3

A subcomplex S of an abstract cellular complex C is semi-closed if and only if Int(Cl(S)) ⊆ S.

Proof

Proof follows directly from the Theorem 3.1 and Lemma 3.1.

Lemma 3.2

If S 1 and S 2 are any two subcomplexes of an abstract cellular complex C and if S 1 ⊆ S 2, then

  1. i

    Int(S 1) ⊆ Int(S 2)

  2. ii

    Fr(S 1) ⊆ Cl(S 2)

  3. iii

    Cl(S 1) ⊆ Cl(S 2)

Proof

  1. i

    Proof follows directly from the Definition 2.7

  2. ii

    Let x ∈ Fr(S 1). This implies that SON(x) intersects with both S 1 and C–S 1. If SON(x) ⊆ S 2 , then x ∈ Int(S 2) and if SON(x) ⊄ S 2, then x ∈ Fr(S 2). Hence, x ∈ Int(S 2) ∪ Fr(S 2) = Cl(S 2).

  3. iii

    Proof follows directly from (i) and (ii)

Theorem 3.4

If S 1 and S 2 are any two subcomplexes of an abstract cellular complex C, then S 1 ∪ S 2 is also semi-open subcomplex.

Proof

Given S 1 and S 2 are two semi-open subcomplexes of C. This implies that S 1 ⊆ Cl(Int(S 1)) and S 2 ⊆ Cl(Int(S 2)). This implies that S 1 ∪ S 2 ⊆ Cl(Int(S 1)) ∪ Cl(Int(S 2)) ⊆ Cl(Int(S 1 ∪ S 2)). Hence, S 1 ∪ S 2 is a semi-open subcomplex in C.

Remark 3.3

The intersection of any two semi-open subcomplexes need not be a semi-open subcomplex.

Theorem 3.5

Let S 1 be a semi-open subcomplex of an abstract cellular complex C and S 1 ⊆ S 2 ⊆ Cl(S 1). Then S 2 is semi-open.

Proof

Given S 1 is semi-open. This implies that there exists an open subcomplex O such that O ⊆ S 1 ⊆ Cl(O). Hence, O ⊆ S 2 . By the Lemma 3.2 (iii), we get Cl(S 1) ⊆ Cl(O).Therefore, S 2 is also semi-open.

Theorem 3.6

If S is homogeneously n-dimensional subcomplex of an n-dimensional complex C, then Fr(S) = Fr(Int(S)).

Proof

Suppose Fr(S) ≠ Fr(Int(S)), it implies that there is at least one lower-dimensional cell k of Fr(S) does not belong to Fr(Int(S)). This implies that the cell k does not bound any n-cell of S. This contradicts the fact that S is homogeneously n-dimensional.

Theorem 3.7

If S is homogeneously n-dimensional subcomplex of an n-dimensional complex C, then it is semi-open.

Proof

Given S is homogeneously n-dimensional subcomplex. By definition of interior, all the principal cells of S belong to Int(S). Suppose S ⊄ Cl(Int(S)), then there exists a lower-dimensional cell c ∈ S such that c ∉ Cl(Int(S)). This implies that the cell c does not bound any n-cell of Int(S). This contradicts the fact that S is homogeneously n-dimensional.

Theorem 3.8

If S is strongly connected homogeneously n-dimensional subcomplex of an n-dimensional complex C, then it is semi-open.

Proof

Proof follows directly from the Theorem 3.6 and the definition of semi-open.

Theorem 3.9

If a subcomplex S of an n-dimensional complex C is solid, then it is semi-open.

Proof

Proof follows directly from the definition of solid and semi-open.

Definition 3.3

Let S be a non-empty subcomplex of an abstract cellular complex C. Then, the semi-frontier of S is the set of all elements k of C–S, such that each neighborhood of k contains elements of both S and its complement C–S. It is denoted by SFr.

Lemma 3.3

If S is a subcomplex of an abstract cellular complex C, then SFr(S) ⊆ Fr(S).

Lemma 3.4

If S is a subcomplex of an abstract cellular complex C, then SFr(S) ∪ SFr(C–S) = Fr(S).

Proof

Proof follows directly from the definition of Fr and SFr

Definition 3.4

Let S be a subcomplex of an abstract cellular complex C. The subcomplex S–SFr(S) is called the semi-interior of S, and it is denoted by SInt.

Lemma 3.5

If S is a subcomplex of an abstract cellular complex C, then Int(S) ⊆ SInt(S).

Lemma 3.6

If S is a subcomplex of an abstract cellular complex C, then SInt(S) is semi-open.

Theorem 3.10

A subcomplex S of an abstract cellular complex C is semi-open if and only if SInt(S) = S.

Proof

Proof follows directly from the definition of semi-frontier and semi-interior.

Definition 3.5

Let S be a subcomplex of an abstract cellular complex C. The subcomplex S ∪ SFr(S) is called the semi-closure of S. It is denoted by SCl.

Definition 3.6

A subcomplex S of an abstract cellular complex C is called semi-open connected if S is connected and semi-open.

Remark 3.4

If a subcomplex S of an abstract cellular complex C is open connected, then it is semi-open connected. But the converse is not true.

Definition 3.7

A subcomplex S of an abstract cellular complex C is called semi-region if S is semi-open, connected, and solid.

Theorem 3.11

Every semi-open connected subcomplex S of an n-dimensional complex C is homogeneously n-dimensional.

Proof

Proof follows directly from the definition of semi-open connected and homogeneously n-dimensional.

Definition 3.8

A subcomplex S of an n-dimensional complex C is called quasi-solid if and only if it is homogeneously n-dimensional and is contained in Cl(Int(S, C),C).

Theorem 3.12

If a subcomplex \( S^{n} \) of an n-dimensional complex is quasi-solid, then it is semi-open.

Proof

Proof follows directly from the definition of quasi-solid and semi-open.

Theorem 3.13

Every solid subcomplex is quasi-solid.

Proof

Proof follows directly from the definition of solid and by the Theorem 3.9.

Remark 3.5

The converse of Theorem 3.13 need not be true.

4 Algorithm on Tracing the Semi-Frontier of an Image

This algorithm is defined to tracing the semi-frontier of an image. The proposed algorithm is more efficient for the image, which contains less number of components. Conceptually, the algorithm is divided into two major steps.

  1. Step 1:

    Before starting the tracing, the membership of the lower-dimensional cells (semi-open subcomplex) must be defined by the user whether it belongs to foreground or background of the image. The user can make the decision on the ground of some knowledge about the image.

  2. Step 2:

    Then, the image must be scanned row by row to find the starting point of each component. After finding the starting point, make the step along the boundary crack to the next boundary point using Kovalevsky’s chain code [7]. The crack and end point of the crack both belong to semi-frontier if it does not belong to foreground. The process stops when the starting point is reached again.

During each pass, the already visited cracks must be labeled to avoid multiple tracing.

4.1 Algorithm

The following is the formal description of the algorithm:

  • Input: Given a digital pattern as a two-dimensional abstract cellular complex Image containing points, cracks, and pixels.

  • Output: A sequence SF of semi-frontier cracks and points.

  • Let p denote the current semi-frontier point.

  • Let c denote the current semi-frontier crack.

  • Begin

    • Set Label to be empty

    • Set SF to be empty

    • Scan the Image row by row until two subsequent pixels of different colors are found

    • Set the upper end point of the crack c lying between the pixels of different colors as starting point s

    • Insert s, c in SF if it does not belong to foreground of the image

    • Fix the direction as 1

    • Move to next boundary point p along boundary crack c

    • Do

      • Insert p, c in SF if it does not belong to foreground of the image

      • To recognize the next boundary crack test left and right pixels lying ahead of actual crack

      • If Image [left] is foreground

      • Change the direction into (direction +1) %4

      • If Image [right] is background

      • Change the direction into (direction +3) %4

      • Insert c in Label, if the direction is 1

      • Move to the next boundary point p

  • End while if p is equal to s

  • End

4.2 Results and Discussion

Our proposed algorithm that extracts semi-frontier finds potential applications in pattern recognition. With the simple preprocessing steps, the algorithm directly traces the semi-frontier of an image. It is thus computationally effective in extracting semi-frontier of an image. The semi-frontier elements are generally a small subset of the total number of elements that represent a boundary. Therefore, the allocation of memory space is highly reduced and also the amount of computation is reduced when the images are processed by means of certain semi-frontier features. The time complexity of an algorithm is O(n 4). The proposed algorithm is implemented in MATLAB (Fig. 2).

Fig. 2
figure 2

a X-ray image of hands. b and c Semi-frontier of (a). d Image of torn photograph. e Semi-frontier of (d)

Full size image