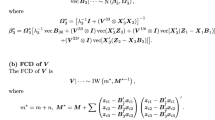Keywords

15.1 Introduction

Time use surveys usually include activities such as work, school, travel to/from work/school, housework, eating, shopping, childcare, reading, sleeping, sports, entertaining friends, hobbies, religious activities, and social activities at various locations (e.g., home, workplace, school, restaurants, and hotels: but without geocoding) throughout a period of one or several days. For example, 41 activitiesFootnote 1 are coded in the Multinational Time Use Study (Gauthier et al. 2006). With the support of various data,Footnote 2 time use has been studied in various disciplinesFootnote 3 to analyze topics such as economic activities, labor, gender, quality of life, leisure, and travel behavior (Michelson 2006; Pentland et al. 2013; Kimberly 2015).

Decision-making processes in daily activities (including relevant trips) involve the planning, execution, and adaptation of a number of interrelated choices across space and over time. Such choices include what to do (generation of activities) and when and how long to do it (time use, including timing), where to do it (destination), with whom (companion), and how to reach a destination (choice of travel mode and/or travel route). Understanding these choices over time and across space is essential for decisions on policies related to transportation, such as flexible or staggered working hours, transportation network planning, road pricing, and travel information provision. A good understanding of the above decisions is also crucial to provide a logical measurement of the value of time (VOT), which is extremely important in evaluating various urban policies. Time is limited and therefore valuable. As a result, the meaning (i.e., the value) of time in a certain time period may be different from that in other periods, even though the same activity is performed. People may choose to participate in a certain activity because of time (timing) constraints, or purposely choose the timing of a particular activity, even taking into account the influence of biological responses (e.g., sleeping habit and tiredness). In either case, it seems that logically quantifying the value of time in consideration of the above decision-making mechanisms and phenomena is needed.

When time use decisions are quantified, transportation researchers have done a better job within the framework of the activity-based approach, which argues that travel is derived from activity participation (e.g., Hensher and Stopper 1979; Jones 1990; Gerike et al. 2015). The activity-based approach has played an extremely important role in understanding why people travel, and has also provided various useful insights into decisions on transportation policies since its birth in the 1980s. In fact, most transportation studies seek to devise ways to reduce traffic congestion during peak hours. In line with such considerations, understanding why people travel at a specific time, i.e., timing decisions, is crucial. However, existing insights are extremely limited. Since the 2000s, some relevant studies have emerged about the development of activity–travel scheduling models, which examine the underlying behavioral mechanisms that give rise to activity sequencing over a period of time (e.g., Garling et al. 1998; Arentze and Timmermans 2000, 2005; Ettema and Timmermans 2003; Joh et al. 2003; Zhang et al. 2005a). In addition, recent changes in policy and forecasting needs have led to the development of an emerging class of activity–trip scheduling process surveys (Doherty 2004; Doherty and Papinski 2004). In essence, activity–trip scheduling behavior concerns the organization of an activity agenda in space and over time, and thus involves decisions regarding destinations, timing, and duration. Destination choices have been widely studied, and nested choice models [e.g., the nested logit and generalized nested logit models (Koppelman and Wen 2000), the nested paired combinatorial logit model (Fujiwara and Zhang 2005)] have dominated the literature. With respect to duration of activity, two research streams have emerged: one applying proportional or accelerated hazard models (see Lee and Timmermans (2007) for a review of recent studies), and another that is mainly based on Becker’s (1965) time allocation model [e.g., the individual-based model by Kitamura and Fujii (1998), the household-based model by Zhang et al. (2002, 2005b), and Zhang and Fujiwara (2006)]. In addition, the introduction of temporal constraints makes it possible to simultaneously represent durations of various activities across the course of a given time period (e.g., a day). More recently, more appealing models and theories have been proposed (e.g., Joh et al. 2002, 2006).

Compared with destination choice and duration, research on timing decisions remains scarce. For activity–travel scheduling behavior, timing decisions are problematic because decision-makers must make various interdependent timing decisions (i.e., multidimensional decisions) in a given time period. If the focus of analysis shifts from an individual to a multiperson household, the problem becomes even more complicated because some timing decisions are influenced by intrahousehold interactions. Therefore, ideally, interdependencies must be systematically incorporated not only into timing decisions across activities but also when factoring household members into modeling timing decisions.

In household decision-making, different members may need to adjust their schedules to meet various household needs, especially when participation in allocated or shared activities is required. An allocated activity such as daily shopping is an activity performed by one or more household members, and it involves a household task. Because the “products” of participation in allocated activities are usually consumed later, timing constraints may occur with respect to the end time. For example, to prepare a dinner with fresh vegetables, a household member may need to buy these vegetables and this trip needs to be completed before preparation of dinner starts. In contrast to allocated activities, participation in shared activities usually involves a negotiation process, because different members need to agree about the start and end times. Such coupling constraints reflect the fact that one has to be with particular people at the same location at (approximately) the same time. As a result, decisions about the timing of shared activities are more complicated than those of other activities.

Existing models have at best treated coupling constraints exogenously. In contrast, this study attempts to develop a multidimensional timing decision model of household activity–travel behavior with endogenous coupling constraints. The model is developed according to the principle of random utility maximization, which assumes that a household tries to maximize its utility. Household utility is defined as an additive-type function, which is the sum of the household members’ utilities. The utility of a member is further specified using a similar additive-type function, which is the sum of utilities of activities/trips. In turn, the utility of an activity/trip is defined as an integral of its timing utility, i.e., the utility of performing the activity/trip at a specific point of time. From the concept of timing utility, the influence of timing constraints and sequential correlation can easily be incorporated. Multidimensional timing is emphasized to take into account the interdependencies of timing decisions related to different activities/trips over the course of a day. The proposed model can also be applied to represent the sequence of activity–travel behavior endogenously. Representing timing endogenously makes it possible to clarify when and why an activity/trip is conducted during a calendar unit of time, and derives a meaningful value for time.

This chapter is organized as follows. Section 15.2 discusses some conceptual issues related to household scheduling behavior, especially from the perspective of timing decisions. Section 15.3 derives a multidimensional household timing decision model. Section 15.4 first describes the data used in this study, and then explains the model estimation, which is followed by a discussion of the implications of the estimation results. Finally, this case study concludes with a discussion of important future research issues.

15.2 Conceptual Issues

15.2.1 Definition of Scheduling Behavior

Scheduling decisions usually involve the following four major choice facets: (1) schedule content, (2) time, (3) space, and (4) agent. “Content” describes what the decision is about. In this study, content refers to all possible activities and trips. Time is concerned with when the content is executed. This is the central concern of this study. “Space” refers to where the activity is executed. Spatial concerns are especially important from the perspective of urban/regional and transportation planning. However, a study of spatial choices is beyond this study. “Agent” refers to the person(s) and/or organization(s) involved in a scheduling decision. An agent can be an independent individual, or several interdependent group members (e.g., household members, colleagues in the same office, a businessperson and his/her clients, friends, or organizations). This study examines scheduling behavior, focusing on an endogenous representation of multidimensional timing in the context of multiperson households.

15.2.2 Group Behavior, Activity Classification, and Sequence

Existing research has shown that decisions made by different members of a household are not independent, suggesting the existence of intrahousehold interaction (Timmermans et al. 1992; Borgers and Timmermans 1993; Molin et al. 1997; Vovsha et al. 2004; Zhang et al. 2005b). The nature of such intrahousehold interaction is strongly influenced by the nature of the activity. Studies of family decision-making show that the involvement of household members varies with decision type (Davis 1976). This is also true for activity–travel behavior. A compulsory activity is by definition constrained to a particular household member, and is often also constrained by time, location, and duration. This means that such activities are likely to be given a high priority and leave the household member less flexibility to perform them. In turn, this may affect the allocation of other activities. However, allocated activities will also be influenced by role patterns within the household.

Activity scheduling involves interdependent choices of what activities to conduct, where and when to conduct them, coupled with mode and route choices. Although individuals and households may decide on these various choice facets in a variety of ways, existing models have typically assumed that decisions concerning activity type, the people involved, location, timing, and travel are made in a fixed sequence in an attempt to reduce the complexity of the problem.

15.2.3 Timing: Multidimensional Considerations

Some activities and trips may be performed by an individual at any time. For others, start and/or end times may be designated a priori. In such cases, individual decisions about timing are constrained. For example, a businessperson has to be on time for a meeting with his/her clients at a designated time and place. Airline passengers face strict departure times for flights. In this sense, timing decisions vary according to types of activities/trips and may be influenced by timing constraints. Participation in an activity reduces the available remaining time and consequently places time pressure on performing other activities scheduled later that day. The existence of such time constraints forces individuals to decide how to make effective use of their limited available time. For example, the more time they spend on one activity, the less they can spend on another; the later they leave a place, the later they start performing another activity. In this sense, it seems unrealistic to assume that activity timing can be determined independently. Decisions about various duration/timing episodes interact. Needless to say, utility of activity participation may depend on when the activity is performed. Traditional unidimensional timing models, such as hazard models, cannot reflect such interdependent timing behavior in a satisfactory manner. Multispell competing risk models (e.g., Popkowski Leszczyc and Timmermans 2002) can be used to represent multidimensional timing decisions from a statistical perspective. In contrast, simultaneous representations of timing decisions based on utility theory may be a better alternative from a behavioral perspective.

15.3 Model Development

15.3.1 Specification of Timing Utility

Previous studies have suggested that the utility of activity participation or travel is dependent upon its timing (Arentze and Timmermans 2000; Ashiru et al. 2003; Zhang et al. 2005a). The concept of timing utility is useful in the study of timing decisions. Because decision-makers may exhibit heterogeneous timing preferences, it is necessary to adopt some general utility functions with operational forms. In theory, a timing function could have either a continuous or a discrete form. These two forms have both advantages and disadvantages. By assuming the discrete form of timing utility, one can adopt the widely applied discrete choice modeling approaches to represent timing decisions (e.g., Zhang et al. 2004); however, categorizing continuous time into the appropriate number of time slots is problematic. For example, Fujiwara et al. (2001) attempted to solve such problems partially by using a paired combinatorial logit (PCL) model; however, such a categorization inevitably involves arbitrary and subjective judgments. Too many categories could result in a nonoperational model specification. To avoid such arbitrariness in model specification, the continuous form is adopted for the timing utility function in this study. Two major timing utility functions seem worthy of further investigation. One is the gamma probability density (GPD) function [Eq. (15.1)], the effectiveness of which has been examined by Zhang et al. (2005a). Another is the bell-shaped function proposed by Joh et al. (2003). Because the bell-shaped function has a much more complex form with more unknown parameters than the GPD function, this study adopts the following GPD function.

$$u_{ni} (t) = \frac{{\beta_{ni}^{{\alpha_{ni} }} t^{{\alpha_{ni} - 1}} }}{{\varGamma \left( {\alpha_{ni} } \right)}} \cdot { \exp }\left( { - \beta_{ni} t} \right)$$
(15.1)
$$\varGamma \left( {\alpha_{ni} } \right) = \int\limits_{0}^{\infty } {y^{{\alpha_{ni} - 1}} {\text{e}}^{ - y} \,dy}$$
(15.2)
$$\alpha_{ni} > 0,\;\beta_{ni} > 0$$
(15.3)

Here, \(\alpha_{ni}\) and \(\beta_{ni}\) indicate the shape and scale parameters of utility \(u_{ni} (t)\) that individual n derives from performing activity or trip i, respectively, and \(\varGamma(\cdot)\) is the gamma function.

Different values of \(\alpha_{ni}\) and \(\beta_{ni}\) result in different timing distributions, and the shape of the utility function can be either skewed or symmetric (see Fig. 15.1). As a result, the GPD function can include various forms of distribution as special cases, such as the exponential function or the normal distribution function. Adoption of the GPD function implicitly assumes that for each activity or trip, the timing utility follows a one-peak distribution, i.e., the timing utility first increases and starts to decrease after reaching a certain point in time. It should be recognized that this is also a limitation of the GPD function. In other words, if a timing distribution has two or more peaks, it is necessary to introduce additional rational logics into the model specification. This paper only examines the applicability of the GPD function to the representation of household timing decisions. Exploring other forms of timing functions is left as a future research issue.

Fig. 15.1
figure 1

Special cases of gamma probability density function

Full size image

15.3.2 Modeling Observed Interdependency: The Individual Level

Because each individual’s available time is limited (here, 24 h in a day), conducting an activity for a longer period of time implies that another activity needs to be either shortened or canceled. In this sense, interdependencies among activities/trips over the course of a day need to be introduced into the model of activity participation, including timing decisions. Taking this into account, it is assumed here that utility is time-additive and time-separable, and that an individual determines the timing of an activity or a trip by maximizing his/her total utility over a given period of time. Individual n’s total utility \(U_{n}\) is defined as the sum of utilities of all activities and trips over the target period of time [Eq. (15.4)]. Note that the start time of the ith activity or trip is also the end time of the i − 1th activity or trip. Start and end times are the dependent variables in this study. Optimal timing can be obtained by solving the following optimization problem consisting of Eqs. (15.4) and (15.5), where Eq. (15.5) indicates the available time constraint.

Maximize

$$U_{n} = \sum\limits_{i} {U_{ni} } = \sum\limits_{i} {\int\limits_{{t_{ni - 1} }}^{{t_{ni} }} {u_{ni} (s)\;ds} }$$
(15.4)

Subject to

$$\sum\limits_{i} {\tau_{ni} } = \sum\limits_{i} {(t_{ni} - t_{ni - 1} )} = T_{n}$$
(15.5)

where,

n, i :

individual and activity/trip, respectively,

\(U_{ni}\) :

individual n’s utility from performing the ith activity/trip,

\(u_{ni} (s)\) :

individual n’s timing utility from performing the ith activity/trip at time s,

\(t_{ni - 1}\) :

the start or departure time when individual n performs the ith activity/trip,

\(t_{ni}\) :

the end or arrival time when individual n performs the ith activity/trip,

\(\tau_{ni}\) :

the duration that individual n performs the ith activity/trip, and

\(T_{n}\) :

the time available to individual n.

15.3.3 Modeling Observed Interdependency: The Household Level

In household decisions, interactions among household members with respect to multidimensional timing decisions take place because of participation in joint or shared activities and trips, which result in coupling constraints. To incorporate such coupling constraints into the model, the activities/trips should be properly classified. In this study, activities are first classified into in-home activities and out-of-home activities. The out-of-home activities are further divided into independent, allocated, and shared (joint) activities. An independent activity is an activity that does not involve a household task and is performed by a single household member. Shared activities are those activities that require the presence of all or a subset of household members. An allocated activity is usually a household task that is assigned to a specific household member. The shared activities may be synchronized or unsynchronized. In the former case, household members conduct the shared activity together from beginning to end. In the latter case, household members share parts of the activity. This study only deals with synchronized activities. The classification described above assumes that decisions on activities in each category are homogeneous. However, this may not be true in the sense that task allocation mechanisms may differ between activities. If such heterogeneity is a concern, a finer classification involving more detailed categories of activities is required.

Applying this classification, the modeling framework defined in Eqs. (15.4) and (15.5) can be rewritten for the context of household decisions as follows:

Maximize

$$U_{h} = \sum\limits_{n} {\sum\limits_{i} {U_{hni} } } = \sum\limits_{n} {\sum\limits_{i} {\int\limits_{{t_{hni - 1} }}^{{t_{hni} }} {u_{hni} (s)\;ds} } }$$
(15.6)

Subject to

$$\sum\limits_{i} {\tau_{hni} } = \sum\limits_{i} {(t_{hni} - t_{hni - 1} )} = T_{hn}$$
(15.7)

where,

h, n, i :

household, individual member, and activity/trip, respectively,

\(U_{hni}\) :

the utility of individual n of household h performing the ith activity or trip,

\(u_{hni} (s)\) :

timing utility of individual n of household h performing the ith activity or trip at time s,

\(t_{hni - 1}\) :

start or departure time of individual n of household h performing the ith activity or trip (equal to the end time of i − 1th activity/trip),

\(t_{hni}\) :

end or arrival time of individual n belonging to household h performing the ith activity or trip (equal to start time of i + 1th activity/trip),

\(\tau_{hni}\) :

duration of the ith activity or trip performed by individual n of household h, and

\(T_{hn}\) :

the time available to individual n of household h.

It may be seen that household utility takes an additive type of utility function, which consists of the members’ utilities. Such a specification assumes that the final decision-maker is the household rather than an individual household member. However, to reach a final decision, the household takes each member’s preferences into account. Decisions about shared activities first require such a model specification because the resultant timing needs to reflect the preferences of all the members involved. Each member must take such shared activities into account to determine the timing of his/her nonshared activities. In other words, members may need to adjust the schedules of their activities/trips. Thus, the abovementioned additive type of household utility function is adopted here to incorporate the preferences of all the household members involved in the decision-making process. Of course, there are other possible household utility functions including multilinear and isoelastic types (see Zhang et al. 2005b; Zhang and Fujiwara 2006). Because introducing those types of function results in nonoperational model structures, such as the first attempt to examine household multidimensional timing decisions from the perspective of group decision-making, this paper only examines the effectiveness of the additive type of household utility function. In line with our previous research about household decisions (see Zhang et al. 2005b; Zhang and Fujiwara 2006), the principle of household utility maximization is applied.

15.3.4 Deriving the Household Timing Decision Model

In Eqs. (15.6) and (15.7), the dependent variable is timing (start time or end time) \(t_{hni}\) at which individual n belonging to household h performs activity i or makes a trip i. Maximization of Eq. (15.6) subject to Eq. (15.7) leads to the household timing decision model. To derive this model, the first derivative is calculated with respect to each timing variable \(t_{hni}\). The timing variable of the shared activity/trip is included in all the household members’ utility functions, but that of a nonshared activity/trip is only related to the member of interest. Therefore, to derive the optimal timing, it is necessary to distinguish between shared and nonshared activities/trips.

15.3.4.1 Timing Function of a Nonshared Activity/Trip

The first-order derivative for the timing of nonshared activity/trips is given below.

$$\begin{aligned} \frac{{\partial U_{hn} }}{{\partial t_{hni} }} & = \frac{\partial }{{\partial t_{hni} }}\left[ {\int\limits_{{t_{hni - 1} }}^{{t_{hni} }} {u_{hni} (s)\,ds} + \int\limits_{{t_{hni} }}^{{t_{hni + 1} }} {u_{hni + 1} (s)\,ds} } \right] \\ & = u_{hni} (t_{hni} ) - u_{hni + 1} \left( {t_{hni} } \right) \\ \end{aligned}$$
(15.8)

Substituting Eq. (15.1) into Eq. (15.8) and setting Eq. (15.8) to equal zero, the following equation, including the optimal timing \(\hat{t}_{hni}\), can be obtained.

$$\hat{t}_{hni}^{{\alpha_{hni + 1} - \alpha_{hni} }} \cdot { \exp }\left\{ { - \left( {\beta_{hni + 1} - \beta_{hni} } \right)\,\hat{t}_{hni} } \right\} = \frac{{\varGamma \left( {\alpha_{hni} } \right)}}{{\varGamma \left( {\alpha_{hni + 1} } \right)}} \cdot \frac{{\beta_{hni + 1}^{{\alpha_{hni + 1} }} }}{{\beta_{hni}^{{\alpha_{hni} }} }}$$
(15.9)

To obtain an explicit function of optimal timing, Eq. (15.9) is rewritten below based on a logarithm transformation.

$$\left( {\alpha_{hni + 1} - \alpha_{hni} } \right)\ln \left( {\hat{t}_{hni} } \right) - \left( {\beta_{hni + 1} - \beta_{hni} } \right)\hat{t}_{hni} = { \ln }\left( {\frac{{\varGamma \left( {\alpha_{hni} } \right)}}{{\varGamma \left( {\alpha_{hni + 1} } \right)}} \cdot \frac{{\beta_{hni + 1}^{{\alpha_{hni + 1} }} }}{{\beta_{hni}^{{\alpha_{hni} }} }}} \right)$$
(15.10)

Further transformation of Eq. (15.10) results in the following timing function for nonshared activities/trips.

$$\hat{t}_{hni} = \frac{{\left( {\alpha_{hni + 1} - \alpha_{hni} } \right)\ln \left( {\hat{t}_{hni} } \right) - { \ln }\left( {\frac{{\varGamma \left( {\alpha_{hni + 1} } \right)}}{{\varGamma \left( {\alpha_{hni} } \right)}}\frac{{\beta_{hni}^{{\alpha_{hni} }} }}{{\beta_{hni + 1}^{{\alpha_{hni + 1} }} }}} \right)}}{{\left( {\beta_{hni + 1} - \beta_{hni} } \right)}}$$
(15.11)

15.3.4.2 Timing Function of a Shared Activity/Trip

Similarly, the first-order derivative condition for the timing of shared activities/trips can be derived as below.

$$\begin{aligned} \frac{{\partial U_{h} }}{{\partial t_{hni}^{j} }} & = \sum\limits_{n} {\frac{{\partial U_{hni} }}{{\partial t_{hni}^{j} }}} = \sum\limits_{n} {\frac{\partial }{{\partial t_{hni}^{j} }}\left\{ {\int\limits_{{t_{hni - 1} }}^{{t_{hni}^{j} }} {u_{hni} (s)\;ds} + \int\limits_{{{\kern 1pt} t_{hni}^{j} }}^{{t_{hni + 1} }} {u_{hni + 1} (s)\;ds} } \right\}} \\ & = \sum\limits_{n} {\left( {u_{hni} \left( {t_{hni}^{j} } \right) - u_{hni + 1} \left( {t_{hni}^{j} } \right)} \right)} = 0 \\ \end{aligned}$$
(15.12)

where \(\hat{t}_{hni}^{j}\) is the jth timing variable of household h’s shared activity/trip, but the ith timing variable of individual n’s activity/trip.

As a result, transformation of Eq. (15.12) leads to the following optimal timing function \(\hat{t}_{hni}^{j}\) for the shared activity/trip.

$$t_{hni}^{j} = \frac{{\sum\nolimits_{n} {\left( {\frac{{\beta_{hni + 1}^{{\alpha {\kern 1pt}_{hni + 1} }} (t_{hni}^{j} )^{{\alpha_{hni + 1} }} }}{{\varGamma \left( {\alpha_{hni + 1} } \right)}} \cdot { \exp }\left( { - \beta_{hni + 1} t_{hni}^{j} } \right)} \right)} }}{{\sum\nolimits_{n} {\left( {\frac{{\beta_{hni}^{{\alpha {\kern 1pt}_{hni} }} (t_{hni}^{j} )^{{\alpha_{hni} - 1}} }}{{\varGamma \left( {\alpha_{hni} } \right)}} \cdot { \exp }\left( { - \beta_{hni} t_{hni}^{j} } \right)} \right)} }}$$
(15.13)

15.3.5 Simplifying Household Timing Decision Model Structure

Observing Fig. 15.1, it is obvious that as the value of positive shape parameter \(\alpha_{ni}\) increases, both mean and variance of timing distribution increase, resulting in a flatter timing distribution and change in the shape of the distribution from left skewed toward the normal distribution. In contrast, the scale parameter \(\beta_{ni}\) shows the opposite trend. In other words, if the explanatory variable for \(\alpha_{ni}\) and \(\beta_{ni}\) has different signs for shape and scale parameters, the timing distribution changes in a consistent way. Otherwise, the timing distribution varies with the values of the same explanatory variable for scale/shape parameters. On the other hand, allowing the coexistence of activity/trip-specific shape and scale parameters not only makes the estimation of Eqs. (15.11) and (15.13) very complicated, but also makes the parameter interpretations very confusing, especially from a policy perspective. Therefore, this study attempts to simplify the model structure without loss of generality by assuming that the shape parameter differs across individual household members, but is invariant across activities/trips. Based on this assumption, Eqs. (15.11) and (15.13) can be rewritten as below.

$$t_{hni} = \frac{{\alpha_{hn} \left( {{ \ln }\left( {\beta_{hni + 1} } \right) - { \ln }\left( {\beta_{hni} } \right)} \right)}}{{\left( {\beta_{hni + 1} - \beta_{hni} } \right)}}$$
(15.14)
$$\hat{t}_{hni}^{j} = \frac{{\sum\nolimits_{n} {\left( {\frac{{\beta_{hni + 1}^{{\alpha {\kern 1pt}_{hn} }} (\hat{t}_{hni}^{j} )^{{\alpha {\kern 1pt}_{hn} }} }}{{\varGamma \left( {\alpha_{hn} } \right)}} \cdot { \exp }\left( { - \beta_{hni + 1} \hat{t}_{hni}^{j} } \right)} \right)} }}{{\sum\nolimits_{n} {\left( {\frac{{\beta_{hni}^{{\alpha_{hn} }} (\hat{t}_{hni}^{j} )^{{\alpha {\kern 1pt}_{hn} - 1}} }}{{\varGamma \left( {\alpha_{hn} } \right)}} \cdot { \exp }\left( { - \beta_{hni} \hat{t}_{hni}^{j} } \right)} \right)} }}$$
(15.15)

15.3.6 Behavioral Implications of Timing Functions

As described above, the timing function for each activity/trip is derived based on the principle of household random utility maximization. This assumption is made because it is expected that the proposed model could be useful for economic evaluations of transportation policies. Moreover, because of the differing levels of involvement of household members, different forms of timing functions are derived with respect to shared and nonshared activities/trips. It is obvious that there is no structural difference in the timing functions for an activity and a trip in the same position in the schedule, or within each type of activity/trip. To capture the differences between activity and trip, activity-specific and trip-specific attributes could be introduced into the timing function. This will be explained below. If the homogeneity of each type of activity/trip were a problem, one could simply make a finer classification of activities and trips. Some major behavioral features of the derived timing functions are summarized below.

15.3.6.1 Modeling Interdependencies Among Activities/Trips

  • Endogenous representation of observed interdependencies

As shown in Eqs. (15.11) and (15.13), each timing variable is derived as a function not only of its own shape and scale parameters, but also of the parameters of the next activity or trip. In this sense, the derived timing functions can represent such observed interdependencies among activities and/or trips over the course of a day endogenously. Because the timing decision of an activity or a trip is influenced by that of the subsequent one, it is first-order interdependence that is incorporated into the model. As described below, the scale and shape parameters are defined as a function of the attributes of the household and its members, so the observed heterogeneity existing in the aforementioned interdependencies may be properly captured.

  • Endogenous representation of unobserved interdependencies

In addition to observed interdependencies among activities/trips, interdependencies may also be caused by the influence of unobserved factors. Because the parameters \(\alpha_{hn}\) and \(\beta_{hni}\) are both positive, we propose to meet these two conditions and incorporate heterogeneity into timing decisions by defining these two parameters using the following functions.

$$\alpha_{hn} = { \exp }\left( {\varDelta_{hn} + e_{hn}^{\alpha } } \right)$$
(15.16)
$$\beta_{hni} = { \exp }\left( {\varDelta_{hni} + e_{hni}^{\beta } } \right)$$
(15.17)

where, \(\varDelta_{hn} ,\,\varDelta_{hni}\) are deterministic terms consisting of the observed factors influencing the shape parameter \(\alpha_{hn}\) and the scale parameter \(\beta_{hni}\), respectively, and \(e_{hn}^{\alpha } ,e_{hni}^{\beta }\) are stochastic terms reflecting the influence of unobserved factors on \(\alpha_{hn}\) and \(\beta_{hni}\).

15.3.6.2 Representation of Activity/Trip Sequence in an Indirect Manner

It is not difficult to observe that to derive the timing function, it is only necessary to know where the relevant activity or trip is located in the overall schedule for a given time period. It is not necessary to identify the content of the activity/trip beforehand. In other words, index i in Eqs. (15.11) and (15.13) refers to the ith event in the overall schedule, and it can be either an activity or a trip. Note that \(\varDelta_{hn} ,\,\varDelta_{hni}\) in Eqs. (15.16) and (15.17) can include any kind of observed factors that influence the shape and scale parameters. If a dummy variable about activity type or trip type is introduced as one of the influential factors, then one can obtain all the timing utilities with respect to both activities and trips corresponding to each optimal timing variable. In other words, as long as the number of activities and trips performed in a day is given, it is possible to calculate the timing utilities for both activity and trip at each ordered location of the schedule over the course of a day. For example, it is expected that a household member may decide whether to participate in an activity or to make a trip by comparing the utilities of the activity and the trip. Thus, the calculated timing utilities could be used to represent the activity/trip sequence indirectly in theory.

15.3.6.3 Endogenous Representation of Coupling Constraints

A coupling constraint means that two or more people have to be together in a specific time period and at a specific place. Such coupling can involve either an activity or a trip. In this paper, a synchronized shared activity/trip is classified to represent such coupling constraints in household scheduling behavior. The presence of coupling constraints may force household members to adjust their schedules. It can also be expected that each member’s timing decisions concerning the nonshared activities/trips may influence the timing when household members undertake them. Thus, the timings of shared and nonshared activities/trips interact, and it is difficult to assume that either a one-way or a two-way influence is more realistic. Therefore, instead of making such an assumption, this paper proposes to derive each timing function by defining each member’s utility as a function of the utilities obtained from performing all the possible activities/trips in a choice set. As a result, the timing functions for both shared and nonshared activities/trips are derived simultaneously in an endogenous way. The influence of coupling constraints is explicitly incorporated into the relevant timing function(s), as shown in Eqs. (15.14) and (15.15).

15.3.7 Model Estimation Method

As Eqs. (15.18) and (15.19) show, each timing variable is derived as a function not only of its own information, but also of information from the next activity/trip. This means that the derived optimal timing variables interact and may both be influenced by the same set of unobserved attributes of the household and its members, suggesting that it is necessary to represent the statistical correlation in the model. Because of the error terms \(e_{hn}^{\alpha } ,e_{hni}^{\beta }\) in Eqs. (15.16) and (15.17), it is quite difficult to estimate the timing functions shown in Eqs. (15.14) and (15.15) directly. To estimate the timing functions based on an operational method, it is assumed that Eqs. (15.14) and (15.15) can be transformed as follows:

$$\hat{t}_{hni} = v_{hni} + \varepsilon_{hni} = \frac{{\tilde{\alpha }_{hn} \left( {{ \ln }\left( {\tilde{\beta }_{hni + 1} } \right) - { \ln }\left( {\tilde{\beta }_{hni} } \right)} \right)}}{{\left( {\tilde{\beta }_{hni + 1} - \tilde{\beta }_{hni} } \right)}} + \varepsilon_{hni}$$
(15.18)
$$\hat{t}_{hni}^{j} = v_{hni}^{j} + \varepsilon_{hni}^{j} = \frac{{\sum\limits_{n} {\left( {\frac{{\tilde{\beta }_{hni + 1}^{{\tilde{\alpha }_{hn} }} (\hat{t}_{hni}^{j} )^{{\tilde{\alpha }_{hn} }} }}{{\varGamma \left( {\tilde{\alpha }_{hn} } \right)}} \cdot { \exp }\left( { - \tilde{\beta }_{hni + 1} \hat{t}_{hni}^{j} } \right)} \right)} }}{{\sum\limits_{n} {\left( {\frac{{\tilde{\beta }_{hni}^{{\tilde{\alpha }_{hn} }} (\hat{t}_{hni}^{j} )^{{\tilde{\alpha }_{hn} - 1}} }}{{\varGamma \left( {\tilde{\alpha }_{hn} } \right)}} \cdot { \exp }\left( { - \tilde{\beta }_{hni} \hat{t}_{hni}^{j} } \right)} \right)} }} + \varepsilon_{hni}^{j}$$
(15.19)
$$\tilde{\alpha }_{hn} = { \exp }\left( {\varDelta_{hn} } \right)$$
(15.20)
$$\tilde{\beta }_{hni} = { \exp }\left( {\varDelta_{hni} } \right)$$
(15.21)

where \(\varepsilon_{hni} ,\varepsilon_{hni}^{j}\) are the transformed error terms.

15.3.7.1 Introduction of the First-Order Sequential Correlation

The above transformation has some positive features for representing timing decisions. First, the unobserved interdependencies among activities/trips can be incorporated into the model by assuming that the error terms \(\varepsilon_{hni} ,\varepsilon_{hni}^{j}\) are correlated. One can define such correlations in various ways. The multivariate normal distribution may be the most desirable in the sense that it can flexibly represent the correlations between error terms. However, one of the difficulties in applying the multivariate normal distribution is the calculation of the multidimensional integral. Even though some advanced methods have recently been proposed to overcome such calculation issues, the calculation itself is still very complicated and time consuming. In this study, to overcome this computational problem and make the estimation of the timing function more practical, a concept of first-order sequential correlation is introduced. The sequential correlation is defined as the correlation between error terms of neighboring activities/trips (i.e., \(\varepsilon_{ni}\) and \(\varepsilon_{ni + 1}\)). It is further assumed that these two error terms follow a bivariate normal distribution.

$$f\left( {\varepsilon_{ni} ,\varepsilon_{ni + 1} } \right) = \frac{1}{{2\pi \sigma_{i} \sigma_{i + 1} \sqrt {1 - \rho^{2} } }}{ \exp }\left\{ { - \frac{{\left[ {\left( {\frac{{\varepsilon_{ni} }}{{\sigma_{i} }}} \right)^{2} - 2\rho \frac{{\varepsilon_{ni} }}{{\sigma_{i} }}\frac{{\varepsilon_{ni + 1} }}{{\sigma_{i + 1} }} + \left( {\frac{{\varepsilon_{ni + 1} }}{{\sigma_{i + 1} }}} \right)^{2} } \right]}}{{2\left( {1 - \rho^{2} } \right)}}} \right\}$$
(15.22)

where \(\rho\) is correlation between error terms \(\varepsilon_{ni}\) and \(\varepsilon_{ni + 1}\), and \(\sigma_{i} ,\sigma_{i + 1}\) are the corresponding standard deviations.

15.3.7.2 Representing Nonnegative Timing and Sequencing Constraints

In this study, the timing of each activity or trip is defined as the length of time from a predefined reference time (referred to as 0:00 here). Therefore, the derived optimal timing variable should first meet this nonnegative condition. In addition, because of activity/trip sequences, the timing (start time in this study) of the ith activity/trip should occur before the timing of the i + 1th activity/trip (i.e., sequencing constraint). Such conditions are described in the following Eqs. (15.23)–(15.25).

$$\hat{t}_{ni} > 0,\;\hat{t}_{ni + 1} > \hat{t}_{ni}$$
(15.23)
$$\hat{t}_{ni} > 0\quad \Rightarrow \quad \hat{t}_{ni} = v_{ni} + \varepsilon_{ni} > 0\quad \Rightarrow \quad \varepsilon_{ni} > - v_{ni}$$
(15.24)
$$\hat{t}_{ni + 1} > \hat{t}_{ni} \quad \Rightarrow \quad \hat{t}_{ni + 1} = v_{ni + 1} + \varepsilon_{ni + 1} > \hat{t}_{ni} \quad \Rightarrow \quad \varepsilon_{ni + 1} > \hat{t}_{ni} - v_{ni + 1}$$
(15.25)

As a result, the probability that describes the nonnegativity and sequencing constraints is given below.

$$\begin{aligned} {\text{Prob}}\left( {\hat{t}_{ni} > 0,\hat{t}_{ni + 1} > \hat{t}_{ni} } \right) & = {\text{Prob}}\left( {\varepsilon_{ni} > - v_{ni} ,\varepsilon_{ni + 1} > \hat{t}_{i} - v_{ni + 1} } \right) \\ & = \int\limits_{{ - v_{i} }}^{\infty } {\int\limits_{{\hat{t}_{i} - v_{i + 1} }}^{\infty } {f\left( {\varepsilon_{ni} ,\varepsilon_{ni + 1} } \right)} } d\varepsilon_{ni} \,d\varepsilon_{ni + 1} \\ \end{aligned}$$
(15.26)

Equation (15.26), with a double integral, can be further transformed into the following equation with a single integral based on coordinate rotation (Zhang et al. 2004).

$${\text{Prob}}\left( {\hat{t}_{ni} > 0,\hat{t}_{ni + 1} > \hat{t}_{ni} } \right) = \left\{ {1 - \varPhi \left( {\frac{{\hat{t}_{ni} - v_{ni + 1} }}{{\sigma_{i + 1} \sqrt {1 - \rho^{2} } }}} \right)} \right\}\left\{ {1 - \varPhi \left( {\frac{{v_{ni} }}{{\sigma_{i} \sqrt {1 - \rho^{2} } }}} \right)} \right\}$$
(15.27)

Equation (15.27) represents the nonshared activity/trip. In the case of a shared activity/trip, because its timing may influence all members’ timing decisions about consecutive activities/trips, Eq. (15.27) needs to be revised to reflect intrahousehold decision-making mechanisms. Instead of \(\hat{t}_{ni}\) in Eq. (15.23), the shared activity/trip timing \(\hat{t}_{hni}^{j}\) is introduced. Then the following conditions need to be met with respect to each household member.

$$\hat{t}_{hni}^{j} > 0,\quad \hat{t}_{hni + 1} > \hat{t}_{hni}^{j}$$
(15.28)

For each member, the relevant probability related to Eq. (15.28) can be written as follows:

$${\text{Prob}}\left( {\hat{t}_{hni}^{j} > 0,\hat{t}_{ni + 1} > \hat{t}_{hni}^{j} } \right) = \left\{ {1 - \varPhi \left( {\frac{{\hat{t}_{hni}^{j} - v_{hni + 1} }}{{\sigma_{i + 1} \sqrt {1 - \rho^{2} } }}} \right)} \right\}\left\{ {1 - \varPhi \left( {\frac{{v_{hni}^{j} }}{{\sigma_{i} \sqrt {1 - \rho^{2} } }}} \right)} \right\}$$
(15.29)

Because the shared activity timing \(\hat{t}_{hni}^{j}\) is included in Eq. (15.29) for each member, it is necessary to estimate these equations simultaneously. Note that \(\hat{t}_{hni + 1}\) may also be the timing of a shared activity/trip.

Needless to say, timing decisions may be influenced by timing constraints (e.g., the designated time of a meeting and departure time of a flight). In addition, because an activity–travel survey is usually conducted within a predesignated time period, it cannot be expected that each respondent started the first activity/trip precisely at the beginning of the time period, and/or ended the last one at the end of the survey period. Therefore, it is necessary to represent this censored timing properly in the model. Zhang et al. (2005a) discussed such issues in the context of individual decision-making. However, their approach can be directly applied to the context of household decision-making, which is the main focus of this study. Because this case study does not deal with these issues, detailed model specifications will not be shown here, and readers are recommended to refer to Zhang et al. (2005a).

15.3.7.3 Applying a Maximum Likelihood Method for Model Estimation

Because only nonnegative timing and activity/trip sequencing constraints are relevant in this case study, the resultant household activity–travel timing decision model can be specified by Eqs. (15.30)–(15.33). The model can be estimated using the conventional maximum likelihood method.

$${ \log }\,{\text{L}} = \sum\limits_{h = 1}^{H} {\sum\limits_{n = 1}^{N} {\sum\limits_{i = 1}^{I} {{ \ln }({\text{p}}_{\text{hni}} )} } }$$
(15.30)
$$p_{hni} = \left\{ {1 - \varPhi \left( {\frac{{\varTheta_{hni + 1} }}{{\sigma_{i + 1} \sqrt {1 - \rho^{2} } }}} \right)} \right\}\left\{ {1 - \varPhi \left( {\frac{{\varTheta_{hni} }}{{\sigma_{i} \sqrt {1 - \rho^{2} } }}} \right)} \right\}$$
(15.31)
$$\varTheta_{hni} = \delta_{hni}^{j} v_{hni}^{j} + \delta_{hni} v_{hni}$$
(15.32)
$$\varTheta_{hni + 1} = (\delta_{hni}^{j} \hat{t}_{hni}^{j} + \delta_{hni} \hat{t}_{hni} ) - (\delta_{hni + 1} v_{hni + 1} + \delta_{hni + 1}^{j + 1} v_{hni + 1}^{j + 1} )$$
(15.33)

where \(p_{hni}\) indicates the probability with respect to the ith (nonshared or shared) activity/trip performed by individual n, belonging to household h, and \(\delta\) is a dummy variable to indicate whether an activity/trip is shared (1: Yes, 0: No).

15.4 Model Estimation Results

15.4.1 Data

The proposed model was estimated using the activity diary data originally collected for the Albatross model (Arentze and Timmermans 2005), which was developed to explore the potential of a new generation of rule-based transport demand models. Albatross predicts the schedule of a maximum of two adult members of a given household on a given day. Because this study attempts to represent household activity–travel timing decision behavior, data from single-member households and the households with missing attributes were excluded from this study. To simplify the discussion of the proposed household timing decision model, the original 48 types of activities were first recategorized into two major types: shared and nonshared activities. Shared activities are distinguished only for out-of-home activities. To avoid inconsistencies in the reported timing data, activities here are considered to be shared if both the husband and wife have the same start and end times. The nonshared activities are further classified into in-home activities and out-of-home independent and allocated activities, even though they have the same form of timing function.

In total, 3075 households provided their activity data. Figures 15.2, 15.3 and 15.4 show the distribution of the numbers of nonshared and shared activities. It is clear that females perform more activities than their spouses (on average, 16 activities/day versus 14 activities/day) both on weekdays and weekends (t values of tests of the differences between husband and wife are 14.30 for activities overall, 13.64 on weekdays and 4.39 on weekends). Irrespective of whether it is a weekday or weekends, each household performs about one shared activity on average. There are significant differences between weekdays and weekends with respect to females’ activities and shared activities (t values of tests of the differences between weekdays and weekends are 4.43 for the female’s activities and 5.74 for the shared activities), but no difference is observed concerning the husband’s activities (the relevant t value is just 0.09).

Fig. 15.2
figure 2

Distribution of number of activities performed by husband

Full size image
Fig. 15.3
figure 3

Distribution of number of activities performed by wife

Full size image
Fig. 15.4
figure 4

Distribution of number of shared activities by husband and wife

Full size image

Even though each member conducts many activities every day, because it is the first attempt to apply the proposed household timing decision model, this paper deals with only two successive activities (the fifth and sixth activities in the day of the survey) on weekdays. In other words, trip-making behavior is excluded from this case study. The resulting sample includes 593 households. The timing distributions related to the fifth and sixth activities are shown in Fig. 15.5. A trial using the full data set is left for future research.

Fig. 15.5
figure 5

Timing distributions of nonshared and shared activities (upper part: husband, middle part: wife, lower part: shared activity)

Full size image

15.4.2 Explanatory Variables

Factors influencing household timing decision behavior are introduced into the model via the scale and shape parameters of the derived timing utility functions. For that purpose, \(\varDelta_{hn} ,\,\varDelta_{hni}\) in Eqs. (15.17) and (15.18) are rewritten as follows:

$$\varDelta_{hn} = \pi_{n}^{\alpha } + \theta_{n}^{\alpha } \,\varOmega_{h} + \mu_{n}^{\alpha } \,\varPsi_{hn}$$
(15.34)
$$\varDelta_{hni} = \pi_{ni}^{\beta } + \theta_{ni}^{\beta } \,\varOmega_{h} + \mu_{ni}^{\beta } \,\varPsi_{hn} + \sum\nolimits_{k} {\gamma_{k} X_{hnik}}$$
(15.35)
$$\varOmega_{h} = \sum\limits_{p} {\rho_{p} Z_{hp} }$$
(15.36)
$$\varPsi_{hn} = \sum\limits_{q} {\kappa_{q} Y_{hnq} }$$
(15.37)

where the variables are as follows:

\(X_{hnik}\) :

the kth activity-specific variable used to explain scale parameter \(\beta_{hni}\),

\(Y_{hnq}\) :

the qth individual attribute used to explain both \(\alpha_{hn}\) and \(\beta_{hni} ,Z_{hp}\) the pth household attribute used to explain both \(\alpha_{hn}\) and \(\beta_{hni}\),

\(\theta_{n}^{\alpha }\) :

the influence of household attributes on shape parameter \(\alpha_{hn}\); the parameter for one household member needs to be fixed at unity,

\(\theta_{ni}^{\beta }\) :

the influence of household attributes on scale parameter \(\beta_{hni}\) of the ith activity; one activity parameter needs to be fixed at unity for each member,

\(\mu_{n}^{\alpha }\) :

the influence of individual attributes on shape parameter \(\alpha_{hn}\); the parameter for one household member needs to be fixed at unity,

\(\mu_{ni}^{\beta }\) :

the influence of individual attributes on scale parameter \(\beta_{hni}\) of the ith activity; one activity parameter needs to be fixed at unity for each member,

\(\gamma_{k} ,\rho_{p} ,\kappa_{q}\) :

the parameters of relevant variables, and

\(\pi_{n}^{\alpha } ,\pi_{ni}^{\beta }\) :

constant terms.

Individual and household attributes may have different influences on a decision about the timing of each activity. Because these two types of attributes are common to all activities, their direct introduction to each timing function will considerably reduce the degree of freedom in the model estimation. To overcome this problem, as shown in the above equations, individual attributes are combined into one composite variable, and household attributes into another. These are then introduced into Eqs. (15.34) and (15.35). Table 15.1 shows household and individual attributes, and activity-specific attributes.

Table 15.1 Explanatory variables
Full size table

15.4.3 Model Estimation

15.4.3.1 Effectiveness of the Proposed Model

Estimation results are shown in Table 15.2. MacFadden’s Rho-squared is 0.4952. Most of the explanatory variables are statistically significant at the 99 % level, suggesting observed heterogeneity in household timing decisions. Most of the correlations and standard deviations related to sequential correlation are statistically significant. This supports the adoption of the bivariate normal distribution to represent sequential correlations. All these results suggest that the proposed model is good enough to represent household activity timing decision behavior in this case study.

Table 15.2 Model estimation resultsa
Full size table

15.4.3.2 Effect of the Shape Parameter on Timing Utility

Because the gamma probability density function is adopted as the timing utility function, an increase in the value of the shape parameter results in an increasing mean and variance of the timing distribution, and consequently the left-skewed timing distribution becomes flatter and moves toward the right-hand side of the time axis. In contrast, the scale parameter shows the opposite trend. In other words, if an explanatory variable has different signs for the shape and scale parameters, the timing distribution changes in a consistent way. If the signs of these parameters differ, the timing distribution varies with the difference in the scale/shape parameters of the same explanatory variable. Therefore, by interpreting the signs of the shape and scale parameters, the influences of various factors on timing distribution can be captured. Because the influences of the scale and shape parameters on timing distribution go in different directions, the meaning of each variable under study must be interpreted carefully. Note that the shape parameter is assumed to vary with household and member, but to be invariant across activities. The explanatory variables for the shape parameter are simply each member’s attributes, including car availability, bicycle availability, and official work hours per week. All these variables are statistically significant and have positive parameters. This means that when the scale parameter is fixed, the high availability of cars or bicycles and longer working hours result in a left-skewed timing utility function tending toward the right-hand side of the time axis. In other words, households with a high availability of cars or bicycles and longer working hours prefer to start activities later. On the other hand, the constant term for the scale parameter of the female timing utility function is significantly negative, implying that women prefer an early start to each activity.

15.4.3.3 Influential Factors of Coupling Constraints

This study derives the timing utility function for shared activities. This includes information on all the household members involved. Focusing on synchronized shared activities allows the endogenous representation of coupling constraints in the model. The influence of coupling constraints on each member’s activity timing decision is incorporated into the model with the aid of sequential correlations. In this case study, percentages of the shared activities are 3 and 3.5 % of the total sample for the fifth and sixth activities. Of course, such a small sample is insufficient to reveal the general decision-making mechanisms related to the timing of shared activities, but it is still useful to explore the influential factors of such decision-making mechanisms. The variables introduced to explain the shared activity timing decisions are simply each member’s attributes, because it is assumed that each member has a different preference for shared activities. The scale parameter is assumed to vary across household members.

The parameter \((\beta_{hni} )\), representing the influence of individual attributes on the scale parameter, shows positive values except for the wife’s sixth activity. This means that households with a greater availability of cars or bicycles and longer working hours prefer an earlier start for each activity. Because the shape and scale parameters play contrary roles in determining the timing utility, in general the actual preferences of each household can be only calculated by comparing shape and scale parameters. However, in this case, the wife’s sixth activity timing shows a consistent direction of variation for both parameters.

15.4.3.4 Influential Factors of Timing Decisions About the Nonshared Activity

Activity-specific attributes are activity types: in-home activities, out-of-home independent activities, and out-of-home allocated activities. The model estimates negative parameters for the first two types of activities, and positive parameters for the last activity. Negative scale parameters mean that household members prefer a later start for in-home activities and out-of-home independent activities. In contrast, a positive parameter pulls the timing distribution curve back from the right- to the left-hand side along the time axis.

  • Household attributes

Household attributes show a similar influence on the timing of both the husband and the wife: a positive parameter for the fifth activity and a negative parameter for the sixth activity. Because the parameters for single members with jobs, socioeconomic class and number of bicycles are negative, and the other parameters are all positive, these results show that households with a single employed member, higher socioeconomic class, and more bicycles tend to start the fifth activity later and the sixth activity earlier than do others. The degree of influence is stronger for the fifth activity of the husband, and for the sixth activity of the wife. Other attributes show the opposite influence.

  • Individual attributes

The estimated parameters of husband and wife attributes are positive for the fifth activity and negative for the sixth activity. Because all individual attributes, including car and bicycle availability and official work hours have positive parameters, households with greater availability of cars and bicycles and longer working hours tend to start the fifth activity earlier and the sixth activity later.

15.5 Conclusions and Future Research Issues

The utility of performing an activity or making a trip changes over time. When an individual makes decisions about the timings of activities/trips, he/she usually faces various constraints, for example, the existence of designated start (departure) and/or end (arrival) times (i.e., authority constraints). Timing decisions within a given period of time (e.g., a day) also interact across activities/trips. These mechanisms become much more complicated in the context of household decisions, where household members usually share a certain period of time to conduct some activities jointly and/or take trips together, and/or some members must take responsibility for household maintenance tasks such as shopping, and picking up and dropping off children. Coupling constraints are especially problematic in modeling household timing decisions because it is necessary to incorporate the preferences of all the members involved in decisions. Conventional modeling approaches have typically incorporated such coupling constraints exogenously, i.e., by treating the constraints as explanatory variables for decision-making. From the behavioral perspective, timing not only constrains other decision(s), but also involves decisions, just as other choices do. Therefore, it is necessary to represent the abovementioned mechanisms related to timing endogenously.

As a case study focusing on daily time use, this study first adopts a gamma probability density function to represent timing utility. Two types of timing functions are successfully derived: one for nonshared activities/trips and the other for shared activities/trips. The function for a nonshared activity/trip performed by a household member only includes information about a member, while that for a shared activity/trip includes information of all the household members involved. To incorporate interdependencies among activities/trips over a day, this study further introduces the concept of the first-order sequential correlation between error terms of timing functions of neighboring activities/trips based on a bivariate normal distribution. In theory, all the nonnegative conditions of timing variables, activity/trip sequencing, timing constraints, and censored timings can be endogenously represented based on the same bivariate normal distribution. Timing functions for shared activities/trips are used to represent a household’s coupling constraints endogenously by using sequential correlations related to all relevant members. The resulting household timing decision model can be estimated using the conventional maximum likelihood method.

The estimation results of the household timing model show that husbands and wives do not have homogeneous preferences for timing decisions. The factors explaining the shape and scale parameters of the gamma distribution reveal inconsistent influences of coupling constraints on the timing distribution. This not only reflects the complexities of household timing decisions, but also raises the question of how to justify the derived influences. However, it is not sufficient to justify this conclusion based on the data/model adopted in this study (i.e., internal validity). External validity is also required. In other words, the justification should also be based on external information.

Because the results obtained from this study are based on a limited sample size with only two successive activities on weekdays, future research must first estimate the model by collecting data from more people. Second, it is necessary to investigate how to select more suitable variables to explain timing decisions. In this study, we adopted a very limited set of variables including household and individual attributes and activity attributes. The explanatory power is insufficient. Selection of explanatory variables should be based on theoretical reasoning, rather than the availability of data. Third, different people may prefer to participate in different activities at different points in time, so a finer classification of activities may be helpful. A change in preferences may be also caused by space–time settings, such as a wish to avoid congestion on roads or at activity locations. Incorporating factors related to space–time settings seems important. There may exist various types of timing distributions. Even though the gamma probability density function has a general form of distribution, to reflect the actual timing distributions more properly it may be necessary to explore the possibility of applying other types of distributions such as the bell-shaped function (Joh et al. 2003). Because representing various timing constraints is one good feature of the derived household timing model, this should be examined in the future. This study adopted an additive-type utility function to represent timing decisions without weighting any activities/trips. In reality, people attach different levels of importance to each activity/trip, suggesting the necessity of introducing such weight parameters into the model. This study assumes one form of timing distribution. Depending on the types of activities/trips and their spatial–temporal constraints, the timing distributions may yield curves that are considerably different. The simultaneous representation of different timing distributions in the same modeling framework clearly generates new difficulties for model estimation. Therefore, a methodological breakthrough is expected to overcome the tradeoff between model complexity and operationalization. Finally, incorporating budget constraints could contribute to the improved measurement of the value of time over time, which is very important in the evaluation of transportation policy.