The Network Analysis of Transportation

Abstract

Since the deregulation of the airline market in 1978, airline networks have rapidly changed. During this time, regional carriers and low-cost carriers (LCCs) have entered or exited airline markets. According to Bamberger and Carlton [1], in 2003, LCCs other than Southwest entered 38 hub routes and 31 non-hub routes (Southwest entered only two non-hub routes). In the same year, major carriers entered 76 own hub routes, 40 other hub routes, and 216 non-hub routes.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Since the deregulation of the airline market in 1978, airline networks have rapidly changed. During this time, regional carriers and low-cost carriers (LCCs) have entered or exited airline markets. According to Bamberger and Carlton [1], in 2003, LCCs other than Southwest entered 38 hub routes and 31 non-hub routes (Southwest entered only two non-hub routes). In the same year, major carriers entered 76 own hub routes, 40 other hub routes, and 216 non-hub routes.

In Japan, the airline market was deregulated in 2000, after which new carriers entered. For example, Skymark Airlines entered the market in July 2000, Air-do in October 2000, and Solaseed Air (Skynet-Asia Airline) in May 2002. In this chapter, we examine a number of outstanding questions. Which routes do new carriers enter? How do incumbent carriers change their operating routes? Based on these interests, this chapter assumes that the incumbent carrier chooses the entry route in the first stage and that the new carrier chooses the entry route in the second stage to investigate which route each carrier enters.

Of the scarce literature on the carrier’s route problem, Lin and Kawasaki [8] assume that the entry route of the incumbent carrier is given and analyze which route, the hub route of the major carrier or the non-hub route, to enter. They demonstrate that the regional carrier has an incentive to enter the non-hub route in order to avoid competition with the incumbent carrier. Similar to Lin and Kawasaki [8], Kawasaki and Lin [7] assume that the incumbent entry route is given and analyze which route (the hub route or non-hub route of the incumbent carrier) to enter. However, the later study addresses the cost differential between incumbent carriers and entrants. As this cost differential increases from a small (large) basis, the new carrier strengthens its incentive to enter the incumbent’s hub (non-hub) route.

Although these two studies consider the new carrier’s entry route problem, they ignore the strategy of the incumbent carrier. To address this shortcoming, the present chapter addresses both the incumbent’s operating route and the entrant’s entry route. We imagine that if the incumbent expects the new carrier to enter its hub–spoke airline market , the incumbent may change its operating route. We also assume that three markets exist in this model and that the potential number of one market is smaller than that of the other two markets. In addition, the incumbent carrier has already entered one market, which has more potential passengers. Given this situation, each incumbent and entrant chooses only one entry route. That is, the incumbent carrier expects the entry route of the new carrier and chooses the entry route for the first time. Then, realizing the incumbent’s entry route, the new carrier chooses the entry route. Considering this situation, which network is formed in equilibrium?

Furthermore, this chapter interprets the selection of the hub airport by the incumbent carrier when it faces potential competition with the entrant carrier. With regard to the hub selection problem in a monopolistic market, Kawasaki [6] demonstrates that a monopolistic carrier does not always choose the hub to minimize the potential number of connecting passengers. Then, by considering the situation in which the incumbent faces competition with the entrant, do the same results as those presented by Kawasaki [6] appear? Finally, by comparing social welfare for each entry pattern, this chapter examines the socially preferable entry pattern.

The main results obtained in this chapter are as follows. The subgame perfect Nash equilibrium with regard to the entry route decision is described below. When the difference in the potential number of passengers between two markets is not small, the incumbent carrier (or the major carrier) enters a route that has a smaller potential number of passengers and the entrant carrier (or the regional carrier) enters a route that has a greater potential number of passengers. However, when this difference is small, both the major carrier and the regional carrier enter the route that has a smaller potential number of passengers.

From the viewpoint of social welfare, the following results are obtained. When the difference in the potential number of passengers between markets is not small, it is socially preferable that both major and regional carriers enter the route that has a smaller potential number of passengers. When this difference is small, it is socially preferable that the regional carrier enters the route that has a smaller potential number of passengers and the major carrier enters the route that has a greater potential number of passengers. Furthermore, by introducing the per-seat cost, this chapter re-analyzes the entry route problem and finds that when this cost is large, the major carrier does not enter the route that has a large potential number of passengers. That is, the major carrier chooses its entry route to decrease the number of connecting passengers.

The remainder of this chapter is organized as follows. In Sect. 10.2, we present the model. Section 10.3 analyzes the flight frequency and quantity of each carrier assuming a restrictive entry pattern. In Sect. 10.4, we compare each carrier’s demand with each entry pattern. Section 10.5 analyzes the entry route decision by the entrant carrier given the result obtained in Sect. 10.3. In Sect. 10.6, given the result presented in Sect. 10.5, we analyze the incumbent carrier’s entry route and derive the subgame perfect equilibrium. In Sect. 10.7, we derive the socially preferable entry pattern. In Sect. 10.8, we introduce the per-seat cost and discuss its influence. Section 10.9 concludes and discusses further research.

2 Model

Following Kawasaki and Lin [7] and Lin and Kawasaki [8], this chapter uses a model with three cities: A, B, and C. The individuals living in each city travel to other cities. All travel is assumed to be in the form of a round trip. There exist two carriers in this economy: a major carrier (or an incumbent carrier) that always uses a hub–spoke network¹ and a regional carrier (or an entrant carrier) that always uses city C’s airport and flies only one route. Hereafter, we call the former carrier airline M and the latter airline R.

Each carrier flies between each city pair. We express airline ℓ’s (ℓ = M, R) number of flights between cities i( = A, B, C) and j( = A, B, C,  i ≠ j) as f _ij ^ℓ. Each carrier incurs operating costs when flying between each city pair. In this chapter, following Kawasaki [6] and Kawasaki and Lin [7], we assume for simplicity that the per-seat cost is zero and the constant cost per flight is K.

The two carriers compete by simultaneously choosing the flight frequency and quantity (total traffic) of their market(s). Throughout our analysis, the airfares of airline ℓ ( = 1, 2) for each city pair ij (i, j = A, B, C,  i ≠ j) are represented as p _ij ^ℓ; the flight frequency and quantity of airline ℓ for city pair ij are represented as f _ij ^ℓ and q _ij ^ℓ, respectively.

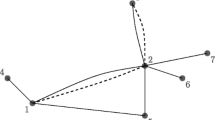
Before deciding its flight frequency and quantity, each carrier decides its operating routes. We assume that the major carrier always uses a hub–spoke network and operates on route AB, but chooses route BC or AC. On the contrary, we assume that the regional carrier operates on only one route and chooses route AC or BC. Figure 10.1 expresses the network structure used in this chapter.

Fig. 10.1

Network structure

Finally, following Kawasaki [5], Kawasaki [6], and Kawasaki and Lin [7], we assume that each flight has unlimited capacity.

2.1 Passengers’ Utility Function

Each passenger benefits from using airline services. Following Brueckner [2] and Kawasaki [6], we assume that total benefit is composed of the travel benefits and schedule delay cost .

We assume that the travel benefits derived from flight services vary among passengers. Here, a passenger’s travel benefit is expressed as w. Following Kawasaki [6], benefit w is assumed to be uniformly distributed between $[-\underline{W},\ W]$. We assume that a passenger who has $w = -\underline{W}$ heavily dislikes airline services and never flies on an aircraft. Furthermore, we assume that the density of benefit w is different between each city pair; the density in city pairs AB and AC is 1 and that in city pair BC is β( ≤ 1).

The waiting time of passengers using a carrier decreases when the carrier increases flight frequency. This additional convenience means that passengers’ benefits increase when flight frequency increases.² Hereafter, we call this effect the “scheduling effect ” and represent the reduction in the schedule delay cost (i.e., the benefit of the increased flight frequency) as $\sqrt{f}$.

We separately formulate the benefit function for connecting passengers because flight frequencies differ for each route. When passengers travel via the hub city, they must use two routes. Consequently, their convenience depends on the frequencies of both routes. Following Oum et al. [9], Flores-Fillol [4], and Kawasaki [6], we assume that the benefit of a one-stop service is the average of the two relevant frequencies.

In general, a connecting passenger’s travel time cost T when flying through the hub city might be higher than the one incurred if direct flights were available (see Brueckner [2]; Kawasaki [5]). However, when introducing this additional travel time cost, the calculation becomes burdensome. Therefore, this chapter omits this additional travel time cost. By ignoring this cost, the assumption that the major carrier adopts a hub–spoke network becomes rational.³

In the following analysis, we assume the following.

Assumption.

Connecting passengers do not change carriers at the hub airport.

The interpretation of this assumption is as follows. When connecting passengers change carriers at the hub airport, they incur heavy disutility from moving to a different terminal, repeating check-in procedures, or having to wait an excessively long time. Therefore, connecting passengers prefer connecting flights provided by the same carrier or an alliance member; hence, few passengers change carriers.⁴

Here, we assume that the airfare for the connecting flight is lower than the sum of the airfares for the two routes. This assumption ensures that connecting passengers do not purchase tickets for two routes. In the following analysis, this assumption always holds. As a result, the utility function is expressed as follows:

$$\displaystyle{ U_{ij=}\left \{\begin{array}{@{}l@{\quad }l@{}} w + \sqrt{f_{ij }^{\ell}} - p_{ij}^{\ell}\ \ \quad &\text{if traveling directly} \\ w + \frac{1} {2}(\sqrt{f_{ih }^{\ell}} + \sqrt{f_{jh }^{\ell}}) - p_{ij}^{\ell}\ \ \quad &\text{if traveling via hub city}\ h. \end{array} \right. }$$

(10.1)

The timeline of this game is as follows. In the first stage, the major carrier chooses its entry route. Then, the regional carrier decides its entry route. In the third stage, each carrier decides its flight frequency and quantity simultaneously.

3 The Decision on Flight Frequency and Quantity

This section analyzes the flight frequency and quantity decided by each carrier. Because the result depends on the entry route chosen by each carrier, we derive four cases.

3.1 Major Carrier Enters Route BC and Regional Carrier Enters Route AC

First, we assume that the major carrier enters route BC and the regional carrier enters route AC. Hereafter, we call this Case 1 (see Fig. 10.1a). In this case, markets AB and BC are monopolized by the major carrier; in market AC, the major carrier competes with the regional carrier. Therefore, each market’s demand function becomes as follows:

$$\displaystyle\begin{array}{rcl} & p_{AB}^{M} = W + \sqrt{f_{AB }^{M}} - q_{AB}^{M},&{}\end{array}$$

(10.2)

$$\displaystyle\begin{array}{rcl} & p_{BC}^{M} = W + \sqrt{f_{BC }^{M}} - q_{BC}^{M},&{}\end{array}$$

(10.3)

$$\displaystyle\begin{array}{rcl} & p_{AC}^{M} = W + \frac{1} {2}\left (\sqrt{f_{AB }^{M}} + \sqrt{f_{BC }^{M}}\right ) - (q_{AC}^{M} + q_{AC}^{R}),&{}\end{array}$$

(10.4)

$$\displaystyle\begin{array}{rcl} & p_{AC}^{R} = W + \sqrt{f_{AC }^{R}} - (q_{AC}^{M} + q_{AC}^{R}).&{}\end{array}$$

(10.5)

Consequently, the profit function of each carrier is

$$\displaystyle\begin{array}{rcl} & \pi _{M} = p_{AB}^{M}q_{AB}^{M} +\beta p_{BC}^{M}q_{BC}^{M} + p_{AC}^{M}q_{AC}^{M} - (f_{AB}^{M} + f_{BC}^{M})K,&{}\end{array}$$

(10.6)

$$\displaystyle\begin{array}{rcl} & \pi _{R} = p_{AC}^{R}q_{AC}^{R} - f_{AC}^{R}K.&{}\end{array}$$

(10.7)

By solving the profit maximization problem, we obtain the following flight frequency and quantity:

$$\displaystyle\begin{array}{rcl} f_{AB}^{M}& =& \left ( \frac{W(1 + 4K(-7 + 16K - 3\beta ) + 5\beta )} {(1 - 4K)(1 + 48K^{2} + 5\beta - 12K(2+\beta ))}\right )^{2},{}\end{array}$$

(10.8)

$$\displaystyle\begin{array}{rcl} f_{BC}^{M}& =& \left ( \frac{W(1 + 5\beta - 4K(1 + 3\beta ))} {1 + 48K^{2} + 5\beta - 12K(2+\beta )}\right )^{2},{}\end{array}$$

(10.9)

$$\displaystyle\begin{array}{rcl} f_{AC}^{R}& =& \left ( \frac{W(1 + 4K(-5 + 8K - 3\beta ) + 5\beta )} {(1 - 4K)(1 + 48K^{2} + 5\beta - 12K(2+\beta ))}\right )^{2},{}\end{array}$$

(10.10)

$$\displaystyle\begin{array}{rcl} q_{AB}^{M}& =& 2KW\left ( \frac{1} {-1 + 4K} + \frac{1} {1 + 48K^{2} + 5\beta - 12K(2+\beta )}\right ),{}\end{array}$$

(10.11)

$$\displaystyle\begin{array}{rcl} q_{BC}^{M}& =& \frac{2KW(-5 + 12K)} {1 + 48K^{2} + 5\beta - 12K(2+\beta )},{}\end{array}$$

(10.12)

$$\displaystyle\begin{array}{rcl} q_{AC}^{M}& =& \frac{4KW(-1 + 4K)} {1 + 48K^{2} + 5\beta - 12K(2+\beta )},{}\end{array}$$

(10.13)

$$\displaystyle\begin{array}{rcl} q_{AC}^{R}& =& 2KW\left ( \frac{1} {-1 + 4K} - \frac{4K} {1 + 48K^{2} + 5\beta - 12K(2+\beta )}\right ).{}\end{array}$$

(10.14)

Consequently, the maximized profits become as follows:

$$\displaystyle\begin{array}{rcl} \pi _{M}^{1}& =& KW^{2}\{(1+\beta )^{2} + 128K^{4}(13 + 9\beta ) - 2K(1 + 5\beta )(20 + 17\beta ) \\ & & -32K^{3}(50 + 9\beta (7+\beta )) + 8K^{2}(59 +\beta (143 + 48\beta ))\} \\ & & /(4K - 1)(1 - 24K + 48K^{2} + 5\beta - 12K\beta )^{2}, {}\end{array}$$

(10.15)

$$\displaystyle\begin{array}{rcl} \pi _{R}^{1}& =& \frac{KW^{2}\{1 + 4K(-5 + 8K - 3\beta ) + 5\beta \}^{2}} {(1 + 48K^{2} + 5\beta - 12K\beta )^{2}}.{}\end{array}$$

(10.16)

3.2 Major Carrier Enters Route BC and Regional Carrier Enters Route BC

In the following, we assume that both the major carrier and the regional carrier enter route BC. Hereafter, we call this Case 2 (see Fig. 10.1b). In this case, markets AB and AC are monopolized by the major carrier; in market BC, the major carrier competes with the regional carrier. Therefore, each market’s demand function becomes as follows⁵:

$$\displaystyle{ p_{BC}^{M} = W + \sqrt{f_{ BC}^{M}} - (q_{BC}^{M} + q_{BC}^{R}), }$$

(10.17)

$$\displaystyle{ p_{BC}^{R} = W + \sqrt{f_{ BC}^{R}} - (q_{BC}^{M} + q_{BC}^{R}), }$$

(10.18)

$$\displaystyle{ p_{AC}^{M} = W + \frac{1} {2}\left (\sqrt{f_{AB }^{M}} + \sqrt{f_{BC }^{M}}\right ) - q_{AC}^{M}. }$$

(10.19)

Consequently, the profit function of each carrier is

$$\displaystyle{ \pi _{M} = p_{AB}^{M}q_{ AB}^{M} +\beta p_{ BC}^{M}q_{ BC}^{M} + p_{ AC}^{M}q_{ AC}^{M} - (f_{ AB}^{M} + f_{ BC}^{M})K, }$$

(10.20)

$$\displaystyle{ \pi _{R} =\beta p_{BC}^{R}q_{ BC}^{R} - f_{ BC}^{R}K. }$$

(10.21)

By solving the profit maximization problem, we obtain the following flight frequency and quantity:

$$\displaystyle{ f_{AB}^{M} = \left ( \frac{W(-3K + 72K^{2} +\beta -46K\beta + 5\beta ^{2})} {192K^{3}\beta (1 + 5\beta ) - 8K^{2}(9 + 16\beta ) + K(3 + 4\beta (11 + 4\beta ))}\right )^{2}, }$$

(10.22)

$$\displaystyle{ f_{BC}^{M} = \left ( \frac{W(\beta +5\beta ^{2} + 8K^{2}(3 + 4\beta ) - K(3 + 2\beta (9 + 8\beta ))))} {192K^{3}\beta (1 + 5\beta ) - 8K^{2}(9 + 16\beta ) + K(3 + 4\beta (11 + 4\beta ))}\right )^{2}, }$$

(10.23)

$$\displaystyle{ f_{BC}^{R} = \left ( \frac{W\beta (1 + 32K^{2} + 5\beta - 16K(1+\beta ))} {192K^{3}\beta (1 + 5\beta ) - 8K^{2}(9 + 16\beta ) + K(3 + 4\beta (11 + 4\beta ))}\right )^{2}, }$$

(10.24)

$$\displaystyle{ q_{AB}^{M} = \frac{KW(96K^{2} - 64K\beta +\beta (-1 + 8\beta ))} {192K^{3}\beta (1 + 5\beta ) - 8K^{2}(9 + 16\beta ) + K(3 + 4\beta (11 + 4\beta ))}, }$$

(10.25)

$$\displaystyle{ q_{BC}^{M} = \frac{KW(-1 + 8K(-1 + 8K - 4\beta ) + 8\beta )} {192K^{3}\beta (1 + 5\beta ) - 8K^{2}(9 + 16\beta ) + K(3 + 4\beta (11 + 4\beta ))}, }$$

(10.26)

$$\displaystyle{ q_{AC}^{M} = \frac{2KW(-3 + 24K - 2\beta )(2K-\beta )} {192K^{3}\beta (1 + 5\beta ) - 8K^{2}(9 + 16\beta ) + K(3 + 4\beta (11 + 4\beta ))}, }$$

(10.27)

$$\displaystyle{ q_{BC}^{R} = \frac{2KW(1 + 32K^{2} + 5\beta - 16K(1+\beta )} {192K^{3}\beta (1 + 5\beta ) - 8K^{2}(9 + 16\beta ) + K(3 + 4\beta (11 + 4\beta ))}. }$$

(10.28)

Consequently, the maximized profits become as follows:

$$\displaystyle\begin{array}{rcl} \pi _{M}^{2}& =& KW^{2}\{2048K^{5}(9\,+\,2\beta )\,-\,2\beta ^{2}(1\,+\,5\beta )^{2}\,+\,K\beta (1\,+\,5\beta )(13 + 48\beta (3+\beta )) \\ & & -128K^{4}(63 + 40\beta (5+\beta )) + 16K^{3}(45 + 4\beta (155 +\beta (203 + 32\beta ))) \\ & & -2K^{2}(9 + 4\beta (88 +\beta (533 + 8\beta (45 + 4\beta )))\} \\ & & /\{192K^{3} -\beta (1 + 5\beta - 8K^{2}(9 + 16\beta ) + K(3 + 4\beta (11 + 4\beta ))\}^{2},{}\end{array}$$

(10.29)

$$\displaystyle\begin{array}{rcl} \pi _{M}^{2}& =& \frac{KW^{2}(4K-\beta )\beta (1 + 32K^{2} + 5\beta - 16K(1+\beta ))^{2}} {\{192K^{3} -\beta (1 + 5\beta ) + K(3 + 4\beta (11 + 4\beta ))\}^{2}}.{}\end{array}$$

(10.30)

3.3 Major Carrier Enters Route AC and Regional Carrier Enters Route AC

In this subsection, we assume that both the major carrier and the regional carrier enter route AC. Hereafter, we call this Case 3 (see Fig. 10.1c). In this case, markets AB and BC are monopolized by the major carrier; in market AC, the major carrier competes with the regional carrier. Therefore, each market demand function becomes as follows:

$$\displaystyle{ p_{BC}^{M} = W + \frac{1} {2}\left (\sqrt{f_{AB }^{M}} + \sqrt{f_{AC }^{M}}\right ) - q_{BC}^{M}, }$$

(10.31)

$$\displaystyle{ p_{AC}^{M} = W + \sqrt{f_{ AC}^{M}} - (q_{AC}^{M} + q_{AC}^{R}), }$$

(10.32)

$$\displaystyle{ p_{AC}^{R} = W + \sqrt{f_{ AC}^{R}} - (q_{AC}^{M} + q_{AC^{R }}). }$$

(10.33)

Consequently, the profit function of each carrier is

$$\displaystyle{ \pi _{M} = p_{AB}^{M}q_{ AB}^{M} +\beta p_{ BC}^{M}q_{ BC}^{M} + p_{ AC}^{M}q_{ AC}^{M} - (f_{ AB}^{M} + f_{ AC}^{M})K, }$$

(10.34)

$$\displaystyle{ \pi _{R} = p_{AC}^{R}q_{ AC}^{R} - f_{ AC}^{R}K. }$$

(10.35)

By solving the profit maximization problem, we obtain the following flight frequency and quantity:

$$\displaystyle{ f_{AB}^{M} = \left ( \frac{W(2(2+\beta ) + K(-32 - 17\beta + 24K(2+\beta )))} {-2(2+\beta ) + K(48 + 8K(-22 + 24K - 3\beta ) + 15\beta )}\right )^{2}, }$$

(10.36)

$$\displaystyle{ f_{AC}^{M} = \left ( \frac{W(2(2+\beta ) + K(-24 - 13\beta + 8K(4 + 3\beta )))} {-2(2+\beta ) + K(48 + 8K(-22 + 24K - 3\beta ) + 15\beta )}\right )^{2}, }$$

(10.37)

$$\displaystyle{ f_{AC}^{R} = \left ( \frac{2W(-1 + 4K)(-2 + 4K-\beta )} {-2(2+\beta ) + K(48 + 8K(-22 + 24K - 3\beta ) + 15\beta )}\right )^{2}, }$$

(10.38)

$$\displaystyle{ q_{AB}^{M} = \frac{KW(8 + 32K(-2 + 3K)-\beta )} {-2(2+\beta ) + K(48 + 8K(-22 + 24K - 3\beta ) + 15\beta )}, }$$

(10.39)

$$\displaystyle{ q_{BC}^{M} = \frac{KW(5 - 34K + 48K^{2})} {-2(2+\beta ) + K(48 + 8K(-22 + 24K - 3\beta ) + 15\beta )}, }$$

(10.40)

$$\displaystyle{ q_{AC}^{M} = \frac{KW(8 -\beta +8K(-6 + 8K+\beta )))} {-2(2+\beta ) + K(48 + 8K(-22 + 24K - 3\beta ) + 15\beta )}, }$$

(10.41)

$$\displaystyle{ q_{AC}^{R} = \frac{4KW(-1 + 4K)(-2 + 4K-\beta )} {-2(2+\beta ) + K(48 + 8K(-22 + 24K - 3\beta ) + 15\beta )}. }$$

(10.42)

Consequently, the maximized profits become as follows:

$$\displaystyle\begin{array}{rcl} \pi _{M}^{3}& =& 2KW^{2}\{ - 4(2+\beta )^{2} + 512K^{5}(13 + 9\beta ) + K(2+\beta )(144 + 61\beta ) \\ & & -64K^{4}(170 +\beta (124 + 9\beta )) - 8K^{3}(848 +\beta (663 + 94\beta )) \\ & & -K^{2}(2016 +\beta (1712 + 333\beta ))\} \\ & & /\{ - 2(2+\beta ) + K(48 + 8K(-22 + 24K - 3\beta ) + 15\beta ))\}^{2},{}\end{array}$$

(10.43)

$$\displaystyle\begin{array}{rcl} \pi _{R}^{3}& =& \frac{4KW^{2}(4K - 1)^{3}(2 - 4K+\beta )^{2}} {\{-2(2+\beta ) + K(48 + 8K(-22 + 24K - 3\beta ) + 15\beta ))\}^{2}}.{}\end{array}$$

(10.44)

3.4 Major Carrier Enters Route AC and Regional Carrier Enters Route BC

Finally, we assume that the major carrier enters route AC and the regional carrier enters route BC. Hereafter, we call this Case 4 (see Fig. 10.1d). In this case, markets AB and AC are monopolized by the major carrier; in market BC, the major carrier competes with the regional carrier. Therefore, each demand function becomes as follows:

$$\displaystyle{ p_{BC}^{M} = W + \frac{1} {2}\left (\sqrt{f_{AB }^{M}} + \sqrt{f_{AC }^{M}}\right ) - (q_{BC}^{M} + q_{ BC}^{R}), }$$

(10.45)

$$\displaystyle{ p_{BC}^{R} = W + \sqrt{f_{ BC}^{R}} - (q_{BC}^{M} + q_{BC}^{R}), }$$

(10.46)

$$\displaystyle{ p_{AC}^{N} = W + \sqrt{f_{ AC}^{M}} - q_{AC}^{M}. }$$

(10.47)

By solving the profit maximization problem, we obtain the following flight frequency and quantity:

$$\displaystyle{ f_{AB}^{M} = \left ( \frac{W(-\beta (2+\beta ) + 2K(3+\beta ))} {24K^{2} +\beta (2+\beta ) - 6K(1 + 2\beta )}\right )^{2}, }$$

(10.48)

$$\displaystyle{ f_{AC}^{M} = \left ( \frac{W(-\beta (2+\beta ) + 2K(3+\beta )))} {24K^{2} +\beta (2+\beta ) - 6K(1 + 2\beta )}\right )^{2}, }$$

(10.49)

$$\displaystyle{ f_{BC}^{R} = \left ( \frac{W\beta (-2 + 4K-\beta )} {24K^{2} +\beta (2+\beta ) - 6K(1 + 2\beta )}\right )^{2}, }$$

(10.50)

$$\displaystyle{ q_{AB}^{M} = \frac{KW(12K - 5\beta )} {24K^{2} +\beta (2+\beta ) - 6K(1 + 2\beta )}, }$$

(10.51)

$$\displaystyle{ q_{BC}^{M} = \frac{2KW(1 + 4K - 2\beta )} {24K^{2} +\beta (2+\beta ) - 6K(1 + 2\beta )}, }$$

(10.52)

$$\displaystyle{ q_{AC}^{M} = \frac{KW(12K - 5\beta )} {24K^{2} +\beta (2+\beta ) - 6K(1 + 2\beta )}, }$$

(10.53)

$$\displaystyle{ q_{BC}^{R} = \frac{2KW(-2 + 4K-\beta )} {24K^{2} +\beta (2+\beta ) - 6K(1 + 2\beta )}. }$$

(10.54)

Consequently, each carrier’s profit becomes as follows:

$$\displaystyle\begin{array}{rcl} \pi _{M}^{4}& =& 2KW^{2}\{ -\beta ^{2}(2+\beta )^{2} + 16K^{3}(9 + 2\beta (+K\beta (2+\beta )(13 + 12\beta ) \\ & & -4K^{2}(9 +\beta (32 + 9\beta ))\}/\{24K^{2} +\beta (2+\beta ) - 6K(1 + 2\beta )\}^{2},{}\end{array}$$

(10.55)

$$\displaystyle\begin{array}{rcl} \pi _{R}^{4}& =& \frac{KW^{2}(4K-\beta )\beta (2 - 4K+\beta )^{2}} {\{24K^{2} +\beta (2+\beta ) - 6K(1 + 2\beta )\}^{2}}.{}\end{array}$$

(10.56)

4 Comparison of the Number of Passengers

In this section, we compare the number of passengers by using each carrier in each market. Hereafter, we express case m’s number of passengers using airline ℓ in market ij as q _ij ^{ℓ m}.

4.1 Comparison of Airline M’s Number of Passengers

First, we present the comparison result of market AB. The following Lemma 10.1 shows the result.

Lemma 10.1.

When β ≤ 0.838127, q _AB ^M2 ≥ q _AB ^M1 ≥ q _AB ^M3 ≥ q _AB ^M4 holds. When β > 0.838127, q _AB ^M2 ≥ q _AB ^M3 ≥ q _AB ^M1 ≥ q _AB ^M4 holds.

First, the number of passengers using airline services depends on the flight frequency of the major carrier. In other words, a larger flight frequency increases demand throughout the larger scheduling effect . Therefore, we mainly discuss flight frequency.

In Case 1, route AB, which influences the number of passengers in market AB, has two markets: market AB is a monopoly for the major carrier and market AC is a duopoly for the major carrier. Here, the monopolistic market has larger marginal revenues of flight frequency than the duopolistic market. Furthermore, monopolistic market AB gives full-sized marginal revenues for flight frequency on route AB but duopolistic market AC gives smaller (i.e., half-sized) marginal revenues for it. Therefore, flight frequency becomes large.

In Case 2, route AB has markets AB and AC, which are both monopolies. Therefore, in Case 2, flight frequency depends on the marginal revenues of these two monopolistic markets. Therefore, flight frequency becomes very large.

In Case 3, route AB has markets AB and BC, which are both monopolies. Here, market BC has a smaller potential number of passengers (i.e., the density of market BC is smaller than that of the other markets). In Case 3, flight frequency depends on the marginal revenues of these two monopolistic markets, one of which has a smaller passenger density. Therefore, flight frequency becomes somewhat large.

In Case 4, route AB has market AB, which is a monopoly, and market BC, which is a duopoly. As mentioned above, because market BC has a smaller potential number of passengers, the marginal revenue from market BC becomes smaller than that from the duopoly market. Therefore, flight frequency becomes small.

From the above characteristics of each case, we see that Case 2’s scheduling effect is the largest and Case 4’s scheduling effect is the smallest among these four cases. Because the larger scheduling effect that arises from the larger flight frequency leads to a larger number of passengers, it is apparent that q _AB ^M2 is the largest among the four cases, while q _AB ^M4 is the smallest. On the contrary, the comparison result between q _AB ^M1 and q _AB ^M3 depends on β. When β is large, the marginal revenue from monopolistic market BC is larger than that from duopolistic market AC, which leads to a larger flight frequency on route AB for Case 3 than Case 1. Therefore, Case 3’s scheduling effect is larger than that of Case 1’s, resulting in q _AB ^M3 becoming larger than q _AB ^M3. Contrarily, when β is not large, the marginal revenue from duopolistic market AC is larger than that from monopolistic market BC, which makes Case 1’s flight frequency on route AB larger than that of Case 3. Consequently, Case 1’s scheduling effect is larger than that of Case 3, and thus q _AB ^M1 becomes larger than q _AB ^M3.

In the following, we present the comparison result of market AC. The following Lemma 10.2 shows the result.

Lemma 10.2.

When β ≤ 0.697224, q _AC ^M4 ≥ q _AC ^M2 ≥ q _AC ^M1 ≥ q _AC ^M3 holds. When β > 0.697224, q _AC ^M2 ≥ q _AC ^M4 ≥ q _AC ^M1 ≥ q _AC ^M3 holds.

To interpret this lemma, we note that the number of passengers in market AC depends on the flight frequency of both routes AB and BC in Case 1 and Case 2.

In Case 1, market AC is a competitive market. At the same time, as mentioned above, the number of passengers depends on flight frequency on routes AB and BC. There are two marginal revenues on both routes; one is a full-sized marginal revenue from the monopolistic market and the other is a half-sized marginal revenue from the duopolistic market. Furthermore, because the potential number of passengers in market BC is small compared with other markets, the marginal revenues from market BC become somewhat small.

In Case 2, market AC is a monopolistic market for the major carrier. In addition, as with Case 1, the number of passengers depends on the flight frequency of both routes AB and BC. On route AB, there exist two monopolistic markets, meaning that the marginal revenue on route AB is large. On the contrary, on route BC, there exist a duopolistic market that has full-sized marginal revenues and a monopolistic market that has half-sized marginal revenues. Additionally, market BC has a smaller potential number of passengers than the other markets. Therefore, flight frequency on this route becomes somewhat small.

In Case 3, market AC is a competitive market. On the contrary, different from Case 1, the number of passengers depends on only flight frequency on route AC. On route AC, there exist two marginal revenues: the full-sized marginal revenue from duopolistic market AC and the half-sized marginal revenue from monopolistic market BC. Additionally, market BC has a smaller potential number of passengers. Therefore, flight frequency on route AC becomes very small.

In Case 4, market AC is a monopolistic market. On the contrary, different from Case 2, the number of passengers depends on only flight frequency on route AC. Flight frequency on route AC has two marginal revenues. One is from monopolistic market AC and is full-sized. The other is from duopolistic market BC and is half-sized. Additionally, market BC has a smaller potential number of passengers than the other markets.

From the above characteristics of each case, we see that Case 3’s scheduling effect is the smallest among the four cases; hence, q _AC ^M3 is the smallest. Next, we discuss the other comparison results. First, however, market AC in Case 1 is a competitive market but its market in the other cases is a monopolistic market. Consequently, q _AC ^M1 becomes the smallest among the three cases (Cases 1, 2, and 4).

Finally, we discuss the comparison result between Cases 2 and 4. First, we consider the extreme case of β = 0. In Case 4, there are no connecting passengers; therefore, flight frequency on route AC depends only on the marginal revenue from market AC. Hence, flight frequency on route AC becomes very small. On the contrary, in Case 2, although flight frequency on route BC is small, that on route AB is very large. Therefore, Case 2’s scheduling effect becomes larger than that of Case 4. As a result, when β = 0, q _AC ^M2 is larger than q _AC ^M4. This characteristic holds when β is small. However, as β becomes very large, the reverse characteristic occurs. For example, we consider another extreme case that β = 1. Then, in Case 4, flight frequency on route AC is large and thus the scheduling effect for a passenger in market AC becomes large. On the contrary, in Case 2, flight frequency on route BC is very small; hence, the scheduling effect for a passenger in market AC becomes small. Consequently, when β = 1, q _AC ^M4 is larger than q _AC ^M2. This relationship holds when β is large.

In the following, we present the comparison result of market BC. The following Lemma 10.3 shows the result.

Lemma 10.3.

When β ≤ 0.982143, q _BC ^M3 ≥ q _BC ^M1 ≥ q _BC ^M4 ≥ q _BC ^M2 holds. When β > 0.982143, q _BC ^M1 ≥ q _BC ^M3 ≥ q _BC ^M4 ≥ q _BC ^M2 holds.

To interpret this lemma, we note that the number of passengers in market BC depends on the flight frequency of both routes AB and AC in Case 3 and Case 4. Additionally, this lemma’s interpretation is similar to that of Lemma 10.2.

In Case 1, market BC is a monopolistic market. In addition, the number of passengers depends on flight frequency on route BC. Flight frequency on route BC has two marginal revenues. One is from monopolistic market BC, which has full-sized marginal revenue, and the other is from duopolistic market AC, which has half-sized marginal revenue. Furthermore, the potential number of passengers in market BC is smaller than that in the other markets.

In Case 2, market BC is a competitive market. In addition, the number of passengers depends on flight frequency on route BC. Flight frequency on route BC has two marginal revenues. One is from duopolistic market BC, which has full-sized marginal revenue, and the other is from monopolistic market AC, which has half-sized marginal revenue.

In Case 3, market BC is a monopolistic market. At the same time, as mentioned earlier, the number of passengers depends on flight frequency on both routes AB and AC. On route AB, there are two monopolistic markets. Therefore, flight frequency on route AB becomes very large. On route AC, there are two markets. One is duopolistic market AC, which has full-sized marginal revenue, and the other is monopolistic market BC, which has half-sized marginal revenue. Therefore, flight frequency becomes small.

In Case 4, market BC is a competitive market. At the same time, the number of passengers depends on flight frequency on both routes AB and AC. Here, there are two markets on each route. One is a monopolistic market that has full-sized marginal revenue and the other is a duopolistic market that has half-sized marginal revenue. Therefore, the flight frequency on each route is somewhat large.

From the above characteristics of each case, we see that Case 2’s scheduling effect is the smallest among the four cases. Consequently, q _BC ^M2 is the smallest. In addition, among the other three cases, market BC faces competition in Case 4. Consequently, q _BC ^M4 becomes the smallest among the three cases.

Finally, we compare Case 1 with Case 3. First, we consider the extreme case of β = 1. Then, in Case 3, although flight frequency on route AC is not large, flight frequency on route AB becomes very large. Consequently, by comparing with Case 1, we see that Case 3’s scheduling effect becomes large for a passenger in market BC. Therefore, q _BC ^M3 is larger than q _BC ^M1. This result holds in the range within which β is sufficiently large. Contrarily, in the range within which β is not sufficiently large, the reverse result occurs. In Case 3, as β decreases, flight frequency on route AC decreases; hence, the scheduling effect for a passenger in market BC becomes small. Although Case 1’s scheduling effect also decreases, this becomes larger than that for Case 3 in the range within which β is not sufficiently large. Therefore, q _BC ^M1 becomes larger than q _BC ^M3.

4.2 Comparison of Airline R’s Number of Passenger

Finally, we show the comparison result for airline R’s number of passengers. The following Lemma 10.4 shows the result.

Lemma 10.4.

When β ≤ 0.685546, q _AC ^R3 ≥ q _AC ^R1 ≥ q _BC ^R2 ≥ q _BC ^R4 holds. When β > 0.685546, q _AC ^R3 ≥ q _BC ^R2 ≥ q _AC ^R1 ≥ q _BC ^R4 holds.

Because airline R always faces competition with airline M, this competition influences the comparison results. Therefore, we first discuss airline M’s flight frequency and then airline R’s flight frequency and the number of passengers.

In Case 1, airline M and airline R compete with each other in market AC. As mentioned in the above subsection, the major carrier’s number of passengers in market AC depends on flight frequency on the two routes, AB and BC. On both routes, the flight frequency of airline M has both a monopolistic market that has full-sized marginal revenue and a duopolistic market that has half-sized marginal revenue. Additionally, the competitive market has a smaller potential number of passengers than the other market. Therefore, the flight frequency of airline M has somewhat large marginal revenues, meaning that the flight frequency of airline M becomes somewhat large. Contrarily, the flight frequency of airline R is somewhat small due to the small marginal revenue.

In Case 2, they compete with each other in market BC. The major carrier’s number of passengers in market BC depends on route BC’s flight frequency. Its flight frequency has two marginal revenues. One is from duopolistic market BC that has full-sized marginal revenue and the other is from monopolistic market AC that has half-sized marginal revenue. Therefore, the flight frequency of airline M has somewhat small marginal revenue; hence, the flight frequency of airline M becomes somewhat small. Contrarily, the flight frequency of airline R somewhat increases.

In Case 3, they compete with each other in market AC. The major carrier’s number of passengers in market AC depends on route AC’s flight frequency. Its flight frequency has two marginal revenues. One is from duopolistic market AC that has full-sized marginal revenue and the other is from monopolistic market BC that has half-sized marginal revenue. Therefore, the marginal revenues of airline M become small and thus the flight frequency of airline M becomes small. Contrarily, the flight frequency of airline R increases.

In Case 4, they compete with each other in market BC. As mentioned in the above subsection, the major carrier’s number of passengers in market BC depends on the flight frequency of two routes, AB and AC. On both routes, the flight frequency of airline M has both a monopolistic market that has full-sized marginal revenue and a duopolistic market that has half-sized marginal revenue. Additionally, the monopolistic market’s potential number of passengers is larger than that of the duopolistic market. Therefore, flight frequency on both routes is very large, meaning that the scheduling effect of airline M becomes very large. On the contrary, because of the larger scheduling effect of airline M, airline R loses more passengers.

From the above characteristics and assumption that market BC has a lower potential number of passengers than markets AB and AC, it is apparent that q _BC ^R4 is the smallest among the four cases. Therefore, q _AC ^R3 is larger than q _BC ^R2. Additionally, by comparing Case 1 with Case 3, because airline M’s scheduling effect in Case 1 is larger than that in Case 3 due to the larger marginal revenues in Case 1, we see that q _AC ^R3 becomes larger than q _AC ^R1. Consequently, q _AC ^R3 is the largest among the four cases. Finally, we discuss the comparison result of Case 1 and Case 2. First, we consider the extreme case that β = 1. In this extreme case, the potential number of passengers in each market is the same. By comparing Case 1’s scheduling effect of airline M in market AC with Case 2’s scheduling effect of airline M in market BC, because airline M has larger marginal revenues in Case 1 than in Case 2, we see that Case 1’s scheduling effect in market AC is larger than Case 2’s scheduling effect in market BC for airline M. Therefore, q _AC ^M1 is larger than q _BC ^M2. Because the number of passengers in the competitive market has a strategic substitution relationship, q _AC ^R1 < q _BC ^R2 holds. Given this result, as β decreases, because the potential number of passengers decreases, q _BC ^R2 largely decreases. Consequently, when β is small, q _AC ^R1 > q _BC ^R2 holds.

5 Entry Route Decision by the Regional Carrier

In this section, we analyze the route that the regional carrier enters. Hereafter, without loss of generality, we assume K = 1.

5.1 Given that the Major Carrier Enters Route BC

First, we derive the entry route decision by the regional carrier given that the major carrier enters route AC. By comparing π _R ¹ and π _R ², we obtain Lemma 10.5.

Lemma 10.5.

Given that the major carrier enters route BC, if the potential number of passengers in market BC (i.e., the density of w in market BC) is larger than 0.853, the regional carrier enters route BC. Otherwise, it enters route AC.

This mechanism is similar to that presented in Kawasaki and Lin [7]. If the regional carrier enters route AC, the major carrier becomes a monopoly in both AB and BC markets, which strengthens its scheduling effect. Because of the very high scheduling effect of the major carrier, the regional carrier loses passengers in market AC. On the contrary, if the regional carrier enters route BC, although the major carrier becomes a monopoly in both AB and AC markets, the influence of market AB (as a monopoly) disappears on route BC. Therefore, the regional carrier does not suffer from the major carrier’s strong scheduling effect compared with the case of entering route AC.

On the contrary, in market BC, the potential number of passengers is smaller than that in market AC. Therefore, if the regional carrier enters route BC, it loses passengers. In other words, the regional carrier has an incentive to enter route AC.

Considering the above trade-off, if β is smaller than 0.853, the latter effect is larger than the former. Consequently, the regional carrier enters route AC. In other words, although the regional carrier suffers from the major carrier’s strong scheduling effect , it does not want to lose potential passengers. If β is larger than 0.853, the former effect is larger than the latter. That is, the regional carrier does not want to compete with the major carrier, which has a strong scheduling effect.

5.2 Given that the Major Carrier Enters Route AC

In the following, we derive the entry route decision by the regional carrier given that the major carrier enters route AC. By comparing π _R ³ and π _R ⁴, we obtain Lemma 10.6.

Lemma 10.6.

Given that the major carrier enters route AC, the regional carrier always enters route AC.

When the major carrier enters route AC, the entry route decision by the regional carrier is different from the case that the major carrier enters route BC. In this case, if the regional carrier enters route BC, it suffers from the major carrier’s strong scheduling effect as mentioned earlier. Furthermore, because the potential number of passengers in market BC is smaller than that in market AC, the regional carrier weakens the incentive to enter route BC. Consequently, in this case, the regional carrier always enters route AC.

6 Entry Route Decision by the Major Carrier

In the previous section, we analyzed the regional carrier’s reaction to the major carrier’s decision in the first stage. Given the above results, this section derives which route (AC or BC) the major carrier enters in the first stage.

6.1 The Case that β ≤ 0. 853

In this case, the regional carrier always enters route AC if the major carrier enters route BC or AC. Therefore, by comparing π _M ¹ with π _M ³, we obtain Lemma 10.7.

Lemma 10.7.

The major carrier enters route BC in the range within which β is smaller than 0.853.

Intuitively, because the potential demand of market BC is small, we expect the major carrier to enter route AC. However, Lemma 10.7 demonstrates that our expectation is violated. In this range, the regional carrier originally has no incentive to enter route BC. Then, if the major carrier enters route BC, it has a large scheduling effect. On the contrary, if it enters route AC, its scheduling effect becomes somewhat weak due to competition in market AC.⁶ Here, noting that the larger scheduling effect brings about larger profits, the major carrier enters route BC. Thus, the major carrier chooses the entry route to seek competitive advantage.

6.2 The Case that β ≥ 0. 853

In this case, if the major carrier enters route BC, the regional carrier also enters route BC; if the major carrier enters route AC, the regional carrier also enters route AC. Therefore, by comparing π _M ¹ with π _M ⁴, we obtain Lemma 10.8.

Lemma 10.8.

The major carrier enters route BC in the range within which β is larger than 0.853.

In this case, the regional carrier enters the same route as the major carrier. Therefore, the major carrier cannot achieve competitive advantage throughout the larger scheduling effect even when it enters route AC or BC. In the following, the major carrier is unwilling to compete with the regional carrier in the market that has a large potential number of passengers. In other words, the major carrier does not want to compete in market AC. The major carrier realizes that if it enters route AC, the regional carrier enters route AC; if it enters route BC, the regional carrier enters route BC. Therefore, to avoid competition in market AC, which has a large potential number of passengers, the major carrier enters route BC.

By summarizing Lemmas 10.5–10.8, we obtain Theorem 10.9, which is the subgame perfect Nash equilibrium of the entry route decision game.

Theorem 10.9.

The subgame perfect Nash equilibrium with regard to the entry route decision is that the major carrier enters route BC and the regional carrier enters route AC (i.e., Case 1) for β ≤ 0.853, while both the major carrier and the regional carrier enter route BC (i.e., Case 2) for β ≥ 0.853.

Here, we discuss the hub location in the competitive situation. In Kawasaki [6], it was concluded that the monopolistic carrier does not always choose the hub airport to minimize the potential number of connecting passengers. This chapter demonstrated that when the major carrier and entrant carrier compete with each other, the former does not choose the hub airport to minimize the potential number of connecting passengers.

In the monopolistic situation, because the carrier wants to strengthen the scheduling effect, the hub airport is not chosen to minimize the potential number of connecting passengers. On the contrary, in the competitive situation, if the potential number of BC passengers is small, to retain competitive advantage, the major carrier does not choose the hub airport to minimize the potential number of connecting passengers. Moreover, if it is not small, to avoid competition in the market that has a larger potential number of passengers, the major carrier does not choose the hub airport to minimize the potential number of connecting passengers. Summarizing, although the objective is different for the monopolistic and competitive situations, the major carrier’s strategy does not change in the competitive situation.

7 Social Welfare

In this section, we derive and compare social welfare in each case. Assuming that K = 1, the social welfare of each case becomes as follows:

$$\displaystyle{ SW_{1} = \frac{7W^{2}(997 + 7\beta (-20+\beta ))} {9(25 - 7\beta )^{2}}, }$$

(10.57)

$$\displaystyle{ SW_{2} = \frac{W^{2}(38412 +\beta (-35197 +\beta (4805 + 2224\beta - 294\beta ^{2})))} {2(123 +\beta (-85 + 11\beta ))^{2}}, }$$

(10.58)

$$\displaystyle{ SW_{3} = \frac{W^{2}(4016 +\beta (1038 - 79\beta )} {(60 - 11\beta )^{2}}, }$$

(10.59)

$$\displaystyle{ SW_{4} = \frac{W^{2}(360 -\beta (146 +\beta (85 + 3\beta (-14+\beta ))))} {(18 +\beta (-10+\beta ))^{2}}. }$$

(10.60)

We first find that SW ₃ is always smaller than SW ₁. In the following, we compare the other levels of social welfare. As a result, we can obtain Fig. 10.2. As a result, we obtain Theorem 10.10.

Fig. 10.2

Comparison result of social welfare

Theorem 10.10.

When β is smaller than 0.9657711, the case that both the major carrier and the regional carrier enter route BC (i.e., Case 2) is socially preferable. When β is larger than 0.9657711, the case that the major carrier enters route AC and the regional carrier enters route BC (i.e., Case 4) is socially preferable.

Theorem 10.10 argues that the regional carrier should always enter route BC, which has a smaller potential number of passengers, from the viewpoint of social welfare. On the contrary, the socially preferable entry route of the major carrier depends on β. First, we discuss the case that β is larger than 0.9657711. In this range, when both carriers enter the same route, the flight frequency of the major carrier on its route becomes small. Consequently, the scheduling effect of the major carrier becomes small. Hence, the larger scheduling effect brings about larger demand and larger utility. Therefore, as the scheduling effect of the major carrier decreases, its demand decreases and the utility of using the major carrier also decreases. Consequently, the case that both carriers enter the same route is not socially preferable in this range.

Furthermore, the case that the major carrier enters route BC and the regional carrier enters route AC is also not socially preferable. In the market that has a greater potential number of passengers, by allowing the major carrier to operate monopolistically, the flight frequency of the major carrier increases. As a result, more passengers can enjoy the larger scheduling effect. If the major carrier enters route BC and the regional carrier enters route AC, the flight frequency of the major carrier becomes somewhat small due to the small potential demand of market BC, meaning no more passengers enjoy the larger scheduling effect. Consequently, the case that the major carrier enters route AC and the regional carrier enters route BC is socially preferable in this range.

On the contrary, in the range within which β is smaller than 0.9657711, the socially preferable case differs. In this range, because the potential number of passengers in the BC market is small, even when a passenger in market BC uses connecting services, the larger scheduling effect hardly occurs. Consequently, to bring about a larger scheduling effect, a passenger in market AC should use connecting services. On the contrary, if the major carrier and regional carrier compete with each other in market AC, demand for the major carrier decreases; thus, the flight frequency of the major carrier decreases, which decreases the major carrier’s scheduling effect. Therefore, to avoid competition in market AC, the regional carrier should enter route BC from the viewpoint of social welfare.

8 Extension

The above analysis assumed that the per-seat cost is zero. However, according to Brueckner [2] and others, this cost is also important for expressing economies of density, which is an important characteristic in the airline industry. Therefore, following Brueckner [2], we introduce the per-seat cost and re-analyze each carrier’s entry route problem.

Following Brueckner [2], this chapter denotes the per-seat cost as τ, which is common to both carriers. To satisfy a positive quantity, we assume that 0 ≤ τ ≤ 1∕3. Then, when expressing the number of seats per flight as s _ℓ , the carrier’s operating cost per flight is $C_{\ell} = K +\tau s_{\ell}$. Because airline ℓ flies f _ℓ times on one route, the total cost on one route becomes $f_{\ell} \times C_{\ell} = f_{\ell}K +\tau s_{\ell}f_{\ell}$. Here, because it is assumed that the load factor equals 100 %, the total number of passengers on one route always equals the total number of seats ( ≡ s _ℓ × f _ℓ ). Therefore, each carrier’s cost on one route can be expressed as f _ℓ K +τ Q _ℓ , where Q _ℓ denotes the total number of passengers on one route.

From the above discussion, each carrier’s profit function becomes as follows:

$$\displaystyle{ \pi _{M} =\beta _{ih}(p_{ih}^{M}-\tau )q_{ ih}^{M}+\beta _{ jh}(p_{jh}^{M}-\tau )q_{ jh}^{M}+\beta _{ ij}(p_{ij}^{M}-2\tau )q_{ ij}^{M}-(f_{ ih}^{M}+f_{ jh}^{M})K, }$$

(10.61)

$$\displaystyle{ \pi _{R} =\beta _{mn}(p_{mn}^{R}-\tau )q_{ mn}^{R} - f_{ mn}^{R}K. }$$

(10.62)

Here, i, h, j ≡ A, B, C (i ≠ j ≠ h), and m, n ≡ A, B, C (m ≠ n). Additionally, $\beta _{AB} =\beta _{AC} = 1$ and β _BC  = β. By solving each profit maximization problem by quantity and flight frequency as in Sect. 10.3, we obtain the profit-maximizing quantity and flight frequency. Here, we omit the detailed values.

Then, by using the profit-maximizing values, we obtain each case’s profits. Here, we assume that $K = W = 1$. In the following, we denote Case s’s profit of carrier ℓ as π _ℓ ^s

$$\displaystyle\begin{array}{rcl} \pi _{M}^{1}& =& \left \{14(71 + 8 - 7\beta )\beta ) + 4\tau (-866 +\beta (43 + 49\beta ))\right. \\ & & \left.+\tau ^{2}(3946 + (-1049+\beta )\beta )\right \}/3(25 - 7\beta )^{2}{}\end{array}$$

(10.63)

$$\displaystyle\begin{array}{rcl} \pi _{R}^{1}& =& \frac{((13 - 7\beta ) +\tau (11+\beta ))^{2}} {3(25 - 7\beta )^{2}},{}\end{array}$$

(10.64)

$$\displaystyle\begin{array}{rcl} \pi _{M}^{2}& =& \{\beta (-12275 + (37510 - 31211\tau )\tau ) +\beta ^{3}(-84 + (1058 - 1493\tau )\tau ) \\ & & +11\beta ^{4}(-6 +\tau (8+\tau )) + 738(15 +\tau (-44 + 35\tau )) \\ & & +\beta ^{2}(3815 +\tau (-13152 + 12133\tau ))\}/(123 +\beta (-85 + 11\beta ))^{2},{}\end{array}$$

(10.65)

$$\displaystyle\begin{array}{rcl} \pi _{R}^{2}& =& \frac{\beta (4-\beta )(17 + 11\beta (-1+\tau ) - 14\tau )^{2}} {(123 +\beta (-85 + 11\beta ))^{2}},{}\end{array}$$

(10.66)

$$\displaystyle\begin{array}{rcl} \pi _{M}^{3}& =& \frac{\begin{array}{l} 1632(-1+\tau )^{2} - +2\beta ^{2}(-2 + 3\tau )(-50 + 119\tau ) \\ \qquad + 4\beta (257 + 31\tau (-35 + 4\tau )) \end{array} } {(60 - 11\beta )^{2}},{}\end{array}$$

(10.67)

$$\displaystyle\begin{array}{rcl} \pi _{R}^{3}& =& \frac{27(4(1-\tau ) +\beta (-2 + 3\tau ))^{2}} {(60 - 11\beta )^{2}},{}\end{array}$$

(10.68)

$$\displaystyle\begin{array}{rcl} \pi _{M}^{4}& =& \{432 - 4\beta (70 +\beta (3 + (-8+\beta )\beta ) - 864\tau + 4\beta (20 +\beta (104 \\ & & +\beta (-41 + 4\beta )))\tau + (432 +\beta (488 +\beta (-596 + 3(58 - 5\beta )\beta ))\tau ^{2}\} \\ & & /((2(18 + (-10+\beta )\beta )^{2}), {}\end{array}$$

(10.69)

$$\displaystyle\begin{array}{rcl} \pi _{R}^{4}& =& \frac{\beta (4-\beta )(2 +\beta (-4+\tau )+\tau )^{2}} {(18 + (-10+\beta )\beta )^{2}}.{}\end{array}$$

(10.70)

The comparison results of π _R ¹ with π _R ² and of π _R ³ with π _R ⁴ are shown in Fig. 10.3.

Fig. 10.3

The comparison results of π _R ¹ with π _R ² and of π _R ³ with π _R ⁴

Given these comparison results, we derive the major carrier’s entry route. In range (a), we compare π _M ¹ with π _M ³. As a result, we find that when τ is large (small), π _M ³ is larger (smaller) than π _M ¹. In range (b), we compare π _M ¹ with π _M ¹ with π _M ⁴. As a result, we find that π _M ⁴ is always larger than π _M ¹. In range (c), we compare π _M ² with π _M ³. As a result, we find that π _M ² is always larger than π _M ³. Consequently, we obtain Fig. 10.4, which denotes the subgame perfect Nash equilibrium of each range.

Fig. 10.4

Subgame perfect Nash equilibrium

When τ is small, the result obtained in Sect. 10.6 now holds. However, as τ becomes large, the equilibrium drastically changes as follows. When introducing the per-seat cost τ, the major carrier does not want to increase the number of connecting passengers because these incur the per-seat cost twice. Actually, in range (a) in Fig. 10.3, when τ is small, the major carrier enters route BC to increase the number of connecting passengers and the scheduling effect. However, as τ increases, the major carrier does not enter route BC, and alternatively enters route AC to decrease the number of connecting passengers. In range (b), even airline R does not want to increase costs. Consequently, if airline M enters route AC, airline R chooses to enter route BC to decrease costs. At the same time, when airline M enters route BC in this range, more passengers use connecting services. Consequently, to avoid more passengers using connecting services, airline M enters route AC even though the scheduling effect decreases.

9 Concluding Remarks

This chapter examined which routes (i.e., those having a large or a small potential number of passengers) major and entrant carriers enter as well as the socially preferable entry pattern. To address these problems, we assumed that three markets exist in this model and that the potential number of one market is smaller than that of the other two markets. Moreover, the incumbent carrier has already entered the market that has a greater potential number of passengers. Given this situation, each incumbent and entrant carrier chooses only one entry route. First, the incumbent carrier expects the entry route of the entrant carrier and chooses the entry route for the first time. Then, realizing the incumbent’s entry route, the entrant carrier chooses its entry route. By considering this situation, this chapter derived the subgame perfect Nash equilibrium with regard to the entry route of each carrier.

A number of findings can be drawn. When the potential number of passengers in a market is large, both the major carrier and the entrant carrier enter the same route (i.e., the one that has a small potential number of passengers). When the potential number of passengers in its market is not large, the major carrier enters the route that has the small potential number of passengers and the entrant carrier enters the route that has the large potential number of passengers. This result can be interpreted as that the major carrier does not choose the hub airport to minimize the potential number of connecting passengers in a competitive situation.

From the viewpoint of social welfare, the following results were obtained. When the difference in the potential number of passengers between markets is not small, it is socially preferable for both the major and the regional carrier to enter the route that has a smaller potential number of passengers. When its difference is small, however, it is socially preferable for the regional carrier to enter the route that has a smaller potential number of passengers and the major carrier to enter the route that has a greater potential number of passengers.

Furthermore, by introducing the per-seat cost, we derived the subgame perfect Nash equilibrium. We found that if the per-seat cost is small, the same result as obtained earlier holds; however, if this cost becomes large, different results occur. Thus, to avoid an increase in operating costs, a major carrier does not choose the entry route to increase the number of connecting passengers.

Finally, we discuss the limitations of this chapter. First, it omitted the difference in operating costs between the major carrier and the entrant carrier. Recently, new carriers are mainly LCCs. Therefore, future research should discuss how this cost difference influences the results obtained here. Second, this chapter omitted the additional travel time cost for connecting passengers. Many studies of airline network formation argue that the additional travel time cost is also important for network formation. With regard to this shortcoming, this chapter also ignored the probability of adopting a point-to-point network. Assuming that there is no additional travel time cost meant that omitting the point-to-point network is rational. However, if an additional travel time cost is introduced, the point-to-point network should also be considered. Finally, this chapter assumed that the entrant carrier enters only one route. Future research might consider these important problems.