Abstract
Combining rewriting modulo an equational theory and SMT solving introduces new challenges in the area of term rewriting. One such challenge is unification of terms in the presence of equations and of uninterpreted and interpreted function symbols. The interpreted function symbols are part of a builtin model which can be reasoned about using an SMT solver. In this article, we formalize this problem, that we call unification modulo builtins. We show that under reasonable assumptions, complete sets of unifiers for unification modulo builtins problems can be effectively computed by reduction to usual E-unification problems and by relying on an oracle for SMT solving.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
A recent line of work [1, 3, 5,6,7, 11, 16, 17, 20] aims at combining rewriting modulo E with SMT solving. The goal is to enable the modelling and analysis of systems beyond what is possible by rewriting modulo E or by SMT solving alone. The unifying idea among the approaches above is that rewriting is constrained by some logical formula and that it also involves elements like integers, reals, bitvectors, arrays, etc. that are handled by the SMT solver. As an example, consider the following constrained rewrite system computing the Collatz sequence:
The rewrite system above reduces a state of the form \(\textsf {n} \mapsto N\), where N is a natural number, to a final state of the form \(\textsf {result} \mapsto C\), where C is the number of steps taken by N to reach 1 in the Collatz transformation. If the Collatz conjecture is false, then \(\textsf {n} \mapsto N\) does not necessarily terminate.
The symbols appearing in the rewrite system are the following: 1. \(\_ \mapsto \_\) (the underscore denotes the place of an argument) is a two-argument free symbol, and \(\textsf {n}, \textsf {cnt},\textsf {result}\) are free constants; 2. \(\_ , \_\) is an ACI symbol (making, e.g., \(\textsf {cnt} \mapsto 0, \textsf {n} \mapsto N\) the same as \(\textsf {n} \mapsto N, \textsf {cnt} \mapsto 0\)); 3. N, C are integer variables and the symbols \(\times , +, >, 0, 1, 2, \ldots \) have their usual mathematical interpretation.
Unification modulo builtins is motivated by the computation of the possible successors of a term with variables in a constrained rewrite system such as the one above. Assuming that we are in a symbolic state of the form \(\textsf {cnt} \mapsto C' + N', \textsf {n} \mapsto N' + 3\), which of the four constrained rewrite rules above could be applied to this state? To answer this question, we should first solve the following equations:
Solving such an equation is E-unification modulo builtins. Whereas usual (E-)unification is solving an equation of the form \(t_1 =t_2\) in the algebra of terms (or in the quotient algebra of terms in the case of E-unification), E-unification modulo builtins is solving an equation of the form \(t_1 =t_2\) in an algebra combining three types of symbols: 1. free symbols (such as \(\_ \mapsto \_\)), 2. symbols satisfying an equational theory E (such as \(\_, \_\), satisfying ACI) and 3. builtin symbols such as integers, bitvectors, arrays or others (handled by an SMT solver).
Unlike regular syntactic unification problems (or E-unification problems), where the solution to a unification problem is a unifier (or complete set of unifiers), the solution to an E-unification modulo builtins problem is a logical constraint. We provide an algorithm that reduces E-unification modulo builtins to usual E-unification. As an example, consider the third equation above:
As the symbol \(\_, \_\) is commutative, the equation reduces to solving the builtin constraint \(2 \times N = N' + 3 \wedge C = C' + N'\) (for example, by relying on the SMT solver). We show that any E-unification modulo builtins problem reduces to a set of logical constraints involving only builtin symbols, plus some substitutions in the range of which there are only non-builtin symbols. Our approach works for any set of builtins, not just integers.
Contributions. 1. We formalize the problem of E-unification modulo builtins, which appears naturally in the context of combining rewriting and SMT solving; 2. We define the notions of E-unifier modulo builtins, which generalizes the usual notion of E-unifier, and of complete set of E-unifiers; 3. We propose an algorithm for the problem of E-unification modulo builtins, which works by reduction to regular E-unification problems, given an oracle for SMT solving; 4. The algorithm not only decides E-unification modulo builtins, but it can also construct a complete set of E-unifiers modulo builtins; 5. We prove that the algorithm is correct and we also implement the algorithm as a Maude prototype.
Related Work. Our algorithm relies on abstractions of terms, various forms of which have been known for a long time and used, for example, in algorithms for combining decision procedures for theories in [15]. The abstractions of terms used here were defined and used for the first time in [2] for automatically obtaining a symbolic execution framework for a given program language definition. In parallel, abstractions were used in [17] for rewriting modulo SMT, where a builtin equational theory is used instead of the data sub-signature and its model. Both approaches use an SMT solver to check satisfiability of the constraints. In [1], Aguirre et al. introduce narrowing for proving reachability in rewriting logic enriched with SMT capabilities. In [20], Skeirik et al. extend the idea from [14] and show how Reachability Logic (defined in [8]) can be generalized to rewrite theories with SMT solving and how safety properties can be encoded as reachability properties. In [17], Rocha et al. were the first to combine rewriting and SMT solving in order to model and analyze an open system; they solve a particular case of the problem of E-unification modulo builtins that can be reduced to matching. In [5], Bae and Rocha introduce guarded terms, which generalize constrained terms. Logically constrained term rewriting systems (LCTRSs), which combine term rewriting and SMT constraints are introduced in [11, 13]. LCTRSs generalize previous formalisms like TRSs enriched with numbers and Presburger constraints (e.g., as in [10]) by allowing arbitrary theories that can be handled by SMT solvers. Early ideas on adding constraints to deduction rules in general and unification in particular date back to the 1990s, with articles such as [9, 12]. Mixed terms, defined in [9], are similar to our terms that mix free symbols with builtins, except that in [9] builtins are treated as constants. Constrained unification, introduced in [9] as a particular type of constrained deduction, can be seen as a sound and complete (but not necessarily terminating) proof system for a special case of E-unification modulo builtins, where the equational theory E is empty. Additionally, in both [9] and [12], it is assumed that constraints always have a solved form, assumption that is critical in order to present the deduction rules. As we do not make this assumption, and only rely on off-the-shelf SMT solvers, our approach is more general from this point of view. Our work can be seen in the abstract as a combination of E-unification and SMT solving, similar to combinations of unification algorithms for (disjoint) theories (e.g., as in [4, 19]).
Organization. In Sect. 2 we formalize constrained terms, which occur naturally in rewriting modulo builtins. Section 3 introduces the concept of E-unification modulo builtins and the notion of (complete set of) E-unifiers. In Sect. 4 we present an algorithm for solving E-unification modulo builtins by reduction to usual E-unification. Section 5 concludes the paper and provides possible directions for future work.
2 Constrained Terms
We first formalize builtins, which represent the parts of the model handled by an SMT solver. This section extends our formalism introduced in [6] by the presence of an equational theory E and by the introduction of defined operations.
Definition 1
(Builtin Signature). A builtin signature \({\varSigma }^\mathsf{b}\triangleq ({S}^\mathsf{b},{F}^\mathsf{b})\) is any many-sorted signature that includes the following distinguished objects: 1. a sort \( Bool \), together with two constants \(\top \) and \(\bot \) of sort \( Bool \); 2. the propositional operation symbols \(\lnot : Bool \rightarrow Bool \), \(\wedge ,\vee ,\rightarrow {}: Bool \times Bool \rightarrow Bool \) and 3. an equality predicate symbol \({=}:s\times s\rightarrow Bool \) for each sort \(s\in {S}^\mathsf{b}\).
Example 1
We consider the builtin signature \(\varSigma ^{ INT} = (S^{ INT}, F^{ INT})\), where \(S^{ INT} = \{ Bool , Int , Arr , Id \}\) and \(F^{ INT} \) includes, in addition to the required symbols (boolean connectives \(\lnot , \wedge , \vee \), boolean constants \(\top \) and \(\bot \) and the equality predicates for \( Bool \) and \( Int \)), the following function symbols:
When working over this builtin signature, we take the liberty to write terms using infix notation for function symbols, so that \(x+y\) is a term of sort \( Int \) and \(x + y \le z\) is a term of sort \( Bool \) whenever x, y and z are of sort \( Int \). We also use infix notation for the boolean operations: \(\lnot b, a \wedge b, a \vee b, a \rightarrow b\).
Definition 2
(Builtin Model). A builtin model \({M}^\mathsf{b}\) is a model of a builtin signature \({\varSigma }^\mathsf{b}\), where the interpretation of the distinguished objects of the builtin signature is fixed as follows: \({M}^\mathsf{b}_{ Bool } = \{ \top , \bot \}, {M}^\mathsf{b}_\top =\top \), \({M}^\mathsf{b}_\bot =\bot , {M}^\mathsf{b}_{ =}(a,b)=\top \) iff \(a=b\), \({M}^\mathsf{b}_\lnot (\top )=\bot , {M}^\mathsf{b}_\lnot (\bot )=\top \), \({M}^\mathsf{b}_\wedge (\top ,b)={M}^\mathsf{b}_\wedge (b,\top )=b\), \({M}^\mathsf{b}_\wedge (\bot ,b)={M}^\mathsf{b}_\wedge (b,\bot )=\bot \), and so on.
Example 2
Continuing Example 1, we consider the builtin model \(M^{ INT} \) that interprets \( Bool \) as required in Definition 2, the sort \( Int \) as the set of integers: \(M^{ INT} _ Int = \mathbb {Z}\), the sort \( Id \) as the set of identifiers (strings) and the sort \( Arr \) as the set of arrays, where both the indices and the values are integers. The builtin model \(M^{ INT} \) also interprets \(+, \times , \textit{mod}\) and \(\le \) as expected: integer addition, integer multiplication, remainder (defined arbitrarily when the divisor is 0) and respectively the less-than-or-equal relation on integers. The symbol \( get\) is interpreted as the selection of an array element from a given index, and \( put\) is interpreted as the update of an array on a given index with a new given element. First-order logical constraints over this model can be solved by an SMT solver implementing the theories of integers, booleans and arrays.
Next, we introduce a formalization of terms extended with builtins.
Definition 3
(Signature Modulo a Builtin Model). A signature modulo a builtin model is a tuple \(\varSigma \triangleq (S,\le , F,{M}^\mathsf{b})\) consisting of 1. an order-sorted signature \((S, \le , F)\), and 2. a builtin \({\varSigma }^\mathsf{b}\)-model \({M}^\mathsf{b}\), where \({\varSigma }^\mathsf{b}\triangleq ({S}^\mathsf{b},{F}^\mathsf{b})\) is a builtin subsignature of \((S,\le , F)\), and 3. the set \(F\setminus {F}^\mathsf{b}\) is partitioned into two subsignatures: constructors \({F}^\mathsf{c}\) and defined operations \({F}^\mathsf{d}\) such that \({F}^\mathsf{c}_{w,s}=\emptyset \) for each \(s\in {S}^\mathsf{b}\).
We further assume that the only builtin constant symbols in \(\varSigma \) are the elements of the builtin model, i.e., \({F}^\mathsf{b}_{\varepsilon ,s}={M}^\mathsf{b}_s\). \({\varSigma }^\mathsf{b}\) is called the builtin subsignature of \(\varSigma \) and \({\varSigma }^\mathsf{c}=(S,\le , {F}^\mathsf{c}\cup \bigcup _{s\in {S}^\mathsf{b}}{F}^\mathsf{b}_{\varepsilon ,s})\) the constructor subsignature of \(\varSigma \).
Terms over only one of the builtin subsignature and respectively constructor subsignature are pure. Terms mixing both constructors and builtins have the builtins as alien terms. Due to the restrictions on builtins, we cannot arbitrary nest of builtins and constructors, as is the case when combining arbitrary disjoint signatures (in our case, constructors cannot occur under builtins).
Example 3
We consider the signature \(\varSigma = (S, \le , F, M^{ INT})\), where the set of sorts \(S = \{ Id , Int , Bool , Arr , Val , State \}\) consists of the four builtin sorts \( Int , Bool , Id \) and \( Arr \), together with the additional sorts \( State \) and \( Val \), where the subsorting relation \({\le } = \{ Int \le Val , Arr \le Val \}\subseteq S \times S\), and where the set of function symbols F includes, in addition to the builtin symbols in \(F^{ INT} \), the following function symbols:

The set \({F}^\mathsf{c}\) of constructor symbols consists of the symbols defined by the first three declarations above and the set of defined symbols is \({F}^\mathsf{d}=\{ keyOcc \}\).
Note that a ground term t defined on the constructor subsignature has the property that any of its builtin subterms is an element of \({\varSigma }^\mathsf{b}_{\varepsilon ,s}={M}^\mathsf{b}_s\). In the rest of this section, \(\varSigma = (S,\le , F,{M}^\mathsf{b})\) denotes a signature modulo a builtin model.
Definition 4
(Model \(M^\varSigma \) Generated by a Signature Modulo a Builtin Model). Let \(\varSigma \triangleq (S,\le ,F,{M}^\mathsf{b})\) be a signature modulo a builtin model. The model \({M}^\mathsf{b}\) is extended to a \((S,\le ,F)\)-model \(M^\varSigma \), defined as follows: 1. \(M^\varSigma _s=T_{{\varSigma }^\mathsf{c},s}\) for each \(s\in S\setminus {S}^\mathsf{b}\), i.e. \(M^\varSigma _s\) includes the constructor terms; 2. \(M^\varSigma _f={M}^\mathsf{b}_f\) for each \(f\in {F}^\mathsf{b}\); 3. \(M^\varSigma _f\) is the term constructor \(M^\varSigma _f(t_1,\ldots ,t_n) = f(t_1,\ldots ,t_n)\) for each \(f\in {F}^\mathsf{c}\); 4. \(M^\varSigma _f\) is a function \(M^\varSigma _f:M^\varSigma _{s_1}\times \cdots \times M^\varSigma _{s_n}\rightarrow M^\varSigma _s\) for each \(f\in {F}^\mathsf{d}_{s_1\ldots s_n,s}\).
Note that elements of the carrier sets of \(M^\varSigma \) are ground terms of the appropriate sort over the signature \(\varSigma \) (as mentioned earlier, builtin elements are constants in \(\varSigma \)). We make the standard assumption that \(M_s\not =\emptyset \) for any \(s\in S\). Since the defined function symbols can be interpreted in various ways, it follows that \(M^\varSigma \) is not uniquely defined, but its carrier sets are uniquely defined by the builtin model and the constructors.
Example 4
Continuing Example 3, we consider the model \(M^\varSigma \) obtained by extending \(M^{ INT} \). We have that \(M^\varSigma _ Val =M^\varSigma _ Int \cup M^\varSigma _ Arr , M_ State \) is the set of finite sets of the form \(\{x_1\mapsto v_1,\ldots ,x_n\mapsto v_n\}\) with \(n > 0, x_i\in M^\varSigma _ Id \) and \(v_i\in M^\varSigma _ Val \) for \(i=1,\ldots ,n, M^\varSigma _{\_{\mapsto }\_}(X,Y)\) is the singleton set \(\{X\mapsto Y\}\), and \(M^\varSigma _{\_{,}\_}(S_1,S_2)\) is the union of the sets \(S_1\) and \(S_2\).
The defined function \(M^\varSigma _{ keyOcc}\) is recursively defined as follows:
where \(\delta \) is the Kronecker delta. We consider a set E of identities such as associativity, commutativity or idempotence for certain function symbols in \(\varSigma \). We let \(\cong \) to be the equivalence relation induced by E on \(M^\varSigma \). We make the assumption that \(\cong \) is a congruence on \(M^\varSigma \), i.e., that it is compatible with the functions, including the defined ones. We define \(M^\varSigma _{\cong }\triangleq M^\varSigma \!\!/{\cong }\) to be the quotient algebra induced by the congruence \(\cong \) on \(M^\varSigma \).
Example 5
Continuing Example 4, we consider the model \(M^\varSigma \). Let E consist of the ACI identities for the operation \({\_{,}\_}\). We have that the equivalence relation \(\cong \) induced by E on \(M^\varSigma \) is a congruence.
Definition 5
(Constraint Formulas). The set \(\mathrm{CF}(\varSigma , \mathcal {X})\) of constraint formulas over variables \(\mathcal {X}\) is inductively defined as follows:
where b ranges over \(T_{\varSigma , Bool }(\mathcal {X}), t_i\) over \(T_{\varSigma ,s_i}(\mathcal {X})\).
That is, the constraints are the usual formulas in first-order logic with equality. The only non-standard feature, which does not restrict generality, is that we use terms of sort \( Bool \) as atomic formulas. The role of predicates is played by functions returning \( Bool \). As usual, we may also use the following formulas defined as sugar syntax: 1. \(t_1\not =t_2\) for \(\lnot (t_1 =t_2)\), 2. \(\forall x.\phi \) for \(\lnot \exists x.\lnot \phi \), 3. \(\forall X.\phi \) for \(\forall x_1.\ldots .\forall x_n.\phi \), where \(X=\{x_1,\ldots ,x_n\}\), 4. \(\phi _1\vee \phi _2\) for \(\lnot (\lnot \phi _1\wedge \lnot \phi _2)\), 5. \(\phi _1\rightarrow \phi _2\) for \(\lnot \phi _1\vee \phi _2\). We denote by \( var (\phi )\) the set of variables freely occurring in \(\phi \).
Example 6
The following formulas are in \( \mathrm{CF}(\varSigma , \mathcal {X})\):
We have \( var (\phi _1) = \{ N, A \}, var (\phi _2) = \{ S \}\) and \( var (\phi _3) = \{ N \}\), assuming that \(\{ I, U, V, N \} \subseteq \mathcal {X}_ Int , A\in \mathcal {X}_ Arr \), and \(X\in \mathcal {X}_ Id \).
Definition 6
(Semantics of Constraint Formulas). The satisfaction relation \(\vDash \) is inductively defined over the model \(M^\varSigma _{\cong }\), valuations \(\alpha : \mathcal {X}\rightarrow M^\varSigma _{\cong }\), and formulas \(\phi \in \mathrm{CF}(\varSigma , \mathcal {X})\), as follows:
-
1.
\(M^\varSigma _{\cong },\alpha \vDash b\) iff \(\alpha (b) = \top \), where \(b \in T_{\varSigma ,\textit{Bool}}(\mathcal {X})\);
-
2.
\(M^\varSigma _{\cong },\alpha \vDash t_1 =t_2\) iff \(\alpha (t_1)=\alpha (t_2)\);
-
3.
\(M^\varSigma _{\cong },\alpha \vDash \exists \, x.\phi \) iff \(\exists a \in M_s\) (where \(x \in \mathcal {X}_s\)) such that \(M^\varSigma _{\cong },\alpha [x \mapsto a] \vDash \phi \);
-
4.
\(M^\varSigma _{\cong },\alpha \vDash \lnot \phi \) iff \(M^\varSigma _{\cong },\alpha \not \vDash \phi \);
-
5.
\(M^\varSigma _{\cong },\alpha \vDash \phi _1\wedge \phi _2\) iff \(M^\varSigma _{\cong },\alpha \vDash \phi _1\) and \(M^\varSigma _{\cong },\alpha \vDash \phi _2\),
where \(\alpha [x \mapsto a]\) denotes the valuation \(\alpha '\) defined by \(\alpha '(y)=\alpha (y)\), for all \(y\not =x\), and \(\alpha '(x)=a\).
Example 7
Continuing the previous example, the formula \(\phi _3\) is satisfied by the model \(M^\varSigma _{\cong }\) defined in Example 5 and any valuation \(\alpha \) such that \(\alpha (N)\) is a composite number.
Definition 7
(Builtin Constraint Formulas). The set \(\mathrm{CF}^b(\varSigma , \mathcal {X})\) of builtin constraint formulas over the variables \(\mathcal {X}\) is the subset of \(\mathrm{CF}(\varSigma , \mathcal {X})\) defined inductively as follows:
where b ranges over \(T_{\varSigma ^b, Bool }(\mathcal {X}), t_i\) over \(T_{\varSigma ,s}(\mathcal {X})\) such that s is a builtin sort, and x ranges over all variables of builtin sort.
Note that in builtin constraint formulas, no symbol that is not builtin is allowed. The constraint formulas \(\phi _1, \phi _3\) in the previous example are builtin.
Definition 8
(Constrained Terms). A constrained term \(\varphi \) of sort \(s\in S\) is a pair  with \(t\in T_{\varSigma ,s}(\mathcal {X})\) and \(\phi \in \mathrm{CF}(\varSigma ,\mathcal {X})\).
with \(t\in T_{\varSigma ,s}(\mathcal {X})\) and \(\phi \in \mathrm{CF}(\varSigma ,\mathcal {X})\).
Let \(\mathrm{CT}(\varSigma ,\mathcal {X})\) denote the set of constrained terms defined over the signature \(\varSigma \) and the variables \(\mathcal {X}\).
Example 8
In the context of the previous examples, we have the following constrained terms in \(\mathrm{CT}(\varSigma , \mathcal {X})\): 1. arrays with N nonnegative values:  2. legal states, where an \( Id \) is bound to at most one value:
2. legal states, where an \( Id \) is bound to at most one value:  3. states where the \( Id \) n is bound to a composite integer:
3. states where the \( Id \) n is bound to a composite integer:  .
.
Definition 9
(Valuation Semantics of Constraints). The valuation semantics of a constraint \(\phi \) is the set of valuations \(\lfloor \!\!\lfloor {\phi }\rfloor \!\!\rfloor \triangleq \{\alpha :\mathcal {X}\rightarrow M^\varSigma _{\cong }\mid M^\varSigma _{\cong },\alpha \vDash \phi \}\).
Definition 10
(Semantics of Constrained Terms). The semantics of a constrained term  is defined by
is defined by

Note that the semantics of constrained terms cannot distinguish between constrained terms with different sets of free variables.
3 E-Unification Modulo Builtins
We discuss as an example the four E-unification modulo builtin problems in the Introduction:
-
1.
\(\textsf {n} \mapsto N =\textsf {cnt} \mapsto C' + N', \textsf {n} \mapsto N' + 3\)
Even if the \(\_,\_\) symbol is ACI, there are no values of \(N, N', '\) that make the lhs equal to the rhs (even if \(C' + N' = N' + 3\), the atoms \(\textsf {cnt} \mapsto C' + N'\) and respectively \(\textsf {n} \mapsto N' + 3\) cannot be identified by the idempotence axiom because \(\textsf {n}\) and \(\textsf {cnt}\) are two different \( Id \)entifiers). Therefore, the solution to this E-unification problem is \(\bot \) (false), i.e., there is no solution.
-
2.
\(\textsf {n} \mapsto 2 \times N + 1, \textsf {cnt} \mapsto C =\textsf {cnt} \mapsto C' + N', \textsf {n} \mapsto N' + 3\)
There are values for \(N, C, N', C'\) that make the terms above equal. In particular, any values that satisfy \(C' + N' = C \wedge N' + 3 = 2 \times N + 1\) make the terms equal. Therefore, the constraint \(C' + N' = C \wedge N' + 3 = 2 \times N + 1\) is the solution of the E-unification problem.
-
3.
\(\textsf {n} \mapsto 2 \times N, \textsf {cnt} \mapsto C =\textsf {cnt} \mapsto C' + N', \textsf {n} \mapsto N' + 3\)
Similar to the case above, the solution is \(C' + N' = C \wedge N' + 3 = 2 \times N\).
-
4.
\(\textsf {n} \mapsto 1, \textsf {cnt} \mapsto C =\textsf {cnt} \mapsto C' + N', \textsf {n} \mapsto N' + 3\)
The constraint \(N' + 3 = 1 \wedge C' + N' = C\) makes the two terms equal and is the solution to the E-unification problem.
It is helpful to split the solution to a E-unification modulo builtins problem into two parts: a substitution and a logical constraint:
Definition 11
(E-Unifiers Modulo Builtins). An E-unifier modulo builtins (E-umb) of two terms \(t_1, t_2\) is a pair \(u = (\sigma , \phi )\), where \(\sigma \) is a substitution and \(\phi \) is a builtin constraint, such that
Note that we require \(\phi \) to be a builtin constraint (see Definition 7), not just a constraint. In particular, \(\phi \) is not allowed to contain any non-builtin symbols. This requirement allows to handle \(\phi \) by using an SMT solver. If \(\phi \) is unsatisfiable, then \((\sigma , \phi )\) is vacuously an E-unifier of any two terms.
Definition 12
(Complete Set of E-Unifiers Modulo Builtins). A set C of pairs of substitutions and builtin logical constraints is called a complete set of E -unifiers of \(t_1\) and \(t_2\) if:
-
1.
each pair \((\sigma , \phi ) \in C\) is an E-umb of \(t_1\) and \(t_2\): \(M^\varSigma _{\cong } \vDash \phi \rightarrow \sigma (t_1) = \sigma (t_2)\);
-
2.
for any partial valuation \(\alpha : var (t_1, t_2) \rightarrow M^\varSigma _{\cong }\) such that \(\alpha (t_1) = \alpha (t_2)\), there is an E-unifier \((\sigma , \phi ) \in C\) and a valuation \(\alpha ^r\) such that \(M^\varSigma _{\cong }, \alpha ^r \vDash \phi \) and \(\alpha = {(\alpha ^r \circ \sigma )}|_{ var (t_1,t_2)}\).
Example 9
Consider the E-unification modulo builtins problem \(\textsf {n} \mapsto 1, \textsf {cnt} \mapsto C =\textsf {cnt} \mapsto C', \textsf {n} \mapsto N'\). A complete set of E-unifiers modulo builtins is the singleton set \(\{(\textit{id}, C = C' \wedge 1 = N')\}\), where \(\textit{id}\) denotes the identity substitution.
Example 10
Consider the E-unification modulo builtins problem
A complete set of E-unifiers modulo builtins is
Example 11
Consider the E-unification modulo builtins problem
A complete set of E-unifiers modulo builtins is the singleton set
where \(\textit{dom}(\sigma ) = \{ M \}\) and \(\sigma (M) = I \mapsto N\).
4 An Algorithm for E-Unification Modulo Builtins
We propose an algorithm that computes, given two terms \(t_1\) and \(t_2\) without any defined operation symbols, a finite and complete set of E-unifiers modulo builtins of \(t_1\) and \(t_2\), assuming that a finitary E-unification algorithm exists. The algorithm critically relies on the notion of abstraction. In order to formally introduce abstractions, we first require a technical helper definition:
Definition 13
(Substitutions as Formulas). Each substitution \(\sigma :\mathcal {X}\rightarrow T_\varSigma (\mathcal {X})\) defines a constraint formula \(\phi ^\sigma =\bigwedge _{x\in dom (\sigma )}x =\sigma (x)\).
Intuitively, an abstraction of a term t is a pair \((s, \sigma )\) such that \(t = \sigma (s)\), where all subterms of builtin sorts have been “moved” from s into the substitution \(\sigma \), and where the domain of \(\sigma \) consists of fresh variables. Formally:
Definition 14
(Abstractions). An abstraction of a term \(t\in T_{\varSigma \setminus {\varSigma }^\mathsf{d}}(\mathcal {X})\) w.r.t. Y, where \( var (t)\subseteq Y\), is a constrained term  , where the pair \((t^\circ ,\sigma ^\circ )\) is inductively defined as follows: – if \(t\in T_{{\varSigma }^\mathsf{b}(\mathcal {X})}\) (i.e., t is a builtin subterm), then \(t^\circ \) is a fresh variable w.r.t. Y and \(\sigma ^\circ (t^\circ )=t\); – if \(t=f(t_1,\ldots ,t_n)\) and \(f\in \varSigma \setminus {\varSigma }^\mathsf{b}\), then \(t^\circ =f(t_1^\circ ,\ldots ,t_n^\circ )\) and \(\sigma ^\circ =\sigma _1^\circ \uplus \cdots \uplus \sigma _n^\circ \), where
, where the pair \((t^\circ ,\sigma ^\circ )\) is inductively defined as follows: – if \(t\in T_{{\varSigma }^\mathsf{b}(\mathcal {X})}\) (i.e., t is a builtin subterm), then \(t^\circ \) is a fresh variable w.r.t. Y and \(\sigma ^\circ (t^\circ )=t\); – if \(t=f(t_1,\ldots ,t_n)\) and \(f\in \varSigma \setminus {\varSigma }^\mathsf{b}\), then \(t^\circ =f(t_1^\circ ,\ldots ,t_n^\circ )\) and \(\sigma ^\circ =\sigma _1^\circ \uplus \cdots \uplus \sigma _n^\circ \), where  is the abstraction of \(t_i\) w.r.t.
is the abstraction of \(t_i\) w.r.t.  (i.e. each argument \(t_i\) has its own fresh variables).
(i.e. each argument \(t_i\) has its own fresh variables).
In Definition 14, we assume for simplicity that any occurrence of a builtin term is replaced by a fresh variable. Therefore, two different occurrences of the same builtin term are abstracted by two different variables. However, this is not critical to the soundness of our approach: all results in the paper hold, even if the same abstracting variable is used for several occurrences of the same builtin term.

Algorithm 1 computes a complete set of E-unifiers. Note that, if \(x \in {\mathcal {X}}^\mathsf{b}\) is a builtin variable, then \(\tau _i(x)\) can only be a builtin variable (by the construction of the abstraction). Due to our assumptions on the builtin sorts, any builtin variable can only be unified with another builtin variable. Therefore builtin variables are treated by the E-unification algorithm used on Line 5 of Algorithm 1 as real variables, and not as free constants. As an optimization of the algorithm, any pair \((\tau _i', \phi _i')\) can be dropped (without losing completeness) if \(\phi _i'\) is unsatisfiable.
Algorithm 1 produces a complete set of E-unifiers modulo builtins. By Definition 11, any satisfiable instance \(\alpha (\phi _i')\) of a constraint \(\phi _i'\) induces the concrete E-umb \(\alpha (\tau _i')\) of \(t_1\) and \(t_2\). Therefore, two terms are E-unifiable modulo builtins iff at least one of the constraints \(\phi _i'\) in the result of Algorithm 1 is satisfiable.
Example 12
Consider the E-unification modulo builtins problem
Let \(t_1 = \textsf {n} \mapsto 1, \textsf {cnt} \mapsto 42\) and \(t_2 = Z, \textsf {n} \mapsto 1\). Let \((s_1, \sigma _1)\) be an abstraction of \(t_1\) defined as follows: \(s_1 = I \mapsto N, J \mapsto M\) and \(\sigma _1(I) = \textsf {n}, \sigma _1(N) = 1, \sigma _1(J) = \textsf {cnt}, \sigma _1(M) = 42\). Let \((s_2, \sigma _2)\) be an abstraction of \(t_2\) defined as follows: \(s_2 = Z, K \mapsto L\) and \(\sigma _2(K) = \textsf {n}\) and \(\sigma _2(L) = 1\). A complete set of ACI-unifiers of \(s_1\) and \(s_2\) is the set \(\{ \tau _1, \tau _2 \}\), where:
-
1.
\( dom (\tau _1) = \{ Z, K, L \}\) and \(\tau _1(Z) = I \mapsto N\), \(\tau _1(K) = J, \tau _1(L) = M\) (the first mapping in \(s_1\) is identified to the first mapping in \(s_2\) and the second mapping in \(s_1\) to the second mapping in \(s_2\));
-
2.
\( dom (\tau _2) = \{ Z, K, L \}\) and \(\tau _2(Z) = J \mapsto M\), \(\tau _2(K) = I, \tau _2(L) = N\) (the first mapping in \(s_1\) is identified to the second mapping in \(s_2\) and the second mapping in \(s_1\) to the first mapping in \(s_2\));
The case where all four mappings are identified is subsumed by any of the two cases. For this example, the algorithm computes \((\tau _i', \phi _i')\) as follows:
-
1.
 is
is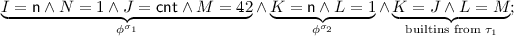
-
2.
 is
is
The algorithm returns the complete set \(\{ (\tau _1', \phi _1'), (\tau _2', \phi _2') \}\) of E-unifiers modulo builtins of the terms \(t_1 = \textsf {n} \mapsto 1, \textsf {cnt} \mapsto 42\) and \(t_2 = Z, \textsf {n} \mapsto 1\). As \(\phi _1'\) is unsatisfiable, the first unifier can be pruned away and therefore \(\{ (\tau _2', \phi _2') \}\) is also a complete set of unifiers of \(t_1 = \textsf {n} \mapsto 1, \textsf {cnt} \mapsto 42\) and \(t_2 = Z, \textsf {n} \mapsto 1\).
The next result shows that Algorithm 1 is correct:
Theorem 1
The set \(\{(\tau _1', \phi _1'), \ldots , (\tau _n', \phi _n')\}\) computed by Algorithm 1 is a complete set of E-unifiers modulo builtins of \(t_1\) and \(t_2\).
Proof
(Sketch). Let \(t_1\) and \(t_2\) be two terms without defined function symbols.
Let  be an abstraction of \(t_1\).
be an abstraction of \(t_1\).
Let  be an abstraction of \(t_2\).
be an abstraction of \(t_2\).
Let \(\{ \tau _1, \ldots , \tau _n \}\) be a complete set of E-unifiers of \(s_1\) and \(s_2\).
Let \(\tau _i' = \tau _i|_{\mathcal {X}\setminus {X}^\mathsf{b}}\). Let \(\phi _i' = \phi ^{\sigma _1} \wedge \phi ^{\sigma _2} \wedge \bigwedge _{x \in dom (\tau _i) \cap {\mathcal {X}}^\mathsf{b}}\tau _i(x) = x\).
We show that the set \(\{(\tau _1', \phi _1'), \ldots , (\tau _n', \phi _n')\}\) is a complete set of unifiers modulo builtins of \(t_1\) and \(t_2\). Firstly, we have to show soundness: that each pair \((\tau _1', \phi _1')\) is indeed a unifier of \(t_1\) and \(t_2\) (easy).
Secondly, we show completeness. Let \(\alpha : var (t_1, t_2) \rightarrow M^\varSigma _{\cong }\) be a partial valuation such that \(\alpha (t_1) = \alpha (t_2)\). We will work with the analogous approach, with \(\alpha : var (t_1, t_2) \rightarrow M^\varSigma \) such that \(\alpha (t_1) \cong \alpha (t_2)\). Note that, by our definition of the model generated by a signature modulo builtins, \(M^\varSigma = \mathcal {T}_{{\varSigma }^\mathsf{c}}(\emptyset )\), and therefore valuations such as \(\alpha \) can also be seen as substitutions.
Let \(\alpha ' : var (s_1, s_2) \rightarrow \mathcal {T}_{{\varSigma }^\mathsf{c}}(\emptyset )\) be defined as follows:

We have \(\alpha '(s_1) \cong \alpha '(s_2)\). By construction, we also have: 1. \(\alpha '|_{ var (s_1)} = \alpha \circ \sigma _1\); 2. \(\alpha '|_{ var (s_2)} = \alpha \circ \sigma _2\). As \(\alpha '\) is a substitution unifying \(s_1\) and \(s_2\) modulo E (recall that \(\cong \) is generated by E), it follows that there exists a unifier \(\tau _i \in \{ \tau _1, \ldots , \tau _n \}\) of \(s_1\) and \(s_2\) and a substitution \(\alpha ^c\) such that: 1. \(\tau _i(s_1) \cong \tau _i(s_2)\); 2. \(\alpha ' = (\alpha ^c \circ \tau _i)|_{ var (t_1, t_2)}\). Note that, as \(\alpha '|_{ var (s_j)} = \alpha \circ \sigma _j\) (\(1 \le j \le 2\)), we also have that\((\alpha ^c \circ \tau _i)|_{ var (s_1)} = \alpha \circ \sigma _1\) and \((\alpha ^c \circ \tau _i)|_{ var (s_2)} = \alpha \circ \sigma _2\).
Let \(\tau _i' = \tau _i|_{\mathcal {X}\setminus {X}^\mathsf{b}}\). Let \(\alpha ^r : var (t_1, t_2, \phi ) \rightarrow \mathcal {T}_{{\varSigma }^\mathsf{c}}(\emptyset )\) be defined as follows:
The substitution \(\alpha ^r\) defined above satisfies all conditions in Definition 12:
-
1.
\(\alpha = (\alpha ^r \circ \tau _i')|_{ var (t_1, t_2)}\):
Let \(x \in var (t_1, t_2)\). We distinguish two cases: – if \(x \in {X}^\mathsf{b}\), then we have \(\alpha ^r(\tau _i'(x)) =\alpha ^r(x) = \alpha (x)\); – if \(x \not \in {X}^\mathsf{b}\), then \(\alpha ^r(\tau _i'(x)) =\alpha ^r(\tau _i(x)) =\alpha ^c(\tau _i(x)) =\alpha '(x) = \alpha (x)\);
-
2.
\(M^\varSigma _{\cong }, \alpha ^r \vDash \phi _i'\):
-
(a)
\(M^\varSigma _{\cong }, \alpha ^r \vDash \phi ^{\sigma _1}\), since: – if \(x \not \in dom (\sigma _1)\), then \(\sigma _1(x) = x\) and therefore trivially \(\alpha ^r(\sigma _1(x)) = \alpha ^r(x)\); – if \(x \in dom (\sigma _1)\), then \(\alpha ^r(\sigma _1(x)) =\alpha (\sigma _1(x)) =\alpha '(x) =\alpha ^r(x)\);
-
(b)
\(M^\varSigma _{\cong }, \alpha ^r \vDash \phi ^{\sigma _2}\), analogously;
-
(c)
\(M^\varSigma _{\cong }, \alpha ^r \vDash \tau _i(x) = x\) for all \(x \in dom (\tau _i) \cap {X}^\mathsf{b}\) trivially, by the third branch in the definition of \(\alpha ^r\).
-
(a)
We have shown that for any \(\alpha \) that unifies modulo builtins \(t_1\) and \(t_2\), there is an E-umb \((\tau _i', \phi _i')\) and a substitution \(\alpha ^r\) with the properties required in Definition 12, and therefore this proves the completeness of the algorithm.
Complexity. Algorithm 1, which reduces E-unification modulo builtins to E-unification, has a linear-time overhead and therefore the running time is dominated by the algorithm for E-unification and, optionally, by some calls to the SMT solver. Lines 3 and 4 are linear in the size of the input. The running time of Line 5 is determined by the E-unification algorithm. The postprocessing step in lines 6–8 is linear in the size n of the output of the E-unification algorithm. Additionally, if we want to check the satisfiability of the constraints \(\phi _i'\) on Line 9, there will be n calls to the SMT solver. In summary, the running time of the algorithm is dominated by one call to the E-unification algorithm, and, optionally, n calls to the SMT solver, where n is the number of unifiers returned by the E-unification algorithm.
5 Conclusion and Future Work
We introduced the problem of E-unification modulo builtins. While regular (E)-unification is about solving an equation in the algebra of terms (or the algebra of terms modulo E), E-unification modulo builtins is solving an equation in an algebra combining terms (modulo E) with builtin elements such as booleans, integers, arrays, or any other elements that can be handled by an SMT solver.
Our main contribution is to formalize the problem of E-unification modulo builtins and to provide an algorithm for it that is based on the notion of abstraction of a term. The algorithm reduces E-unification modulo builtins to regular E-unification. This allows to lift all existing E-unification algorithms to E-unification modulo builtins.
Unlike regular E-unification algorithms, which produce (sets of) substitution(s) as their output, algorithms for E-unification modulo builtins produce sets of pairs of substitutions and logical constraints. The equation being solved holds when instantiated by one of the substitutions, in the cases where the attached logical constraint holds. We show how to produce logical constraints that only contain builtins, which means that they can be fully handled by an SMT solver. We implement our approach as a Maude prototypeFootnote 1 at the meta-level. Given two terms, the prototype computes a complete set of E-unifiers modulo builtins as described in Algorithm 1. As an optimization, it filters out the E-unifiers modulo builtins that have an unsatisfiable constraint, by using the integrated SMT solver. We describe the prototype in Appendix A. Our result answers in part an open question in [18], namely of finding elements that match two matching logic patterns, which is essential in developing a matching-logic prover.
The main question that needs to be answered in future work is what kind of new applications are enabled by the combination of rewrite and SMT solving. On the theoretical side, all known results in rewriting (confluence, etc.) also need to be developed in the new framework. Another open question is how to perform E-unification modulo builtins in the presence of defined operations.
Notes
- 1.
The prototype is available at: https://github.com/andreiarusoaie/unification-modulo-builtins.
References
Aguirre, L., Martí-Oliet, N., Palomino, M., Pita, I.: Conditional narrowing modulo SMT and axioms. In: PPDP, pp. 17–28 (2017)
Arusoaie, A., Lucanu, D., Rusu, V.: A generic framework for symbolic execution. In: Erwig, M., Paige, R.F., Van Wyk, E. (eds.) SLE 2013. LNCS, vol. 8225, pp. 281–301. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-02654-1_16
Arusoaie, A., Lucanu, D., Rusu, V.: Symbolic execution based on language transformation. Comput. Lang. Syst. Struct. 44, 48–71 (2015)
Baader, F., Schulz, K.U.: Unification in the union of disjoint equational theories: combining decision procedures. JSC 21(2), 211–243 (1996)
Bae, K., Rocha, C.: Guarded terms for rewriting modulo SMT. In: Proença, J., Lumpe, M. (eds.) FACS 2017. LNCS, vol. 10487, pp. 78–97. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68034-7_5
Ciobâcă, Ş., Lucanu, D.: A coinductive approach to proving reachability properties in logically constrained term rewriting systems. IJCAR (2018, to appear)
Ciobâcă, Ş., Lucanu, D.: RMT: proving reachability properties in constrained term rewriting systems modulo theories. Technical report TR 16–01, Alexandru Ioan Cuza University, Faculty of Computer Science (2016)
Ştefănescu, A., Ciobâcă, Ş., Mereuta, R., Moore, B.M., Şerbănută, T.F., Roşu, G.: All-path reachability logic. In: Dowek, G. (ed.) RTA 2014. LNCS, vol. 8560, pp. 425–440. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08918-8_29
Darlington, J., Guo, Y.: Constrained equational deduction. In: Kaplan, S., Okada, M. (eds.) CTRS 1990. LNCS, vol. 516, pp. 424–435. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-54317-1_111
Falke, S., Kapur, D.: Dependency pairs for rewriting with built-in numbers and semantic data structures. In: Voronkov, A. (ed.) RTA 2008. LNCS, vol. 5117, pp. 94–109. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70590-1_7
Fuhs, C., Kop, C., Nishida, N.: Verifying procedural programs via constrained rewriting induction. ACM TOCL 18(2), 14:1–14:50 (2017)
Kirchner, C., Kirchner, H., Rusinowitch, M.: Deduction with symbolic constraints. Research report RR-1358, INRIA (1990). Projet EURECA
Kop, C., Nishida, N.: Term rewriting with logical constraints. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 343–358. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_24
Lucanu, D., Rusu, V., Arusoaie, A., Nowak, D.: Verifying reachability-logic properties on rewriting-logic specifications. In: Martí-Oliet, N., Ölveczky, P.C., Talcott, C. (eds.) Logic, Rewriting, and Concurrency. LNCS, vol. 9200, pp. 451–474. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-23165-5_21
Nelson, G., Oppen, D.C.: Simplification by cooperating decision procedures. ACM TOPLAS 1(2), 245–257 (1979)
Nigam, V., Talcott, C., Aires Urquiza, A.: Towards the automated verification of cyber-physical security protocols: bounding the number of timed intruders. In: Askoxylakis, I., Ioannidis, S., Katsikas, S., Meadows, C. (eds.) ESORICS 2016. LNCS, vol. 9879, pp. 450–470. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45741-3_23
Rocha, C., Meseguer, J., Muñoz, C.: Rewriting modulo SMT and open system analysis. JLAMP 86(1), 269–297 (2017)
Roşu, G.: Matching logic. LMCS 13(4), 1–61 (2017)
Schmidt-Schauss, M.: Unification in a combination of arbitrary disjoint equational theories. JSC 8(1), 51–99 (1989)
Skeirik, S., Ştefănescu, A., Meseguer, J.: A constructor-based reachability logic for rewrite theories. CoRR, abs/1709.05045 (2017)
Acknowledgments
We thank the anonymous reviewers for their valuable suggestions. This work was supported by a grant of the Romanian National Authority for Scientific Research and Innovation, CNCS/CCCDI - UEFISICDI, project number PN-III-P2-2.1-BG-2016-0394, within PNCDI III.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Maude Prototype
A Maude Prototype
Since the algorithm needs to manipulate terms (for instance, to compute the abstractions) we use the metalevel capabilities of Maude to implement the following functionalities:
-
For a given meta-representation of a term, getAbstraction returns the abstraction of a term w.r.t. the set of builtins sorts, which need to be provided explicitly. When computing abstractions, fresh variables are generated;
-
The E-unifiers of the abstractions are computed by unifyAbstractions;
-
The unsatisfiable formulas are filtered out by filterUnsatUMBs;
-
The E-unification modulo builtins algorithm that we propose is implemented by completeSetOfUMBs, which gets as input the meta-representations of two terms and returns the unifiers modulo builtins in two steps: it first generates the substitution-formula pairs with completeSetOfUMBsUnfiltered, and then it eliminates the unsatisfiable solutions using the aforementioned filterUnsatUMBs.
We show how to use our prototype to find the E-unifiers modulo builtins of the E-unification modulo builtins problem \(\textsf {n} \mapsto 1, \textsf {cnt} \mapsto 42 =Z, \textsf {n} \mapsto 1\), introduced in Example 12. First, Maude finds a complete set of ACI-unifiers for the abstractions of the two terms. Then, from these unifiers we generate the pairs \(\{(\tau _1', \phi _1'), (\tau _2', \phi _2') \}\), as shown in Example 12):

The variables abs0, abs1, ..., are generated during the abstraction process, while %1, %2, ...are generated by the Maude’s variant unifier.
Finally, completeSetOfUMBs – the main function in our prototype – filters out the first unifier, which has an unsatisfiable constraint. Because the interaction between Maude and the SMT solver only supports integers and booleans, we have encoded identifiers (of sort Id) into integers before sending the formula to the SMT solver. The solution is:

The result is essentially that the variable Z must be \(\textsf {cnt} \mapsto 42\), since %1 = abs2:Id = count and %2 = abs3:Id = 42.
We now show how our prototype solves the four E-unification modulo builtins problems discussed in the Introduction:
-
1.
\(\textsf {n} \mapsto N =\textsf {cnt} \mapsto C' + N', \textsf {n} \mapsto N' + 3\)
-
2.
\(\textsf {n} \mapsto 2 \times N + 1, \textsf {cnt} \mapsto C =\textsf {cnt} \mapsto C' + N', \textsf {n} \mapsto N' + 3\)
-
3.
\(\textsf {n} \mapsto 2 \times N, \textsf {cnt} \mapsto C =\textsf {cnt} \mapsto C' + N', \textsf {n} \mapsto N' + 3\)
-
4.
\(\textsf {n} \mapsto 1, \textsf {cnt} \mapsto C =\textsf {cnt} \mapsto C' + N', \textsf {n} \mapsto N' + 3\)
The set of unifiers modulo builtins is computed by our Maude prototype for each case as shown below:

For the first E-umb problem, the tool returns noUMBResults, which means that it does not have any solution. For the other examples, the prototype finds the unifiers, as expected.
Rights and permissions
Copyright information
© 2018 Springer-Verlag GmbH Germany, part of Springer Nature
About this paper
Cite this paper
Ciobâcă, Ş., Arusoaie, A., Lucanu, D. (2018). Unification Modulo Builtins. In: Moss, L., de Queiroz, R., Martinez, M. (eds) Logic, Language, Information, and Computation. WoLLIC 2018. Lecture Notes in Computer Science(), vol 10944. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-57669-4_10
Download citation
DOI: https://doi.org/10.1007/978-3-662-57669-4_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-57668-7
Online ISBN: 978-3-662-57669-4
eBook Packages: Computer ScienceComputer Science (R0)





 is
is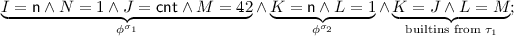
 is
is
