Estimating Lyapunov Exponents from Time Series

Abstract

Lyapunov exponents are important statistics for quantifying stability and deterministic chaos in dynamical systems. In this review article, we first revisit the computation of the Lyapunov spectrum using model equations. Then, employing state space reconstruction (delay coordinates), two approaches for estimating Lyapunov exponents from time series are presented: methods based on approximations of Jacobian matrices of the reconstructed flow and so-called direct methods evaluating the evolution of the distances of neighbouring orbits. Most direct methods estimate the largest Lyapunov exponent, only, but as an advantage they give graphical feedback to the user to confirm exponential divergence. This feedback provides valuable information concerning the validity and accuracy of the estimation results. Therefore, we focus on this type of algorithms for estimating Lyapunov exponents from time series and illustrate its features by the (iterated) Hénon map, the hyper chaotic folded-towel map, the well known chaotic Lorenz-63 system, and a time continuous 6-dimensional Lorenz-96 model. These examples show that the largest Lyapunov exponent from a time series of a low-dimensional chaotic system can be successfully estimated using direct methods. With increasing attractor dimension, however, much longer time series are required and it turns out to be crucial to take into account only those neighbouring trajectory segments in delay coordinates space which are located sufficiently close together.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1.1 Introduction

Lyapunov exponents are a fundamental concept of nonlinear dynamics. They quantify local stability features of attractors and other invariant sets in state space. Positive Lyapunov exponents indicate exponential divergence of neighbouring trajectories and are the most important attribute of chaotic attractors. While the computation of Lyapunov exponents for given dynamical equations is straight forward, their estimation from time series remains a delicate task. Given a univariate (scalar) time series the first step is to use delay coordinates to reconstruct the state space dynamics. Using the reconstructed states there are basically two approaches to solve the estimation problem: With Jacobian matrix based methods a (local) mathematical model is fitted to the temporal evolution of the states that can then be used like any other dynamical equation. Using this approach in principle all Lyapunov exponents can be estimated if the chosen black-box model is in very good agreement with the underlying dynamics. In practical applications such a high level of fidelity is often difficult to achieve, in particular since the time series typically contain only limited information about contracting directions in state space. With the second approach for estimating (at least the largest) Lyapunov exponents the local divergence of trajectory segments in reconstructed state space is assessed directly. Advantage of this kind of direct methods is their low number of estimation parameters, easy implementation, and last but not least, direct graphical feedback about the (non-) existence of exponential divergence in the given time series.

The following presentation is organised as follows: In Sect. 1.2 the standard algorithm for computing Lyapunov exponents using dynamical model equations is revisited. Methods for computing Lyapunov exponents from time series are presented in Sect. 1.3. In Sect. 1.4 four dynamical systems are introduced to generate time series which are then in Sect. 1.5 used as examples for illustrating and evaluating features of direct estimation of the largest Lyapunov exponent. The examples are: the Hénon map, the hyper chaotic folded-towel map, the Lorenz-63 system, and a 6-dimensional Lorenz-96 model. These time discrete and time continuous models exhibit deterministic chaos of different dimensionality and complexity. In Sect. 1.6 a summary is given and the Appendix contains some information for those readers who are interested in implementing Jacobian based estimation algorithms.

1.2 Computing Lyapunov Exponents Using Model Equations

Lyapunov exponents characterize and quantify the dynamics of (infinitesimally) small perturbations of a state or trajectory in state space. Let the dynamical model be a M-dimensional discrete

$$\displaystyle{ \mathbf{x}(n + 1) =\mathbf{ g}(\mathbf{x}(n)) }$$

(1.1)

or a continuous

$$\displaystyle{ \dot{\mathbf{x}} = \frac{d\mathbf{x}} {dt} =\mathbf{ f}(\mathbf{x}) }$$

(1.2)

dynamical system generating a flow

$$\displaystyle{ \phi ^{t}: \mathbb{R}^{M} \rightarrow \mathbb{R}^{M} }$$

(1.3)

with discrete $t = n \in \mathbb{Z}$ or continuous $t \in \mathbb{R}$ time. The temporal evolution of an infinitesimally small perturbation $\mathbf{y}$ of the state $\mathbf{x}$

$$\displaystyle{ D\phi ^{t}(\mathbf{x}) \cdot \mathbf{ y} }$$

(1.4)

is governed by the linearized dynamics where $D\phi ^{t}(\mathbf{x})$ denotes the Jacobian matrix of the flow ϕ ^t. For discrete systems this Jacobian can be computed using the recursion scheme

$$\displaystyle{ D_{x}\phi ^{n+1}(\mathbf{x}) = D_{ x}\mathbf{g}(\phi ^{n}(\mathbf{x})) \cdot D_{ x}\phi ^{n}(\mathbf{x}) }$$

(1.5)

with initial value $D_{x}\phi ^{0}(\mathbf{x}) = I_{M}$ where I _M denotes the M × M identity matrix. For continuous systems (1.2) additional linearized ordinary differential equations (ODEs)

$$\displaystyle{ \frac{d} {dt}Y = D_{x}\mathbf{f}(\phi ^{t}(\mathbf{x})) \cdot Y }$$

(1.6)

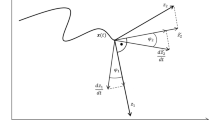
have to be solved where $\phi ^{t}(\mathbf{x})$ is a solution of Eq. (1.2) with initial value $\mathbf{x}$ and Y is a M × M matrix that is initialized as Y (0) = I _M . The solution Y (t) provides the Jacobian of the flow $D\phi ^{t}(\mathbf{x})$ that describes the local dynamics along the trajectory given by the temporal evolution $\phi ^{t}(\mathbf{x})$ of the initial state $\mathbf{x}$. Since Eq. (1.6) is a linear ODE its solutions consist of exponential functions and the Jacobian of the flow $D\phi ^{t}(\mathbf{x})$ maps a sphere of initial values close to $\mathbf{x}$ to an ellipsoid centered at $\phi ^{t}(\mathbf{x})$ as illustrated in Fig. 1.1. This evolution of the tangent space dynamics can be analyzed using a singular value decomposition (SVD) of the Jacobian of the flow $D\phi ^{t}(\mathbf{x})$

$$\displaystyle{ D\phi ^{t}(\mathbf{x}) = U \cdot S \cdot V ^{tr} }$$

(1.7)

where $S =\mathrm{ diag}(\sigma _{1},\ldots,\sigma _{M})$ is a M × M diagonal matrix containing the singular values $\sigma _{1} \geq \sigma _{2} \geq \ldots \geq \sigma _{M} \geq 0$ and $U = (\mathbf{u}^{(1)},\ldots,\mathbf{u}^{(M)})$ and $V = (\mathbf{v}^{(1)},\ldots,\mathbf{v}^{(M)})$ are orthogonal matrices, represented by orthonormal column vectors $\mathbf{u}^{(i)} \in \mathbb{R}^{M}$ and $\mathbf{v}^{(i)} \in \mathbb{R}^{M}$, respectively. V ^tr is the transposed of V coinciding with the inverse V ⁻¹ = V ^tr, because V is orthogonal. For the same reason U ^tr = U ⁻¹ and by multiplying by V from the right we obtain $D\phi ^{t}(\mathbf{x}) \cdot V = U \cdot S$ or

$$\displaystyle{ D\phi ^{t}(\mathbf{x})\mathbf{v}^{(m)} =\sigma _{ m}\mathbf{u}^{(m)}\ \ \ \ \ (m = 1,\ldots,M). }$$

(1.8)

The column vectors of the matrices V and U span the initial sphere and the ellipsoid, as illustrated in Fig. 1.1, where the singular values $\sigma _{m}(t)$ give the lengths of the principal axes of the ellipsoid at time t. On average $\sigma _{m}(t)$ increases or decreases exponentially during the temporal evolution and the Lyapunov exponents $\lambda _{m}$ are the mean logarithmic growth rates of the lengths of the principal axes

$$\displaystyle{ \lambda _{m} =\lim _{t\rightarrow \infty }\frac{1} {t}\ln \sigma _{m}(t). }$$

(1.9)

Fig. 1.1

Temporal evolution of an infinitesimally small sphere in state space

The existence of the limit in Eq. (1.9) is guaranteed by the Theorem of Oseledec [33] stating that the Oseledec matrix

$$\displaystyle{ \varLambda (\mathbf{x}) = \lim _{t\rightarrow \infty }\left ([D\phi ^{t}(\mathbf{x})]^{tr} \cdot D\phi ^{t}(\mathbf{x})\right )^{ \frac{1} {2t} } }$$

(1.10)

exists. For dissipative systems one set of exponents is associated with each attractor and for almost all initial states $\mathbf{x}$ from each attractor $\varLambda (\mathbf{x})$ takes the same value.

The logarithms of the eigenvalues μ _m of this symmetric positive definite M × M matrix are the Lyapunov exponents of the attractor or invariant set the initial state $\mathbf{x}$ belongs to

$$\displaystyle{ \lambda _{m} =\ln \mu _{m}\ \ \ \ (m = 1,\ldots,M). }$$

(1.11)

Using the SVD of the Jacobian matrix of the flow the Oseledec matrix for finite time t can be written

$$\displaystyle{ \left (V \cdot S \cdot U^{tr} \cdot U \cdot S \cdot V ^{tr}\right )^{ \frac{1} {2t} } = \left (V \cdot S^{2} \cdot V ^{tr}\right )^{ \frac{1} {2t} } }$$

(1.12)

with eigenvalues $\sigma _{m}^{1/t}$. Taking the logarithm $\frac{1} {t} \ln \sigma _{m}$ and performing the limit $t \rightarrow \infty$ we obtain the Lyapunov exponents (1.11). Unfortunately, this definition and illustration of the Lyapunov exponents cannot be used directly for their numerical computation, because the Jacobian matrix D ϕ ^t(x) consists of elements that are exponentially increasing or decreasing in time resulting in values beyond the numerical resolution and representation of variables. To avoid these severe numerical problems in 1979 Shimada and Nagashima [45] and in 1980 and Benettin et al. [3] suggested algorithms that exploit the fact that the growth rate of k-dimensional volumes $\lambda ^{(k)}$ (in the M-dimensional state space) is given by the sum of the largest k Lyapunov exponents

$$\displaystyle{ \lambda ^{(k)} =\sum _{ m=1}^{k}\lambda _{ m} }$$

(1.13)

and the Lyapunov exponents can by computed from the volume growth rates as $\lambda _{1} =\lambda ^{(1)}$, $\lambda _{2} =\lambda ^{(2)} -\lambda _{1}$, $\lambda _{3} =\lambda ^{(3)} -\lambda _{2} -\lambda _{1}$, etc. The volume growth rates $\lambda ^{(k)}$ can be computed using a QR decomposition of the Jacobian of the flow $D\phi ^{t}(\mathbf{x})$. Let $O^{(k)} = (\mathbf{o}^{(1)},\ldots,\mathbf{o}^{(k)})$ be an orthogonal matrix whose column vectors $\mathbf{o}^{j}$ span a k-dimensional infinitesimal volume with k ranging from 1 to M. After time t this volume is transformed by the Jacobian matrix into a parallelepiped $P^{(k)}(t) = D\phi ^{t}(\mathbf{x}) \cdot O^{(k)}$. To computed the volume spanned by the column vectors of P ^(k)(t) we perform a QR-decomposition of P ^(k)(t)

$$\displaystyle{ P^{(k)}(t) = D\phi ^{t}(\mathbf{x}) \cdot O^{(k)} = Q^{(k)}(t) \cdot R^{(k)}(t) }$$

(1.14)

where Q ^(k)(t) is a matrix with k orthonormal columns and R ^(k)(t) is an upper triangular matrix with non-negative diagonal elements. The volume V ^(k)(t) of P ^(k)(t) at time t is given by the product of the diagonal elements R _ii ^(k)(t) of R ^(k)(t)

$$\displaystyle{ V ^{(k)}(t) = R_{ 11}^{(k)}(t) \cdot \ldots \cdot R_{ kk}^{(k)}(t) =\prod _{ i=1}^{k}R_{ ii}^{(k)}(t). }$$

(1.15)

The mean logarithmic growth rate of the k-dimensional volume is thus given by

$$\displaystyle{ \lambda ^{(k)} =\lim _{ t\rightarrow \infty }\frac{1} {t}\ln V ^{(k)}(t) =\lim _{ t\rightarrow \infty }\frac{1} {t}\sum _{i=1}^{k}\ln R_{ ii}^{(k)}(t). }$$

(1.16)

Using this relation and Eq. (1.13) we can conclude that the first k Lyapunov exponents $\lambda _{1},\ldots,\lambda _{k}$ are given by

$$\displaystyle{ \lambda _{i} =\lim _{t\rightarrow \infty }\frac{1} {t}\ln R_{ii}^{(k)}(t). }$$

(1.17)

If one would perform the QR-decomposition (1.14) of the Jacobian $D\phi ^{t}(\mathbf{x})$ after a very long period of time (to approximate the limit $t \rightarrow \infty$) then one would be faced with the same numerical problems that were mentioned above in the context of the Oseledec matrix. The advantage of the volume approach via QR-decomposition is, however, that this decomposition can be computed recursively for small time intervals avoiding any numerical over or underflow. To exploit this feature the period of time [0, t] is divided into N time intervals of length T = t∕N and the Jacobian matrices $D\phi ^{T}(\phi ^{t_{n}}(\mathbf{x}))$ are computed at times t _n  = nT (n = 0, …, N − 1) along the orbit. Employing the chain rule the Jacobian matrix $D\phi ^{t}(\mathbf{x})$ can be written as a product of Jacobian matrices $D\phi ^{T}(\phi ^{t_{n}}(\mathbf{x}))$

$$\displaystyle{ D\phi ^{t}(\mathbf{x}) = D\phi ^{T}(\phi ^{t_{N-1} }(\mathbf{x})) \cdot \ldots \cdot D\phi ^{T}(\phi ^{t_{0} }(\mathbf{x})) =\prod _{ n=0}^{N-1}D\phi ^{T}(\phi ^{t_{n} }(\mathbf{x})). }$$

(1.18)

Using QR-decompositions

$$\displaystyle{ \hat{Q}^{(k)}(t_{ n+1}) \cdot \hat{R} ^{(k)}(t_{ n+1}) = D\phi ^{T}(\phi ^{t_{n} }(\mathbf{x})) \cdot \hat{Q} ^{(k)}(t_{ n}) }$$

(1.19)

the full period of time [0, t] used for averaging the local expansion rates can be decomposed into a sequence of relatively short intervals [0, T] with Jacobian matrices $D\phi ^{T}(\phi ^{t_{n}}(\mathbf{x}))$ that are not suffering from numerical difficulties. Applying the QR-decompositions (1.19) recursively we obtain a scheme for computing the QR-decomposition of the Jacobian matrix of the full time step

$$\displaystyle\begin{array}{rcl} D\phi ^{t}(\mathbf{x}) \cdot O^{(k)}& =& D\phi ^{T}(\phi ^{t_{N-1} }(\mathbf{x})) \cdot \ldots \cdot D\phi ^{T}(\phi ^{t_{0} }(\mathbf{x})) \cdot O^{(k)} {}\\ & =& D\phi ^{T}(\phi ^{t_{N-1} }(\mathbf{x})) \cdot \ldots \cdot D\phi ^{T}(\phi ^{t_{1} }(\mathbf{x})) \cdot \hat{Q} ^{(k)}(t_{ 1}) \cdot \hat{R} ^{(k)}(t_{ 1}) {}\\ & =& D\phi ^{T}(\phi ^{t_{N-1} }(\mathbf{x})) \cdot \ldots \cdot D\phi ^{T}(\phi ^{t_{2} }(\mathbf{x})) \cdot \hat{Q} ^{(k)}(t_{ 2}) \cdot \hat{R} ^{(k)}(t_{ 2}) \cdot \hat{R} ^{(k)}(t_{ 1}) {}\\ & \vdots & {}\\ & =& D\phi ^{T}(\phi ^{t_{N-1} }(\mathbf{x})) \cdot \hat{Q} ^{(k)}(t_{ N-1}) \cdot \hat{R} ^{(k)}(t_{ N-1}) \cdot \ldots \cdot \hat{R} ^{(k)}(t_{ 1}) {}\\ & =& \hat{Q}^{(k)}(t_{ N}) \cdot \hat{R} ^{(k)}(t_{ N}) \cdot \ldots \cdot \hat{R} ^{(k)}(t_{ 1}) {}\\ \end{array}$$

which provides $Q^{(k)}(t) = \hat{Q} ^{(k)}(t_{N})$ and the required matrix R ^(k)(t) as a product

$$\displaystyle{ R^{(k)}(t) = \hat{R} ^{(k)}(t_{ N}) \cdot \ldots \cdot \hat{R} ^{(k)}(t_{ 1}). }$$

(1.20)

For the diagonal elements of the upper triangular matrices holds the relation

$$\displaystyle{ R_{ii}^{(k)}(t) =\prod _{ n=1}^{N}\hat{R} _{ ii}^{(k)}(t_{ n}) }$$

(1.21)

and substituting R _ii ^(k)(t) in Eq. (1.17) (with t = NT) we obtain the following expression for the ith Lyapunov exponent (with i ≤ k ≤ M)

$$\displaystyle{ \lambda _{i} =\lim _{N\rightarrow \infty } \frac{1} {NT}\sum _{n=1}^{N}\ln \hat{R} _{ ii}^{(k)}(t_{ n}). }$$

(1.22)

Using this approach the computation of all Lyapunov exponents of a given dynamical system became a standard procedure [12, 19, 46, 51] providing the full set of Lyapunov exponents constituting the Lyapunov spectrum which is an ordered set of real numbers $\{\lambda _{1},\lambda _{2},\ldots,\lambda _{m}\}$. If the system undergoes aperiodic oscillations (after transients decayed) and if the largest Lyapunov exponent $\lambda _{1}$ is positive, then the corresponding attractor is said to be chaotic and to show sensitive dependence on initial conditions. If more than one Lyapunov exponent is positive the underlying dynamics is called hyper chaotic.

The (ordered) spectrum $\lambda _{1} \geq \lambda _{2} \geq \ldots \geq \lambda _{m}$ can be used to compute the Kaplan–Yorke dimension (also called Lyapunov dimension) [34]

$$\displaystyle{ D_{KY } = k + \frac{\sum _{i=1}^{k}\lambda _{i}} {\vert \lambda _{k+1}\vert } }$$

(1.23)

where k is the maximum integer such that the sum of the k largest exponents is still non-negative. D _KY is an upper bound for the information dimension of the underlying attractor.

1.3 Estimating Lyapunov Exponents from Time Series

All methods for computing Lyapunov exponents are based on state space reconstruction from some observed (univariate) time series [11, 42, 43, 49]. For reconstructing the dynamics most often delay coordinates are used due to their efficacy and robustness.

To reconstruct the multi-dimensional dynamics from an observed (univariate) time series {s _n } sampled at times t _n  = n Δ t we use delay coordinates providing the N × D trajectory matrix

$$\displaystyle{ X = (\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{N})^{tr} }$$

(1.24)

where each row is a reconstructed state vector¹

$$\displaystyle{ \mathbf{x}_{n} = (s_{n},s_{n+L},\ldots,s_{n+(D-1)L}) }$$

(1.25)

at time n (with lag L and dimension D). From a time series {s _n } of length N _d a total number of N = N _d − (D − 1)L states can be reconstructed. To achieve useful (nondistorted) reconstructions the time window length (D − 1)L of the delay vector should cover typical time scales of the dynamics like natural periods or the first zero or minimum of the autocorrelation function or the (auto) mutual information [1, 26].

Since Lyapunov exponents are invariant with respect to diffeomorphic changes of the coordinate system the Lyapunov exponents estimated for the reconstructed flow will coincide with those of the original system. Technically, different approaches exist for computing Lyapunov exponents from embedded time series. Jacobian-based methods employ the standard algorithm outlined in Sect. 1.2 except for the computation of the Jacobian matrix $D\phi ^{t}(\mathbf{x})$ which is now based on approximations of the flow in the reconstructed state space. This class of methods will be briefly presented in Sect. 1.3.1. In particular with noisy data reliable estimation of the Jacobian matrix may be a delicate task. This is one of the reasons why several authors proposed methods for estimating the largest Lyapunov exponent directly from diverging trajectories in reconstructed state space. Such direct methods will be discussed in detail in Sect. 1.3.2 and will be illustrated and evaluated in Sect. 1.5. They do not require Jacobian matrices but are mostly used to compute the largest Lyapunov exponent, only. A major advantage of direct methods, however, is the fact that they provide direct visual feedback to the user whether the available time series really exhibits exponential divergence on small scales. Therefore, we shall focus on this class of methods in the following.

1.3.1 Jacobian-Based Methods

With Jacobian methods, first a model is fitted to the data and then the Jacobian matrices of the model equations are used to compute the Lyapunov exponents using standard algorithms (see Sect. 1.2) which have been developed for the case when the equations of the dynamical system are known [3, 12, 19, 45]. In this context usually local linear approximations are used for modeling the flow in reconstructed state space [14, 22, 29, 36, 40, 47, 48, 53, 54]. An investigation of the data requirements for Jacobian-based methods may be found in [13, 15]. Technical details and more information about the implementation of Jacobian-based methods are given in the Appendix.

To employ the standard algorithm for computing Lyapunov exponents (Sect. 1.2) also for time series analysis the Jacobian matrices along the orbit in reconstruction space are required and have to be estimated from the temporal evolution of reconstructed states. Here two major challenges occur:

• (a) The Jacobian matrices (derivatives) have to be estimated using reconstructed states that are scattered along the unstable direction(s) of the attractor but not in transversal directions (governed by contracting dynamics). This may result in ill-posed estimation problems and is a major obstacle for estimating negative Lyapunov exponents. Furthermore, the estimation problem is often even more delicate because we aim at approximating (partial) derivatives (the elements of the Jacobian matrix) from typically noisy data where estimating derivatives is a notoriously difficult problem.

• (b) To properly unfold the attractor and the dynamics in reconstruction space the embedding dimension D has in general to be larger than the dimension of the original state space M (see Sect. 1.3). Therefore, a straightforward computation of Lyapunov exponents using (estimated) D × D Jacobian matrices in reconstruction space and QR-decomposition (see Sect. 1.2) will provide D Lyapunov exponents, although the underlying M-dimensional system possesses M < D exponents, only. The additional D − M Lyapunov exponents are called parasitic or spurious exponents and they have to be identified (or avoided), because their values are not related to the dynamics to be characterized.

Spurious Lyapunov exponents can take any values [8], depending on details of the approximation scheme used to estimate the Jacobian matrices, the local curvature of the reconstructed attractor, and perturbations of the time series (e.g., noise). Therefore, without taking precautions spurious Lyapunov exponents can occur between “true” exponents and may spoil in this sense the observed spectrum (resulting in false conclusion about the number of positive exponents or the Kaplan–Yorke dimension, for example). To cope with this problem many authors presented different approaches for avoiding spurious Lyapunov exponents or for reliably detecting them [44].

To identify spurious Lyapunov exponents one can estimate the local thickness of the attractor along the directions associated with the different Lyapunov exponents [6, 7] or compare the exponents obtained with those computed for the time reversed series [35, 36], because spurious exponents correspond to directions where the attractor is very thin and because in general they do not change their signs upon time reversal (in contrast to the true exponents). The latter method, however, works only for data of very high quality that enable also a correct estimation of negative Lyapunov exponents which in most practical situations is not the case. Furthermore, in some cases also spurious Lyapunov exponents may change signs and can then not be distinguished from true exponents. Another method for identifying spurious Lyapunov exponents employing covariant Lyapunov vectors been suggested in [27, 52].

Spurious Lyapunov exponents can be avoided by globally unfolding the dynamics in a D-dimensional reconstruction space and locally approximating the (tangent space) dynamics in a lower dimensional d-dimensional space (with d ≤ M). This can be done using two different delay coordinates where the set of indices of neighbouring points of a reference point is identified using a D-dimensional delay reconstruction and then these indices are used to reconstruct states representing “proper” neighbours in a d-dimensional delay reconstruction (with d < D) which is used for subsequent modeling of the dynamics (flow and its Jacobian matrices) [6, 7, 14]. To cover relevant time scales it is recommended [14] to use for both delay reconstructions different lags L _D and L _d so that the delay vectors span the same or similar windows in time (i.e., (D − 1)L _D  ≈ (d − 1)L _d ). An alternative approach for evaluating the dynamics in a lower dimensional space employs local projections into d-dimensional subspaces of the D-dimensional delay embedding space given by singular value decompositions of local trajectory matrices [10, 48].

For evaluating the uncertainty in Lyapunov exponent computations from time series employing Jacobian based algorithms bootstrapping methods have been suggested [28].

1.3.2 Direct Methods

There are (slightly) different ways to implement a direct method for estimating the largest Lyapunov exponent and they all rely on the fact that almost all tangent vectors (or perturbations) converge to the subspace spanned by the first Lyapunov vector(s) with an asymptotic growth rate given by the largest Lyapunov exponent $\lambda _{1}$ (see Sect. 1.5.1). In practice, however, from a time series of finite length only a finite number of reconstructed states is available with a finite lower bound for their mutual distances. If the nearest neighbour $\mathbf{x}_{m(n)}$ of a reference point $\mathbf{x}_{n}$ is chosen from the set of reconstructed states the trajectory segments emerging from both states will (on average) diverge exponentially until the distance $\Vert \mathbf{x}_{m(n)+k} -\mathbf{ x}_{n+k}\Vert$ exceeds a certain threshold and ceases to grow but oscillates bounded by the size of the attractor. For direct methods it is crucial that the reorientation towards the most expanding direction takes place and is finished before the distance between the states saturates. Then the period of exponential growth characterised by the largest Lyapunov exponent can be detected and estimated for some period of time as a linear segment in a suitable semi-logarithmic plot. This feature is illustrated in Fig. 1.2a showing the average of the logarithms of distances of neighbouring trajectories vs. time on a semi-logarithmic scale. In phase I the difference vector between states from both trajectories converges towards the most expanding direction. Then in phase II exponential divergence results in a linear segment until in phase III states from both trajectory segments are so far away from each other that nonlinear folding occurs and the mean distance converges to a constant value (which is related to the diameter of the attractor).

Fig. 1.2

(a) Sketch showing the mean logarithmic distance of neighbouring states on different trajectory segments vs. time. (b) Illustration motivating the exclusion of temporal neighbours (Theiler window)

Different implementations of the direct approach have been suggested in the past 25 years [18, 25, 30, 38, 41] that are based on the following considerations.

Let $\mathbf{x}(m(n))$ be a neighbour of the reference state $\mathbf{x}(n)$ (with respect to the Euclidean norm or any other norm) and let both states be temporally separated

$$\displaystyle{ \vert m(n) - n\vert> w }$$

(1.26)

where w is a characteristic time scale (e.g., a mean period) of the time series. The temporal separation (also called Theiler window w [50]) is necessary to make sure that this pair of neighbouring states can be considered as initial conditions of different trajectory segments and the largest Lyapunov exponent can be estimated from the mean rate of separation of states along these two orbits. Figure 1.2b shows an illustration of a case where a Theiler window of w = 3 would be necessary to exclude neighbours of the state marked by a big dot to avoid temporal neighbours on the same trajectory segment (small dots preceding and succeeding the reference state within the circle, indicating the search radius).

We shall quantify the separation of states by the distance

$$\displaystyle{ d(m(n),n,k) =\Vert \mathbf{ x}(m(n) + k) -\mathbf{ x}(n + k)\Vert }$$

(1.27)

of the neighbouring states after k time steps (i.e. a period of time T = k Δ t). Most often [18, 30, 38, 41] the Euclidean norm

$$\displaystyle{ d_{E}(m(n),n,k) =\Vert \mathbf{ x}(m(n) + k) -\mathbf{ x}(n + k)\Vert _{2} }$$

(1.28)

is used to define this distance, although Kantz [25] pointed out that it is sufficient to consider the difference

$$\displaystyle{ d_{L}(m(n),n,k) =\vert x(m(n) + (D - 1)L + k) - x(n + (D - 1)L + k)\vert }$$

(1.29)

of the last components of both reconstructed states, because these projections also grow exponentially with the largest Lyapunov exponent. Here L denotes again the time lag used for delay reconstruction. With the same argument, one can also consider the difference of the first component

$$\displaystyle{ d_{F}(m(n),n,k) =\vert x(m(n) + k) - x(n + k)\vert }$$

(1.30)

and in the following we shall compare all three choices. Within the linear approximation (very small d(m(n), n, k)) the temporal evolution of the distance d(m(n), n, k) is given by

$$\displaystyle{ d(m(n),n,k) \approx d(m(n),n,0)\ e^{\hat{\lambda }_{1}(n)k\varDelta t} }$$

(1.31)

where d(m(n), n, 0) stands for the initial separation of both orbits and $\hat{\lambda }_{1}(n)$ denotes the (largest) local expansion rate of orbits starting at $\mathbf{x}(n)$. Taking the logarithm we obtain

$$\displaystyle\begin{array}{rcl} \hat{\lambda }_{1}(n)& \approx & \frac{1} {k\varDelta t}\left [\ln (d(m(n),n,k)) -\ln (d(m(n),n,0))\right ] \\ & =& \frac{1} {k\varDelta t}\ln \left (\frac{d(m(n),n,k)} {d(m(n),n,0)}\right ). {}\end{array}$$

(1.32)

Here and in the following expansion rates and Lyapunov exponents are computed using the natural logarithm $\ln (\cdot )$.

Since expansion rates vary on the attractor we have to average along the available trajectory by choosing for each reference state $\mathbf{x}(n)$ some neighbouring states $\{\mathbf{x}(m(n)): m(n) \in \mathcal{U}_{n}\}$ where $\mathcal{U}_{n}$ defines the chosen neighbourhood of $\mathbf{x}(n)$ that can be of fixed mass (a fixed number K of nearest neighbours of $\mathbf{x}(n)$) or of fixed size (all points with distance smaller than a given bound ε). Often a fixed mass with K = 1 (i.e., using only the nearest neighbour) is used [18, 38, 41], but a fixed size may in some cases be more appropriate to avoid mixing of scales [25, 30]. In the following $\vert \mathcal{U}_{n}\vert$ denotes the number of neighbours of $\mathbf{x}(n)$.

Furthermore, it may be appropriate to use not all available reconstructed states $\mathbf{x}(n)$ (n = 1, …, N) as reference points but only a subset $\mathcal{R}$ consisting of $N_{r} =\vert \mathcal{R}\vert$ points. This speeds up computations and may even result in better results if $\mathcal{R}$ contains only those reconstructed states that possess very close neighbours (where d(m(n), n, 0) is very small). This issue will be discussed and demonstrated in the results section.

With averaged logarithmic distances

$$\displaystyle{ E(k) = \frac{1} {N_{r}}\sum _{n\in \mathcal{R}} \frac{1} {\vert \mathcal{U}_{n}\vert }\sum _{m\in \mathcal{U}_{n}}\ln (d(m,n,k)) }$$

(1.33)

and

$$\displaystyle{ S(k) = \frac{1} {N_{r}}\sum _{n\in \mathcal{R}} \frac{1} {\vert \mathcal{U}_{n}\vert }\sum _{m\in \mathcal{U}_{n}}\ln \left (\frac{d(m,n,k)} {d(m,n,0)}\right ) = E(k) - E(0) }$$

(1.34)

and the local expansion rates (1.32) the averaged growth rate can be expressed as

$$\displaystyle\begin{array}{rcl} \bar{\lambda }_{1}& =& \frac{1} {N_{r}}\sum _{n\in \mathcal{R}}\hat{\lambda }_{1}(n) \approx \frac{1} {N_{r}} \frac{1} {k\varDelta t}\sum _{n\in \mathcal{R}} \frac{1} {\vert \mathcal{U}_{n}\vert }\sum _{m\in \mathcal{U}_{n}}\ln \left (\frac{d(m,n,k)} {d(m,n,0)}\right ){}\end{array}$$

(1.35)

$$\displaystyle\begin{array}{rcl} & =& \frac{1} {k\varDelta t}S(k) = \frac{1} {k\varDelta t}\left [E(k) - E(0)\right ]{}\end{array}$$

(1.36)

providing the relations

$$\displaystyle{ S(k) \approx k\varDelta t\bar{\lambda }_{1} }$$

(1.37)

and

$$\displaystyle{ E(k) \approx k\varDelta t\bar{\lambda }_{1} + E(0). }$$

(1.38)

Here E(k) stands for E _E (k), E _F (k), or E _L (k) depending on the distance measure d _E , d _F , or d _L used when computing E in Eq. (1.33).

In 1987 Sato et al. [41] suggested to estimated the largest Lyapunov exponent by the slope of a linear segment of the graph obtained when plotting S(k) vs. k Δ t. The same approach was suggested later in 1993 by Gao and Zheng [18]. The same year Rosenstein et al. [38] recommended to avoid the normalization by the initial distance d(m(n), n, 0) in Eqs. (1.32) and (1.34) and to plot E(k) vs. k Δ t. As can be seen from Eqs. (1.37) and (1.38) both procedures are equivalent, because both graphs differ only be a constant shift E(0). Instead of estimating the slope in S(k) vs. k Δ t Sato et al. [41] and Kurths and Herzel [30] independently suggested in 1987 to consider

$$\displaystyle{ \bar{\lambda }_{1} \approx \frac{E(k + l) - E(k)} {l\varDelta t} = \frac{S(k + l) - S(k)} {l\varDelta t} }$$

(1.39)

and to identify a plateau in the graph [E(k + l) − E(k)] vs. k (that should occur for the same range of k values where the linear segment occurs with the previous methods). This is basically a finite differences approximation of the slope of the graph E(k) vs. k Δ t. To obtain best results the time interval l Δ t should be large but (l + k)Δ t must not exceed the linear scaling region(s) where distances grow exponentially (and this range is in general not known a priori).

In 1985 Wolf et al. [51] suggested a method to estimate the largest Lyapunov exponent(s) which avoids the saturation of mutual distances of reference states and local neighbours due to nonlinear folding. The main idea is to monitor the distance between the reference orbit and the neighbouring orbit and to replace (once a threshold is exceeded) the neighbouring state by another neighbouring state that is closer to the reference orbit and which lies on or near the line from the current reference state to the last point of the previous neighbouring orbit in order to preserve the (local) direction corresponding to the largest Lyapunov exponent. Criteria for the replacement threshold and other details of the algorithm are given in [51], including a FORTRAN program. In principle, it is possible to use this strategy also for computing the second largest Lyapunov exponent [51], but this turns out to be quite difficult. When applied to stochastic time series the Wolf algorithm yields inconclusive results and may provide any value for the Lyapunov exponent depending on computational parameters and pre-filtering [9]. Due to its robustness the Wolf-algorithm is often used for the analysis of experimental data (see, for example, [16, 17]). A drawback of this method (similar to Jacobian based algorithms) is the fact that the user has no possibility to check whether exponential growth underlies the estimated values or not. Even if the amount of data available or the type and quality of the time series would not be sufficient to quantify exponential divergence the algorithm would provide a number that might be misinterpreted as the largest Lyapunov exponent of the underlying process. Therefore, we do not consider this method in more detail in the following.

1.4 Example Time Series

To illustrate and evaluate the direct method for estimating the largest Lyapunov exponent, time series generated by four different chaotic dynamical systems are used that will be introduced in the following subsections.

1.4.1 The Hénon Map

The first system is the Hénon map [21]

$$\displaystyle\begin{array}{rcl} x_{1}(n + 1)& =& 1 - ax_{1}^{2}(n) + bx_{ 2}(n){}\end{array}$$

(1.40a)

$$\displaystyle\begin{array}{rcl} x_{2}(n + 1)& =& x_{1}(n){}\end{array}$$

(1.40b)

with parameters a = 1. 4 and b = 0. 3. The Lyapunov exponents of this system are $\lambda _{1} = 0.420$ and $\lambda _{2} = -1.624$ (computed with the natural logarithm $\ln (\cdot )$, note that for the Hénon map $\lambda _{1} +\lambda _{2} =\ln (b) = -1.204$). In the following we shall assume that a x ₁ time series of length N _d  = 4096 is given.² A special feature of the Hénon map is that its original coordinates (x ₁(n), x ₂(n)) coincide with 2-dimensional delay coordinates (x ₁(n), x ₁(n − 1)) = (x ₁(n), x ₂(n)). Figure 1.3a shows the Hénon attractor reconstructed from a clean {x ₁(n)} time series and in Fig. 1.3b a reconstruction is given based on a time series with additive measurement noise of signal-to-noise ration (SNR) of 30 dB (generated by adding normally distributed random numbers).

Fig. 1.3

Attractor of the Hénon map (1.40) (a) without noise and (b) with noise (SNR = 30 dB)

1.4.2 The Folded-Towel Map

The second system is the folded-towel map introduced in 1979 by Rössler [39]

$$\displaystyle\begin{array}{rcl} x(n + 1)& =& 3.8x(n)(1 - x(n)) - 0.05(y(n) + 0.35)(1 - 2z(n)){}\end{array}$$

(1.41a)

$$\displaystyle\begin{array}{rcl} y(n + 1)& =& 0.1[(y(n) + 0.35)(1 - 2z(n)) - 1](1 - 1.9x(n)){}\end{array}$$

(1.41b)

$$\displaystyle\begin{array}{rcl} z(n + 1)& =& 3.78z(n)(1 - z(n)) + 0.2y(n){}\end{array}$$

(1.41c)

which generates the chaotic attractor shown in Fig. 1.4. The folded-towel map has two positive Lyapunov exponents $\lambda _{1} = 0.427$, $\lambda _{2} = 0.378$, and a negative exponent $\lambda _{3} = -3.30$. The Kaplan–Yorke dimension of this attractor equals D _KY  = 2. 24.

Fig. 1.4

Hyperchaotic attractor of the folded-towel map (1.41), original coordinates (x, y, z) (length N _d  = 65, 536)

Figure 1.5 shows delay reconstructions based on x, y, and z time series of length N _d  = 65, 536 (i.e. 64k). In the first row (Fig. 1.5a–c) clean data are used while for the reconstructions shown in the second row (Fig. 1.5d–f) noisy data (64k) with signal-to-noise ratio (SNR) of 30 dB are used that were obtained by adding normally distributed random numbers to the clean data shown in the first row. These noisy time series will be used to evaluate the robustness of methods for estimating Lyapunov exponents.

Fig. 1.5

Delay reconstructions of the attractor of the folded-towel map (1.41). (a)–(c) Without and (d)–(f) with additive (measurement) noise of SNR 30 dB. Reconstruction from (a), (d) {x(n)} time series, (b), (e) {y(n)} time series, and (c), (f) {z(n)} time series

1.4.3 Lorenz-63 System

As an example of a low dimensional continuous time system we use the Lorenz-63 system [31] given by the following set of ordinary differential equations (ODEs)

$$\displaystyle\begin{array}{rcl} \dot{x}_{1}& =& \sigma (x_{2} - x_{1}){}\end{array}$$

(1.42a)

$$\displaystyle\begin{array}{rcl} \dot{x}_{2}& =& x_{1}(R - x_{3}) - x_{2}{}\end{array}$$

(1.42b)

$$\displaystyle\begin{array}{rcl} \dot{x}_{3}& =& x_{1}x_{2} - bx_{3}.{}\end{array}$$

(1.42c)

With parameter values $\sigma = 16$, R = 45. 92, and b = 4 this systems generates a chaotic attractor with Lyapunov exponents $\lambda _{1} = 1.51$, $\lambda _{2} = 0$, and $\lambda _{3} = -22.5$.

1.4.4 Lorenz-96 System

As an example of a continuous time system exhibiting complex dynamics we shall employ a 6-dimensional Lorenz-96 system [32] describing a ring of 1-dimensional dynamical elements. The differential equations for the model read

$$\displaystyle{ \frac{dx_{i}(t)} {dt} = x_{i-1}(t)(x_{i+1}(t) - x_{i-2}(t)) - x_{i}(t) + f }$$

(1.43)

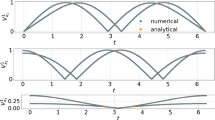
with i = 1, 2, …, 6, x ₋₁(t) = x ₅(t), x ₀(t) = x ₆(t), and x ₇(t) = x ₁(t). With a forcing parameter f = 10 the system generates a chaotic attractor characterized by a Lyapunov spectrum {1. 249, 0. 000, −0. 098, −0. 853, −1. 629, −4. 670} and a resulting Kaplan–Yorke dimension of D _KY  = 4. 18. Figure 1.6a shows the convergence of the six Lyapunov exponents upon their computation using the full model equations (1.43) and in Fig. 1.6b, a typical time series of the Lorenz-96 system is plotted.

Fig. 1.6

(a) Convergence of Lyapunov exponents of the 6-dimensional Lorenz-96 system (1.43) generated with parameter value f = 10. (b) Typical oscillation

1.5 Estimation of Largest Lyapunov Exponents Using Direct Methods

1.5.1 Convergence of Small Perturbations

As illustrated in Fig. 1.2a any (random) perturbation first undergoes a transient phase I and converges to the direction of the Lyapunov vector(s) corresponding to the largest Lyapunov exponent. Then, in phase II, it grows linearly (on a logarithmic scale) until the perturbation exceeds the linear range (phase III). In the following we shall study this convergence process for the four example systems which were introduced in the previous section. The asymptotic average stretching of almost any initial perturbation (tangent vector) $\mathbf{z}(0)$ is given by the largest Lyapunov exponent $\lambda _{1}$. Using the tangent space basis $\{\mathbf{v}^{(1)},\ldots,\mathbf{v}^{(m)}\}$ provided by the SVD (1.7) the initial tangent vector can be written as

$$\displaystyle{ \mathbf{z}(0) =\sum _{ m=1}^{M}c_{ i}\mathbf{v}^{(m)} = V \cdot \mathbf{ c} }$$

(1.44)

where $\mathbf{c} = (c_{1},\ldots,c_{M})$ denotes the vector of projection coefficients. Its temporal evolution is thus given by

$$\displaystyle{ \mathbf{z}(t) = D\phi ^{t}(\mathbf{x}) \cdot \mathbf{ z}(0) = U \cdot S \cdot V ^{tr} \cdot \mathbf{ z}(0) = U \cdot S \cdot \mathbf{ c} =\sum _{ m=1}^{M}c_{ m}\sigma _{m}\mathbf{u}^{(m)}. }$$

(1.45)

If we approximate the singular values $\sigma _{m}$ by $e^{\lambda _{m}t}$ we obtain for (the square of) the Euclidean norm of $\mathbf{z}(t)$

$$\displaystyle{ Z^{2}(t) =\Vert \mathbf{ z}(t)\Vert ^{2} =\sum _{ m=1}^{M}c_{ m}^{2}e^{2\lambda _{m}t} }$$

(1.46)

and this yields

$$\displaystyle{ \lim _{t\rightarrow \infty }\frac{1} {t}\ln \left (Z(t)\right ) =\lim _{t\rightarrow \infty }\frac{1} {t}\ln \left (\Vert \mathbf{z}(t)\Vert \right ) =\lim _{t\rightarrow \infty }\frac{1} {2}\ln \left (\sum _{m=1}^{M}c_{ m}^{2}e^{2\lambda _{m}t}\right )^{1/t} =\lambda _{ 1} }$$

(1.47)

because the term $e^{\lambda _{m}t}$ with the largest $\lambda _{m}$ dominates the sum as time t goes to infinity. The speed of convergence depends on the full Lyapunov spectrum. Figure 1.6 shows $\ln (Z(t)) =\ln (\Vert \mathbf{z}(t)\Vert )$ (as defined in Eq. (1.47)) vs. t for the Hénon map (1.40), the folded towel map (1.41), the Lorenz-63 system (1.42), and the Lorenz-96 system (1.43). While the local slopes of the Hénon map and the folded towel map reach the value of the largest Lyapunov exponent after a period of time of about t ≈ 1 the random initial tangent vectors $\mathbf{z}(0)$ of the Lorenz-96 system need about twice the time and converge to $\lambda _{1}$ only after t ≈ 2 (Fig. 1.7).

Fig. 1.7

(a) Average values of $\ln (Z(t)) =\ln (\Vert z(t)\Vert )$ vs. t (see Eq. (1.47)) for the Hénon map (red), the folded towel map (blue, dotted line), The Lorenz-63 system (green, dashed-dotted line) and the Lorenz-96 system (dashed line). The curves are computed by averaging 2000 realizations with randomly chosen initial vectors $\mathbf{z}(0)$ with $\Vert \mathbf{z}(0)\Vert = 1$. (b) Local slopes of curves shown in (a) indicating the convergence to the value of the corresponding largest Lyapunov exponent (given by horizontal dashed lines)

1.5.2 Hénon Map

Figure 1.8 shows an application of the direct estimation method to a {x ₁(n)} time series of the Hénon map (1.40). The time series has a length of N = 4096 samples, the lag equals L = 1, and different reconstruction dimensions D = 2, D = 4, and D = 6 are used. Figure 1.8a shows E _E (k) vs. k Δ t where Δ t = 1 denotes the sampling time and E _E (1.33) is computed with the Euclidean distance d _E (1.28). In Fig. 1.8b the slope

$$\displaystyle{ \frac{dE_{E}} {dt} ((k + 0.5)\varDelta t) \approx \frac{E_{E}(k + 1) - E_{E}(k)} {\varDelta t} = \frac{\varDelta E_{E}} {\varDelta t} }$$

(1.48)

is plotted. Figure 1.8c, d and e, f show the corresponding diagrams obtained with the distance measures d _F (1.30) and d _L (1.29), respectively. In all diagrams three phases occur (see also Fig. 1.2):

• First the difference vector $\mathbf{x}(m(n) + k) -\mathbf{ x}(n + k)$ converges for increasing k to the subspace spanned by the first Lyapunov vector(s). The slope increases.

• Then the difference vector experiences the expansion rate given by the largest Lyapunov exponent. The slope is constant indicating exponential divergence.

• Finally, the lengths of the difference vector exceeds the range of the linearized dynamics and its length saturates due to nonlinear folding in the (reconstructed) state space. The slope decreases.

Fig. 1.8

Direct estimation of the largest Lyapunov exponent from a Hénon time series for different reconstruction dimensions D = 2, D = 4, D = 6 using a lag of L = 1. The diagrams (a), (c), and (e) show E _E , E _L and E _F vs. k Δ t with Δ t = 1 for different measures of distance (1.28), (1.29), and (1.30). In (b), (d), and (f) the corresponding slopes Δ E∕Δ t vs. k Δ t (Eq. (1.48)) are shown. The dashed lines indicate the true result $\lambda _{1} = 0.42$

The lengths of the linear scaling regions in Fig. 1.8a, c, e and of the plateaus in Fig. 1.8b, d, f shrink with increasing embedding dimension. They also shrink, if the length of the time series is reduced or the number of nearest neighbours K is increased.

The results shown in Fig. 1.8 are computed by using each reconstructed state as a reference point. Reliable estimates may be obtained, however, already with a subset of reference points which reduces computation time almost linearly. This subset can be randomly selected from all reconstructed states or it can be chosen to include only those reconstructed states that possess the nearest neighbours. The latter choice has the advantage that more steps of the diverging neighbouring trajectory segments are governed by the linearised flow and exhibit exponential growths resulting in longer scaling regions. Figure 1.9 shows results based on those 25 % of the total number N of reference points that possess the closest neighbours (i.e., where the chosen distance measure d _E , d _F , or d _L (see Eqs. (1.28)–(1.30)) takes the smallest values). The scaling regions are extended compared to Fig. 1.8 but the local slopes plotted in Fig. 1.9c, d, f show more statistical fluctuations due to the smaller number of reference points (for D = 6 we have N _r  = 1018 reference points in Fig. 1.9e, f compared to N _r  = 4070 inFig. 1.8e, f).

Fig. 1.9

Direct estimation of the largest Lyapunov exponent from a Hénon time series for different reconstruction dimensions D = 2, D = 4, D = 6 using a lag of L = 1. The diagrams (a), (c), and (e) show E _E , E _L and E _F vs. k Δ t with Δ t = 1 for different measures of distance (1.28), (1.29), and (1.30). In (b), (d), and (f) the corresponding slopes Δ E∕Δ t vs. k Δ t (Eq. (1.48)) are shown. The dashed lines indicate the true result $\lambda _{1} = 0.42$. In contrast to Fig. 1.8 only those 25 % of the reconstructed states with closest neighbours have been used as reference points

To illustrate the impact of (additive) measurement noise Fig. 1.10 shows results obtained with a noisy Hénon time series (compare Fig. 1.2b). As can be seen in all diagrams noise leads to shorter scaling intervals and a bias towards smaller values underestimating the largest Lyapunov exponent. Decreasing the number N _r of reference points (with nearest neighbours) reduces the bias but increases statistical fluctuations.

Fig. 1.10

Direct estimation of the largest Lyapunov exponent from a noisy Hénon time series (SNR 30 dB) for different reconstruction dimensions D = 2, D = 4, D = 6 using a lag of L = 1. The diagrams (a), (c), and (e) show E _E , E _L and E _F vs. k Δ t with Δ t = 1 for different measures of distance (1.28), (1.29), and (1.30). In (b), (d), and (f) the corresponding slopes Δ E∕Δ t vs. k Δ t (Eq. (1.48)) are shown. All reconstructed states are used as reference points and the dashed lines indicate the true result $\lambda _{1} = 0.42$

1.5.3 Folded Towel Map

To address the question whether the direct methods also work with hyper-chaotic dynamics we shall now analyze time series generated by the folded-towel map (1.41). Figure 1.11 shows results obtained from a {x(n)} time series of length N _d  = 65, 536 using all N reconstructed states as reference points. As can be seen no linear scaling region exists, because this time series provides poor reconstructions of the underlying attractor (compare the reconstruction shown in Fig. 1.4a). Results can be improved by using a longer time series and only those reference points with very close neighbours. Alternatively, one may consider reconstructions based on a {y(n)} time series which provide better unfolding of the chaotic attractor (compare Fig. 1.4b). Figure 1.12 shows results computed using a {y(n)} time series from the folded-towel map (1.41) with length N _d  = 65, 536, where only 10 % of the reconstructed states (with closest neighbours) are used for estimating exponential divergence. As can be seen the {y(n)} time series is more suited for estimating the largest Lyapunov exponent of the folded towel map and exhibits for reconstruction dimensions D = 4 and D = 6 the expected scaling behaviour. For D = 2 no clear scaling occurs and results differ significantly from those obtained with D = 4 and D = 6, because 2-dimensional delay coordinates are not sufficient for reconstructing this chaotic attractor (with Kaplan–Yorke dimensionD _KY  = 2. 24).

Fig. 1.11

Direct estimation of the largest Lyapunov exponent from a {x(n)} time series of the folded-towel map of length N _d  = 65, 536 for different embedding dimensions D = 2, D = 4, D = 6 using a lag of L = 1. The diagrams (a), (c), and (e) show E vs. k Δ t with Δ t = 1 for the Euclidean norm. In (b), (d), and (f) the corresponding slopes Δ E∕Δ t vs. k (Eq. (1.48)) are shown. The dashed lines indicate the true result $\lambda _{1} = 0.43$

Fig. 1.12

Direct estimation of the largest Lyapunov exponent from a {y(n)} time series of the folded-towel map of length N _d  = 65, 536 for different embedding dimensions D = 2, D = 4, D = 6 using a lag of L = 1. The diagrams (a), (c), and (e) show E vs. k Δ t with Δ t = 1 for the Euclidean norm. In (b), (d), and (f) the corresponding slopes Δ E∕Δ t vs. k (Eq. (1.48)) are shown. The dashed lines indicate the true result $\lambda _{1} = 0.43$. Only those 10 % of the reconstructed states possessing the most nearest neighbours are used as reference points for estimating exponential divergence (N _r  = 6551 for D = 6)

Figure 1.13 shows results obtained with a noisy {y(n)} time series (SNR 30 dB) generated by the folded-towel map (compare Fig. 1.4e) with reconstruction dimension D = 4, D = 6, and D = 8 and 10 % reference points. Scaling intervals are barely visible due to the added measurement noise.

Fig. 1.13

Direct estimation of the largest Lyapunov exponent from a noisy {y(n)} time series (SNR = 30 dB) of the folded-towel map of length N _d  = 65, 536 for different embedding dimensions D = 4, D = 6, D = 8 using a lag of L = 1. The diagrams (a), (c), and (e) show E vs. k Δ t with Δ t = 1 for the Euclidean norm. In (b), (d), and (f) the corresponding slopes Δ E∕Δ t vs. k (Eq. (1.48)) are shown. The dashed lines indicate the true result $\lambda _{1} = 0.43$. Only 10 % of the reconstructed states with the smallest distances to their neighbours are used for estimating (exponential) growth rates

1.5.4 Lorenz-63

We shall now use as data source the Lorenz-63 system which is an example of a low dimensional continuous system exhibiting deterministic chaos. Figure 1.14 shows results for a x ₁ time series of length N _d  = 65, 536 sampled with Δ t = 0. 025 for reconstruction dimensions D = 4, D = 12, and D = 21 using a delay of L = 1. The resulting time windows (D − 1)L covered by the delay vectors are 3, 11, and 20, respectively, where the latter corresponds to a typical oscillation period of the Lorenz-63 system. Here the sampling time Δ t = 0. 025 is much smaller compared to the iterated maps considered so far. To avoid strong fluctuations of the slope values the derivative Δ E∕Δ t is estimated by

$$\displaystyle{ \frac{\varDelta E} {\varDelta t} (t) \approx \frac{E(t + 3\varDelta t) - E(t - 3\varDelta t)} {6\varDelta t} }$$

(1.49)

where E-values at t ± 3Δ are used when estimating Δ E∕Δ t at time t. Note that the oscillations are less pronounced for higher reconstruction dimensions. Only 20 % of the reconstructed states are used as reference points (those which possess the closest neighbours). The linear scaling regions are clearly visible in the semi-logarithmic diagrams.

Fig. 1.14

Direct estimation of the largest Lyapunov exponent from a {x(n))} time series of the Lorenz-63 system of length N _d  = 65, 536 for different reconstruction dimensions D = 4, D = 12, and D = 21, all with a lag of L = 1. As reference points only those 20 % of the reconstructed states are used that possess the nearest neighbours. The diagrams (a), (c), and (e) show E vs. k Δ t with Δ t = 0. 025 for the Euclidean norm. In (b), (d), and (f) the corresponding slopes Δ E∕Δ t vs. k (Eq. (1.48)) are shown. The dashed lines indicate the true result $\lambda _{1} = 1.51$

Figure 1.15 shows diagrams with reconstruction dimensions D = 6, D = 11, and D = 21 and corresponding lags L = 4, L = 2, and L = 1, respectively. In this case all reconstructed states represent the same windows in time with a length of (D − 1)L = 5 ⋅ 4 = 10 ⋅ 2 = 20 ⋅ 1 = 20 time steps of size Δ t = 0. 025, i.e. a period of time of length 20 ⋅ 0. 025 = 0. 5 which is close to the period of the natural oscillations of the Lorenz-63 system. The results for all three state space reconstruction coincide very well and the amplitude of oscillations of the slope is much smaller compared to the results shown in Fig. 1.14.

Fig. 1.15

Direct estimation of the largest Lyapunov exponent from a {x(n))} time series of the Lorenz-63 system of length N _d  = 65, 536 for different reconstruction dimensions D = 6, D = 11, and D = 21, with lags L = 4, L = 2, and L = 1, respectively. As reference points only those 20 % of the reconstructed states are use that possess the nearest neighbours. The diagrams (a), (c), and (e) show E vs. k Δ t with Δ t = 0. 025 for the Euclidean norm. In (b), (d), and (f) the corresponding slopes Δ E∕Δ t vs. k (Eq. (1.48)) are shown. The dashed lines indicate the true result $\lambda _{1} = 1.51$

1.5.5 Lorenz-96

Although it possesses only a single positive Lyapunov exponent the 6-dimensional Lorenz-96 systems turns out to be a surprisingly challenging case for estimating the largest Lyapunov exponent from time series. Figure 1.16 shows estimation results for time series of different lengths (first column: N _d  = 10, 000, second column N _d  = 100, 000, third column N _d  = 1, 000, 000) and a different number of reference points given by those reconstructed states with closest neighbours (first row: 1 %, second row: 10 %). All examples employing 10 % of the reconstructed states as reference points provide diagrams where no suitable scaling region exists (even with N _d  = 1, 000, 000 data points, see Fig. 1.16F, f). If only 1 % of the reconstructed states is used, the diagram based on N _d  = 100, 000 samples (Fig. 1.16B, b) gives a rough estimate of $\lambda _{1}$ and with N _d  = 1, 000, 000 data points a linear scaling regime (with the correct slope) is clearly visible in Fig. 1.16C, c. The reconstruction dimensions used here are D = 9, 18, and 36 with lags L = 4, 2, and 1, respectively, resulting in window lengths 8 ⋅ 4 = 32, 17 ⋅ 2 = 34, and 35 ⋅ 1 = 35. The slopes given in Fig. 1.16 were computed with Eq. (1.48) and only the case of the Euclidean norm E _E is shown here, because E _F and E _L show very similar results. The observation that a time series of length N _d  = 1, 000, 000 (at least) is required to obtain reliable and correct results is consistent with the results of Eckmann and Ruelle [13] who estimated that the amount of required data points increases as a power of the attractor dimension. For comparison, the Kaplan–Yorke dimension of the Lorenz-96 attractor (D _KY  = 4. 18) is more than twice as large as the dimension of the Lorenz-63 model and so instead of 64k data a time series of length longer than 64²k = 4M would be necessary to obtain comparable results.³

Fig. 1.16

Direct estimation of the largest Lyapunov exponent from a {x ₁(n))} time series of the Lorenz-96 system for different reconstruction dimensions D = 9, D = 18, and D = 36 with corresponding lags L = 4, L = 2, and L = 1, respectively. Diagrams (A)–(F) show E _E vs. k Δ t with Δ t = 0. 025 and diagrams (a)–(f) give the corresponding local slopes Δ E∕Δ t vs. k (Eq. (1.48)) (E _E is the error with respect to the Euclidean norm). The dashed lines indicate the true result $\lambda _{1} = 1.249$. In diagrams (A)–(C), (a)–(c) only 1 % of the reconstructed states with the smallest distances to their neighbours are selected for estimating (exponential) growth rates, while in (D)–(F), (d)–(f) 10 % are used. Diagrams (A), (a) and (D), (d) are generated using N _d  = 10, 000 samples, figures (B), (b) and (E), (e) are computed from N _d  = 100, 000 data points, and diagrams (C), (c) and (F), (f) show results obtained from a time series of length N _d  = 1, 000, 000

1.6 Conclusion

Estimating Lyapunov exponents from time series is a challenging task and since any algorithm provides “results” (i.e., numbers) some error control is very important to avoid misleading interpretation of the values obtained. From the variety of estimation methods, currently only the direct methods provide some feedback to the user whether local exponential divergence is properly identified or not. The presented examples included cases where this was not the case, due to:

• (a) a too short time series (compared to the dimension of the underlying attractor), resulting in neighbouring reconstructed states whose distances exceed the range of validity of locally linearized dynamics, see for example Fig. 1.16A, B

• (b) (measurement) noise, see for example Fig. 1.13, or

• (c) an observable which is not suitable (to faithfully unfold the dynamics in reconstruction space), see for example Fig. 1.11.

This failure was in all cases directly visible in the semi-logarithmic diagrams showing the average growth of mutual distances of neighbouring states vs. time, where no linear scaling region could be identified. If, on the contrary, such a linear scaling region exists then it provides strong evidence for deterministic chaos and the estimated slope can be trusted to be a good estimate of the largest Lyapunov exponent. The choice of the norm for quantifying the divergence of trajectories turned out to be noncritical because all three norms used (E _E , E _F , and E _L , see Sect. 1.3.2) used exhibited equivalent performance.

A particular challenge are time series from high dimensional chaotic attractors. Eckmann and Ruelle [13] estimated that the number of required data points N _d exponentially grows with the attractor dimension D _a as $N_{d} \approx const^{D_{a}}$. The results obtained for the folded-towel map (Sect. 1.5.3) and the 6-dimensional Lorenz-96 model (Sect. 1.5.5) confirmed this (‘pessimistic’) prediction. Although the 6-dimensional Lorenz-96 model possesses a chaotic attractor with a single positive Lyapunov exponent it possesses a Kaplan–Yorke dimension of D _KY  = 4. 18. Due to this relatively high attractor dimension, satisfying estimates of the largest Lyapunov exponent were obtained only from very long time series (Fig. 1.16C) and if only those trajectory segments are used for estimating local divergence which started from very closely neighbouring reconstructed states (1 % in Fig. 1.16C). This selection of suitable reference points is very similar to a fixed size approach (see Sect. 1.3.2) using a relatively small radius ε and the results obtained for the folded-towel map and the Lorenz-96 model indicate its importance for coping with high dimensional chaos. On the other hand, these examples clearly show that data requirements (and practical difficulties) increase exponentially with the dimension of the underlying attractor (at least for the direct estimation methods employed here) and this fact imposes fundamental bounds for estimating Lyapunov exponents from time series generated by processes of medium or even high complexity.

Appendix

Let $\varphi ^{k}: \mathbb{R}^{D} \rightarrow \mathbb{R}^{D}$ be the induced flow in reconstruction space mapping reconstructed states $\mathbf{x}_{n} = (s_{n},s_{n+L},\ldots,s_{n+(D-1)L})$ to their future values $\varphi ^{k}(\mathbf{x}_{n}) =\mathbf{ x}_{n+k}$. To estimate the D × D Jacobian matrices $D\varphi ^{k}(\mathbf{x})$ from the temporal evolution of the reconstructed states $\{\mathbf{x}_{n}\}_{n=1}^{N}$ the flow $\varphi ^{k}$ has to be approximated by a general ansatz (black-box model) like a neural network [20] or a superposition of I basis functions $b_{i}: \mathbb{R}^{D} \rightarrow \mathbb{R}$ providing an approximating function

$$\displaystyle{ \psi ^{k}(\mathbf{x}) = \left (\psi _{ 1}^{k}(\mathbf{x}),\ldots,\psi _{ D}^{k}(\mathbf{x})\right ) = \left (\sum _{ i=1}^{I}c_{ i1}b_{i}(\mathbf{x}),\ldots,\sum _{i=1}^{I}c_{ iD}b_{i}(\mathbf{x})\right ) =\mathbf{ b}(\mathbf{x}) \cdot C }$$

(1.50)

where C = (c _ij ) denotes a I × D matrix of coefficients with columns $\mathbf{c}^{(\,j)}$ ( j = 1, …, D) that have to be estimated and $\mathbf{b}(\mathbf{x}) = (b_{1}(\mathbf{x}),\ldots,b_{I}(\mathbf{x}))$ is a row vector consisting of the values of all basis functions evaluated at the state $\mathbf{x}$.⁴

For the special choice k = L (evolution time step equals the lag of the delay coordinates) the first D − 1 components of the map $\psi ^{k}(\mathbf{x}_{n})$ are known (due to the delay reconstruction) and only for the last component an approximation is required

$$\displaystyle\begin{array}{rcl} \psi ^{L}(\mathbf{x})& =& \left (s_{ n+L},s_{n+2L},\ldots,s_{n+(D-1)L},\sum _{i=1}^{I}c_{ i}b_{i}(\mathbf{x})\right ){}\end{array}$$

(1.51)

$$\displaystyle\begin{array}{rcl} & =& (x_{n2},\ldots,x_{nD},\mathbf{b}(\mathbf{x}) \cdot \mathbf{ c}).{}\end{array}$$

(1.52)

With this notation the approximation $D\psi ^{k}(\mathbf{x})$ of the desired Jacobian matrix $D\varphi ^{k}(\mathbf{x})$ of the (induced) flow $\varphi (\mathbf{x})$ in embedding space can be written as

$$\displaystyle{ D\psi ^{k}(\mathbf{x}) = \left (\begin{array}{ccc} \frac{\partial b_{1}} {\partial x_{1}} & \ldots & \frac{\partial b_{I}} {\partial x_{1}}\\ \vdots & \ddots & \vdots \\ \frac{\partial b_{1}} {\partial x_{D}} & \ldots & \frac{\partial b_{I}} {\partial x_{D}} \end{array} \right )\cdot C = G\cdot C }$$

(1.53)

where G will be called derivative matrix in the following.

For k = L the Jacobian matrix of the approximating function ψ ^k is given as

$$\displaystyle{ D\psi ^{L}(\mathbf{x}) = \left (\begin{array}{ccccc} 0 &1&0&\ldots & 0\\ 0 &0 &1 &\ldots & 0\\ \vdots & \vdots & \vdots &\ddots & \vdots \\ 0 &0&0&\ldots & 1 \\ \sum _{i=1}^{I}c_{i} \frac{\partial b_{i}} {\partial x_{1}} & \ldots & \ldots & \ldots & \sum _{i=1}^{I}c_{i} \frac{\partial b_{i}} {\partial x_{D}} \end{array} \right ) }$$

(1.54)

Linear basis functions $b_{i}(\mathbf{x})$ can be used to model the (linearized) flow (very) close to the reference points $\mathbf{x}_{n}$ along the orbits. To approximate the flow in a larger neighbourhood of $\mathbf{x}_{n}$ or even globally, nonlinear basis functions are required, like multidimensional polynomials [2, 4–7], or radial basis functions [23, 24, 35].

To estimate the coefficient matrix C in Eq. (1.50) or the coefficient vector $\mathbf{c}$ in Eq. (1.51) we select a set of representative states $\{\mathbf{z}^{j}\}$ whose temporal evolution $\varphi ^{k}(\mathbf{z}^{j})$ is known. For local modeling this set of states consists of nearest neighbours $\{\mathbf{x}_{m(n)}: m(n) \in \mathcal{U}_{n}\}$ of the reference point $\mathbf{x}_{n}$ where $\mathcal{U}_{n}$ defines the chosen neighbourhood that can be of fixed mass (a fixed number K of nearest neighbours of $\mathbf{x}_{n}$) or of fixed size (all points with distance smaller than a given bound ε). For global modeling of the flow the set $\{\mathbf{z}^{j}\}$ is usually a (randomly sampled) subset of all reconstructed states. Let

$$\displaystyle{ Y = \left (\begin{array}{cccc} \varphi _{1}^{k}({\boldsymbol z^{1}}) &\ldots & \varphi _{D}^{k}({\boldsymbol z^{1}})\\ \vdots &\vdots & \vdots \\ \varphi _{1}^{k}({\boldsymbol z^{J}})&\ldots &\varphi _{D}^{k}({\boldsymbol z^{J}})\\ \end{array} \right ) }$$

(1.55)

be a J × D matrix whose rows are components the (known) future values $\varphi ^{k}(\mathbf{z}^{j})$ of the J states $\{\mathbf{z}^{j}\}$ and let

$$\displaystyle{ B = \left (\begin{array}{cccc} b_{1}({\boldsymbol z^{1}}) &\ldots & b_{I}({\boldsymbol z^{1}})\\ \vdots &\vdots & \vdots \\ b_{1}({\boldsymbol z^{J}})&\ldots &b_{I}({\boldsymbol z^{J}})\\ \end{array} \right ) }$$

(1.56)

be the J × I (design) matrix [37] whose rows are the basis functions b _i (⋅ ) evaluated at the selected states $\{\mathbf{z}^{j}\}$. Using this notation the approximation task can be stated as a minimization problem with a cost function

$$\displaystyle{ g(\mathbf{c}^{(j)}) =\Vert B \cdot \mathbf{ c}^{(j)} -\mathbf{ y}^{(j)}\Vert ^{2} }$$

(1.57)

where y ^(j) denotes the j-th column of the matrix Y (given in Eq. (1.55)), or

$$\displaystyle{ g(C) =\Vert B \cdot C - Y \Vert _{F}^{2} }$$

(1.58)

where $\Vert \cdot \Vert _{F} =$ denotes the Frobenius matrix norm (also called Schur norm).

The solution of this optimization problem may suffer from the fact that typically the states $\{\mathbf{z}^{j}\}$ cover only some subspace of the reconstructed state space. Therefore, in particular for local modeling ill-posed optimization problems may occur with many almost equivalent solutions. For estimating Lyapunov exponents we prefer to select solutions for the coefficient matrix C that provide partial derivatives (elements of the Jacobian matrix) with small magnitudes, because in this way spurious Lyapunov exponents are shifted towards $-\infty$. This goal can be achieved by Tikhonov–Philips regularization where the cost function of the optimization problem (1.58) is extended by a term ρ ∥ A ⋅ C ∥ resulting in

$$\displaystyle{ g(\mathbf{c}^{(j)}) =\Vert B \cdot \mathbf{ c}^{(j)} -\mathbf{ y}^{(j)}\Vert ^{2} +\rho ^{2}\Vert A \cdot \mathbf{ c}^{(j)}\Vert ^{2} }$$

(1.59)

where A denotes a so-called stabilizer matrix and $\rho \in \mathbb{R}$ is the regularization parameter that is used to control the impact of the regularization term on the solution of the minimization problem. If the identity matrix is used as stabilizer A = I then $\Vert \mathbf{c}(j)\Vert$ is minimized and the solution with the smallest coefficients is selected (also called Tikhonov stabilization). Another possible choice is the derivative matrix (1.53) A = G. In this case we minimize the sum of all squared singular values $\sigma _{i}$ of $D\psi ^{k}(\mathbf{x}) = U \cdot S \cdot V ^{tr}$, because

$$\displaystyle\begin{array}{rcl} \Vert G \cdot C\Vert _{F}^{2}& =& \Vert D\psi ^{k}(\mathbf{x})\Vert _{ F}^{2} = \mbox{ trace}\left ([D\psi ^{k}(\mathbf{x})]^{tr} \cdot D\psi ^{k}(\mathbf{x})\right ){}\end{array}$$

(1.60)

$$\displaystyle\begin{array}{rcl} & =& \mbox{ trace}\left (V \cdot S^{2} \cdot V ^{tr}\right ) = \mbox{ trace}(S^{2}) =\sum _{ i=1}^{D}\sigma _{ i}^{2}{}\end{array}$$

(1.61)

and so we minimize Lyapunov exponents by maximizing contraction rates.

To solve the optimization problem (1.59) we rewrite it as an augmented least squares problem with a cost function

$$\displaystyle{ g(\mathbf{c}^{(j)}) =\Vert \left (\begin{array}{c} B \\ \rho A \end{array} \right )\cdot \mathbf{c}^{(j)}-\left (\begin{array}{c} \mathbf{y}^{(j)} \\ 0\end{array} \right )\Vert ^{2} =\Vert \hat{B} \cdot \mathbf{c}^{(j)}-\hat{\mathbf{y}} ^{(j)}\Vert ^{2} }$$

(1.62)

that can be minimized by a solution of the corresponding normal equations

$$\displaystyle{ \left (B^{tr} \cdot B +\rho ^{2}A^{tr} \cdot A\right ) \cdot \mathbf{ c}^{(j)} = B^{tr} \cdot \mathbf{ y}^{(j)} }$$

(1.63)

using a sequence of Householder transformations [35] or by employing the singular value decomposition of the matrix $\hat{B} = U_{\hat{B} } \cdot S_{\hat{B} } \cdot V _{\hat{B} }^{tr}$ providing the minimal solution [37]

$$\displaystyle{ \mathbf{c}^{(j)} = V _{\hat{ B} } \cdot S_{\hat{B} }^{-1} \cdot U_{\hat{ B} }^{tr} \cdot \hat{\mathbf{y}} ^{(j)}. }$$

(1.64)

for each column $\hat{\mathbf{c}} ^{(j)}$ or

$$\displaystyle{ C = V _{\hat{B} } \cdot S_{\hat{B} }^{-1} \cdot U_{\hat{ B} }^{tr} \cdot \hat{Y } }$$

(1.65)

for the full coefficient matrix C where $\hat{Y } = \left (\begin{array}{c} Y\\ 0 \end{array} \right )$.

For the stabilizer A = I the elements of the diagonal matrix $S_{\hat{B} }^{-1}$ are given by

$$\displaystyle{ \frac{\hat{\sigma }_{i}} {\hat{\sigma }_{i}^{2} +\rho ^{2}} }$$

(1.66)

where $\hat{\sigma }_{i}$ are the diagonal elements of $S_{\hat{B} }$ (i.e., the singular values of$\hat{B}$).