Optimal Algorithms and a PTAS for Cost-Aware Scheduling

Abstract

We consider a natural generalization of classical scheduling problems in which using a time unit for processing a job causes some time-dependent cost which must be paid in addition to the standard scheduling cost. We study the scheduling objectives of minimizing the makespan and the sum of (weighted) completion times. It is not difficult to derive a polynomial-time algorithm for preemptive scheduling to minimize the makespan on unrelated machines. The problem of minimizing the total (weighted) completion time is considerably harder, even on a single machine. We present a polynomial-time algorithm that computes for any given sequence of jobs an optimal schedule, i.e., the optimal set of time-slots to be used for scheduling jobs according to the given sequence. This result is based on dynamic programming using a subtle analysis of the structure of optimal solutions and a potential function argument. With this algorithm, we solve the unweighted problem optimally in polynomial time. Furthermore, we argue that there is a $(4+{\varepsilon })$-approximation algorithm for the strongly NP-hard problem with individual job weights. For this weighted version, we also give a PTAS based on a dual scheduling approach introduced for scheduling on a machine of varying speed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

We consider a natural generalization of classical scheduling problems in which occupying a time slot incurs certain cost that may vary over time and which must be paid in addition to the actual scheduling cost. Such a framework has been proposed recently in [11] and [7]. It models additional cost for operating servers or machines that vary over time such as, e.g., labor cost that may vary by the day of the week, or the hour of the day [11], or electricity cost fluctuating over day time [7]. On the one hand, the latter have economically a huge impact on facilities with enormous power consumption such as large data centers, and on the other hand, these fluctuations reflect the imbalance between generation and consumption of electricity on a daily or weekly basis. Hence, cost aware scheduling is economically profitable and supports an eco-aware usage and generation of energy. Another motivation stems from cloud computing. Users of such services, e.g., Amazon EC2, are offered time-varying pricing schemes for processing jobs on a remote cloud server [1]. It is a challenging task for them to optimize the tradeoff between resource provisioning cost and the scheduling quality.

Problem Definition. We first describe the underlying classical scheduling problems. We are given a set of jobs $J:= \left\{ 1,\ldots ,n\right\}$ where every job $j\in J$ has given a processing time $p_j\in \mathbb {N}$ and possibly a weight $w_j \in \mathbb {Q}_{\ge 0}$. The task is to find a preemptive schedule on a single machine such that the total (weighted) completion time, $\sum _{j\in J}w_jC_j$, is minimized. Here $C_j$ denotes the completion time of job j. In the standard scheduling notation, this problem is denoted as $1 \,|\, pmtn \,|\, \sum (w_j)C_j$. We also consider makespan minimization on unrelated machines, typically denoted as $R \,|\, pmtn \,|\, C_{\max }$. Here we are given a set of machines M, and each job $j\in J$ has an individual processing time $p_{ij}\in \mathbb {N}$ for running on machine $i\in M$. The task is to find a preemptive schedule that minimizes the makespan, that is, the completion time of the latest job.

In this paper, we consider a generalization of these scheduling problems within a time-varying reservation cost model. We are given a cost function $e:\mathbb {N} \rightarrow \mathbb {R}$, where e(t) denotes the reservation cost for processing job(s) at time t. We assume that e is piecewise constant with given breakpoints at integral time points. We assume, more formally, that time is discretized into unit-size time slots, and the time horizon is partitioned into given intervals $I_k =\left[ s_k,d_k\right)$ with $s_k,d_k \in \mathbb {N}$, $k=1,\ldots ,K$, within which unit-size time slots have the same unit reservation cost $e_k$. To ensure feasibility, let $d_K\ge \sum _{j\in J} \min _{i\in M} p_{ij}$.

Given a schedule ${\mathcal {S}}$, let y(t) be a binary variable indicating if any processing is assigned to time slot $\left[ t,t+1\right)$. The reservation cost in ${\mathcal {S}}$ is $E({\mathcal {S}})=\sum _{t} e(t) y(t)$. That means, for any time unit that is used in ${\mathcal {S}}$ we pay the full unit reservation cost, even if the unit is only partially used. We also emphasize that in case of multiple machines, a reserved time slot can be used by all machines. This models applications in which reserving a time unit on a server gives access to all processors on this server.

The overall objective now is to find a schedule that minimizes the scheduling objective, $C_{\max }$ resp. $\sum _{j\in J}w_jC_j$, plus the reservation cost E. We refer to the resulting problems as $R \,|\, pmtn \,|\, C_{\max } + E$ and $1 \,|\, pmtn \,|\, \sum w_jC_j + E$.

Related Work. Scheduling with time-varying reservation cost (aka variable time slot cost) has been studied explicitly in [11] and [7]. The seminal paper [11] is concerned with several non-preemptive single machine problems, which are polynomial-time solvable in the classical setting, such as minimizing the total completion time, lateness, and total tardiness, or maximizing the weighted number of on-time jobs. These problems are shown to be strongly NP-hard when taking reservation cost into account, while efficient algorithms exist for restricted reservation cost functions. In particular, the problem $1 \,|\, \,|\, \sum C_j + E$ is strongly NP-hard, and it is efficiently solvable when the reservation cost is increasing or convex non-increasing [11]. The research focus in [7] is on online flow-time minimization using resource augmentation. Their main result is a scalable algorithm that obtains a constant performance guarantee when the machine speed is increased by a constant factor and there are only $K=2$ distinct unit reservation cost. They also show that, in this online setting, for arbitrary K there is no constant speedup-factor that allows for a constant approximate solution.

In this paper, we study the simpler—but not yet well understood—offline problem without release dates. For this problem, the authors in [7] announce the following results: a pseudo-polynomial $(4+{\varepsilon })$-approximation for $1 \,|\, pmtn \,|\, \sum w_jC_j + E$, which gives an optimal solution in case that all weights are equal, and a constant approximation in quasi-polynomial time for a constant number of distinct reservation costs or when using a machine that is processing jobs faster by a constant factor.

The general concept of taking into consideration additional (time-dependent) cost for resource utilization when scheduling has been implemented differently in other models. We mention the area of energy-aware scheduling, where the energy consumption is taken into account (see [2] for an overview), or scheduling with generalized non-decreasing (completion-) time dependent cost functions, such as minimizing $\sum _j w_jf(C_j)$, e.g. [5, 6, 10], or even more general job-individual cost functions $\sum _j f_j(C_j)$, e.g. [3]. Our model differs fundamentally since our cost function may decrease with time, because delaying the processing in favor of cheaper time slots may decrease the overall cost. This is not the case in the above-mentioned models. Thus, in our framework we have the additional dimension in decision-making of choosing the time slots to be reserved.

There is also some similarity between our model and scheduling on a machine of varying speed. Notice that the latter problem (with $\sum _j w_jC_j$ as objective function) can be reformulated as minimizing $\sum _j w_jf(C_j)$ on a single machine with constant speed. Interestingly, the independently studied problem of scheduling with non-availability periods, see e.g. the survey [9], is a special case of both, the time-varying speed and the time-varying reservation cost model. Indeed, machine non/availability can be expressed either by 0 / 1-speed or equivalently by $\infty /0$ unit reservation cost. Results shown in this context imply that our problem $1 \,|\, pmtn \,|\, \sum _j w_j C_j + E$ is strongly NP-hard, even if there are only two distinct unit reservation costs [12].

Our Contribution. We present new optimal algorithms and best-possible approximation results for a generalization of standard scheduling problems to a framework with time-varying reservation cost.

Firstly, we give an optimal polynomial-time algorithm for the problem $R \,|\, pmtn \,|\, C_{\max }+E$ (Sect. 2). It relies on a known algorithm for the problem without reservation cost [8] to determine the optimal number of time slots to be reserved, together with a procedure for choosing the time slots to be reserved.

Our main results concern single-machine scheduling to minimize the total (weighted) completion time (Sect. 3). We present an algorithm that computes for a given ordered set of jobs an optimal choice of time slots to be used for scheduling. We derive this by first showing structural properties of an optimal schedule, which we then exploit together with a properly chosen potential function in a dynamic program yielding polynomial running time. Based on this algorithm, we show that the unweighted problem $1 \,|\, pmtn \,|\, \sum C_{j} + E$ can be solved in polynomial time and that there is a $(4+{\varepsilon })$-approximation algorithm for the weighted version $1 \,|\, pmtn \,|\, \sum w_j C_{j} + E$. A pseudo-polynomial $(4+{\varepsilon })$-approximation has been known before [7]. While pseudo-polynomial time algorithms are rather easy to derive, it is quite remarkable that our DP’s running time is polynomial in the input, in particular, independent of $d_K$.

Finally, we design for the strongly NP-hard weighted problem variant (Sect. 4) a pseudo-polynomial algorithm that computes for any fixed ${\varepsilon }$ a $(1+{\varepsilon })$-approximate schedule for $1 \,|\, pmtn \,|\, \sum w_jC_j + E$. If $d_K$ is polynomially bounded, then the algorithm runs in polynomial time for any ${\varepsilon }$, i.e., it is a polynomial-time approximation scheme (PTAS). In terms of approximation, our algorithm is best possible since the problem is strongly NP-hard even if there are only two different reservation costs [12].

Our approach is inspired by a recent PTAS for scheduling on a machine of varying speed [10] and it uses some of its properties. As discussed above, there is no formal mathematical relation known between these two seemingly related problems which allows to directly apply the result from [10]. The key is a dual view on scheduling: instead of directly constructing a schedule in the time-dimension, we first construct a dual scheduling solution in the weight-dimension which has a one-to-one correspondence to a true schedule. We design an exponential-time dynamic programming algorithm which can be trimmed to polynomial time using techniques known for scheduling with varying speed [10].

For both the makespan and the min-sum problem, job preemption is crucial for obtaining worst-case bounds. For non-preemptive scheduling, a reduction from 2-Partition shows that no approximation within a polynomial ratio is possible, unless P$=$NP, even if there are only two different reservation costs, 0 and $\infty$.

Finally, we remark that in general it is not clear that a schedule can be encoded polynomially in the input. However, for our completion-time based minimization objective, it is easy to observe that if an algorithm reserves p unit-size time slots in an interval of equal cost, then it reserves the first p slots within this interval, which simplifies the structure and output of an optimal solution.

2 Minimizing the Makespan on Unrelated Machines

The standard scheduling problem without reservation $R \,|\, pmtn \,|\, C_{\max }$ can be solved optimally in polynomial time [8]. We show that taking into account time-varying reservation cost does not significantly increase the problem complexity.

Consider the generalized preemptive makespan minimization problem with reservation cost. Recall that we can use every machine in a reserved time slot and pay only once. By [8] it is sufficient to find an optimal reservation decision.

Observation 1

Given the set of time slots reserved in an optimal solution, we can compute an optimal schedule in polynomial time.

Given an instance of our problem, let Z be the optimal makespan of the relaxed problem without reservation cost. Notice that Z is not necessarily integral. To determine an optimal reservation decision, we use the following observation.

Observation 2

Given an optimal makespan $C_{\max }^*$ for $R \,|\, pmtn \,|\, C_{\max }+E$, an optimal schedule reserves the $\lceil Z \rceil$ cheapest slots before $\lceil C_{\max }^* \rceil$.

Note that we must pay full reservation cost for a used time slot, no matter how much it is utilized, and so does an optimal solution. In particular, this holds for the last reserved slot. Hence, it remains to design a procedure for computing an optimal value $C^* :=\lceil C_{\max }^* \rceil$.

We compute for every interval $I_k = \left[ s_k,d_k\right)$, $k=1,\ldots ,K$, an optimal point in time for $C^*$ assuming that $C^* \in I_k$. Start from the value $C^*=s_{k}$, if feasible, with the corresponding cheapest $\lceil Z \rceil$ reserved time slots. Notice that any of these reserved time slots that has cost e such that $e > e_{k} +1$ can be replaced by a time slot from $I_{k}$ leading to a solution with less total cost. Thus, if such a time slot does not exist, then $s_{k}$ is the best choice for $C^*$ in $I_{k}$. Otherwise, let $R \subseteq \left\{ 1,\dots ,k-1\right\}$ be the index set of intervals that contain at least one reserved slot. We define $I_{\ell }$ to be the interval with $e_{\ell } = \max _{h\in R} e_h$ and denote by $r_{h}$ the number of reserved time slots in $I_{h}$. Replace $\min \{r_{\ell },d_k-s_k-r_k\}$ reserved slots from $I_{\ell }$ by slots from $I_k$ and update R, $I_{\ell }$ and $r_k$. This continues until $e_{\ell } \le e_{k}+1$ or the interval $I_k$ is completely reserved, i.e., $r_k = d_k-s_k$. This operation takes at most O(K) computer operations per interval to compute the best $C^*$-value in that interval. It yields the following theorem.

Theorem 1

The scheduling problem $R \,|\, pmtn \,|\, C_{\max } + E$ can be solved in polynomial time equal to the running time required to solve an LP for $R \,|\, pmtn \,|\, C_{\max }$ without reservation cost plus $O(K^2)$.

3 Minimizing $\sum _j (w_j)C_j$ on a Single Machine

In this section, we consider the problem $1 \,|\, pmtn \,|\, \sum (w_j) C_{j} + E$. We design an algorithm that computes, for a given (not necessarily optimal) scheduling sequence $\sigma$, an optimal reservation decision for $\sigma$. We firstly identify structural properties of an optimal schedule, which we then exploit in a dynamic program. Based on this algorithm, we show that the unweighted problem $1 \,|\, pmtn \,|\, \sum C_{j} + E$ can be solved optimally in polynomial time and that there is a $(4+{\varepsilon })$-approximation algorithm for the weighted problem $1 \,|\, pmtn \,|\, \sum w_j C_{j} + E$.

In principle, an optimal schedule may preempt jobs at fractional time points. However, since time slots can only be reserved entirely, any reasonable schedule uses the reserved slots entirely as long as there are unprocessed jobs. The following lemma shows that this is also true if we omit the requirement that time slots must be reserved entirely. (For the makespan problem considered in Sect. 2 this is not true.)

Lemma 1

There is an optimal schedule $\mathcal {S}^*$ in which all reserved time slots are entirely reserved and jobs are preempted only at integral points in time.

In the following, we assume that we are given a (not necessarily optimal) sequence of jobs, $\sigma =(1,\ldots ,n)$, in which the jobs must be processed. We want to characterize an optimal schedule $\mathcal {S}^*$ for $\sigma$, that is, in particular the optimal choice of time slots for scheduling $\sigma$. We first split $\mathcal {S}^*$ into smaller sub-schedules, for which we introduce the concept of a split point.

Definition 1

(Split Point). Consider an optimal schedule $\mathcal {S}^*$ and the set of potential split points $\mathcal {P}:=\bigcup _{k=1}^{K} \left\{ s_k , s_k+1 \right\} \cup \{d_K\}$. Let $S_j$ and $C_j$ denote the start time and completion time of job j, respectively. We call a time point $t\in \mathcal {P}$ a split point for $\mathcal {S}^*$ if all jobs that start before t also finish their processing not later than t, i.e., if $\left\{ j\in J : S_j < t \right\} = \left\{ j\in J : C_j \le t\right\}$.

Given an optimal schedule $\mathcal {S}^*$, let $0=\tau _1< \tau _2 < \cdots < \tau _\ell = d_K$ be the maximal sequence of split points of $\mathcal {S}^*$, i.e. the sequence containing all split points of $\mathcal {S}^*$. We denote the interval between two consecutive split points $\tau _x$ and $\tau _{x+1}$ as region $R_x^{\mathcal {S}^*} :=\left[ \tau _x,\tau _{x+1}\right)$, for $x=1,\ldots ,\ell -1$.

Consider now any region $R_x^{\mathcal {S}^*}$ for an optimal schedule $\mathcal {S}^*$ with $x\in \left\{ 1,\ldots ,\ell -1\right\}$ and let $J_x^{\mathcal {S}^*} := \left\{ j \in J : S_j \in R_x^{\mathcal {S}^*} \right\}$. Note that $J_x^{\mathcal {S}^*}$ might be empty. Among all optimal schedules we shall consider an optimal solution $\mathcal {S}^*$ that minimizes the value $\sum _{t=0}^{d_K-1} t\cdot y(t)$, where y(t) is a binary variable that indicates if time slot $\left[ t,t+1\right)$ is reserved or not.

Observation 3

There is no job $j\in J_x^{\mathcal {S}^*}$ with $C_j \in R_x^{\mathcal {S}^*} \cap \mathcal {P}$.

Namely, every $C_j$ with $C_j=s_k\in R_x^{\mathcal {S}^*}$ or $C_j=s_k+1\in R_x^{\mathcal {S}^*}$ would make $s_k$ or $s_k+1$ a split point, whereas $R_x^{\mathcal {S}^*}$ is defined as the interval between two consecutive split points.

We say that an interval $I_k$ is partially reserved if at least one slot in $I_k$ is reserved, but not all.

Lemma 2

There exists an optimal schedule $\mathcal {S}^*$ in which at most one interval is partially reserved in $R_x^{\mathcal {S}^*}$.

We are now ready to bound the unit reservation cost spent for jobs in $J_x^{\mathcal {S}^*}$. Let $e_{\max }^j$ be the maximum unit reservation cost spent for job j in $\mathcal {S}^*$. Furthermore, let $\varDelta _x := \max _{j\in J_x^{\mathcal {S}^*}} (e_{\max }^j + \sum _{j' < j} w_{j'})$ and let $j_x$ be the last job (according to sequence $\sigma$) that achieves $\varDelta _x$. Suppose, there are $b\ge 0$ jobs before and $a\ge 0$ jobs after job $j_x$ in $J_x^{\mathcal {S}^*}$. The following lemma gives for every job $j \in J_x^{\mathcal {S}^*}\setminus \{j_x\}$ an upper bound on the unit reservation cost spent in the interval $\left[ S_j,C_j\right)$.

Lemma 3

Consider an optimal schedule $\mathcal {S}^*$. For any job $j\in J_x^{\mathcal {S}^*}\setminus \{j_x\}$ a slot $\left[ t,t+1\right) \in \left[ S_j,C_j\right)$ is reserved if and only if the cost of $\left[ t,t+1\right)$ satisfies the upper bound given in the table below.

Proof

Consider any job $j:=j_x -\ell$ with $0< \ell \le b$. Suppose there is a job j for which a slot is reserved with cost $e_{\max }^{j} > e_{\max }^{j_x} + \sum _{j'=j}^{j_x -1} w_{j'}$. Then $e_{\max }^{j} + \sum _{j'<j} w_{j'} > e_{\max }^{j_x} + \sum _{j'<j_x} w_{j'}$, which is a contradiction to the definition of job $j_x$. Thus, $e_{\max }^{j}\le e_{\max }^{j_x} + \sum _{j'=j}^{j_x -1} w_{j'}$.

Now suppose, there is a slot $\left[ t,t+1\right) \in \left[ S_j,C_j\right)$ with cost $e(t) \le e_{\max }^{j_x} + \sum _{j'=j}^{j_x -1} w_{j'}$ that is not reserved. There must be a slot $\left[ t',t'+1\right) \in \left[ S_{j_x},C_{j_x}\right)$ with cost exactly $e_{\max }^{j_x}$. If we reserve slot $\left[ t,t+1\right)$ instead of $\left[ t',t'+1\right)$, then the difference in cost is non-positive, because the completion times of at least $\ell$ jobs ($j=j_x-\ell , \ldots , j_x-1$ and maybe also $j_x$) decrease by one. This contradicts either the optimality of $\mathcal {S}^*$ or our assumption that $\mathcal {S}^*$ minimizes $\sum _{t=0}^{d_K-1} t \cdot y(t)$.

The proof of the statement for any job $j_x +\ell$ with $0< \ell \le a$ follows a similar argument, but now using the fact that for every job $j:=j_x+\ell$ we have $e_{\max }^{j} < e_{\max }^{j_x} - \sum _{j'=j_x}^{j-1} w_{j'}$, because $j_x$ was the last job with $e_{\max }^j + \sum _{j' < j} w_{j'} =\varDelta _x$.    $\square$

To construct an optimal sub-schedule, we need the following two lemmas.

Lemma 4

Let $\left[ t',t'+1\right) \in \left[ S_{j_x},C_{j_x}\right)$ be the last time slot with cost $e_{\max }^{j_x}$ that is used by job $j_x$. If there is a partially reserved interval $I_k$ in $R_x^{\mathcal {S}^*}$, then either (i) $I_k$ is not the last interval of $R_x^{\mathcal {S}^*}$ and $I_k$ contains $\left[ t',t'+1\right)$ as its last reserved time slot or (ii) $I_k$ is the last interval of $R_x^{\mathcal {S}^*}$.

Lemma 5

Let $\left[ t',t'+1\right) \in \left[ S_{j_x},C_{j_x}\right)$ be the last time slot with cost $e_{\max }^{j_x}$ that is used by job $j_x$. There exists an optimal solution $\mathcal {S}^*$ such that if there is a partially reserved interval $I_k$ in $R_x^{\mathcal {S}^*}\!$ and it is the last one in $R_x^{\mathcal {S}^*}\!$, then there is no slot $\left[ t,t+1\right) \in \left[ S_{j_x},C_{j_x}\right)$ with cost at most $e_{\max }^{j_x}$ that is not reserved.

We now show how to construct an optimal partial schedule for a given ordered job set in a given region in polynomial time.

Lemma 6

Given a region $R_x$ and an ordered job set $J_x$, we can construct in polynomial time an optimal schedule for $J_x$ within the region $R_x$, which does not contain any other split point than $\tau _x$ and $\tau _{x+1}$, the boundaries of $R_x$.

Proof

Given $R_x$ and $J_x$, we guess the optimal combination $\left( j_x,e_{\max }^{j_x}\right)$, i.e., we enumerate over all nK combinations and choose eventually the best solution.

We firstly assume that a partially reserved interval exists and it is the last one in $R_x$ (case (ii) in Lemma 4). Based on the characterization in Lemma 3 we find in polynomial time the slots to be reserved for the jobs $j_x-b,\ldots ,j_x-1$. This defines $C_{j_x-b},\ldots ,C_{j_x-1}$. Then starting job $j_x$ at time $C_{j_x-1}$, we check intervals in the order given and reserve as much as needed of each next interval $I_h$ if and only if $e_h\le e_{\max }^{j_x}$, until a total of $p_{j_x}$ time slots have been reserved for processing $j_x$. Lemma 5 justifies to do that. This yields a completion time $C_{j_x}$. Starting at $C_{j_x}$, we use again Lemma 3 to find in polynomial time the slots to be reserved for processing the jobs $j_x+1,\ldots ,j_x+a$. This gives $C_{j_x+1},\ldots ,C_{j_x+a}$.

Now we assume that there is no partially reserved interval or we are in case (i) of Lemma 4. Similar to the case above, we find in polynomial time the slots that $\mathcal {S}^*$ reserves for the jobs $j_x-b,\ldots ,j_x-1$ based on Lemma 3. This defines $C_{j_x-b},\ldots ,C_{j_x-1}$. To find the slots to be reserved for the jobs $j_x+1,\ldots ,j_x+a$, in this case, we start at the end of $R_x$ and go backwards in time. We can start at the end of $R_x$ because in this case the last interval of $R_x$ is fully reserved. This gives $C_{j_x+1},\ldots ,C_{j_x+a}$. Job $j_x$ is thus to be scheduled in $\left[ C_{j_x-1}, S_{j_x+1}\right)$. In order to find the right slots for $j_x$ we solve a makespan problem in the interval $\left[ C_{j_x-1}, S_{j_x+1}\right)$, which can be done in polynomial time (Theorem 1) and gives a solution that cannot be worse than what an optimal schedule $\mathcal {S}^*$ does.

If anywhere in both cases the reserved intervals can not be made sufficient for processing the job(s) for which they are intended, or if scheduling the jobs in the reserved intervals creates any intermediate split point, then this $\left( j_x,e_{\max }^{j_x}\right)$-combination is rejected. Hence, we have computed the optimal schedules over all nK combinations of $\left( j_x,e_{\max }^{j_x}\right)$ and over both cases of Lemma 4 concerning the position of the partially reserved interval. We choose the schedule with minimum total cost and return it with its value. This completes the proof.    $\square$

Now we are ready to prove our main theorem.

Theorem 2

Given an instance of $1 \,|\, pmtn \,|\, \sum w_j C_{j} + E$ and an arbitrary processing sequence of jobs $\sigma$, we can compute an optimal reservation decision for $\sigma$ in polynomial time.

Proof

We give a dynamic program. We define a state for every possible potential split point $t \in \mathcal {P}$. By definition, there are $2K+1$ of them. A state also includes the set of jobs processed until time t. Given the sequence $\sigma$, this job set can be uniquely identified by the index of the last job, say j, that finished by time t. By relabeling the job set J, we can assume w.l.o.g. that $\sigma =(1,\ldots ,n)$.

For each state (j, t) we compute and store recursively the optimal scheduling cost plus reservation cost Z(j, t) by

$$\begin{aligned} Z(j, t) = \min \!\bigg \{ Z(j'\!,t') + z\big (\big \{j'\!+1,\ldots ,j\big \}, [t',t)\big )\!: t'\!,t\in \mathcal {P},t'\!< t,&j'\!,j \in J, j'\!<j \bigg \}, \end{aligned}$$

where $z\big (\big \{j'+1,\ldots ,j\big \},[t',t)\big )$ denotes the value of an optimal partial schedule for job set $\{j'+1,j'+2,\ldots ,j\big \}$ in the region $[t',t)$, or $\infty$ if no such schedule exists. This value can be computed in polynomial time, by Lemma 6. Hence, we compute Z(j, t) for all O(nK) states in polynomial time, which concludes the proof.    $\square$

The following observation follows from a standard interchange argument.

Observation 4

In an optimal schedule $\mathcal {S}^*$ for the problem $1 \,|\, pmtn \,|\, \sum C_{j} + E$, jobs are processed according to the Shortest Processing Time First (SPT) policy.

Combining this observation with Theorem 2 gives the following corollary.

Corollary 1

There is a polynomial-time algorithm for $1 \,|\, pmtn \,|\, \sum C_j + E$.

For the weighted problem $1 \,|\, pmtn \,|\, \sum w_j C_{j} + E$, there is no sequence that is universally optimal for all reservation decisions [5]. However, in the context of scheduling on an unreliable machine there has been shown a polynomial-time algorithm that computes a universal $(4+{\varepsilon })$-approximation [5]. More precisely, the algorithm constructs a sequence of jobs which approximates the scheduling cost for any reservation decision with a factor at most $4+{\varepsilon }$.

Consider an instance of problem $1 \,|\, pmtn \,|\, \sum w_j C_{j} + E$ and compute such a universally $(4+{\varepsilon })$-approximate sequence. Applying Theorem 2 to $\sigma$, we obtain a schedule $\mathcal {S}$ with an optimal reservation decision for $\sigma$. Let $\mathcal {S'}$ denote the schedule which we obtain by changing the reservation decision of $\mathcal {S}$ to the reservation in an optimal schedule $\mathcal {S}^*$ (but keeping the scheduling sequence $\sigma$). The schedule $\mathcal {S'}$ has cost no less than the original cost of $\mathcal {S}$. Furthermore, given the reservation decision in the optimal solution $\mathcal {S}^*$, the sequence $\sigma$ approximates the scheduling cost of $\mathcal {S}^*$ within a factor of $4+{\varepsilon }$. This gives the following result.

Corollary 2

There is a $(4+{\varepsilon })$-approx. algorithm for $1 \,|\, pmtn \,|\, \sum w_j C_j + E$.

4 A PTAS for Minimizing Total Weighted Completion Time

The main result of this section is an approximation scheme for minimizing the total weighted completion time with time-varying reservation cost.

Theorem 3

For any fixed $\varepsilon >0$, there is a pseudo-polynomial time algorithm that computes a $(1+\varepsilon )$-approximation for the problem $1 \,|\, pmtn \,|\, \sum _j w_j C_j + E$. This algorithm runs in polynomial time if $d_K$ is polynomially bounded.

In the remainder of this section we describe some preliminaries, present a dynamic programming (DP) algorithm with exponential running time, and then we argue that it can be trimmed down to (pseudo-)polynomial size. As noted in the introduction, our approach is inspired by a PTAS for scheduling on a machine of varying speed [10], but a direct application does not seem possible.

4.1 Preliminaries and Scheduling in the Weight-Dimension

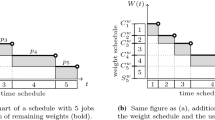
We describe a schedule $\mathcal {S}$ not in terms of completion times $C_j\!\left( \mathcal {S}\right)$, but in terms of the remaining weight function $W^{\mathcal {S}}\!\left( t\right)$ which, for a given schedule ${\mathcal {S}}$, is defined as the total weight of all jobs not completed by time t. Based on the remaining weight function we can express the cost for any schedule $\mathcal {S}$ as

$$\int _0^\infty W^{\mathcal {S}}\!\left( t\right) = \sum _{j\in J} w_j C_j\!\left( \mathcal {S}\right) .$$

This has a natural interpretation in the standard 2D-Gantt chart, which was originally introduced in [4].

For a given reservation decision, we follow the idea of [10] and implicitly describe the completion time of a job j by the value of the function W at the time that j completes. This value is referred to as the starting weight $S_j^w$ of job j. In analogy to the time-dimension, the value $C_j^w := S_j^w +w_j$ is called completion weight of job j. When we specify a schedule in terms of the remaining weight function, then we call it a weight-schedule, otherwise a time-schedule. Other terminologies, such as feasibility and idle time, also translate from the time-dimension to the weight-dimension. A weight-schedule is called feasible if no two jobs overlap and the machine is called idle in weight-dimension if there exists a point w in the weight-dimension with $w\notin \left[ S_j^w, C_j^w\right]$ for all jobs $j\in J$.

A weight-schedule together with a reservation decision can be translated into a time-schedule by ordering the job in decreasing order of completion weights and scheduling them in this order in the time-dimension in the reserved time slots. For a given reservation decision, consider a weight-schedule $\mathcal {S}$ with completion weights $C_1^w > \cdots > C_n^w > C_{n+1}^w:=0$ and the corresponding completion times $0=:C_0 < C_1 < \cdots < C_n$ for the jobs $j=1,\ldots ,n$. We define the (scheduling) cost of a weight schedule $\mathcal {S}$ as $\sum _{j=1}^n \left( C_{j+1}^w -C_j^w \right) C_j$. This value equals $\sum _{j=1}^n \pi _j^{\mathcal {S}} C_j^w$, where $\pi _j^{\mathcal {S}}:= C_j -S_j$, if and only if there is no idle weight. If there is idle weight, then the cost of a weight-schedule can only be greater, and we can safely remove idle weight without increasing the scheduling cost [10].

4.2 Dynamic Programming Algorithm

Let ${\varepsilon }>0$. Firstly, we apply standard geometric rounding to the weights to gain more structure on the input, i.e., we round the weights of all jobs up to the next integer power of $(1+\varepsilon )$, by losing at most a factor $(1+{\varepsilon })$ in the objective value. Furthermore, we discretize the weight-space into intervals of exponentially increasing size: we define intervals $W\!I_u := [\left( 1+\varepsilon \right) ^{u-1}, \left( 1+\varepsilon \right) ^{u} )$ for $u = 1, \ldots , \nu$ with $\nu := \lceil \log _{1+\varepsilon } \sum _{j\in J} w_j\rceil$.

Consider a subset of jobs $J' \subseteq J$ and a partial weight-schedule of $J'$. In the dynamic program, the set $J'$ represents the set of jobs at the beginning of a corresponding weight-schedule, i.e., if $j\in J'$ and $k\in J\setminus J'$, then $C_j^w < C_k^w$. As discussed in Sect. 4.1, a partial weight-schedule $\mathcal {S}$ for the jobs in $J'$ together with a reservation decision for all jobs in J can be translated into a time-schedule. Note that the makespan of this time-schedule is completely defined by the reservation decision and the total processing volume $\sum _{j\in J} p_j$. Moreover, knowing the last $p\!\left( J'\right) :=\sum _{j\in J'} p_j$ reserved slots is sufficient for scheduling the jobs in $J'$ in the time-dimension, since we know that the first job in the weight-schedule finishes last in the time-schedule, i.e., at the makespan. This gives a unique completion time $C_j$ and a unique execution time $\pi _j^{\mathcal {S}} := C_j - S_j$ for each job $j\in J'$. The total scheduling and reservation cost of this partial schedule is $\sum _{j\in J'} \pi _j^{\mathcal {S}} C_j^w + E$.

Let $\mathcal {F}_u := \{ J_u \subseteq J : \sum _{j\in J_u}w_j \le \left( 1+\varepsilon \right) ^u \}$. The set $\mathcal {F}_u$ contains all the possible job sets $J_u$ that can be scheduled in $W\!I_u$ or before. With every possible pair $\left( J_u, t\right)$, $J_u \in \mathcal {F}_u$ and $t\in \left[ 0,d_K\right)$, we associate a recursively constructed weight-schedule together with a reservation decision starting at time t so that the current scheduling and reservation cost is a good approximation of the optimal total cost for processing the set $J_u$ starting at t. More precisely, given a $u~\in ~\left\{ 1,\ldots , \nu \right\}$, a set $J_u \in \mathcal {F}_u$, and a time point $t\in \left[ 0,d_K\right)$, we create a table entry $Z\!\left( u,J_u,t\right)$ that represents a $\left( 1+\mathcal {O}\!\left( \varepsilon \right) \right)$-approximation of the scheduling and reservation cost of an optimal weight-schedule of $J_u$ subject to $C_j^w \le \left( 1+\varepsilon \right) ^u$ for all $j\in J_u$ and $S_j \ge t$ for all $j\in J_u$. Initially, we create table entries $Z\!\left( 0,\emptyset ,t\right) := 0$ for all $t=0,\ldots ,d_K$ and we define $\mathcal {F}_0 = \left\{ \emptyset \right\}$. With this, basically, we control the makespan of our time-schedule.

The table entries in iteration u are created based on the table entries from iteration $u-1$ in the following way. Consider candidate sets $J_u \in \mathcal {F}_u$ and $J_{u-1} \in \mathcal {F}_{u-1}$, a partial weight-schedule $\mathcal {S}$ of $J_u$, in which the set of jobs with completion weight in $W\!I_u$ is exactly $J_u\setminus J_{u-1}$, and two integer time points $t,t'$ with $t< t'$.

We let $APX_u\!\left( J_u \setminus J_{u-1}, \left[ t,t'\right) \right)$ denote a $(1+{\varepsilon })$-approximation of the minimum total cost (for reservation and scheduling) when scheduling job set $J_u \setminus J_{u-1}$ in the time interval $[t,t')$, i.e.,

$$APX_u\!\left( J_u \setminus J_{u-1}, \left[ t,t'\right) \right) := \left( 1+\varepsilon \right) ^u \cdot \left( t'-t\right) + RES\!\left( J_u \setminus J_{u-1}, \left[ t,t'\right) \right) ,$$

where $RES\!\left( J_u \setminus J_{u-1}, \left[ t,t'\right) \right)$ denotes the cost of the $p\!\left( J_u \setminus J_{u-1} \right)$ cheapest slots in the interval $\left[ t,t'\right)$. If $p\!\left( J_u \setminus J_{u-1} \right) > t' - t$, then we set $RES\!\left( J_u \setminus J_{u-1}, \left[ t,t'\right) \right)$ to infinity to express that we cannot schedule all jobs in $J_u \setminus J_{u-1}$ within $\left[ t,t'\right)$.

Based on this, we compute the table entry $Z\!\left( u,J_u,t\right)$ with $J_u \in \mathcal {F}_u$ according to the following recursive formula

$$ Z\!(u,J_u,t) := \min \left\{ Z\!(u-1,J_{u-1},t') + APX_u\!( J_u \setminus J_{u-1}, [t,t')): \right. \\ \left. J_{u-1} \in \mathcal {F}_{u-1}, J_{u-1} \subseteq J_u, t\le t'\right\} . $$

We return $Z\!\left( \nu ,J,0\right)$ after iteration $\nu$. From $Z\!\left( \nu ,J,0\right)$ we can construct a schedule and its reservation decision by backtracking.

Notice that the values $APX_u(J_u\setminus J_{u-1}, [t,t'))$ do not depend on the entire schedule, but only on the time interval $[t,t')$ and the total processing volume of jobs in $J_u\setminus J_{u-1}$. Since we approximate the scheduling cost by a factor $1+{\varepsilon }$ and determine the minimum reservation cost, the dynamic programming algorithm obtains the following result.

Lemma 7

The DP computes a $(1+\mathcal {O}({\varepsilon }))$-approximate solution.

4.3 Trimming the State Space

The set $\mathcal {F}_u$, containing all possible job sets $J_u$, is of exponential size, and so is the DP state space. In the context of scheduling with variable machine speed, it has been shown in [10] how to reduce the set $\mathcal {F}_u$ for a similar DP (without reservation decision, though) to one of polynomial size at only a small loss in the objective value. In general, such a procedure is not necessarily applicable to our setting because of the different objective involving additional reservation cost and the different decision space. However, the compactification in [10] holds independently of the speed of the machine and, thus, independently of the reservation decision of the DP (interpret non/reservation as speed 0 / 1). Hence, we can apply it to our cost aware scheduling framework and obtain a PTAS. For more details on the procedure we refer to the full version.

5 Open Problems

Our PTAS for the weighted problem runs in polynomial time when $d_K$ is polynomially bounded. Otherwise, the scheme is a “PseuPTAS”. The question is if, by a careful analysis of the structure of optimal solutions, we can avoid the dependence of the running time on $d_K$, as in our dynamic program from Sect. 3.

Furthermore, it would be interesting to algorithmically understand other scheduling problems in the model of time-varying reservation cost. An immediate open question concerns the problems considered in this paper when there are release dates present. In the full version we show that the makespan problem $1 \,|\, r_j, pmtn \,|\, C_{\max } + E$ can be solved in polynomial time. We can also solve $R \,|\, pmtn,r_j \,|\, C_{\max }$ optimally if we allow fractional reservation. The seemingly most simple open problem in our (integral) model is $1| r_j, pmtn|\sum _j C_j + E$. While the problem without reservation cost can be solved optimally in polynomial time, the complexity status in the time-varying cost model is unclear, even with only two different unit reservation costs.

Machine-individual time-slot reservation opens a different stream of research. While a standard LP can be adapted for optimally solving $R \,|\, pmtn,r_j \,|\, C_{\max }$ with fractional reservation cost, the integrality gap is unbounded for our model.