Real-Time Cycle Slip Detection and Repair Algorithm for SBAS Airborne Receiver

Abstract

SBAS improves performance of GNSS by providing timely corrections and integrity monitoring to meet the requirement for civil aviation. Single frequency SBAS augments GPS L1 signal, such as WAAS and EGNOS, providing APV-I service. Receiver uses GIVD to correct ionosphere delay, in which way the impact of ionosphere storm cannot be eliminated. Thus, SBAS performance is limited. Dual frequency SBAS receiver directly mitigates ionosphere delay. However, receiver will suffer considerably larger noise, proposing a higher demand for carrier smoothing techniques. Cycle slip is frequent in airborne receiver’s carrier measurement, which makes smoothed measurement pulsing, thereby reducing the positioning accuracy. This paper presents a real-time cycle slip detection and repair method, including chi-square detection algorithm and sequence-sum repair algorithm based on the statistical property of fourth order differential of carrier measurement, and its repair error variance. According to the measured data analysis, the algorithm shows good performance in cycle slip detection and repair and is sufficient for carrier smoothing techniques for SBAS airborne receiver.

1 Introduction

Satellite-based augmentation system (SBAS) broadcasts augmentation information frequently to support precision approach operations using global navigation satellite system (GNSS).

WAAS and EGNOS have been put into use, augmenting GPS L1 C/A only, providing APV-I service within their service areas respectively. The main reason why single frequency SBAS cannot provide a higher level of service is that the airborne receiver uses grid ionosphere vertical delay to correct ionosphere delay, in which case the impact of ionosphere storm cannot be eliminated. In the future, dual-frequency multiple-constellation (DFMC) SBAS will provide augmentation information for core GNSS constellations, including GPS, GLONASS, Galileo and BeiDou. The use of two signals at two distinct frequencies enables the airborne receiver to mitigate ionosphere delay directly. However, the airborne receiver will suffer considerably larger pseudorange noise [3].

Carrier smoothing technique is an efficient way to reduce pseudorange noise [1]. Single-frequency SBAS receiver minimum operational performance standards (RTCA DO-229) requires that a receiver must perform carrier smoothing to improve ranging accuracy, and the carrier smoothing equation is clearly given, namely single-frequency carrier smoothing (SFS) filter. Although DFMC SBAS specification is still under developing, it is reasonable to assume that iono-free smoothing (IFree) shall be performed to obtain iono-free pseudorange [2].

Cycle slip in the carrier measurement is common for airborne receivers, which leads to smoothed pseudorange pulsing, thereby positioning accuracy and integrity may be affected. Thus, airborne receivers should have the ability to perform cycle slip detection and repair before carrier smoothing.

There are four typical methods for cycle slip detection and repair, namely polynomial fitting method and high-order differential method for single-frequency receivers, ionosphere residual method and combination method of pseudorange and carrier phase for dual-frequency receivers. These methods have a common problem that the detection threshold is dependent on engineering experience, and is not applicable for different cases. Another common problem is that these methods cannot provide integrity parameters of corrections. In addition, the high-order differential method can’t be used in real-time cycle slip detection, and dual-frequency methods have high computing cost to determine cycle slips on each frequency. Thus, these methods are incapable of cycle slip detection and repair for SBAS airborne receiver. Cycle slip detection and repair using triple-frequency measurements has also been researched [4]. But the plan for utilization of a third frequency hasn’t been proposed by aviation community yet.

Based on the statistics characteristic of fourth order differential of carrier measurement, a real-time cycle slip detection and repair method is proposed, including chi-square detection algorithm and sequence-sum repair algorithm. This method also gives the variance of cycle slip estimated error for integrity calculation.

2 Requirements Analysis

Assuming that sampling interval is one second, the smoothed pseudorange of SFS filter can be written as:

$$ \hat{\rho }\left( t \right) = \frac{1}{\tau }\rho \left( t \right) + \frac{\tau - 1}{\tau }\left[ {\hat{\rho }\left( {t - 1} \right) + \lambda \varphi \left( t \right) - \lambda \varphi \left( {t - 1} \right)} \right] $$

(9.1)

where, $\hat{\rho }$ is the smoothed pseudorange in meters; ρ is the raw pseudorange in meters; φ is the carrier measurement in cycles; λ is the carrier wavelength in meters; $\tau$ is the time constant of 100 s.

The smoothing error with cycle slip occurring at time t can be expressed as:

$$ \begin{aligned}\Delta \hat{\rho }\left( {\text{t}} \right) & = \frac{\tau - 1}{\tau }\lambda\Phi \\\Delta \hat{\rho }\left( {\text{t + k}} \right) & = - \frac{{\left( {\tau - 1} \right)^{k - 1} }}{{\tau^{k} }}\lambda\Phi ,k \ge 1 \\ \end{aligned} $$

(9.2)

where, $\Delta \hat{\rho }$ is the smoothing error in meters; Φ is the cycle slip in cycles.

The smoothed pseudorange on L1 of IFree filter can be written as:

$$ \begin{aligned} \hat{\rho }_{L1} \left( {t + 1} \right) & = \frac{1}{\tau }\left[ {\rho_{L1} \left( {t + 1} \right) - \frac{1}{\alpha }\left( {\rho_{L1} \left( {t + 1} \right) - \rho_{L5} \left( {t + 1} \right)} \right)} \right] + \frac{\tau - 1}{\tau }\left[ {\hat{\rho }_{L1} \left( t \right)} \right. \\ & \quad + \left. {\lambda_{\varphi 1} \left( {1 - \frac{1}{\alpha }} \right) \times \left( {\varphi_{L1} \left( {t + 1} \right) - \varphi_{L1} \left( t \right)} \right) - \frac{{\lambda_{\varphi 5} }}{\alpha }\left( {\varphi_{L5} \left( {t + 1} \right) - \varphi_{L5} \left( t \right)} \right)} \right] \\ \end{aligned} $$

(9.3)

The smoothing error with cycle slip occurring at time t can be expressed as:

$$ \begin{aligned}\Delta \hat{\rho }_{L1} \left( {\text{t}} \right) & { = }\frac{\tau - 1}{\tau }\left[ {\left( {1 - \frac{1}{\alpha }} \right)\lambda_{\varphi 1}\Phi _{L1} - \frac{1}{\alpha }\lambda_{\varphi 5}\Phi _{L5} } \right] \\\Delta \hat{\rho }_{L1} \left( {\text{t + k}} \right) & { = } - \frac{{\left( {\tau - 1} \right)^{k - 1} }}{{\tau^{k} }}\left[ {\left( {1 - \frac{1}{\alpha }} \right)\lambda_{\varphi 1}\Phi _{L1} - \frac{1}{\alpha }\lambda_{\varphi 5}\Phi _{L5} } \right],k \ge 1 \\ \end{aligned} $$

(9.4)

According to Eqs. (9.2) and (9.4), small cycle slip affects the smoothed pseudorange the time it occurs, and has an ignorable effect on the later smoothed pseudoranges.

Assuming that code-tracking noise is a hundredth of code length, and smoothing error threshold is one-tenth of code-tracking noise. Thus, the cycle slip thresholds for SFS filter and IFree filter are 1.56 cycles and 0.688 cycles respectively.

It is necessary to provide not only corrections but also corresponding integrity parameters for SBAS airborne receiver. The alert time for precision approach operations is no more than 10 s, and civil aircraft is in a high-speed motion, so that cycle slip detection and repair shall be real-time.

3 Cycle Slip Detection and Repair Algorithm

In this section, the algorithm is described in detail, and the flowchart is given.

3.1 Fourth Order Differential

Carrier phase measurement can be expressed as:

$$ \lambda \varphi = r + c\left( { - t_{iono} + t_{trop} + t_{u} - t_{s} } \right) + N + \eta $$

(9.5)

where, r is the geometrical distance in meters; c is the speed of light in meters per second; t _iono is the ionosphere delay in seconds; t _trop is the troposphere delay in seconds; t _u is the receiver clock error in seconds; t _s is the satellite clock error in seconds; N is the carrier ambiguity; η is the carrier-tracking noise.

The fourth order differential of carrier measurement at time k is:

$$ \Delta ^{4} \varphi_{k} = \varphi_{k} - 4\varphi_{k - 1} + 6\varphi_{k - 2} - 4\varphi_{k - 3} + \varphi_{k - 4} $$

(9.6)

Assuming that the noises of carrier measurements are independent and normally distributed with the same variance, $\Delta ^{4} \varphi_{k}$ is normally distributed and the variance of $\Delta ^{4} \varphi_{k}$ is:

$$ \sigma_{{\Delta ^{4} \varphi }}^{2} = \frac{70}{{\lambda^{2} }}\sigma_{\varphi }^{2} $$

(9.7)

3.2 Chi-Square Detection Algorithm

As $\Delta ^{4} \varphi_{k}$ is normally distributed, chi-square test can be used to detect cycle slip.

The slide-window sequence is constructed as follows:

$$ z = \left[ {\begin{array}{*{20}c} {z_{1} } & {z_{2} } & \ldots & {z_{n} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {\Delta ^{4} \varphi_{1} } & {\Delta ^{4} \varphi_{2} } & \ldots & {\Delta ^{4} \varphi_{n} } \\ \end{array} } \right]^{T} $$

(9.8)

To detect the cycle slip, the following hypothesis is proposed:

$$ \begin{aligned} & H_{0} :\sigma_{z}^{2} = \sigma_{0}^{2} \\ & H_{1} :\sigma_{z}^{2} \ne \sigma_{0}^{2} \\ \end{aligned} $$

(9.9)

where, σ ² _z is the variance of the sequence z.

The chi-square statistic is given by:

$$ T = z^{T} z/\sigma_{z}^{2} $$

(9.10)

The calculated value T is compared with the threshold value Td of the chi-square distribution, which depends on the allowed error probability P _FA and sequence length n as described below:

$$ \int\limits_{0}^{Td} {f_{n} \left( x \right)dx} = P_{FA} $$

(9.11)

where, f _n (x) is the probability density function with n degrees of freedom.

If T is larger than Td, the hypothesis is rejected and cycle slip is detected, otherwise it is accepted and there is no cycle slip.

3.3 Sequence-Sum Repair Algorithm

Fast Fourier transform is defined by the formula:

$$ Z\left( k \right) = \sum\limits_{j = 1}^{n} {z_{j} w_{n}^{{\left( {j - 1} \right)\left( {k - 1} \right)}} } ,\;w_{n} = e^{{\left( { - 2\pi i} \right)/n}} $$

(9.12)

The fourth order differential with cycle slip can be expressed as:

$$ z_{n} = z_{0,n} +\Phi $$

(9.13)

where, z ₀ is the fourth order differential without cycle slip.

Consequently, Z(1) can be expressed as:

$$ Z\left( 1 \right) = \sum\limits_{j = 1}^{n} {z_{j} } = \sum\limits_{j = 1}^{n} {z_{0,j} } +\Phi $$

(9.14)

The expectation of cycle slip can be expressed as:

$$ E\left[\Phi \right] = E\left[ {\sum\limits_{j = 1}^{n} {z_{j} } } \right] - E\left[ {\sum\limits_{j = 1}^{n} {z_{0,j} } } \right] $$

(9.15)

where, E[·] is mathematical expectation.

Considering that z ₀ is normally distributed with zero mean and that $\Phi$ is an integer, the estimated value of cycle slip is:

$$ {\hat{\Phi }} = Round\left[ {\sum\limits_{j = 1}^{n} {z_{j} } } \right] = Round\left[ {\sum\limits_{j = 1}^{n} {\Delta ^{4} \varphi_{j} } } \right] $$

(9.16)

where, Round[·] rounds the number to the nearest integer.

The estimated error can be expressed as:

$$ {\Delta \Phi } =\Phi - {\hat{\Phi }} $$

(9.17)

In order to evaluate the repair accuracy, some latest samples are selected to calculate the variance of cycle slip estimated error defined as follows:

$$ \sigma_{{\Delta \Phi }}^{2} = \frac{1}{N - 1}\sum\limits_{i = 1}^{N} {\left( {\Delta ^{4} \varphi_{i} -\Delta ^{4} \bar{\varphi }} \right)^{2} } $$

(9.18)

where, N and $\Delta ^{4} \bar{\varphi }$ are the number and the mean value of the samples respectively. N is a variable integer, which increases with time and is set to zero when cycle slip is detected. Considering the correlation of samples, the maximum number of N is set to sixty.

When this method is applied, the variance of smoothed pseudorange is:

$$ \sigma_{{\hat{\rho }}}^{2} = \sigma_{0}^{2} + \lambda \sigma_{{{\Delta \Phi }}}^{2} $$

(9.19)

where, $\sigma_{0}^{2}$ is the variance of smoothing filter output pseudorange.

3.4 Algorithm Flow

The flowchart in Fig. 9.1 describes the algorithm flow. The maximum number of sequence is 6, and the allowed error probability is 10⁻³.

Fig. 9.1

Flowchart of real-time cycle slip detection and repair algorithm for SBAS airborne receiver

• 1. Empty sequence z. Start cycle slip detection and repair after four continuous samples.

• 2. If there is a new measurement, go to step 3, otherwise terminate the procedure of cycle slip detection and repair.

• 3. Calculate fourth order differential $\Delta ^{4} \varphi_{k}$.

• 4. Calculate cycle slip estimated error $\sigma_{{{\Delta \Phi }}}^{2}$.

• 5. Insert $\Delta ^{4} \varphi_{k}$ into sequence. If the sequence length is smaller than six, $z_{k} = \left[ {z_{k - 1,1} ,z_{k - 1,2} , \ldots ,z_{k - 1,n} ,\Delta ^{4} \varphi_{k} } \right]$, otherwise $z_{k} = \left[ {z_{k - 1,2} ,z_{k - 1,3} , \ldots ,z_{k - 1,n} ,\Delta ^{4} \varphi_{k} } \right]$.

• 6. Detect cycle slip using chi-square detection algorithm. If cycle slip is detected, go to step 7, otherwise go to step 2.

• 7. Estimate cycle slip using sequence-sum repair algorithm. If estimated value of cycle slip is zero, go to step 2, otherwise go to step 1.

4 Performance and Analysis

In this section, carrier phase is measured by receiver UR370, whose nominal clock stability is 5 × 10⁻⁷.

4.1 Statistical Property

The carrier measurements were statically collected at July 27, 2014. The sampling interval is one second. There are 357,076 fourth order differential samples. It’s reasonable to assume that fourth order differential without cycle slip is smaller than 10. After excluding those larger than 10, there are 357,072 samples left, of which the mean value is 4.176 × 10⁻⁵ cycles and the standard deviation is 0.7657 cycles.

The Q-Q plot of 357,072 samples is showed in Fig. 9.2, indicating that fourth order differential can be treated as normally distributed.

Fig. 9.2

Q-Q plot of 357,072 samples. The blue cross represents the sample quantiles and the red dashed line represents the theoretical quantiles from a normal distribution

4.2 Detection Performance

In this section, the performance of chi-square detection algorithm has been analyzed and evaluated using 20054 carrier phase samples of GPS PRN 1.

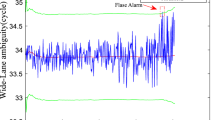
The detection result of raw data is showed in Fig. 9.3. The detection function has been performed 20,046 times, and cycle slip has been detected in the 17115th sample. Assuming that there is no cycle slip in raw data, the probability of false detection is about 0.00499 %.

Fig. 9.3

Detection result of GPS PRN 1 raw data. The red dot represents the sample with cycle slip detected, the blue dot represents the sample with no cycle slip detected, and the green dot represents the sample undetected during initialization

Then, cycle slips are manually added to the raw data every 60 s. Cycle slip value is generated as follows:

$$ \Phi _{k} = Round\left[ {randn_{k} \times 50} \right] $$

(9.20)

where randn _k is a standard normally distributed random variable.

The detection result of data with cycle slips is showed in Fig. 9.4. The detection function has been performed 18,878 times, and cycle slip has been detected 22 times. No cycle slip is added but cycle slip is detected in the 9497th, 11281st, 11551st, 17115th and 17531st samples, thus the probability of false detection is about 0.0265 %. Cycle slip is added but no cycle slip is detected in the 2526th, 2595th, 4407th, 7849th, 7913rd, 7975th, 9012nd, 9207th, 9670th, 10053rd, 11804th, 13240th, 14020th, 15090th, 15289th, 18692nd and 19329th samples, thus the probability of missing detection is about 0.0901 %. These 17 cycle slips are all smaller than 5 cycles.

Fig. 9.4

Same as Fig. 9.3 but the detection result of GPS PRN 1 data with manually added cycle slips

4.3 Repair Performance

The same data has been used to analyze and evaluate the performance of sequence-sum algorithm.

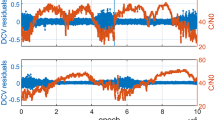
The repair result of raw data is showed in Fig. 9.5. Cycle slip is detected in the 17115th sample, and the estimated value of cycle slip is −2 cycles.

Fig. 9.5

Repair result of GPS PRN 1 raw data. The blue dot represents the sample with zero cycle slip, and the red dot represents the sample with non-zero cycle slip

The repair result of data with cycle slips is showed in Fig. 9.6. There are 132 samples with non-zero estimated error. Three of them are false detected, seventeen of them are missing detected, and the rest of them are caused by the repair algorithm. These 112 estimated errors are all smaller than 3 cycles.

Fig. 9.6

Left Same as Fig. 9.5 but the repair result of GPS PRN 1 data with manually added cycle slips. Right The bounding distribution of estimated error

The repair performance is limited by the standard deviation of fourth order differential. In this case, the standard variance is about 1 cycle, it’s reasonable that cycle slip within 3 cycles is difficult to repair.

The sum of absolute values of these 132 estimated errors is 165 cycles. Considering that cycle slips are added every 60 s, the mean value of estimated errors is about 0.494 cycles per second, which is smaller than the cycle slip threshold of IFree filter.

The estimated error ΔΦ and the corresponding variance of cycle slip estimated error $\sigma_{{\Delta \Phi }}^{2}$ are used to evaluate the repair accuracy. The result plotted in Fig. 9.6 shows that there are 6 times in which cases ΔΦ is larger than 3.29 σ _ΔΦ. Thus, the bounding probability is about 99.97 %.

4.4 Dynamic Test

Carrier measurements were collected in a car moving at speed between 80 and 100 km/h on the Beijing-Xinjiang Expressway.

The dynamic performance has been analyzed and evaluated using 1257 carrier phase samples of BeiDou PRN 9. According to the repair result in Fig. 9.7, cycle slip is detected in the 1054th sample of raw data, and the estimated value of cycle slip is −23 cycles. According to the repair result in Fig. 9.8, there are 19 samples with non-zero estimated error. Two of them are false detected, three of them are missing detected, and the rest of them are all smaller than 7 cycles. The mean value of estimated errors is 3.34 cycles per second. There is no ΔΦ larger than 3.29 σ _ΔΦ.

Fig. 9.7

Same as Fig. 9.5 but the repair result of BeiDou PRN 9 raw data

Fig. 9.8

Same as Fig. 9.6 but the repair result of BeiDou PRN 9 data with manually added cycle slips

There are two reasons why the mean value of estimated errors is larger than the cycle slip threshold of SFS filter. According to the fact that the standard deviation of the fourth order differential of BeiDou satellite carrier is about twice that of GPS satellite carrier, the first reason is the clock stability of BeiDou satellite is worse than that of GPS satellite. The second reason is that the clock stability of UR370 is not good enough for aviation.

5 Conclusion

This paper analyzes the requirement of cycle slip detection and repair for SBAS airborne receiver and describes a real-time cycle slip detection and repair method in detail, which combines chi-square detection algorithm and sequence-sum repair algorithm based on the statistical property of carrier fourth order differential. The cycle slip estimated error formula is given for integrity calculation.

Data collected by receiver UR370 has been used to evaluate the performance of the method. The result shows that cycle slip can be correctly detected and repaired, and that the cycle slip estimated error can bound the estimated error with the probability more than 99.9 %. The proposed method can be used in both the current SF SBAS and the coming DFMC SBAS.

Cycle slip repair accuracy is closely related to the statistical property of fourth order differential, which is affected by the stability of satellite clock and receiver clock, the state of motion and the environment. In order to improve the repair accuracy, SBAS airborne receiver should have a highly stabile inner clock, and selects navigation satellites with highly stabile clock onboard.