Abstract
Proof problems have long been the main target for logical problem solving. A problem in this class is a “yes/no” problem concerning with checking whether one logical formula is a logical consequence of another logical formula. Meanwhile, the importance of anther class of problems, query-answering problems (QA problems), has been increasingly recognized. A QA problem is an “all-answers finding” problem concerning with finding all ground instances of a query atomic formula that are logical consequences of a given logical formula. Several specific subclasses of QA problems have been addressed based on solution techniques for proof problems, without success of finding general solutions. In order to establish solution methods for proof problems and QA problems, we integrate these two classes of problems by embedding proof problems into QA problems. Construction of low-cost embedding mappings from proof problems to QA problems is demonstrated. By such embedding, proof problems can be solved using a procedure for solving QA problems. A procedure for solving QA problems based on equivalent transformation is presented. The presented work provides a new framework for integration of proof problems and QA problems and a solution for them by the general principle of equivalent transformation.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Given a first-order formula \(K\), representing background knowledge, and an atomic formula (atom) \(a\), representing a query, a query-answering problem (QA problem) is to find the set of all ground instances of \(a\) that are logical consequences of \(K\). Characteristically, it is an “all-answers finding” problem, i.e., all ground instances of the query atom satisfying the requirement must be found. A proof problem, by contrast, is a “yes/no” problem; it is concerned with checking whether or not one given logical formula is a logical consequence of another given logical formula.
Historically, works on logic-based automated reasoning have been centered around proof problems [5–7, 10]. Methods for solving proof problems were developed, e.g., tableau-based methods [4] and resolution-based methods [11], and they have been subsequently adapted to address other classes of logical problems, including some specific subclasses of QA problems, e.g., QA problems on definite clauses [8]. As opposed to such a proof-centered approach, we present in this paper a direct approach towards solving QA problems on the basis of the equivalent transformation (ET) principle. We show that proof problems can naturally be considered as QA problems of a special form; therefore, a method for solving QA problems also lends itself to solve proof problems in a straightforward way.
In order to clearly understand the relation between proof problems and QA problems, we introduce the notion of an embedding mapping from one problem class to another problem class. Using an embedding mapping, we demonstrate that proof problems can be formulated as a subclass of QA problems. We propose a framework for solving QA problems by ET. A given input QA problem on first-order logic is converted into an equivalent QA problem on an extended clause space, called the \(\text {ECLS}_\mathrm{F}\) space, through meaning-preserving Skolemization [1]. The obtained QA problem is then successively transformed on the \(\text {ECLS}_\mathrm{F}\) space by application of ET rules until the answer to the original problem can be readily obtained. With an embedding mapping from proof problems to QA problems, this framework can be used for solving proof problems.
To begin with, Sect. 2 formalizes QA problems and proof problems. Section 3 defines an embedding mapping and shows how to embed proof problems into QA problems. Section 4 introduces extended clauses, the extended space \(\text {ECLS}_\mathrm{F}\) and QA problems on this space. Section 5 presents our ET-based procedure for solving QA problems. Section 6 defines unfolding transformation on the \(\text {ECLS}_\mathrm{F}\) space and provides some other ET rules on this space. Section 7 illustrates application of our framework. Section 8 concludes the paper.
2 QA Problems and Proof Problems
2.1 Interpretations and Models
In this paper, an atom occurring in a first-order formula can be either a usual atom or a constraint atom. The semantics of first-order formulas based on a logical structure given in [2] is used. The set of all ground usual atoms, denoted by \(\mathcal{G}\), is taken as the interpretation domain. An interpretation is a subset of \(\mathcal{G}\). A ground usual atom \(g\) is true with respect to an interpretation \(I\) iff \(g\) belongs to \(I\). Unlike ground usual atoms, the truth values of ground constraint atoms are predetermined independently of interpretations. A model of a first-order formula \(E\) is an interpretation that satisfies \(E\). The set of all models of a first-order formula \(E\) is denoted by Models \((E)\). Given first-order formulas \(E_1\) and \(E_2\), \(E_2\) is a logical consequence of \(E_1\) iff every model of \(E_1\) is a model of \(E_2\).
2.2 QA Problems
A query-answering problem (QA problem) is a pair \(\langle K, a \rangle \), where \(K\) is a first-order formula, representing background knowledge, and \(a\) is a usual atom, representing a query. The answer to a QA problem \(\langle K, a \rangle \), denoted by \(\textit{answer}_\mathrm{qa}(\langle K, a \rangle )\), is defined as the set of all ground instances of \(a\) that are logical consequences of \(K\). Using Models \((K)\), the answer to a QA problem \(\langle K, a \rangle \) can be equivalently defined as
where \(\textit{rep}(a)\) denotes the set of all ground instances of \(a\). Accordingly, a QA problem can also be seen as a model-intersection problem. When no confusion is caused, \(\textit{answer}_\mathrm{qa}(\langle K, a \rangle )\) is often written as \(\textit{answer}_\mathrm{qa}(K, a)\).
2.3 Proof Problems
A proof problem is a pair \(\langle E_1, E_2 \rangle \), where \(E_1\) and \(E_2\) are first-order formulas, and the answer to this problem, denoted by \(\textit{answer}_\mathrm{pr}(\langle E_1, E_2 \rangle )\), is defined by

It is well known that a proof problem \(\langle E_1, E_2 \rangle \) can be converted into the problem of determining whether \(E_1 \wedge \lnot E_2\) is unsatisfiable [5], i.e., whether \(E_1 \wedge \lnot E_2\) has no model. As a result, \(\textit{answer}_\mathrm{pr}(\langle E_1, E_2 \rangle )\) can be equivalently defined by

When no confusion is caused, \(\textit{answer}_\mathrm{pr}(\langle E_1, E_2 \rangle )\) is often written as \(\textit{answer}_\mathrm{pr}(E_1, E_2)\).
3 Embedding Proof Problems into QA Problems
3.1 Embedding Mappings
The notion of a class of problems and that of an embedding mapping are formalized below.
Definition 1
A class \(\mathbf {C}\) of problems is a triple \(\langle \textsc {Prob}, {\textsc {Ans}}, \textit{answer} \rangle ,\) where
-
1.
\(\textsc {Prob}\) and \(\textsc {Ans}\) are sets,
-
2.
\(\textit{answer}\) is a mapping from \(\textsc {Prob}\) to \(\textsc {Ans}\).
The sets \(\textsc {Prob}\) and \(\textsc {Ans}\) are called the problem space and the answer space, respectively, of \(\mathbf {C}\). Their elements are called problems and (possible) answers, respectively, in \(\mathbf {C}\). Given a problem prb \(\in \) Prob, \(\textit{answer}(\textit{prb})\) is the answer to \(\textit{prb}\) in \(\mathbf {C}\). \(\square \)
Definition 2
Let \(\mathbf {C}_1 = \langle \textsc {Prob}_1, \textsc {Ans}_1, \textit{answer}_1 \rangle \) and \(\mathbf {C}_2 = \langle \textsc {Prob}_2, \textsc {Ans}_2, \textit{answer}_2 \rangle \) be classes of problems. An embedding mapping from \(\mathbf {C}_1\) to \(\mathbf {C}_2\) is a pair \(\langle \pi , \alpha \rangle \), where \(\pi \) is an injective mapping from \(\textsc {Prob}_1\) to \(\textsc {Prob}_2\) and \(\alpha \) is a partial mapping from \(\textsc {Ans}_2\) to \(\textsc {Ans}_1\) such that for any prb \(\in \) Prob \(_1\), \(\textit{answer}_1(\textit{prb}) = \alpha (\textit{answer}_2(\pi (\textit{prb})))\). \(\square \)
Let \(\mathbf {C}_1\) and \(\mathbf {C}_2\) be classes of problems. Suppose that (i) there exists an embedding mapping \(\langle \pi , \alpha \rangle \) from \(\mathbf {C}_1\) to \(\mathbf {C}_2\), (ii) there exists a procedure \(P\) for solving problems in \(\mathbf {C}_2\), and (iii) there also exist a procedure \(P_\pi \) for realizing \(\pi \) and a procedure \(P_\alpha \) for realizing \(\alpha \). Then a procedure for solving problems in \(\mathbf {C}_1\) can be obtained by making the composition of the procedures \(P_\pi \), \(P\) and \(P_\alpha \). \(\mathbf {C}_1\) is regarded as a subclass of \(\mathbf {C}_2\) iff there exists an embedding mapping \(\langle \pi , \alpha \rangle \) from \(\mathbf {C}_1\) to \(\mathbf {C}_2\) such that \(\pi \) and \(\alpha \) can be realized at low computational cost.
3.2 Embedding Proof Problems into QA Problems
Next, we show how to embed proof problems into QA problems. Assume that:
-
\(\mathbf {C}_\mathrm{qa} = \langle \textsc {Prob}_\mathrm{qa}, \textsc {Ans}_\mathrm{qa}, \textit{answer}_\mathrm{qa} \rangle \) is the class of QA problems defined by Sect. 2.2, i.e., \(\textsc {Prob}_\mathrm{qa}\) is the set of all QA problems, \(\textsc {Ans}_\mathrm{qa}\) is the power set of \(\mathcal{G}\), and \(\textit{answer}_\mathrm{qa}: \textsc {Prob}_\mathrm{qa} \rightarrow \textsc {Ans}_\mathrm{qa}\) is given by Sect. 2.2.
-
\(\mathbf {C}_\mathrm{pr} = \langle \textsc {Prob}_\mathrm{pr}, \textsc {Ans}_\mathrm{pr}, \textit{answer}_\mathrm{pr} \rangle \) is the class of proof problems defined by Sect. 2.3, i.e., \(\textsc {Prob}_\mathrm{pr}\) is the set of all proof problems,
 , and \({answer}_\mathrm{pr}: \textsc {Prob}_\mathrm{pr} \rightarrow \textsc {Ans}_\mathrm{pr}\) is given by Sect. 2.3.
, and \({answer}_\mathrm{pr}: \textsc {Prob}_\mathrm{pr} \rightarrow \textsc {Ans}_\mathrm{pr}\) is given by Sect. 2.3.
Figure 1 gives a pictorial view of an embedding mapping from \(\mathbf {C}_\mathrm{pr}\) to \(\mathbf {C}_\mathrm{qa}\). In order to construct such an embedding mapping, we want to construct from any arbitrary given proof problem \(\langle E_1, E_2 \rangle \) a QA problem \(\langle K, yes \rangle \) such that  iff \(\textit{answer}_\mathrm{qa}(K, yes) = \{ yes \}\), where \(yes\) is a 0-ary predicate symbol and the atom \(yes\) occurs in neither \(E_1\) nor \(E_2\). The following approaches can be taken for constructing such a formula \(K\):
iff \(\textit{answer}_\mathrm{qa}(K, yes) = \{ yes \}\), where \(yes\) is a 0-ary predicate symbol and the atom \(yes\) occurs in neither \(E_1\) nor \(E_2\). The following approaches can be taken for constructing such a formula \(K\):
-
Construct \(K\) such that every model of \(K\) contains \(yes\) iff
 .
. -
Construct \(K\) such that \(K\) has no model iff
 .
.
We refer to the first approach as positive construction, and the second one as negative construction. They are given below.
Embedding Using Positive Construction. Positive construction of an embedding mapping from \(\mathbf {C}_\mathrm{pr}\) to \(\mathbf {C}_\mathrm{qa}\) can be obtained by Proposition 1.
Proposition 1
Let \(E_1\) and \(E_2\) be first-order formulas. Assume that:
-
1.
\(yes\) is a 0-ary predicate symbol and \(yes\) occurs in neither \(E_1\) nor \(E_2\).
-
2.
\(prb_1\) is the proof problem \(\langle E_1, E_2 \rangle \).
-
3.
\(prb_2\) is the QA problem \(\langle yes \leftrightarrow (E_1 \rightarrow E_2), yes \rangle \).
Then  iff \(\textit{answer}_\mathrm{qa}(prb_2) = \{ yes \}\). \(\square \)
iff \(\textit{answer}_\mathrm{qa}(prb_2) = \{ yes \}\). \(\square \)
As depicted by Fig. 2(a), Proposition 1 determines an embedding mapping \(\langle \pi _\mathrm{a}, \alpha _\mathrm{a} \rangle \) from \(\mathbf {C}_\mathrm{pr}\) to \(\mathbf {C}_\mathrm{qa}\) as follows:
-
For any proof problem \(\langle E_1, E_2 \rangle \), \(\pi _\mathrm{a}(\langle E_1, E_2 \rangle ) = \langle yes \leftrightarrow (E_1 \rightarrow E_2), yes \rangle \).
-
 and
and 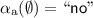 .
.
Embedding Using Negative Construction. The next proposition illuminates negative construction of an embedding mapping from \(\mathbf {C}_\mathrm{pr}\) to \(\mathbf {C}_\mathrm{qa}\).
Proposition 2
Let \(E_1\) and \(E_2\) be first-order formulas. Assume that:
-
1.
\(yes\) is a 0-ary predicate symbol and \(yes\) occurs in neither \(E_1\) nor \(E_2\).
-
2.
\(prb_1\) is the proof problem \(\langle E_1, E_2 \rangle \).
-
3.
\(prb_2\) is the QA problem \(\langle E_1 \wedge \lnot E_2, yes \rangle \).
Then  iff \(\textit{answer}_\mathrm{qa}(prb_2) = \{ yes \}\). \(\square \)
iff \(\textit{answer}_\mathrm{qa}(prb_2) = \{ yes \}\). \(\square \)
As shown in Fig. 2(b), Proposition 2 determines an embedding mapping \(\langle \pi _\mathrm{b}, \alpha _\mathrm{b} \rangle \) from \(\mathbf {C}_\mathrm{pr}\) to \(\mathbf {C}_\mathrm{qa}\) as follows:
-
For any proof problem \(\langle E_1, E_2 \rangle \), \(\pi _\mathrm{b}(\langle E_1, E_2 \rangle ) = \langle E_1 \wedge \lnot E_2, yes \rangle \).
-
 and
and  .
.
4 QA Problems on an Extended Space
To solve a QA problem \(\langle K, a \rangle \) on first-order logic, the first-order formula \(K\) is usually converted into a conjunctive normal form. The conversion involves removal of existential quantifications by Skolemization, i.e., by replacement of an existentially quantified variable with a Skolem term determined by a relevant part of a formula prenex. The classical Skolemization, however, does not preserve the logical meaning of a formula—the formula resulting from Skolemization is not necessarily equivalent to the original one [5]. In [1], a theory for extending the space of first-order formulas was developed and how meaning-preserving Skolemization can be achieved in the obtained extended space was shown. A procedure for converting first-order formulas into extended conjunctive normal forms in an extended clause space, called the \(\text {ECLS}_\mathrm{F}\) space, was also presented.
The basic idea of meaning-preserving Skolemization [1] is to use existentially quantified function variables instead of usual Skolem functions. Figure 3 illustrates the basic difference between meaning-preserving Skolemization and the conventional Skolemization, where \(h\) is a unary function variable, func is a built-in predicate symbol, and \(f\) is a usual unary Skolem function. Function variables, func-atoms, extended clauses, extended conjunctive normal forms, and QA problems on \(\text {ECLS}_\mathrm{F}\) are introduced below.
4.1 Function Constants, Function Variables and func-Atoms
A usual function symbol, say \(f\), in first-order logic denotes an unevaluated function; it is used for constructing from existing terms, say \(t_1, \ldots , t_n\), a syntactically new term, e.g., \(f(t_1, \ldots , t_n)\), possibly recursively, without evaluating the new term \(f(t_1, \ldots , t_n)\). A different class of functions is used in the extended space. A function in this class is an actual mathematical function, say \(h\), on ground terms; when it takes ground terms, say \(t_1, \ldots , t_n\), as input, \(h(t_1, \ldots , t_n)\) is evaluated for determining an output ground term. We called a function in this class a function constant. Variables of a new type, called function variables, are introduced; each of them can be instantiated into a function constant or a function variable, but not into a usual term.
In order to clearly separate function constants and function variables from usual function symbols and usual terms, a new built-in predicate symbol func is introduced. Given any \(n\)-ary function constant or \(n\)-ary function variable \(\bar{f}\), an expression \(\textit{func}(\bar{f}, t_1, \ldots , t_n, t_{n+1})\), where the \(t_i\) are usual terms, is considered as an atom of a new type, called a func -atom. When \(\bar{f}\) is a function constant and the \(t_i\) are all ground, the truth value of this atom is evaluated as follows: it is true iff \(\bar{f}(t_1, \ldots , t_n) = t_{n+1}\).
4.2 Extended Clauses
An extended clause \(C\) is a closed formula of the form
where \(v_1, \ldots , v_m\) are usual variables, each of \(a_1, \ldots , a_{n}, b_1, \ldots , b_p\) is a usual atom or a constraint atom, and \(\mathbf {f}_1, \ldots , \mathbf {f}_q\) are func-atoms. It is often written simply as \((a_1, \ldots , a_n \leftarrow b_1, \ldots , b_p, \mathbf {f}_1, \ldots , \mathbf {f}_q)\). The sets \(\{ a_1, \ldots , a_n \}\) and \(\{ b_1, \ldots , b_p, \mathbf {f}_1, \ldots , \mathbf {f}_q \}\) are called the left-hand side and the right-hand side, respectively, of the extended clause \(C\), denoted by \(\textit{lhs}(C)\) and \(\textit{rhs}(C)\), respectively. When \(n = 0\), \(C\) is called a negative extended clause. When \(n = 1\), \(C\) is called an extended definite clause, the only atom in \(\textit{lhs}(C)\) is called the head of \(C\), denoted by \(\textit{head}(C)\), and the set \(\textit{rhs}(C)\) is also called the body of \(C\), denoted by \(\textit{body}(C)\). When \(n > 1\), \(C\) is called a multi-head extended clause. All usual variables in an extended clause are universally quantified and their scope is restricted to the clause itself. When no confusion is caused, an extended clause, a negative extended clause, an extended definite clause and a multi-head extended clause will also be called a clause, a negative clause, a definite clause and a multi-head clause, respectively.
An extended normal form called existentially quantified conjunctive normal form (ECNF) is a formula of the form \(\exists {v_h}_1, \ldots , \exists {v_h}_m: (C_1 \wedge \cdots \wedge C_n)\), where \({v_h}_1, \ldots , {v_h}_m\) are function variables and \(C_1, \ldots , C_n\) are extended clauses. It is often identified with the set \(\{ C_1, \ldots , C_n \}\), with implicit existential quantifications of function variables and implicit clause conjunction. Function variables in such a clause set are all existentially quantified and their scope covers entirely all clauses in the set.
4.3 QA Problems on \(\text {ECLS}_\mathrm{F}\)
The set of all ECNFs is referred to as the extended clause space (\(\text {ECLS}_\mathrm{F}\)). By the above identification of an ECNF with a clause set, we often regard an element of \(\text {ECLS}_\mathrm{F}\) as a set of (extended) clauses. With occurrences of function variables, clauses contained in a clause set in the \(\text {ECLS}_\mathrm{F}\) space are connected through shared function variables. By instantiating all function variables in such a clause set into function constants, clauses in the obtained set are totally separated.
A QA problem \(\langle \textit{Cs}, a \rangle \) such that \(\textit{Cs}\) is a clause set in \(\text {ECLS}_\mathrm{F}\) and \(a\) is a usual atom is called a QA problem on \(\text {ECLS}_\mathrm{F}\). Given a QA problem \(\langle K, a \rangle \) on first-order logic, the first-order formula \(K\) can be converted equivalently by meaning-preserving Skolemization, using the conversion procedure given in [1], into a clause set \(\textit{Cs}\) in the \(\text {ECLS}_\mathrm{F}\) space. The obtained clause set \(\textit{Cs}\) may be further transformed equivalently in this space for problem simplification, by using unfolding and other transformation rules.
5 Solving QA Problems
Using the notation introduced in Sects. 5.1 and 5.2, our ET-based procedure is presented in Sect. 5.3.
5.1 Inclusion of Query Information
The following notation is used. A set \(A\) of usual atoms is said to be closed iff for any \(a \in A\) and any substitution \(\theta \) for usual variables, \(a\theta \) belongs to \(A\). Assume that (i) \(\mathcal{A}\) is the set of all usual atoms, (ii) \(\mathcal{A}_1\) and \(\mathcal{A}_2\) are disjoint closed subsets of \(\mathcal{A}\), and (iii) \(\phi \) is a bijection from \(\mathcal{A}_1\) to \(\mathcal{A}_2\) such that for any \(a \in \mathcal{A}_1\) and any substitution \(\theta \) for usual variables, \(\phi (a\theta ) = \phi (a)\theta \). For any \(i, j \in \{ 1, 2 \}\), an extended clause \(C\) is said to be from \(\mathcal{A}_i\) to \(\mathcal{A}_j\) iff all usual atoms in \(\textit{rhs}(C)\) belong to \(\mathcal{A}_i\) and all those in \(\textit{lhs}(C)\) belong to \(\mathcal{A}_j\).
Let \(\langle K, a \rangle \) be a QA problem such that \(K\) is a first-order formula in which all usual atoms belong to \(\mathcal{A}_1\) and \(a \in \mathcal{A}_1\). As will be detailed in Sect. 5.3, to solve this problem using ET, \(K\) is transformed by meaning-preserving transformation into a set \(\textit{Cs}\) of extended clauses from \(\mathcal{A}_1\) to \(\mathcal{A}_1\) and a singleton set \(Q\) consisting only of the clause \((\phi (a) \leftarrow a)\) from \(\mathcal{A}_1\) to \(\mathcal{A}_2\) is constructed from the query atom \(a\). The resulting QA problem \(\langle \textit{Cs}\cup Q, \phi (a) \rangle \) is then successively transformed using ET rules.
5.2 Triples for Transformation
In order to make a clear separation between a set of extended clauses from \(\mathcal{A}_1\) to \(\mathcal{A}_1\) and a set of those from \(\mathcal{A}_1\) to \(\mathcal{A}_2\) in a transformation process of QA problems, the following notation is introduced: Given a set \(\textit{Cs}\) of extended clauses from \(\mathcal{A}_1\) to \(\mathcal{A}_1\), a set \(Q\) of extended clauses from \(\mathcal{A}_1\) to \(\mathcal{A}_2\) and an atom \(b\) in \(\mathcal{A}_2\), let the triple \(\langle \textit{Cs}, Q, b \rangle \) denote the QA problem \(\langle \textit{Cs}\cup Q, b \rangle \). A QA problem \(\langle \textit{Cs}, Q, b \rangle \) can be transformed by changing \(\textit{Cs}\), by changing \(Q\), or by changing both \(\textit{Cs}\) and \(Q\).
Definition 3
A transformation of a QA problem \(\langle \textit{Cs}, Q, b \rangle \) into a QA problem \(\langle \textit{Cs}^\prime , Q^\prime , b \rangle \) is equivalent transformation (ET) iff \(\textit{answer}_\mathrm{qa}(\textit{Cs}\cup Q, b)\) and \(\textit{answer}_\mathrm{qa}(\textit{Cs}^\prime \cup Q^\prime , b)\) are equal. \(\square \)
5.3 A Procedure for Solving QA Problems by ET
Let \(\mathcal{A}_1\) be a closed set of usual atoms. Assume that a QA problem \(\langle K, a \rangle \) is given, where \(K\) is a first-order formula in which all usual atoms belong to \(\mathcal{A}_1\) and \(a \in \mathcal{A}_1\). To solve the QA problem \(\langle K, a \rangle \) using ET, perform the following steps:
-
1.
Transform \(K\) by meaning-preserving Skolemization into a clause set \(\textit{Cs}\) in the \(\text {ECLS}_\mathrm{F}\) space.
-
2.
Determine (i) a closed set \(\mathcal{A}_2\) of usual atoms such that \(\mathcal{A}_1\) and \(\mathcal{A}_2\) are disjoint and (ii) a bijection \(\phi \) from \(\mathcal{A}_1\) to \(\mathcal{A}_2\) such that for any \(a \in \mathcal{A}_1\) and any substitution \(\theta \) for usual variables, \(\phi (a\theta ) = \phi (a)\theta \).
-
3.
Successively transform the QA problem \(\langle \textit{Cs}, \{ (\phi (a) \leftarrow a) \}, \phi (a) \rangle \) in the \(\text {ECLS}_\mathrm{F}\) space using unfolding and other ET rules (see Sect. 6).
-
4.
Assume that the transformation yields a QA problem \(\langle \textit{Cs}^\prime , Q, \phi (a) \rangle \). Then:
-
(a)
If \(\textit{Models}(\textit{Cs}^\prime ) = \emptyset \), then output \(\textit{rep}(a)\) as the answer.
-
(b)
If \(\textit{Models}(\textit{Cs}^\prime ) \ne \emptyset \) and \(Q\) is a set of unit clauses such that the head of each clause in \(Q\) is an instance of \(\phi (a)\), then output as the answer the set
$$ \phi ^{-1}(\bigcup _{C \in Q} \textit{rep}(\textit{head}(C))). $$ -
(c)
Otherwise stop with failure.
-
(a)
It is shown in [3] that the obtained answer is always correct.
The set \(\mathcal{A}_2\) and the bijection \(\phi \) satisfying the requirement of Step 2 can be determined as follows: First, introduce a new predicate symbol for each predicate symbol occurring in \(\mathcal{A}_1\). Next, let \(\mathcal{A}_2\) be the atom set obtained from \(\mathcal{A}_1\) by replacing the predicate of each atom in \(\mathcal{A}_1\) with the new predicate introduced for it. Finally, for each atom \(a \in \mathcal{A}_1\), let \(\phi (a)\) be the atom obtained from \(a\) by such predicate replacement.
6 ET Rules on \(\text {ECLS}_\mathrm{F}\)
Next, ET rules for unfolding and definite-clause removal are presented, along with some other ET rules.
6.1 Unfolding Operation on \(\text {ECLS}_\mathrm{F}\)
Assume that (i) \(\textit{Cs}\) is a set of extended clauses, (ii) \(D\) is a set of extended definite clauses, and (iii) occ is an occurrence of an atom \(b\) in the right-hand side of a clause \(C\) in \(\textit{Cs}\). By unfolding \(\textit{Cs}\) using \(D\) at occ, \(\textit{Cs}\) is transformed into
where for each \(C^\prime \in D\), \(\textit{resolvent}(C, C^\prime , b)\) is defined as follows, assuming that \(\rho \) is a renaming substitution for usual variables such that \(C\) and \(C^\prime \rho \) have no usual variable in common:
-
If \(b\) and \(\textit{head}(C^\prime \rho )\) are not unifiable, then \(\textit{resolvent}(C, C^\prime , b) = \emptyset \).
-
If they are unifiable, then \(\textit{resolvent}(C, C^\prime , b) = \{ C^{\prime \prime } \}\), where \(C^{\prime \prime }\) is the clause obtained from \(C\) and \(C^\prime \rho \) as follows, assuming that \(\theta \) is the most general unifier of \(b\) and \(\textit{head}(C^\prime \rho )\):
-
\(\textit{lhs}(C^{\prime \prime }) = \textit{lhs}(C\theta )\)
-
\(\textit{rhs}(C^{\prime \prime }) = (\textit{rhs}(C\theta ) - \{ b\theta \}) \cup \textit{body}(C^\prime \rho \theta ).\)
-
The resulting clause set is denoted by \(\textsc {Unfold}(\textit{Cs}, D, \textit{occ})\).
6.2 ET by Unfolding and Definite-Clause Removal
Let Atoms \((p)\) denote the set of all atoms having a predicate \(p\). ET rules on \(\text {ECLS}_\mathrm{F}\) for unfolding and for definite-clause removal are described below.
ET by Unfolding. Let \(\langle \textit{Cs}, a \rangle \) be a QA problem on \(\text {ECLS}_\mathrm{F}\). Assume that:
-
1.
\(q\) is the predicate of the query atom \(a\).
-
2.
\(p\) is a predicate such that \(p \ne q\).
-
3.
\(D\) is a set of extended definite clauses in \(Cs\) that satisfies the following conditions:
-
(a)
For any \(C \in D\), \(\textit{head}(C) \in \textit{Atoms}(p)\).
-
(b)
For any \(C^\prime \in \textit{Cs}- D\), \(\textit{lhs}(C^\prime ) \cap \textit{Atoms}(p) = \emptyset \).
-
(a)
-
4.
occ is an occurrence of an atom in Atoms \((p)\) in the right-hand side of an extended clause in \(\textit{Cs}- D\).
Then \(\langle \textit{Cs}, a \rangle \) can be equivalently transformed into the QA problem \(\langle \textsc {Unfold}(\textit{Cs}, D, \textit{occ}), a \rangle \).
ET by Definite-Clause Removal. Let \(\langle \textit{Cs}, a \rangle \) be a QA problem on \(\text {ECLS}_\mathrm{F}\). Assume that:
-
1.
\(q\) is the predicate of the query atom \(a\).
-
2.
\(p\) is a predicate such that \(p \ne q\).
-
3.
\(D\) is a set of extended definite clauses in \(\textit{Cs}\) that satisfies the following conditions:
-
(a)
For any \(C \in D\), \(\textit{head}(C) \in \textit{Atoms}(p)\).
-
(b)
For any \(C^\prime \in \textit{Cs}- D\), \(\textit{lhs}(C^\prime ) \cap \textit{Atoms}(p) = \emptyset \).
-
(a)
-
4.
For any \(C^\prime \in \textit{Cs}- D\), \(\textit{rhs}(C^\prime ) \cap \textit{Atoms}(p) = \emptyset \).
Then \(\langle \textit{Cs}, a \rangle \) can be equivalently transformed into the QA problem \(\langle \textit{Cs}- D, a \rangle \).
6.3 Some Other ET Rules on \(\text {ECLS}_\mathrm{F}\)
Next, ET rules for merging func-atoms having the same call pattern, for removing isolated func-atoms, and for removing subsumed clauses are presented. They are used in examples in Sect. 7.
Merging func -Atoms with the Same Invocation Pattern. Let \(\langle \textit{Cs}, a \rangle \) be a QA problem on \(\text {ECLS}_\mathrm{F}\). Suppose that \(C \in \textit{Cs}\) and \(\textit{rhs}(C)\) contains func-atoms \(\mathbf {f}_1\) and \(\mathbf {f}_2\) that differ only in their last arguments. Then:
-
1.
If the last arguments of \(\mathbf {f}_1\) and \(\mathbf {f}_2\) are unifiable, with their most general unifier being \(\theta \), and \(C^\prime \) is an extended clause such that
-
\(\textit{lhs}(C^\prime ) = \textit{lhs}(C\theta )\), and
-
\(\textit{rhs}(C^\prime ) = (\textit{rhs}(C) - \{ \mathbf {f}_2 \})\theta \),
then \(\langle \textit{Cs}, a \rangle \) can be equivalently transformed into the QA problem \(\langle (\textit{Cs}- \{ C \}) \cup \{ C^\prime \}, a \rangle \).
-
-
2.
If their last arguments are not unifiable, then \(\langle \textit{Cs}, a \rangle \) can be equivalently transformed into the QA problem \(\langle \textit{Cs}- \{ C \}, a \rangle \).
Elimination of Isolated func -Atoms. A func-atom \(\textit{func}(h, t_1, \ldots , t_n, v)\), where \(v\) is a usual variable, is said to be isolated in an extended clause \(C\) iff there is only one occurrence of \(v\) in \(C\).
Now let \(\langle \textit{Cs}, a \rangle \) be a QA problem on \(\text {ECLS}_\mathrm{F}\). Suppose that:
-
1.
\(C \in \textit{Cs}\) such that \(C\) contains a func-atom that is isolated in \(C\).
-
2.
\(C^\prime \) is the extended clause obtained from \(C\) by removing all func-atoms that are isolated in \(C\).
Then \(\langle \textit{Cs}, a \rangle \) can be equivalently transformed into the QA problem \(\langle (\textit{Cs}- \{ C \}) \cup \{ C^\prime \}, a \rangle \).
Elimination of Subsumed Clauses. An extended clause \(C_1\) is said to subsume an extended clause \(C_2\) iff there exists a substitution \(\theta \) for usual variables such that \(\textit{lhs}(C_1)\theta \subseteq \textit{lhs}(C_2)\) and \(\textit{rhs}(C_1)\theta \subseteq \textit{rhs}(C_2)\).
A subsumed clause can be removed as follows: Let \(\langle \textit{Cs}, a \rangle \) be a QA problem on \(\text {ECLS}_\mathrm{F}\). If \(\textit{Cs}\) contains extended clauses \(C_1\) and \(C_2\) such that \(C_1\) subsumes \(C_2\), then \(\langle \textit{Cs}, a \rangle \) can be equivalently transformed into the QA problem \(\langle \textit{Cs}- \{ C_2 \}, a \rangle \).
7 Examples
Example 1 demonstrates how the procedure in Sect. 5.3 solves a QA problem using the ET rules in Sect. 6. Example 2 shows how to apply the procedure to solve a proof problem based on the embedding mapping in Sect. 3.2.
Example 1
Consider the “Tax-cut” problem discussed in [9]. This problem is to find all persons who can have discounted tax, with the knowledge that (i) any person who has two children or more can get discounted tax, (ii) men and women are not the same, (iii) a person’s mother is always a woman, (iv) Peter has a child named Paul, (v) Paul is a man, and (vi) Peter has a child, who is someone’s mother. This background knowledge is represented in first-order logic as the formulas \(F_1\)–\(F_6\) below, assuming that \(\textit{hc}\), \(\textit{ns}\), \(\textit{tc}\), \(\textit{mn}\), \(\textit{wm}\) and \(\textit{mo}\) stand, respectively, for \(\textit{hasChild}\), \(\textit{notSame}\), \(\textit{TaxCut}\), \(\textit{Man}\), \(\textit{Woman}\) and \(\textit{motherOf}\):

Accordingly, the “Tax-cut” problem is formulated as the QA problem \(\langle K, \textit{tc}(x) \rangle \), where \(K\) is the conjunction of \(F_1\)–\(F_6\). Using the meaning-preserving Skolemization procedure given in [1], the first-order formula \(K\) is transformed into a clause set \(\textit{Cs}\) consisting of the following extended clauses:

The clauses \(C_6\) and \(C_7\) together represent the first-order formula \(F_6\), where \(h_1\) and \(h_2\) are 0-ary function variables.
Assume that all usual atoms occurring in \(\textit{Cs}\) belong to \(\mathcal{A}_1\), \(\textit{ans}\) is a newly introduced unary predicate symbol, all \(\textit{ans}\)-atoms belong to \(\mathcal{A}_2\), and for any term \(t\), \(\phi (\textit{tc}(t)) = \textit{ans}(t)\). Let
To solve the QA problem \(\langle K, \textit{tc}(x) \rangle \), the QA problem \(\langle \textit{Cs}, \{ C_0 \}, \textit{ans}(x) \rangle \) is successively transformed by applying the ET rules in Sect. 6 as follows:
-
1.
By unfolding \(C_0\) at \(\textit{tc}(x)\) using \(\{ C_1 \}\), \(C_0\) is replaced with:

-
2.
By unfolding \(C_8\) at the last body atom using \(\{ C_2 \}\), \(C_8\) is replaced with:

-
3.
By unfolding \(C_9\) at the third body atom using \(\{ C_5 \}\), \(C_9\) is replaced with:

-
4.
By unfolding \(C_{10}\) at the last body atom using \(\{ C_3 \}\), \(C_{10}\) is replaced with:

-
5.
By unfolding \(C_{11}\) at the last body atom using \(\{ C_7 \}\), \(C_{11}\) is replaced with:

-
6.
By removing an isolated \(\textit{func}\)-atom, \(C_{12}\) is replaced with:

-
7.
By unfolding \(C_{13}\) at the first body atom using \(\{ C_4, C_6 \}\), \(C_{13}\) is replaced with:

-
8.
By merging \(\textit{func}\)-atoms with the same invocation pattern, \(C_{15}\) is replaced with:
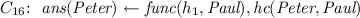
-
9.
Since \(C_{16}\) is subsumed by \(C_{14}\), \(C_{16}\) is removed.
-
10.
By unfolding \(C_{14}\) at the first body atom using \(\{ C_4, C_6 \}\), \(C_{14}\) is replaced with:

-
11.
By definite-clause removal, \(C_1\)–\(C_7\) are removed.
-
12.
By merging \(\textit{func}\)-atoms with the same invocation pattern, \(C_{18}\) is replaced with:

-
13.
By removing an isolated \(\textit{func}\)-atom, \(C_{19}\) is replaced with:

-
14.
Since \(C_{17}\) is subsumed by \(C_{20}\), \(C_{17}\) is removed.
The resulting QA problem is \(\langle \emptyset , \{ C_{20} \}, \textit{ans}(x) \rangle \). Since \(\textit{Models}(\emptyset ) \ne \emptyset \) and \(C_{20}\) is a unit clause whose head is an instance of \(\phi (\textit{tc}(x))\), the answer to the “Tax-cut” problem \(\langle K, \textit{tc}(x) \rangle \) is determined by
i.e., Peter is the only one who gets discounted tax. \(\square \)
Example 2
Refer to the description of the “Tax-cut” problem, the first-order formulas \(F_1\)–\(F_6\), the clauses \(C_0\)–\(C_{20}\) and the clause set \(\textit{Cs}= \{ C_1, \ldots , C_7 \}\) in Example 1. From the background knowledge of the “Tax-cut” problem, suppose that we want to prove the existence of someone who gets discounted tax. This problem is formulated as the proof problem \(\langle E_1, E_2 \rangle \), where \(E_1\) is the conjunction of \(F_1\)–\(F_6\) and \(E_2\) is the first-order formula \(\exists x: \textit{tc}(x)\).
Using Proposition 2, this proof problem is converted into the QA problem \(\langle E_1 \wedge \lnot E_2, yes \rangle \). Using the procedure in Sect. 5.3, this QA problem is solved as follows:
-
Convert \(E_1 \wedge \lnot E_2\) by meaning-preserving Skolemization, resulting in the clause set \(\textit{Cs}\cup \{ C^\prime _0 \}\), where \(C^\prime _0\) is the negative clause \((\leftarrow \textit{tc}(x))\).
-
Transform the QA problem
$$ \langle \textit{Cs}\cup \{ C^\prime _0 \}, \{ (\phi (yes) \leftarrow yes) \}, \phi (yes) \rangle $$using ET rules. By following the transformation Steps 1–14 in Example 1 except that the initial target clause is \(C^\prime _0\) instead of \(C_0\), the clauses \(C^\prime _8\)–\(C^\prime _{20}\) are successively produced, where for each \(i \in \{ 8, \ldots , 20 \}\),
-
\(lhs(C^\prime _i) = \emptyset \), and
-
\(\textit{rhs}(C^\prime _i) = \textit{rhs}(C_i)\),
and \(C_1\)–\(C_7\) are removed. As a result, \(\textit{Cs}\cup \{ C^\prime _0 \}\) is transformed into \(\{ C^\prime _{20} \}\), where \(C^\prime _{20} = (\leftarrow )\), and the QA problem
$$ \langle \{ C^\prime _{20} \}, \{ (\phi (yes) \leftarrow yes) \}, \phi (yes) \rangle $$is obtained.
-
-
Since \(C^\prime _{20}\) is the empty clause, the clause set \(\{ C^\prime _{20} \}\) has no model, i.e., \(\textit{Models} (\{ C^\prime _{20} \}) = \emptyset \). So the procedure outputs \(\textit{rep}(yes) = \{ yes \}\) as the answer to the QA problem \(\langle E_1 \wedge \lnot E_2, yes \rangle \).
It follows from Proposition 2 that the answer to the proof problem \(\langle E_1, E_2 \rangle \) is “yes”, i.e., there exists someone who gets discounted tax. \(\square \)
8 Conclusions
As shown in Fig. 4(a), previous approaches to solving QA problems are proof-centered. The classical first-order logic and the conventional Skolemization provide a foundation for solving proof problems. Based on them, several solution methods for specific subclasses of QA problems have been developed; for example, answering queries in logic programming and deductive databases can be regarded as solving QA problems on definite clauses and those on a restricted form of definite clauses, respectively. There has been no general solution method for QA problems on full first-order formulas. The conventional first-order logic and the conventional Skolemization are not enough for developing a general solution for QA problems.
QA problems on full first-order logic are considered in this paper. We introduced the concept of embedding and proposed how to embed proof problems into QA problems. This embedding leads to a unified approach to dealing with proof problems and QA problems, allowing one to use a method for solving QA problems to solve proof problems. It enables a QA-problem-centered approach to solving logical problems, which is shown in Fig. 4(b).
Equivalent transformation (ET) is one of the most fundamental principles of computation, and it provides a simple and general basis for verification of computation correctness. We proposed a framework for solving QA problems by ET. All computation steps in this framework are ET steps, including transformation of a first-order formula into an equivalent formula in the extended clause space \(\text {ECLS}_\mathrm{F}\) and transformation of extended clauses on \(\text {ECLS}_\mathrm{F}\). To the best of our knowledge, this is the only framework for dealing with the full class of QA problems on first-order formulas.
Since many kinds of ET rules can be employed, the proposed ET-based framework opens up a wide range of possibilities for computation paths to be taken. As a result, the framework enables development of a large variety of methods for solving logical problems. The range of possible computation methods can also be further extended by using computation spaces other than \(\text {ECLS}_\mathrm{F}\). Proof by resolution can be seen as one specific example of these possible methods. As demonstrated in [2], it can be realized by using two kinds of ET rules, i.e., resolution and factoring ET rules, on a computation space that differs slightly from \(\text {ECLS}_\mathrm{F}\).
References
Akama, K., Nantajeewarawat, E.: Meaning-preserving skolemization. In: 2011 International Conference on Knowledge Engineering and Ontology Development, Paris, France, pp. 322–327 (2011)
Akama, K., Nantajeewarawat, E.: Proving theorems based on equivalent transformation using resolution and factoring. In: 2nd World Congress on Information and Communication Technologies, Trivandrum, India, pp. 7–12 (2012)
Akama, K., Nantajeewarawat, E.: Embedding proof problems into query-answering problems and problem solving by equivalent transformation. Technical report, Hokkaido University, Sapporo, Japan (2013)
Beth, E.W.: Semantic Entailment and Formal Derivability. Noord-Hollandsche Uitg. Mij, Amsterdam (1955)
Chang, C.-L., Lee, R.C.-T.: Symbolic Logic and Mechanical Theorem Proving. Academic Press, New York (1973)
Fitting, M.: First-Order Logic and Automated Theorem Proving, 2nd edn. Springer, New York (1996)
Gallier, J.H.: Logic for Computer Science: Foundations of Automatic Theorem Proving. Wiley, New York (1986)
Lloyd, J.W.: Foundations of Logic Programming, 2nd edn. Springer, Heidelberg (1987)
Motik, B., Sattler, U., Studer, R.: Query answering for OWL-DL with rules. J. Web Semant. 3, 41–60 (2005)
Newborn, M.: Automated Theorem Proving: Theory and Practice. Springer, New York (2000)
Robinson, J.A.: A machine-oriented logic based on the resolution principle. J. ACM 12, 23–41 (1965)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Akama, K., Nantajeewarawat, E. (2015). Integration of and a Solution for Proof Problems and Query-Answering Problems. In: Fred, A., Dietz, J., Liu, K., Filipe, J. (eds) Knowledge Discovery, Knowledge Engineering and Knowledge Management. IC3K 2013. Communications in Computer and Information Science, vol 454. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-46549-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-662-46549-3_14
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-46548-6
Online ISBN: 978-3-662-46549-3
eBook Packages: Computer ScienceComputer Science (R0)






 , and
, and  .
. .
.
 and
and 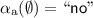 .
. and
and  .
.