Forced Trades in a Free Market

Abstract

A free trade is always Pareto-improving. But some “free trades” are actually forced in the sense that they reflect the trader’s poverty rather than his or her preferences. We propose a rigorous concept of forced trade, and apply it to the ethical evaluation of Walrasian equilibria.

1 Introduction

Everyone but an idiot knows that the lower classes must be kept poor or they will never be industrious.

Arthur Young, The Farmer’s Tour through the East of England, 1771.

The contribution of the theory of social choice to the evaluation of market allocations has been for the most part limited to exploring the general possibilities for aggregating individual preferences into a social ordering. In this mainstream context, the Pareto principle is generally sacrosanct. However, scholars like Nick Baigent have explored beyond the boundaries of this domain, questioning the basic principles of consequentialism, the possibility of carving a space for rights in social evaluation, and examined how to reconcile the social choice approach with policy concerns about merit goods.¹ This paper takes inspiration from this critical tradition.

A few years ago, TV news exhibited the sorrow of an English mother whose daughter died of the new form of Creutzfeld-Jacob disease. Her daughter, she explained, had been fed mostly with hamburgers for years because that was the only kind of food they could afford. At the same period, a French novel made a scandal because it describes sexual tourism as an ordinary business. Between affluent, cynical Westerners and poor people from developing countries, who only own their body, it is, as the author said, ‘an ideal situation of exchange’.

More recurrently a debate is going on about labor market deregulation, and opposes those who point out the new possibilities of mutually beneficial trades that deregulation entails, and those who object that workers will have no choice but to accept badly paid jobs with low guarantee and unsafe working conditions. The project of an international market for pollution permits has also aroused a debate opposing arguments about efficiency to arguments having to do with the fact that poor countries would then be induced to sell permits just because they are, regrettably, not in a position to pollute themselves.

The common thread in all these stories is the following. Although voluntary trade is always mutually beneficial, some trades are less “voluntary” than others, and economic pressure may be such as to make some trades questionable. If two agents engage in a trade, but one of them accepts it only because of a relatively disadvantaged position, it looks like the Pareto-improvement obtained through that trade is a step in the wrong direction. In particular, the surplus obtained by the relatively advantaged agent seems questionable. This agent is only exploiting the relative disadvantage of his trade partner. This is not to say that the disadvantaged agent is not actually benefiting also from the trade. But his benefit is conditional on his relative disadvantage, which is what makes it worrisome.

This problem has long been recognized by the law, which stipulates, with a lot of variation across countries, that contracts accepted under conditions of economic duress have no legal validity. The notion of economic duress that is retained by the law has, however, tended to be quite restrictive in general. But state regulation has added many safeguards and prohibitions surrounding working hours, working conditions, minimum wages, organs and blood, surrogate mothers, prostitution, etc. which all have to do with the risk that without regulation many agents would accept the unacceptable just because they are poor. The issue is not only one of paternalism against dangerous preferences (those who like dangerous work, for instance) or of externalities (bad health entails many negative externalities), but, above all, that the poor must be protected against the consequences of poverty which have to do with their excessive willingness to enter bad contracts.

Be that as it may, economic theory has no formal concept for this problem. Because any voluntary trade is Pareto-improving, and a Pareto-improvement is close to being sacro-sanct in welfare economics, there is no way in which the currently available concepts may help discern a problem when an agent is only apparently free, and is actually forced to accept a trade by economic pressure. When markets are complete and competition is perfect, the only ethical problem that economic theory acknowledges is the distribution of income, when it features inequalities or poverty.

Inequalities and poverty are commonly thought to be undesirable for a variety of reasons. On egalitarian grounds, it is just bad if some have less (resources, consumption, freedom, etc.) than others. In view of sufficiency principles, it is bad if some do not have enough. In the theory of fair allocation, recently surveyed by Thomson [25], it is bad if some agents envy others (in the sense that they would rather consume the others’ bundles), or if they would rather have the average bundle than their own. In [19] theory of exploitation, it is bad if some people would be better-off under an egalitarian distribution of endowments. In [18] theory of justice, it is bad if the worse-off could be better-off. None of these approaches describes or analyzes the phenomenon we want to study here.²

The explanation for this gap in economic theory may lie in the difficulty to disentangle the various factors which give agents incentives to trade. Agents engage in trade essentially for a mixture of three causes: (1) different tastes; (2) qualitatively different endowments; (3) quantitatively unequal endowments. Voluntary trades induced by different tastes or qualitatively different endowments should not give any qualm to the ethical observer, but trades which stem from inequalities or poverty are more problematic. And the reason they are problematic is that in such trades, the disadvantaged agent would no longer accept the trade if his disadvantage was removed.

In this paper we attempt to devise a test for the fact that an agent would no longer accept a trade or part of a bundle if his endowment was higher. Starting with examples, we will progressively elaborate general concepts which will enable the economist to distinguish how much of an agent’s market demand is due to economic pressure.

The availability of such concepts should permit a more complex view of the ethical properties of the market mechanism in welfare economics. A market economy with inequalities is not just an economy with unequal welfare, or with poor households who cannot buy enough consumption goods. It is also an economy where some agents are forced to accept the unacceptable, and, as a consequence, it is an economy where there is too much trade of some kind, such as bad jobs and junk food. An inegalitarian economy is therefore qualitatively different from an egalitarian one. Even the rich cannot have the same way of life in an economy without poverty, because they have no poor available, if only for domestic chores and cheap arts and crafts.

What we set up to do in this paper is to give a precise and rigorous definition to the notion of a forced trade. We will show in particular that one may distinguish an objective notion, having to do with budget constraints and survival, and a subjective notion which involves the agent’s preferences.

The paper is organized as follows. The next two sections essentially provide more intuition, in particular contexts, and propose a heuristic analysis. Section 2 presents a simple model in which the idea that some agents are forced to work more than normal is formalized. Section 3 examines another simple model, with a focus on forced consumption of inferior goods by people with low income. Section 4 extends these preliminary analyses and proposes a more abstract approach in a very general setting. Section 5 concludes.

2 Forced Labor

Consider the following simple model. There are three goods, land, labor and corn. Corn is the numeraire, and prices of land and labor are denoted r and w, respectively. A constant-returns-to-scale technology transforms land (k) and labor (ℓ) into corn (c):

$$\displaystyle{c = f(k,\ell).}$$

The population has n individuals, whose initial endowment consists of land only. They can also work. Their supply of land is inelastic, but they have preferences over corn and labor. Individual i has initial endowment (and supply) of land k _i , yielding a budget constraint

$$\displaystyle{c_{i} = \mathit{rk}_{i} + w\ell_{i},}$$

where c _i is consumption of corn and ℓ _i is labor, supposed to vary between 0 and 1 (see Fig. 1).

Fig. 1

Budget set

Let $c_{i}(w,\mathit{rk}_{i})$ and $\ell_{i}(w,\mathit{rk}_{i})$ denote individual i’s demand of corn and supply of labor, respectively. We assume that these demand and supply functions are determined by maximization of preference satisfaction under individual budget constraint.

Let us assume that a Walrasian equilibrium exists. Such an equilibrium is necessarily Pareto-optimal, and this is often presented as the hallmark of a free market. But are agents really free to trade in such a context?

Obviously, individuals face a budget constraint, and the smaller the budget the less options they have. This is trivial, and one might think that the only meaningful exercise, in this respect, is measuring the size of the opportunity sets of agents. A poor agent has less options than a rich agent, and this apparently raises a problem of inequality only. But, as suggested in the introduction, there is more to it. Poverty does not only reduce the available options, it also puts pressure on accepting some trades. A poor may accept a trade that a rich with similar preferences would refuse.

In order to make sense of this idea, one must first give a rigorous definition of the economic pressure due to poverty.

There is, first, an objective sense in which agents can be considered as constrained. Suppose that a decent (or subsistence) level of consumption is c ₀. Then an agent is objectively forced to work if $\mathit{rk}_{i} < c_{0}.$ More precisely, consider any k > 0 and ℓ > 0 satisfying:

$$\displaystyle{c_{0} = \mathit{rk} + w\ell.}$$

The agent is objectively forced to work at least ℓ whenever his endowment is less than k (see Fig. 2).

Fig. 2

Objective constraint

With this simple definition, one can ask the following questions. First, supposing that a given amount of labor $\ell^{{\ast}}\in \left (0,1\right )$ is taken as a reference, one can identify the agents who are objectively forced to work more than ℓ ^∗, and they are those whose endowment is less than

$$\displaystyle{\mathit{OLE}(\ell^{{\ast}}) = \frac{c_{0} - w\ell^{{\ast}}} {r},}$$

which will be called the “objective liberation endowment”, that is, the endowment which releases the agent from the obligation to work at least ℓ ^∗ in order to attain c ₀. The reference level ℓ ^∗ can be normal legal duration of labor, or average labor, or a physiologically ideal amount of labor.

Second, supposing that a given amount of endowment k ^∗ > 0 is taken as a reference, and that $\mathit{rk}^{{\ast}} + w \geq c_{0},$ one can notice that the agents with a lower endowment are forced to work at least

$$\displaystyle{\mathit{OFL}(k^{{\ast}}) =\max \{ 0, \frac{c_{0} - rk^{{\ast}}} {w} \},}$$

which will be called “objectively forced labor”. The reference k ^∗ can for instance be derived from a poverty line, or simply be the average endowment.

Different amounts of minimal consumption c ₀ can be considered for different agents, for instance as a function of their needs (the agents can be households of different sizes), in which case the functions OLE and OFL are agent-specific.

More interestingly, this objective definition of constrained supply of labor can be generalized so as to incorporate a subjective kind of constraint. When an agent supplies ℓ _i , it may not be because he is objectively forced to do so in order to reach some minimal consumption c ₀, but still, it might be that with a higher endowment this agent would no longer be willing to supply that much labor.

Following this intuition, we will say that agent i is subjectively forced to sell at least ℓ when $\ell_{i}(w,rk_{i}) \geq \ell$ and there is k such that for all $k^{{\prime}} > k,\;\ell_{i}(w,rk^{{\prime}}) <\ell$. Indeed, in such a case, the agent is willing to supply ℓ (or more), but would refuse to do so if his endowment was high enough.

Again, one can use this definition in various ways. Suppose that a reference ℓ ^∗ is considered. Then it may be interesting to register agents who are subjectively forced to work at least ℓ ^∗. One can define the “subjective liberation endowment” as

$$\displaystyle{\mathit{SLE}_{i}(\ell^{{\ast}}) =\max \{ k\mid \ell_{ i}(w,\mathit{rk}) \geq \ell^{{\ast}}\}.}$$

Then, agent i is subjectively forced to sell at least ℓ ^∗ when $\ell_{i}(w,\mathit{rk}_{i}) \geq \ell^{{\ast}}$ and $k_{i} \leq \mathit{SLE}_{i}(\ell^{{\ast}}) < +\infty$. When leisure is normal, the condition $k_{i} \leq \mathit{SLE}i(\ell^{{\ast}}) < +\infty$ is necessary and sufficient (see Fig. 3).

Fig. 3

Subjective liberation endowment. The curve ℓ _i (w, . ) is the locus of pairs (c, ℓ) that are best in the budget $c = w\ell + \mathit{rk}$ for some k

Notice that the higher $\mathit{SLE}_{i}(\ell^{{\ast}}),$ the less economic pressure the agent suffers. When $\mathit{SLE}_{i}(\ell^{{\ast}}) = +\infty,$ the pressure just disappears, because the agent is willing to sell ℓ ^∗ for indefinitely high incomes. When leisure is not a normal good, then $\ell_{i}(w,\mathit{rk}_{i})$ may fluctuate around ℓ ^∗ as k _i increases. We chose to define $\mathit{SLE}_{i}(\ell^{{\ast}})$ as the highest endowment k such that $\ell_{i}(w,rk) =\ell ^{{\ast}}$ and above which $\ell_{i}(w,\mathit{rk}) <\ell ^{{\ast}}.$ Indeed, it would seem strange to consider that the agent suffers a strong pressure just because his labor supply is volatile around ℓ ^∗, while he is willing to sell ℓ ^∗ for very high incomes. Taking the maximum threshold seems the only reasonable option (see Fig. 4).

Fig. 4

SLE in a complex case

The definition of SLE is a formal generalization of OLE, and both coincide when, over the relevant range, the agent works the minimum required to obtain c ₀, i.e.,

$$\displaystyle{\ell_{i}(w,\mathit{rk}) = \frac{c_{0} -\mathit{rk}} {w}.}$$

In the case when c ₀ is a subsistence level which the agent seeks to attain in priority, one always has

$$\displaystyle{\ell_{i}(w,\mathit{rk}) \geq \frac{c_{0} -\mathit{rk}} {w} }$$

and therefore, for any ℓ ^∗, 

$$\displaystyle{\mathit{OLE}(\ell^{{\ast}}) \leq \mathit{SLE}_{ i}(\ell^{{\ast}}).}$$

Symmetrically, if a reference k ^∗ is given, it may be interesting to measure the amounts of labor that agents are subjectively forced to provide when their endowment is less than k ^∗. Subjectively forced labor is then defined as

$$\displaystyle{\mathit{SFL}_{i}(k^{{\ast}}) =\max \{\ell \mid \forall k \leq k^{{\ast}},\;\ell_{ i}(w,\mathit{rk}) \geq \ell\}.}$$

When leisure is normal, one just has

$$\displaystyle{\mathit{SFL}_{i}(k^{{\ast}}) =\ell _{ i}(w,\mathit{rk}^{{\ast}}).}$$

When leisure is not normal, one cannot take $\ell_{i}(w,\mathit{rk}^{{\ast}})$ as forced labor due to endowment below k ^∗ if there exists k < k ^∗ such that $\ell_{i}(w,\mathit{rk}) <\ell _{i}(w,\mathit{rk}^{{\ast}}).$ One should check that for all k < k ^∗ one has ℓ _i (w, rk) no less than the amount of forced labor, and this justifies the above definition (see Fig. 5).

Fig. 5

Subjectively forced labor

Variants of these definitions can be imagined. For instance, suppose that k ^∗ is an ideal amount of endowment, such as the per capita endowment in the economy. Then

$$\displaystyle{\ell_{i}(w,\mathit{rk}_{i}) -\ell_{i}(w,\mathit{rk}^{{\ast}})}$$

is the additional amount of labor that agent i accepts because of an endowment lower than ideal.

The following proposition describes properties of the notions introduced here:

Proposition 1

For all k ^∗ and l ^∗ :

$$\displaystyle\begin{array}{rcl} \mathit{OLE}(\mathit{OFL}(k^{{\ast}}))& =& k^{{\ast}}\;\text{when }\mathit{OFL}(k^{{\ast}}) > 0 {}\\ \mathit{OFL}(\mathit{OLE}(\ell^{{\ast}}))& =& \ell^{{\ast}} {}\\ \mathit{SLE}_{i}(\mathit{SFL}_{i}(k^{{\ast}}))& \geq & k^{{\ast}}\ \text{(with equality if leisure is strictly normal)} {}\\ \mathit{SFL}_{i}(\mathit{SLE}_{i}(\ell^{{\ast}}))& \leq & \ell^{{\ast}}\ \text{(with equality if leisure is normal).} {}\\ \end{array}$$

The simple proof is omitted.³

Up to now we have only provided definitions, and it remains to explain why these new notions can be ethically relevant by implying that some Walrasian trades are problematic. We can distinguish different cases.

Case 1. :

Suppose that for some reason it is regrettable that agent i has $k_{i} < k^{{\ast}},$ where k ^∗ is some ideal endowment. For instance, k ^∗ equals the average endowment, and equality of endowments would be the ideal situation. If one has

$$\displaystyle{\mathit{SLE}_{i}(\mathit{SFL}_{i}(k_{i})) < k^{{\ast}},}$$

one can say that agent i accepts to work the amount SFL(k _i ) (or more) only because his endowment is unduly low. If he had k ^∗ or more, he would refuse to sell that much.

Why introduce SFL _i (k _i ) in the above condition, and not simply consider the condition $\mathit{SLE}_{i}(\ell_{i}) < k^{{\ast}}?$ Because if $\mathit{SFL}_{i}(k_{i}) <\ell _{i},$ which may occur if leisure is not normal, then one may have

$$\displaystyle{\mathit{SLE}_{i}(\ell_{i}) < k^{{\ast}}\leq \mathit{SLE}_{ i}(\mathit{SFL}_{i}(k_{i})),}$$

which means that although the agent would not accept to work ℓ _i if his endowment was k ^∗ or more, he would actually work less than ℓ _i (i.e., $\mathit{SFL}_{i}(k_{i})$) for some endowment that is less than k _i . In such a case it would be strange to say that the situation is problematic, because the agent is not really forced to work ℓ _i  —the agent can at most be considered forced to work as much as $SFL_{i}(k_{i})$ (see Fig. 6).

Fig. 6

A complex case

Case 2. :

Suppose that for some reason it is regrettable that agent i has $\ell_{i} >\ell ^{{\ast}},$ where ℓ ^∗ is some ideal amount of labor. For instance, ℓ ^∗ is an amount of labor which is socially considered “decent”. If one has

$$\displaystyle\begin{array}{rcl} \mathit{SFL}_{i}(k_{i})& >& \ell^{{\ast}} {}\\ \mathit{SLE}_{i}(\ell^{{\ast}})& <& k^{{\ast}} {}\\ \end{array}$$

one can say that it is doubly regrettable that the agent works more than ℓ ^∗, and does so because of an unduly low endowment. Such a situation seems worse than the previous one.

Case 3. :

The situation is also worse than the first one if

$$\displaystyle{\mathit{SLE}_{i}(\mathit{OFL}(k_{i})) < k^{{\ast}},}$$

because in this case the agent is, currently, objectively forced to work an amount he would refuse to work if his endowment was k ^∗. 

Case 4. :

The worst of all is when

$$\displaystyle\begin{array}{rcl} \mathit{OFL}(k_{i})& >& \ell^{{\ast}} {}\\ \mathit{SLE}_{i}(\ell^{{\ast}})& <& k^{{\ast}}, {}\\ \end{array}$$

because the agent has no choice but to work more than ℓ ^∗, and would no longer accept it with a normal endowment.

As this discussion suggests, it is not in itself questionable if only one of $\mathit{SFL}_{i}(k_{i}) >\ell ^{{\ast}}$ or $\mathit{OFL}(k_{i}) >\ell ^{{\ast}}$ holds. After all, the agent might be a workaholic who would work more than ℓ ^∗ no matter how rich he is. In such a case one cannot really say that his insufficient endowment is a relevant cause to his working that much. This is why it is essential to rely on SLE _i to check what the agent would choose if his endowment was sufficient.

The detection of questionable situations relies, here, on reference levels k ^∗ and ℓ ^∗. It seems necessary to rely on such benchmarks. Otherwise one would face the following difficulty. Consider a case when

$$\displaystyle{\mathit{SLE}_{i}(\mathit{SFL}_{i}(k_{i})) < +\infty }$$

but is extremely high, e.g., above the maximum endowment in an affluent population. This means that the agent would no longer accept to work that much only if his wealth was well above the currently observed endowments in this population. It seems hard to criticize this situation, because such high levels of wealth are just irrelevant. What is at stake here is the detection of situations where disadvantage, in terms of inequality or poverty, is at the root of the agent’s supply or demand.

The selection of reference levels is not addressed in this paper, because the point of this analysis is to provide concepts that can be adapted to many different normative views about what a decent endowment is or what a normal amount of labor is. Analysts focused on poverty and health may choose a lower k ^∗ and a greater ℓ ^∗ than analysts focused on inequality. The latter may want to take an average or a median value for these reference levels. Legal norms may also provide useful benchmarks. The legal hours (beyond which overtime pay is mandatory) may have been chosen for various reasons by the legislator, and independently of such reasons, it may be interesting to study if the workers who work overtime do it by choice or by constraint.

Another issue that this analysis raises is whether there is a link between forced trades and exploitation. Does the fact that some workers work more than a reference level under economic constraint mean that those who buy their labor take unfair advantage of the situation? In a Walrasian context with many agents, an employer who hires someone who works under economic constraint is not benefiting from this single worker’s situation, because the market wage rate does not depend on one single agent. But when there are many individuals who are constrained to work more than they would under better circumstances, the effect on market wages is substantial and generally in the direction of lowering wages to the benefit of the employers. Therefore, while no single transaction between two agents can be identified as exploitative in isolation, it may be part of a general pattern in which a “class” of employers benefits from the constraints imposed on the “class” of workers.

One can, however, argue that the concepts introduced here are about forced individual choices, rather than about forced transactions. If the benchmark endowment k ^∗ is defined on the basis of a poverty line and the whole economy is populated by poor individuals, they may be forced to work more than normal because of their poverty, without there being a class of exploiters. One can then recognize that something ethically unpleasant is taking place in this economy, although it not about unfair advantage or exploitation, but simply economic constraint. Moreover, notice that each of the four critical cases described above is compatible with the agent working in her own workshop, or even being a buyer, not a seller, of labor.

But these concepts can easily be applied to specific transactions, as the following simple example illustrates. Assume that, at the prevailing Walrasian equilibrium, every agent actually retains his own land, and works in priority over his own land. All agents use the same technique with factor ratio $\overline{\ell}/\overline{k},$ where $\overline{\ell}$ denotes the average labor and $\overline{k}$ the average endowment. If

$$\displaystyle{k_{i}\; \frac{\overline{\ell}} {\overline{k}} <\ell _{i},}$$

the agent has an excess of labor that he can sell to other agents. If the inequality is the other way around, then the agent does not work enough to make use of his land and he has to hire other agents. Suppose, now, that one takes k ^∗ to be the average endowment $\overline{k}.$ If one wants to avoid forced sale of labor (due to inequality) at the equilibrium, one has to check that there is no agent i such that

$$\displaystyle\begin{array}{rcl} \mathit{SLE}_{i}(\mathit{SFL}_{i}(k_{i}))& <& \overline{k} {}\\ k_{i}\; \frac{\overline{\ell}} {\overline{k}}& <& \ell_{i}. {}\\ \end{array}$$

If leisure is a strictly normal good, then $\mathit{SLE}_{i}(\mathit{SFL}_{i}(k_{i})) = k_{i},$ and one only has to check that for every i, 

$$\displaystyle{\frac{k_{i}} {\overline{k}} \geq \min \{ 1, \frac{\ell_{i}} {\overline{\ell}} \},}$$

i.e., that no agent with less-than-average endowment supplies labor on the market.

3 Forced Consumption

The previous model was also compatible with a different interpretation in terms of trade. It could describe an economy where all agents work on their own workshop, but trade land if their endowment does not fit their own quantity of labor. Then an agent will have to buy land if and only if

$$\displaystyle{k_{i} <\ell _{i}\frac{\overline{k}} {\overline{\ell}},}$$

which is the same condition as above for selling labor. In this new interpretation, one can talk about forced purchase of land instead of forced sale of labor.

But we will turn to another example of forced purchase. Suppose there are two consumption goods in the economy, hamburgers h and caviar c. For standard preferences in the population, the former is an inferior good, while the latter is a luxury good. Hamburger is the numeraire, and the price of caviar is denoted p. 

We will assume that survival requires a minimal consumption

$$\displaystyle{h_{i} + c_{i} \geq 1,}$$

in which hamburger and caviar have a symmetric role, but we will also assume that caviar is more expensive: p > 1. 

Individual i has an income I _i and his budget constraint is (see Fig. 7):

$$\displaystyle{h_{i} + \mathit{pc}_{i} = I_{i}.}$$

Let h _i (p, I _i ) and c _i (p, I _i ) denote the Marshallian demands of individual i.

Fig. 7

Consumption set and budget set

Under these assumptions survival requires I _i  ≥ 1 and

$$\displaystyle{h_{i} + \frac{I_{i} - h_{i}} {p} \geq 1,}$$

or equivalently,

$$\displaystyle{h_{i} \geq \frac{p - I_{i}} {p - 1}.}$$

By analogy to the previous section, we can define an objectively forced consumption of hamburger for 1 ≤ I _i  ≤ p: 

$$\displaystyle{\mathit{OFC}(I_{i}) = \frac{p - I_{i}} {p - 1},}$$

and an objective liberation income for 0 ≤ h _i  ≤ 1: 

$$\displaystyle{\mathit{OLI}(h_{i}) = p\left (1 - h_{i}\right ) + h_{i}.}$$

Figure 8 illustrates the computations.

Fig. 8

Objective constraint

Turning to subjective constraints, we can similarly define subjectively forced consumption as the amount which agent i would consume for any smaller income (see Fig. 9, where the curve h _i (p, . ) is the locus of pairs $\left (c,h\right )$ that are best in the budget $h + \mathit{pc} = I$ for some I ≥ 1):

$$\displaystyle{\mathit{SFC}_{i}(I_{i}) =\max \{ h\;\vert \;\forall I \in [1,I_{i}],\;h_{i}(p,I) \geq h\}}$$

Fig. 9

Subjectively forced consumption

and a subjective liberation income as the income above which the agent i would no longer consume that much (see Fig. 10):

$$\displaystyle{\mathit{SLI}_{i}(h_{i}) =\max \{ I\;\vert \;h_{i}(p,I) \geq h_{i}\}.}$$

Fig. 10

Subjective liberation income

Such notions can be put to use in the following fashion. Suppose that there is some ideal income I ^∗ > 1 such that it is regrettable if I _i  < I ^∗, and some ideal consumption h ^∗ < 1 such that it is regrettable (say, for health purposes) if h _i  > h ^∗. 

If agent i is such that

$$\displaystyle{\mathit{SLI}_{i}(\mathit{SFC}_{i}(I_{i})) < I^{{\ast}},}$$

one can say that this agent is subjectively forced to consume at least $SFC_{i}(I_{i}),$ because of an unduly low income. As a consequence, those agents who sell him that amount (or more) are unduly benefiting from his having I _i  < I ^∗. 

The situation is worse if

$$\displaystyle\begin{array}{rcl} \mathit{SLI}_{i}(h^{{\ast}})& <& I^{{\ast}}, {}\\ \mathit{SFC}_{i}(I_{i})& >& h^{{\ast}}, {}\\ \end{array}$$

because it involves an excessive consumption by the h ^∗ standard.

The situation is also worse if

$$\displaystyle{\mathit{SLI}_{i}(\mathit{OFC}(I_{i})) < I^{{\ast}},}$$

because the agent is objectively forced.

And the worst of all is

$$\displaystyle\begin{array}{rcl} \mathit{SLI}_{i}(h^{{\ast}})& <& I^{{\ast}}, {}\\ \mathit{OFC}(I_{i})& >& h^{{\ast}}, {}\\ \end{array}$$

because the agent is objectively forced to overconsume hamburgers, while he would refuse to do so with ideal income.

The parallelism between this example and the previous one suggests that a generalization of these concepts is not out of reach. Such a generalization is attempted in the next section.

4 Forced Trade: A General Approach

4.1 Framework

Consider a standard Arrow-Debreu model with ℓ goods. We assume that the prevailing price vector $p \in \mathbb{R}_{++}^{\ell}$ is fixed throughout. An individual agent i has an endowment $\omega _{i} \in \mathbb{R}^{\ell}$ in goods. In case of production, we will assume that this endowment contains the shares the agent owns in the m firms of the economy, that is:

$$\displaystyle{\omega _{i} =\bar{\omega } _{i} +\sum _{ j=1}^{m}\theta _{ \mathit{ij}}y_{j}}$$

where $\bar{\omega }_{i}$ denotes his personal endowment (as a household), θ _ij his share in firm j, and $y_{j} \in \mathbb{R}^{\ell}$ the production vector of firm j (with positive components for net outputs, and negative components for net inputs). Obviously, the production vectors depend on the prevailing prices but we will assume here that, like prices, the production plans of firms are fixed.

Agent i also has a consumption set $X_{i} \subset \mathbb{R}^{\ell},$ and a Walrasian demand correspondence for goods $x_{i}(p,\omega _{i}) \subset X_{i},$ derived from maximization of satisfaction over the budget set

$$\displaystyle{B_{i}(p,\omega _{i}) = \left \{x \in X_{i}\mid \mathit{px} \leq p\omega _{i}\right \}.}$$

We adopt the convention that for a bundle x ∈ X and a good k, x _k  > 0 means that good k is consumed, whereas x _k  < 0 means that good k is a labor service provided by the agent. The demand set (or expansion path) of the agent is the set of all demanded bundles at all possible endowments:

$$\displaystyle{D_{i} =\bigcup _{\omega \in \mathbb{R}^{\ell}}x_{i}(p,\omega ).}$$

(We adopt the convention that $x_{i}(p,\omega ) =\emptyset$ whenever $B_{i}(p,\omega ) =\emptyset$.)

We need the following notations. For a given bundle $x \in \mathbb{R}^{\ell},$ let

$$\displaystyle{x^{\nearrow } = \left \{z \in \mathbb{R}^{\ell}\mid \forall k = 1,\ldots,\ell,\;x_{ k}z_{k} \geq x_{k}^{2}\right \},}$$

that is, $x^{\nearrow }$ is the set of bundles whose components have the same sign as components of x, and are larger (when x _k  = 0, this puts no constraint on z _k ). Concretely, $x^{\nearrow }$ is the set of bundles such that the agent consumes at least as much, and works at least as much, as in x. And, for any closed subset $A \subset \mathbb{R}^{\ell},$ let

$$\displaystyle\begin{array}{rcl} A_{\inf }& =& a \in \mathbb{R}^{\ell}\;\text{such that:} {}\\ A& \subset & a^{\nearrow }\;\text{and }\ \forall b \in a^{\nearrow },\;A \subset b^{\nearrow }\Rightarrow b = a. {}\\ \end{array}$$

In other words, A _inf is the maximal bundle a (in the “$^{\nearrow }$” sense) such that $A \subset a^{\nearrow }.$ Notice one always has $A \subset \left (A_{\inf }\right )^{\nearrow }.$ Finally, let pA denote

$$\displaystyle{pA =\{ m \in \mathbb{R}\mid \exists a \in A,\;m = \mathit{pa}\}.}$$

4.2 Forced Consumption and Trade

We are now equipped to give definitions which generalize the previous sections.

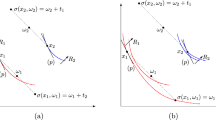
The agent is no longer objectively forced to demand a given bundle x or more, that is, to consume a bundle in $x^{\nearrow },$ when his income allows him to consume something in $X_{i}\setminus x^{\nearrow }.$ One can then define the objective liberation income for x (see Fig. 11) as

$$\displaystyle{OLI_{i}(x) =\inf p\left (X_{i}\setminus x^{\nearrow }\right ).}$$

Figure 11 illustrates two cases, with one in which x is not in X _i .

Fig. 11

Objective liberation income. The continous curve delineates X _i , the dotted lines delineate $x^{\nearrow }$

Conversely, with endowment ω _i the agent is objectively forced to consume at least any bundle x such that $B_{i}(p,\omega _{i}) \subset x^{\nearrow }.$ Therefore, his objectively forced consumption is then:

$$\displaystyle{\mathit{OFC}_{i}(\omega _{i}) = B_{i}(p,\omega _{i})_{\inf }}$$

and, similarly, his objectively forced trade is the maximal trade q such that for any $x \in B_{i}(p,\omega _{i}),$ $x -\omega _{i} \in q^{\nearrow },$ that is (see Fig. 12):

$$\displaystyle{\mathit{OFT}_{i}(\omega _{i}) = \left [B_{i}(p,\omega _{i}) -\omega _{i}\right ]_{\inf }.}$$

This vector is illustrated in Fig. 12 as the arrow from ω _i to $B_{i}(p,\omega _{i})_{\inf }$.

Fig. 12

Objectively forced consumption and trade

Notice that these concepts capture minimal constraints. One may also want to focus on B _i (p, ω _i ) rather than just $B_{i}(p,\omega _{i})_{\inf },$ in some cases, or concatenate some dimensions in order to talk about constraints over aggregate goods or services. For instance, consider a household with a couple without children. Suppose they have no unearned income, and assume that they need at least $15,000 per year to live in a decent way. Both are able to work and earn $30,000, but in different kinds of jobs: he is a nurse while she is a carpenter. According to the $B_{i}(p,\omega _{i})_{\inf }$ concept, they are not objectively forced to work, in the sense that they can live without providing any hour of nurse or any hour of carpenter to the market. But of course, aggregating nurse hours and carpenter hours gives a different picture: at least one of them must work half time.

The extension of these definitions to the idea of subjective constraints is essentially obtained by substituting D _i to X _i in the above definitions, if we assume that preferences are locally non-satiated in order to simplify the analysis (this allows us to have $x_{i}(p,\omega ) = D_{i} \cap \{ z \in X\mid \mathit{pz} = p\omega \}$). However, the definition of a subjective liberation income by the formula

$$\displaystyle{\mathit{SLI}_{i}(x) =\inf p\left (D_{i}\setminus x^{\nearrow }\right )}$$

is not satisfactory when the agent’s demand is not normal, since it may happen that with some high income the agent is still willing to demand a bundle in $x^{\nearrow }$ again. As explained in the previous sections, the subjective liberation income must be such that, above it, the agent is no longer willing to consume in $x^{\nearrow }.$ The appropriate generalization of the definitions of the previous sections is then (see Fig. 13):

$$\displaystyle{\mathit{SLI}_{i}(x) =\sup p\left (D_{i} \cap x^{\nearrow }\right ),}$$

and this definition correctly yields + ∞ whenever the agent is willing to consume in $x^{\nearrow }$ for indefinitely high incomes. This definition can be extended again to accommodate any requirement that an area of X _i should be avoided (and in particular the case when $x_{i}(p,\omega _{i})$ is not a singleton). For any A ⊂ X _i , one may define the subjective liberation income for A as the income above which the agent no longer accepts to consume in A: 

$$\displaystyle{\mathit{SLI}_{i}(A) =\sup p\left (D_{i} \cap A\right ).}$$

Fig. 13

Subjective liberation income. The upward sloping curve is D _i , the demand set defined by a given p and varying endowments

With the other definitions the simple substitution of D _i to X _i provides the correct extension, and this can be denoted here as follows (see Fig. 14):

$$\displaystyle\begin{array}{rcl} \mathit{SFC}_{i}(\omega _{i})& =& \left [B_{i}(p,\omega _{i}) \cap D_{i}\right ]_{\inf }, {}\\ \mathit{SFT}_{i}(\omega _{i})& =& \left [\left (B_{i}(p,\omega _{i}) \cap D_{i}\right ) -\omega _{i}\right ]_{\inf }. {}\\ \end{array}$$

Fig. 14

Subjectively forced consumption and trade

There are general properties to be noted, about these various concepts.

Proposition 2

• (i) For all $x \in \mathbb{R}^{\ell}$ , $\mathit{OLI}_{i}(x) \leq \mathit{SLI}_{i}(x).$

• (ii) For all $x,q \in \mathbb{R}^{\ell},$ $x \in q^{\nearrow }\Rightarrow \mathit{OLI}_{i}(x) \leq \mathit{OLI}_{i}(q)$.

• (iii) For all $A,B \subset \mathbb{R}^{\ell},$ $A \subset B \Rightarrow \mathit{SLI}_{i}(A) \leq \mathit{SLI}_{i}(B).$

• (iv) For all $\omega _{i} \in \mathbb{R}^{\ell},$ $\mathit{SFC}_{i}(\omega _{i}) \in \mathit{OFC}_{i}(\omega _{i})^{\nearrow }.$

• (v) For all $\omega _{i} \in \mathbb{R}^{\ell},$ $\mathit{OLI}_{i}(\mathit{OFC}_{i}(\omega _{i})) \geq p\omega _{i}.$

• (vi) For all $\omega _{i} \in \mathbb{R}^{\ell},$ $\mathit{SLI}_{i}(\mathit{SFC}_{i}(\omega _{i})) \geq p\omega _{i}.$

Proof

 

• (i) One has

  $$\displaystyle\begin{array}{rcl} \mathit{OLI}_{i}(x)& =& \inf p\left (X_{i}\setminus x^{\nearrow }\right ) {}\\ & \leq &\inf p\left (D_{i}\setminus x^{\nearrow }\right ) {}\\ & \leq &\inf p\left (D_{i}\setminus x^{\nearrow }\right ) \cap p\left (D_{ i} \cap x^{\nearrow }\right ) {}\\ & \leq &\sup p\left (D_{i}\setminus x^{\nearrow }\right ) \cap p\left (D_{ i} \cap x^{\nearrow }\right ) {}\\ & \leq &\sup p\left (D_{i} \cap x^{\nearrow }\right ) = \mathit{SLI}_{ i}(x). {}\\ \end{array}$$

• (ii) One has

  $$\displaystyle\begin{array}{rcl} x& \in & q^{\nearrow }\Rightarrow x^{\nearrow }\subset q^{\nearrow } {}\\ &\Rightarrow & X_{i}\setminus q^{\nearrow }\subset X_{ i}\setminus x^{\nearrow } {}\\ &\Rightarrow &\inf p\left (X_{i}\setminus x^{\nearrow }\right ) \leq \inf p\left (X_{ i}\setminus q^{\nearrow }\right ). {}\\ \end{array}$$

• (iii) The reasoning is the same as for (ii).

• (iv) A ⊂ B entails $A_{\inf } \in \left (B_{\inf }\right )^{\nearrow },$ so that

  $$\displaystyle{\mathit{SFC}_{i}(\omega _{i}) = \left [B_{i}(p,\omega _{i}) \cap D_{i}\right ]_{\inf } \in \left [B_{i}(p,\omega _{i})_{\inf }\right ]^{\nearrow }.}$$

• (v) $B_{i}(p,\omega _{i}) \subset \left [B_{i}(p,\omega _{i})_{\inf }\right ]^{\nearrow },$ so that

  $$\displaystyle{\mathit{OLI}_{i}(\mathit{OFC}_{i}(\omega _{i})) =\inf p\left (X_{i}\setminus \left [B_{i}(p,\omega _{i})_{\inf }\right ]^{\nearrow }\right ) \geq \inf p\left (X_{ i}\setminus B_{i}(p,\omega _{i})\right ) = p\omega _{i}.}$$

• (vi) One has

  $$\displaystyle\begin{array}{rcl} \mathit{SLI}_{i}(\mathit{SFC}_{i}(\omega _{i}))& =& \sup p\left (X_{i} \cap \left [\left (B_{i}(p,\omega _{i}) \cap D_{i}\right )_{\inf }\right ]^{\nearrow }\right ) {}\\ & \geq &\sup p\left (X_{i} \cap \left (B_{i}(p,\omega _{i}) \cap D_{i}\right )\right ) {}\\ & =& \sup p\left (B_{i}(p,\omega _{i}) \cap D_{i}\right ) = p\omega _{i}. {}\\ \end{array}$$

 □ 

Let us now turn to the ethical discussion of situations where economic pressure is problematic. Following the same intuition as in the above examples, we can say that if

$$\displaystyle{\mathit{SLI}_{i}(\mathit{SFC}_{i}(\omega _{i})) < I^{{\ast}},}$$

where I ^∗ is an ideal income (such as the average level in the population), then there is a problem, because the agent is subjectively forced to consume bundles which he would no longer accept to consume if his income reached the reference I ^∗. 

In some cases, it also makes sense to worry about the situation

$$\displaystyle{\mathit{SLI}_{i}(x_{i}(p,\omega _{i})) < I^{{\ast}},}$$

for instance in the case illustrated in Fig. 15, where the agent has

$$\displaystyle{\mathit{SLI}_{i}(\mathit{SFC}_{i}(\omega _{i})) = +\infty }$$

but

$$\displaystyle{\mathit{SLI}_{i}(x_{i}(p,\omega _{i})) = p\omega _{i}.}$$

In this example, $\mathit{SFC}_{i}(\omega _{i})$ is just the bottom point of X and is not very relevant. Because good 1 is inferior for high incomes, one may say that the agent is forced to consume much of it because of his low income. The examples of the two previous sections did not provide similar cases because in those examples SFC _i (ω _i ) was not much influenced by the shape of the agent’s demand at very low incomes.

Fig. 15

Inferior good for high incomes

Similarly, suppose that there is a consumption subset X ⁻ ⊂ X _i such that it is considered problematic if an agent consumes x ∈ X ⁻ (for instance, x ∈ X ⁻ means that the agent suffers from malnutrition and overworks). Then, if one indeed observes x ∈ X ⁻, and moreover

$$\displaystyle\begin{array}{rcl} \mathit{SFC}_{i}(\omega _{i})& \in & X^{-} {}\\ \mathit{SLI}_{i}(X^{-})& <& I^{{\ast}}, {}\\ \end{array}$$

then the situation is worse than above. (Notice that it implies $\mathit{SLI}_{i}(\mathit{SFC}_{i}(\omega _{i})) < I^{{\ast}}.$)

Again, the situation is also rather bad if

$$\displaystyle{\mathit{SLI}_{i}(\mathit{OFC}_{i}(\omega _{i})) < I^{{\ast}},}$$

since the agent is objectively forced to accept consumptions he would reject with the ideal income.

Finally, the worst of all is when

$$\displaystyle\begin{array}{rcl} \mathit{OFC}_{i}(\omega _{i})& \in & X^{-} {}\\ \mathit{SLI}_{i}(X^{-})& <& I^{{\ast}}. {}\\ \end{array}$$

4.3 Equilibria With and Without Forced Trade

The concepts defined above allow us to speak rigorously about agents who accept particular consumptions because of inadequate income and not by pure preference. We now proceed to examine whether it is possible to obtain Walrasian equilibria such that no agent suffers from undue economic pressure, and we will focus on equilibria where no agent suffers from

$$\displaystyle{\mathit{SLI}_{i}(x_{i}(p,\omega _{i})) <\bar{ I},}$$

where $\bar{I}$ is the average income in the population, or at least where no agent has

$$\displaystyle{\mathit{SLI}_{i}(\mathit{SFC}_{i}(\omega _{i})) <\bar{ I}.}$$

In other words, is it possible to make sure that no agent accepts certain consumption and work just because of a below-average income? Obviously, full equality of incomes in the population provides a sufficient condition for this to be achieved. But can one characterize the set of situations where any of the above requirement is satisfied?

An equilibrium is such that $\mathit{SLI}_{i}(x_{i}(p,\omega _{i})) \geq \bar{ I}$ for all i if and only if for every agent i such that $I_{i} <\bar{ I},$ one has, by definition:

$$\displaystyle{\sup p\left (D_{i} \cap x_{i}(p,\omega _{i})^{\nearrow }\right ) \geq \bar{ I},}$$

which is equivalent, since $D_{i} \cap x_{i}(p,\omega _{i})^{\nearrow }$ is not empty and $x_{i}(p,\omega _{i})$ is closed, to the condition that there exists ω ^′ such that $p\omega ^{{\prime}}\geq \bar{ I}$ and

$$\displaystyle{ x_{i}(p,\omega ^{{\prime}}) \cap x_{ i}(p,\omega _{i})^{\nearrow }\neq \emptyset. }$$

(1)

A sufficient condition for this to be obtained is that for ω ^′ such that $p\omega ^{{\prime}} =\bar{ I},$

$$\displaystyle{x_{i}(p,\omega ^{{\prime}}) \subset x_{ i}(p,\omega _{i})^{\nearrow }.}$$

And a sufficient condition for the latter to be obtained is that, for incomes over the range $[p\omega _{i},\bar{I}],$ consumption goods (those k such that $x_{\mathit{ik}}(p,\omega _{i}) > 0)$ must be normal, whereas labor services (those k such that x _ik (p, ω _i ) < 0) must be inferior.

One should not hope for more clearcut necessary and sufficient conditions than condition (1) here, because (1) can be satisfied in many different ways by complex demand correspondences.

If one focuses on the weaker condition that $\mathit{SLI}_{i}(\mathit{SFC}_{i}(\omega _{i})) \geq \bar{ I}$ for all i, one obtains the necessary and sufficient condition that for every agent i such that $I_{i} <\bar{ I},$ there must exist $\omega ^{{\prime}}$ and ω ^{′ ′} such that $p\omega ^{{\prime}}\geq \bar{ I},$ $p\omega ^{{\prime\prime}}\leq p\omega _{i}$ and

$$\displaystyle{x_{i}(p,\omega ^{{\prime}}) \cap x_{ i}(p,\omega ^{{\prime\prime}})^{\nearrow }\neq \emptyset.}$$

A sufficient condition for this to be obtained, in addition to the ones described above, is that for low endowments the demand x _i must be close enough to zero. As described in the previous section, in the case of consumption goods, this condition may be automatically satisfied because of the objective pressure of the budget constraint, and this new sufficient condition is then not very relevant, from the ethical standpoint.

Let us now examine the likelihood of observing undue economic pressure, in the sense of the above two conditions, in any market equilibrium. From the above discussion, it is easy to derive the conclusion that if all goods and services are normal, then it is very likely to observe unduly forced labor, but no forced consumption (of ordinary goods) will prevail. On the contrary, if many or most goods and services are inferior over the relevant range (that is, between the lowest and the average incomes), then one will not observe any forced labor, but forced consumption will be commonplace. The situation which is the least favorable is when labor services are normal, while consumption goods are inferior.

The latter situation is actually quite plausible for unpleasant kinds of works (dangerous or dirty chores) and for low quality consumption goods (industrial food of dubious quality, low quality clothes). As a consequence, one may safely conjecture that forced labor and forced consumption, in the sense defined here, do prevail over a large scale in most world economies.

5 Conclusion

The concepts developed here are meant to give a rigorous formulation to the widespread intuition that poor people are not only agents who consume too little, but also agents who work too much (in bad jobs) and consume too much (of bad quality goods). Some ideas for future research are proposed in this conclusion.

First, there is an obvious link between objective and subjective constraint, the latter generalizing the former, as explained in Sect. 2. More precisely, the objective constraint corresponds to the subjective constraint for individuals who seek to minimize the contemplated trade in priority. But another understanding of the objective constraint, as defined in this paper, is that the agent is objectively constrained when he is subjectively constrained for all possible preferences. This formulation suggests a notion that would be intermediate between the objective and subjective notions, and would examine the size of the set of preferences for which the agent is constrained. The larger this set, the more objective is the constraint.

Moreover, one could focus on a subset that is centered on the agent’s actual preferences. Intuitively, the idea would be that the agent is more constrained when it would require a greater change to his preferences in order to obtain a situation in which he is not subjectively constrained. This is an idea that needs topological concepts on preferences, as in topological social choice [3].

A related idea would be to extend the concepts proposed here in the direction of defining a degree of constraint. The definitions offered in this paper only seek to decide whether an individual is or is not constrained. But it would also make sense to seek a measure of economic constraint that would vary between 0 and 1. Two directions could be explored for this purpose. First, the relative size of the set of preferences for which the agent is constrained, or the minimal distance between his preferences and the preferences for which he would no longer be constrained, could be used to construct the index of constraint. Such a measure could focus on a particular trade and measure how much economic pressure the agent endures to accept this particular trade. Another possibility, in the direction of measuring the general economic constraint endured by the agent, would be to measure the size of the set of trades that the agent is forced to accept.

Finally, establishing a rigorous terminology to depict the ethical problems raised by economic pressure obviously suggests to examine remedies. Two general kinds of practical solutions are available. One is based on redistribution, and seeks to radically solve the problem by freeing the poor from the constraint of poverty itself. Another kind of policy consists in regulating the market and prohibiting the bad trades that poor people are likely to accept.

In first approximation, one may guess that the former is the most favorable to the target population, because the latter is likely to make them actually worse off according to their own preferences, at least in the short run. In some contexts, it appears, however, that prohibition may alter market prices so that, in the end, the poor actually benefit. An example dealing with child labor is provided by Basu [5]. The mixed results obtained on the impact of minimal wages on the labor market also suggest that prohibiting low-wage jobs does not necessarily hurt the potential low-wage earners.

The prohibition policy has, at any rate, often been chosen. There may be several reasons for that. For instance, bad trades which endanger health create negative externalities. Paternalistic views may insist on prohibiting certain patterns of consumption. But there might be another explanation, coming from political economy. Of the two policies described above, redistribution is the most effective and favorable to the poor, but is also the most costly to the rich. It may be much more acceptable to the rich to prohibit the most conspicuous and repugnant forms of bad trades without doing any redistribution. This is certainly costly to the rich as well, but probably much less than direct transfers.

When dealing with the issue of bad trades, one should be aware that the boundary between the acceptable and the unacceptable is really a matter of social convention. The work schedules and kinds of jobs that appeared normal in the last century now seem awful. Slavery seemed natural to Aristotle just as wage contracts seem natural to most of our contemporaries. Now, the concept of subjective liberation income may help to get more insight in the trend that affects the boundary of the acceptable. Just take a high income and examine what people would no longer be willing to accept if they had such income. This may give some indication about where the boundary of the acceptable will lie in the next centuries. What this device neglects is the potential impact of culture shifts. But at least some tendencies may be detected in that way.