Binary Oxides of Transition Metals

Abstract

First-principles DFT methods complement the experimental study of the binary oxides (ZnO, TiO$_2$ and ZrO$_2$)-based nanostructures. We begin each section of this chapter with a short discussion of the results of the corresponding bulk crystal and nanosheet properties calculations. This information is important for understanding the structure and properties of binary oxide-based nanotubes and nanowires.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

First-principles DFT methods complement the experimental study of the binary oxides (ZnO, TiO$_2$ and ZrO$_2$)-based nanostructures. We begin each section of this chapter with a short discussion of the results of the corresponding bulk crystal and nanosheet properties calculations. This information is important for understanding the structure and properties of binary oxide-based nanotubes and nanowires.

ZnO-layered crystals have a wurtzite structure, in which the interlayer Van der Waals interaction is weak. Therefore the conventional single-walled ZnO nanotubes are generated by rolling up one-layer slab with a hexagonal 2D lattice. The DFT(PBE) calculations of zigzag (n,0), armchair (n,n) and chiral (n$_1$, n$_2$) rolled up nanotubes show that for all types of ZnO nanotubes, the strain energies are much smaller than for BN nanotubes with the same diameters, but are somewhat sensitive to the chirality of the nanotube. The majority of the computationally studied ZnO nanowires are [0001]-oriented. These include hexagonal and triangular shaped nanowires, having six or three low energy surface facets, respectively, with the c-axis of the wire oriented along the [0001] direction.

In most theoretical simulations on TiO$_2$ nanotubes, the model $3D\longrightarrow 2D\longrightarrow 1D$ of structural transformations was applied, i.e., the bulk ($3D$) phase first formed a lamellar product ($3D\longrightarrow 2D$) and then was bent and rolled to a nanotubular form ($2D\longrightarrow 1D$). The lamellar product was mainly formed by the anatase (101) surface, identified as prevailing in $\mathrm TiO_2$ NTs. A further geometry optimization of the 3-layer O-Ti-O sheet for the $2D\longrightarrow 1D$ transition results in the formation of titania nanotubes, possessing hexagonal fluorite-like (111) morphology with (n,n) and (n,0) chiralities. The results of the first-principles calculations of anatase-based six-layer nanotubes with a rectangular morphology show that rolled up ($-$n,n) nanotubes are energetically preferable to (n,n) nanotubes.

Two types of rutile-based [001]—and [110]—oriented nanowires are considered: Ti-atom-centered and hollow-site centered. It was found that the hollow-site centered NTs have smaller strain energy than the Ti-atom centered ones. Both LCAO and PW calculations clearly demonstrate that the more energetically preferable titania nanowires in the rutile phase display (110) facets when they are [001]-oriented and (110) and (001) facets when they are [110]-oriented. The orientation effects in the morphology and electronic properties of rutile nanowires, anatase nanowires and facetted nanotubes are discussed using the results of PW DFT calculations.

In consideration of the rolled up ZrO$_2$ nanotubes it was taken into account that thin sheets of zirconia exhibit a variety of structures because of the existence of several crystalline bulk polymorphs. We consider cubic, tetragonal, and monoclinic faces with different (low) crystallographic indices one after another. It is found that the formation energy of ZrO$_2$ nanotubes with a sufficiently large diameter is mainly determined by the formation energy of the corresponding nanosheet. The analysis of nanotube formation and strain energies has determined that the most stable tubes with thin (one ZrO$_2$ layer) walls should have hexagonal morphology corresponding to the rolling of (111) sheets from the cubic fluorite phase. The tubes with walls composed of two ZrO$_2$ layers presumably have lepidocrocite morphology. The tubes with thicker walls can possess a different structure originating from the cubic, tetragonal or orthorhombic phases. The lowest strain energy was found for a nanotube with rutile morphology exhibiting zigzag ZrO bond arrangement.

The comparison of zirconia-based and titania-based nanotubes shows that the former may have smaller strain energies, while the latter may have smaller formation energies relative to the stable bulk phases.

1 Zinc Oxide

Zinc oxide materials are now widely applied to electronic and optoelectronic devices [1] and nano-engineering [2]. An overview of the bulk ZnO fundamental properties (electronic, phononic, magnetic and optical) is given in [3, 4].

Using different growth techniques, researchers have shown that ZnO can be grown in a wide variety of shapes and structures, possibly larger in number than any other material [5–7]. Most ZnO nanostructures are grown by three main methods: vaporliquidsolid (VLS) process, solution-based chemical synthesis, and chemical vapor deposition (CVD) [8]. Depending on the specific growth conditions, the nanostructures can be obtained with a wide range of geometric features. In particular, new nanostructured 2D- and 1D-morphologies (nanosheets, nanoribbons, nanotubes and nanowires) have been discovered and applied to gas sensing. A common feature of these nanostructures is the very high aspect ratio, which is due to the lowest surface energy of a certain crystalline facet.

Over the last decade the progress in ZnO-based nanostructures research has been very fast [9, 10]. The results of the experimental studies of ZnO-based nanostructure synthesis and growth mechanism can be found in books [2, 9, 10] and original papers [11–18].

The theoretical modeling of bulk ZnO and the ZnO-based nanostructures has become an important field in ZnO-based nanostructure research. Review [7] focuses on studies that employ DFT electronic structure calculations, useful for understanding the reaction mechanism, binding strength, charge transfer as well as other electronic and structural properties of ZnO-based nanomaterials and gas-sensor interaction. A summary and outlook for future directions of this exciting area of research is also provided.

1.1 Bulk Zinc Oxide and Nanolayers

At ambient conditions ZnO crystallizes in a layered wurtzite structure in which each oxygen atom is tetrahedrally coordinated with four zinc atoms along the crystallographic c-axis, and vice versa (see Fig. 7.1). The primitive unit cell consists of two formula units. The wurtzite structure of bulk ZnO with the symmetry of the non-symmorphic space group $C_{6v}^4$ has a threefold rotation axis and a $6_3$ improper rotation axis. Both axes are parallel to the c-direction but do not coincide with each other. Whereas the atoms of the lattice lie on the threefold axis, the $6_3$ axis does not bear any atom, [19] (Fig. 7.2).

Fundamentals of the zinc oxide as a semiconductor are discussed in review article [20]. The results of the bulk ZnO DFT calculations are also reviewed in [20]. However, a common problem of most of these calculations is the use of the standard DFT exchange-correlation functionals (LDA/GGA) or parameter-dependent functionals like hybrid Heyd-Scuseria-Ernzerhof (HSE) or DFT+U. The LDA/GGA approach significantly underestimates the band gap in ZnO. On the other hand, different fractions of the HartreeFock (HF) exact exchange were used for ZnO within the HSE functional (see below).

Fig. 7.1

The wurtzite crystal structure of ZnO with the lattice parameters a and c indicated in (a), and the band structure of ZnO calculated using the HSE hybrid functional in (b) [20]. The energy of the valence-band maximum was set to zero (Reprinted figure with permission from Janotti and Van de Walle [20], Copyright (2009) by the IOP Publishing)

Fig. 7.2

Location of threefold rotation and $6_3$ improper rotation axes and of symmetry and glide planes in the wurtzite lattice. Filled circles Zn (O) site within the $z = 0$ plane. Open circles site with an atom of the same species as within the $z = 0$ plane but located within the first upper layer. Each atomic site is located on a threefold rotation axis perpendicular to the $z = 0$ plane. Crosses location of an improper rotation axis perpendicular to the $z = 0$ plane (Reprinted figure with permission from Tronc et al. [19], Copyright (2006) by the WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim)

In recent bulk zinc oxide calculations [22], the LCAO basis set (BS) and PerdewBurke Ernzerhof (PBE0) hybrid exchange-correlation functional (implemented in the CRYSTAL09 computer code [23]) were used. The used in ZnO Hartree Fock calculations all electron BS by Jaffe et al. [24] has been chosen for Zn and O atoms; the exponents of Gaussian type orbitals smaller than 0.7 Bohr$^{-2}$ were reoptimized for the PBE0 functional. The BS optimization in ZnO led to a considerable energy gain of 0.29 eV per primitive unit cell. The MonkhorstPack scheme [25] 6 6 4 $\mathbf {k}$-point mesh in the Brillouin zone (BZ) was applied, the tolerances 8 8 8 8 and 16 for the Coulomb and exchange integral calculations were taken. Furthermore, the SCF convergence threshold on the total electronic energy is 10$^{-7}$ was used for the ZnO structure optimization. High-frequency dielectric constants were estimated using the coupled perturbed HF (Kohn-Sham) method [26].

The comparison of PBE0 and HSE results made in [22] is given in Table 7.1. The calculated lattice parameters and bulk moduli agree very well with the experimental data and previous hybrid functional calculations. The Mulliken atomic charges evidence a considerable covalency of ZnO bonding ($\pm 0.95$ e for Zn and O, respectively). The underestimated band gaps in ZnO within the standard LDA, GGA-type functionals were a subject of many discussions in the literature. The band gap $\varDelta E_g$ is significantly underestimated in both plane wave and LCAO calculations (0.73 eV) [27]. In order to solve this problem, one should go beyond the standard DFT functionals, e.g. by using the hybrid functional, the DFT+U approach [20] or self-interaction correction (SIC)-LDA technique [28]. It is also well established for ZnO that the DFT+U approach is unable to reproduce correctly $\varDelta E_g$ by a simple variation of the U-parameter for the d electrons of the transition metal, i.e. the value of $\varDelta E_g$ remains underestimated by almost 1.5 eV in comparison with the experimental value for ZnO. A very sophisticated DFT+U study on ZnO was recently performed by Boonchun and Lambrecht [29], where they separately adjusted the U parameters for the s, p, d electrons of Zn and s, p electrons of O, in order to obtain the correct $\varDelta E_g$ from their accurate GW calculation. On the other hand, Oba et al. [27] have shown that the fraction of HF exact exchange must be increased to 0.375 for the HSE functional, in order to reproduce $\varDelta E_g$ (3.42 eV in Table 7.1) in ZnO, if the screening parameter is set to 0.2. In calculations [22] with PBE0 $\varDelta E_g$ = 3.56 eV, see Table 7.1. The calculated value $\varDelta E_g$ for ZnO is only by 0.12 eV larger than the experimental one.

Table 7.1 Bulk properties of Zinc Oxide[22]: a,c,u-lattice parameters;$z_{Mull}$-Mulliken atomic charge; $z_{Born}$-Born effective atomic charge (two components are separated by /); $\epsilon ^0$ and $\epsilon ^{\propto }$ are static and high frequency dielectric constants, respectively; $\varDelta E_g$-band gap; $\mathrm B$-bulk modulus

In the work of Diebold et al. [34] it was revealed using highresolution scanning tunneling microscopy (STM), that the surface morphology of wurtzite ZnO is strongly dominated by five low Miller index planes: the nonpolar prism (10$\overline{1}$0) and (11$\overline{2}$0) faces as well as the polar (000$\overline{1}$), (0001) and (11$\overline{2}$1) faces, see Fig. 7.3 and [35].

Fig. 7.3

Side views of the optimized bulk and surface structures of wurtzite ZnO: a bulk ZnO crystal, b O-terminated (000$\overline{1}$) with pseudohydrogen atoms of nuclear charge $Z = 1/2$, c Zn-terminated (0001) with pseudohydrogen atoms of $Z = 3/2$, d (10$\overline{1}$0), e (11$\overline{2}$0) and f (11$\overline{2}$1) with pseudohydrogen atoms of Z = 1/2. All artificial atoms (small white balls) were attached to the bottom of the slab for each polar surface. The medium red spheres stand for O atoms and the large blue spheres for Zn atoms (Reprinted figure with permission from Tang and Luo [35], Copyright (2013) by the American Chemical Society)

The mixed-terminated $(10\overline{1}0)$ and $(11\overline{2}0)$ facets can be seen as containing exclusively neutral Zn-O ion pairs, thus leading to the nonpolarity of the two flat surfaces. The two basal planes -O-terminated (000$\overline{1}$) and Zn-terminated (0001)-are always created together by cutting the hexagonal crystal perpendicular to the c-axis, wherein the first surface is located on one side of the as-cleaved stoichiometric sheet and, concurrently, the second surface is located on the other, opposite side. The stepped surface (11$\overline{2}$1) is constituted by terraces of four atomic rows and monatomic steps, which are $[11\overline{2}0]$ and $[0001]$ orientations, respectively. All step edges are terminated by 2-fold coordinated oxygen sites.

The PW DFT (LDA and PBE) calculations of both the nonpolar ZnO $(10\overline{1}0)$ and $(11\overline{2}0)$ as well as the polar (000$\overline{1}$) and (0001) surfaces were performed in [36]. All the surfaces were represented by periodically repeated slabs consisting of several atomic layers and separated by a vacuum region of 9.4–12.4 Å. For the polar surfaces a dipole correction was used to prevent artificial electrostatic interactions between the repeated units. To simulate the underlying bulk structure, the slab lattice constant in the direction parallel to the surface was always set equal to the theoretical equilibrium bulk value.

The nonpolar surfaces are obtained by cutting the crystal perpendicular to the hexagonal Zn and O layers. In both cases, equivalent surfaces are created for the $(10\overline{1}0)$ and $(11\overline{2}0)$ planes so that stoichiometric slabs with the same surface termination on top and at the bottom can always be formed.

The polar surfaces were modelled by slabs consisting of Zn–O double layers, exhibiting a dipole moment perpendicular to the surface. The polar surfaces can only be stable if a rearrangement of charges between the Zn- and the O-terminated surfaces takes place. In calculations [36] the polar surfaces were stabilized by allowing the electrons to move from the (000$\overline{1}$)-O surface to the (0001)-Zn surface. The charge in the top and bottom layer of the slab was modified in such a way that the dipole moment of the slab became independent of the slab thickness and the internal electric field vanishes. This charge transfer is equivalent to applying an external dipole, which compensates for the internal electric field.

The cleavage energies calculated in [36] for the two nonpolar surfaces are close $-$2.3 (1.6) J/m$^2$ in the LDA (PBE) calculations. For the two polar surfaces these energies are also close but are higher than those for the nonpolar surfaces: 4.3 (3.4) J/m$^2$ in LDA (PBE) calculations. These reasults were confirmed in the LDA+U calculations [37].

A precondition of the forming single-walled ZnO nanotubes is the stability of the graphene phase of the corresponding material. The component atoms in the graphitic structure adopt planar sp$^2$ hybridization, while those in the wurtzite structure undergo tetrahedral sp$^3$ hybridization. The stability of the graphitic structure of ZnO relative to Zn- and O-terminated films was discussed in [38, 39]. The experimental evidence related to the morphology of Zn-terminated polar (0001) thin films was presented in [39]. From first principles PW DFT calculations with the Perdew-Wang exchange-correlation functional and the ultra-soft Vanderbilt psedopotentials, it was also found in [39] that the graphitic structure persists up to 16 layers in the Zn-terminated film and the surface atoms exhibit trigonal sp$^2$ hybridization. This implies that the ultra-thin ZnO film might have a tendency to form ZnO graphitic sheets. The same conclusion was made in [40]: after the structure optimization of the single Zn–O layer in the DFT calculations a planar graphite-like structure was obtained, see Fig. 7.4.

Fig. 7.4

ZnO single layers. The left part is a single layer taken from the wurtzite ZnO crystal while the right one is the optimized structure which is a planar hexagonal lattice. The small and large balls represent zinc and oxygen atoms, respectively [40]

Under appropriate conditions, single-layered ZnO graphene may coalesce in a tubular form. Moreover, the electronegative difference of 1.8 between Zn and O is comparable to the difference of 1.0 between B and N. Thus, the similarity in the bonding character of BN and ZnO may lead to an analogous growth sequence of the one-dimensional nanostructures [41], in particular single-walled nanotubes, as do C and BN. These results were confirmed in [36], where surface x-ray diffraction and scanning tunneling microscopy was made for the 2 monolayer thick ZnO(001) films grown on Ag(111). The conclusion was made that Zn and O atoms are arranged in planar sheets as in the hexagonal boron-nitride prototype structure. The observed depolarization is accompanied by a significant lateral 1.6 % expansion of the lattice parameter and a 3 % reduced Zn–O bond length within the sheets. The nonpolar structure stabilizes the atomically flat surface morphology. The transition to the bulk wurtzite structure occurs in the 34 monolayer coverage.

An alternative stabilization mechanism for the polar ZnO(0001)-Zn surface is discussed in [42]. Basing on the results of PW DFT (PAW) calculations the authors discuss various stabilization mechanisms, such as metallization of the surface layer, adsorption of OH groups or O adatoms, the formation of Zn vacancies, and large scale triangular reconstructions. The calculations indicate that isolated Zn vacancies or O adatoms are unfavorable compared to triangular reconstructions. In the absence of hydrogen, these triangular features are stable under any realistic temperature and pressure. When hydrogen is present, the reconstruction is lifted, and hydroxyl groups stabilize the ideal otherwise unreconstructed surface. The transition between the unreconstructed hydroxyl-covered surface and the triangular shaped features occurs abruptly; OH groups lift the reconstruction, but their adsorption is energetically unfavorable on the triangularly reconstructed surface.

The PW DFT (PBE) calculations [43] were performed for six bilayers of Zn- and O-terminated surfaces, in which the lower four bilayers are fixed as the bulk configuration while the upper two bilayers and adatoms (or adlayers) are allowed to relax. Figure 7.5 shows the schematic structures of c-axis ZnO polar surfaces, where each anion is surrounded by four cations at the corners of a tetrahedron, and vice versa.

Fig. 7.5

Three-dimensional views of the upper part of a the perfect (0001) surface, and b the (000$\overline{1}$) surface. The black and the gray are O and Zn atoms, respectively. Four pseudohydrogen atoms (shown as white balls) are placed at the bottom of the cell (Reprinted figure with permission from Yufei et al. [43], Copyright (2010) by the IOP Publishing)

The tetrahedral coordination is typically of sp$^3$ covalent bonding, but ZnO has a substantial ionic characteristic. To prevent unphysical charge transfer between the top and bottom slab surfaces, pseudohydrogens with fractional charges were used. The surface energies calculated for the 8-layer and 12-layer slab models show that the relative error is very small. By comparison, it was found that the surface energy of the Zn-terminated polar (0001) surface is bigger than that of the O-terminated polar (000$\overline{1}$) surface, which shows that the ZnO–Zn surface is more active than the ZnO–O surface. This is in good agreement with the experimental data [44].

1.2 Symmetry of Zinc Oxide Nanostructures

ZnO nanowires usually grow along the (0001) direction and have a hexagonal or triangular cross section, see [45, 46] and Fig. 7.6a, b. The faceted ZnO nanotubes can be regarded as nanowires with hollow interior centers that preserve their bulk-like configuration, Fig. 7.6c. The conventional single-walled and thicker ZnO nanotubes are generated by rolling up one- or multi-layer slabs with a hexagonal 2D lattice, see Fig. 7.6d.

Fig. 7.6

Models of ZnO 1D nanostructures: a nanowires with hexagonal cross sections, b nanowires with triangular cross sections, c faceted nanotubes, and d conventional single-walled nanotubess. Red and gray balls denote O and Zn atoms, respectively (Reprinted figure with permission from Zhou et al. [46], Copyright (2008) by the American Chemical Society)

The symmetry of wurtzite-based quantum wells and superlattices was studied in [47] which allowed the determination of the electron states symmetry and optical selection rules in these nanostructures.

The analysis of ZnO nanorods (nanowires) and faceted nanotubes symmetry was performed in [19, 48]. The hexagonal rods and tubes considered are built from the wurtzite structure of bulk ZnO, their axis being parallel to the c-axis of the wurtzite lattice. The lateral faces are assumed to be parallel to the sides of the hexagons within the (x, y) plane.

It has been shown that the symmetry of ZnO hexagonal nanorods and nanotubes depends on the location of their axes with respect to the ZnO wurtzite lattice. When the axis coincides with the threefold rotation axis of the lattice (type I structure), the point and space symmetries are described by the $C_{3v}$ point group and the family 6 rod group RG49 (p3m1), respectively. When the axis coincides with the 6$_{3}$ improper rotation axis (type II structure), the symmetries are described by the $C_{6v}$ point group and the family 8 rod group R70 (p$6_3$mc), respectively, see Table D.3. The site symmetry of an atom in the structure is $C_{3v}$, $C_s$, or $C_1$, depending on its location.

Fig. 7.7

Nanotubes of type I. Left panels top view of the bulk. Points denote zinc atoms at z = 0 (the black ones) and at z = c/2 (the grey ones). Lines depict positions of the vertical mirror planes. The third-order rotational axis is at their intersection. The symmetry cell is shaded. Right panels type I (3, 5) and (3, 6) nanotubes (Reprinted figure with permission from Milošević et al. [48], Copyright (2006) by the IOP Publishing)

Figures 7.7 and 7.8 show type I and the type II ZnO nanotubes.

At any point of the one-dimensional Brillouin zone the direct optical transitions in the nanostructures obey the selection rules governed by the $C_{3v}$ group (type I) or $C_{6v}$ one (type II). The latter group is that of the $\varGamma$ point of the bulk ZnO. The rules for transitions involving bound states differ from those in the bulk since they are generally governed by smaller groups. The effect of a magnetic or/and an electric field on the symmetry properties of the nanostructures was established in [19].

The conventional ZnO nanotubes are modelled by the rolling up procedure (see Chap. 2): the hexagonal lattice with the symmetry of layer group 69 (P3m1) is used to generate the chiral (n$_1$,n$_2$) and the achiral (n,n), (n,0) nanotubes.

The symmetry groups of the chiral NTs belong to Family 1, the symmetry groups of the achiral (n,n) and (n,0) NTs belong to families four and eight, respectfully, see C.1. The number of the atoms in the one-periodic unit cell is equal to 4n for the achiral nanotubes, the screw axis order is 2n.

At any point of the one-dimensional Brillouin zone the direct optical transitions in the achiral ZnO nanotubes obey the selection rules governed by the $C_{2nv}$ group.

The high symmetry restrictions, introduced for the rolled up ZnO nanotubes, can increase the calculated formation energy.

Fig. 7.8

Nanotubes of type II. Left panels top view of the bulk. The walls are enumerated. Points denote zinc atoms at z = 0 (the black ones) and at z = c/2 (the grey ones). Mirror and glide planes are indicated by thick and thin lines, respectively. The sixth-order screw axis is at their intersection. The symmetry cell is shaded. Right panels (6,12) and (3,6) nanotubes (Reprinted figure with permission from Milošević et al. [48], Copyright (2006) by the IOP Publishing)

1.3 ZnO Nanotubes

Different techniques have been used to grow ZnO nanotubes and study their properties [49–53].

ZnO nanotubes with a regular polyhedral shape, hollow core, and a wall thickness as small as 4 nm, were prepared in a large-area substrate by vapor phase growth [52]. The formation of the ZnO nanotubes was found to be closely related to the hexagonal structure of the ZnO crystal and the peculiar growth conditions used. In particular, high aspect ratio nanotubes are obtained by a three-step low temperature process involving ionic layer absorption, deposition of the ZnO seed layer followed by hydrothermal annealing of the seed layer and deposition of the 1D ZnO nanostructures [49]. These ZnO nanotubes have a single-crystalline wurtzite structure with lengths exceeding 10 $\mu$ m and diameters of around 27 nm. By hydrothermal annealing, ZnO nanotubes grown along the $\langle {001}\rangle$ direction have been obtained [49].

Fig. 7.9

Different nanostructures of ZnO that have been modelled using DFT: a hexagonal, b triangular, c other nanowires, d facetted (polyhedral) nanotubes, e facetted nanotubes (Zn atoms shown in blue and O atoms in red) (Reprinted figure with permission from Spencer [7], Copyright (2011) by the Elsevier Ltd. All rights reserved)

The reaction of $\mathrm{{Zn(NO_3)_2}}$ with methenamine in aqueous medium under hydrothermal conditions also gives rise to ZnO nanotubes. These nanotubes are hollow with rough surfaces, indicating a layer-stack structure. The ZnO nanotubes have a hexagonal wurtzite structure with lengths in the range of 13 ${\upmu }$m and a wall thickness in the 50–100 nm range. The cross section is hexagonally faceted, providing strong evidence that the single nanotube grows along the c-axis direction [49], see Fig. 7.9d. The optical properties of ZnO nanotubes were studied at room temperature in [53]. Raman peaks arising from the ZnO nanotubes were analyzed, which correspond well to those of the bulk ZnO sample.

Fig. 7.10

Binding energy $E_b$ and radius $R$ of different SWZONTs [40]

Fig. 7.11

Cleaving atoms on the ZnO surface via cylinders of different sizes (indicated in green) yields nanowires and nanotubes (left). ZnO planar sheet showing rolling directions to yield armchair (A), zigzag (Z) and chiral (C) nanotubes (right) (Reprinted figure with permission from Spencer [7], Copyright (2011) by the Elsevier Ltd. All rights reserved)

One of the first PW DFT (LDA) calculations of the rolled up (see Fig. 7.11) single-walled ZnO nanotubes (SWZONTs) was performed in [40]. Without regard for the two ends, an SWZONT was treated as a cylinder rolled up from a single sheet of ZnO layer such that two equivalent sites of the hexagonal lattice coincide. Figure 7.10 shows the binding energy of SWZONTs with different chirality indices (n,m). From this figure one can find that (i) the binding energy for different SWZONTs is negative, which suggests that these SWZONTs can exist in principle; (ii) the binding energy E$_b$ decreases with the increase of the radius R of SWZONTs and can be well described by (7.1). Obviously, $E_b\rightarrow -8.242$ eV/ZnO for R$\rightarrow \infty$. This value is quite close to the binding energy $-8.246$ eV/ZnO of a ZnO single planar layer. The term $1.371/R^2$ reflects the curvature effect of the nanotubes.

$$\begin{aligned} E_b = - 8.242 + 1.371/R^2 (\mathrm{{eV/ZnO}}) \end{aligned}$$

(7.1)

The classic shell theory also gives the same form, $D\varOmega /R^2$, for the curvature effect, where D is the rigidity of the ZnO single layer and $\varOmega =8.91$Å$^2$ is the area of the parallelogram generated by the hexagonal lattice primitive translation vectors. Thus we obtain $D=0.15$ eV, which is a lot smaller than the rigidity (1.17) eV [54] of a single graphite layer. The ZnO single layer is much softer than the graphite layer so that it is more easily wrapped up into a nanotube [40].

Table 7.2 is taken from [7] and gives references to the DFT calculations of both facetted and cylindrical shape single-walled chiral (n,m), zigzag (n,0) and armchair (n,n) ZnO-nanotubes, rolled up from the graphitic (001) ZnO plane.

Table 7.2 ZnO nanostructures modelled with wurtzite structure; including nanowires and nanotubes, [7]

To form the nanotube shape, a large supercell of bulk wurtzite ZnO is created, with one repeat unit kept in the z-direction. The supercell is then cut into cylinders of different diameters, removing the atoms outside and inside the cylinder and relaxing the structure to form a cylindrical shape. Facetted nanotubes are created the same way as the nanotubes but two cylinders of different diameters are used, with both the atoms outside the larger cylinder and those within the second smaller cylinder being removed. Both the facetted and rolled up nanotubes are infinite in the (0001) direction.

Table 7.3 The optimised supercell length L(Å), the average Zn-O bond length R(Å), the diameter D(Å), the number of atoms per unit cell N, the strain energy SE (eV/atom), the binding energy BE (eV/atom), bandgap $\varDelta$ (eV) and net Milliken charge Q (e) of the ZnO nanotubes, the calculated band gap for the bulk ZnO is 0.895 eV [41]

Table 7.3 shows results obtained in DFT (PBE) calculations (with the numerical atomic orbital basis set) on chiral, armchair and zigzag ZnO- nanotubes [41]. Density functional semi-core pseudopotentials (DSPP) fitted to all-electron relativistic DFT results, and a double numerical basis set including dpolarization functions (DND) were employed. The accuracy of the PBE and DND/DSPP combination was tested for the ZnO molecule and wurtzite bulk. It is seen that the zigzag nanotubes are more stable than the armchair ones, in contrast to the trend for carbon NTs. For all types of ZnO nanotubes, the strain energies are much smaller than for BN nanotubes with the same diameters [86], but are somewhat sensitive to the chirality of the nanotube. For the NTs studied in [41], the strain energies were approximately proportional to the inverse square of the tube diameter.

It is well known that DFT calculations underestimate the band gap of the bulk crystals. In particular, the DFT (PBE) calculation [41] gives for the bulk ZnO bandgap a value 0.895 eV (the experimental value is 3.25 eV, see Table 7.1). All the published DFT calculations of ZnO nanotubes (both facetted and rooled up ones) give NT band gaps that are larger than the gap of the bulk ZnO [7]. It is especially obvious from Table 7.3 showing the results of DFT(PBE) calculations [41] of single-walled ZnO nanotubes.

Previous studies have shown that DFT with hybrid functionals can give a quantitatively more accurate band gap of the bulk ZnO, see Table 7.1. The DFT(B3LYP) method, implemented in the CRYSTAL package [23], was used in [41] to calculate the band structures of bulk ZnO and ZnO (6,0) SWNT. It was found in [41] that the overall features of the ZnO (6,0) band structure are nearly the same as those based on the DFT(PBE) method, except for enlarged band gap, that is, 3.29 and 4.35 eV for bulk ZnO and ZnO (6,0) SWNT, respectively which matches the experimental band gap of bulk ZnO (3.4 eV) quite well. Because both DFT-B3LYP and DFT-PBE calculations indicate that the band gap of ZnO (6,0) SWNT is larger than that of bulk ZnO, it is expected that DFT(PBE) calculations can, after all, give a qualitatively correct trend in the band structure, see Table 7.3.

ZnO rolled up nanotubes with and without defects (including vacancies and antisites) were examined in [66, 69, 83]. It was found that the presence of oxygen vacancies yields the lowest formation energies. Furthermore, antisites, that have high formation energies in the bulk, could have relatively low formation energies in nanotubes.

Facetted ZnO NTs (structures 13, 14 and 15, Fig. 7.9) were examined in [55]. The calculated binding energy (BE) values (per atom) increased in magnitude as the size of the facetted NTs increased, showing that the larger structures are more stable. To represent the BE of infinitely large NTs the BE of a single sheet of ZnO was calculated in [55]. It was found that the smallest facetted NTs were more stable than infinitely large NTs. As it was indicated in [55] the facetted ZnO NTs unlike facetted boron nitride and carbon NTs, can only be hypothetical, due to the significant differences in the atomic radius and electronegativity of Zn and O atoms. Due to the large difference in the atomic radii, the orbital overlap is quite small resulting in weaker p bonding and hence lower stability. Furthermore, the large difference in electronegativity enhances the ionic component of the Zn-O bonds, diminishing the conjugated effect of p bonding. For boron nitride NTs, however, the atomic radii of B and N are similar and hence the overlapping of p$_z$ orbitals between B and N results in a strong delocalised $\pi$–system and a more stable structure. Zhou et al. [46] showed that the binding energies of various facetted NTs were linearly related to the ratio of the surface atoms (number of unsaturated Zn and O atoms in the surface divided by the total number of Zn and O atoms in the system) and not to the tube size.

A more detailed discussion of the results of the ZnO nanotubes DFT calculations can be found in [7].

1.4 ZnO Nanowires

Several methods have been employed to synthesize ZnO nanowires [49]. In particular, they were grown by a vapour-phase transport process using a gold catalyst. Zn vapour is generated by carbo-thermal or hydrogen reduction of ZnO and the size of the nanowires is controlled by the thickness of the Au film. ZnO nanowires are single-crystalline with a wurtzite structure and grow along the c-axis. ZnO NWs were also obtained by a carbo-thermal route involving the reaction of Zn oxalate or ZnO powders mixed with activated carbon or MWNTs. The nanowires obtained are single-crystalline with a wurtzite structure and have diameters of 300–400 nm, with lengths extending to tens of microns.

The majority of 1D ZnO nanowires that have been studied computationally are [0001] oriented nanowires [7]. These include hexagonal and triangular shaped nanowires, having six or three low energy (10$\overline{1}$0) surface facets, respectively, with the c-axis of the wire oriented along the [0001] direction, see Fig. 7.9a, b.

The hexagonal nanowire structures that have been investigated include structures 1–5 as presented in Fig. 7.9a. The nanostructures are created by building a bulk ZnO structure and cleaving atoms around a virtual ring of a specific diameter (see Fig. 7.11). Structure 1 results from cleaving the atoms around the central ZnO hexagon, indicated by the smallest ring in Fig. 7.11, while structures 2–5 are created by cleaving atoms around the larger rings indicated in Fig. 7.11. The nanowire with structure 2 features is the most commonly investigated hexagonal nanowire in the DFT studies of ZnO 1D nanostructures.

The triangular nanowires that have been investigated theoretically are shown in Fig. 7.9 (structures 6, 7 and 8). Instead of cleaving atoms around a ring, the nanowire is created by cleaving along three planes aligned at 60$^\circ$ to each other, producing a triangular cross section. ZnO nanowires that do not have a hexagonal or triangular cross section have also been investigated and include structures 9–12 (Fig. 7.9).

Table 7.4 Theoretical structural parameters and electronic and mechanical properties of the single crystal ZnO wurtzite (B) and hexagonal (H) nanowire structures studied

The results of the DFT calculations of ZnO nanowire stability, structure and electronic properties are discussed in [7].

A number of studies have examined the relative stability of wurtzite and hexagonal nanowires. Hexagonal (wurtzite and graphitic) and zinc blende ZnO hexagonal NWs with structure 2 and 3 were investigated in [81]. All the phases are energetically less stable than the bulk phase, with the wurtzite phase calculated to be most energetically favourable, followed by the hexagonal and then zinc blende phases. The latter two phases change order for NWs with diameters $\ge {1.6\,\mathrm{{nm}}}$. A comparison of the binding energies of hexagonal and triangular nanowires (structures 1, 2 and 6 in Fig. 7.9) with wurtzite or hexagonal structures, as a function of supercell length, was made in [75]. The results obtained show that both the wurtzite and hexagonal phases correspond to distinct energy minima, indicating that the phase transition from wurtzite to hexagonal phases occurs under compression. For supercell length $\ge { 0.44\,\mathrm{{nm}}}$ the NWs exist in the wurtzite phase, while for lengths $\le {0.44\,\mathrm{{nm}}}$, they exist in the hexagonal phase. The hexagonal NW with structure 1 was more stable in the hexagonal phase than the wurtzite phase, while structures 2 and 6 were more stable in the wurtzite phase. An earlier study [76] of ZnO nanowires with structures 1, 2 and 3 showed a similar trend where the wurtzite phase was more stable. In particular, their results indicated that the graphitic/hexagonal phase was more stable for the smaller NWs (structures 1 and 2) while the larger NW (structure 3) was more stable in the wurtzite phase.

Table 7.4 shows the results obtained in [73] and gives a comparison of the wurtzite and hexagonal phase NWs (structures 2, 3, 6, 10) with two bi-layers along the z-direction of the supercell, showing that both phases are distinct minima, with the binding energies becoming stronger with increasing diameter. This table gives the calculated properties of NWs with the facets (${00\overline{1}0}$) forming trigonal (W1), quadrangular (W2) and two hexagonal (W3 and W4) cross sections with a diameter of 1.5–2.0 nm, which is one of the most typical growth morphologies for ZnO nanowires found in experiments. Binding energies of ZnO nanowires increase with increasing diameters from 6.752 eV per ZnO for (W1) to 6.974 eV/ZnO for (W4), and from 6.734  eV/ZnO for (W1) to 7.072 eV/ZnO for (W4).

Compared to the bulk ZnO wurtzite solid, for ZnO nanowires with the B structure, Zn(O) atoms in the side surfaces exhibit small inward (outward) relaxation and each polar bilayer slightly expands in the direction of the wire axis. This effect results in decreases in the average bond lengths of Zn-O (1.978, 1.986, 1.989, and 1.999 Å for W1, W2, W3, and W4, respectively), which are smaller than the theoretical Zn-O bond length 2.005 Å for the bulk phase. Both the surface oxygen and zinc atoms on the first layer relax toward the bulk region with different amplitudes, forming a buckled Zn-O dimer. For H-type ZnO nanowires, Zn(O) atoms on the side surfaces exhibit inward (outward) expansion and each polar bilayer contracts in the direction of the nanowire axis, implying the flattening of the buckled wurtzite basal plane (Zn and O atoms become coplanar). This increases the average bond lengths of ZnO (2.068, 2.071, 2.079, and 2.083 Å for W1, W2, W3, and W4, respectively), which are larger than the bulk bond length of 2.005 from calculations [73]. As a result, Zn atoms sit at equal distances from O atoms along the $[0001]$ axis and the structure acquires an additional symmetry of a mirror plane perpendicular to the $[0001]$ axis. This process goes on while the orientation of the basal plane remains invariant.

The coordination in the H-type nanowire is fivefold, compared to the fourfold coordination in the B structure. The formation of additional bonds along the $[0001]$ axis implies a change in the chemical bond and charge density distributions, which differ from the graphitic structure with in-plane threefold coordination. The unusual fivefold coordination in H-type nanowires that is crystallographically similar to the rocksalt structure suggests that the observed BH transformation corresponds to enhanced ionic bonding with a higher coordination. Along the $[0001]$ axis, the H structure has the same hexagonal symmetry as the B structure. During BH transformation with contracting supercell length, the graphitic structure is an unstable transition state.

According to calculations [73], the average binding energy of the H-type ZnO wire, W1 (H), is 0.018 eV/ZnO larger than that of the B-type W1(B), i.e. the H structure of W1 is more stable than the B structure. For the W2 wire, the binding energy difference between the H and B phase structures is only 0.014 eV per ZnO, whereas the B phase becomes energetically is preferred. The difference of binding energy between the H and B phase structures is 0.045 and 0.098 eV/ZnO for W3 and W4 wires, respectively. For ZnO nanowires of larger diameters, the H-type structure would become increasingly more and more unstable. Therefore such H phase structure can be experimentally detected since the diameter of the H wire is as small as $\approx$2.0 nm. This may explain why so far experiments have only observed wurtzite structures in the ZnO nanowires.

The dependence of band gaps on the structure and thickness the ZnO nanowires is also presented in Table 7.4. A well-known deficiency of the standard DFT technique, is that DFT calculations significantly underestimate the band gap of ZnO systems (in calculations [73] the $\varGamma$–point band gap for the bulk ZnO wurtzite is only 0.895 eV, much smaller than the experimental band gap 3.37 eV). As the nanowire diameter increases, the band gap decreases monotonously and approaches the bulk value. This behavior is quite different from that of single-walled ZnO nanotubes that the band gap is nearly independent of tubular structures and diameters. With the same wire diameter, the band gaps of the B phase wire are larger than that of the H phase.

Mulliken population analysis shows that the charge transfer from zinc to oxygen in the B phase wires is about 0.72–0.76 e, comparable to that in the bulk ZnO wurtzite solid. The amount of charge transfer only slightly varies with nanowire diameter. As shown in Table 7.4, the Zn-to-O charge transfer in H phase nanowires is more pronounced than that in B phase structures, suggesting that H phase nanowires are more ionic. All the ZnO nanowires studied exhibit semiconducting behavior with direct band gap.

Table 7.4 demonstrates that the computed Youngs moduli (Y) for ZnO nanowires are significantly higher than those of bulk solid (140 GPa). Although the modulus oscillates with the wire radius, it generally decreases with increasing size. The results of the Youngs moduli calculation are in accordance with the atomic force microscopy measurements of Youngs modulus for ZnO nanowires, in which the increase in the elastic modulus for the thinner wires is attributed to the surface effect. Most importantly, the calculations [73] show strong structure dependence of Y. With the same size, the H-type wires usually have higher values of Y than those of the B phases. This indicates that the H-type wires possessing a more ionic character are mechanically stronger under external tensions.

A more detailed discussion of the results obtained in numerous DFT calculations of ZnO-based nanowires stability, structure, band gaps and density is given in [7].

We conclude this section by a short description of ZnO nanotubes and nanowires relative stability, see [56, 74, 87].

The cohesive energy values for zigzag NTs $(n{,}0)$ with $n = 8, 10, 12, 15, 20$, as well as a ZnO graphitic layer (representing a NT with the largest diameter) were in the range from $-7.10$ to $-7.17$ eV, which was slightly larger in magnitude than their values for the ultrathin NWs with structures 1 or 6, see Fig. 7.9, but much lower in magnitude than the NWs or facetted NTs with lower surface atom ratios [7]. For NWs with high surface-atom to bulkatom ratios, NTs are energetically preferable.

The size-dependent cohesive energy $E_c(n)$ of nanowires and single-walled nanotubes of ZnO was calculated in [74, 87] where n denotes atom number per periodic unit consisting of two ZnO layers. The calculations show that, for small n, a single-walled nanotube has a lower energy than a nanowire. A crossover point near $n\approx$ 38 is predicted in [74], while the crossover point at $n\approx$ 48 was found in [87].

2 Titanium Oxide

2.1 Bulk and Nanolayers

Titania ($\mathrm TiO_2$) is a well-known semiconductor with a number of promising properties and numerous technological applications comprehensively studied in materials science [88]. The number of discovered $\mathrm TiO_2$ polymorphs is seven [89], with rutile and anatase undoubtedly prevailing in practical applications because of their higher energetic stability as compared to other titania phases [90]. These polymorphs exhibit different properties. Anatase is the most common product of low-temperature synthesis pathways, and is an important component of materials, e.g. those developed for gasphase separation and catalysis [91]. At the same time, in order to synthesize selected samples of rutile, which is a reliable material for both the ultrathin gate oxide in field-effect transistors and the dielectric layer in capacitors for dynamic random access memory [92], a number of experimental treatment have been performed in conditions of ultra-high vacuum (UHV) with preliminary treatments (Ar$^+$ ion bombardment, irradiation, high temperature) [93]. Anatase transforms irreversibly to rutile at elevated temperatures. The temperature of this transformation is not unique and the processes involved in the transformation were comprehensively reviewed in [90].

The symmetry of the ${\mathrm{TiO}}_2$ rutile structure is described by a 3D tetragonal lattice and the space group P$4_2$/mnm with two titania formula units per primitive cell (the upper bulk models in Fig. 2.19a–d). Table 7.5 presents the results of calculations [94] compared to those obtained from both theoretical simulations and experimental neutron scattering measurements at 15 K. The first principles calculations [94] were made by the DFT-LCAO method, as implemented in the CRYSTAL09 code [23], which describes 2D slabs and 1D nanotubes in their original space form, without spurious 3D periodicity used in the alternative planewave DFT-PW method, for example, in the VASP code [95]. A new version of the crystal code CRYSTAL14 [96] also includes the NANOROD option and extends the possibilities of nanostructure calculations.

Table 7.5 The structure and electronic properties of optimized TiO$_2$ bulk (rutile phase), calculated in [94]

The small-core pseudopotential [98] of the Ti atom was used in titania nanotube calculations ($3s, 3p, 3d$ and $4s$-electrons were taken as valence electrons), while the all-electron BS for the O-atom was taken from [99]. It is well known that in the LCAO calculations of crystals the BS of a free atom has to be modified as the diffuse functions cause numerical problems because of the large overlap with the core functions of the neighboring atoms in a densely packed crystal [100]. To optimize the BS, the minimization method without calculations of the total energy derivatives (the method of conjugate directions, developed by Powell [101]) was used in [102]. The diffuse exponents of valence $s, p$ and $d$-orbitals have been optimized for the stable anatase phase of bulk titania. Its atomic and electronic properties have been reproduced in the good agreement with the experiment (the experimental values are given in brackets): the lattice parameters a $=$ 3.784 Å (3.782 Å) and c $=$ 9.508 Å (9.502 Å), the dimensionless parameter for the relative position of the oxygen atom u $=$ 0.2074 (0.2080), although the values of the gap are still less accurate, again because of being overstimated: 4.1 eV versus 3.2 eV. Any way, these results for the bulk titania (anatase) agree with the experimental data better than those given in [97] for both the plane wave (PW) and LCAO calculations when one uses different exchange-correlation potentials. A certain improvement over the substantially underestimated values of the gap for the bulk anatase in the DFT PW calculations has been achieved recently [103] using the LDA+U method (2.7 eV).

Monoperiodic translation symmetry has been adopted for nanotube calculations as it was implemented in CRYSTAL09 code [23], containing also a special input option which allows the generation of 1D nanotubes from 2D slabs.

The symmetry of the $\mathrm TiO_2$ anatase structure is described by a 3D tetragonal lattice and the space group I4$_1$/amd with four titania formula units per tetragonal (crystallographic) cell (the upper bulk models in Fig. 2.20a–d). Table 7.6 presents the results of our calculations [102] compared to those obtained from both theoretical simulations and experimental neutron scattering measurements at 15 K. In the anatase DFT LCAO calculations the same atomic basis set and computational parameters were used as were applied in rutile calculations. Total geometry optimization was performed both in the rutile and anatase calculations.

Table 7.6 The structure and electronic properties of optimized TiO$_2$ bulk (anatase phase) [102]

Tables 7.5 and 7.6 demonstrate that the parameters of the rutile and anatase bulk $\mathrm TiO_2$ structure (a, c and u) calculated using different methods show both qualitative correlation and correspondence to the experimental values, although a certain dispersion is observed of the results obtained. The same is also true for Ti–O bond lengths inside the first (I) and second (II) coordination shells.

The calculated values of the effective charges $q_{O}$ and $q_{Ti}$ as they are found to be look quite reasonable and qualitatively comparable with the corresponding data obtained earlier [97]. As to the large difference between the experimental and calculated values of band gaps $\varDelta \varepsilon _g$ between the top valence band composed mainly of O(2p) states and the bottom of the conduction band with prevailing contribution from Ti(3d) states, the standard DFT calculations essentially underestimate $\varDelta \varepsilon _g$ for semiconductors and insulators. It is only when the hybrid exchange-correlation functionals, like PBE0 are applied that the band gaps can be reproduced with a relatively high accuracy. To estimate the effective atomic charges on O and Ti atoms, the Mulliken population analysis was adopted.

The knowledge of the relative stability of densely-packed rutile and anatase slabs is important for the study of titania nanostructures. The slab models of rutile and anatase were dealt with in Chap. 2.

The following densely-packed stoichiometric titania rutile surfaces have been previously described and systematized as stable, according to the results of DFT calculations on the corresponding slab models (their hierarchy corresponds to the growth of surface energy), see Fig. 2.19: (110), (100), (101) and (001) [88, 104–107], in accordance with the Tasker’s analysis applied to predicting energetic stability for the surfaces of ionic and partly ionic metal oxides [108]. To display the relative energetics of those rutile surfaces, a Wulff construction formalism [109] can be applied when constructing a possible macroscopic TiO$_2$ crystal terminated by the corresponding four types of facets. The relaxation of the outermost atoms on these surfaces was found to be substantial and responsible for a large reduction of the calculated surface energies as compared to the non-optimized slabs cut from a single-crystal [104].

The following densely-packed stoichiometric titania anatase surfaces have been previously described and systematized as stable, according to the results of DFT calculations on the corresponding slab models (their hierarchy corresponds to the growth of surface energy), see Fig. 2.20: (101), (100), (110) and (001). The surface energies of the two last anatase faces are very close to each other [88, 110, 111].

Table 7.7 Diperiodic symmetry groups and key structural parameters of four relaxed densely packed TiO$_2$ rutile slabs (Fig. 2.19)

Table 7.8 Diperiodic symmetry groups and key structural parameters of four relaxed densely packed TiO$_2$ anatase slabs (Fig. 2.20)

The layer group symmetry of the thinnest slab layers and geometry parameters of relaxed densely-packed rutile and anatase slabs are systematized in Tables 7.7 and 7.8. Here the thinnest slab layer means a (TiO$_2$)$_2$ layer (the bulk rutile or anatase primitive cell contains two TiO$_2$ formula units). The number of atomic planes in the thinnest layer depends both on the bulk titania phase (rutile or anatase) and the surface chosen. These structural data correlate well with with the model images of all the slabs (see Figs. 2.19 and 2.20) and give detailed information on the morphology of all the surfaces.

We define the surface areas of slab unit cells $S_{slab\_UC}$ depending on the lattice parameters a and c. The numbers of atomic planes in minimal repeating layer units $n^{(min)}_{layer}$ are also given in Tables 7.7 and 7.8. These parameters describe the morphological peculiarities of four types of densely-packed rutile and anatase surfaces.

Table 7.9 Results of our PBE and PBE0 calculations on surface energies (E$_{surf}$) for four densely-packed types of relaxed TiO$_2$ rutile slabs (Fig. 2.19) containing 12, 20 and 32 formula units per surface unit cell (UC) and their comparison with the corresponding data obtained in previous DFT calculations

Table 7.10 Results of our PBE and PBE0 calculations on surface energies (E$_{surf}$) for four densely-packed types of relaxed TiO$_2$ anatase slabs (Fig. 2.20) containing 12, 20 and 32 formula units per surface unit cell (UC) and their comparison with the corresponding data obtained in previous DFT calculations

Table 7.11 Results of PBE and PBE0 calculations on geometry and electronic properties for four densely-packed types of relaxed TiO$_2$ rutile slabs (Fig. 2.19) containing 32 formula units per surface unit cell and their comparison with the corresponding data obtained in previous DFT calculations

The convergence of the surface energies for all types of densely–packed slabs is demonstrated in Tables 7.9 and 7.10 using the slabs with 12, 20 and 32 formula units per surface unit cell. These slabs consist of 6, 10 and 16 thinnest slab layers, respectively.

The converged results of PBE and PBE0 calculations [94] performed on (110), (100), (101) and (001) rutile slabs of large thickness (corresponding to N$_{FU}=$ 32) are systematized in Table 7.11, where they are compared between themselves and with the results of other ab initio calculations performed using different DFTmethods, see [104–107]. The relaxation of all the slab models is estimated when comparing the minimal inter-layer spacings near either the surface $h_{layer}^{(s)}$ or the mirror plane $h_{layer}^{(m)}$ in slabs with optimized geometry (Table 7.11). It has been found that $h_{layer}^{(s)}$ (s) is larger than $h_{layer}^{(m)}$ in (110) and (100) slabs, while in the other two slab types the surface layer is compressed, in accordance with the results of recent simulations [107]. The growth of slab thickness leads to the averaged optimized thickness approaching that in non-relaxed slab cut from bulk, i.e., $h_{layer}^{(m)}$ $\rightarrow$ $h_{layer}^{(o)}$. The effective charges on both O and Ti atoms positioned on either surface ($q_O^{(s)}$ vs. $q_{Ti}^s$) or mirror plane ($q_O^{(m)}$ vs. $q_{Ti}^m$) of 96-atom unit cells UCs per slab have been also compared (Table 7.11), the latter practically coincide with those in the rutile bulk. However, the effective charges of surface O and Ti atoms are certainly smaller than those in bulk, due to a smaller coordination number with the adjacent atoms, depending on the slab morphology, which also confirm published results [107]. Hierarchy of surface energies calculated for all the four slabs of different thickness (Table 7.9) completely confirms the conclusions drawn earlier [104–107], whereas the growth of slab thickness results in the corresponding surface energies approaching certain limits. Thus, (110) is the energetically most stable surface while (001) is only marginally stable [104]. The calculations [94] also yield the estimate of band gap depending on the slab morphology and thickness. The thinner are the slabs, the larger are the values of $\varDelta \varepsilon _g$, calculated using both PBE and PBE0 methods, which approach those for the rutile bulk with increasing slab thickness. Band gaps are qualitatively similar for slabs containing the same number of formula units per surface unit cells (N$_{FU}$), irrespective of slab morphology.

Obviously, the results discussed in this section are important not only in terms of verification, confirming as they do the validity of models and computational procedure used, and mainly in terms of further understanding of both the construction of four-facetted TiO$_2$ nanowires and, even, the possible mechanism of their growth upon the substrate.

2.2 Rolled-Up Single- and Double-Wall TiO$_2$ Nanotubes with Hexagonal Morphology

${\mathrm{TiO}}_2$-based nanotubes (NTs) of different morphology have been systematically synthesized and carefully studied as promising technological materials [112, 113]. One of the recently discovered nanotube applications was the doping of ${\mathrm{TiO}}_2$ NTs by boron and nitrogen atoms [114] gradually varying their band gaps.

In most theoretical simulations on titania nanotubes, the model $3D\longrightarrow 2D\longrightarrow 1D$ of structural transformations described in [115] was applied, i.e., the bulk ($3D$) phase first formed a lamellar product ($3D\longrightarrow 2D$) and then was bent and rolled to a nanotubular form ($2D\longrightarrow 1D$). The lamellar product was mainly formed by anatase (101) surface, identified as prevailing in ${\mathrm{TiO}}_2$ NTs [103, 116–119]. A further geometry optimization of the 3-layer O-Ti-O sheet for the $2D\longrightarrow 1D$ transition results in the formation of titania nanotubes possessing hexagonal fluorite-like (111) morphology with (n,n) and (n,0) chiralities [120]. In reality this hexagonal structure can only exist in the metastable phase of bulk titania under extremely high pressure [89].

Theoretical simulations on ${\mathrm{TiO}}_2$ nanosheets originating from the three-layer O–Ti–O model were widespread as simpler systems for simulations [118]. When the structures of a 3-layer (101) slab cut from anatase bulk were being optimized only the structure of the (111) fluorite-type slab was recently obtained [120], which exhibits six-fold coordinated titanium atoms, and two-fold coordinated oxygens. The three-layer nanosheets cut from the fluorite phase of the bulk ${\mathrm{TiO}}_2$ (the space group 225 $Fm{\overline{3}}m$) have the symmetry of the layer group 72 $P{\overline{3}}m1$, see Table 7.12.

Using the rolling up correspondence of the line and layer groups (see Table 2.10) one obtains line groups for special chiralities of graphene, BN and ${\mathrm{TiO}}_2$ nanotubes (see Table 7.12). The corresponding isogonal point groups $\mathbf{P}_I$ and line groups for general chiralities $(n_1,n_2)$ are also given in Table 7.12.

Table 7.12 Line symmetry groups of SW BN and ${\mathrm{TiO}}_2$ nanotubes rolled up from hexagonal nanosheets

Table 7.13 The atomic and electronic structure of the optimized TiO$_2$ anatase bulk versus the fluorite-like (111) titania slab, [102]

The first principles LCAO calculations on hexagonal titania nanosheets and nanotubes were performed in [102] using the hybrid Hartree-Fock/Kohn-Sham exchange-correlation functional (PBE0). TiO$_2$ sheets with a thickness of a few atomic layers were found to be remarkably stable [121].

The main results obtained by means of the LCAO PBE0 calculations [102] for this slab are compared with the corresponding bulk properties of the titania anatase phase in Table 7.13. The relaxation energy for the 3-layer TiO$_2$ slab cut from the anatase bulk and transformed into (111) fluorite-type morphology is really large, while its surface and formation energies are qualitatively similar to those calculated earlier [103, 121]. Since the optimized 3-layer slab has a hexagonal structure, its parameters cannot be compared directly with those for the titania anatase bulk.

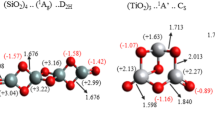
Three-layer titania nanosheets with a hexagonal fluorite-like (111) structure can be rolled up to 3-layer titania SW NTs with (i) armchair-type (n,n) chirality and (ii) zigzag-type (n,0) chirality. The structural and electronic properties of several hexagonal three-layer titania nanotubes are given in Table 7.14. The optimized structures of four selected nanotubes of both chiralities (two nanotube models per each chirality) are shown in Fig. 7.13.

Fig. 7.12

6-fold coordination of Ti atoms in a stoichiometric three-layer hexagonal titania nanosheet (a) and its top and cross-sectional images (b)

As to the Ti-O bond lengths, their deformation is more noticeable for smaller values of $d_\mathrm{Ti-O}$, gradually approaching those in a three-plane nanosheet, see Table 7.13. Obviously, this is also true for the convergence of $E_{relax}$ with $D_{NT}$ increasing (Table 7.14). The strain energies and band gap dependence on $D_{NT}$ for all the four sets of three-layer TiO$_2$ NTs is shown in Figs. 7.14 and 7.15, respectively.

The range of nanotube diameters considered is sufficiently large, from 0.5 to 4.0 nm, with the number of atoms per NT unit cell increased from 30 to 288. The calculations with the total geometry optimization for a total of 20 one-periodic models of TiO$_2$ NTs of different morphologies were performed in [102].

The two curves $E_{strain}(D_{NT})$ shown in Fig. 7.14 for two chiralities of titania nanotubes confirm the conclusions drawn above from Table 7.14. When the diameters of nanotubes increase up to 40 Å all the strain energies substantially decrease and approach each other. One expects that a further increase of $D_{NT}$ can result in slightly smaller values of $E_{strain}$ for 3-layer nanotubes. In three-layer nanotubes of similar diameters, the difference of the strain energies for fluorite-type (n,n) and (n,0) chiralities is fairly negligible, which supports qualitatively similar results obtained earlier for these types of nanotubes [103, 116, 118]. Figure 7.15 presents $\varDelta \varepsilon _{gap}$ dependence on $D_{NT}$. When nanotube diameters markedly increase, their band gaps $\varDelta \varepsilon _{gap}$ asymptotically approach those for the corresponding 2D slabs (Table 7.13), in a similar way to hexagonal. However, the nanotube diameters considered are too small for a direct comparison with the slabs.

Table 7.14 The structural and electronic properties of hexagonal 3-layer TiO$_2$ NTs(definitions of values are the same as in Tables 7.2–7.4)

Fig. 7.13

Cross-sectional (across) and lateral (aside) images of hexagonal single-wall TiO$_2$ nanotubes with different chiralities and diameters. a Across and aside images of optimized 3-layer (6,6) TiO$_{2}$ NT with $D_{{\mathrm{{NT}}}}=1.01$ nm. b Across and aside images of optimized 3-layer (12,0) TiO$_{2}$ NT with $D_{{\mathrm{{NT}}}}=1.17$ nm. c Across and aside images of optimized 3-layer (18,0) TiO$_{2}$ NT with $D_{{\mathrm{{NT}}}}=1.72$ nm. d Across and aside images of optimized 3-layer (12,12) TiO$_{2}$ NT with $D_{{\mathrm{{NT}}}}=1.97$ nm

Fig. 7.14

Strain energies $E_{strain}$ versus $D_{NT}$ for the two sets of single-wall TiO$_2$ nanotubes with various chiralities

Fig. 7.15

Band gaps $\varDelta$ $\epsilon$ $_{gap}$ versus D$_{NT}$ for the two sets of single-wall TiO$_2$ nanotubes with various chiralities

The line symmetry group $L_2$ = $Z_2$ $P_2$ of a double-wall (DW) nanotube can be treated as an intersection of the symmetry groups $L_0$ and $L_1$ of its single-wall constituents, see Sect. 2.5 and [122, 123]. The coaxial hexagonal DW NTs $(n_1,n_1)@(n_2,n_2)$ and $(n_1,0)@(n_2,0)$ are commensurate; the translation period of such DW NTs is the same as for their constituents.

Table 7.15 Symmetry of DW TiO$_2$ NTs with hexagonal morphology

Table 7.16 The structural and electronic properties of optimized DW TiO$_2$ NTs

Table 7.17 Ionic charges $(q)$ and bond populations $(p)$ for DW TiO$_2$ NTs

Table 7.15 gives the symmetry of commensurate DW TiO$_2$ NTs with hexagonal morphology, including both multiple DW nanotubes (armchair (n,n)@M(n,n) and zigzag (n,0)@M(n,0), part a), and nonmultiple DW nanotubes containing arbitrary SW constituents (armchair $(n_1,n_1)@(n_2,n_2)$ and zigzag $(n_10)@$ $N(n_2,0)$, part b).

LCAO PBE0 calculations of DW TiO$_2$ nanotubes with hexagonal morphology are made in [124] and allow one to compare their properties with those of the corresponding single-wall nanotubes. The calculations were performed using the CRYSTAL-09 computer code [23] and the HELIX option, which takes into account only rototranslational symmetry. As seen from Table 7.15, the DW NTs under consideration have twice more symmetry operations than the order of the rotohelical axis (reflections in vertical or horizontal planes are added to the rotohelical rotations). Using the TESTGEOM-NANOTUBE option as foreseen in the CRYSTAL-09 code, all the atomic coordinates in the monoperiodic unit cell were generated from 2D slabs for both constituent SW NTs separately. Added to the input, they describe the initial DW NT atomic coordinates.

The calculations of double-wall nanotubes that have large unit cells (containing up to 288 atoms in the case of (12,0) @ (36,0) and TiO$_2$ NTs) were performed using the full exploitation of the helical rototranslational symmetry. The coordinates of all the atoms in the nanotube unit cells were allowed to relax when the optimization procedure was performed.

Two different commensurate DWNTs can be constructed from a given pair of SW NTs rolled up from the hexagonal sheets of TiO$_2$. There is no second-order symmetry axis perpendicular to the TiO$_2$ layers under consideration. This means that the rotation through 180$^{\circ }$ around the U axis, normal to the nanotube translation vector, is not a symmetry operation and the SW rotated NT cannot be superimposed onto the original one by any rototranslational operation. When rotating one of the constituents (for example the outer shell) around the U axis, one obtains an inversed DW NT structure, which is different from the straight structure initially constructed by the folding procedure. If the U axis belongs to the one of the existing (common) mirror planes $\sigma _h$ or $\sigma _v$, the total symmetry of DW NT is unaffected. For TiO$_2$ DW NT, the U axis should pass through the Ti atom and can coincide with the x-axis.

The binding energy ${ E}_{bind}$ between the constituent shells of a double-wall nanotube was chosen as a criterion for nanotube stability, see 7.2.

$$\begin{aligned} -E_{bind}\left( D^{in}_{NT}@D^{out}_{NT}\right) =E_{tot}\left( D^{in}_{NT}@D^{out}_{NT}\right) -E_{tot}\left( D^{in}_{NT}\right) -E_{tot}\left( D^{out}_{NT}\right) \end{aligned}$$

(7.2)

where ${ E}_{tot}$ is the calculated total energy of the DW NT and its constituent SW NTs with optimized structure. Also estimated were the relaxation energies $E_{relax}$ (the difference between the total energies of the DW NT before and after geometry optimization) which are usually large for the small values of $\varDelta$ $R_{NT}$ and $D^{in}_{NT}$.

Unlike DW BN NTs, ab initio simulations on double-wall titania nanotubes are few.

Tables 7.16 and 7.17 present the results of the first ab initio LCAO calculations [124] on titania DW nanotubes (see also Figs. 7.17 and 7.18). Owing to the electroneutrality of each O-Ti-O shell of DW TiO$_2$ NTs, the inter-wall polarization effects in DW TiO$_2$ NTs are much less noticeable than in zz-DW BN NTs. This is why only straight configurations for both ac- and zz-chiralities of double-wall titania nanotubes with hexagonal morhphology were considered in [124].

Tables 7.16 and 7.17 contain data obtained in the calculations of DW TiO$_2$ NTs. Combining the latter with the binding energy curves $-E_{bind}$($\varDelta R_{NT}$) for titania nanotubes of both chiralities one can localize the minima of $-E_{bind}$($D_{NT}$) functions which correspond to (6,6)@(12,12) and (10,0)@(20,0) configurations with inter-wall $\varDelta R_{NT}$ distances 4.6–4.8 Å ($\varDelta R_{NT}$ is defined as a difference between the radii of middle Ti subshells). Meanwhile, when $\varDelta R_{NT}$ in DW TiO$_2$ NTs was reduced below the optimal values ($\le 4.1-4.3$) Å structural overstrains were observed, much larger than in DW BN NTs. This is especially true for ac-nanotubes of titania (4,4)@(8,8), (6,6)@(10,10), (5,5)@(10,10), and (6,6)@(11,11), where geometry optimization resulted in the destruction of double-wall morphology and the formation of complicated nonhexagonal quasi-single-wall morphology. The binding energies estimated per formula unit for the optimal configurations of hexagonal DW NTs are considerably larger for titania as compared to boron nitrides, while the reliefs of minima on $-E_{bind}$($\varDelta R_{NT}$) curves are sharper for titania. Obviously, this is caused by a substantially larger ionic contribution to interwall interaction between the titania SW constituents (Table 7.17). In both cases, the double-wall nanotube configurations with zz-chirality are energetically more favorable compared to those with ac-chirality. As with DW BN NTs, the small values of $\varDelta R_{NT}$ and $D_{NT}$ in Table 7.16 accompanied by the large values of $E_{relax}$ result in the instability of DW TiO$_2$ NTs, while the large values of $\varDelta R_{NT}$ correspond to cases when the interaction within the pairs of the constituent SW NTs is almost negligible. As with to DW BN NTs, $E_{bind}$ is rather negligible (Table 7.16).

The straightly stacked configurations for both ac- and zz chiralities of DW TiO$_2$ NTs with hexagonal morhphology (panels a and b of Fig. 7.16, respectively) were calculated in [124]. Unlike DW BN NTs, no permutation of Ti and O atoms occurs in the case of inverted configurations. In ac-DW TiO$_2$ NTs, such an inversion means the angular reorientation of O-Ti-O shells (Fig. 7.16a), which does not cause any noticeable rearrangement of the intershell bonding. A similar conclusion can also be drawn for the zz-DW TiO$_2$ NT, although the interwall polarization causes the $\varDelta$z shift when the cross section of the nanotube contains Ti and O atoms belonging to different shells (Fig. 7.16b).

Fig. 7.16

Cross sections and lateral images of hexagonal DW TiO$_2$ NTs (i.e., left and right parts of models a and b, respectively) corresponding to optimized diameters for armchair and zigzag chiralities. For zz-DW TiO$_2$ NTs (model b), the atoms of the nearest ring behind the cross section are shown as half-shaded balls. The arrows above each lateral image are shown twice as long as the directions of the cross sections. For convenience, the lateral images of the inner shells of the nanotubes are shown as twice as long as those of the outer shells. a optimized model of double-wall (6,6)@(12,12) ac-TiO$_{2}$ NT. b optimized model of double-wall (10,0)@(20,0) zz-TiO$_{2}$ NT

Fig. 7.17

Binding energies E$_{bind}$ versus $\varDelta$R$_{NT}$ for the two sets of DW TiO$_2$ NTs with ac- and zz-chiralities. Spline treatment of the curves was performed to make them smooth

Fig. 7.18

Difference electron density plots $\varDelta$ $\rho$(r) of DW TiO$_2$ NTs calculated for the cross sections of nanotubes depicted in Fig. 7.16: a (6,6)@(12,12), b (8,8)@(24,24), c (10,0)@(20,0), d (12,0)@(36,0). The solid, dashed and dot-dashed isolines describe positive, negative and zero values of the difference density, respectively. Isodensity curves are drawn from $-$0.001 to + 0.001 e Å$^{-3}$ with increments of 0.00004 e Å$^{-3}$

It was found in [124] that the binding energies estimated per formula unit for the optimal configurations of hexagonal DW NTs are considerably larger for titania as compared to boron nitrides. Obviously, this is caused by a substantially larger ionic contribution to the interwall interaction between the titania SW constituents. In both cases, the double-wall nanotube configurations with zz-chirality are energetically more favorable than those with ac-chirality. As with DW BN NTs, the small values of $\varDelta$R$_{NT}$ and D$_{NT}$ $^{in}$ (Table 7.16) accompanied by the large values of E$_{relax}$ result in the instability of DW TiO$_2$ NTs, while the large values of $\varDelta$R$_{NT}$ correspond to an almost negligible interaction within the pairs of constituent SW NTs. As with DW BN NTs, E$_{bind}$ for titania nanotubes is sensitive to $\varDelta$R$_{NT}$, while the influence of D$_{NT}$ $^{in}$ on E$_{bind}$ is rather negligible (Table 7.16).

The comparison of the difference electronic charge redistributions drawn for both optimal and increased values of $\varDelta R_{NT}$ within ac- and zz-DW NTs (both BN and TiO$_2$) [124] demonstrates higher electron density localization within the latter (especially for armchair-type nanotubes),while the comparison of the results presented in Table 7.17 show a noticeably higher bond ionicity in DW TiO$_2$ NTs. The bond populations between the shells in DW TiO$_2$ NTs were found to be close to zero. For large $\varDelta R_{NT}$ in double-wall titania nanotubes (Fig. 7.13) the intershell interaction becomes weak again, i.e. the stability of these DW TiO$_2$ NTs is quite low, as with DW BN NTs (Figs. 7.17 and 7.18).

Unlike BN nanotubes, the difference between the values of the band gap for double-wall and single-wall TiO$_2$ NTs is considerably larger. An additional difference occurs for the small values of $\varDelta R_{NT}$. The band gaps of zz-DW TiO$_2$ NTs are indirect, while for zz-DW BN NTs, these band gaps are direct for all configurations. This can be explained by a substantially smaller stability of DW TiO$_2$ NTs with reduced values of $\varDelta R_{NT}$. Moreover, when both the inner $D_{NT}$ and $\varDelta R_{NT}$ increase, the band gaps of double-wall titania nanotubes are still too far from the band gap limit of the TiO$_2$(111) three layer slab (4.89 eV), [102]. However, the dependence of band gaps on both $\varDelta R_{NT}$ and inner $D_{NT}$ is similar for both DW BN and TiO$_2$ NTs, i.e. the band gap depends the most on the diameter of the inner shell. The Mulliken population analysis shows that O(2p) states prevail near the top of the valence band, while Ti(3d) states are mainly distributed near the bottom of the conduction band.

The comparison of the total energies between optimal DW TiO$_2$ NTs with hexagonal fluorite-type morphology and SW TiO$_2$ NTs with anatase-type centered rectangular morphology [120] containing the same number of atoms per nanotube unit cell allows one to make the following conclusions. For similar chiralities, one observes that the latter are energetically preferable: (i) the energy gain for ($-$9,9) SW NT vs (6,6)@(12,12) DW NT with the number of atoms equal to 108 has been found to be 0.09 eV per TiO$_2$ formula unit; (ii) an analogous energy gain for 180-atomic unit cells of SW and DW nanotubes with chiralities (15,15) and (10,0)@(20,0) achieves 0.17 eV per TiO$_2$ formula unit. Therefore, the growth of anatase-type NTs is preferable.

2.3 Rolled up Singlewall $\mathrm{{TiO_2}}$ Nanotubes with Rectangular Morphology

The morphology of titania nanotubes is governed by the structure of atomic layers in the bulk phases and it is much more complicated than that of carbon and BN nanotubes. The distance between two six layer slabs (1.2 Å) is two times larger than that between the neighbouring three layer slabs (0.6 Å) used in the calculations of the simplified hexagonal three layer model of TiO$_2$ nanotubes considered above. A more realistic six layer titania nanotube model was used in [117, 119, 125]. The model uses six atomic planes of the (101) anatase slab (three Ti- and three O- planes), and the slab obtained belongs to the rectangular lattice, see Fig. 7.19. As follows from (2.39), there are restrictions on the NT chiralities compatible with the translational symmetry.

Fig. 7.19

Five-fold coordination for Ti atoms in six-layer centered rectangular titania sheets

Fig. 7.20

Models of stoichiometric (101) titania sheets of different thickness optimized from the corresponding slabs with initial geometry of bulk anatase (lateral and cross sections images): a 6-layer slab (thickness 0.24 nm); b 12-layer slab (thickness 0.58 nm)

The bulk anatase structure is described by the space group I$4_1/amd$ with four TiO$_2$ formula units in the tetragonal (conventional) unit cell with the edges $a$ and $c$. Figure 2.20b shows a (1 0 1) slab consisting of 6 atomic planes (four oxygen and two titanium planes). The 2D translation symmetry of the slab corresponds to the centered rectangular lattice with 12 atoms in the conventional unit cell with the edges $a$ and $\sqrt{a^2+c^2}$. The nanotubes ($-$n,n) and (n,n) are constructed by rolling an anatase (1 0 1) sheet along the $(\overline{1}01)$ and $(0 1 0)$ directions, respectively. The 1D line symmetry groups of the ($-$n,n) and (n,n) titania nanotubes contain $(2n)_n$ screw axis. This axis is oriented along the tube one-dimensional translation vector $\mathbf {a}$. Just after the rolling up the reflection planes contain $\mathbf {a}$ for the ($-$n,n) nanotubes and are perpendicular to $\mathbf {a}$ for the (n,n) ones. During nanotube structure relaxation new symmetry elements (reflection planes and twofold axes) can appear.

Table 7.18 Line symmetry groups of SW ${\mathrm{TiO}}_2$ NTs, rolled from two periodic titania layers

Table 7.18 gives the line symmetry groups of SW TiO$_2$ NTs, rolled from two-periodic titania layers. Figure 7.16 shows the ways of constructing SW nanotubes for three types of titania sheets: one 3-layered with hexagonal morphology and two 6-layered ones with rectangular morphology. The 3-layer model of the anatase (101) slab considered in the preceding section consists of three atomic layers (O-Ti-O), its structural optimization results in the formation of a fluorite-type (111) slab [118, 126], whose symmetry can be attributed to the layer 2D group $72(P{\overline{3}} m1)$. It is the same for the 3-layer slab with both anatase and fluorite structures, although the space symmetry of the fluorite TiO$_2$ bulk crystal is described by cubic space group 225($Fm\overline{3}m$). In the case of the 6-layer model (O–O–Ti–Ti–O–O), all the six atoms of the bulk primitive unit cell are included and both centered and primitive rectangular lattices have to be considered. The 12-layer (O–O–Ti–Ti–O–O–O–O–Ti–Ti–O–O) model contains two quasi-separated 6-layer slabs. The layer group $18(C2/m11)$ with a centered rectangular lattice describes the symmetry of both 6- and 12-layer slabs. The bulk titania with lepidocrocite structure can be attributed to orthorhombic space group 63 (Cmcm). The 6-layer model of the lepidocrocite (010) slab consists of six atomic layers (O–Ti–O–O–Ti–O) [127]. Layer group $46 (Pmmn)$ with a primitive rectangular lattice describes its symmetry. Table 7.18 gives the line symmetry groups of SW TiO$_2$ NTs, rolled from two periodic titania slabs.

The first-principle calculations of six layer TiO$_2$ NTs were made in [117, 119, 125, 127]. As the number of atoms in the six layer model of the TiO$_2$ nanotube quickly increases with increasing diameter the ab initio calculations are very time consuming for the structural optimization. Therefore in [117] molecular mechanics-based calculations were performed to obtain the optimized nanotube structure, while electronic band structures were obtained by performing DFT (LDA) calculations. As in all the plane wave calculations, the three-periodic nanotube model was used in [117]: a tetragonal supercell with the lattice parameter $a$ much larger than the nanotube translation periodicity was adopted, but the result dependence on the parameter $a$ was not investigated. The two types (-n,n) and (n,n) of titania nanotubes (called A- and B-types,respectively [117]) were studied. It was found that A-nanotubes are energetically preferable to B-nanotubes. According to [117], the band gap of the A-nanotube was reduced by 0.60 eV as the tube diameter decreases from 12 to 5 Å. The first hybrid HF/DFT LCAO calculations of both the structure and electronic properties of the TiO$_2$ nanotube obtained by rolling a six-layer (1 0 1) anatase slab were made in [119, 125]. In the LCAO calculations of TiO$_2$ NTs no artificial 3D periodicity is necessary.

We now proceed to discuss the results of the first principles hybrid HF-DFT LCAO calculations [120, 125] on the 6- and -12 layer models of TiO$_2$ NTs with rectangular morphology. The CRYSTAL09 computer code [23] was used. As in the three-layer model calculations [102, 124] of TiO$_2$ NTs with hexagonal morphology the small-core pseudopotential [98] of the Ti atom was used ($3s, 3p, 3d$ and $4s$-electrons were taken as valence electrons), while the all-electron basis set for the O-atom was taken from [99].

The diffuse exponents of valence s, p and d-orbitals were optimized for the stable anatase phase of the bulk titania. Its atomic and electronic properties were reproduced in the good agreement with the experiment (the experimental values are given in brackets): the lattice parameters a $=$ 3.784 Å (3.782 Å) and c = 9.508 Å (9.502 Å), the dimensionless parameter for the relative position of the oxygen atom $u = 0.2074 (0.2080)$, the values of the energy gap are reproduced worse, because of being overstimated: 4.0 eV versus 3.2 eV. In any case, these results for the bulk titania (anatase) agree with the experimental data better than those given in [97] for both the plane wave (PW) and LCAO calculations when the different exchange-correlation potentials were used. A certain improvement of the substantially underestimated values of the energy gap for the bulk anatase in the DFT PW calculations has been achieved recently [103] using the LDA+U method (2.7 eV).

The structures of 6- and 12-layer anatase (101) slabs (see Fig. 7.19) were optimized in [120, 125] and their properties were calculated. Both 6- and 12-layer anatase (101) slabs keep their initial symmetry after structural optimization, although their lattice parameters differ from those in the bulk, see Table 7.20.

Six-layer titania slabs with anatase-type (101) structure can be rolled up to 6-layer titania SW NTs with (i) $(-n{,}n)$ chirality and (ii) $(n{,}n)$ chirality. Figure 7.21a shows the optimized structures of the selected 6-layer nanotubes of both chiralities. A specific feature of these six-layer titania sheets and nanotubes is that both Ti sublayers are rearranged in the middle between the surfaces of both the sheets and nanotubes, see Figs. 7.20a and 7.21a, i.e., their optimized structure is O–O–Ti–Ti–O–O, which is different from O–Ti–O–O–Ti–O owing to the sequence of TiO$_2$ formula units in the bulk anatase structure.

Fig. 7.21

A top (Lateral) and across (cross sections) views of 6-layered anatase-like SW TiO$_2$ nanotubes for different chiralities: a ($-$3,3), b (10,10), c (15,15), d ($-$6,6)

Fig. 7.22

Strain energies E$_{strain}$ versus D$_{NT}$ for the two sets of six-layer SW TiO$_2$ NTs with various chiralities

Table 7.21 presents the results obtained after the structural optimization of 6-layer TiO$_2$ NTs with (i) ($-$n,n) chirality (for n $=$ 3, 4, 6, 9, 12) and (ii) (n,n) chirality (for n = 6, 10, 15, 20, 24). One of the main parameters of the nanotube stability, i.e., the strain energy $E_{strain}$, is defined as a difference between the total energies of the optimized nanotube $E_{NT}$ and the corresponding slab before rolling up $E_{slab}$, with regard to the number $k$ of slab unit cells in the nanotube unit cell containing $m$ formula units TiO$_2$ (measured in kJ/mol per TiO$_2$ formula unit): $E_{strain}=(E_{NT}-kE_{slab}/m)$. Obviously, the number of atoms per surface unit in ($-$n,n) nanotubes is markedly smaller than that in (n,n) NTs of the same diameter. Therefore the former can be calculated faster. For the small diameter $D_{NT}$ (low chirality indices), the absolute values of both $E_{relax}$ and $E_{strain}$ are quite large, and trying to reduce these diameters further, one faces an enhanced instability of NTs. For example, the convergence of calculations on (4,4) nanotubes has been found to be rather poor. Since hypothetical nanotubes with an infinite diameter should coincide with sheets of the same thickness, a consequent growth of the NT diameters leads to a substantial decrease in both relaxation and strain energies (down to zero at infinity), whereas the values of other properies (Table 7.21) approach those for the 6-layer titania slab with hexagonal structure (Table 7.20).

To analyze the dependence of $E_{strain}$ and the energy gap on the diameter of six-layer TiO$_2$ NTs a sufficiently large range of nanotube diameters, from 0.5 to 4.0 nm, with the number of atoms per NT unit cell increased from 36 up to 288, was considered in [125]. Two curves $E_{strain}$($D_{NT}$) shown in Fig. 7.22 demonstrate that the strain energy of six-layer NTs with ($-$n,n) chirality is smaller than that of (n,n) NTs of a similar diameter, i.e., the former are more stable energetically. This difference remains noticeable for nanotubes with diameters $\le$30 Å. When the diameters of nanotubes increase to 40 Å the strain energies decrease and approach one another.

For six-layer titania nanotubes of both chiralities, $\varDelta E_{gap}$($D_{NT}$) curves possess maxima at the diameter range 13–17 Å (Fig. 7.23). For larger values of DNT, both the relaxation and strain energies of TiO$_2$ nanotubes substantially decrease, while their band gaps asymptotically approach the band gaps of the corresponding 2D slab (Table 7.20).

Fig. 7.23

Band gaps versus D$_{NT}$ for the two sets of six-layer SW TiO$_2$ NTs with various chiralities

Table 7.19 The structural and electronic properties of four pairs of symmetry-compatible TiO$_2$ NTs ((i), (d) means indirect and direct gap, respectively)

Table 7.19 presents the comparison of the results of calculations on four pairs of structurally similar TiO$_2$ nanotubes. The optimized values of $D_{NT}$ in each pair of these NTs were selected (the relative difference of the diameters in different pairs varied from 0.57 to 1.34 %). The structural compatibility of all the four pairs can be explained by their belonging to the same line groups (Table 7.18), i.e. the chiralities of 3-layer (n,n) and 6-layer ($-$n,n) nanotubes can be described by the same line group $(2n)_n/m$, whereas the line group $(2n)_nmc$ corresponds to both 3-layer (n,0) and 6-layer (n,n) NTs. Alongside the proximity of diameters, this symmetry factor makes reasonable a direct comparison of the structural and electronic properties in each pair of these nanotubes. One can conclude from the data presented in Table 7.19 that in 3- and 6-layer nanotubes with close diameters described by the $(2n)_n/m$ symmetry group the number of atoms per unit cell is the same, whereas the length of the unit cell of the 6-layer nanotube is about 20 % larger. In analogous NT pairs described by the $(2n)_nmc$ symmetry group the number of atoms per unit cell is larger by about 70 % for 6-layer nanotubes, while their lengths are more than twice larger compared to 3-layer NTs. Thus, if one estimates the density of atoms per NT length, it will be larger for 3-layer nanotubes. The 6-layer NT thickness is about 30 % larger than that of 3-layer nanotubes for all chiralities. As to Ti-O bond lengths, their deformation is noticeably larger in 6-layer nanotubes, and it is not decreased for $D_{NT}$ up to 30 Å, whereas in the 3-layer NTs, the values of $d_\mathrm{{Ti-O}}$ approach those in the three-layer slab (Table 7.2) much faster. Obviously, this is also true for the convergence of $E_{ relax}$ with DNT increasing (Table 7.20).

The chemical nature of the Ti-O bonds in both three- and six-layer titania nanotubes is slightly different. The values of effective charges $q_{Ti}$ on titanium atoms presented in Table 7.20 clearly show that the chemical bonding in hexagonal nanotubes is more ionic. On the other hand, the calculated Ti-O bond populations in 6-layer NTs were found to be 2–3 times larger than those in 3-layer slabs achieving 0.16–0.18 e per internal wall bonds, i.e., the bonding in the former is more covalent. A series of calculations for the total and projected densities of states (DOS and PDOS) for the TiO$_2$ anatase bulk, 3, 6 and 12-layer titania sheets were also made in [120]. It was found that the DoSs of the 6- and 12-layer sheets and the 6-layer are qualitatively similar to the DOSs of the bulk anatase. When both $D_{NT}$ and the number of atoms are increased, the profiles of DOSs and PDOSs become more complicated, since the number of one-electronic states increases. The total density of states projected on different atomic states implies that the states of the highest valence band (VB) mainly arise from the 2p states of oxygen atoms, while those of the lowest conduction band (CB) come from the 3d states of Ti atoms. In 6-layer nanotubes, the contributions of O and Ti states in CB and VB states are found to be larger than in 3-layer nanotubes. It means that the $\mathrm{{O}}(2p)-\mathrm{{Ti}}(3d)$ bond hybridization is more pronounced at PDOSs calculated for the equilibrium six-layer TiO$_2$ nanotube structures, i.e., their covalent bonding is stronger.

Twelve-layer single-walled TiO$_2$ nanotubes with rectangular morphology were also simulated in [125]. The middle of the 12-layer TiO$_2$ slab consists of two sublayers containing oxygen atoms (Fig. 7.20a), and when a single-walled titania nanotube is obtained by rolling up this twelve-layer sheet its thickness is about 2.5 times larger than that of a six-layer TiO$_2$ nanotube. As a result, the atomic structure of the internal wall surface of this 12-layer NT is overstrained even for the moderate values of $D_{NT}$. A comparison of images for both six- and twelve-layer NTs with the same ($-$6,6) and (12,12) chiralities (Fig. 7.24) clearly shows quite small geometry relaxation of the former and a drastic change of morphology of the latter, which cannot be optimized at all, due to a divergence of the SCF calculations after several steps of geometry optimization.

This effect can be also illustrated by a drastic difference between the calculated strain energies $E_{strain}$ for six- and twelve-layer SW TiO$_2$ NTs (with the initial geometry after rolling up the corresponding slabs), for ($-$6,6) and (12,12) chiralities: 23.76 and 41.78 versus 224.04 and 498.62 kJ/mol per TiO$_2$ formula unit, respectively. Thus, one can predict that for 12-layer titania nanotubes, the more preferable morphology has to be not SW but the double-walled (DW) NT consisting of a pair of six-layer nanotubes of different diameters and chirality indices.

Table 7.20 The atomic and electronic structure of TiO$_2$ bulk versus various slabs

It is seen that ab initio LCAO calculations using the hybrid PBE0 Hamiltonian allow one to perform the analysis of the atomic and electronic structure of TiO$_2$ sheets, as well as nanotubes simulated using different models. It was found in [120] that the structural optimization of the 3-layer slab results in a spontaneous (barrier-less) reconstruction into the hexagonal (111) fluorite structure. The structural optimization of three- and six-layer single-walled titania nanotubes leads to a growth of the NT diameter for all the morphologies considered. Noticeable differences between the calculated properties of 3- and 6-layer TiO$_2$ sheets and nanotubes were found. First of all, the strain energies of the six-layer nanotubes are smaller than those of the 3-layer NTs of close diameters (for $D_{NT}$ $\le$ 20–25 Å). The most probable reason for this 6-layer NT energetical stability is that in six-layer titania sheets and nanotubes with anatase structure both Ti sublayers are positioned in the middle between the surfaces of both the sheets and the nanotubes, i.e., their formal bulk structure is O–O–Ti–Ti–O–O. On the other hand, the relaxation energies of 6-layer NTs are larger than those of 3-layer nanotubes (especially for small NT diameters), due to a more complicated structure of the former. The band gaps of six-layer titania nanotubes (typical semiconductor with $\varDelta E_{gap}$ $\le$ 5 eV) are found to be noticeably larger (up to 0.5  eV) compared to three-layer NTs of the same diameter. When these diameters markedly increase, the nanotube band gaps asymptotically approach those for 2D slabs of the corresponding thickness.

Fig. 7.24

Cross-sections of 6- and 12-layer SW TiO$_2$ NTs with ($-$6; 6) and (12; 12) chiralities, respectively (D$_NT$ for nanotubes with initial geometry are defined as described in Table 7.21)

Table 7.21 The structural and electronic properties of six-layer SW ${\mathrm{TiO}}_2$ NTs (Fig. 7.21)$^\mathrm{{a}}$

The strain energies of 6-layer SW TiO$_2$ NTs decrease with the growth of the nanotube diameter, approaching a minimum for the infinite $D_{NT}$. $\varDelta E_{gap}$ curves for both nanotube chiralities achieve maxima at the diameter range 13–17 Å and after its further growth both gaps asymptotically approach that for the corresponding 2D slab. Twelve-layer SW TiO$_2$ NTs were found in [125] to be as energetically unstable as single-walled nanotubes. One can predict that for these nanotubes the most preferable morphology has to be double-walled (DW) NTs of the same chirality consisting of a pair of six-layer nanotubes of different diameters and chirality indices.

2.4 TiO$_2$ Nanowires

Titania nanowires (TiO$_2$ NWs) attract enhanced attention in modern nanotechnology due to a variety of promising applications such as humidity sensors, photovoltaic and photocatalytic cells, optical devices, field-effect transistors, etc. [128]. TiO$_2$ NWs based on the rutile phase were mainly synthesized using thermal evaporation [129, 130] via vaporliquidsolid and vaporsolid growth mechanisms, applying Ni or Au as a catalyst, and by chemical vapor deposition [131]. Such titania nanowires were found to be single crystalline with diameters of 10–100 nm possessing the $[110]$, [132] and $[001]$, [133] orientations of growth. On the other hand, TiO$_2$ NWs were recently synthesized with diameters on the Angstrem scale [134]. In this case, nanowires show effects not present in the bulk, thus opening up new applications.

A number of theoretical studies on atomic-scale TiO$_2$ nanowires have already been published. Simulations on the formation energy for titania nanowires showed the stability of structures assembled from Ti$_2$O4 building blocks (with a tetrahedral coordination of the Ti atoms instead of the usual octahedral one) [135]. Large-scale calculations on the thinnest filaments consisting of periodically repeated TiO and TiO$_2$ molecules along chosen 1D axes as well as on bulk-like TiO$_2$ [110]-oriented NWs were performed, too [136]. First-principles simulations indicated an increase in band gap values due to the quantum confinement effects of hydrogenated rutile-based TiO$_2$ NWs with the $[001]$ orientation [137]. In particular, $[001]$—oriented nanowires were cut along the central axis passing through the Ti atoms (resulting in mirror plane symmetry but without a screw axis in nanowires).

Large-scale ab initio calculations on thermodynamically preferable TiO$_2$ NWs in the rutile phase [128] clearly display only the energetically preferable $\{110\}$ facets in the case of their $[001]$ orientation, as well as the alternating $\{110\}$ and $\{001\}$ facets in the case of the $[110]$ NW orientation, in accordance with the Wulff construction formalism [109]. The influence of O and Ti vacancies on the energetic, structural, and electronic properties of rutile-based titania $[110]$ nanowires and their reactivity toward water molecules were evaluated as well [138].

Two main reasons cause the simulation of both $[001]$ and $[110]$ orientations of rutile-based TiO$_2$ NWs to be a necessity, [128]: (i) the thermodynamic contribution to nanowire stability is independent of NW morphology for diameters greater than 10 nm synthesized experimentally (while ab initio calculations can be performed only for nanowires with diameters $\le$5 nm) and (ii) the interface between a catalytic substrate and the nucleation titania seed should display a sufficiently low energy to surpass the nucleation barrier. This is why $[110]$- oriented rutile-based TiO$_2$ NWs have been synthesized more frequently so far [129–132].

The structure and electronic properties of TiO$_2$ anatase–based nanowires were calculated as well, with different orientations and surface terminations varied as a function of diameter [139, 140]. In particular, the stability and electronic structure of both anatase-based and rutile-based $[001]$ nanowires were compared for a series of first-principles calculations [141]. With diameters of up to 2.1 nm in anatase-based and 3.7 nm in rutile-based nanowires, those ${100}$-walled anatase and ${110}$-walled rutile NWs were found to be the most stable, which retains the nonsymmorphic character of the bulk space group. As for the construction of 1D atomistic models for titania nanowires, both the Ti atom- and hollow-centered symmetry axes (i.e., translation 2-fold rotation axis and 4-fold screw axis, respectively) were considered in studies [137, 141].

According to Wulff’s formalism [109], the quasi-square cross-sections of titania nanowires correspond to a minimum of dangling bonds per titania formula units [128].

From numerous possible shapes of symmetric prism models used for the simulation of rutile-based titania nanowires, [128, 136–138, 141] the two energetically most favorable configurations have been chosen in rutile-based TiO$_2$ nanowires calculations [94, 142]: square the rhomb-type (Figs. 7.25 and 7.26) and quasi-square rectangle-type (Figs. 7.28 and 7.29) possessing Ti atom-centered symmetry axes. As found recently [128], it is only for these shapes of TiO$_2$ NWs, that the total nanowire energy per formula unit achieves minimum values. The hollow site-centered TiO$_2$ $[001]$ nanowire, see Fig. 7.27, has also been used in calculations [94, 141].

Fig. 7.25

Transformation of $5\times 5$ supercells of two-plane rutile (001) slabs to cross-sections of either hollow site-centered (a $\rightarrow$ b) or Ti atom-centered (c $\rightarrow$ d) $[001]$ NWs. Dot-dashed blue lines (a, c) show the borders of adjacent slab supercells. The centers of hollow site- and Ti atom-centered nanowires are shown by crosses and ballsof a larger diameter, respectively. The consequent transformation of Ti$_{-1}$, Ti$_{-2}$, Ti$_{-3}$ and Ti$_{-4}$ (b), as well as Ti$_{-1}$ and Ti$_{-2}$ (d) atoms can be described by C$_{4h}$ and D$_{2h}$ point groups, respectively (see explanation in the text). The lengths of rhombic square sides in the slab supercells and NW cross-sections are defined for arbitrary extensions

Fig. 7.26

Cross-sectional a and lateral b images of the non-optimized $[001]$-oriented Ti atom-centered nanowire possessing the D$_{2h}$ symmetry and containing 81 formula units per NW unit cell with aside (110) and (1$\overline{1}$0) facets shown in b. The red rhombs in a show the borders for prism models of middle, small and smallest TiO$_2$ NWs (49, 25 and 9 formula units per UC, respectively). The images of the $[001]$-oriented hollow site-centered titania nanowire (c, d) possessing the C$_{4h}$ point symmetry and containing 64 formula units per unit cell are shown in a manner similar to a and b, respectively, including the prism models of middle, small and smallest TiO$_2$ NWs containing 36, 16 and 4 formula units per unit cell. The diameter of the nanowire is shown in a by a twice-terminated arrow (d$_{[001]}$), while its period (length of UC) is shown in b as (l$_{[001]}$)

Fig. 7.27

Cross-sectional image of a non-optimized hollow site-centered TiO$_2$ $[001]$ NW possessing a four-fold screw axis (its track is shown by a cross) and containing 64 formula units per NW UC. Small arrows show the shifts of the nanowire axis during alternating transformations from hollow site- to Ti atom-centered structures and vice versa. Two adjacent rhombohedral sides imaged by solid lines show the facet borders of Ti atom-centered titania nanowires, while those limited by dashed lines correspond to hollow site-centered TiO$_2$ NWs. Two other lateral facets described here fixed remain, coinciding with the lower sides of the cross-sectional image

The construction of rutile-based nanowires for the calculations [94, 142] was made from the supercells of rutile slabs in such a way that the 2D slab surface was normal to the chosen NW periodicity direction with the subsequent removal of both slab translations and restoring the translation for the NW. The translational period of the nanowire is defined by the minimal slab unit cell along the direction normal to the slab surface. This period consists of two and four titania formula units for the orthogonal [001] and [110] nanowires, respectively. The length unit $l_{NW_{UC}}$ of the nanowires generated corresponds the minimal slab periodicity along the normal axis $h_{layer}^{min}$ in the case of the (001) cross-sections, Fig. 2.19 d while for the (110) cross-section, NW orthogonality is provided for the double thickness 2$h_{layer}^{min}$, Fig. 2.19a. Non-orthogonal [110] NWs with axes inclined from the normal by $\pi /4$ can be simulated too (as they were really observed in experiment [132]) if $l_{NW_{UC}}=h_{layer}^{min}$. On the other hand, the periodic cross-section of the 1D nanowire can be transformed from the supercell of the 2D slab possessing periodic boundary conditions (PBC). At first we consider an [001]-oriented rutile nanowire. The surface unit cell of the (001) slab with an arbitrary thickness consists of an even number of TiO$_2$ formula units since the two formula units of the titania bulk primitive cell are projected on the two neighbor slab planes forming periodically repeating 2D layers along the z-axis (see Fig. 2.19d and Table 7.7). There are two possibilities for the choice of four-faceted NWs since the primitive cell of the square plane lattice can be transformed into supercells with $\begin{pmatrix} n&{} 0 \\ 0&{} n \\ \end{pmatrix}$ or $\begin{pmatrix} n&{} n \\ -n&{} n \\ \end{pmatrix}$ matrices which correspond to either (100), ($\overline{1}$00), (010) and (0$\overline{1}$0) lateral NW facets (according to Fig. 2.19d) or (110), ($\overline{1}$10), (1$\overline{1}$0) and ($\overline{1}$ $\overline{1}$0) ones (Fig. 7.25), respectively.

Table 7.9 shows that the surface energy of the (110) and related slabs is substantially smaller than that of the (001)-type of slabs. Therefore, we have to generate [001]-oriented NWs using $\begin{pmatrix} n&{} n \\ -n&{} n \\ \end{pmatrix}$ slab supercells. Any such supercell consists of 2$n^2$ minimal slab unit cells along the z-axis, i.e., 4n$^2$ TiO$_2$ formula units (n $=$ 1, 2, 3). To generate the nanowire, one removes the 2D periodicity of the slab, i.e., the cyclic boundary conditions for the facets and introduces periodicity along the z-axis (two TiO$_2$ formula units in the 1D unit cell).

Upper part of Fig. 7.25 shows the two possible types of slab supercells which differ by origins of coordinate systems centered at either the hollow site (Fig. 7.25a) or the Ti atom (Fig. 7.25c). Both rhombic-type supercells with periodic boundary conditions shown in the aforementioned models by dot-dashed lines contain the same number of formula units 4n$^2$ and have the same surface area, while their size can be described by the length of square side: $na\sqrt{2}$. When removing PBC one obtains a nanowire with the translation vector perpendicular to the titania (001) rutile slab, whose unit length equals to thickness of slab layer unit: $l_{NW001}=h_{001}^{min}$. In the case of the hollow-centered [001] nanowire, both the NW shape and the composition of O and Ti atoms in its cross-section are the same as those in hollow-centered (001) slab supercell (cf. Fig. 7.25a, b), however, a length of its square side decreases from $na\sqrt{2}$ to $a\sqrt{2}(n+1/2-2u)$ due to an absence of 2D supercell periodicity (u is the rutile structure parameter defining the positions of oxygen atoms). Symmetry of such a nanowire is described by rod group P4$_2$/m with a screw axis. The rotations around this axis transform corner Ti$_{1}$, Ti$_{2}$, Ti$_{3}$ and Ti$_{4}$ atoms (consistently located in adjacent atomic planes) to each other. Thus, when the origin of coordinate system is centered at hollow site, one does not needs any structural transformation for transition 2D slab1D NW.

However, when removing the PBC from the supercell centered at the Ti atom one receives the cross-section of the NW requiring an additional transformation and generates a nanowire with symmetric composition of the edge O and Ti atoms similar to the composition obtained in the hollow site-centered [001]-oriented NW. To achieve this aim, the two upper rows of the edge O and Ti atoms, as well as the lowest row of the edge O atoms (Fig. 7.25c) must be removed, giving altogether $(4n1)$ formula units. The symmorphic Pmmm rod group describes the symmetry of the newly-formed Ti atom-centered nanowire (Fig. 7.25d) transforming corner $Ti_{1}$ and $Ti_{2}$ atoms (located in the same atomic plane) to each other. The length of the NW square cross section is found to be $a\sqrt{2}(n-2u)$, while number of formula units per unit cell of this transformed nanowire is $(2n1)^2$. Obviously, the square cross-sections of Ti atom-centered nanowires (Fig. 7.25d) cannot form a 2D slab since they contain the odd number of Ti atoms in each equivalent side and cannot be translated along the side directions, resulting in the appearance of adjacent supercells which are complementary to the slab prototype. On the contrary, the cross-sections of hollow site-centered NWs containing an even number of Ti atoms (Fig. 7.25b) allow the introduction of periodic boundary conditions.

Thus, in rutile-based [001] titania nanowires (Fig. 7.26) the direction of the translation axis is orthogonal to the pair (110) and (1$\overline{1}$0) vectors of the cross-sectional rhombic square. If the translational two-fold rotation axis goes through a Ti atom (Fig. 7.26a, b), one can see that the reflection in the horizontal plane and the rotations around the two second order axes in this plane are the symmetry operations for [001]-oriented nanowires described by the point symmetry group D$_{2h}$ [142]. Both the cross-sectional and lateral views of this type of nanowire define its diameter, d$_{NW}$ and length unit, l$_{NW}$. As to the translation axis for a [001] rutile—based nanowire with a 4-fold screw axis going through the interstitials in the middle of the squares formed by Ti atoms (Fig. 7.26c, d), its point symmetry group is C$_{4h}$ and the corresponding rod group P4$_2$/m is non-symmorphic, [141]. It means that the number of point symmetry operations used for the description of the [001]–oriented hollow site-centered nanowire (eight) equals that of the Ti atom-centered nanowire. Figure 7.27 clearly shows how nanowires with hollow site-centered symmetry axes can be transformed to NWs with Ti atom-centered axes and vice versa by the removal of external stoichiometric shells from the two adjacent facets.

Fig. 7.28

Transformation of 84 supercells of six-plane rutile (110) slabs to cross-sections of either Ti atom-centered (a $\rightarrow$ b) or hollow site-centered $[110]$ nanowires (c $\rightarrow$ d). The dot-dashed lines in Fig. 7.28a, c show the borders of adjacent slab supercells. The centers of hollow site- and Ti atom-centered nanowires are shown by crosses and balls of a larger diameter, respectively. The consequent transformation of Ti$_{-1}$ and Ti$_{-2}$ (b) as well as Ti$_{-1}$ and Ti$_{-2}$ (d) atoms can be described by D$_{2h}$ and C$_s$ point groups, respectively (see explanation in the text). The lengths of rectangular sides in the slab supercells and NW cross-sections are defined analytically for arbitrary extensions

For [110] oriented nanowires the structural generation is more complex than in the case of [001]-oriented NWs. In the former case the lateral facets are (001), (00$\overline{1}$), ($1\overline{1}$0) and ($\overline{1}$10). Analyzing the values of surface energies given in Table 7.9 one can suppose that the nanowires generated from (110) slab supercells have noticeably larger surface energies than [001] nanowires. The 2D lattice for a (110) slab is rectangular with the lengths of translation vectors proportional to c and $a\sqrt{2}$ (Fig. 2.19a). According to Table 7.7, the surface area of a (110) slab unit cell is a stretched rectangle, i.e., $c\mathrm{x }a\sqrt{2}$. Moreover, unlike the (001) slab, the ratio of unit lengths in the (110) surface area is transcendental. To provide a generation of a quasi-square supercell for the (110) slab with close lengths of sides, the transformation matrix $\begin{pmatrix} 2n&{} 0 \\ 0&{} n \\ \end{pmatrix}$ can be used. Both choices of the coordinate system origin giving Ti atom- and hollow site-centered supercells (cf. Fig. 7.28a, c) are equivalent when periodic boundary conditions are introduced. However, after the removal of PBC one needs to make additional transformations in order to obtain stoichiometric nanowires. Rectangular quasi-square supercells with PBC shown in Fig. 7.28 by dot-dashed lines contain the same number of formula units 8n$_2$ and have the same surface area, while their sizes can be described by a pair of lengths: $2nc$ and $na\sqrt{2}$ (Fig. 7.28a, c). After the removal of PBC the shapes of cross-sections in [110]-oriented NWs are the same as those in (110) slab supercells, however, the lengths of rectangle sides decrease: $c(2n1/2)$ and $a\sqrt{2}(n+1/2-2u)$. For both Ti atom- and hollow site-centered [110] nanowires, additional transformations are necessary, to generate a nanowire with a symmetric composition of edge O and Ti atoms. In the first case, $(6n1)$ excessive formula units must be removed from the corresponding supercell of the (110) rutile slab (Fig. 7.28a), in order to obtain a Ti atom-centered titania nanowire, while in order to obtain a hollow site-centered [110]-oriented nanowire (Fig. 7.28c) $2n$ missing formula units must be added. These transformations generate NWs consisting of $(2n1)(4n1)$ and $2n(4n+1)$ formula units whose symmetry is determined by the rod groups Pmmm and Pm2m for Ti atom- and hollow site-centered cases, respectively (Fig. 7.28b, d). In the former case, the symmetry group transforms Ti$_{1}$ and Ti$_{2}$ atoms in the middle of opposite sides to each other (Fig. 7.28b), while the latter analogously transforms the titanium atoms located at the upper corners of the same side (Fig. 7.28d). Both pairs of Ti atoms are positioned in the same atomic plane. The lengths of corresponding pairs of rectangular sides are $c(2n1)$ and $a\sqrt{2}(n-2u)$ versus $2nc$ and $a\sqrt{2}(n+1/2-2u)$, respectively. Obviously, the cross-sections of [110]-oriented nanowires cannot be translated along the side directions, to provide the formation of adjacent supercells which are complementary to the prototype for the $2D\rightarrow 1D$ structural transition (Fig. 7.28).

Fig. 7.29

The cross sectional a and lateral b images of a non-optimized $[110]$-oriented Ti atom-centered NW possessing the D$_{2h}$ symmetry and containing 105 formula units per NW UC, with aside (001) and (110) facets (the former is shown as b image). The red rectangles in the cross-section a show the borders of prism models for middle and small titania nanowires containing 55 and 21 formula units per UC, respectively. The images of the $[110]$-oriented hollow site-centered titania nanowire (c, d) possessing the C$_{2v}$ point symmetry and containing 78 formula units per unit cell are shown in a manner similar to a and b, respectively, including prism models of middle and small TiO$_2$ NWs containing 36 and 10 formula units per unit cell. The diameter of a nanowire is shown in a by a twice-terminated arrow (d$_{[001]}$) while its period (length of UC) is shown in b as (l$_{[001]}$)

For the orthogonal [110] TiO$_2$ NWs, the four formula units of the primitive cell lie in the six cross-sectional atomic planes (Fig. 7.29b). The symmetry of a [110] nanowire coincides with the symmetry of the analogous type of [001] NW if the translation axis with rotation by $\pi$ goes through the Ti atom (the rod group Pmmm). Indeed, Fig. 7.29a, b shows that the symmetry operations for [110] NWs are reflection in the vertical (v) plane (containing the translation axis) and rotation around the two-fold translation axis in this plane. The symmetry operations also include rotations around the two-fold axis in the horizontal plane (orthogonal to the translation axis). Thus, the point group of this nanowire type is again D$_{2h}$, analogous to the Ti atom-centered [001] nanowire. As to the symmetry of [110] NWs with hollow site-centered symmetry axes (Fig. 7.29c, d) it can be described by a rather poor C$_s$ point group characterized by the presence of the mirror plane across the nanowire cross-section only. However, since the lateral $\{110\}$ facets of this NW configuration are described by the C$_{2v}$ point group, the latter can be used to characterize the whole nanowire.

Let us discuss the properties of rutile-based [001] and [110] nanowires calculated in [94].

The main results of large-scale PBE and PBE0 calculations with total energy optimization on both Ti atom- and hollow site-centered titania [001] nanowires with four diameters for PBE and PBE0 exchange-correlation functionals are presented in Tables 7.22 and 7.23.

Figures 7.30 and 7.31 demonstrate the distorted structure of [001]-oriented NWs with the initial morphology discussed above. In both figures, the distorted geometry of the [001]-oriented NWs calculated using the PBE0 method is shown since PBE calculations give qualitatively similar images. Structural relaxation leads to an increase in the optimized $d_{NW}$ and a decrease in $l_{NW}$. The larger the $d_{NW}$, the closer its equilibrium value to the initial non-optimized $d_{NW}$ (Fig. 7.26), whereas $l_{NW}$ also approaches the initial value of the NW unit cell length. Figures 7.30 and 7.31 demonstrate a decrease in the NW distortion with increasing $d_{NW}$, this distortion is more noticeable in the case of hollow site-centered nanowires. At the edges and corners of [001]-oriented NWs the Ti–O bonds have been found to be more covalent than those in the proximity of nanowire axis or in the bulk, thus explaining the appearance of structural distortion after geometry relaxation, e.g., shortening of the corner and edge Ti–O bonds. These conclusions are confirmed by the consequent decrease of the surface energy in both types of TiO$_2$ nanowires approaching that for the lateral $\{110\}$ and $\{1\overline{1}0\}$facets, which are energetically the most favorable (Table 7.9). Comparative analysis of surface energies for the [001] and [110]-oriented nanowires is illustrated by Fig. 7.32, clearly showing energetic preference for the former, which correlates well with the recently published results of simulations on rutile-based TiO$_2$ NWs with varying diameters [143]. Moreover, the rutile-based NWs with hollow–centered symmetry axes have been found to be energetically slightly more stable than Ti atom-centered ones, especially when nanowire diameter increases. As the change of band gaps with increasing $d_{NW}$, these values approach those for the bulk beginning with the smaller gaps for ultrathin Ti atom-centered NWs. Conversely, the decrease in the calculated band gap with increasing $d_{NW}$ has been observed for hollow site-centered nanowires beginning with large gaps in the case of small diameters, this peculiarity was confirmed in other theoretical simulations [137, 141, 143]. Analogous changes of band gap occur for slabs with increasing thickness. Irrespective of the NW type, the convergence to the value of band gap for the titania rutile bulk has been observed for both models. In [94], the results obtained for a Ti atom-centered nanofilament containing only one formula unit per NW unit cell were not analyzed since the properties of this nanostructure drastically differed from those for more thick nanowires [128]. The corresponding oscillations of surface energy and band gap for nanowires of small diameters were observed in study [143].

Figure 7.33 presents the total densities of states for rutile-based TiO$_2$ nanowires and those projected on the surface and internal atoms calculated using the PBE0 method for Ti atom- and hollow site-centered [001]-oriented NWs of largest diameters (Fig. 7.26 as well as Tables 7.22 and 7.23). By comparison, gray–filled areas on both plots show the total DOS for the titania rutile bulk. One can observe a slight

Table 7.22 The structural and electronic properties of optimized Ti atom-centered $[001]$-oriented NWs (Fig. 7.26a, b)

Table 7.23 The structural and electronic properties of optimized Ti atom-centered $[001]$-oriented NWs (Fig. 7.26a, b)

Fig. 7.30

Cross-sectional views of optimized Ti atom-centered titania $[001]$ NWs of smallest (a), small (b), middle (c) and large (d) diameters calculated using the LCAO-PBEmethod (parameters of relaxation are present in Table 7.22). Section planes for present images are chosen to be the same as in Fig. 7.13

Fig. 7.31

Cross-sectional views of optimized hollow site-centered titania $[001]$ NWs of smallest (a), small (b), middle (c) and large (d) diameters calculated using the LCAO-PBE method (parameters of relaxation are present in Table 7.23). Section planes for present images are chosen to be the same as in Fig. 7.13

Fig. 7.32

Dependences of surface energies for Ti atom- and hollow site-centered titania nanowires of $[001]$ and $[110]$ orientations on the number of formula units per NW unit cells (Tables 7.11 and 7.22 and 7.23 and 7.24) calculated using the LCAO PBE (a) and PBE0 (b) methods. The labels of different shapes correspond to the calculated values of the surface energy for different NW configurations. Spline treatment of lines initially joined the nearest labels of the same shapes has been performed to obtain the smooth curves

Fig. 7.33

The total densities of states (shown by bold lines) as well as the densities projected on either surface or internal atoms (solid or dashed lines, respectively) for $[001]$-oriented NWs of largest diameters (Fig. 7.26) centered on the Ti atom (a) and hollow site (b) containing 81 and 64 formula units per nanowire’s UC, respectively. The filled gray areas correspond to the total DOS of the titania rutile bulk

shift of the DOS projected on the surface (outer) or internal NW atoms towards the larger versus the lower energies, respectively, compared to the total DOS. The latter is qualitatively similar to the total DOS of the titania bulk. On the other hand, no essential qualitative difference between the DOSs for Ti atom- and hollow site-centered NWs exists. This can be explained by different coordination of surface and internal atoms. Obviously, the PDOSs of Ti and O one-electronic states imply that the states of the highest valence band (VB) zones mainly arise from the 2p states of oxygen atoms, while those of the lowest conduction band (CB) zones come from the 3d states of Ti atoms. The analysis of parameters for both 3d(Ti)–3d(Ti) and 3d(Ti)–2p(O) bonding states was performed elsewhere [143].

The results obtained in [94] for TiO$_2$ [110]-oriented NWs are presented in Tables 7.24 and 7.25 and Figs. 7.32, 7.34 and 7.35.

It is important to find similarities and differences between the properties of [001] and [110] types of structurally different TiO$_2$ NWs. The main qualitative conclusions for NW properties depending on $d_\mathrm{NW}$ are found to be close to being similar to those drawn in [143]. However, the comparison of surface energies gives substantial energetic preference for [001]-oriented NWs over [110]-oriented nanowires, which are terminated by the alternating $\{001\}$ and $\{1\overline{1}0\}$ facets (Table 7.9 clearly demonstrates that (001) rutile surfaces are less-stable).

A distorted structure of Ti atom-centered [110]-oriented NWs has been obtained using the rod group symmetry Pmmm, while relaxed hollow site-centered nanowires are described by the Pm2m rod group. As in the case of [001] nanowires, [110]-oriented NWs with hollow–centered symmetry axes have been found to be energetically slightly more stable than Ti atom-centered ones (Fig. 7.32, as well as Tables 7.24 and 7.25). Figures 7.34 and 7.35 illustrate a decrease in the [110] NW distortion with increasing d$_{NW}$, that is analogous to [001] NW. Again, such a distortion is more noticeable in the case of hollow site-centered nanowires.

The results for the Ti atom-centered [110]-oriented nanofilament containing only 3 formula units per NW UC, presented in [142] clearly showed that this nanofilament noticeably differs from bulk-like nanowires, which are simulated in [94].

The corner and edge Ti–O bonds are again more covalent and slightly shorter than those in the proximity of the symmetry axes of [110]-oriented NWs. The same is true for the change of band gaps with increasing $d_{NW}$ since these values approach the band gap for the bulk beginning with the nanowire containing 21 formula units per unit cell. Again, in the case of Ti atom-centered TiO$_2$ NWs the values of the band gap increase with a growth of $d_{NW}$, while in the case of hollow site-centered NWs they decrease, analogously to the (110) slab with increasing thickness (cf. Tables 7.9, 7.24 and 7.25).

The conclusions, which can be drawn when analyzing the total and projected densities of states imaged in Fig. 7.36 and calculated using the PBE0 method for Ti atom–and hollow site-centered [110]-oriented titania NWs of largest diameters (Fig. 7.29, as well as Tables 7.24 and 7.25), are qualitatively similar to those for [001]-oriented NWs.

Table 7.24 The structural and electronic properties of optimized Ti atom-centered $[110]$-oriented NWs (Fig. 7.29a, b)

Table 7.25 The structural and electronic properties of optimized Ti atom-centered $[110]$-oriented NWs (Fig. 7.29a, b)

Fig. 7.34

Cross-sectional views of optimized Ti atom-centered titania $[110]$ NWs of small (a), middle (b) and large (c) diameters calculated using the LCAO-PBE method (parameters of relaxation are present in Table 7.22). The section planes for the present images are chosen the same as in Fig. 7.29

Fig. 7.35

Cross-sectional views of optimized hollow site-centered titania $[110]$ NWs of small (a), middle (b) and large (c) diameters calculated using the DFT-PBE method (parameters of relaxation are present in Table 7.24). The section planes for the present images are chosen the same as in Fig. 7.29

Fig. 7.36

The total densities of states (shown by bold lines) as well as the densities projected on either surface or internal atoms (solid or dashed lines, respectively) for $[110]$-oriented NWs of largest diameters (Fig. 7.29) centered on the Ti atom (a) and hollow site (b) containing 105 and 78 formula units per nanowire’s UC, respectively. The filled gray areas correspond to the total DOS of the titania rutile bulk

Let us summarize the results obtained in [94] for rutile-based nanowires. 1. The procedure of the structural generation of rutile-based [001]– and [110]–oriented four-facetted TiO$_2$ nanowires with symmetric prism-type shapes from titania (001) and (110) slabs, respectively, was suggested in [94]. In the case of rhombic–like square hollow site-centered [001] NWs, the nanowire cross-section is structurally compatible with the corresponding supercell of the (001) rutile slab. Thus, no additional geometry transformation is required to generate this NW configuration. For the generation of other configurations of rutile-based nanowires, either addition or removal of certain number of formula units is necessary from the corresponding slab supercells after a release of the periodic 2D boundary conditions. Moreover, rutile-based NWs with hollow–centered symmetry axes have been found to be slightly more stable than the Ti atom-centered ones, especially when the nanowire diameter increases. 2. The properties of rutile-based nanowires are both size and shape dependent. The large-scale calculations of the bulk crystal surface energy per formula unit allow a direct comparison of the relative stability of both 2D slabs and 1D nanowires and gives the main criterion of their stability. The values of d$_{NW}$ slightly increase, whereas the periodicity length l$_{NW}$ has been found to be reduced after NW geometry optimization. The larger NW diameter, the closer are its geometry parameters as well as the band gap to those of rutile-based TiO$_2$ bulk and non-optimized (001) and (110) slabs, whereas the NW surface energy approaches that of the facets terminating the nanowire. In the case of Ti atom-centered NWs, the values of the band gap grow with increasing d$_{NW}$, while in hollow site-centered NWs, these values decrease in analogous conditions, analogously to the band gaps of slabs with increasing thickness. 3. The comparative ab initio calculations using the DFT PBE and hybrid DFT HF PBE0 methods confirm that the stability of nanowires is determined mainly by the stability of their lateral facets, that is why [001]-oriented NWs terminated by $\{110\}$ facets are energetically more preferable than [110] NWs terminated by alternating $\{110\}$ and $\{001\}$ facets. The surface energy calculation for (110) and (001) slabs allows one to estimate the NW surface energy. Indeed, for hollow site-centered [001] and [110] nanowires the converged PBE0 surface energies are 0.83 and 1.39 $\mathrm{{J/m^2}}$. The use of the slab averaged energies for all the facets gives 0.74 and 1.22 $\mathrm{{J/m^2}}$. 4. Due to a structural compatibility between the TiO$_2$ slab supercells and the cross-sections of growing NWs, the results obtained in [94] can be used for further simulation of TiO$_2$ nanowire growth upon titania–containing substrate. On the other hand, some balance between the stability of supercell slabs with a large surface area and thick nanowires can exist. That is why the results of calculations [94] do not contradict experimental observations that the growth of thick TiO$_2$ NWs with [110] orientation (whose diameters are larger than 10 nm) can be more preferable than the stable (110) facets of the polycrystalline TiO$_2$/sapphire substrate [132].

Only a limited number of studies performed so far considered not just bare titania nanowires but NWs with vacancies, their chemical reactivity [144] and hydrogen-passivated NWs [137]. Such a limitation can be explained by the reduced symmetry of defective NWs, down to the P1 rod group (C$_1$ point group), and thus by a substantial increase of computational time. The substantial increase in the CPU time necessary for the calculations on titania nanowires described by the point group C$_1$ is accompanied by a noticeable limitation of NW size considered.

The LCAO calculations discussed above for bare titania nanowires use the full RG symmetry of rutile-based NWs. However the total energy per 1D unit cell and NW translation period can change if the initial structure RG symmetry is lowered. Table 7.26, see [142], clearly demonstrates that these changes are small both for [001] and [110] oriented nanowires. Therefore the calculations on titania nanowires possessing middle and large diameters $\le 2$ nm (which are considered to be more realistic for a comparison with the experiment [128]) become possible.

Table 7.26 Dependence of the Total Energy per TiO$_2$ NW Unit Cell, E$_{tot\_NW}$, and Its Period, $l$, Calculated Using CRYSTAL Code$^{15}$, on Point Groups Set in Inputs for [001]- and [110]-Oriented Nanowires

When comparing the parameters calculated for titania slabs and both NW orientations using DFT PBE and hybrid the DFTHF PBE0 methods we can observe their qualitative proximity, except for the densities of one-electron energy states including band gaps [94]. Since calculations using the hybrid method are considerably more time-consuming, especially when using plane wave codes, the parameters of structure and total energy for both slabs and nanowires can be calculated using the standard GGA DFT methods. This conclusion is important as PW calculations are made mainly using the GGA methods.

The localized atomic function (LCAO) method allows one to describe single 1D nanowires, whereas the plane wave (PW) method is more widespread for large-scale calculations on low dimensional periodic systems. However, to restore the 3D periodicity in the PW nanowire calculations, the 1D nanostructure supercell is artificially introduced; i.e., the NWs are placed into a square array with sufficiently large intertube distances. At such separations, the NW-NW interaction is usually found to be rather small. However, the convergence of results obtained using DFT-PW calculations depends on the artificial interwire interactions, thus additional computational efforts should be provided to ensure their negligibility. Such an artifact is certainly absent in the LCAO nanowire calculations. From this point of view, a comparison of results obtained in DFT-LCAO and DFT-PW calculations can be very important for their verification. Such a comparison was made in [142] in the calculations of rutile-based $[001]$ and $[110]$-oriented TiO$_2$ nanowires with Ti atom-centered symmetry axes. The details of the DFT LCAO and DFT PW computational schemes are the same as those used in the bulk rutile comparative LCAO and PW calculations (see Sect. 3.8).

Tables 7.27 and 7.28 present the results of comparative DFT– LCAO and DFT– PW calculations of rutile TiO$_2$ [001] and [110] Ti–atom centered NWs [142]. Both methods have been used for calculations of the key NWs structural and electronic properties depending on the orientation, shape and diameter of TiO$_2$ [001] and [110] NWs (i.e., the changes of the diameters d$_{NW}$ and unit cell lengths l$_{NW}$ of nanowires during geometry optimization, as well as effective atomic charges correlated with the formation energies per formula unit $E_{rel}$ and band gaps). A good quantitative correlation is observed between the results of the DFT-LCAO and DFT-PW calculations. In particular, the values of d$_{NW}$ slightly increase, whereas l$_{NW}$ are found to be reduced after NW geometry optimization, except for the thinnest [110] NW ($d_{NW}\approx 3$ Å), whose 1D unit cell contains three formula units making this nanostructure more like a nanofilament. The larger the NW diameter is, the closer its geometry parameters as well as the band gap to those of the rutile-based TiO$_{2}$ bulk. The NW morphology affects the stability of TiO$_2$ NWs at very small diameters ($\le$3 Å), while at larger diameters its role is attenuated.

Both LCAO and PW calculations clearly demonstrate that the more energetically preferable titania nanowires in the rutile phase (without hydrogen passivation and the presence of vacancies) display (110) facets when they are [001]-oriented and $\{110\}$ and $\{001\}$ facets when they are [110]-oriented. Thus a good quantitative correlation between the results of the DFT-LCAO and DFT-PW calculations on nanowires was established in [142].

Table 7.27 Structural and Electronic Properties of Optimized Rutile-Based TiO$_2$ [001]-Oriented Nanowires

Table 7.28 Structural and Electronic Properties of Optimized Rutile-Based TiO$_2$ [110]-Oriented Nanowires

2.5 Orientation Effects in the Morphology and Electronic Properties of Rutile Nanowires, Anatase Nanowires and Facetted Nanotubes

Nanostructure orientation is important in the calculation of the properties of nanostructures. The orientation effects in the morphology and electronic properties of TiO$_2$ nanostructures have been studied for rutile nanowires [128] and anatase nanowires [145] and nanotubes [146] by means of ab initio DFT PW calculations with structural optimization.

[001] and [110] oriented rutile NWs display the three possible morphology (the rhomb, the polyhedron, and the square), see Fig. 2.26. The knowledge of the relative surface energies is useful in predicting the shape of a nanostructure whose facets display low surface energies [128]. As we have seen above in the case of TiO$_2$ in the rutile phase, the (110) surface has been shown to possess the lowest surface energy, followed by the (100), (011), and (001) surfaces, respectively. Therefore [001]-oriented rutile NWs with rhomb topology (four $\{110\}$ facets) are expected to have the lowest surface energy. This conclusion is confirmed both by the results of calculations [94, 128] and experimental study [133].

A short summary of the results obtained in [128] is as follows. The most thermodynamically preferable TiO$_2$ NWs in the rutile phase without hydrogen passivation or O vacancies display $\{110\}$ facets when they are [001]-oriented and the $\{110\}$ and $\{001\}$ facets when they are [110]-oriented. The morphology affects the stability of the rutile TiO$_2$ NWs at small diameters, while at larger diameters its role is attenuated. The most stable [001]-oriented NWs are characterized by band gap values that are invariable with respect to the diameter of the nanostructures and close to that of the bulk. Such band gap behavior is anomalous with respect to the expected changes in the gap values due to quantum confinement effects. This happens because of the stabilization role of the states in the top valence bands and in the bottom conduction bands that come from atoms located close to and at the surface of these nanostructures. One can suggest that the interaction between the edges of adjacent $\{110\}$ and $\{100\}$ facets in NWs with the [001] axis leads to a sizable band gap reduction. In the case of [110]-oriented NWs, the presence of the flat bands, similar the localized levels in the gap region, is found to be an intrinsic feature of such nanostructures, which is not connected with the O vacancies or surface states. These flat bands composed of Ti–d states also provide a decrease in the band gaps. The calculated band structures of different NWs do not show any sign of surface dangling bonds in the gap region, indicating that the hydrogen passivation is not appropriate for these nanostructures. The absorption coefficients for rutile NWs with different morphology and orientations do not follow the changes in the gaps and do not display any shift of the absorption edge to the lower energy range. [001]-oriented NWs with a rhomb morphology can be considered as a suitable material for photovoltaic and photocatalytic cells, however an efficient way to shift the absorption edge to the lower energy range and to improve the transport properties of these NWs should be found.

According to experimental observations, there are three different growth orientations of TiO$_2$ NWs in the anatase phase: $[001],[100]$ and $[110]$, see references in [145]. The smallest experimentally observed diameter of anatase TiO$_2$ NWs has been detected to be 4–5 Å, [134].

Theoretical investigations of anatase NWs [139–141] mainly focus on the band gap variation with diameter and the data obtained are different and contradictory to the experimental data. The study of the orientation effects on the electronic structure of anatase-based NWs allows one to understand the situation: ab initio calculations [145] revealed a sizable anisotropy in the electronic properties of anatase TiO$_2$ nanowires to exist with respect to the orientation: nanowires with $[001], [100]$ and $[110]$ axes are found to be direct band gap, indirect band gap and degenerate semiconductor materials, respectively.

Structural optimization and band structure calculations of TiO$_2$ NWs were performed in [145] by utilizing the first principles total energy PAW method (see Chap. 3) and the PW basis (an energy cutoff was introduced at 420 eV). PBE exchange and correlation potentials were included, and periodic boundary conditions were applied along the nanowire axis with the unit cell parameter $a_{||}$. In order to ensure a negligible interaction between the neighboring NWs, at least 7 Å of vacuum were introduced (a further increase in the vacuum thickness did not noticeably affect the total energy). All the atoms in TiO$_2$ NWs were allowed to relax. The grid of 1 $\times$ 1 $\times$ 6 Monkhorst-Park points was used in the calculations and the atomic relaxation was made. To ensure convergence, the final iterations were performed on the 1x1x10 grid. The optimization of $a_{||}$ was done by gradually increasing/decreasing its value along with a relaxation of the atomic positions till an equilibrium was reached. Calculations of the band structures were performed using the self-consistent charge densities. The charge distributions and transfers were analyzed by the Bader method. After the optimization the bulk lattice parameters of TiO$_2$ in the anatase phase were found to be $a=3.80 (3.79)$ Å and $c=9.57 (9.52)$ Å. The experimental values of these parameters are given in brackets, the LCAO PBE0 calculations give $a=3.78$ Å and $c=9.51$ Å, see Table 7.6.

The initial structures of TiO$_2$ NWs were generated in [145] on the basis of the bulk, which was specifically oriented, by cutting it along different atomic planes in order to form facets parallel to the NW axis. According to the selected orientation of NWs, $a_{||}$ was set at c, a and 2a for such nanostructures with the $[001], [100]$ and $[110]$ axes, respectively. The TiO$_2$ stoichiometry of NWs was kept invariable. As in the case of NWs, the same energy cutoff, vacuum thickness as well as the procedure of structural optimization and band structure calculation were applied for (001), (100) and (110) TiO$_2$ slabs which have two equal surfaces and different thickness.

Fig. 7.37

Cross sections of TiO$_2$ NWs after full structural optimization. The large, blue balls stand for Ti atoms, the small, red balls represent O atoms. NW orientations, morphology and facets are indicated (Reprinted figure with permission from Migas et al. [145], Copyright (2014) by the Royal Society of Chemistry)

The morphology of TiO$_2$ NWs with $[001]$ axes can be characterized by $\left\{ 100\right\}$ and $\left\{ 110\right\}$ facets. The cross sections of such NWs are shown in Fig. 7.37, where cases conventionally called the square, the polyhedron and the rhomb are considered. In the square NWs only $\left\{ 100\right\}$ facets are present, while in the rhomb NWs one can notice $\left\{ 110\right\}$ facets. In the case of the polyhedron NWs both $\left\{ 100\right\}$ and $\left\{ 110\right\}$ facets, which are almost equal in size, define their shape. The diameters of these NWs are $2.6$, $2.5$ and $2.5$ nm for the square, the polyhedron and the rhomb morphology, respectively.

After the structural optimization of TiO$_2$ NWs only slight changes can be spotted in their shape, that are mostly caused by the O atoms. In fact, TiO interatomic distances are found to be in the range of 1.80–2.28 Å. However, in the case of the rhomb morphology there are four undercoordinated Ti atoms in the unit cell which are located at edges between adjacent$\left\{ 110\right\}$ facets because they have only one O atom from the first coordination shell and two O atoms from the second coordination shell. Moreover, some O atoms at edges display outward relaxation, possess the largest distance from the center of the NW among the other atoms and have only one Ti atom at each edge as their neighbor with the TiO interatomic distance equal to 1.65 Å. The unit cell parameter $a_{||}$ is decreased after the optimization for all the NWs irrespective of their morphology. The largest changes in $a_{||}$ are found for the square $(2.6\,\%)$ and the rhomb $(3.6\,\%)$ NWs with the smallest diameters of 1.0 and 1.4 nm, respectively.

The morphology of [100]–oriented rutile NWs can be characterized by $\{001\}$, $\{010\}$ and $\{011\}$ facets. In study [145] two possible cross sections were chosen : a square one with $\{001\}$ and $\{010\}$ facets and a polyhedron one with $\{001\}$, $\{010\}$ and $\{011\}$ facets, as presented in Fig. 7.37. The corresponding diameters of NWs are 3.8 and 3.4 nm for the square and the polyhedron morphology, respectively. The polyhedron morphology can be easily obtained from the square morphology by introducing $\{011\}$ facets at edges between adjacent $\{001\}$ and $\{010\}$ facets. Structural optimization does not sizably affect the shape of the NWs with respect to the initial configurations cut from the bulk. Moreover, after relaxation the TiO interatomic distances have turned out to be in the range of 1.79–2.16 Å, which is very close to the case of [001]-oriented anatase NWs. In addition, $a_{||}$ is found to be decreased for both the square and the polyhedron NWs displaying, a 5 and 3 % reduction for a diameter of about 2.0 and 3.8 nm, respectively.

For [110]-oriented TiO$_2$ NWs, $\{001\}$ and $\{112\}$ facets were observed during the growth [147], leading to the polyhedron morphology as illustrated in Fig. 7.37. In addition to $\{001\}$ and $\{112\}$ facets, the appearance of $\{110\}$ facets in the morphology of anatase NWs is also possible. Thus, morphology with polyhedron, rhomb, square and round cross sections was considered in [145]. Square morphology involves $\{110\}$ and $\{001\}$ facets orthogonal to each other in the plane of the cross section. Round morphology possesses $\{112\}$ facets in between $\{110\}$ and $\{001\}$ facets, while rhomb morphology displays only $\{112\}$ facets. For the latter case the larger rhomb diagonal (1.8 nm), which defines the diameter of the NW, is almost twice as large as the smaller diagonal (1.2 nm). The diameters of the square, the round and the polyhedron TiO$_2$ NWs are 2.7, 2.2 and 2.1 nm, respectively. After structural optimization the interatomic distances are found to be in the range of 1.77–2.27 Å, which is in agreement with the data for [001]- and [100]-oriented anatase NWs. The authors of [145] also revealed that the Ti-Ti interatomic distances of Ti atoms, which are in the plane of the cross section and located on the surface of $\{112\}$ and $\{110\}$ facets, get shorter (2.80–2.94 Å) with respect to the bulk values. This effect is probably responsible for the expansion in $a_{||}$ since the latter one is larger than the unoptimized value by 0.8, 1.0, 2.5 and 3.5 % for the square, the round, the polyhedron and the rhomb NWs, respectively.

These results demonstrate the presence of structure anisotropy in anatase NWs with respect to their growth orientation. Such an anisotropy was also found in anatase NWs electronic properties [145]. Indeed, [001]-oriented NWs, regardless of their morphology and diameter, display a direct band gap and an almost identical dispersion of the bands close to the gap region. Similar features are typical of [100]-oriented NWs except for the indirect band-gap nature. On the contrary, anatase NWs with [110] axes and different morphology can be treated as degenerate semiconductors because the Fermi level crosses some bands at the bottom of the conduction band. This issue is attributed to a slight deviation from TiO$_2$ stoichiometry since two O atoms are always lacking in [110]-oriented NWs. Even though there are at least four possible places to add two O atoms and restore TiO$_2$ stoichiometry, these two additional O atoms cause a significant distortion in the NW structure along with the appearance of several flat bands in the gap region. Thus, the degenerate semiconducting properties of [110]-oriented anatase NWs can be viewed as their intrinsic feature.

The calculated band-gap dependence on the diameter of anatase NWs does not follow the common $\approx$ $1/d^{2}$ law due to the quantum confinement effects and displays instead the mainly the linear dependence or even invariable values of the gap. Partly this issue can be explained by a variation in $a_{||}$ (the unit cell parameter along the NW axis) during full structural optimization, which affects the band-gap values of anatase NWs, and partly by the influence of the surface state effects. The latter should be always taken into account because surface states do not shift in energy due to quantum confinement effects and, at the same time, they characterize the top valence band and the bottom conduction band in anatase NWs. In fact, pure surface hole states usually appear at the top of the valence band in NWs with different orientations, while an admixture of surface states and bulk-like states is present in the bottom conduction band. Moreover, a similar behavior was observed for TiO$_2$ thin films (slabs) and the same features can be expected to occur for TiO$_2$ nanocrystals because their shape is characterized by facets. In addition to that, the appearance of $\{001\}$ facets (or (001) surface) can lead to band-gap values in TiO$_2$ nanostructures being smaller than in the bulk. The prevalence of $\{110\}$ facets (or (110) surface) stabilizes the band gaps at values slightly higher than the one in the bulk, whereas presence of $\{100\}$ and $\{110\}$ facets can result in complex band-gap behavior with the diameter in TiO$_2$ nanostructures similar to that of the [001]-oriented polyhedron TiO$_2$ NWs.

The orientation effects in the morphology and electronic properties of anatase facetted nanotubes are considered in [146]. The same computational PW DFT (PBE) method was used as was applied to study the orientatation effects in anatase TiO$_2$ nanowires [145]. [001]-, [100]- and [110]-oriented anatase facetted NTs with different cross sections and diameters were considered, while periodic boundary conditions were applied along the NT axis with the unit cell parameter (a$_{||}$). In order to provide a negligible interaction between the neighboring NTs at least 7 Å of vacuum were introduced because a further increase of the vacuum thickness did not noticeably affect the total energy. All the atoms in TiO$_2$ NTs were allowed to relax.

The initial structures of TiO$_2$ NTs were generated on the basis of the anatase NWs by forming a hole along the NW axis. The corresponding anatase NWs are described above. By making a hole along the NW axis centered at its middle one can easily obtain an NT, whose inner surface also possesses facets. Thus, in the case of anatase facetted NTs one can expect the same set of facets to be taken into account for both the inner and the outer surfaces. In order to describe the morphology of facetted NTs, it is convenient to use the same notations as for anatase NWs (for example: the square, the polyhedron, the rhomb) and also indicate in a similar way the shape of the hole (for example: a polyhedron NT with a square hole). According to the selected orientation of the NTs, (a$_{||}$) was set at c, a and a$\sqrt{2}$ for NTs with the [001], [100] and [110] axes, respectively.

Fig. 7.38

Cross sections of [001]-oriented square anatase TiO$_2$ facetted NTs with different shape of the hole and diameters of 2.6 nm after full structural optimization. The corresponding square anatase NW is shown in Fig. 7.37. The large, blue balls stand for Ti atoms. The small, red balls represent O atoms. The facets of the inner surface the case numbers are indicated. For the #2 case the $\{100\}$ facets are shown pointed out by arrows (Reprinted figure with permission from Migas et al. [146], Copyright (2014) by the Royal Society of Chemistry)

Figure 7.38 shows the cross sections of the square anatase facetted NTs with different shapes of the hole. The #1 case is characterized by a square hole involving $\{100\}$ facets, while for the #2 case a polyhedron hole is chosen along with $\{100\}$ and $\{110\}$ facets to form the inner surface. After relaxation the thickness of NT walls consisting of three TiO$_2$ layers is about 0.39 nm which is comparable with the size of the bulk unit cell a. The hole size varies within 1.0–1.5 nm. The #3 case possesses a rhomb hole with $\{110\}$ facets. After structural optimization the wall thickness is equal to the Ti-O interatomic distance of 1.63 Å  because of the outward relaxation of the O atoms in the middle of $\{100\}$ facets of the outer surface, while initially the wall in this place is only represented by one TiO$_2$ layer. Such a short Ti-O interatomic distance is due to the under coordinated Ti atoms, as in the case of the rhomb TiO$_2$ NWs. The #3 case can also be considered as a conglomerate of four touching nanocrystals which form the NT. The #4 case is similar to the #1 case except for the NT walls which have only two TiO$_2$ layers, however the wall thickness is enlarged to 0.30 nm with respect to 0.19 nm of the initial structure due to the outward relaxation of the surface O atoms. Structural optimization does not sizably affect the shape of the square TiO$_2$ NTs (the cases #1–#4) as compared with the initial structures, leading to the interatomic distances being close to those of TiO$_2$ NWs. Contrary to the TiO$_2$ NWs, $a$ increases for the square TiO$_2$ NTs by 3.4–3.7 % and 5.1 % for the #1, #2 and #4 cases, respectively. This effect is probably due to interatomic interactions at the edges between the adjacent facets of the inner surface. However, a reduction in a$_{||}$is detected for the #3 case (1.7 %), which is most likely caused by the presence of under coordinated Ti atoms, as for the rhomb TiO$_2$ NWs.

Fig. 7.39

Cross sections of [001]-oriented anatase facetted NTs with different shapes of the hole. The diameters of NTs are about 1.9–2.2 nm. The top and middle panels the #5–#7 cases as cut from the bulk and after structural optimization, respectively. The bottom panel the #8–#10 cases with thicker walls after structural optimization. The large, blue balls stand for Ti atoms. The small, red balls represent O atoms. The facets of the inner surface (the top panel) and the case numbers are indicated. For the #6 case the $\{100\}$ facets as shown by arrows (Reprinted figure with permission from Migas et al. [146], Copyright (2014) by the Royal Society of Chemistry)

The top panel of Fig. 7.39 represents the cross sections of the rhomb and polyhedron TiO$_2$ NTs cut from the bulk with different shapes of the hole. The #5 case shows the rhomb anatase facetted NT with a square hole characterized by the $\{100\}$ facets of the inner surface and the wall thickness in the thinnest place of about 0.27 nm (three TiO$_2$ layers). The polyhedron TiO$_2$ NT (the #6 case) possesses a polyhedron hole with $\{100\}$ and $\{110\}$ facets. The wall thickness is also about 0.27 nm (three TiO$_2$ layers). The #7 case is essentially the same as the #6 case except for the wall thickness which is reduced by half down to 0.13 nm (two TiO$_2$ layers). Conversely, square TiO$_2$ NTs (Fig. 7.38), structural optimization crucially modifies the shape of the rhomb and polyhedron TiO$_2$ NTs, as can be seen in the middle panel of Fig. 7.39. In fact, the hole is rounded for the #5 and #6 cases and their cross section can be also viewed as a conglomerate of nanoclusters because some the Ti and O atoms in the thinest part of the NT walls (the middle of the $\{110\}$ facets of the outer surface) shift towards each other from different sides of the wall, leading to the formation of four nanocluster–like structures connected to each other by a thin isthmus. Amazingly, the #7 case, which is initially a polyhedron NT with a wall thickness of two TiO$_2$ layers and a polyhedron hole, has transformed into a cylindrical and single-walled-like structure. It is clearly seen that most of the O atoms on the inner and outer surfaces display outward relaxation, and the wall thickness varies in the plane of the cross section of the NT. Significant changes have been spotted for $a_{||}$, indicating its expansion of 9.5, 6.3 and 8.7 % for the #5, #6 and #7 cases, respectively. It is interesting to trace how an increase in the wall thickness of the rhomb and polyhedron NTs affects their shape. The #8 case with a square hole (Fig. 7.39, bottom panel) differs from the #5 case in the wall thickness, which is 0.40 nm (four TiO$_2$ layers), compared to 0.27 nm (three TiO$_2$ layers) of the #5 case. It is also evident that structural optimization does not modify the shape of the square hole and or the whole NT for the #8 case. Moreover, the conglomeration effect is attenuated, indicating that the wall thickness of 0.40 nm (four TiO$_2$ layers) for rhomb NTs turns out to be a critical one. Thus, for thicknesses smaller than 0.4 nm crucial changes in the NT shape are expected. The same conclusions can be drawn for polyhedron TiO$_2$ NTs. In fact, the #9 and #10 cases, which are characterized by a wall thickness of 0.40 nm (four TiO$_2$ layers), have square and rhomb holes, respectively. The square hole (the #9 case) has deliberately been selected with the hope to enhance the conglomeration effect observed in the #6 case; however, neither the square hole (the #9 case), nor the rhomb hole (the #10 case) causes any significant change in the NT shape. Moreover, #8 case possesses the under coordinated Ti atoms at the edges between the adjacent $\{110\}$ facets. These atoms have sizable outward relaxation displaying the Ti-Ti (2.88 Å) and Ti-O (1.66 Å) distances. It is found that a$_{||}$ substantionally increases for the #8 (10.6 %) and #9 (10.4 %) cases, while a marginal reduction (0.02 %) is revealed for the #10 case.

Fig. 7.40

Cross sections of [100]-oriented polyhedron anatase facetted NTs with a diameter of 3.4 nm (the corresponding NW cross sections are shown in Fig. 7.37) and different holes after full structural optimization. The large, blue balls stand for Ti atoms, the small, red balls represent O atoms. The facets of the inner surface and the case numbers are indicated (Reprinted figure with permission from Migas et al. [146], Copyright (2014) by the Royal Society of Chemistry)

Two types of [100]-oriented TiO$_2$ polyhedron NTs are shown in Fig. 7.40. The first type (the #11 case) has a square hole with a diameter of about 1.2 nm and a wall thickness close to 0.84 nm (four TiO$_2$ layers). The second type (the #12 case) is characterized by a polyhedron hole of 1.5–2.2 nm and it displays significantly thinner walls. In fact, 0.38 nm (two TiO$_2$ layers) and 0.63 nm have been determined for the walls with $\{001\}$ and $\{011\}$ facets, respectively. In addition, the thickness of the walls with $\{010\}$ facets varies from 0.63 nm to almost zero because of a thin isthmus of TiOTi bands in the middle of these facets. However, structural optimization does not affect the shape of such NTs with respect to the initial structures. Moreover, the Ti-O distances for the #11 case are similar to those of the parent NW (1.79, 2.19 Å), while for the #12 case they are 1.75, 2.28 Å. a$_{||}$ has been found to drop by 4 and 9 % for NTs with thicker (the #12 case) and thinner (the #11 case) walls, respectively. The square TiO$_2$ NTs are shown to display similar structural features as the polyhedron NTs. For this reason, these NTs are not predicted to have a critical wall thickness, as in the case with polyhedron and rhomb TiO$_2$ NTs with [001] axes because walls as thin as two TiO$_2$ layers preserve the shape of [100]-oriented TiO$_2$ NTs regardless of their morphology.

Fig. 7.41

The top panel cross sections of the [110]-oriented round anatase facetted NTs with a polyhedron hole and different wall thickness after full structural optimization. The diameter of the NTs is 3.1 nm. The bottom panel cross section of the [110]-oriented polyhedron anatase facetted NTs with a polyhedron hole before (from the left) and after (from the right) full structural optimization. The diameter of the NT is 2.1 nm. The corresponding round and polyhedron NW cross sections are shown in Fig. 7.37. The large, blue balls stand for Ti atoms, the small, red balls represent O atoms. The facets of the inner surface and case numbers are indicated (Reprinted figure with permission from Migas et al. [146], Copyright (2014) by the Royal Society of Chemistry)

For [110]-oriented TiO$_2$ NTs round and polyhedron TiO$_2$ NTs with a polyhedron hole involving 001 and 112 facets for the inner surface were selected, whose cross sections are shown Fig. 7.41, as representatives of TiO$_2$ NTs with [110] axes. Thus, the round TiO$_2$ NTs are chosen to have two different wall thicknesses: three TiO$_2$ layers of about 0.60–0.62 nm (the #13 case) and two TiO$_2$ layers (the #14 case). After relaxation the latter case possessed a wall thickness of 0.39 nm for the walls with $\{001\}$ facets, 0.26 nm for the walls with $\{110\}$ facets and 0.50 nm for the walls with $\{112\}$ facets. A significant increase in the wall thickness with $\{112\}$ facets is attributed to an outward relaxation of the surface O atoms along with a sizable extension of the Ti-Ti interatomic distances (3.42 Å). Different from the #13 case, where no crucial change in shape can be spotted, the #14 case displays a slight inward relaxation of the walls with $\{112\}$ and $\{110\}$ facets, as if the NT were squeezed. This effect is more pronounced for the polyhedron TiO$_2$ NT with a smaller diameter and two TiO$_2$ layers to form walls (the #15 case), where the shape of the NT transformed into a rectangular one as if $\{001\}$ and $\{110\}$ facets characterized its initial morphology. It is evident that the critical wall thickness is three TiO$_2$ layers. The hole sizes are 1.6–1.9, 2.1–2.3 and 1.0–1.4 nm for the #13, #14 and #15 cases, respectively. Typical Ti-O interatomic distances are in the range of 1.75–2.21 A. a$_{||}$ increases by 1.7 % for the #13 case and by 3.0 % for the #15 case, while it decreases by 0.4 % for the #14 case.

Fig. 7.42

The top panel different lateral views of the anatase facetted NT with a polyhedron hole (the #7 case). Three unit cells along the NT axis are presented. Crystallogrphic directions are shown. Elements of NT walls (triangles, which are vertex downwards oriented, and chains) are indicated by arrows. The middle panel individual elements of NT walls including triangles, which are vertex upwards oriented, and chains. The bottom panel different lateral views of the anatase facetted NT with a rhomb hole (#10 case). Three unit cells along the NT axis are presented. Crystallogrphic directions are shown (Reprinted figure with permission from Migas et al. [146], Copyright (2014) by the Royal Society of Chemistry)

Only the [001]-oriented polyhedron NT with a polyhedron hole (the #7 case, Fig. 7.39) displays a prefect cylindrical shape and a single-walled-like structure. The lateral view of an NT is presented in the top panel of Fig. 7.42 indicating the facelike structure of the NT wall. In fact, four rows of isosceles triangles in addition to chains form the wall. Moreover, each vertex of the triangle is connected to the middle of the base of a neighbor triangle. Two equal sides of the triangles have a length of 10.2 Å, whereas the base side is about 7.1 Å (Fig. 7.42, the middle panel). Since the orientation of the triangles (vertex upwards or downwards) alternates along the NT perimeter, chains as long as 10.7 Å (Fig. 7.42, middle panel) always link the vertexes of neighbor triangle bases. These chains closely resemble the thinnest anatase (101) slab of one monolayer [148]. However, some empty space or elongated holes as long as 22 Å are also clearly seen in the NT wall. The lateral views of the polyhedron TiO$_2$ NT with a rhomb hole (the #10 case) are also presented in Fig. 7.42 indicating that the $\{100\}$ facets have a wedge structure, while the rows of chains diagonal to the NT axis are clearly seen for the $\{110\}$ facets. The former ones are similar to the triangle structure observed for the #7 case, whereas the latter ones resemble the chains of the #7 case. The same can be seen from the lateral views of polyhedron TiO$_2$ NWs. Moreover, the #7 case (cut from the bulk initial structure) displays a lace-like structure. Thus, if the wall thickness of the polyhedron TiO$_2$ NT is smaller than the critical wall thickness, structural optimization rounds the NT cross section without a sizable reshuffle of atoms in the walls.

The morphology of walls of the facetted (polyhedron) TiO$_2$ NTs and TiO$_2$ NTs described and formed by rolling up a thin TiO$_2$ layer is different because in the latter case it is uniform while in the former case it inherits a structure which depends on the alternation of different facets. It is likely expected that in the cylindrical and single-walled- like structure (the #7 case) the interatomic distances are affected by relaxation. In fact, the Ti-O distances in the triangles and chains are in the range of 1.80–2.18 Å and 1.84–1.87 Å, respectively. Whereas the Ti–Ti distances get shorter with respect to the bulk value, shrinking down to 2.72–2.90 Å for the triangles and to 2.72 Å for the chains.

Fig. 7.43

Cross sections of [001]-oriented polyhedron anatase facetted NTs with a polyhedron hole and diameters of 1.6 nm (the #16 case) and of about 2.7 nm (the #17– #19 cases) for initial (as cut from the bulk)-left panel) and after full structural optimization (right panel). The large, blue balls stand for Ti atoms. The small, red balls represent O atoms. The facets of the inner surface and the case numbers are indicated. For the #16 case the $\{100\}$ facets are shown by arrows (Reprinted figure with permission from Migas et al. [146], Copyright (2014) by the Royal Society of Chemistry)

Fig. 7.44

The band gaps in [001]-, [100]- and [110]-oriented anatase facetted NTs as a function of the number of TiO$_2$ layers in walls. Case numbers are indicated for some of the NTs. The horizontal dotted line indicates the band-gap value in the anatase TiO$_2$ bulk, while the vertical dotted line corresponds to the upper limit of the wall thickness (Reprinted figure with permission from Migas et al. [146], Copyright (2014) by the Royal Society of Chemistry)

It has been revealed that the #7 case is not unique and similar cylindrical and single-walled-like structures can be formed in TiO$_2$ NTs with smaller and larger diameters. Figure 7.43 presents polyhedron TiO$_2$ NTs with polyhedron holes and diameters of 1.6 (the #16 case) and 2.7 nm (the #18 case). The lace-like structure of their walls is essentially the same as for the #7 case, while sizes of triangles get larger (the #18 case) or smaller (the #16 case) along with the length of chains. However, the polyhedron morphology of the initial NW along with a polyhedron hole is not sufficient to guarantee the cylindrical and single-walled-like structure of TiO$_2$ NTs. In fact, the #17 and #19 cases do not display the cylindrical shape, probably because the $\{100\}$ and $\{110\}$ facets are not close in size, while they can only be viewed as a single-walled-like structure with a polyhedron cross section, which is, nevertheless, visually rounded. After optimization a$_{||}$ is found to be increased by 9.7 % (the #16 case), 6.9 % (the #17 case), 8.6 % (the #18 case) and 7.9 % (the #19 case).

Experimental observations indicate that the [100] orientation occurs in cylindrical and multi-walled TiO$_2$ NTs [115, 149, 150]. The results discussed above suggest that the appearance of cylindrical and singlewalled- like TiO$_2$ NTs with [001] axes is not excluded. Moreover, one can assume that a multi-walled-like structure can easily be obtained by combining single-walled-like TiO$_2$ NTs with smaller and larger diameters.

Band gap variation with diameter in anatase facetted TiO$_2$ is affected by at least two issues. First of all, it is the value of a$_{||}$ because full structural optimization changes this lattice parameter in TiO$_2$ NTs by several percent with respect to the initial value corresponding to the one in the bulk. TiO$_2$ NTs and NWs display a similar variation in band gaps with uniaxial strain. Secondly, it is the surface states effects, which can attenuate or even block the influence of the quantum confinement effects, that can decrease the shift in the energy of band edges or lead to invariable band-gap values, which may be smaller than the one in the bulk. In the case of TiO$_2$ NTs, where one has both outer and inner surfaces, the band-gap dependence on the wall thickness can be more complicated than in NWs. Such a dependence is shown in Fig. 7.44, where TiO$_2$ NTs with the same orientation have equal diameters and morphology. The number of TiO$_2$ layers forming the NT walls are used instead of thickness expressed in Å because the surface O atoms often display a sizable outward relaxation artificially increasing the wall thickness. The data for TiO$_2$ NWs are used as an upper limit of the NT wall thickness. It is evident that only [001]-oriented square TiO$_2$ NTs follow the common law of a band-gap decrease with increasing wall thickness, while a possible limiting gap value corresponds to the one in the bulk (Fig. 7.44). Conversely, [100]-oriented polyhedron TiO$_2$ NTs and [110]-oriented round TiO$_2$ NTs are predicted to have band-gap values smaller than that in the bulk (Fig. 7.44) most probably because of the presence of $\{001\}$ facets. In addition, for the round TiO$_2$ NT with the [110] axis and a wall thickness of four TiO$_2$ layers the maximum of the valence band is characterized by p-states of O atoms located on the inner surfaces of the adjacent $\{112\}$ facets, while the $\{001\}$ facets almost disappear, leading to the band-gap value being smaller than the bulk value. Cylindrical and single-walled-like TiO$_2$ NTs (the #16, #7 and #18 cases) with the same wall thickness and different diameters display almost invariable band-gap values. In fact, band gaps of 3.12, 3.11 and 3.09  eV were detected for the #16, #7 and #18 cases, respectively, indicating that changes in band-gap values of TiO$_2$ NTs are expected with changes in the wall thickness. Figure 7.44 shows the band-gap dependence on the effective hole size for NTs with different orientations and a fixed outer diameter, i.e. the figure represents the band gap dependence when the NTs transform into NWs.

The results of ab initio calculations [146] clearly demonstrate crucial changes in the morphology of facetted TiO$_2$ NTs, as obtained from TiO$_2$ NWs by making a hole along their axes, and these changes are closely connected with the critical wall thickness and orientation. A critical wall thickness of four and three TiO$_2$ layers was predicted for TiO$_2$ NTs with [001] and [110] axes, respectively, while [100]-oriented TiO$_2$ NTs do not display any variation in shape with respect to the wall thickness.

Anisotropy effects in the band dispersion of the TiO$_2$ NTs are very close to those of the parent TiO$_2$ NWs. Thus, the competitive direct/indirect character of the gap is found to be typical of [001]-oriented TiO$_2$ NTs because of the small dispersion of the bottom conduction bands and the top valence bands, whereas [100]-oriented TiO$_2$ NTs are characterized by indirect transition. The facetted TiO$_2$ NTs with [110] axes possess a direct band gap. Unlike the [110]-oriented TiO$_2$ NWs, the corresponding TiO$_2$ NTs have TiO$_2$ stoichiometry due to specific atomic arrangements on the inner and outer surfaces at the edges and such NTs do not display degenerate properties. Moreover, band-gap values smaller than that in the bulk can occur for the TiO$_2$ NTs due to the influence of the surface states effects. Calculations [146] have also shown an alternative way to form cylindrical and single-walled-like structures for the [001]-oriented TiO$_2$ NTs—without rolling up a thin titania layer into a NT.

3 ZrO$_2$

3.1 Bulk Zirconia

We saw above that TiO$_2$-based nanostructure calculations have been made by different authors who employmed different theoretical models.

As for first-principles calculations of ZrO$_2$-based nanostructures, however, it is only recently that they have been performed for the first time [151]. A large array of zirconia nanotubes was constructed in [151] from the nanosheets derived. In each case the positions of all the atoms were optimized to obtain the most stable nanotube structure while preserving the rototranslational symmetry. Formation and strain energies were calculated to provide nanotube stability analysis. It was found that the formation energy of ZrO$_2$ nanotubes with a sufficiently large diameter is mainly determined by the formation energy of the corresponding nanosheet. The closeness of the nanotube surface energy to the surface energy of the corresponding thin films confirms the principal role of the parent nanolayer structure.

Zirconia is an oxide which exhibits a large variety of polymorphs. The properties of the bulk ZrO$_2$ are well studied experimentally [152] and theoretically [153–160]. It has been established that ZrO$_2$ has three zero-pressure modifications. At high temperatures (higher than 2350 $^\circ$C), zirconia adopts a cubic fluorite structure (Fm$\overline{3}$m), while at low temperatures (lower than 1150 $^\circ$C), a monoclinic baddeleyite (P2$_1$/c) structure is more likely preferred [161] and represents a ground state of zirconia. A tetragonal phase exists at intermediate temperatures; it can be viewed as a simple perturbation of the cubic phase in which the oxygen atoms are displaced alternately along the 4$_2$ axis by $\pm 0.2$ Å, resulting in a P4$_2$/nmc symmetry.

Besides the well-known monoclinic, tetragonal, and cubic phases, two orthorhombic high pressure phases with space group symmetry Pbca (orthorhombic-I) and Pnma (orthorhombic-II) are stable above 3 and 20 GPa, respectively [162, 163]. The dense orthorhombic-II phase (isostructural with cotunnite) is of particular interest because it can be quenched to ambient conditions [163].

The relative stability of ZrO$_2$ phases can be influenced by the crystallite size. It is well known that small zirconia particles suspended in a host matrix do not transform from tetragonal to monoclinic, even well below the bulk transition temperature unless subjected to an external stress field or heating above 700 $^\circ$K [164, 165]. Moreover, Wang et al. [112] have found that tetragonal zirconia can be obtained in particles with sizes below 40 nm at room temperature. Structure studies [166] of ZrO$_2$ deposition on amorphous silica have shown that thin ZrO$_2$ film growth starting from the formation of an amorphous phase proceeds with the preferential growth of crystallites of tetragonal and cubic structures in the direction $[001]$. Structure analysis of the fabricated: ZrO$_2$-based NT-ZNT also gives evidence that the small particle size may stabilize the virtually unstable phases. This means that ZNT can possess cubic, tetragonal or orthorhombic morphology. It should also be noted that the additional tetragonal, orthorhombic, and hexagonal phases of ZrO$_2$ have also been reported at high pressures and/or high temperatures [162, 167, 168].

We now proceed to consider in more detail the first-principles calculations [151] of bulk zirconia, ZrO$_2$ sheets and nanotubes. The hybrid exchange-correlation functional PBE0 within LCAO approximation has been employed to investigate the properties of ZrO$_2$ nanotubes constructed from different zirconia polymorphs, in an attempt to understand the relation between bulk zirconia atomic structure and the stability of zirconia nanotubes. Thin sheets generated from cubic, tetragonal and monoclinic phases as the precursors to nanotubes have been considered.

As the first step, the study was started with calculations of the structure and properties of the corresponding bulk crystals. At the same time, these crystals play a role of benchmark systems for testing the applicability of the computation method selected. Further, the calculations [151] demonstrated that one of the sheets considered was reconstructed to a cotunnite-type layer. Because of this, the high-pressure orthorhombic-II phase was appended to the set of three low-pressure phases. For similar reasons, the rutile-like hypothetical phase of ZrO$_2$ was calculated in [169]. The hypothetical anatase-like phase of ZrO$_2$ was studied in [169] primarily because of the prospective comparison with TiO$_2$ nanotubes.

The CRENBL effective small-core pseudopotential was adopted in [151] for the Zr atom [170]. This pseudopotential replaces only inner core electrons, whereas sub-valence electrons (4s and 4p in Zr case), as well as valence electrons, are calculated self-consistently. To prevent quasi-linear dependences, diffuse exponents less than 0.1 a.u. were removed from the original [170] basis and the exponents of other polarization functions were re-optimized for the periodic calculations. Oxygen atoms were treated with an all-electron basis [171]. Reciprocal space integration was performed by sampling the Brillouin zone of the cubic crystal with the 12 $\times$ 12 $\times$ 12 Monkhorst Pack mesh [25], which was reduced inversely to the cell constants in other periodical systems to provide approximately uniform k-point spacing. The lattice parameters and fractional positions of all the atoms in the systems considered were fully optimized. Ionic and cell relaxations were performed until the rootmean- square forces on the atoms were less than 0.003 eV/Å  in the bulk and slab systems, and less than 0.03 eV/Å in the nanotubes.

In Table 7.29 we compare the calculated properties of four ZrO$_2$ phases with the experimental data. As follows from this table, the theoretical structure parameters differ from the experimental estimations by (1 %) or less. The values reported are of a better quality than those obtained in other works [155, 159] using the DFT(GGA) exchange-correlation functional. Calculations [151] also reproduce the cohesion and relative energies of the different phases. The bulk moduli values were obtained via the Birch Murnaghan third-order equation of state, and they are in agreement with both the experimental and theoretical results. Table 7.29 also reports the values of the band gap, which, as expected, are much better reproduced using the hybrid exchange—correlation functional compared the plain GGA.

Table 7.29 Calculated and experimental$^\mathrm{{a}}$ properties of monoclinic, tetragonal, cubic, and orthorhombic ZrO$_2$ phases [151]

Table 7.30 Relaxed strucure and stability$^\mathrm{{a}}$ of ZrO$_2$ thin sheets generated from different bulk phases [151]

3.2 Structure and Stability of ZrO$_2$ Sheets

Thin sheets of zirconia exhibit a variety of structures because of the existence of several crystalline bulk polymorphs. We consistently consider cubic, tetragonal, and monoclinic faces with different (low) crystallographic indexes. A hypothetical zirconia tetragonal phase with anatase structure was also included in our consideration just for the purpose of comparison of ZrO$_2$ and TiO$_2$ nanotubes with anatase morphology. In each case the stoichiometric slabs consisting of 212 atomic planes with a thickness of 26 Å  were constructed by cleaving the bulk crystals. Oxygen-terminated slabs were chosen whenever it was possible. It is known [164] that metallic terminations, as a rule, make the surface unstable to oxidation or to strong reconstruction. We do not consider non-stoichiometric slabs, so our 2D unit cells consist of an integer number of ZrO$_2$ formula units, as well as 1D cells of the subsequent NTs. All the surface layers were allowed to relax. There were several cases where the reconstructed structures of nanolayers generated from different phases or with different indices became identical. Consequently, the final number of unique 2D structures proved to be less than the total number of the surfaces considered.

The calculated surface energies and formation energies of the relaxed slabs are given in Table 7.30 together with the corresponding structural information. When calculating the formation energy, the values of E$_{bulk}$, n$_{bulk}$ for the low-temperature monoclinic phase were used in most cases. When calculating the formation energy the following notations were used: p. xxx l n, where p is the first letter of the parent phase, xxx is the Miller index, l is the type of 2D lattice (r rectangular, c centered rectangular, s square, h hexagonal), and n is the number of ZrO$_2$ layers after slab relaxation or reconstruction.

Fig. 7.45

Relaxed or reconstructed structure of nanosheets cut from the cubic ZrO$_2$ crystal parallel to the (110) face viewed along the $[\overline{1}10]$ direction. a c110r2—relaxed bilayer; b c110r3—1 $\times$ 1 reconstructed trilayer with rutile morphology; and c c110r4—1 $\times$ 1 reconstructed tetralayer. Large light balls, O atoms; small dark balls, Zr atoms; black lines, 2D unit cell boundaries

The cubic crystal has three types of nonequivalent low index surfaces: (001), (110), and (111). However, it is clear that the first one is just a special case of the (001) surface for the less symmetric tetragonal phase. So, the last two faces were only considered in [151]. Each atomic (110) plane includes two O atoms per one Zr atom per 2D unit cell, so any number of (110) planes provides the correct stoichiometry. The single-plane sheet was excluded from the consideration because its formation energy was too high. The final relaxed or reconstructed structures of slabs consisted of 2, 3, and 4 atomic planes, as shown in Fig. 7.45. During the optimization of the (110) slab the top oxygen atoms move outward, the top zirconium atoms move inward, and the number of atomic planes is thus redoubled. The relaxation of the two-plane slab is limited to the displacements mentioned (Fig. 7.45a). However, after the initial D$_{2h}$ (Pmmm) symmetry was removed, a deeper relaxation of the three-plane slab was found. The final structure of a 3-layer slab (Fig. 7.45b) includes nine atomic planes and it resembles the relaxed (100) rutile surface slab with the top bridging oxygens [105]. The 4-plane slab also obeys a considerable reconstruction. If the initial Pmmn symmetry is preserved, it spontaneously splits into two separated 2-layer slabs. However, after the initial symmetry is removed, the two upper layers shift along the $[001]$ direction by approximately one fourth of the period, thus facilitating the restoration of ZrO bonds between the two middle ZrO$_{2}$ layers (Fig. 7.45c). The resulting 8-plane slab has low surface and formation energies (see Table 7.30). The 2D lattice of the (111) slabs (Fig. 7.46) has a well-known hexagonal symmetry (P$\overline{3}$m1). The zirconium atom is 6-fold coordinated in a 3-plane slab (c111h1), while in a 6-plane slab (c111h2) it is bonded to an additional O atom in the next layer. According to the data in Table 7.30, the hexagonal layers have low formation and surface energies. They are compact, very stable, and not reconstructed even if the symmetry constrains are totally removed. The ionic relaxations are small and confined to the outmost O planes.

Fig. 7.46

Relaxed structure of nanosheets cut from the cubic ZrO$_2$ crystal parallel to the (111) face viewed along the $[\overline{1}10]$ direction. a c111h1—relaxed monolayer and b c111h2—relaxed bilayer. See Fig. 7.45 for labeling

Fig. 7.47

Relaxed structure of nanosheets cut from the tetragonal ZrO$_2$ crystal parallel to the (001) face viewed along the $[100]$ direction. a t001s1—relaxed monolayer and b t001r2—relaxed bilayer with lepidocrocite morphology. See Fig. 7.45 for labeling

Among the five low-index tetragonal-phase surfaces, (100), (001), (110), (101), and (111), the second and third ones can only be used for generating the proper thin sheets which have not been coincided previously. The last low-symmetry surface (111) has an oblique 2D lattice, so it is not suitable for NT rolling [119, 182]. It has been found that the thin slabs created from (100) and (101) t-ZrO$_2$ faces relax to the slabs generated from (110) and (111) cubic ZrO$_2$ faces, correspondingly. The relaxation of a (001) 3-plane sheet resulted in a simple structure with a square 2D lattice belonging to the P $\overline{4}$m2 layer group (Fig. 7.47a). The undercoordination of the Zr atom in this monolayer structure (its coordination number is 4) provides large formation and surface energies, making this structure unfavorable (see Table 7.2). The adjoining of two layers together into a 6-plane slab improves the structure considerably because of the increase of the Zr coordination number up to 6 (Fig. 7.47b). Moreover, the initially equal lattice constants become different upon the optimization. The final slab structure (Fig. 7.47b) has a rectangular 2D lattice, and it is identical to that of the layer in lepidocrocite-type laminated crystals, having low formation and surface energies (Table 7.30). The (110) slabs of the tetragonal zirconia consist of alternated Zr and O planes, so that the stoichiometric sheets must include an even number of atomic planes and their initial (bulk) structure would be polar and, therefore, unstable. During the optimization, the 2-plane (110) slab with an imposed Pba2 (originating from the bulk) symmetry converts to a single flat layer. After the symmetry constrains are removed, this slab transforms to a 3-plane hexagonal sheet which has been already considered for the cubic phase. The strongly reconstructed structure of the 4-plane slab is shown in Fig. 7.48a. The reconstruction of the 6-layer (110) slab was more surprising, and a compact 7-plane structure was obtained, as displayed in Fig. 7.48b. After structure analysis the conclusion was made that this nanolayer can really be attributed to the orthorhombic-II ZrO$_2$ phase. The individual optimization of a 3-plane (010) cotunnite nanosheet confirmed our supposition.

Fig. 7.48

1 $\times$ 1 reconstructed structure of nanosheets cut from the tetragonal ZrO$_2$ crystal parallel to the (110) face viewed along the $[001]$ direction. a t110r2—reconstructed bilayer and b t110r3—reconstructed trilayer with cotunnite morphology. See Fig. 7.45 for labeling

The orthogonality condition [119] is satisfied for (100), (001), (101), and ($\overline{1}$01) monoclinic faces. The monoclinic crystal was cleaved parallel to those faces to produce thin slabs with 6, 12, 12, and 12 atomic planes, correspondingly. These slabs provide the right connectivity and a sufficiently large Zr coordination number with having equal top and bottom O-terminated surfaces. However, only one pair, namely (100) and ($\overline{1}$01), was selected for further consideration. The 12-plane (001) slab is reconstructed into the lepidocrocite-type sheet considered above, while the (101) slab is converted into a 4-plane sheet obtained after the relaxation of the (110) slab cut from the cubic phase. The final relaxed structures of (100) and ($\overline{1}$01) nanosheets are shown in Fig. 7.49. Obviously, the first possesses a 6-plane bilayer structure, while the second consists of four Zr-planes and eight O-planes. However, some of the oxygen planes almost coincide, and the actual number of the oxygen layers in the relaxed structure is 6. The final structure can be considered as a pseudobilayer because it is impossible to split the oxygen planes in between the four ZrO$_2$ layers.

Fig. 7.49

Relaxed structure of nanosheets cut from the monoclinic ZrO$_2$ crystal. a m100r2—relaxed bilayer parallel to the (100) face viewed along the $[001]$ direction. b m$\overline{1}$01r2 relaxed pseudobilayer parallel to the ($\overline{1}$01) face viewed along the $[010]$ direction. See Fig. 7.45 for labeling

It follows from Table 7.30 that the compact hexagonal sheet c111h1 has the smallest surface energy. Previous results [164, 183–186] for the zirconia surface energies were based on the calculation of substantially thicker slabs; nevertheless, our values are basically in accordance with the prediction that the surfaces of the cubic and/or tetragonal phases are generally more stable than the monoclinic surfaces considered here. In works [102, 119, 120, 125, 187] titania nanotubes folded from slabs of different TiO$_2$ bulk phases were studied. It has been found that 1- and 2-TiO$_2$ layer slabs cut from (101) anatase surfaces can form NT with low formation and strain energies, as discussed in the next subsection. Whereas a 3-plane layer can be reconstructed easily to a sheet with hexagonal structure, the 6-plane bilayer preserves the modified anatase structure [119]. The ab initio modeling of TiO$_2$ nanosheets has been performed earlier by Vittadini and coworkers [121, 188]. In particular, they have established that two TiO$_2$-layer (001) anatase films rearrange to very stable lepidocrocite- like nanosheets. To compare zirconia- and titania-based nanotubes, we include the zirconia 6-plane sheet with anatase structure (a101c2) in this consideration (see Table 7.30). This zirconia nanosheet possesses rather high formation energy of 147 kJ/mol in contrast to that of 71 kJ/mol for similar titania nanosheet [120]. In the last column of Table 7.30 we list the electronic band gaps, E$_g$, in the calculated structures. In most cases, E$_g$ is lying in the interval from 6 to 7 eV, and it is greater than the band gap in the parent bulk phase (see Table 7.29). The only exception is the sheet t110r2, for which E$_g$ $=$ 3.8 eV. By the way, we could not identify the parent bulk phase for this extremely reconstructed structure. We found the maximal Eg value (6.9 eV) in the lepidocrocite-like structure, t001r2, to be greater by 1 eV than that in the tetragonal ZrO$_2$ crystal.

3.3 ZrO$_2$ Nanotubes

The knowledge of the layer symmetry group of the precursor sheet (see Table 7.30) allows one to find the line group symmetry of nanotubes rolled up with different chiralities, see Chap. 2. The initial structures of the nanotubes considered in [151] were obtained by rolling up the relaxed or reconstructed ZrO$_2$ thin sheets discussed previously. The precursor sheets form 2D lattices consisting of three types: primitive rectangular (c110r2, c110r3, c110r4, t001r2, t110r3, m100r2, m$\overline{1}$01r2), centered rectangular (a101c2), and hexagonal (c111h1, c111h2). Different ZNT chiralities compatible with the 2D lattice of the listed nanosheets were considered in [151]. The nanosheets t110r2 and t001s1 were excluded from further consideration because of their large formation energy.

Two chiralities are possible for the commensurate NTs folded from simple or centered rectangular lattices: (n,0) and (0,n), or (n,n) and ($-$n,n), respectively [119, 120]. In the case of the hexagonal lattice, the study was restricted to the achiral NTs, (n,0) and (n,n). The line group symmetry and its family can be found for each initial NT structure using Table 2.10.

A bulk monoclinic phase has been used as the reference state for the NTs formation energy calculation just as it was done for nanolayers.

Atomic planes in slabs are transformed to atomic shells (cylinders) in tubes upon folding. The inner and outer shells undergo stress due to the stretching or shrinking of the interatomic distances in the initial relaxed slab. The smaller the tube diameter and the thicker the tube wall the larger is the strain. The most critical is the repulsion between the nearest oxygen atoms in the inner shells. Because of the shrinking, the distance between the O atoms may become less than 2.72$\,\times \,$5 Å, thus leading to a considerable increase in repulsion. The inner and outer shells are strained in opposite directions, and reducing tension in the former may increase the tension in the latter. As a result, for any chirality and tube wall thickness w, there exists a minimum diameter d below which the NT becomes unstable and undergoes spontaneous destruction. For example, if we assume that $\delta$ is the maximal linear strain admissible for the layer, we can easily obtain the condition: $\delta \,\ge$ w/d. This means that the ratio w/d should have an upper limit $\delta$ for each NT type folded from a single slab. Nanotubes having w/d above this limit should possess a multi-walled structure or polygonal morphology. In this discussion we consider NTs of sufficiently large diameters (w/d $\le$ 0.2) with wall thicknesses of 2–7 Å to exclude the instability mentioned. To reduce the number of calculated NT structures the stability of different NTs at a constant total number (288) of atoms was examined. In each case the positions of all the atoms were optimized to obtain the most stable ZNT structure, preserving only the rototranslational symmetry. The resulting structural parameters, formation and strain (rolling) energies of the nanotubes are given in Table 7.31. Additionally, the selected ZNTs were recalculated at an approximately equal diameter of about 40 Å (Table 7.32). In Table 7.32, instead of the formation energies we listed the NT surface energies estimated by the equation:

$$\begin{aligned} E_{surf} = (E_{NT} -n_{NT}E_{bulk}/n_{bulk})/S_{NT};S_{NT}=\pi l(d_{in}+d_{out})=2\pi ld \end{aligned}$$

(7.3)

where l and d are the period and the average diameter of the nanotube, correspondingly. The external (d $_{out}$) and internal (d $_{in}$) diameters of the NTs were estimated as the double distance from the NT axis to the most remote or to the nearest atom (in almost all of the NTs above considered the most remote and the nearest atoms were oxygens). Therefore, the NT surface area (S $_{NT}$) depends on the NT average diameter and period only. Consequently, E$_{surf}$ is insensitive to the exact definition of the radii of the NT cylindrical surfaces. The last columns of Tables 7.31 and 7.32 demonstrate the electronic band gaps in the ZNT considered. Mostly, these values are only slightly (by 0.10 – 0.2 eV) less than the values in the appropriate slabs because of the sufficiently large NT diameters. In the case of ZNTs based on c110r4 and t001r2 slabs, the reduction is greater: 0.4–1.1 eV. Low—energy tubes with fluorite and lepidocrocite morphology exhibit maximal E$_g$ values. However, no overall correlation was found between the band gap and the formation energy.

Table 7.31 Relaxed structure, symmetry and stability of ZNT’s consisting of 96 ZrO$_2$ formula units, [151]

Table 7.32 Relaxed structure$^\mathrm{{a}}$, stability and band gaps of selected ZNT’s with an average diameter of about 40 Å [151]

To simplify the analysis of the data obtained, it is possible assume that all the ZNTs considered can be divided into three groups according to their wall thickness: (1) tubes with a wall thickness of 23 Å; (2) tubes with a wall thickness of 35 Å; and (3) tubes with a wall thickness of 57 Å. The first group includes ZNTs with thin walls consisting of 36 atomic shells (one or two compact ZrO$_2$ shells), while the last one includes relatively thick ZNTs with walls consisting of 79 atomic shells (three or four ZrO$_2$ shells). The tube walls for the middle group generally contain 6 atomic shells (two ZrO$_2$ shells), except for c110r3 (n,0) and m$\overline{1}$01r2, where the number of atomic shells is greater, but the intershell distance within the ZrO$_2$ layers is smaller.

The first group contains one type of NT folded from the rectangular 2D lattice (c110r2), one type folded from the centered rectangular 2D lattice (a101c 2), and one type folded from the hexagonal 2D lattice (c111h1). The tubes generated from the layers of cubic phase, c110r2 and c111h1, have relatively small formation and strain energies (Table 7.31). However, the data in Table 7.32 show that the tubes with hexagonal morphology (Fig. 7.50) are preferable at equal diameter. Thus, ZNTs with thin walls, if they really exist, are thought to have hexagonal morphology corresponding to the cubic zirconia phase.

The structure and energetics of nanotubes folded from TiO$_2$ hexagonal layers have been studied before ([102, 116, 118, 120, 187]). In particular, in previous works [102, 120, 187] the same computational approach was used. It was found that the structural optimization of the 3-plane TiO$_2$ slabs cut from the anatase phase resulted in a spontaneous (barrierless) reconstruction to the hexagonal (111) fluorite structure. Thus, hexagonal morphology is also preferable for NTs folded from a TiO$_2$ monolayer. In Table 7.33 we compare the results obtained for some tinania and zirconia nanotubes. The strain energies of TNTs reported in [102, 120, 187] are nearly two times larger than those derived here for ZNTs with an equal chirality. This means that ZNTs are more stable than TNTs relative to the precursor nanosheets.

However, the formation and surface energies of the hexagonal ZrO$_2$ monolayer slab (see Table 7.30) are considerably greater than the corresponding energies for the hexagonal TiO$_2$ monolayer slab (E$_{form}$ = 47 kJ/mol, E$_{surf}$ = 0.44 J/m$^2$). Consequently, E$_{form}$ (ZNT) is greater than E$_{form}$(TNT), and ZNTs with monolayer walls should be less stable than similar TNTs relative to the parent bulk phases.

Zirconia nanotubes with anatase morphology belong to the first group possessing a wall thickness below 3 Å. Analogous titania nanotubes generated from 6-planes (101) anatase sheets were modeled in works [119, 120, 125]. Calculation results are given in Table 7.32 for ZNT a101c2 with chirality (12,12). Such chirality was found to be more favorable for TNTs [120, 125].

Comparison of similar ZNT and TNT leads to the same conclusions that were made for NTs with hexagonal morphology (see Table 7.33). Supposedly, E$_{form}$ $\approx$150 kJ/mol is too high for the potential existence of anatase-type ZNTs in spite of their low strain and surface energy.

Fig. 7.50

A cross-section of the relaxed structure of zirconia nanotubes folded from the hexagonal monolayer c111h1. a With chirality (30,0) and b with chirality (18,18). See Fig. 7.45 for labeling

Table 7.33 Comparison of stability for selected TNTs and ZNTs with an average diameter of about 40 Å

The second group includes nanotubes of different structure with a wall thickness of 45 Å. Among the ZNTs generated from the cubic phase, only the 6-shell tube of type c111h2 with hexagonal morphology and chirality (n,n) has a relatively low formation energy and the medium strain energy. During the relaxation of the NT c111h2 (20,20), the average diameter increases considerably from 38 to 41 Å. This leads to the stretching of Zr O bonds up to their break on the outward NT surface. As a result, one sees a noticeable increase in the strain energy for a 6-shell NT with hexagonal morphology compared to a similar 3-shell NT. On the other hand, nanotubes t001r2 (n,0) generated from the tetragonal phase with lepidocrocite morphology (Fig. 7.51a) have approximately the same stability, although their strain energy is half the strain energy of c111h2 (n,n) with an equal diameter (see Table 7.32). For this reason, nanotubes with lepidocrocite structure are more preferable among other ZNTs with a wall thickness of 45 Å. As was stated above, TiO$_2$-layer anatase (001) films, consisting of two layers, rearrange into stable lepidocrocite-like layers [188]. Szieberth et al. [127] investigated the structure and energy of TiO$_2$ nanotubes with lepidocrocite morphology using a computational method which is very close to ours. Some systems were recalculated in [151] with other basis sets and gave identical results, see Table 7.33. The designated NT chirality corresponds to the choice of a and b slab vectors (see Table 7.30). The values obtained show that titania (n, 0) NTs with lepidocrocite morphology have almost the same strain energies as were found for the equivalent ZNTs. Similar to the hexagonal and anatase cases (see above), the formation energies of t001r2 (n,0) ZNTs are two times larger than the formation energies of the lepidocrocite-like TNTs.

Fig. 7.51

A cross-section of the relaxed structure of zirconia nanotubes folded from the bilayers with a wall thickness of 4–5 Å. a Using nanosheet t001r2 with lepidocrocite morphology with chirality (18,0) and b using nanosheet m$\overline{1}$01r2 with baddeleyite morphology with chirality (12,0). See Fig. 7.45 for labeling

Tubes generated from the monoclinic (baddeleyite) phase have the formation energy close to 150 kJ/mol, and consequently they are less stable than the two above-mentioned. Nevertheless, one of these ZNTs (Fig. 7.51b), namely m$\overline{1}$01r2 (n,0), may be interesting due to its flexible structure and low strain energy.

The walls with a width of 5 Å or thicker are attributed to the ZNT based on c110r4, c110r3, and t110r3 nanolayers. Presumably, the computational results for such tubes are more important. Nanotubes based on c110r4 consist of eight atomic shells and have a large strain and/or formation energy (see Table 7.31). The relatively small formation and strain energies pertain to 9-shell (with rutile morphology) and 7-shell (with cotunnite morphology) tubes with chirality (0,n). These ZNTs are depicted in Fig. 7.52a, b, respectively. The low strain energy of the first one is probably due to a spring-like ZrO bond arrangement, which provides a soft expansion and shrinking of the surface layers during the structure relaxation. The structure of the second ZNT consists of two ZrO$_2$ layer blocks connected with flexible one ZrO$_2$ layer sectors (see t110r3 slab structure in Fig. 7.48b). This explains the low strain energy of the ZNT with cotunnite morphology. Both types of tubes can be proposed as models for NT with a wall thickness greater than 5 Å, although the relatively high formation energy of those tubes ($\approx$120 kJ/mol) should be kept in mind. Presumably, further calculations of zirconia multi-walled and/or polygonal nanotubes are needed to make more realistic the comparison between the theoretical and experimental results.

Fig. 7.52

A cross-section of relaxed structure of zirconia nanotubes folded from the trilayers with wall thickness of 5–7 Å. a Using nanosheet c110r3 with rutile morphology with chirality (0,24) and b using nanosheet t110r3 with cotunnite morphology with chirality (0,16). See Fig. 7.45 for labeling

Upon relaxation, the enlargement of the initial diameter of the nanotubes considered is small, except for the above-mentioned case of ZNT c111h2, where the internal strain leads to a substantial nanotube expansion. Relaxation of the ZNT obtained from a t110r3 sheet results in a small reduction of diameter. Insignificant diameter change indicates that relaxation does not displace the atoms considerably from their positions just after folding for tube diameters of 40 Å and above, with a wall thickness less than 7 Å. This conclusion is confirmed by comparing the surface energy of the nanotubes with the surface energy of the corresponding thin films: the proximity of these values proves the principal role of the parent nanolayer structure.

The dependence of the strain energy on the tube average diameter is plotted in Fig. 7.53 for the ZNTs discussed above. It is seen that most of the selected ZNTs have low E$_{str}$ at diameters d $>$ 25. The difference in the strain energies of fluorite-type ZrO$_2$ monolayer tubes with chiralities (n,n) and (n,0) is quite negligible, thus supporting the similar results obtained earlier [102] for titania nanotubes folded from hexagonal layers.

Three ZrO$_2$-layer tubes with rutile (c110r3) morphology provide the smallest strain energy. The curves for tubes with baddeleyite (m-101r2) and cotunnite (t110r3) morphology lie slightly above. The strain energy dependence jumps down for cotunnite-type tubes at d $<$ 24 Å due to an increase of the Zr atom coordination number from 5 to 6 on the innermost tube surface. The tubes with two ZrO$_2$-layer walls (at lepidocrocite and hexagonal morphology) have a greater value of E$_{str}$ than that for other cases depicted in Fig. 7.53. However, we can suppose that the importance of lepidocrocite-like structure should increase in multiwall nanotubes because of its laminate nature and low formation energy. This assumption needs examination in the subsequent calculations.

Fig. 7.53

Strain energy dependence on the average diameter for selected zirconia nanotubes (see text for nanotube labels)

Let us summarize the most important conclusions made in [151] basing on the results of the first-principles zirconia nanotubes calculations.

It has been found that the formation energy of ZrO$_2$ nanotubes with a sufficiently large diameter is mainly determined by the formation energy of the corresponding nanosheet.

The proximity of the nanotube surface energy to the surface energy of the corresponding thin films confirms the principal role of the parent nanolayer structure. As a rule, the nanotube strain energy is positive and decreases with enlarging diameter. Several factors can contribute to the increase of the strain energy at relatively small nanotube diameters: (1) steric obstacles upon folding, especially those caused by repulsion between the nearby-base NT calc oxygen atoms in the inner tube shells; (2) shrinking of the chemical bonds in the inner tube shells, and (3) stretching or breaking of chemical bonds in the outer tube shells due to their expansion. The potential flexibility of the chemical bond network in the parent sheet helps to reduce the contribution of the factors listed.

The analysis of nanotube formation and strain energies has determined that the most stable tubes with thin (one ZrO$_2$ layer) walls should have hexagonal morphology corresponding to the rolling of (111) sheets from the cubic fluorite phase. The tubes with walls composed of two ZrO$_2$ layers presumably have lepidocrocite morphology. The tubes with thicker walls can possess a different structure originating from cubic, tetragonal or orthorhombic phases. The lowest strain energy has been derived for a nanotube with rutile morphology exhibiting zigzag ZrO bond arrangement.

The comparison of zirconia-based and titania-based nanotubes shows that the former may have smaller strain energies, while the latter may have smaller formation energies relative to the stable bulk phases. One can suppose that the formation energy is a more fundamental quantity than the strain (or rolling) energy to collate the nanotubes with different chemical composition, since the former includes the latter as its part. From this point of view, titania-based single-walled nanotubes can be obtained more easily than zirconia-based single-walled nanotubes. This conclusion is in accordance with the fact that synthesized titania nanotubes may have thinner walls than those observed in the fabricated zirconia nanotubes.