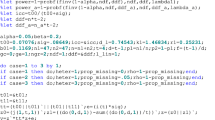
Abstract
In this chapter, an overview is given of different methods to analyse data from a randomised controlled trial (RCT) with more than one follow-up measurement. For a continuous outcome variable, a classical GLM for repeated measurements can be used to analyse the difference in development over time between the intervention and control group. However, because GLM for repeated measurements has some major disadvantages (e.g., only suitable for complete cases), it is advised to use more advanced statistical techniques such as mixed model analysis or Generalised Estimating Equations (GEE). The biggest problem with the analysis of data from an RCT with more than one follow-up measurement is the possible need for an adjustment for baseline differences. To take these differences into account a longitudinal analysis of covariance, an autoregressive analysis or a ‘combination’ approach can be used. The choice for a particular method depends on the characteristics of the data. For dichotomous outcome variables, an adjustment for baseline differences between the groups is mostly not necessary. Regarding the more advanced statistical techniques it was shown that the effect measures (i.e. odds ratios) differ between a logistic mixed model analysis and a logistic GEE analysis. This difference between these two methods was not observed in the analysis of a continuous outcome variable. Based on several arguments (e.g., mathematical complexity, unstable results, etc.), it was suggested that a logistic GEE analysis has to be preferred above a logistic mixed model analysis.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Randomise Control Trial
- Generalise Linear Model
- Correlation Structure
- Recurrent Event
- Longitudinal Analysis
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
10.1 Introduction
Randomized controlled trials (RCT’s) are considered to be the gold standard for evaluating the effect of a certain intervention [10]. In a randomized controlled trial, the population under study is randomly divided into an intervention group and a non intervention or control group (e.g., a placebo group or a group with ‘usual’ care). Regarding the analysis of RCT data a distinction must be made between studies with only one follow-up measurement and studies with more than one follow-up measurement. When there is only one follow-up measurement relatively simple statistical techniques can be used to evaluate the effect of the intervention, while when more than one follow-up measurement is considered, in general, more advanced statistical techniques are necessary.
In the past decade, an RCT with only one follow-up measurement has become very rare. At least one short-term follow-up measurement and one long-term follow-up measurement ‘must’ be performed. However, more than two follow-up measurements are usually performed in order to investigate the ‘development over time’ of the outcome variable, and to compare the ‘developments over time’ among the intervention and control group. Sometimes these more complicated experimental designs are analysed with simple cross-sectional methods, mostly by analysing the outcome at each follow-up measurement separately, or sometimes even by ignoring the information gathered from the in-between measurements, i.e. only using the last measurement as outcome variable to evaluate the effect of the intervention. Besides this, summary statistics are often used. The general idea behind a summary statistic is to capture the longitudinal development of an outcome variable over time into one value; the summary statistic. With a relative simple cross-sectional analysis these summary statistics can be compared between the intervention and control group in order to analyse the effect of the intervention. One of the most frequently used summary statistics is the area under the curve (AUC) [14]. However, nowadays mostly more advanced statistical methods such as mixed model analysis or generalised estimating equations (GEE analysis) [8, 19] are used to analyze RCT data with more than one follow-up measurement. In this chapter, the different methods will be discussed by using an example dataset in which the effect of a new therapy (i.e. intervention) for low back pain is evaluated. The example dataset is a manipulated dataset from an RCT in which patients who seek care in a private physical therapy clinic with low back pain as primary complaint were included. Besides a baseline measurement, three follow-up measurements were performed at 6, 12 and 18 months respectively. In the present example, two outcome variables will be considered: one continuous outcome variable and one dichotomous outcome variable. The continuous outcome variable is a score on a questionnaire aiming to measure complaints, while the dichotomous outcome variable reflects whether the patient is recovered or not; this is based on subjective self-report.
10.2 Continuous Outcome Variables
Table 10.1 shows descriptive information for both the intervention and control group at baseline and at the three follow-up measurements.
10.2.1 Generalised Linear Model (GLM) for Repeated Measurements
Although GLM for repeated measurements can not be seen as a new (more advanced) statistical technique to analyse longitudinal data, it can be used to analyse a continuous outcome variable measured in an RCT with more than one follow-up measurement. The basic idea behind GLM for repeated measurements (which is also known as (multivariate) analysis of variance ((M)ANOVA) for repeated measurements) is the same as for the well known paired t-test. The statistical test is carried out for the T − 1 absolute differences between subsequent measurements. In fact, GLM for repeated measurements is a multivariate analysis of these T − 1 absolute differences between subsequent time-points. Multivariate refers to fact that T − 1 differences are used simultaneously as outcome variable. Besides the ‘multivariate’ approach, the same research question can also be answered with a ‘univariate’ approach. This ‘univariate’ procedure is comparable to the procedures carried out in simple analysis of variance (ANOVA) and is based on the ‘sum of squares’, i.e. squared differences between observed values and average values. In most software packages, the results of both the ‘multivariate’ and ‘univariate’ approach are provided at the same time. From a GLM for repeated measurements with one dichotomous determinant (i.e. intervention versus control), basically three ‘effects’ can be derived [14]. An overall time-effect (i.e. is there a change over time, independent of the different groups), an overall group effect (i.e. is there a difference between the groups on average over time) and, most important, a group*time interaction effect (i.e. is there a difference between the groups in development over time). Table 10.2 shows the results of a GLM for repeated measurements performed on the example dataset, while Fig. 10.1 shows the so called ‘estimated marginal means’ resulting from the GLM for repeated measurements.
From Table 10.2 it can be seen that there is an overall time effect, an overall intervention effect but no intervention*time interaction effect. From Fig. 10.1 (and also from Table 10.1), however, it can be seen that the baseline values of both groups are different. This is a problem that often occurs in RCT data which should be taken into account in the analysis evaluating the effect of the intervention. Different baseline values for the therapy and the control group causes ‘regression to the mean’. If the outcome variable at a certain time-point t = 1 is a sample of random numbers, and the outcome variable at the next time-point t = 2 is also a sample of random numbers, then the subjects in the upper part of the distribution at t = 1 are less likely to be in the upper part of the distribution at t = 2, compared to the other subjects. In the same way, the subjects in the lower part of the distribution at t = 1 are less likely than the other subjects to be in the lower part of the distribution at t = 2. The consequence of this is that, just by chance, the change between t = 1 and t = 2 is correlated with the initial value. For the group with higher baseline values, a decrease in the outcome variable is much easier to achieve than for the group with the lower baseline value. It is clear that this problem arises in the analysis of the example dataset. Therefore, the consequence is that when the intervention group and control group differ at baseline, a comparison of the changes between the groups can lead to either an overestimation or an underestimation of the intervention effect [15].
There is, however, a nice way to adjust for the phenomenon of regression to the mean. This approach is known as ‘analysis of covariance’. With this technique the value of the outcome variable Y at the second measurement is used as outcome variable in a linear regression analysis, with the observation of the outcome variable Y at the first measurement as one of the covariates:
where Y it2 = observations for subject i at time-point t = 2; β 1 = regression coefficient for Y it1; Y it1 = observations for subject i at time-point t = 1; β 2 = regression coefficient for X i ; X i = intervention variable and \(\varepsilon _{i} =\) error for subject i.
In the analysis of covariance, the change is defined relative to the value of Y at t = 1. This relativity is expressed in the regression coefficient β 1 and, therefore, it is assumed that this method adjusts for the phenomenon of regression to the mean. In fact the effect of the intervention is evaluated assuming the same baseline value for both groups. The same idea can be used in a GLM for repeated measurements; i.e. the analysis can be adjusted for the baseline value. This approach is also known as (M)ANCOVA for repeated measurements. Table 10.3 and Fig. 10.2 show the results of a GLM for repeated measurements adjusting for the baseline value performed on the example dataset.
Although GLM for repeated measurements is often used, it has a few major drawbacks. First of all, it can only be applied to complete cases; all subjects with one or more missing observation are not part of the analyses. Secondly, GLM for repeated measurements is mainly based on statistical significance testing, while there is more interest in effect estimation. Because of this, nowadays, new more advanced statistical techniques, such as mixed model analysis and GEE analysis are mostly used.
10.2.2 More Advanced Analysis
The questions answered by a GLM for repeated measurements could also be answered by more advanced methods, such as mixed model analysis and GEE analysis [14]. The advantage of the more advanced methods is that all available data is included in the analysis, while with GLM for repeated measurements only those subjects with complete data are included. Another important advantage of the more advanced analyses is that they are basically regression techniques, from which the effect estimates (i.e. the magnitude of the effect of the intervention) and the corresponding confidence intervals can be derived.
The general idea behind all statistical techniques to analyse longitudinal data is that because of the dependency of observations within a subject an adjustment must be made for ‘subject’. The problem, however, is that the variable ‘subject’ is a categorical variable that must be represented by dummy variables. Suppose there are 200 subjects in a particular study. This means that 199 dummy variables are needed to adjust for subject. Because this is practically impossible, the adjustment for ‘subject’ has to be performed in a more efficient way and the different longitudinal techniques differ from each other in the way they perform that adjustment [14].
Mixed model analysis is also known as multilevel analysis [4, 13], hierarchical linear modeling or random effects modeling [6]. As has been mentioned before, the general idea behind all longitudinal statistical techniques is to adjust for ‘subject’ in an efficient way. Adjusting for ‘subject’ actually means that for all subjects in the longitudinal study, different intercepts are estimated. The basic principle behind the use of mixed model analysis in longitudinal studies is that not all separate intercepts are estimated, but that (only one) variance of those intercepts is estimated, i.e. a random intercept. It is also possible that not only the intercept is different for each subject, but that also the development over time is different for each subject, in other words, there is an interaction between ‘subject’ and time. In this situation the variance of the regression coefficients for time can be estimated, i.e. a random slope for time. In fact, these kind of individual interactions can be added to the regression model for all covariates. In a regular RCT, however, assuming a random slope for the intervention effect is not possible, because the intervention variable is time-independent [13]. When a certain subject is assigned to either the intervention or control group, that subject stays in that group along the intervention period. An exception is the cross-over trial, in which the subject is his own control and the intervention variable is time-dependent. In this situation the intervention effect can be different for each subject and therefore a random slope for the intervention variable can be assumed. For mixed model analysis, one has to choose which coefficients have to be assumed random. This choice can be based on the result of a likelihood ratio test.
Within GEE, the adjustment for the dependency of observations is done in a slightly different way, i.e. by assuming (a priori) a certain ‘working’ correlation structure for the repeated measurements of the outcome variable [8, 19]. Depending on the software package used to estimate the regression coefficients, different correlation structures are available. They basically vary from an ‘exchangeable’ (or ‘compound symmetry’) correlation structure, i.e. the correlations between subsequent measurements are assumed to be the same, irrespective of the length of the measurement interval, to an ‘unstructured’ correlation structure. In this structure no particular structure is assumed, which means that all possible correlations between repeated measurements have to be estimated.
In the literature it is assumed that GEE analysis is robust against a wrong choice for a correlation structure, i.e. it does not matter which correlation structure is chosen, the results of the longitudinal analysis will be more or less the same [9, 12]. However, when the results of analysis with different working correlation structures are compared to each other, the magnitude of the regression coefficients are different [14]. It is therefore important to realize which correlation structure should be chosen for the analysis. Although the unstructured working correlation structure is always the best, the simplicity of the correlation structure also has to be taken into account. The number of parameters (in this case correlation coefficients) which needs to be estimated differs for the various working correlation structures. The best option is therefore to choose the simplest structure which fits the data well. The first step in choosing a certain correlation structure can be to investigate the observed within-person correlation coefficients for the outcome variable. It should be kept in mind that when analyzing covariates, the correlation structure can change (i.e. the choice of the correlation structure should better be based conditionally on the covariates).
Within the framework of the more advanced statistical techniques, several models are available to evaluate the effect of an intervention. In an RCT with more than one follow-up measurement, the simplest model that can be used is
where Y it = observations for subject i at time t; β 0 = intercept; β 1 = regression coefficient for X i ; X i = intervention variable and \(\varepsilon _{\mathit{it}} =\) error for subject i at time t.
With this model the outcome variable at the different follow-up measurements is compared between the therapy and control group simultaneously. This is comparable to the comparison of the post-test value between two groups in a pre-post test design. It should be noted that with this model, the influence of possible differences at baseline between the two groups is ignored. In the example dataset, however, it was seen that there is a (big) difference in baseline values between the intervention and control group and that this difference can cause regression to the mean. The intervention effect estimated with the standard model shown in (10.2), is therefore not correct. To adjust for differences at baseline, a longitudinal analysis of covariance can be used:
where Y i t = observations for subject i at time t; β 0 = intercept; β 1 = regression coefficient for X i ; X i = intervention variable; β 2 = regression coefficient for observation at t 0; Y it0 = observation for subject i at time t 0 and \(\varepsilon _{\mathit{it}} =\) error for subject i at time t.
The general idea behind a longitudinal analysis of covariance is that the outcome variable at each of the follow-up measurements is adjusted for the baseline value. The regression coefficient of interest, i.e. the regression coefficient for the intervention variable reflects the overall ‘adjusted’ difference between the intervention and control group over time.
Another possible way to analyse RCT data with more than one follow-up is to use a so-called autoregressive analysis. In an autoregressive analysis the outcome variable is not adjusted for the baseline value, but each measurement of the outcome variable is adjusted for the value of the outcome variable one time-point earlier:
where Y it = observations for subject i at time t; β 0 = intercept; β 1 = regression coefficient for X i ; X i = intervention variable; \(Y _{\mathit{it}-1} =\) observation for subject i at time t − 1; β 2 = regression coefficient for observation at t − 1 (autoregression coefficient) and \(\varepsilon _{\mathit{it}} =\) error for subject i at time t.
The idea underlying an autoregressive analysis is that the value of an outcome variable at each time-point is primarily influenced by the value of this variable one measurement earlier. To estimate the ‘real’ influence of the intervention variable on the outcome variable, the model should therefore adjust for the value of the outcome variable at time-point t − 1. In fact, with an autoregressive analysis, the ‘adjusted’ changes between subsequent measurements are compared between the therapy and the control group. Table 10.4 shows the results of the three analyses performed on the example dataset. For all analyses the results of both a mixed model analysis and a GEE analysis are shown.
From Table 10.4 it can first be seen that the results derived from a mixed model analysis and the results derived from a GEE analysis are more or less the same. Furthermore, it can be seen that the standard analysis gives a higher effect measure compared to the other two methods. This has to do with the fact that with the standard analysis, the differences at baseline between the intervention and control group are not taken into account. Because the intervention group has lower values all over the follow-up period, the intervention effect obtained from the standard analysis is overestimated. In the example dataset the differences between an analysis of covariance and an autoregressive analysis are small. Slightly higher effect estimates for the autoregressive analysis and slightly smaller 95 % confidence intervals.
Although the longitudinal analysis of covariance is mostly used, it is questionable whether or not this is correct. In fact, the adjustment for baseline for all the follow-up measurements can overestimate the overall therapy effect. This is especially true when the effect of the therapy is particularly found in the first part of the follow-up period [14]. In the present example this is not really the case, so therefore, the longitudinal analysis of covariance and the autoregressive analysis gave more or less the same results. It is sometimes argued that both analyses are not correct. This has to do with the fact that in a RCT only the differences at baseline are caused by chance. Differences between the groups at the follow-up measurements are probably mostly caused by the intervention and should therefore not be adjusted for. To take that into account, a so-called ‘combination’ approach is suggested [17]. In this ‘combination’ approach, the first follow-up measurement is adjusted for the baseline differences, but the next follow-up measurements are not adjusted anymore for either the baseline differences (as in the longitudinal analysis of covariance) or the value of the outcome one time-point earlier (as in the autoregressive analysis). Although this approach makes sense, it is not much used in practice.
Up to now, the more advanced analyses performed were aimed to estimate an overall intervention effect. Sometimes, however, one is more interested in the estimation of effects at the different follow-up measurements. This can be done in a simple way by performing separate analyses at the different follow-up measurements, either by comparing the change between the baseline measurements and the three follow-up measurements or by performing three separate analyses of covariance (see Tables 10.5 and 10.6).
As expected, the results derived from the analysis of change scores are totally different from the results derived from the analyses of covariance. This has to do with the fact that the analyses of change scores not adjust for the difference at baseline. The analyses of covariance take into account these differences and because the intervention group has a lower value for the outcome variable at baseline, the effect derived from analyses of covariance are much higher than the ones derived from the analyses of change scores. Performing separate analyses, however, is theoretically wrong because the separate analyses are highly dependent on each other. To obtain the separate effects in one analysis, time and the interaction between the intervention variable and time can be added to the longitudinal analysis of covariance and the autoregressive analysis.
Table 10.7 shows the results of the analyses performed on the example dataset in order to obtain the effects of the intervention at the three follow-up measurements.
From Table 10.7 it can be seen that the differences between the results obtained from a longitudinal analysis of covariance and the ones obtained from an autoregressive analysis are comparable to the differences between the two analyses in the estimation of the overall effect over time (see Table 10.4). Table 10.7 only shows the results from a mixed model analysis. It is obvious that the results obtained from a GEE analysis are comparable.
An approach to evaluate the effect of an intervention at different time-points is provided by Fitzmaurice et al. [3]. In this approach all measurements are used as outcome (including the baseline measurement). The following model (which is basically an extension of the standard model shown in (10.2)) is then used:
where Y it = observations for subject i at follow-up time t, β 1 = the regression coefficient for X i ; X i = intervention variable and time1, time2, time3 = dummy variables for time and \(\varepsilon _{\mathit{it}} =\) error for subject i at time t.
In this model, the β 1 coefficient reflects the differences between the two groups at baseline, β 1 +β 5 reflects the differences between the two groups at the first follow-up measurement, while β 1 +β 6 reflects the differences between the two groups at the second follow-up measurement and β 1 +β 7 the differences between the two groups at the third follow-up measurement. Although, this is a nice way of analysing the effect of the intervention at the different time-points, it does not adjust for the differences between the groups observed at baseline, or in other words, it does not adjust for possible regression to the mean.
An alternative approach to tackle this problem is to use the same model but without the intervention variable:
where Y it = observations for subject i at follow-up time t, X i = intervention variable and time1, time2, time3 = dummy variables for time and \(\varepsilon _{\mathit{it}}\) = error for subject i at time t.
Because the intervention variable is not in the model, the baseline values for both groups are assumed to be equal and are reflected in the intercept of the model (i.e. β 0). In this model, the coefficients of interest are the same as in the model with the intervention variable. The only difference is that now the effects of intervention at the different time-points are adjusted for the differences at baseline (Fig. 10.8).
The analyses based on (10.6) (i.e. the model without the intervention variable) are basically the same as a longitudinal analysis of covariance. The difference in the effect estimates between the two approaches is caused by a different number of observations (due to missing values). When the two analyses would have been performed on a full dataset without any missing values, the results of the two analyses would have been exactly the same.
Although longitudinal analysis of covariance is mostly used to analyse the effect of an RCT with more than one follow-up measurement one should be careful with the interpretation of the results of such an analysis. In some situations, it is better to use an autoregressive analysis. However, when differences at baseline occur between the groups, they must be taken into account in the analysis.
10.3 Dichotomous Outcome Variables
The statistical models used for the analysis of dichotomous outcome variables derived from an RCT with more than one follow-up measurement are somewhat less complex than the models discussed for the analysis of a continuous outcome variable. This has to do with the fact that in general an adjustment for differences in baseline values is not necessary, because all subjects have the same value at baseline (e.g. all subjects are not recovered). As has been mentioned before, the example dataset used in this section is derived from the same RCT that has been used in the example with a continuous outcome variable. However, in this section the outcome is dichotomous reflecting whether the patient is recovered or not. Table 10.9 shows the number of subjects recovered versus the number of subjects not recovered in the intervention and in the control group at the three follow-up measurements, while Fig. 10.3 shows the percentages over time for both groups.
The classical way to analyse the results of such an RCT is to analyse the difference in proportion of patients experiencing recovery between the intervention and the control group at each of the three follow-up measurements, by simply applying a Chi-square test. Furthermore, at each of the follow-up measurements, the effect of the intervention can be estimated by calculating the relative risk (and corresponding 95 % confidence interval). The relative risk is defined as the proportion of subjects recovered in the intervention group, divided by the proportion of subjects recovered in the control group [10]. Table 10.10 summarizes the results of the analyses.
From Table 10.10 it can be seen that the effect of the intervention at the first and second follow-up measurement is more or less the same, while at the third follow-up measurement the effect of the intervention is somewhat greater and also statistically significant.
It is, of course, also possible to estimate the effect of the intervention with a more advanced longitudinal technique. Because of the nature of the outcome variable, a logistic mixed model analysis or a logistic GEE analysis should be used instead of a linear mixed model analysis or a linear GEE analysis. It should be noted that for a dichotomous outcome variable GLM for repeated measurements is not possible. Furthermore, it should be realized that as a result of a logistic longitudinal analysis, odds ratios are calculated. Odds ratios are often interpreted as relative risks, but they are not the same. Owing to the mathematical background of the odds ratios and relative risks, the odds ratios are always an overestimation of the ‘real’ relative risk. This overestimation becomes stronger as the proportion of ‘cases’ (i.e. recovered patients) increases. To illustrate this, the odds ratios for intervention versus control were calculated at each of the follow-up measurements (see Table 10.11).
From the results in Table 10.11 it can be seen that the calculated odds ratios are bigger than the relative risks shown in Table 10.10, and that the confidence intervals are wider, but that the significance levels are the same. So, when a logistic GEE analysis is carried out, one must realize that the results (i.e. odds ratios) obtained from such an analysis cannot be interpreted as relative risks.
Table 10.12 presents the results of a logistic mixed model analysis and a logistic GEE analysis in which the average effect of the intervention over time is analysed.
The most intriguing finding regarding the comparison of the two analyses is that the odds ratio obtained from a logistic mixed model analysis is much higher compared to the odds ratio obtained from a logistic GEE analysis. This is not just a coincidence, but this has a theoretical background; i.e. the odds ratio obtained from a logistic mixed model analysis will always be bigger than the one obtained from a logistic GEE analysis.
Basically, both ‘longitudinal’ techniques take all measurements into account, and use a logistic regression approach with an adjustment for the dependency of the observations. This is done either by assuming a certain ‘working’ correlation structure (GEE analysis) or by allowing random regression coefficients (mixed model analysis). The difference between the two techniques is that GEE analysis is a so-called population average approach, while mixed model analysis is a so-called subject specific approach [14]. The different estimation procedures cause the difference in the magnitude of the odds ratios, which is always in favour of the mixed model analysis, i.e. the effects estimated with a logistic mixed model analysis are always bigger than the effects estimated with a logistic GEE analysis. Because the standard errors are also bigger for a logistic mixed model analysis (and therefore the 95 % confidence intervals are wider), the corresponding p-values are not much different and when conclusions are based on these p-values, they will be more or less the same. However, when the conclusions are based on the magnitude of the odds ratios, the conclusions will differ remarkably between the two techniques.
It should further be noted that the estimations of the regression coefficients (i.e. odds ratios) with logistic mixed model analysis can be very complicated and often lead to instable results. Furthermore, the results of these analyses can differ between software packages [7, 14, 18].
It is of course also possible to estimate the effects of the intervention at the three follow-up measurements in one analysis. This can be done in exactly the same way as has been described for continuous outcome variables, i.e. by adding dummy variables for time and the interaction between these dummy variables and the intervention variable to the model. Again, this is far less complicated as for a continuous outcome variable because in general an adjustment for differences in baseline values is not necessary.
Table 10.13 shows the results derived from a both a logistic mixed model analysis and a logistic GEE analysis.
From Table 10.13 it can be seen again that the odds ratios derived from a logistic mixed model analysis are much higher than the ones derived from a logistic GEE analysis. It can also be seen that the odds ratios derived from a logistic GEE analysis are much closer to the ones obtained from the three separate analyses than the odds ratios derived from a logistic mixed model analysis (Table 10.11). This suggests that regarding the more advanced longitudinal techniques, logistic GEE analysis has to be preferred above logistic mixed model analysis.
The data used in the present example is an example of ‘recurrent event’ data. To analyse ‘recurrent event’ data, also some other approaches are available. Based on a survival approach, Cox proportional hazards regression for recurrent events can be performed [5, 11, 16]. Although there are different estimation procedures available the general idea behind Cox proportional hazards regression for recurrent events is that the different time periods are analysed separately adjusted for the fact that the time periods within one patient are dependent. The idea of this adjustment is that the standard error of the regression coefficient of interest is increased proportional to the correlation of the observations within one subject. One of the problems using Cox proportional hazards regression for recurrent events for RCT data is that it is assumed that the events under study are short lasting, which means that after an event the particular subject is directly at risk to get another event. This assumption does not hold for most RCT’s, including the example RCT used in this chapter. Although the events can be recurrent, most of the events are long lasting. So in this situation, Cox proportional hazards regression for recurrent events is not very suitable.
There are also other possibilities to model recurrent events data, such as the continuous-time Markov process model for panel data [1] or the conditional frailty model [2]. However, most of those alternative methods are mathematically complicated and not much used in practice.
10.4 Discussion
In this chapter several methods were discussed that can be used to analyse data from an RCT with more than one follow-up measurement. The data of the examples were analysed with different software packages. GLM for repeated measurements was performed with SPSS, while both mixed model analysis and GEE analysis were performed with STATA. Nowadays, it is possible to perform both linear and logistic mixed model analysis as well as linear and logistic GEE analysis with all popular (commercial) software packages such as SPSS, STATA, SAS and R. It should be realised that the results of linear mixed model analysis and linear GEE analysis are very stable; i.e. there is no difference in results obtained from the different software packages. This also holds for logistic GEE analysis. However, for logistic mixed model analysis this is not the case. The use of different software packages lead to different results as well as the use of different estimation procedures within a software package [14]. Therefore, the results obtained from a logistic mixed model analysis should be interpreted with great caution.
References
Berkhof, J., Knol, D., Rijmen, F., Twisk, J., Uitdehaag, B., Boers, M.: Relapse - remission and remission - relapse switches in rheumatiod arthritis patients were modelled by random effects. Journal of Clinical Epidemiology 62, 1085–1094 (2009)
Box-Steffensmeier, J., De Boef, S.: Repeated events survival models: the conditional frailty model. Statistics in Medicine 25, 3518–3533 (2006)
Fitzmaurice, G.M., Laird, N.M., Ware, J.H.: Applied longitudinal data analysis. Wiley, Hoboken, New Jersey, USA (2004)
Goldstein, H.: Multilevel statistical models, 3rd edn. Edward Arnold, London (2003)
Kelly, P.J., Lim, L.Y.: Survival analysis for recurrent event data: An application to childhood infectious diseases. Statistics in Medicine 19, 13–33 (2003)
Laird, N.M., Ware, J.H.: Random effects models for longitudinal data. Biometrics 38, 963–974 (1982)
Lesaffre, E., Spiessens, B.: On the effect of the number of quadrature points in a logistic random-effects model: an example. Annals of Applied Statistics 50, 325–335 (2001)
Liang, K., Zeger, S.L.: Longitudinal data analysis using generalized linear models. Biometrika 73, 45–51 (1986)
Liang, K.Y., Zeger, S.L.: Regression analysis for correlated data. Annual Review of Public Health 14, 43–68 (1993)
Rothman, K.J., Greenland, S.: Modern Epidemiology. Lippincott-Raven Publishers, Philidelphia (1998)
Stürmer, T., Glynn, R.J., Kliebsch, U., Brenner, H.: Analytic strategies for recurrent events in epidemiologic studies: background and application to hospitalization risk in the elderly. Journal of Clinical Epidemiology 53, 57–64 (2000)
Twisk, J.W.R.: Longitudinal data analysis. A comparison between generalized estimating equations and random coefficient analysis. European Journal of Epidemiology 19, 769–776 (2004)
Twisk, J.W.R.: Applied multilevel analysis. Cambridge University Press, Cambridge, UK (2006)
Twisk, J.W.R.: Applied longitudinal data analysis for epidemiology: a practical guide, 2nd edn. Cambridge University Press, Cambridge, UK (2013)
Twisk, J.W.R., Proper, K.: Evaluation of the results of a randomized controlled trial: how to define changes between baseline and follow-up. Journal of Clinical Epidemiology 57, 223–228 (2004)
Twisk, J.W.R., Smidt, N., de Vente, W.: Applied analysis of recurrent events: a practical overview. The Journal of Epidemiology and Community Health 59, 706–710 (2005)
Twisk, J.W.R., de Vente, W.: The analysis of randomised controlled data with more than one follow-up measurement. A comparison between different approaches. European Journal of Epidemiology 23, 655–660 (2008)
Yang, M., Goldstein, H.: Multilevel models for repeated binary outcomes: attitudes and voting over the electoral cycle. Journal of the Royal Statistical Society 163, 49–62 (2000)
Zeger, S.L., Liang, K.Y.: Longitudinal data analysis for discrete and continuous outcomes. Biometrics 42, 121–130 (1986)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Twisk, J.W.R. (2014). Different Methods to Analyse the Results of a Randomized Controlled Trial with More Than One Follow-Up Measurement. In: van Montfort, K., Oud, J., Ghidey, W. (eds) Developments in Statistical Evaluation of Clinical Trials. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-55345-5_10
Download citation
DOI: https://doi.org/10.1007/978-3-642-55345-5_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-55344-8
Online ISBN: 978-3-642-55345-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)