Non-adiabatic Photochemistry: Ultrafast Electronic State Transitions and Nuclear Wavepacket Coherence

Abstract

Chemistry that takes place exclusively in the ground electronic state can be well described by a reaction path in which the reactants pass over a transition state to the products. After photoexcitation, a molecule is in an excited electronic state and new topographical features joining different states, known as conical intersections, also need to be considered to describe the time-evolution from reactants to products. These intersections are due to the coupling between electrons and nuclei. In addition to providing new pathways, they provide a quantum-mechanical phase to the system which means that to describe the nuclear motion properly methods are required that include the resulting quantum-mechanical coherences in the nuclear motion. In this chapter, we review the nature and topography of conical intersections and simulation methods that have been developed to describe a molecule passing through one. These range from the full solution of the time-dependent Schrödinger equation to approximate methods based on Newtonian mechanics. Using examples the advantages and disadvantages of each are discussed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

7.1 Introduction

The development of software able to efficiently treat a range of problems can have a huge effect on the development of science. This is exemplified in the field of chemistry where the existence of quantum chemistry programs such as Gaussian and Molpro has resulted in molecular structure calculations and energetic analysis becoming a ubiquitous tool providing mechanistic information in chemical research. Similarly, classical molecular dynamics programs such as CHARMm and AMBER have helped to focus thinking onto the dynamical nature of, in particular, condensed phase and biological processes.

Photochemistry, however, has mechanistic features that cannot be adequately described by standard quantum chemistry and classical molecular dynamics calculations. First, the reaction is initiated by absorption of a photon, which means we need to be able to treat excited electronic states. Second, it is found that there are molecular geometries where the excited- and ground state potential energy surfaces are close in energy or even meet. At these geometries the nuclear and electronic motions couple and the molecule undergoes non-adiabatic dynamics.

Given the importance of photochemistry in actual and emerging technologies, such as solar energy, photodynamic therapy, and optical storage, methods to understand and describe the energy flow in these molecular systems have an important role to play in the development of these fields of research. Also, time-resolved spectroscopy and coherent control experiments, in which a laser field is used to observe, or even direct, a molecule as it goes from photo-excited reactant to product are now well established. Being able to perform appropriate simulations is essential for understanding these experiments probing the fundamental behaviour of molecules.

In non-adiabatic dynamics it is necessary to treat the nuclei as moving over a set of coupled potential energy surfaces rather than the single surface of classical molecular dynamics. The surfaces can then approach to form avoided crossings or meet as conical intersections that provide pathways where the initially excited molecule can cross back to the ground electronic state in a non-radiative manner. This crossing is particularly efficient at a conical intersection, which is why these features play a central role in the mechanistic description of photochemistry, in a similar way to the role played by the transition state in thermal chemistry.

The recent availability of theoretical developments implemented in widely available quantum chemistry software means that the theoretical study of non-adiabatic chemistry is also “coming of age”, with many applications oriented practitioners now using calculations to support their ideas and experiments. For example, an algorithm for finding the minimum energy point on a conical intersection [1] was made available in Gaussian in the 1990s, and most quantum chemistry codes now have this feature.

Just knowing the positions and energies of conical intersections is, however, not enough to understand the mechanism of a reaction and dynamical information is also required. For example, how efficient the crossing process is requires knowledge of the time scale and population transfer at an intersection. Here, dynamics methods embedded in quantum chemistry programs can be used to great effect once adapted to treat non-adiabatic processes. For example, the direct dynamics methods developed by Schlegel in the Gaussian program have been adapted to non-adiabatic dynamics since the late 1990s [2].

Just as for thermal chemistry, for photochemistry the easiest and most pictorial dynamics uses classical trajectories. The non-adiabatic process is then modelled by computing the probability of hopping between the surfaces using some approximate solution of the Schrödinger equation [3, 4]. From the starting point given by absorbing a photon, the trajectories thus show where the system can go, and where and when it can cross to the ground state. The hopping probabilities then give how efficient this process is. For an excellent overview of non-adiabatic dynamics from the semi-classical perspective the reader may consult the recent review of Tully [5] and the many papers in the same edition of J. Chem. Phys.

Trajectory surface hopping is, however, only an approximate treatment of the dynamics and the full quantum dynamics description requires a full solution of the time-dependent Schrödinger equation (TDSE) [6]. The main failure of the semi-classical surface hopping approach is that the different trajectories are independent and so the coherence of the nuclear motion as it passes through a conical intersection is lost. How important is this coherence? The answer to this is not known in general, but coherence will play a role in the short-term dynamics of phenomena. For example, recrossing at an intersection is known from full quantum dynamics simulations, but is not seen in surface hopping. Such methods are therefore potentially essential for understanding short time-scale fundamental processes such as electron transfer and proton transfer–essential for many chemical and biological systems. Furthermore, recent experiments have implicated nuclear coherence as being involved in certain biological processes over a long time-scale [7, 8].

The computational resources required to solve the TDSE meant that until recently only a few atoms could be treated in this way. However, programs to treat molecular systems with quantum dynamics are now becoming more widely used. The Heidelberg MCTDH package is probably the only quantum dynamics code that has been developed with the aim of generality [9]. Recent advances in algorithms such as the development of the variational multi-configuration Gaussian (vMCG) method [10, 11] and multiple spawning [12, 13] also are moving quantum dynamics to become a mainstream simulation tool and comparisons with the simpler surface hopping can now be made [14].

This chapter sets out to focus on the information available from computational tools to describe non-adiabatic dynamics and photochemical reactivity. From a general mechanistic point of view the non-adiabatic event takes place near a conical intersection. It is the “shape” of the extended seam of the intersection and its position on the reaction path that controls the outcome of a photochemical reaction. The concepts of this topic are reviewed, with examples, in Sect. 7.2. In Sect. 7.3 we introduce the main methods for performing dynamics using a potential derived from quantum chemistry electronic structure methods, starting from an exact solution of the TDSE and moving to more approximate techniques. In Sect. 7.4 we “showcase” these methods with some representative examples.

7.2 Classifying Conical Intersections: Shapes and Positions

We shall begin our exploration of conical intersections with an example constructed from a classic textbook photochemistry case, the 2+2 cyclo-addition of two ethylene molecules [15–17]. The potential energy surface is illustrated schematically in Fig. 7.1. We shall consider the face to face approach (centred on points with geometry A or A′ in Fig. 7.1a) where the new σ-bonds are formed synchronously, as well as a bi-radical approach (passing through the geometry C in Fig. 7.1a), where one σ-bond is formed first to yield a diradical intermediate. The coordinate that connects the two approaches is a trapezoidal distortion coordinate A–C. The potential energy surface in the space of these two coordinates for the ground and excited states is shown in Fig. 7.1. In thermal chemistry, reactivity is confined to the ground state or the lower potential energy surface. In photochemistry, the reaction begins by excitation from the ground state potential energy surface to the excited state potential energy surface. For our purposes, we imagine that the starting point of the photochemical cyclo-addition, the so-called Franck–Condon geometry, corresponds to two isolated ethylene molecules, and the product is cyclobutane in a square planar geometry.

Fig. 7.1

Cartoons of the potential energy surfaces describing the 2+2 cyclo-addition of two ethylene molecules (adapted from [16])

We can use the potential surfaces shown in Fig. 7.1 to compare and contrast what might happen in thermal and photochemical reaction, and thus to illustrate the role of a conical intersection. We have distinguished two molecular motions X₁ and X₂ in which to plot the surfaces. The variable X₁ is a reaction coordinate corresponding to the approach of the two ethylenes passing via point A A′. The variable X₂ is a rhomboidal distortion passing through E and connecting A and C. As we will presently discuss, a photochemical mechanism via a conical intersection must involve two distinguished coordinates, while a transition state associated with a thermal reaction is associated with one distinguished coordinate, X₁ in this case, corresponding to the reaction path.

In a 2+2 thermal reaction, there are two possible transition states, shown as A′ for the synchronous reaction, where both bonds are formed simultaneously, and C for the asynchronous reaction where one bond was formed first. The Woodward–Hoffman (WH) [17] rules predict that the asynchronous reaction (via C) has the lower energy. Now let us examine a region of the potential energy surface along a line connecting the two transition states A′ and C. We can see that the ground state energy passes through a very high-energy point E where the ground state and excited state become degenerate. This is known as a conical intersection [18]. Of course, a thermal reaction would not pass close to point E that is so high in energy. At this point, we also observe that the double cone at point E requires two coordinates X₁X₂ to describe it.

Now, let us consider the photochemical reaction. The reaction begins with photoexcitation at the FC geometry, corresponding to two separated ethylenes. The reaction would progress along a coordinate leading to a minimum A, if the system were constrained to have a rectangular geometry. However, the potential energy is unstable along this coordinate with respect to rhomboidal distortion. Notice that along a reaction path directed towards the point E, there is a negative direction of curvature so that A, rather than being a local minimum, is in fact, a transition state along the reaction path leading to the point E. Thus the geometrical changes corresponding to reaction paths on the excited state are quite different than on the ground state. On the one hand, the motion which brings the two ethylenes together along the coordinate which preserves rectangular symmetry is a maximum on the ground state involving a transition state at A′ while it is a local minimum on the excited state at A. This one-dimensional picture is shown in Fig. 7.1b. However, this excited state reaction path is not stable, and a lower energy pathway is available which involves motion along the rhomboidal distortion coordinate, leading via point E to the ground state asynchronous pathway at point C. Thus, reaction pathways (the geometries traced out) along excited state or ground state evolution are in general very different in the ground and excited states. Also, we can see from Fig. 7.1 that the reaction path from the excited state to the ground state passes via a point E where the two states have the same energy. This is the point where radiationless decay takes place and the system moves from the excited state to the ground state without emitting light. This type of degenerate point is known as a conical intersection [17] and we will have more to say about that as we continue our development.

Before leaving discussion of Fig. 7.1 it is important to mention that this figure is a “cartoon”. With present-day computational methods, one computes the geometries of points where the gradient is zero, such as minima and transition states. One can also compute the energies and geometries of low-energy conical intersection points such as E [19]. The cartoon that one draws in Fig. 7.1 is intended to convey the shape of the potential energy surface and the way in which various critical points (minima, etc.) are connected rather than presenting the results of actual computations on a grid.

Fig. 7.2

Cartoon of a “classic” double cone conical intersection, showing the excited state reaction path and two ground state reaction paths (adapted from Paterson et~al. [21])

If the mechanistic information just discussed in Fig. 7.1 is to be really useful then it must be an intrinsic property of the chromophores themselves, i.e. the two ethylene molecules. For example, it is the key feature in intra-strand thymine dimerisation and these dimers can disrupt the function of DNA and trigger complex biological responses, including apoptosis, immune suppression, and carcinogenesis. One can identify the geometry corresponding to the point E in Fig. 7.1 as well as the computed directions [20] X₁ and X₂ for the 2+2 cyclo-addition reaction of two thymine molecules.

Using Fig. 7.1 we briefly introduced the idea that a conical intersection requires two geometrical coordinates in order to define the double cone. We now extend these ideas more rigorously.

Fig. 7.3

A representation of the electronic wavefunction around a conical intersection. The black and white tessellations correspond to different “diabatic states”

In Fig. 7.2, we show a general cartoon of a conical intersection. In addition to the energy, the double cone like structure is defined by two geometrical coordinates X₁ and X₂ (first introduced in Fig. 7.1). Thus, as one moves away from the apex of the cone, the degeneracy is lifted. In Fig. 7.3 we show another important effect, the nature of the wavefunction represented by a superimposed tessellation pattern. The tessellation indicates the nature of the diabatic states at any point on the conical intersection; pure white is one diabat and pure black a different diabat. The essential idea is that if one takes a point on the upper surface and suppose that it has electronic structure A, then the corresponding point A′ on the lower surface, related by inversion (180^o rotation plus reflection in the X₁X₂ plane) has the same electronic structure. Similarly, at an avoided crossing (e.g. Fig. 7.1) one has an overall wavefunction composed of both states Ψ₊ = c ₁ ψ _Black + c ₂ ψ _White on the upper surface and Ψ₋ = c ₁ ψ _White − c ₂ ψ _Black on the lower surface.

The two coordinates X₁X₂ thus play a central role in mechanistic photochemistry. In a thermal reactivity problem, we are normally interested in the energy and the reaction path. In a photochemical problem, where the reaction path passes through a conical intersection, we are interested in the energy and two coordinates X₁ and X₂. Thus the thermal reaction path, a single coordinate, gets replaced in photochemistry, by the two coordinates X₁ and X₂. In a thermal reactivity problem, the reaction path is precisely defined at the transition state itself. It is just the direction associated with the normal coordinate corresponding to the imaginary frequency. The imaginary frequency is associated with the curvature of the potential energy surface at the transition state (i.e. the second derivative of the energy). In contrast at a conical intersection, the two directions X₁ and X₂ are defined by the equations

$$ {x}_1^{\left( i\gamma \right)}=\frac{\partial \left({E}_{\mathrm{B}}-{E}_{\mathrm{A}}\right)}{\partial {\xi}_{i\gamma}} $$

(7.1a)

$$ {x}_2^{\left( i\gamma \right)}=\frac{\partial \left\langle {\Psi}_{\mathrm{A}}\left|\widehat{H}\right|{\Psi}_{\mathrm{B}}\right\rangle }{\partial {\xi}_{i\gamma}}, $$

(7.1b)

i.e. associated with gradients and transition gradients. They are usually referred to as the gradient difference and derivative coupling vectors.

In Eq. (7.1), states A and B are the two electronic states: ground and excited states associated with the conical intersection, ξ _iγ is the γth mass-weighted Cartesian coordinate of the ith atom, the index i labels the N atoms and γ the Cartesians components, x, y, and z. These quantities are in principle obtainable only from a theoretical calculation. Nevertheless, as we shall discuss subsequently, they have a simple interpretation and one can often make a reasonable guess as to the nature of these two vectors using qualitative valence bond theory.

The coordinates X₁ and X₂ are precisely defined quantities that can be computed explicitly [22] from electronic structure theory. Similarly, the apex of the cone corresponds in general to an optimised molecular geometry [23]. (See also the more recent works of Sicilia et~al. [24], Martinez et~al. [25] and Thiel et~al. [26].) The shape or topology in the region of the apex of the double cone will change from one photochemical system to another [27], and it is the generalities associated with the shape that form part of the mechanistic scenario that we will discuss. All ideas follow from a development of a two-level quadratic expansion (for S₁ and S₀) simultaneously. Such an expansion involves gradients (X₁) and off-diagonal gradients (X₂). However, such developments require more specialised knowledge and for details the reader is referred to the literature [21, 24, 27–33].

Now let us turn to the situation where the reaction path does not lie in the plane X₁X₂. In this case we need three coordinates to define the course of a photochemical reaction through a conical intersection: the reaction path X₃ and the coordinates X₁X₂. In order to draw a picture similar to Fig. 7.2, we would need four dimensions. Thus for simplicity, we will plot the energy as a function of one (X_1/2) of the two coordinates X₁ or X₂ and the reaction path X₃. The corresponding cartoon is shown in Fig. 7.4. In this case, the conical intersection appears as a line or a seam which we shall refer to as a conical intersection seam. In Fig. 7.4, we use the coordinate X₃ to denote the reaction coordinate, and the axis (X_1/2) labelled “branching space coordinate X₁ X₂” is designed to indicate a vector which is a linear combination of X₁ X₂. Motion along this composite coordinate, X_1/2, is at right angles to the seam, and the degeneracy is lifted. In the figure, we have shown the double cone along this seam in order to remind ourselves that there are three geometrical coordinates involved in this picture.

Fig. 7.4

The conical intersection hyperline traced out by a coordinate X₃ plotted in a space containing the coordinate X₃ and one coordinate from the degeneracy-lifting space X₁ X₂ (adapted from Paterson et~al. [21])

Thus, Fig. 7.4 illustrates the general situation where the reaction path is not contained in the branching plane, X₁ X₂. There are many examples where this type of topology presents itself [34–38].

In Figs. 7.2 and 7.4 we have illustrated cartoons for different ways of visualising the topology of a conical intersection. In general, there are two coordinates X₁ and X₂, which form what is known as the branching space where the degeneracy of the common intersection is lifted. Then we introduced a third coordinate as X₃, which we referred to as the reaction coordinate. Of course, there are more than three geometrical variables in the typical photochemical reactivity problem. In modern computational methods one uses all the molecular degrees of freedom in numerical computations. Then, a posteriori, we identify three variables to visualise and understand any particular problem. However, the two directions X₁ and X₂ computed according to Eq. (7.1) are precisely defined.

To conclude this section on local topology we briefly discuss two other concepts: the slope [27] of the conical intersection and the position of the conical intersection on the reaction coordinate [39]. These concepts are illustrated in Figs. 7.5 and 7.6.

Fig. 7.5

Classification of conical intersections according to their local topography (from [27, 39])

Fig. 7.6

Different topographies of conical intersections along a reaction coordinate (extended version adapted from [39])

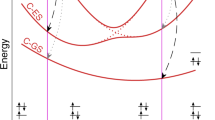
In Fig. 7.5 we indicate the slope of the conical intersection [27]. Of course X₃ does not appear on these figures. The peaked intersection corresponds to the simple case where the system simply “falls down” from one state to the other. The sloped/intermediate intersection is particularly interesting mechanistically. This type of topology is associated with photostability (i.e. no new chemical species is produced after decay from the conical intersection) and we will return to discuss this in our section on case studies. However, it should be apparent that in a sloped intersection a trajectory may recross the apex of the cone many times before decaying to the ground state energy sheet.

The position of the surface crossing and whether or not it is preceded by a local minimum on the excited state reaction path is illustrated in Fig. 7.6. Comparing Fig. 7.6a versus b we can examine the competition between passing over a barrier when a conical intersection is separated from a local minimum (Fig. 7.6a) versus passing directly from the Franck–Condon region of the potential energy surface to the conical intersection (Fig. 7.6b). In the first case, there must be a competition between fluorescence decay at the minimum versus passage over the barrier to the conical intersection. In the second case there is no barrier and the system decays on the time scale of vibrational motion after excitation to the Franck–Condon region: an ultrafast reaction. In Fig. 7.6c we show the sloped conical intersection discussed in the previous figure. It is now obvious that such a topology must be associated with photostability because the excited state intermediate when it decays at the conical intersection returns to the ground state intermediate. Figures 7.6d and 7.6e are intended to illustrate, in a schematic way, the effect of the position of the surface crossing on the reaction coordinate. In Fig. 7.6d we illustrate the case where the surface crossing occurs on the product side of a ground state transition state. In such a case one has an adiabatic reaction, and the decay to the ground state takes place in the product region. In Fig. 7.6e we show the situation with an adiabatic reaction terminating at a sloped conical intersection.

Thus in the same way that one can characterise topographical features on a potential energy surface where the gradient goes to zero at maxima and minima, it is possible to systematically map out and characterise the seam. These ideas lie beyond the scope of this review. However, they can be useful in further characterising mechanistic effects [21, 24, 27–33, 40–44].

7.3 Simulating Non-adiabatic Transitions

When a molecule has a configuration near to that of a conical intersection it is able to undergo non-adiabatic transitions, whereby it can move from one electronic state to another instantaneously in a radiationless manner. These transitions are due to coupling between the nuclear and electronic motion and as a result are quantum-mechanical processes. Thus to simulate them requires solving the TDSE

$$ i\mathit{\hslash}\frac{\partial \varPsi}{\partial t}=\widehat{H}\varPsi $$

(7.2)

for the nuclear wavefunction Ψ to capture the evolution of the molecular system as it flows over the coupled potential energy surfaces.

The potential energy information is contained in the Hamiltonian, $\widehat{H}$, which can be written in two different ways: the adiabatic or diabatic form [6, 45]. In the adiabatic form the coupling is part of the kinetic energy operator and the potential energy surfaces are simply ordered in energy. In the diabatic form the coupling is part of the potential operator and potential energy surfaces can be associated with an electronic configuration or molecular property. The relationship between the two forms is not straightforward, but the adiabatic picture is that used in quantum chemistry, while in general the TDSE is solved in the diabatic picture as in the adiabatic picture conical intersections result in singularities that provide problems.

Over the last 20 years powerful methods to solve the TDSE have been developed [46, 47]. These are based on using a grid-based representation of the wavefunction and Hamiltonian and have provided detailed descriptions of non-adiabatic events. Unfortunately, such numerically exact solutions of the TDSE require huge computer resources as they scale exponentially with the number of degrees of freedom and approximations must be introduced to treat systems with more than 20 atoms, which include the majority of photochemistry.

There are two classes of approximations that are commonly used. The first is to use what are called Gaussian wavepackets (GWPs) to describe the wavefunction. This wavepacket description means a grid is not required, and the scaling is improved. Often the GWPs follow classical trajectories and other approximations are made to improve efficiency.

The second approach is to discretise the wavepacket into a “swarm of trajectories” that evolve according to Newton’s equations of motion. Non-adiabatic events are then simulated either by “hopping” between potential energy surfaces, in what is termed trajectory surface hopping, or by each trajectory carrying an evolving weight associated with each potential energy surface in Ehrenfest dynamics.

In addition to the bottleneck due to memory requirements, grid-based quantum dynamics suffers from the basic problem that they are global methods, i.e. the potential energy surfaces and wavefunctions must be defined globally before the propagation can be made. Calculating accurate global potential energy surfaces, particularly for multi-state calculations where couplings are also required, is a huge challenge. The more approximate GWP- and trajectory-based methods have the advantage that they can be used in a direct dynamics approach in which the potential energy surfaces are calculated on-the-fly as and when required.

7.3.1 Grid-Based Quantum Dynamics

The wavefunction can be expanded in a basis set of functions for each degree of freedom, {χ}^(κ). The wavefunction is then written

$$ \varPsi ={\displaystyle \sum_{j_1{j}_2\cdots {j}_f}{A}_{j_1{j}_2\cdots {j}_f}(t){\chi}_{j_1}^{(1)}\left({q}_1\right){\chi}_{j_2}^{(2)}\left({q}_2\right)\dots {\chi}_{j_f}^{(f)}\left({q}_f\right)} $$

(7.3)

And the TDSE is reduced to solving a set of equations for the time-evolution of the expansion coefficients

$$ i{\dot{A}}_I={\displaystyle \sum_J{H}_{IJ}{A}_J} $$

(7.4)

where J = j ₁ j ₂ … j _f is a composite index and H _IJ are the matrix elements of the Hamiltonian represented in the basis set. These basis functions may be harmonic oscillator eigenfunctions or some other suitable set. Discrete variable representations are particularly useful as they allow the wavefunction to be mapped onto a spatial grid as well as providing accurate integrals of the matrix elements (see Appendix B in [49]).

Equation (7.4) is very easy to implement on a computer. The matrix is built once at the beginning and then straightforward matrix–vector operations are used to propagate the wavefunction forwards in time. A number of integration schemes have been developed to do this [47]. The scaling problem is, however, obvious. For a system with f degrees of freedom and N basis functions for each there are N ^f expansion coefficients that must be propagated. As of the order of 50–100 basis functions per degree of freedom are required, these numerically exact calculations are in general restricted to 3–4 atom systems.

The multi-configuration time-dependent Hartree (MCTDH) method [48–50] is a grid-based method that is able to treat larger systems. It uses a similar wavefunction ansatz

$$ \varPsi ={\displaystyle \sum_{j_1{j}_2\cdots {j}_f}{A}_{j_1{j}_2\cdots {j}_f}(t){\varphi}_{j_1}^{(1)}\left({q}_1,t\right){\varphi}_{j_2}^{(2)}\left({q}_2,t\right)\dots {\varphi}_{j_f}^{(f)}\left({q}_f,t\right)} $$

(7.5)

But now the basis functions are also time-dependent. The resulting description is more compact as the basis functions follow the evolving wavepacket using variationally derived equations of motion and so effort is not wasted describing regions of space where the wavefunction is negligible. Using this method up to 15 atoms may be treated [51].

The method is still a grid-based one as the basis functions (known as single-particle functions) are still described using time-independent DVR functions

$$ {\varphi}_i^{\left(\kappa \right)}={\displaystyle \sum_{\alpha }{c}_{i\alpha}{\chi}_{\alpha}^{\left(\kappa \right)}} $$

(7.6)

It also has a higher overhead than the standard numerically exact method as the Hamiltonian matrix elements are also now time-dependent and the potential energy function requires a special form for maximum efficiency.

7.3.2 Gaussian-Based Quantum Dynamics

Methods based on GWPs, also known as coherent states (CSs), all derive from the seminal work of Heller [52]. They can capture the full quantum-mechanical character of molecular processes and promise better scaling than grid-based methods. A big advantage is that they allow direct dynamics approaches [6], whereby the potential energy and its derivatives with respect to the nuclear coordinates are calculated “on-the-fly”, such as in trajectory-based classical and semi-classical dynamics (e.g. ab initio molecular dynamics and trajectory surface hopping). This strategy thus promises reasonable multidimensional quantum dynamics simulations at low effort. They may, however, suffer from numerical problems in terms of convergence, which often restricts them to semi-quantitative applications, as opposed to the more involved—but more accurate—grid-based methods.

The ideal field of application of Gaussian-based quantum dynamics methods is certainly non-adiabatic photochemistry [53]. In this context, they hold a midway position between grid-based quantum dynamics methods and trajectory-based semi-classical methods. The former are plagued by the time and memory requirements of first generating analytical multidimensional expressions for the potential energy surfaces and non-adiabatic couplings. This is an involved task that often implies the preliminary identification of a subset of active nuclear coordinates and a simplified model for the treatment of the remaining degrees of freedom. In contrast, semi-classical methods, such as trajectory surface hopping or Ehrenfest dynamics, are easier to utilise and yield correct estimates for the characteristic rates and efficiencies of non-adiabatic transitions. However, they remain limited to describing the very first radiationless events because of their inadequate treatment of quantum coherence or entanglement (excess or lack of) among the coupled electronic states.

GWP or CS methods have in common the expansion of the total wavepacket in a basis set of multidimensional time-dependent Gaussian functions, ${g}_j^{(s)}\left({\bf R},t\right)$, on one or several coupled electronic states, $\left|s;{\bf R}\right\rangle$,

$$ \left|\varPsi \left({\bf R},t\right)\right\rangle ={\displaystyle \sum_s{\displaystyle \sum_j{A}_j^{(s)}(t){g}_j^{(s)}\left({\bf R},t\right)\left|s;{\bf R}\right\rangle }} $$

(7.7)

where s denotes the state index and ${\bf R}$ the nuclear coordinate vector. In the majority of these methods the centres of the frozen-width Gaussian basis functions follow classical trajectories and so are unable to model individually certain situations such as tunnelling. The latter is retrieved through the quantum superposition of trajectories of various total energies through the coupled propagation of the expansion coefficients, A ^(s) _j (t). These evolve according to a secular formulation of the TDSE in a non-orthogonal basis set.

The full multiple spawning (FMS) method [12, 13, 54–58] is an adaptive-basis-set approach that uses classically driven Gaussian functions. Simulations start with a relatively small basis set on the initial electronic state. The spawning procedure generates extra basis functions if branching events require them, such as when a conical intersection is reached, and population must be transferred to the other electronic state. This method will in principle be numerically exact at convergence. The multiple independent spawning (MIS) approach is an approximate classical-like variant based on uncoupled trajectories.

In the variational multi-configuration Gaussian wavepacket (vMCG) method [10, 11, 59–63] the basis functions follow coupled “quantum trajectories” whereby the mean positions and momenta are treated as variational basis-function parameters that evolve according to the Dirac–Frenkel principle applied to the TDSE. Each basis function directly simulates quantum phenomena in a rigorous way, and the method thus promises much faster convergence than classical-trajectory-based methods due to a better sampling of the phase space.

Somewhat midway between FMS and vMCG techniques, the multi-configurati- onal Ehrenfest (MCE) method [64–68] assumes Gaussian basis functions following coupled Ehrenfest trajectories that are thus governed by a weighted average of several potential energies. Ehrenfest trajectories are more quantum in essence than FMS trajectories but are generated from an approximate solution to the vMCG equations of motion where only the leading term is accounted for and thus the Gaussian functions again follow classical trajectories. The multi-configurational character of the description relieves them of the typical issue of contradictory average gradients in single-configuration Ehrenfest dynamics.

The limited spatial expansion of frozen-width Gaussian functions means that a local harmonic approximation of the potential energy surface around the centre of each GWP is a decent approximation (“thawed” Gaussian functions have proved to be inadequate numerically due to excessive spreading compared to the range of validity of the local harmonic approximation). The potential energy and its derivatives can thus be calculated along the trajectories followed by their centres. Such treatments free quantum dynamics of the numerically expensive and time-consuming requirement of calculating and fitting potential energy surfaces beforehand. The corresponding extensions of the three aforementioned methods are termed ab initio multiple spawning (AIMS), direct dynamics vMCG (DD-vMCG), and ab initio MCE (AI-MCE).

Direct dynamics implementations of Gaussian-based quantum dynamics methods are a turning point from a computational perspective. Fully accounting for the quantum nature of Gaussian basis functions over their widths requires repeated evaluations of gradients and Hessians at their centres. Obviously, despite the exponential scaling of grid-based methods, long-lived trajectories also require a large number of electronic-structure calculations, which can also happen to be a practical bottleneck. However, using Hessian-update procedures and/or a physically sound hierarchical description based on a QM/MM treatment in lieu of fully ab initio calculations is a promising strategy for the adequate description of quantum effects in large systems or medium-sized systems embedded in an environment [69].

7.3.3 Trajectory-Based Semi-classical Dynamics

The lowest level of approximation that can be used to solve the TDSE is also the one that gives the best scaling with system size. Using a polar representation of the wavefunction, in the classical limit ℏ → 0, it is possible to model the evolving density

$$ \rho \left({\bf R},t\right)={\Psi}^{*}\left({\bf R},t\right)\Psi \left({\bf R},t\right) $$

(7.8)

as a set of trajectories that follow classical equations of motion [70], often referred to as a swarm, i.e. for each coordinate

$$ M\ddot{R}=-\frac{\partial V}{\partial R} $$

(7.9)

This approach, originated by Bohm, has the further advantage that it can be used in direct dynamics in a straightforward way: calculating the potential and gradient at each point along the trajectories is straightforward using quantum chemistry methods.

Initial conditions for the trajectories must be chosen by sampling an appropriate distribution. To sample a particular initial wavefunction, the ground vibrational state, for example, the Wigner distribution can be used [6]. This is a transformation of the density in configuration space to a set of phase space variables and so randomly sampling this distribution provides trajectories that effectively discretise the quantum density. For states where the Wigner function has negative regions that cannot be interpreted as a probability, the Husimi function may be used. Alternatively, simpler sampling can be used based on a single representative trajectory or on a microcanonical distribution that can include the zero-point energy in an approximate way.

What happens if more than one potential energy surface is present? The standard way to tackle this problem is to use “surface hopping”, which recognises that the main result of non-adiabatic coupling is to effect a transfer of population between states in the region of the coupling [71–74]. Each trajectory is propagated on a surface until it reaches a non-adiabatic region where the coupling is non-negligible. The trajectory may then hop to the other surface with a probability calculated to model the quantum-mechanical population transfer. This inclusion of some degree of quantum-mechanical behaviour to the nuclear motion is why these methods are referred to as semi-classical.

There are a variety of ways in which the hop can be calculated. The most commonly used variant is Tully’s least switches algorithm [73]. This is designed to reproduce the correct electronic state populations with the least number of hops. The probability of changing from electronic state 2 to 1 is here given by

$$ {P}_{2\to 1}=-\frac{\mathrm{d}}{\mathrm{d}t} \log {\left|{c}_2\right|}^2\varDelta t $$

(7.10)

where c ₂ is the coefficient of the upper state component in the electronic wavefunction

$$\Psi_{\rm el}(\mathrm{r},t)={c}_1(t)\psi_1({\rm r})+{c}_2(t)\psi_2(\rm r)$$

(7.11)

and Δt the step size in the propagation. A simpler method is inspired by the

Landau–Zener crossing probability [74]

$$ {P}_{2\to 1}= \exp \left(-\frac{2\pi {V}_{12}^2}{\mathit{\hslash v}\left|{F}_2-{F}_1\right|}\right)\Delta t $$

(7.12)

where V ₁₂ is the coupling between the states, F _i the forces on the atoms on the different surfaces, and v the velocity of the atoms passing through the intersection.

Trajectory surface hopping is inherently an approximate method. There is no rigorous derivation for the hop probability, hence the different possibilities, and various ad hoc corrections need to be made to conserve energy after a hop and to cope with “frustrated hops” when a hop is required but energetically not possible. A potentially more serious problem is that as the trajectories are independent nuclear coherences are not included. Quantum effects such as tunnelling and zero-point energy are thus not correctly treated and much work, particularly by Truhlar and co-workers, has been made to assess the validity of surface hopping [75, 76]. New approaches are also still being developed to correct for these problems [77, 78].

An alternative formulation that uses classical trajectories to model non-adiabatic behaviour is the Ehrenfest approach [79, 80]. In this, each trajectory point (p, q) is driven by a “mean-field” force

$$ \dot{p}=-\frac{\mathrm{d}}{\mathrm{d}q}\left\langle \Psi_{\mathrm{el}} (t)\left|{H}_{\mathrm{el}}\right|\Psi_{\mathrm{el}} (t)\right\rangle$$

(7.13)

with the electronic wavefunction being given by Eq. (7.11). It thus has components on all electronic states and so the trajectory has associated with it a probability for being on the various states. The force is also an average of forces from the various states. This can lead to unphysical behaviour [81].

Despite the problems due to the inexact nature of the approximations being made, the simplicity of surface hopping and Ehrenfest dynamics means it can be used to extract information on the dynamics of large systems. This is exemplified by the work of Tavernelli and co-workers who combine surface hopping with TDDFT to study protein and condensed phase systems [80].

7.4 Case Studies of Non-adiabatic Photochemistry

We report here on some of our recent case studies that highlight the methods presented in Sect. 7.3 and how they help interpret experimental findings. This selection is, of course, partial and non-exhaustive. We show an example per method with challenges of different natures that require different treatments: the most adequate depending on the context. At one end of the spectrum, we exemplify how full quantum information can be retrieved with a grid-based approach on a non-trivial case involving a four-state crossing. Multiple recrossings and complicated interferences are observed, but a simplified model must be used for the potential energies. Other examples along this line can be found in Chap. 6. At the other end of the spectrum, our third example considers a semi-classical-trajectory-based treatment, which includes quantum effects only approximately, but is able to treat the photodynamics of a large molecule embedded in a protein environment. The second example illustrates how a Gaussian-based method can be a good compromise between efficiency and accuracy, with quantum effects described from first principles while keeping a simple trajectory-based picture that makes the interpretation of results easier.

7.4.1 MCTDH Study of the Homolysis of the O–O Bond in Anthracene-9,10-endoperoxide

Anthracene-9,10-endoperoxide (APO, see Fig. 7.7) is an aromatic endoperoxide which, upon excitation to S₁, shows a cleavage of the oxygen–oxygen bond, leading to rearrangement products such as diepoxides or to the decomposition into quinones, whereas excitation to higher excited states leads to cycloreversion and the release of singlet molecular oxygen [82].

Fig. 7.7

Structure of anthracene-9,10-endoperoxide (APO)

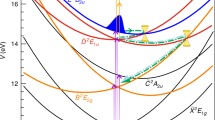
The photodynamics of the O–O cleavage is modulated by a four-state conical intersection (4CI) [83]. The most important modes are the opening angle of the O–O bond (β) and the twisting angle of the oxygen atoms around the molecular axis (τ). These two degrees of freedom were employed to calculate two-dimensional potential energy surfaces for the four interacting singlet states (see Fig. 7.8).

Fig. 7.8

The four adiabatic potential energy surfaces along β and τ close to the 4CI point (adapted from [84])

Using the grid-based MCTDH method, simulations were performed, first in two dimensions [84]. The resulting dynamics show that the 4CI point is reached very fast (in less than 30 fs after photoexcitation), and the wavepacket distributes over all states (see Fig. 7.9).

Fig. 7.9

Selected snapshots of the four adiabatic wavepacket densities. The black cross indicates the position of the 4CI point and the dot the FC point (adapted from [84])

The efficiency of the population transfer is due to the strong couplings in the twisting mode, even though the wavepacket does not spread in this degree of freedom; instead, the wavepacket only spreads along the O–O opening mode. In order to allow for a more adequate dissipation of the energy, two sets of different bath modes were added as harmonic oscillators, and quantum dynamics simulations were run in up to nine dimensions. The degree of distribution into the four states proved to be very much dependent on which modes are included in the simulation.

All the quantum dynamics simulations performed show that upon excitation to S₁, the β-coordinate dominates the photodynamics, whereas splitting off singlet molecular oxygen (for which the τ-coordinate is an important mode) does not play any role. This result is in agreement with the available experiments that found that ¹O₂ is obtained after excitation to states higher than S₁ [82].

The present grid-based quantum dynamics simulations retrieve quantum effects such as recrossings and interferences but are too limited in terms of number of degrees of freedom to provide the reaction pathways to form rearrangement products. This study could thus be complemented by less accurate trajectory-based semi-classical dynamics simulations or Gaussian-based quantum dynamics simulations in full dimensions like those presented in the next application cases.

7.4.2 DD-vMCG Study of the Photoisomerisation of a Cyanine Model

Cyanines are a class of conjugate organic dyes. Fluorescence of the trans species is in competition with a photoisomerisation towards the cis species, which represents a technological obstacle to their use as fluorescent molecular probes in imagery [85].

Calculations on model cyanines (H₂N–(CH) _n –NH₂ ⁺ with n = 3, 5 or 7) showed [86, 87]: (1) a systematic relationship between the size of the polymethine chain and the time scale of the cis–trans torsion; (2) an extended seam of conical intersection along the torsional coordinates; and (3) that high-frequency skeletal deformations were required to access the seam. The last two points were demonstrated with qualitative results based on semi-classical trajectories for the simplest trimethine cyanine (see Fig. 7.10).

Fig. 7.10

Structure of the trimethine cyanine model H₂N–(CH)₃–NH₂ ⁺

This work prompted optimal control experiments on a large cyanine [88, 89], which confirmed that the branching ratio could be controlled by a pulse leading to excitation of the same skeletal deformations in the initial wavepacket (see Fig. 7.11). This control strategy was further validated in a quantum dynamics context with Gaussian-based direct dynamics simulations [90].

Fig. 7.11

Cartoon of the two radiationless decay mechanisms for the cyanine model. The white line represents the seam of intersection between the S₁ and S₀ potential energy surfaces (from [90])

These simulations showed that directly addressing the torsional modes was not efficient. After the initial in-plane relaxation has taken place, twisting dominates the reaction coordinate, so that in the absence of control the system naturally decays down the minimum-energy path to a twisted conical intersection. The only way to avoid twisting is to excite orthogonal motions such that the dynamical pathway can deviate from the minimum-energy path. Increasing/decreasing the momentum in the skeletal deformation coordinates is thus expected to induce radiationless decay at small/large twist angles (see Fig. 7.11). This was proved by running simulations whereby the initial wavepacket was given an extra mean momentum pointing from the Franck–Condon point to a point on the seam corresponding to a quasi-planar geometry. Systematically reducing the magnitude of the momentum vector resulted in a larger average twist angle of the crossing geometries.

This work also was an opportunity to analyse the concept of quantum coherence and non-locality in the context of Gaussian-based methods. Semi-classical non-locality is related to the statistical spreading of the points where surface hopping occurs. The population transfer occurs at different times for different trajectories. Of course, this also means different geometries, but we will refer to such results as non-local in time. In contrast, quantum non-locality has to do with the fact that quantum trajectories communicate with each other at all times. Results will be called non-local in space if the population transfer involves a decrease of the weight of a given function on a given electronic state correlated with an increase of the weight of a different function on a different state (see Fig. 7.12). For example, some limited non-local transfer occurs between 18 and 20 fs for the first and the fourth basis functions in Fig. 7.13.

Fig. 7.12

Local transfer (left panel) versus non-local transfer (right panel) for a generic nuclear coordinate x (from [90])

Fig. 7.13

S₁/S₀ adiabatic energy differences for the trajectories followed by the centres of four coupled Gaussian basis functions over time (red); weight of each individual basis function to the global wavepacket (green), and corresponding S₀ and S₁ populations (purple and orange, respectively) over time (from [90])

In contrast with grid-based methods, there is no need to first build analytical models for the potential energy surface, which makes Gaussian-based methods easier to use. In addition, an approximate description based on a limited number of “quantum trajectories” can provide a more intuitive interpretation of the reaction mechanism than the evolution of a wavepacket on a grid. However, increasing the size and complexity of the system may require an even more approximate description such as semi-classical trajectories presented below.

7.4.3 TSH Study of the Photoactivation of the Photoactive Yellow Protein

Treating the non-adiabatic photochemistry of large systems in an environment is computationally demanding. A possible strategy can be QM/MM trajectory-based semi-classical dynamics, as exemplified by simulations of the photoactivation of the photoactive yellow protein (PYP) [91–93], a bacterial photoreceptor believed to be responsible for negative phototactic response to blue light of Halorhodospira halophila bacteria.

Trans-to-cis isomerisation of photoactive chromophores usually occurs through a standard one-bond-flip mechanism in the gas phase. In contrast, spatial constraints in a protein environment probably favour volume-conserving mechanisms where concerted atomic motions are expected. The isomerisation of the p-coumaric acid chromophore in PYP (see Fig. 7.14) has recently been observed with time-resolved X-ray crystallography experiments [94, 95]. These have suggested the involvement of an early twisted intermediate that can bifurcate into two structurally distinct cis intermediates via hula-twist and bicycle-pedal pathways. This highly strained structure had been predicted from the aforementioned theoretical study [92].

Fig. 7.14

Snapshots from semi-classical trajectories of PYP, showing the p-coumaric acid chromophore in the active site pocket. The first snapshot is at the photoexcitation. The second shows the configuration at the radiationless transition from S₁ to S₀. The third snapshot shows the photoproduct (from [93])

Simulations showed that the isomerisation is enhanced in the protein by altering the stability of the global S₁ minimum (i.e. by moving the position of the S₁/S₀ seam and lowering the trans-to-twisted barrier on S₁, see Fig. 7.15), and by sterically constraining the motion of the chromophore, which allows the isomerisation of the double bond (torsion b) to be favoured over isomerisation of the single bond (torsion a). These interactions significantly restrain the torsional motion of the ring about the single bond and enhance the torsional motion about the double bond. The increased population of the twisted global minimum ultimately ensures a higher quantum yield.

Fig. 7.15

Potential energy surfaces of the excited and ground states of the deprotonated chromophore in the trans-to-cis isomerisation coordinate (torsion b) and a skeletal deformation of the bonds in vacuo (a) and in the protein (b) (from [91])

Table 7.1 Dynamics studies of photochemistry

Semi-classical simulations are not aimed at providing an exhaustive and definitive understanding of photoreactivity. They should be improved on different fronts to become more predictive. Gaussian-based quantum dynamics could also provide a more accurate description of the quantum effects involved in such processes. However, semi-classical simulations are useful to generate ideas for designing new experiments, which in turn can be designed to validate specific aspects of the theoretical explanation (involvement of single-bond isomerisation, role of Arg52 in the protein, etc.) and to calibrate the level of theory required for an adequate computation.

7.5 Conclusions

In this chapter we have reviewed the central features of the theoretical aspects of non-adiabatic processes in photochemistry that can be computed using standard electronic structure methods: conical intersections and dynamics through an intersection using either trajectories with surface hoping or quantum dynamics. We have illustrated these ideas with some case studies. Of course these case studies are a small sample drawn from our own work. Thus to extend this we have prepared a non-exhaustive bibliography (Table 7.1) where the reader can find other interesting examples.

As we have mentioned in the Introduction, we believe that the age of dynamics and quantum dynamics in particular is upon us. The applications to photochemistry that have been performed so far have progressed beyond benchmarks and are uncovering new mechanistic features. Within our own research groups we have non-specialists carrying out computations to support experimental work. The general codes will be available in general packages soon.