Vibrational Spectroscopy and Molecular Dynamics

Abstract

Quantum dynamical simulations in full dimensionality play an essential role in the field of molecular dynamics. This is shown with the help of two examples: (1) the simulation of the infrared spectrum of the Zundel cation (H₅O₂ ⁺) and (2) the investigation of the tunneling splitting in malonaldehyde (C₃H₄O₂). For the Zundel cation, full, 15-dimensional dynamics calculations are presented for different isotopomers and experimental spectra are assigned to vibrational transitions. Furthermore, the internal proton transfer process within the Zundel cation is discussed. For malonaldehyde, full, 21-dimensional calculations of the ground state, the four lowest fundamentals, and their tunneling splittings are presented. The results are, along with assignments, compared to experimental data and findings of other researchers.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 Introduction

In a classical picture, a molecule is often seen as collection of N atoms, connected by chemical bonds that are formed by light electrons orbiting the heavy atomic nuclei. The particular geometrical configuration of the molecule is determined by type and character of the chemical bonds, which are seen as spring-like elastic connections between the atoms, and the kind of atoms involved. As a consequence of the elasticity of the inter-atomic bonds, the molecule can vibrate, i.e., the atoms can perform periodic motions relative to each other. Within a harmonic approximation, these vibrations can be expressed as superpositions of N − 6 (N − 5 for linear molecules) so-called normal mode vibrations, i.e., global vibrations of the molecule where all atoms vibrate with the same phase and the same normal mode frequency. Most of those normal mode vibrations involve a large number of the atoms of the molecule, but, depending on the particular structure, some of the normal mode vibrations can be quite localized and the corresponding frequency can be very typical for a certain chemical bond or groups of involved atoms.

In a quantum mechanical description, the simple spring-like picture of chemical bonds, of course, breaks down and the molecule has to be described as a many-body system of interacting particles including electrons and nuclei. Nevertheless, the normal mode vibrations have their counterpart in the fundamental excitations of the nuclear vibrational degrees of freedom (DOF) of the molecule. The fundamentals can be excited by infrared radiation (IR) and characteristic absorption bands in the IR spectra immediately point to the existence of certain chemical bonds or to functional groups and hence IR (and Raman) spectroscopy are powerful tools to investigate and study the chemical structure of molecules.

However, not all of the experimentally observed absorption bands can be assigned to characteristic bonds or groups. Here, model calculations can be a useful tool to assign transitions to the involved vibrational states and may help to identify a variety of properties such as the molecular structure itself, the determination of reaction mechanisms, characterization of transition states, etc. The advantage of model calculations is that the quantum mechanical wavefunction can be inspected in detail and to arbitrary precision, only limited, of course, by the available computational capacities.

For the theoretical modeling of IR absorption spectra there exist in essence two strategies which are commonly used, both based on the semi-classical dipole approximation for light–matter interaction: a time-independent one where eigenstates and energies of the molecular Hamiltonian are obtained by solving the time-independent Schrödinger equation and, hence, giving direct access to transition frequencies and dipole matrix elements. The second ansatz is based on a perturbative approach within a time-dependent framework. It aims for the calculation of the linear response[1] of the molecule upon IR irradiation. The latter method requires solving the time-dependent Schrödinger equation for a dipole operated initial system state and subsequently obtaining the absorption spectrum as the frequency components of the linear response function. The advantage of the time-dependent approach is that multiple spectral lines and their intensities are obtained within a single calculation, while, on the other hand, it lacks the possibility to inspect particular eigenstates. A characterization of the eigenstates, i.e., an assignment of the spectral lines, however, can be performed in the time-dependent picture as well.

The key ingredient for both approaches is solving the molecular Schrödinger equation and a large variety of methods are known to accomplish this task, both within the time-dependent and a time-independent framework. However, most of these methods can only be applied to very small and rather rigid molecules, containing three to four atoms with limited flexibility. The challenges of today lie in the accurate modeling of larger and flexible molecules beyond the limit of so few atoms. Large and flexible molecules, especially those exhibiting large amplitude motions and reorganization processes, usually need to be described by highly correlated multi-dimensional wavefunctions which makes these systems difficult to treat numerically. However, it is also in particular these problems which are stimulating the exploration of new methodologies in the field of quantum dynamics.

One such approach is the multi-configuration time-dependent Hartree (MCTDH) method [2–5] which first emerged in 1990 and since then has been further developed and applied to a large variety of problems. With MCTDH two major breakthroughs could be achieved, one of which we are presenting in the present contribution. The first one was the calculation of the absorption spectrum of pyrazine[6, 7] using a realistic 24-mode model Hamiltonian. The second one was the calculation of IR spectra and assignment of states[8–12] of the Zundel cation, a system with 15 internal DOF. The latter is discussed in detail in Sect. 5.3. We also present recent calculations of state energies and tunneling splittings of malonaldehyde (21 DOF) in Sect. 5.4 in comparison with experimental results, recently published by Lüttschwager et al. [13].

The present chapter is organized as follows: in Sect. 5.2 we briefly review present limitations and current challenges for solving the time-dependent and time-independent Schrödinger equation in multiple dimensions and outline the MCTDH approach in contrast to “standard” methods. In Sect. 5.3 we present full-dimensional calculations on the protonated water dimer, also called the Zundel cation, including the assignment of recorded spectral lines. In Sect. 5.4 we present calculations on the proton tunneling splittings of malonaldehyde in comparison with experimental data. We finally summarize in Sect. 5.5.

5.2 High-Dimensional Quantum Dynamics

An accurate numerical description of molecular vibrations in the field of physical chemistry often requires explicit solutions of the time-dependent or time-independent Schrödinger equation. A full quantum mechanical treatment of all involved particles, i.e., all electrons and nuclei, however, is only possible for very small and rather simple systems such as H₂ ⁺. For larger systems one must rely an approximations, because the demands on CPU time and memory of a numerically exact treatment quickly exceed today’s numerical capacities.

The most powerful approximation for treating molecular systems even today was already published in 1927, almost a 100 years ago: the famous Born–Oppenheimer approximation [14]. The key ingredient to this approximation is the separation of the electronic and the nuclear motions, motivated by the different masses of the two types of particles. The electronic wavefunction is treated as being parametrically dependent on the nuclear DOFs while the nuclei evolve within a set of PESs which reflect the energies of the electronic eigenstates.

This separation into subsystems is even today indispensable. It reduces the number of particles in each of the two problems, and, most importantly, it also enables the use of specialized methods and algorithms which take into account the different nature of the involved particles: indistinguishable Fermions within the electronic system and (in most cases) distinguishable nuclei. Especially for the calculation of the electronic states a large variety of quantum chemistry methods and programs on different levels of theory exist. Nevertheless, the calculation of full-dimensional PESs on which the nuclei of a molecule evolve is even for small molecules a formidable task. Many research groups spend much effort in calculating and fitting these PESs and make them available as numerical subroutines that can be integrated in other program codes which then may use them as a kind of “black box” routines that allow to calculate the potential at any given configuration of the nuclei.

In this spirit we will consider the problem of obtaining the potential as solved for our purposes and focus on the description of the nuclear DOF. Here one usually concentrates on the internal DOFs and chooses a well-suited set of coordinates q = { q _κ } to describe the system. Once having defined this set of coordinates one usually represents the nuclear wavefunction Ψ in terms of basis functions on a product grid, that is, for each DOF one chooses a set of basis functions $\chi _{i_{\kappa }}(q_{\kappa })$, in practice often grid points in coordinate representation, on which the wavefunction is sampled such that it can be written as

$$\displaystyle{ \varPsi (\mathbf{q,t}) =\sum \limits _{ i_{1}}^{N_{1} }\cdots \sum \limits _{i_{f}}^{N_{f} }C_{i_{1}\cdots i_{f}}\chi _{i_{1}}^{(\kappa )}(q_{ 1})\cdots \chi _{i_{f}}^{(\kappa )}(q_{ f}), }$$

(5.1)

where the coefficients $C_{i_{1}\cdots i_{f}}$ take the form of a complex valued f-way tensor and are the quantities that need to be stored in a computer to describe the systems state.

The representation Eq. (5.1) is sometimes also called the standard form of the wavefunction. Given that on average N basis functions per DOF are sufficient for an accurate description of Ψ the amount of information that needs to be stored and processed scales exponentially with N ^f, where N is usually of the order of 10. The standard form therefore de facto limits the size of the molecules that can be treated to about 4 atoms, i.e., 6 internal DOF.

MCTDH therefore takes a different route. The basis functions that are used to represent the wavefunction are chosen variationally optimal and typically span a few (one to four) physical DOF. Numerically, this corresponds to combining a subset of the indices in Eq. (5.1) into one single index and subsequently finding an optimal basis to describe this subset of DOF. In this way only a few most important basis functions and their expansion coefficients on the primitive grid as well as the expansion coefficients of the wavefunction in this optimal basis have to be stored. This leads to an enormous reduction of data.

The MCTDH ansatz of the wavefunction reads

$$\displaystyle\begin{array}{rcl} \varPsi (q_{1},\ldots,q_{f},t)& \equiv & \varPsi (Q_{1},\ldots,Q_{p},t) \\ & =& \sum _{j_{1}}^{n_{1} }\cdots \sum _{j_{p}}^{n_{p} }A_{j_{1},\ldots,j_{p}}(t)\,\prod _{\kappa =1}^{p}\varphi _{ j_{\kappa }}^{(\kappa )}(Q_{\kappa },t) \\ & =& \sum _{J}A_{J}\,\varPhi _{J}\;. {}\end{array}$$

(5.2)

Here $A_{j_{1},\ldots,j_{p}}$ are the MCTDH expansion coefficients and $\varphi$ are optimal basis functions for this particular wavefunction, also called single particle functions (SPF), that are (exclusively) defined on one combined coordinate Q _κ , the latter comprising the aforementioned d (one to four) physical DOF. Note that the ansatz Eq. (5.2) is a generalized form of the standard Hartree ansatz and reduces to the very same if one sets n _i  = 1.

As mentioned before, the SPF are expanded on the primitive grid such that

$$\displaystyle{ \varphi _{j_{\kappa }}^{(\kappa )}(Q_{\kappa },t) =\sum _{ l_{1}=1}^{N_{1,\kappa } }\cdots \sum _{l_{d}=1}^{N_{d,\kappa } }c_{j_{\kappa }l_{1}\cdots l_{d}}^{(\kappa )}(t)\;\chi _{ l_{1}}^{(\kappa,1)}(q_{ 1,\kappa })\cdots \chi _{l_{d}}^{(\kappa,d)}(q_{ d,\kappa }), }$$

(5.3)

where the χ represent the primitive basis functions as in Eq. (5.1), usually grid points within a discrete-variable representation (DVR), and the c are again expansion coefficients.

Note, that other than in the standard form Eq. (5.1) not only the coefficients, but both the basis functions (SPFs) and the MCTDH expansion coefficients, are taken to be time-dependent in Eq. (5.2). Inserting this ansatz in the Dirac–Frenkel variational principle leads to equations of motion (EOM) for the SPF and the coefficients ($\hslash = 1$),

$$\displaystyle{ i \frac{\partial } {\partial t}A_{J} =\sum \limits _{L}\left < \varPhi _{J}\right \vert \hat{H}\left \vert \varPhi _{L}\right >A_{L}, }$$

(5.4)

and

$$\displaystyle{ i \frac{\partial } {\partial t}\varphi _{j}^{(\kappa )} = \left (1 - {P}^{(\kappa )}\right )\sum \limits _{ k,l=1}^{n_{\kappa }}\left ({\rho }^{(\kappa )}\right )_{ j,k}^{-1}\left < \hat{H}\right >_{ k,l}^{(\kappa )}\varphi _{ l}^{(\kappa )}, }$$

(5.5)

where $\hat{H}$ is the system Hamiltonian, $\left < \hat{H}\right >_{k,l}^{(\kappa )}$ are the so-called mean fields, ρ ^(κ) is the reduced system density matrix for the κth coordinate, and (1 − P ^(κ)) projects outside the space currently spanned by the SPF of DOF κ. Like for the standard form Eq. (5.4) resembles the matrix form of the time-dependent Schrödinger equation and Eq. (5.5) ensures that the basis set follows the motion of the wavefunction as it evolves in time.

Note that Eqs. (5.4) and (5.5) are coupled via the mean fields and the matrix elements. In practice, the EOMs are decoupled during an update time step, by the so called constant mean-field approach. Nevertheless, the evaluation of the EOMs (5.4) and (5.5) is rather costly as the calculation of the mean fields and matrix elements involves multi-dimensional integrals over all physical DOF. A key ingredient of the MCTDH algorithm therefore is that the Hamiltonian operator can be expressed in terms of products of low-dimensional terms $\hat{h}_{r}^{(\kappa )}$ such that

$$\displaystyle{ \hat{H} =\sum _{ r=1}^{s}c_{ r}\prod _{\kappa =1}^{p}\hat{h}_{ r}^{(\kappa )}, }$$

(5.6)

where the $\hat{h}_{r}^{(\kappa )}$ operate only on the κth composite coordinate. With this ansatz the multi-dimensional integrals reduce to sums of products of low-dimensional integrals:

$$\displaystyle{ \langle \varPhi _{J}\vert \hat{H}\vert \varPhi _{L}\rangle =\sum _{ r=1}^{s}c_{ r}\prod _{\kappa =1}^{p}\langle \varphi _{ j_{\kappa }}^{(\kappa )}\vert \hat{h}_{ r}^{(\kappa )}\vert \varphi _{ l_{\kappa }}^{(\kappa )}\rangle \;. }$$

(5.7)

In this form the evaluation of the right-hand sides of the EOMs can be effectively performed. (An alternative to the product form discussed here is the correlated DVR (CDVR) method of Manthe [15].)

The MCTDH ansatz Eq. (5.2) is also suitable for the calculation of eigenstates in which case the expectation value of the Hamiltonian is minimized. This leads to an eigenvalue problem for the A-vector

$$\displaystyle{ \sum _{L}\langle \varPhi _{J}\vert \hat{H}\vert \varPhi _{L}\rangle \,A_{L} = E\,A_{J}, }$$

(5.8)

which constitutes an ordinary eigenvalue equation that can be solved using a Krylow subspace method, and a propagation of the SPF in negative imaginary time $\tau = -\mathit{it}$, i.e., a relaxation, with the EOM

$$\displaystyle{ \frac{\partial } {\partial \tau }\varphi _{j}^{(\kappa )}:= -\left (1 - {P}^{(\kappa )}\right )\sum _{ k,l=1}^{n_{\kappa }}\left ({\rho }^{(\kappa )}\right )_{\mathit{ jk}}^{-1}\left < \hat{H}\right >_{\mathit{ kl}}^{(\kappa )}\varphi _{ l}^{(\kappa )} \rightarrow 0. }$$

(5.9)

Since both equations have to be fulfilled simultaneously, one again uses the constant mean-field approach to iteratively solve both equations until convergence is achieved.

One of the main challenges at the present time, however, is not so much the compact representation of the wavefunction but of the Hamiltonian. While the kinetic energy operator is in most cases known analytically and of the form Eq. (5.6) this is not the case for the PES. As stated above, accurate PES are often available only as intricate numerical subroutines resulting from previous quantum chemistry calculations. The sheer size of the primitive basis prohibits sampling of the PES or calculating the potential points on the fly for larger systems.

For smaller systems (six to eight DOF) one can use a similar ansatz for the potential as for the wavefunction Eq. (5.2) and use the so-called POTFIT algorithm[3, 16–19] or its multi-grid extension[20], to transform the PES into product form. This, however, requires multiple integrals over the complete grid such that POTFIT can only be used up to a certain number of DOF. For larger systems, one needs to use alternative techniques.

Within the present contribution we resorted to the so-called cluster expansion (CE)[10], a variant of the n-mode representation[21, 22], also called high-dimensional model representation or cut-high dimensional model representation (cut-HDMR)[23–26]. Within the CE the potential is approximated by n-particle interaction terms. These terms are called clusters. Again the Q _α refer to the composite coordinates as detailed above. The PES is approximated by the expansion

$$\displaystyle{ \begin{array}{rl} V (\mathbf{Q}) =&v_{\mathrm{ref}}^{(0)}(Q_{\mathrm{ref}}) +\sum \limits _{\alpha =1}v_{\alpha,\mathrm{ref}}^{(1)}(Q_{\alpha },Q_{\mathrm{ref}}) +\sum \limits _{\alpha <\beta }v_{\alpha,\beta,\mathrm{ref}}^{(3)}(Q_{\alpha },Q_{\beta },Q_{\mathrm{ref}}) \\ & +\sum \limits _{\alpha <\beta <\gamma }v_{\alpha,\beta,\gamma,\mathrm{ref}}^{(3)}(Q_{\alpha },Q_{\beta },Q_{\gamma },Q_{\mathrm{ref}}) + \cdots \end{array} }$$

(5.10)

with

$$\displaystyle{ \begin{array}{rl} v_{\mathrm{ref}}^{(0)}(Q_{\mathrm{ref}})& = V (0,\ldots,Q_{\mathrm{ref}}) \\ v_{\alpha,\mathrm{ref}}^{(1)}(Q_{\alpha },Q_{\mathrm{ref}})& = V (0,\ldots,Q_{\alpha },0,\ldots,Q_{\mathrm{ref}}) - v_{\mathrm{ref}}^{(0)}(Q_{\mathrm{ref}}), \end{array} }$$

(5.11)

etc. Q _ref here may either be a reference configuration or contain reference coordinate which is present in all clusters. The main advantage of this technique is that the series can often be truncated at low orders n and that the n-particle interaction terms v ⁽ⁿ⁾ only depend on a few (composite) coordinates such that POTFIT can be used to transform these low-dimensional terms into product form. The main disadvantage, on the other hand, is that this method is not variational and hence additional terms are not always guaranteed to improve the global accuracy of the expansion. It is also unknown which terms are significant and which ones can be neglected prior to their actual calculation, however, it can be estimated using statistical methods. Moreover, especially in the edges of the primitive grid the error of the expansion Eq. (5.10) is known to be rather uncontrollable. The CE often leads to numerical instabilities due to unphysically and strongly negative parts of the approximated potential which need to be “repaired” by adding either additional higher order terms of the CE or artificial external potentials. But even with these limitations, the CE is a powerful tool to represent potentials with a large number of DOF and hence this method is used for all calculations presented in this chapter.

5.3 Infrared Spectroscopy and Dynamics of the Protonated Water Dimer

Protonated water clusters (H(H₂O) _n ⁺) of various sizes and geometries have captured the attention of many researchers in recent years due to their importance to many areas of chemistry and biology. Advancements in understanding the dynamics and spectroscopy of this kind of systems were made possible owing to important improvements in the measurements of IR action spectra in the gas phase [27–32]. In order to assign the recorded spectra and extract meaningful structural and dynamical information, computational simulations are needed in conjunction with experiments. However, we are still far from accurate and reliable simulations of the IR spectra of all but the smallest clusters. This is caused by the coupled, anharmonic interatomic potential governing the motion of these systems, featuring many accessible minima connected through shallow barriers, and the need of a quantum dynamical treatment of the system to obtain accurate vibrational eigenstate energies and absorption cross-sections. Among the various clusters, the protonated water dimer (H(H₂O)₂ ⁺), also known as Zundel cation, has been the subject of intense research efforts, both from the experimental [28–32] and from the theoretical [8, 10, 11, 31–38] perspectives. The cleanest experimental IR spectra for the Zundel cation could be obtained by messenger atom tagging techniques using Ar [30–32] and Ne [31, 32] as the tagging agents. Previous multiphoton spectra measured by IR free electron lasers had presented substantially different features to the linear spectra measured at lower light intensities and had been very difficult to interpret [28, 29]. The spectrum obtained with Ne-tagging could be shown to be very close to the linear absorption spectrum of the bare cation. This spectrum could be assigned and fully understood only after full-dimensional quantum-dynamical simulation [8–10]. IR spectra of various isotopically substituted forms of the Zundel cation were also reported using the messenger predissociation technique with Ar-tagging in the range 600–4,000 cm⁻¹[32]. The large observed variation in the spectral features of the different isotopomers clearly pinpoints the complex nature of the cluster dynamics, dominated by anharmonicities and Fermi resonances.

5.3.1 Infrared Spectroscopy

The infrared spectra are calculated in the time-dependent representation of quantum mechanics by Fourier transformation of the auto-correlation of the dipole-operated initial state [1]:

$$\displaystyle\begin{array}{rcl} I(E)& =& \frac{E} {3\,c\,\epsilon _{0}\,{\hslash }^{2}}\mathrm{Re}\int \limits _{0}^{\infty }\exp (i\,(E + E_{ 0})\,t/\hslash ) \\ & & \times \langle \varPsi _{\mu,0}\vert \exp (-i\,\hat{H}\,t/\hslash )\vert \varPsi _{\mu,0}\rangle \ \;\mathit{dt} {}\end{array}$$

(5.12)

where E ₀ is the ground-state energy and $\vert \varPsi _{\mu,0}\rangle \equiv \hat{\mu }\,\vert \varPsi _{0}\rangle$. This corresponds to the first order time-dependent perturbation theory result for absorption spectroscopy. The great advantage of the time-dependent approach is that no full Hamiltonian diagonalization is required in order to obtain the vibrational eigenstates from which later transition dipole matrix elements would be computed. The latter becomes simply impracticable in systems of just moderate dimensionality due to the large number and density of states. Instead, the application of Eq. (5.12) requires an efficient wavepacket propagation method. As outlined in Sect. 5.2 an efficient propagation method for the time-dependent Schrödinger equation is given by MCTDH [2–5]. The choice of coordinates is crucial in quantum dynamics calculations of large molecules. The coordinates should correspond as much as possible to what could be called “natural motions” of the system. In rigid and weakly coupled systems these correspond to normal modes of vibration calculated from second order expansion of the PES around a suitable stationary point. In molecules and clusters featuring large amplitude motions and with strong mode couplings the best choice is usually to use internal coordinates consisting of, e.g., bond distances, bond angles or dihedral angles. Internal coordinates of this kind lead usually to complicated kinetic energy operators (KEO), and this is discussed elsewhere. Once the coordinates are fixed and the KEO has been obtained, the potential energy operator (PEO) part of the Hamiltonian has to be expressed in such coordinates in a form that makes the subsequent quantum dynamics calculations as efficient as possible. Various possibilities to attack this question are also discussed elsewhere. All details on the setup of the vibrational Hamiltonian of the Zundel cation can be found in [9, 39]. For the sake of completeness we mention that a set of curvilinear coordinates was used to describe the configuration of the system and that the exact KEO in this set of coordinates was employed. The 15 internal coordinates describing the system are: the distance between the oxygen atoms of both water molecules (R), the position of the central proton with respect to the center of mass of both oxygen atoms (x,y,z), the Euler angles defining the relative orientation between the two water molecules (waggings: γ _A , γ _B ; rockings: β _A , β _B ; internal relative rotation: α) and the Jacobi coordinates which account for the particular configuration of each water molecule ($R_{1(A,B)},R_{2(A,B)},\theta _{(A,B)})$) where R _1x is the distance between the oxygen atom and the center of mass of the corresponding H₂ fragment, R _2x is the H–H distance and θ _x is the angle between these two vectors. Figure 5.1 presents a scheme of the 15 coordinates that describe the configuration of the system.

Fig. 5.1

Diagram of the 15 internal coordinates describing the configuration of the Zundel cation. The internal coordinates of the water molecules ($R_{1X},R_{2X},\theta _{X}$) correspond to the Jacobi vectors connecting the oxygen atom to the center of the H–H fragment, the vector joining both hydrogen atoms and the angle between both vectors, respectively. The bending mode of a monomer is well described by the R _2X coordinate in the absence of large oscillations in the OH-stretching modes

To account for the interatomic potential we made use of the PES of Bowman and coworkers, which constitutes the most accurate ab initio surface available to date for this system [34]. The PEO was constructed as a CE or n-mode representation [21] as outlined in Sect. 5.2.

We will now discuss the accurate calculation and assignment of the IR spectra of the isotopically substituted forms of the Zundel cation D(D₂O)₂ ⁺, H(D₂O)₂ ⁺, and D(H₂O)₂ ⁺ [12]. These spectra are compared to the non-deuterated H(H₂O)₂ ⁺ cation, whose main features are extensively discussed in [8, 10].

Fig. 5.2

Comparison of MCTDH spectra with available experimental measurements from [32] for (a) H(H₂O)₂ ⁺ and (b) D(D₂O)₂ ⁺

Figure 5.2a presents the computed MCTDH spectrum for H(H₂O)₂ ⁺ in comparison with spectra from [32] measured using Ne and Ar as tagging agents. The agreement of the computed IR linear absorption spectrum with the Ne-tagging spectrum is excellent. The Ar-tagging spectrum presents splitting and broadening of its features due to the stronger interaction of Ar with the cation. For the deuterated species only Ar-tagged spectra have been reported to date [32]. Figure 5.2b presents the comparison of the computed D(D₂O)₂ ⁺ spectrum with the one obtained with Ar-tagging. The last presents relatively broad features, but the agreement in the positions of the main absorptions with theory is good. Therefore we can conclude that the spectra of the various Zundel forms computed with MCTDH will display a very good agreement with messenger predissociation spectra whenever the perturbation due to the tagging agent is small. This is in itself an important result that could only be established after comparison of the messenger tagging spectra with spectra calculated by a full-dimensional quantum mechanical treatment using MCTDH.

The interpretation of the IR spectra requires definite assignments of the spectral lines and an understanding of their origin. Zeroth-order states are used as a tool to perform such assignments. They correspond to well-defined local excitations of the system, e.g. the bending mode of the water molecules or the one-quantum excitation of the proton-transfer mode, and they are constructed as products of eigenfunctions of low-dimensional Hamiltonians. A more specific definition and procedures to obtain them in the context of MCTDH was presented elsewhere [10]. In the following, | Φ _l ⟩ refers to the vibrational wavefunction of a zeroth-order state while | Ψ _m ⟩ corresponds to a vibrational eigenstate. The quantities used for assignments are the $\vert \mbox{ $\langle \varPhi _{l}\vert \varPsi _{m}\rangle $}{\vert }^{2}$ products, which tell us to which extent a particular and well-defined zeroth-order vibration participates in a certain spectral line. Even though each line contains contributions from all or some of the considered zeroth-order states (non-vanishing $\vert \mbox{ $\langle \varPhi _{l}\vert \varPsi _{m}\rangle $}{\vert }^{2}$ elements), there is usually a zeroth-order state that contributes to a specific transition appreciably more than the others. Thus, when we refer to a certain spectral line as the (X) transition or to the corresponding eigenstate as | Ψ _X ⟩, it is because it is possible to identify the zeroth-order state | Φ _X ⟩ as the leading contribution to | Ψ _X ⟩. In the case of very large coupling it may not be possible to cleanly disentangle the spectrum into one-to-one assignments of spectral peaks to zeroth-order states, since a given transition may present similar contributions from two or more zeroth-order states. Tables containing the most important $\vert \mbox{ $\langle \varPhi _{l}\vert \varPsi _{i}\rangle $}{\vert }^{2}$ elements for the four considered isotopologues are provided in [40].

Fig. 5.3

Computed IR spectra of the (a) H(H₂O)₂ ⁺, (b) D(D₂O)₂ ⁺, (c) H(D₂O)₂ ⁺, and (d) D(H₂O)₂ ⁺ isotopologues of the Zundel cation with assignments of the most important peaks

Figure 5.3 presents the IR spectra of H(H₂O)₂ ⁺, D(D₂O)₂ ⁺, H(D₂O)₂ ⁺ and D(H₂O)₂ ⁺. The lowest frequency parts of the four spectra are composed of two lines related to the one-quantum wagging motions and its combination with the internal rotation motion of one of the monomers with respect to the other. The highest frequency parts of the spectra are composed of two bright lines related to the terminal O–H(D) vibrations of the water molecules. Neither the assignment of the just discussed peaks in the lowest and highest energy domain nor the relative positions between each other change after deuteration. Only the expected red-shifts take place for D(D₂O)₂ ⁺ and H(D₂O)₂ ⁺, i.e. when the terminal hydrogens are substituted by deuterium atoms.

The situation turns out to be much more complex in the spectral region between 600 and 2,000 cm⁻¹. The middle range spectrum of the H(H₂O)₂ ⁺ cation in Fig. 5.3a features five clearly visible absorptions in the range between 900 and 1,900 cm⁻¹. They could be assigned and explained as arising from a set of five coupled zeroth-order states composed of [8, 10]: $\vert \varPhi _{1R,w_{3}}\rangle$, a combination of two modes, a two-quanta asymmetric wagging (w ₃) mode and the one-quantum (1R) mode, where R is the O–O stretching coordinate; | Φ _1z ⟩, the one-quantum asymmetric proton stretch along the central O–O axis (z refers to the proton position along the O–O axis); | Φ _1z, 1R ⟩, the combination of the 1z and 1R excitations; | Φ _1z, 2R ⟩, the combination of the 1z and two-quanta O–O excitations; | Φ _bu ⟩, the ungerade water-bending mode.

The most intense line of the H(H₂O)₂ ⁺ spectrum centered at 1,040 cm⁻¹ is related to the (1z) transition since the displacement of the central proton along the O–O axis causes the largest variation of the dipole moment. Thus the | Φ _1z ⟩ zeroth-order state has a large contribution to this eigenstate, but the second most important contribution to this line arises from the $\vert \varPhi _{1R,w_{3}}\rangle$ zeroth-order state. The situation is reversed for the transition centered at 915 cm⁻¹, whose leading contribution is $\vert \varPhi _{1R,w_{3}}\rangle$ and the second most important one is | Φ _1z ⟩. Therefore the doublet of peaks centered at about 1,000 cm⁻¹ in the H(H₂O)₂ ⁺ arises from a Fermi resonance between the strongly coupled, zeroth-order states | Φ _1z ⟩ and $\vert \varPhi _{1R,w_{3}}\rangle$ [8, 10, 11]. The next three lines of the spectrum correspond to the 1,415 cm⁻¹ (1z, 1R), 1,750 cm⁻¹ (bu) and 1,905 cm⁻¹ (1z, 2R) transitions, respectively. All three transitions, and specially (bu), have a non-negligible contribution from the | Φ _1z ⟩ zeroth-order state, from which they obtain a large part of their spectral intensity [10]. Moreover, the strong coupling between the | Φ _1z ⟩ and | Φ _bu ⟩ modes is responsible for shifting the (1z) and (bu) lines about 150 cm⁻¹ down and up, respectively, with respect to their estimated uncoupled positions [10, 11].

The IR spectrum of D(D₂O)₂ ⁺ is shown in Fig. 5.3b. The (1z) peak is found here at 678 cm⁻¹ and is, as in H(H₂O)₂ ⁺, the most intense IR absorption. The (1R, w ₃) peak is found at 807 cm⁻¹. Therefore the characteristic doublet at about 1,000 cm⁻¹ in H(H₂O)₂ ⁺ is also found in D(D₂O)₂ ⁺, but with its constituent peaks in reverse order [12]. The (bu) peak is found at 1,298 cm⁻¹, about 450 cm⁻¹ below its position in H(H₂O)₂ ⁺. Neither (1z, 1R) nor (1z, 2R) peaks appear in the spectrum of D(D₂O)₂ ⁺. The position of these two eigenstates has been computed to be 1,150 and 1,600 cm⁻¹, respectively. Therefore they are located far from absorptions from which they could borrow intensity. Moreover, after deuteration the coupling between z (proton position) and R (O–O distance) is reduced since the system remains in deeper, less anharmonic regions of the potential, thus reducing even more the possibility for direct absorption of the (1z, 1R) and (1z, 2R) combinations [12]. Immediately above the (bu) peak a line is found, which can be assigned to (w ₃, 2R) [40]. This peak therefore borrows some intensity from (bu) in order to become bright in D(D₂O)₂ ⁺ via a similar mechanism that gives rise to the main doublet in H(H₂O)₂ ⁺. This absorption is seen as a shoulder to the (bu) peak in experimental spectra in this region [32].

The most complex of all considered spectra is H(D₂O)₂ ⁺, shown in Fig. 5.3c. Here the deuteration of the external positions brings the position of the zeroth-order state | Φ _bu ⟩ down to lower frequencies by about 300 cm⁻¹, while the zeroth-order states | Φ _1z ⟩ and | Φ _1z, 1R ⟩ remain almost unaffected. This results in a situation in which the zeroth-order | Φ _bu ⟩ is found between | Φ _1z ⟩ and | Φ _1z, 1R ⟩. These three zeroth-order states strongly couple to each other and are responsible for the triplet absorption with peaks at 938, 1,355, and 1,564 cm⁻¹ [12, 40]. The peak at 938 cm⁻¹ has almost equal relative contribution from | Φ _1z ⟩ and | Φ _bu ⟩. The central peak at 1,355 cm⁻¹ has almost equal participation from | Φ _1z ⟩, | Φ _bu ⟩, and | Φ _1z, 1R ⟩, while the peak at 1,564 cm⁻¹ is a mixture of | Φ _bu ⟩ and | Φ _1z, 1R ⟩ with a slightly larger participation of the latest. The strong couplings shaping the middle region of the spectrum are reflected in the loss of diagonal dominance of the matrix composed of the $\vert \mbox{ $\langle \varPhi _{l}\vert \varPsi _{m}\rangle $}{\vert }^{2}$ elements (see table in [40]) for H(D₂O)₂ ⁺. The use of a tilde in these three assignments in Fig. 5.3c indicates that the tag assignments are a bit arbitrary because of the strong mixing of underlying zeroth-order states, in contrast to other assignments in which one zeroth-order state is mainly responsible for a given peak. The (1R, w ₃) peak is of reduced intensity due to its red shift and consequent decoupling from the zeroth-order (1z). The (1z, 2R) state is located far from peaks from which it can borrow intensity and shows no IR absorption.

In contrast to H(D₂O)₂ ⁺, deuteration of the central position alone in D(H₂O)₂ ⁺ leads to the simplest and most diagonally dominant IR spectrum of this series. Here the zeroth-order (1z) shifts to lower frequencies and decouples from (1R, w ₃). The peak at 785 cm⁻¹ is cleanly assigned to (1z). (1z) decouples as well from (bu). This brings the position of the (bu) peak down to 1,662 cm⁻¹, closer to the bending frequency of an isolated water molecule and explains the reduced intensity [12, 40]. Note that the position of (bu) at 1,758 cm⁻¹ in H(H₂O)₂ ⁺ was due to strong coupling with the central proton (1z) mode. Due to the isotopic substitution the (1z, 2R) peak is shifted down, ending relatively close to (bu). The doublet formed by (bu) and (1z, 2R) is the only structure related to a resonance in D(H₂O)₂ ⁺. However, both lines can be cleanly assigned, as seen by inspecting the contribution of the corresponding zeroth-order states [12, 40].

We have seen that the effect of a full or partial deuteration of the cation not only leads to line shifts but also significantly changes the intensities and modifies the assignment of the infrared signatures of the different isotopologues. This is due to the soft, anharmonic, and coupled potential of the Zundel cation, where the dynamics and spectroscopy are strongly dominated by Fermi resonances between various coupled zeroth-order vibrations. The discussed quantum dynamical calculations represent an important milestone in our understanding of the spectroscopy and dynamics of protonated water clusters and on their dramatic isotope effects [41], and could only be achieved after a full-dimensional quantum dynamical treatment of the clusters.

5.3.2 Dynamics of the Excess Proton

We are now in a position to further explore the dynamics of the protonated water dimer and attempt to learn about the details of proton transfer dynamics in acidic water. These issues can be naturally addressed within the same methodological framework presented above to calculate the IR spectrum. The first proposal of a plausible mechanism for charge migration in water dates from two centuries ago and depicts the excess charge as hoping between neighboring waters [42]. In more recent times two limiting structures were proposed, namely the Zundel [43] (H₅O₂ ⁺) and Eigen [44] (H₉O₄ ⁺) cations, which represented excluding views of the hydrated proton in water. With the advent of sophisticated experimental and computational techniques during recent years a concordant view emerged for the transfer of an excess proton between two hydrogen-bonded water molecules [38, 45–47]. Both the Eigen and Zundel structures play a role as limiting ideal configurations in such mechanism. Basically, the breakage of a hydrogen bond in the second solvation shell of the Eigen cation allows for the excess proton to advance towards a neighboring water molecule while forming a Zundel-like transient structure. Based on the analysis of classical trajectories of an excess proton in bulk water two different time regimes were identified. On the one hand, the rate-limiting hydrogen bond breakage occurs in the time-scale of 1–2 ps. On the other hand, the ultra-fast rattling of the transferring proton between water molecules before the transfer is complete occurs in the time-scale of 100–200 fs or even less [48, 49]. Femtosecond pump-probe experiments in the infrared domain were able to access such ultra-fast proton oscillations between neighboring water molecules, which would even occur in a time-scale shorter than the resolution of the experiment, below 100 fs [50], thus supporting the view of an ultra-fast PT taking place only after the right coordination of the implied water molecules has been achieved, this last being the rate-limiting step of the overall process.

Fig. 5.4

(a) Expectation value ⟨R⟩ and (b) expectation value ⟨z⟩. The vibrational energy of the system is 2,575 cm⁻¹ (7.36 kcal/mol) above the ZPE. The expectation value ⟨z⟩ at t = 0 is −0.61 Bohr

In the following we will analyze the very fundamental proton transfer event between the fragments H₃O⁺ and H₂O from a quantum dynamical, time-dependent perspective, and provide a connection to the IR spectroscopy results presented above. An initial wavepacket to study the collision and proton transfer is prepared by applying a perturbing potential depending on the z and R coordinates in order to place the proton closer to one of the two water molecules [11] and to increase their intermolecular distance. This wavepacket corresponds to fragments H₃O⁺ and H₂O immediately before their encounter and exchange of a proton. This wavepacket is then propagated on the unperturbed Hamiltonian. At t = 0 we have ⟨R⟩ = 5. 20 Bohr (2. 75 Å), which roughly corresponds to the equilibrium distance of the hydrogen bond between water molecules. The proton is initially closer to water A (left in the plot). The total vibrational energy of the system in this propagation lies 2,575 cm⁻¹ (7. 36 kcal/mol) above the ZPE. Figure 5.4a, b present the time evolution of the ⟨R⟩ and ⟨z⟩ expectation values, respectively. After the dynamics starts the hydrogen bond quickly compresses and reaches its shortest value of ⟨R⟩ = 4. 37 Bohr (2. 31 Å) after 40 fs. After 75 fs it reaches its outer turning point at ⟨R⟩ = 4. 98 Bohr, which is, however, shorter than the initial O–O separation. The amplitude of the ⟨R⟩ oscillations is damped at each new cycle. The dynamics of the central proton depends to a large extent on the position of the R coordinate. The plot of ⟨z⟩ shows how the proton executes a fast motion towards the acceptor oxygen during the first half cycle of the ⟨R⟩ oscillation. The proton continues to be transferred during the second half of the ⟨R⟩ oscillation, between t = 40 and t = 75 fs while the R distance is becoming larger again. The rate of proton transfer is, however, slower during the second half-period. In the next full cycle of ⟨R⟩ the proton transfer proceeds slightly in the opposite direction, and after two cycles of ⟨R⟩ the expectation value ⟨z⟩ stabilizes around 0.

Fig. 5.5

Snapshots of the probability density ρ(z, R) for the simulation with a total vibrational energy of 2,575 cm⁻¹ (7.36 kcal/mol) above the zero point energy of the system

The probability density ρ(z, R) at different times during the dynamics is depicted in Fig. 5.5. After the first two oscillations of ⟨R⟩ during the first 150 fs the probability density ρ(z, R) reaches a nearly symmetric distribution in z, which is also evident from the fact that ⟨z⟩ ≈ 0. Although ⟨z⟩ attains an equilibrium value in this short period, the ρ(z, R) distribution changes in time by performing almost symmetric motions in z. This is seen by comparing the snapshots of ρ(z, R) at times 180, 210, 240, and 270 fs in Fig. 5.5. After about 120 fs a node develops in the (R) coordinate direction which then remains clearly visible for the rest of the simulation. This indicates that, once internally equilibrated, the (R) coordinate has about one quanta of excitation. Here we would like to emphasize again that the densities in Fig. 5.5 and expectation values in Fig. 5.4 are averaged quantities extracted from the full-dimensional (15-dimensional) propagation of the cluster. The dramatic effect of the strong coupling among vibrational modes becomes now apparent if one compares these dynamics to the kind of periodic and undamped motion that would be expected for a one- or two-dimensional model composed of only the (z) or (z, R) coordinates.

Fig. 5.6

Energy partition among combined modes (for details on the calculation, see [11]). Panel (a) presents the change in vibrational energy in the (z, R) coordinates and the sum of the changes of the vibrational energy in all other modes. The initial energy in each mode is used as the energy origin, so that energy changes relative to t = 0 are shown. The sum of these two energy changes equals the energy dumped to the coupling terms of the Hamiltonian, and hence differs from zero. Panel (b) displays the change in vibrational energy of all combined modes except (z, R) individually

Next, we discuss the dynamics of energy transfer from the (z, R) coordinates to the rest of the system [11]. During the first 50 fs these modes lose about 1,200 cm⁻¹ vibrational energy. At the end of the propagation a bit more than 1,500 cm⁻¹ of vibrational energy has been redistributed to the rest of the system. Interestingly, the energy transfer is markedly monotonic: the energy transferred from the (z,R) coordinates to the rest of the system is never transferred back during the length of the simulation. Such ultra-fast, irreversible energy transfer is the consequence of strong couplings between the various DOF of the system, which open very effective channels for vibrational energy redistribution. It is interesting to investigate how the vibrational energy redistributes among various vibrational modes. Figure 5.6b shows the vibrational energy in each combined-mode along time. The energy of (α,x,y) highly oscillates with a period that matches the motion of ⟨R⟩. These oscillations are not compensated by other modes, which indicates that these energy oscillations are related to an energy transfer from and to the coupling terms, i.e. $\hat{H} -\sum \hat{ {H}}^{(\kappa )}$ (where $\hat{{H}}^{(\kappa )}$ are separable Hamiltonians of the corresponding subpart of the cluster [11]), of the Hamiltonian. The rocking coordinates (β _A , β _B ) also have an oscillatory component, but underlying there is again a monotonic energy increase. The wagging coordinates ($\gamma _{A},\gamma _{B}$) gain energy in a smooth and steady way during the whole dynamics, while the internal coordinates of the water molecules gain energy in a much more abrupt way during the first 50–100 fs. By projection of the total wavefunction onto eigenstates of the $\hat{{H}}^{(\kappa )}$ Hamiltonians it is possible to learn more about the details of the energy redistribution during the proton transfer process. We find out that the vibrational energy in the (R) coordinate efficiently flows into the orientational DOF of the water monomers via their gerade motions [11]. From the internal motions within each water monomer only the bending modes play a significant role in the dynamics, while the O–H stretchings remain completely unaffected. All vibrational energy flowing into the internal coordinates of the water molecules is taken by the bending modes, even if the total energy of the system would be enough to appreciably excite the O–H stretchings. The strong coupling between proton transfer and bending modes has been analyzed in the IR spectra discussed previously, where it was shown that it leads to pronounced energy shifts of a few hundred wavenumbers of the corresponding absorption lines. The fact that the energy transfer occurs mostly within the first 100 fs, in which the central proton reaches a distribution close to equilibrium, suggests that there is a very efficient energy flow from the proton-transfer mode to the water bendings, in particular to the ungerade bending mode, which has the adequate symmetry for such coupling.

5.4 Tunneling Splitting of Malonaldehyde

Malonaldehyde (propanedial) is studied in many fields of the natural sciences. It is, for instance, an important product of the lipid metabolism and also serves as a biomarker for oxidative stress. In this function it plays an important role in many clinical studies. Also in food processing the presence of malonaldehyde indicates lipid oxidation and hence can be used for quality control purposes. Malonaldehyde is also one of the most prominent molecules that exhibit a keto-enol tautomerization and mainly exists in the enol form, of which in total eight possible but only one stable stereoisomers exist. The stable enol form consists of a horseshoe-shaped backbone of three carbon atoms with conjugated double bonds saturated with hydrogen. To one end of the carbon chain a hydroxyl group is attached while the other end is formed by an aldehyde group. The molecule is planar and the two oxygen atoms are oriented to the same side of the carbon chain (cis-form) such that they are in close proximity and an intra-molecular hydrogen bond forms between the hydroxyl and the aldehyde group [51].

This particular geometric arrangement gives rise to an interesting effect. The hydrogen of the hydroxyl group can tunnel through a potential barrier towards the other oxygen atom of the aldehyde group, thereby triggering a reorganization of the double bonds—and hence bond lengths—within the carbon backbone. This tunneling process is depicted in Fig. 5.7. The resulting structure corresponds to the perfect mirror image of the original molecule such that the proton transfer process occurs in a symmetric double well potential.

Fig. 5.7

Chemical structure and proton tunneling within the enol form of malonaldehyde. The proton of the hydroxyl group (a) is transferred via a transition state (b) to the oxygen of the (former) aldehyde group (c). During the transfer the single- and double-bonds as well as hydroxyl and aldehyde groups are interchanged resulting in a mirrored variant of the original molecule

The small size of the molecule and the occurrence of an intra-molecular hydrogen bond alongside with the existence of an intra-molecular tunneling process makes malonaldehyde a model system to study these kinds of processes. In particular the tunneling process has drawn quite some attention within the scientific community and has been described in numerous publications, both experimentally and theoretically. Spectroscopic measurements have already been performed in the late 1970s and early 1980s [52] and first estimates of the ground state tunneling splitting have been given as approximately 21 cm⁻¹ by Wilson and coworkers. Later this value could be refined and the value of the ground state tunneling splitting has been given very accurately as 21. 5831383(6) cm⁻¹ [53, 54].

Higher vibrational eigenstates and tunneling splittings have been measured and reported in a number of papers, most notably already by Wilson et al. [51, 52, 55] and Seliskar and Hoffman [56] in the early 1980s. Most recently Lüttschwager et al. reported [13] spectroscopic measurements and assignments of a larger number of vibrational states. These measurements allow a detailed comparison of calculated and measured data and hence can be used to construct and test model systems with large amplitude motions such as proton transfer reactions.

From a theoretical point of view an accurate treatment of these kind of processes is a challenging task. For a full quantum treatment, electronic structure calculations to a high level of theory need to be performed which became feasible in the early 2000s [57–60]. The first PES featuring full dimensionality was published by Yagi et al. [61] and a second one by Wang et al. [62]. Following the authors, the latter PES is the most accurate one published to date and in particular features the correct barrier height which the authors state as 4.1 kcal/mol.

However, a numerical reproduction of experimental spectra requires not only a correct PES but also the corresponding wavefunction of the system needs to be accurately represented. The proton motion is strongly coupled to the motion of the backbone atoms and the reorganization processes therein which makes the wavefunction highly correlated. Accurate calculations require a full quantum mechanical treatment of all involved particles. Nevertheless, in the past, a number of approximate methods have been used to overcome this bottleneck. These are, of course, models of reduced dimensionality where some DOF have been neglected [55], reaction surface methods, [63–65], more general methods [60, 62, 66–71], semi-classical approaches [72–77]. However, excitations in other modes than the transfer mode can change the effective barrier height and width for the tunneling process and therefore lead to different splittings. An illustrative example is the vibrational mode describing the distance of the two oxygen atoms. Excitation of this mode facilitates the proton transfer by effectively lowering the barrier and leads to a much larger tunneling splitting than observed for the ground state. The opposite effect can be seen upon excitation of the asymmetric out-of-plane motion of the two oxygen atoms which effectively increases the barrier height as the oxygen atoms move away from the proton.

Recently, a number of full quantum mechanical calculation on malonaldehyde employing MCTDH have been reported [66, 70, 78–80] using the potential energy surface of Yagi et al. [61] as well as for the PES of Wang et al. [62]. Here, the authors report that even the estimation of the ground state energy already reached the limit of today’s computational capacities as detailed in the following section, where we present state energies that were obtained using the PES of Wang et al. [62].

5.4.1 Calculated State Energies

The choice of coordinates is of particular importance for the calculations using MCTDH. The length of the A-vector (cf. Eq. (5.2)) is determined by the amount of correlation between the combined modes or particles as discussed in Sect. 5.2. The coordinates should therefore be chosen such that they minimize this correlation in the sense that a simple Hartree ansatz for the wavefunction already yields a good approximation of the wavefunction. Complicated curvilinear coordinates may reduce these “artificial” correlations but, on the other hand, they may complicate the calculation of expressions for the kinetic energy operator to such an extent that they become hardly feasible. Often one needs to find a compromise between these two.

Table 5.1 Labeling, frequencies in cm⁻¹, type and physical interpretation of the normal mode coordinates obtained at the transition state

For the calculations on malonaldehyde we used a set of mass- and frequency scaled normal mode coordinates $\left \{\tilde{q}_{i}\right \}$ obtained at the transition state depicted in Fig. 5.7b. The coordinate labeling, normal mode frequencies and physical description are outlined in Table 5.1. The coordinates were subsequently modified [78] to minimize the correlation induced by the reorganization of the double bonds. The shifts of the inter atomic distances only depend on the position of the proton along the transfer coordinate $\tilde{q}_{21}$. They can be compensated by the modified coordinates $\left \{q_{i}\right \}$ obtained by the transformation

$$\displaystyle{ \begin{array}{@{}ll@{}} q_{i} & =\tilde{ q}_{i} - F_{i}(\tilde{q}_{21}),\ \ \ \ i = 1\ldots 20,\\ q_{ 21} & =\tilde{ q}_{21}. \end{array} }$$

(5.13)

The F _i describe the displacements and were determined by minimization of the potential and subsequent fitting to polynomials such that the kinetic energy operator can still be obtained in analytic form as given in [78]. Note that in the following global rotation and vibration–rotation interaction terms have been neglected and a non-rotating system is assumed. In this case the vibration–rotation interaction contributes approximately 2.4 cm⁻¹ to the vibrational ground state energy and increases the tunneling splitting about 0.2 cm⁻¹ [78].

Details about the kinetic and potential operators can be found in [78] and [79]. The latter in particular contains a detailed description of the CE technique Eq. (5.10) used to model the PES. Here, we just note that other than in the previous section, the reference geometry always included the transfer coordinate and that relevant clusters have been identified using a Metropolis algorithm prior to their actual sampling on the primitive grid since a brute force calculation of all clusters was not possible.

For the representation of the wavefunction in MCTDH form, the 21 physical coordinates have been combined into six logical ones, where each mode contains three to four physical coordinates. The mode combination scheme is outlined in Table 5.2. It was chosen such that, where possible, physical coordinates that are strongly correlated are grouped together. This has the advantage that correlations between those modes are already represented on the SPF level and do not enter the A-vector. (Note that when computing the CE, Eq. (5.10), we have used less strongly combined particles. See [79].)

Table 5.2 Mode combinations for MCTDH calculations

Once having defined the computational setup, the ground state energy was estimated using an extrapolation scheme [78] based on the variational character of the MCTDH algorithm. The extrapolation scheme exploits the fact that adding SPF always leads to lower state energies. Provided an (in terms of number of SPF) almost converged wavefunction this energy drop is mode-local, i.e., it does (almost) not depend on changes in the number of SPF in other modes, so that the sum of energy drops one obtains by independently increasing the number of SPF in all modes, one by one, is an upper estimate for the energy lowering one would obtain if one increases the number of SPF in all modes simultaneously.

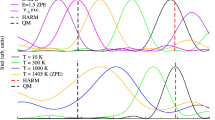
The extrapolation scheme is outlined in Table 5.3. Starting from a reference calculation the numbers of SPF are doubled for each mode independently and the energy drops are summed to obtain the true ground state energy and tunneling splitting. Since the energy drop for modes 3 and 6 where larger then for all other modes, we also performed an additional extrapolation by increasing the number of SPF in these two modes simultaneously.

Table 5.3 Extrapolation of the state energies

After careful convergence checks the zero point energy was obtained as 14,667.3 cm⁻¹ and the ground state tunneling splitting as 23.2 cm⁻¹. Additional calculations confirmed these results with an error of less than 2 cm⁻¹ for the ground state and less than 0.1 cm⁻¹ for the tunneling splitting. Concerning the dynamical calculation, the error introduced by the CE of the potential is difficult to estimate. However, we have performed CEs using different mode combinations and different selections of clusters (not discussed here) and obtained very similar results. Upon adding the estimated contributions of the vibration–rotation coupling terms (2.4 and 0.2 cm⁻¹) [78] a zero point energy of 14,670 cm⁻¹ and a tunneling splitting of 23.4 cm⁻¹ were obtained for the PES of Wang et al. [62]. These results are in very good agreement with the splitting of 23.8 cm⁻¹ obtained by Hammer and Manthe [78] who used a multi-layer variant of MCTDH together with the correlation DVR scheme. However, the tunneling splitting differs somewhat from the experimental value of 21.6 cm⁻¹. The zero point energy calculated by us is about 8 cm⁻¹ below the one obtained by Hammer and Manthe [78]. Again, this could be due to the CE, but we think the lower ground state energy reflects the fact that the present calculations are better converged.

Excited states and tunneling pairs were obtained using the block improved relaxation algorithm. The calculations were performed in blocks of four using the same computational setup as before but with a larger set of SPFs than for the reference state in Table 5.3 (Q ₁:18, Q ₂:10, Q ₃:16, Q ₄:11, Q ₅:11, Q ₆:22) and the blocks were chosen such that they overlap by one state. Calculated state energies from this work in comparison with values obtained in [80] and experimental energies [13] as well as tunneling splittings are outlined in Table 5.4 together with their assignments. Note that within the calculated energies and splittings the rotation–vibration interaction has been neglected. Since the wavefunctions become more and more structured the higher the state energy, it is not surprising that their accuracy decreases as emerging correlations cannot be completely covered by the A-vector anymore. However, the structure of the corresponding tunneling pairs is very similar such that this error cancels to quite some extent for the splittings. We therefore consider the splittings reported in Table 5.4 as converged while the state energies are likely to be slightly too large.

Table 5.4 Vibrational state energies relative to the ground state energy and tunneling splittings, both, calculated (this work and from [80]) and measured (from [13]), as well as their assignment

The calculated state energies and splittings we obtained as outlined in Table 5.4 are in reasonable agreement with the experiment. This is especially true for the state energies for which we obtain a difference to the experimental values of at most 14 cm⁻¹. However, it is interesting to see that for states q ₃ and q ₄ the energies are larger than the experimental values, while this is not the case for the q ₁ and q ₂ fundamentals. Here the experimental value are larger.

For the two lowest eigenstates we obtain very similar splittings as Hammer and Manthe [80], which are, however, somewhat larger than the experimental values. For the two following splittings (q ₁ and q ₂) Hammer and Manthe observe excellent agreement with the experiment while overestimating the absolute state energies by 35–50 cm⁻¹, presumably because of a lag of full convergence of the wavefunction. In contrast, we observe good agreement of our calculated state energies with the experiment while obtaining larger splittings than Hammer and Manthe. This is especially true for the fundamental of q ₁ for which we obtain a splitting of about 17 cm⁻¹, while the experimental value lies between 6 and 9 cm⁻¹. The situation changes for the splitting of q ₃. Here, the result of Hammer and Manthe is approximately 4 cm⁻¹ larger than the experimental one, while our result lies 2 cm⁻¹ above the experiment.

In addition to the fundamentals we also show two doubly excited states in Table 5.4. The first double excitation is observed in the mode q ₄ (O–O—distance) and the second one as a combination of an excitation within mode q ₁ and q ₄, which were both obtained among the fundamentals within the block improved relaxation scheme. Note that the sum of the fundamental frequencies yields almost exactly the frequencies of the double excitations, indicating that the anharmonic coupling between these states is small.

The comparison of the calculated values both, of Hammer and Manthe [80] and ourselves as well as the comparison with the experiment is quite interesting. While our results for the absolute state energies are in very good, the tunneling splitting are in reasonable, but not excellent, agreement with the experiment, the situation is vice versa for the results of Hammer and Manthe. Their splittings are indeed in excellent agreement with the experiment; however, the state energies are consistently too large as discussed above. At this point the origin of these differences remains unclear and further investigations are needed. Hammer and Manthe are using the CDVR scheme [15] and hence do not need to represent the PES in product form. The main source of inaccuracies in their work is most likely due to a not completely converged wavefunction and the errors introduced by the CDVR scheme (which are difficult to estimate). On the other hand, our wavefunction is better converged (although still not completely) and the main source of error may be introduced by the CE. As mentioned above, however, test calculations with different mode combinations and different selections of clusters lead to very similar results as outlined above. This makes us confident that our PES representation is reliable. Moreover, errors in the PES representation should largely cancel when inspecting tunneling splittings. Considering the results outlined above and their discussion, again, shows that the treatment of quantum dynamics in high dimensions is still a formidable task.

5.5 Summary

The protonated water dimer (or Zundel cation) constitutes an anharmonic and vibrationally coupled cluster featuring a complex IR spectrum. This system has been the subject of numerous experimental and theoretical investigations owing to its challenging nature and its importance as a fundamental building block in acidic chemistry. Here we presented a full-dimensional (15D) quantum mechanical calculation and assignment of the IR spectrum of the cluster using the MCTDH method. Vibrational spectroscopy inherently probes quantized vibrational excitations and a quantum mechanical treatment is critical to obtain the right absorption band positions and intensities. For such a strongly coupled and anharmonic system the description has to be full-dimensional and based on curvilinear coordinates, which render the correlation between modes tractable if chosen to represent physically meaningful bond lengths and angles of the system.

The IR spectrum of various isotopomers was discussed. Isotopomers of a system have identical PES but their IR spectra present shifts with respect to each other due to the different masses of some atoms. In the Zundel cation, we showed how different isotopomers have completely different spectra, which is a consequence of the complexity of coupling mechanisms and resonances shaping the IR absorption profile. The proton transfer dynamics of the Zundel cation was discussed as well and related to the IR signatures of the system.

Malonaldehyde with its intra-molecular proton transfer is another important model system to study these kind of processes and is hence a well-studied molecule. Experimental IR and Raman spectra have been recorded over the last decades and allow a detailed evaluation of full-dimensional (21-D) model calculations which only became possible in the recent years. In the present contribution we have presented full-dimensional calculations on the ground state energy and the lowest excited states. The calculations were performed using the MCTDH algorithm and the most accurate PES published to date [62]. Similarly as done in the Zundel studies, the PES was brought to a numerically useful form by adopting a CE. This re-fitting of the potential is likely the largest source of errors in our calculations.

With this setup and after careful convergence checks a ground state energy of 14,670 cm⁻¹ and a tunneling splitting of 23.4 cm⁻¹ have been obtained. Also, the first four fundamentals and their tunneling splittings as well as two double excitations were calculated and compared to experimental values as well as numerical results of Hammer and Manthe [80]. Reasonable agreement between calculated and experimental results was found. Slightly different results obtained with different, but related, numerical methods still show that large systems like malonaldehyde are a challenging task for accurate calculations.