Abstract
In this chapter, recent developments of the quantum wave packet methods for calculating differential cross sections (DCSs) of tetra-atomic reaction, for calculating DCSs of triatomic reaction using wave packet method only with reactant Jacobi coordinates, for calculating and analyzing the reactive resonance wave functions, and for simulating and explaining experimental observables of a reactive scattering, are given. Applications to the F + H2 reaction, especially some fundamental understandings of its short-lived reactive resonances, the H + O2 reaction, the H2 + OH → H + H2O reaction, and the OH + CO → H + CO2 reaction are presented for illustration.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
4.1 Introduction
For decades it has been witnessed the persistent endeavors from both experimental and theoretical sides in the attempts to reveal the ever detailed minutes of how the reactants evolve to products during a chemical reaction process in various conditions. A chemical reaction may be envisioned as a scattering collision in which the original chemical bonds are cleaved and new ones are formed. Considering the large mass difference between electrons and nuclei, it is advantageous to separate the treatment of a reaction into solutions of two Schrödinger equations: first for the electrons at fixed nuclear positions, and then for the nuclei. This is the Born–Oppenheimer (BO) approximation, and it is valid for many chemical reactions. The treatment of the motions of electrons allows the definition of potential energy surface (PES) as a function of all nuclear coordinates, and then the dynamic motions of nuclei during a reaction are governed by the PES, which provides the force acting on each nuclei in the system. A chemical reaction takes place on the PES along a minimum energy path connecting the reactant region to the product region, and it is called the reaction coordinate for the chemical reaction. In a typical chemical reaction, the path traverses a reaction intermediate region, which is defined as the transition state [34, 35].
Theoretically, the very early theory was pioneered by Hirschfelder and his coworkers dated back to the later 1930s and early 1940s [49, 52], but it takes more than 30 years to see the report of the fully quantum mechanical method on the simplest three-dimensional H + H2 exchange reaction [110, 111], even though various model calculations were implemented on H + H2 [62, 108, 109, 133, 134, 143] and F + H2 [106, 112, 144]. With the tremendous progress of various theoretical and numerical methods to deal with the partial differential equations and associated boundary conditions in the field of quantum reaction dynamics [4, 15, 50, 90, 96, 107], it has now become just a routine to perform full-dimensional quantum scattering calculations for atom–diatom systems with both accurate ICS and DCS at the state-to-state level [3, 100, 119, 124, 140], especially after the introduction of reactant coordinate-based method [43, 126, 127]. Previously one had to transform the wave function between the reactant Jacobi coordinates and the product Jacobi coordinates (Jacobi coordinate is defined in Sect. 4.3), in order to efficiently express the reactant ro-vibrational states and the product ro-vibrational states and further obtain the state-to-state information. This leads to the well-known coordinate problem in time-dependent quantum wave packet calculation for extracting state-to-state reactive scattering information. Therefore quantum wave packet method had only been considered as a convenient method for calculating initial state-specific total reaction probabilities. Nowadays the quantumwave packet method has also been proved an effectivemethod for extracting state-to-state information.
Once the atom–diatom reactive scattering problem had essentially been solved, attention naturally turned to more complicated reactions involving more than three atoms—as the first step, to systems involving four atoms. Unfortunately, this is not a trivial task, as the number of degrees of freedom increases from three for a three-atom system to six for a four-atom system. In the past decades, significant progress has been made on accurate quantum reactive scattering studies of four-atom chemical reactions. Starting from time-independent (TI) reduced dimensionality approaches [15, 26], it is now possible to calculate fully converged integral cross sections [42, 155, 164], and state-to-state dynamical quantities for the total angular momentum J = 0 [29, 156, 165] without any dynamical approximation for some four-atom reactions, mainly through the development of the initial state selected wave packet method. Other quantum dynamical approaches have also received great success in four-atom reactions, such as the Multi-configurational Time-Dependent (TD) Hartree (MCTDH) approach for thermal rate constant calculations [72]. Various TID and TD reduced dimensionality calculations were also reported on different systems [118, 149, 154, 163, 166]. Recently, time-dependent wave packet (TDWP) method was developed to compute differential cross sections (DCSs) for four-atom reactions and applied to the prototypical HD + OH → H2O + D [70, 145] and D2 + OH → HOD + D reactions [69]. Excellent agreements were achieved for the first time for a four-atom reaction between the full-dimensional DCS and high-resolution crossed-molecular beam experimental results. Because it only takes a relatively short time to obtain fully converged DCS for the reaction, it is conceivable that the wave packet-based quantum scattering method has matured to the stage where it can afford yielding complete dynamical information for many four-atom reactions, as have been done for three-atom reactions in the past decades.
While fully quantum mechanical calculations on larger reactive system are always limited by the current computational power, the quasi-classical trajectory (QCT) method provides a feasible alternative by describing the scattering collisions with classical equations of motion [54, 99]. However, despite its high efficiency and intuitive nature, QCT is not a rigorous method to deal with quantum dynamics in reactive scattering, such as reactive resonance, zero-point energy, quantum tunneling, and interference. Even atoms other than hydrogen and its isotopes usually are not believed to have strong tunneling effect at room temperature, it is not clear what is exact the role of the zero-point energy in a molecular dynamics process.
In this chapter, we aim to provide quantum mechanical methods to simulate and explain some interesting experimental observables of reactive scatterings, especially some fundamental understandings of the short-lived reactive resonances.
4.2 Resonance in a Reactive Scattering
Three types of reactive resonances near the transition state region in chemical reactions, adapted from [66]. Panel (a) illustrates the case associated with a deep potential well along the reaction coordinate. The resulting bound and pre-dissociative quasi-bound states can be characterized, for a three-atom system, by three vibrational modes. (b) Threshold resonance for which only the two motions orthogonal to the unbound reaction coordinate are quantized and thus assignable by vibrational quantum numbers. The dynamical trapped-state resonance is schematically shown in panel (c). Despite the repulsive potential energy surface along the reaction coordinate, this metastable state can be assigned by three vibrational quantum numbers
For a reactive scattering, the properties of the reaction system near the transient region have the dominant role that determines various details of reactive collisions including the nature of potential surfaces, nonadiabaticity, direct and complex-forming collision dynamics, energy partitioning, product state and angular distributions, quantum tunneling and resonances in the transient region, and other interference effects.
The literature has seen several comprehensive reviews that summarized the recent advances in the understanding of reactive resonance [22, 37, 66, 67, 148], and for the consideration of integrity, here we shall only briefly explain the basic concepts.
The properties of the reaction system near the transient region determine how the reactant evolves to the product side, and in a typical chemical reaction, reactions form short-lived intermediate reactive complex at the transition state region and finally decay into the final reaction products. The transition state region can be an energetic barrier, which separates the reactants from products, and in some cases after this barrier the reaction coordinate shows itself with a deep potential well, shown in Fig. 4.1a, which attracts the intermediate complex for a long time before it decays into the final products. The latter is always named as complex-forming reaction, and we shall not go into too much details in this kind of resonance, as recently it has been intensely reviewed by an elegant article [46]. We shall from now on only focus on the reactive resonance in direct reactions.
Schematic illustration of the threshold resonances (a) and quantum dynamical resonance (b), adapted from [67]. In each panel, the left figure illustrates the effective dynamical potential along the reaction coordinate R, and the middle and the right ones are the E c-dependence of the reaction probability \(P_{J}(E_{\mathrm{c}})\) and the reaction cross section σ(E c). In the case of threshold resonance, the non-zero values of the reaction probability and cross section start at a smaller collision energy than the height of the barrier, which manifests the effect of zero-point energy
In a direct reaction, the minimum energy path along the reaction coordinate shows itself with repulsive feature on the PES, and no discrete quantum state exists in the transition state region along the reaction coordinate R, shown in Fig. 4.1b, c. The directions perpendicular to R are the internal coordinates u of the reaction system, and the motions along u are quasi-bound, which is the character of the saddle-point nature in the transition state region, shown in Fig. 4.1b. In a typical atom–diatom reaction, A + BC, the reaction coordinate approaches the asymmetric stretch motion of the ABC complex in the transition state region, and the two quasi-bound states are the symmetric stretching and bending modes. Due to the discrete nature of the two quasi-bound states, they would serve as a bottleneck to gate the flux going from the reactant region to product side. This is named as the threshold resonance or barrier resonance, and the discrete quasi-bound states are the quantized bottleneck states. As a result, stair-like feature is observed in the reaction probability \(P_{J}(E_{\mathrm{c}})\) from a single partial wave J as a function of the collision energy, as shown in Fig. 4.2a (middle). The effect of zero-point energy manifests itself in the reaction probability as the smaller reaction threshold energy than the height of the barrier.
The other reactive resonance is called the trapped-state resonance or Feshbach resonance, shown in Fig. 4.1c. In this case, the ABC complex is dynamically trapped along the reaction coordinate, even the minimum energy path on the BO PES is totally repulsive. The trapping of the short-lived ABC complex is caused by the vibrationally adiabatic potential, which is based on the concept of vibrational adiabaticity [23, 75, 76, 120]. As the vibrational motions along the directions perpendicular to R are fast compared with the motion along R, the vibrational modes should approximately conserve the quantum number n, which is in the spirit of BO separation of motions with different time scale. A typical vibrationally adiabatic potential along the reaction coordinate R is shown in Fig. 4.2b (left), and it can be constructed as
in which V MEP(R) is the minimum energy path along the reaction coordinate, and \(\varepsilon _{\mathbf{n}}(R)\) is the quantized vibrational energy of the orthogonal motions. In the vicinity of the transition state region, the strong couplings between the vibrational motions and the reaction coordinate lead to the dramatic vibrational frequency decrease due to the weakening of the bonds, and consequently dynamic potential well would appear along the reaction coordinate, especially for high vibrational quantum numbers. If the well is deep enough to support discrete resonance quantum state along the reaction coordinate, an isolated sharp peak should be observed in the reaction probability \(P_{J}(E_{\mathrm{c}})\), as shown in Fig. 4.2b (middle) for \(P_{J}(v^{\prime} = 1;E_{\mathrm{c}})\) of the v′ = 1 product state from a single partial wave J. The appearance of the isolated sharp peak before the reaction threshold energy is due to the resonant tunneling process through the barrier, which enhances the formation of the resonance complex state, and at higher collision energy, the direct reaction of the broad over-the-barrier probability dominates the process. In a one-dimensional model, the resonance produced by a potential like in Fig. 4.2b (left) is called as shape resonance [37]. While in multi-dimensional case, energy exchange occurs between various collective modes of the compound molecule, and it is named as the Feshbach resonace.
Even though the reaction probability provides distinctly different characteristics for the above two types of reactive resonance, the experimental observables of the reaction cross sections are often smeared out due to the summation of all possible \(P_{J}(E_{\mathrm{c}})\), which is inevitable because of the existence of many partial. The interpretation of the experimental observables and further understanding of the effects of reactive resonance require the intense interplay between theory and experiment. For example, the transition state region is often tight, and only a small range of partial waves contributing to the DCS in certain direction, which is amenable to quantum mechanical calculations. We shall be able to focus on reaction probabilities of a certain range of partial waves, from which the different kinds of reactive resonance manifest themselves with distinct features.
In the following part, we will review the current quantum wave packet method for simulating reactive scattering processes and its applications, especially on understandings of reactive resonances. The quantum dynamical studies have greatly deepened our understandings of the reaction dynamics in some prototypical systems. The following part is full of technical details and one may skip it for a general interest.
4.3 Theory by Quantum Wave Packet Method
4.3.1 Overall Theory
In a reactive scattering, the full Hamiltonian H needs to be partitioned in different arrangement channels ν,
in which \(H_{0}^{\nu } = {T}^{\nu }(R) + {h}^{\nu }(\boldsymbol{q})\) is the asymptotic Hamiltonian, V ν is the interaction potential, and T ν(R) is the kinetic energy operator in the translational degree of freedom, R, \({h}^{\nu }(\boldsymbol{q})\) is the internal Hamiltonian in the internal degrees of freedom, \(\boldsymbol{q}\). In the limit that the separation of the two fragments R goes to infinity, the interaction potential would be vanished, and the eigenfunction of the system is simply the product of a plane wave and the eigenfunction \(\chi _{n}(\boldsymbol{q})\) of the internal Hamiltonian \({h}^{\nu }(\boldsymbol{q})\),
in which \(\chi _{n}^{\nu }(\boldsymbol{q})\) is related to E n by
and the translational plan wave is directly written as
where \(k = \sqrt{2\mu (E - E_{n } )/{\hslash }^{2}}\), μ is the reduced mass of the translational motion. The eigenfunction \(\psi _{n,E}^{\nu,\pm }\) of the full Hamiltonian H is related to the asymptotic wave function through the Møller operator, Ω ± [153],
Given the definition of S matrix operator, \(S =\varOmega _{ -}^{\dag }\varOmega _{+}\), the probability amplitude to scatter from an initial state i of the reactant arrangement α to a final state f of the product arrangement β is written as the matrix element of the S operator [153],
There are generally two methods to calculate the S matrix element. The first one is the time-independent (TI) method, which solves the eigenvalues of the full Hamiltonian H to obtain the scattering matrix \(\psi _{f,E^{\prime}}^{\beta,-}\) and ψ i, E α, +. In a single run of the TI method, the entire S-matrix is obtained at a particular energy E. TI method is especially suitable for the case with low energy, such as cold collision problem. However, the TI method is notorious for its bad scaling relation N 3, with respect to the number of basis functions, N. Alternatively, the time-dependent (TD) method or wave packet method has a better scaling of N 2, and it is carried out by solving the TD Schrödinger equation of a first-order differential equation.
In a typical wave packet method, three steps are involved to calculate the S matrix. First, an initial wave packet Ψ i of definite internal quantum states is launched in the reactant region with normally a Gaussian shape wave packet in the scattering coordinate, and this determines the range of collision energy. Then the wave packet is propagated for a sufficient length of time until the reaction is finished. Finally, the state-to-state S-matrix element is obtained for the reactive scattering. In the TD method, the S-matrix element is reformulated by wave packet correlation function [132],
where Ψ f is the final wave packet, a i (E) and a f (E) are the energy amplitudes of the energy normalized eigenfunctions contained in the initial and final wave packets. It can be seen that the S matrix element is obtained by the Fourier transform of the time correlation function C fi (t) between the final wave packet and the propagated initial wave packet, \(C_{\mathit{fi}}(t) =\langle \varPsi _{f}\vert \varPsi _{i}(t)\rangle\).
It should be noted that the initial and final wave packets are usually expressed in the Jacobi coordinates of their own arrangements, which results in the difficult coordinate problem in state-to-state reactive scattering as we mentioned previously. One may either choose the product Jacobi coordinate [47, 53, 65, 151], or reactant Jacobi coordinate to propagate the initial wave packet, and there also exist two other methodologies but may be both named as reactant coordinate-based (RCB) method: the first one is to employ interpolation schemes for the coordinate transformation [41, 89, 126, 127, 156], and the second one is realized by projection of both reactant and product wave packets to an intermediate coordinate [43, 127], Alternatively, in the reactant–product decoupling (RPD) method [6, 7, 96], both the reactant and product coordinates are used, and they are divided and combined by a complex absorbing potential.
4.3.2 Quantum Wave Packet Method
The ever increasing popularity of the wave packet approach to reactive scattering is attributed largely to its intuitive time dependence and better scaling laws [87]. However, the concept of wave packet was originally postulated long time ago by Schrödinger in 1926 [115] as a coherent superposition of states, with localization in its position representation. The states can be electronic states, vibrational states, or rotational states, but in molecular wave packet method, the wave packet represents the coherent nuclei motion on certain electronic PES under Born–Oppenheimer approximation. Since the formulation of these original works, molecular wave packet theory has undergone a huge development, as reviewed by Manz in his comprehensive historical survey of molecular wave packet theory in the period of 1926–1996 [74].
Since the numerical details for a triatomic reactive scattering can be directly extended to more complicated systems and are very typical, we will focus on the triatomic reactions in this part.
4.3.2.1 Hamiltonian and Discretization
To study the atom–diatom reactive scattering, A + BC(v i , j i ) → AB(v f , j f ) + C/AC(v f , j f ) + B at a state-to-state level, body-fixed (BF) frame Jacobi coordinates are used to represent the corresponding wave packets in their arrangements: normally the reactants A + BC is for the α arrangement, and the two product channels AB + C and AC + B are for the β and γ arrangements, respectively. The Jacobi coordinates for the three arrangements are shown in Fig. 4.3. In each arrangement, the coordinate is denoted as \((R_{\nu },r_{\nu },\theta _{\nu };\boldsymbol{\varOmega _{\nu }})\), where ν represents any one of the above arrangements. For example, when ν represents the reactant arrangement, R ν is the length of vector \(\boldsymbol{R}_{\nu }\) pointing from the BC center of mass to A, r ν the BC bond length, and θ ν the angle between BC bond and \(\boldsymbol{R}_{\nu }\); \(\boldsymbol{\varOmega _{\nu }}\) denotes the Euler angles orienting \(\boldsymbol{R}_{\nu }\) in the space-fixed (SF) frame.
Considering the reaction scattering as an isolated system, the calculation is always carried out using a partial wave representation, in which the total angular momentum J is a good quantum number and one can take advantage of the conservation of the total angular momentum to break the problem into separate calculations for each value of the total angular momentum quantum number J. The Hamiltonian for a given total angular momentum \(\boldsymbol{J}\) is given in the reactant Jacobi coordinate as
where the arrangement label α is removed for clarity consideration, μ R and μ r are the corresponding reduced mass for R and r, respectively. The squared orbital angular momentum operator is responsible for the centrifugal potential and expressed as
where \(\hat{\boldsymbol{J}}\) and \(\hat{j}\) are the total and BC diatomic rotational angular momentum operators, with \(\hat{\boldsymbol{J}}_{z}\) and \(\hat{j}_{z}\) as their corresponding projections onto the BF z-axis, which coincides with the vector R. The raising/lowering operators in the last two terms, \(\hat{\boldsymbol{J}}_{\pm }\) and \(\hat{j}_{\pm }\), represent the Coriolis coupling, which couples the adjacent helicity quantum number K. K is the projection of both J and j onto the BF z-axis, and it is a good quantum number in the BF frame.
For each partial wave J and parity ε, the Hamiltonian and wave packet are discretized in the BF frame in mixed representation [21, 64, 80, 89, 160]: discrete variable representation (DVR) is employed for the two radial degrees of freedom and finite basis representation (FBR) of normalized associated Legendre function \(\mathcal{Y}_{\mathit{jK}}(\theta )\) for the angular degree of freedom. Thus the wave packet in the BF frame is written as
where \(\mathcal{D}_{\mathit{MK}}^{J\epsilon {\ast}}(\boldsymbol{\varOmega })\) is the parity-adapted normalized rotation matrix, depending only on the Euler angles \(\boldsymbol{\varOmega }\),
where ε is the parity of the system defined as ε = (−1)j+l with l being the orbital angular momentum quantum number, and \(D_{\mathit{MK}}^{J{\ast}}(\boldsymbol{\varOmega })\) is Wigner rotation matrix [16, 152]. The usage of the parity-adapted normalized rotation matrix restricts the K to be nonnegative and the basis size is reduced almost by half. ψ(t, R, r, θ K; K) only depends on three internal coordinates and K, and it is expanded as
where n and m are the radial basis labels, u n (R) and ϕ m (r) are the corresponding basis functions, respectively, and \(\mathcal{Y}_{\mathit{jK}}(\theta )\) is the normalized associated Legendre function.
4.3.2.2 Construction of the Initial Wave Packet
As has been mentioned above, the first step of the wave packet method is to set up the initial wave packet. The initial wave packet is advantageous to be defined in the SF frame, because the Coriolis couplings in the BF frame are long ranged and it requires to define the initial wave packet at rather large position of R. There are not many ways to account for them in a reasonable grid. On the other hand, in the SF frame, the asymptotic form of the scattering wave function can be described by the Riccati–Hankel function, and the long-range centrifugal term is diagonal, l(l + 1)∕2μ R R 2 [3, 30]. Consequently, the initial wave packet can be placed as close as the interaction potential is negligible. In such a manner, the initial wave packet is defined as the product of the diatomic ro-vibrational eigenstate \(\phi _{v_{0}j_{0}}(r)\) of BC and a Gaussian wave packet G(R) in the translational coordinate [3, 65, 126],
where \(\vert \mathit{JMj}_{0}l_{0}\epsilon \rangle\) is the eigenfunction of the total angular momentum operator in the coupled representation of the SF frame with parity of system \(\epsilon = {(-1)}^{j_{0}+l_{0}}\), and the Gaussian wave packet G(R) in the translational coordinate is given as
in which δ, R 0, and k 0 are the width, mean position, and mean momentum of the translational wave packet, respectively, and they determine the range of collision energy.
Wave packet is always propagated in the BF frame, and the initial wave packet needs to be transformed from the SF to the BF frames before the propagation, which is to transform the SF eigenfunction \(\vert \mathit{JMj}_{0}l_{0}\epsilon \rangle\) of the total angular momentum operator in the coupled representation to the BF frame,
where \(\boldsymbol{C}_{l_{0}K}^{\mathit{Jj}_{0}\epsilon }\) is the parity-adapted orthogonal transform matrix between the SF and BF frames [65, 101, 153, 157] and given as
where \(\langle \,\mathit{jK}l0\vert \mathit{JK}\rangle\) is the Clebsch–Gordan coefficient.
4.3.2.3 Propagation of the Wave Packet
After the preparation of the initial wave packet, it is then propagated under the operation of system Hamiltonian by the unitary propagator \(U(t,t_{0}) = {e}^{-\frac{i} {\hslash } H(t-t_{0})}\).
Usually, the propagator U(t, t 0) is approximated by various schemes [55, 60, 137], and there are plenty of wonderful articles that have explained each in detail, such as the split operator method and higher order split operator methods [11, 36, 130], Chebyshev polynomial expansion [131], Faber polynomial expansion [51, 146], short iterative Lanczos propagation method [95], Crank–Nicholson second-order differencing [10, 56, 57], symplectic method [14, 45], recently proposed real Chebyshev method [24, 44, 125], and Multi-configuration Time-Dependent Hartree (MCTDH) Method [12, 73, 81–83]. For details, one may refer to the corresponding references.
4.3.3 State-to-State Method: The RPD Approach
It has been a long time that only the product Jacobi coordinates were used in the propagation for extracting state-to-state information: the initial wave function, which is constructed in reactant Jacobi coordinate, is first transformed into product Jacobi coordinate, directly or after some propagation time to focus the initial wave packet in interaction region. Then the wave function propagation and product state-resolved information is calculated. Later, RPD method was proposed [96], particularly for direct reactive scattering process where it has been proved being very efficient. Recently, efficient RCB method was put forward by Sun et al. and Roncero et al. [43, 126, 127], particularly for reactive scattering process involving intermediate complex. The RCB method has been applied with H + O2 [124], O + O2 [128], N + NO → N2 + O etc., which clearly demonstrated its efficiency and convenience for usage. In this part we only briefly introduce the RPD method, which is the only technique capable of extracting state-to-state DCS of tetra-atomic molecules currently.
The RPD method, originally introduced by Peng and Zhang [96] in order to extract the state-to-state information efficiently, transforms no-return part of reacted wave packet continuously in time from reactant to product coordinates with the help of absorption potentials. It divides the full time-dependent wave function into the reactant and product components and the calculation of each component can be carried out using the Jacobi coordinates of the corresponding arrangement channel separately. The RPD method solves, to a large extent, the problem of the choice of coordinates in quantum reactive scattering.
In the time domain, the RPD scheme partitions the full time-dependent (TD) wave function into a sum of reactant component (Ψ r ) and all product components (Ψ p , p = 1, 2, 3, …) that satisfy the following decoupled equations:
where −iV p is the negative imaginary potential (absorption potential) used to prevent the wave function Ψ r (t) from entering the pth product arrangement. The solution for Ψ r (t) is independent of those for Ψ p (t) and the latter are independent of each other. Therefore, Ψ r (t) can be propagated in the reactant Jacobi coordinates just as for total reaction probability calculations,
Every product wave function, Ψ p , can be propagated in its own coordinates as in a normal wave packet propagation except with a source term, ξ p , provided by Eq. (4.19),
Finally, one can extract the final state information, such as state-to-state S matrix elements or reaction probabilities, from the Fourier transformation of Ψ p (t).
The RPD approach is very efficient on dealing with direct reactants with barriers as demonstrated by Althorpe and coworkers [3, 8], because in this case the absorption potential can be applied right after the barrier as in initial selected total reaction probability calculations and it is also rather cheap to carry out the continuous propagation for the absorbed wave packet in a product channel. In particular, Althorpe and coworkers have realized that the absorption of reacted wave packet can be performed after multiple propagation steps [5, 29].
In the original RPD approach, the source term \(\xi _{p}(t) = (1 - {e}^{-V _{p}\varDelta /\hslash })\varPsi _{r}(t)\) is saved and transformed from reactant to product Jacobi coordinates at every propagation time step. By using the multiple-step reactant–product decoupling (MRPD) scheme, one can be saving and transforming the source term at every M time [68, 70, 71].
where t 0 is the starting point for performing wave function transformation. At other time steps, we carried out the standard split-operator propagation for Ψ r (t) and Ψ p (t) without the absorption potential, V p , related terms. In this way, we can cut the computational time for wave function transformation from reactant coordinates to product coordinates by a factor of M.
Since the efficiency of RPD method for a state-to-state calculation of a direct reactive scattering process, it is crucial for extracting product state-resolved information of tetra-atomic reaction limited by current computer resource. The applications below of tetra-atomic reaction are accomplished by using the RPD method.
4.3.4 Calculation of the Experimental Observations
4.3.4.1 Calculation of S-Matrix of Triatomic Reaction Using the RCB Method
To calculate the state-to-state S-matrix in Eq. (4.8), the time correlation function \(C_{\mathit{fi}}(t) =\langle \Psi _{f}\vert \Psi _{i}(t)\rangle\) needs to be calculated at each time step during the propagation. A projection plane is often defined as R ν = R ν0 for the νth (ν = β or γ) arrangement using the corresponding product Jacobi coordinate, and the time correlation function is always carried out on this projection plane but the projection action can be carried out in either reactant or product Jacobi coordinate. The final product wave packet \(\varPsi _{f}(R_{\nu })\) is also defined in the SF frame due to the merits already mentioned above,
in which R′, r′, and θ′ describe the product Jacobi coordinate, and \(\boldsymbol{\varOmega }^{\prime}\) are the Euler angles for \(\boldsymbol{R}^{\prime}\) in the SF frame. In practice, one often calculates the scattering wave function in the energy domain before taking overlap with the final product state, and it is obtained by a time-energy Fourier transform from the propagated wave packet,
With the strategy to deal with the coordinate problem as mentioned in Sect. 4.3.1, the state-to-state S-matrix can be readily evaluated,
where a i (E) and a f (E) are given by
in which μ R′ is the reduced mass for the product translational degree of freedom, \(\mathcal{H}_{l}\) is the outgoing Riccati–Hankel function.
Finally, the S-matrix needs to be transformed from the SF frame to the helicity representation by the standard transformation,
4.3.4.2 Calculation of ICS and DCS
By substituting the S-matrix \(S_{v^{\prime}j^{\prime}K^{\prime}\leftarrow \mathit{vjK}}^{J}(E)\) in the helicity representation into the standard formulas, the state-to-state ICS can be obtained by summing over the contributions from all partial waves [157],
and the state-to-state DCS [157],
in which \(\vartheta\) is the scattering angle between the direction of incoming reactant A and outgoing product AB/AC in the center of mass frame, and \(d_{K_{\nu }K_{0}}^{J}(\vartheta )\) is the reduced rotational matrix [16, 152].
4.3.4.3 Calculation of Reaction Rate
With the calculated initial state-specific ICS, the initial state-specific temperature-dependent reaction rate constant can be expressed as
where k b is Boltzmann’s constant. The thermal rate constant can be calculated from the Boltzmann averaging of the initial state-specific reaction rate constants as
where \(E_{v_{0}j_{0}}\) is the ro-vibrational energy of the reactant diatomic molecule, and Z elec(T) is the possible electronic partition function for the system.
For a reaction with a defined transition state and without recrossing, reaction rate can be well approximated by many methods. For such reaction, we can assume that there is a dynamics bottleneck located at the transition state (conventional transition state theory, TST) or at a generalized transition state obtained by a canonical (CTV) or microcanonical (μVT) criterion. In the later cases, the dividing surface is optimized variationally to minimize the recrossing. Evans first proposed to place the transition state at the location that maximizes the free energy of activation which provides a key conceptual framework for modern variational transition state theory [33]. However, recrossing always possibly exists and only a full-dimensional reactive scattering dynamics calculations are able to provide us the exact rate constant on a defined PES. For a detailed discussion, one may refer to the reviews by Truhlar et al. [38, 136].
4.3.4.4 Calculation and Characterization of the Reactive Resonance Wavefunction
It is crucial to characterize the features of the reactive resonance wave function, in order to understand the nature and role of a particular reactive resonance state in the reaction.
The nomenclature “resonance” refers to a transient metastable species produced in the reaction scattering processes, and it results in peaks in the plots of reaction probabilities as a function of collision energy. Although its observation and assignment in scattering experiments usually is difficult because the coherent summation of many partial waves tends to wash out most of the resonance structures, numerically the quantum calculation is carried out with a specified partial wave and the resonance is much easier to pick out. The existence signature of a dynamical resonance is the arising of a peak in the collision energy-dependent reaction probability enhanced by the metastable transient state with long enough lifetime. Thus, such dynamical resonance wavefunctions can be figured out by using the so-called spectral quantization method. The bottleneck state in the H + H2 and its isotopes reactions scattering processes [104] and the reactive resonance state in the F + HD reaction processes [116] have been investigated using the spectral quantization method. In that method a carefully designed initial wave function was applied to obtain the time-independent wave function at the peak energies in the reaction probabilities by Fourier transform of the time-propagated wave packet. The reactive resonance wave function calculated in this way strongly depends on the initial wave function, and one must be careful for further studying with it.
Instead, a rigorous, robust, and convenient method to calculate the dynamical resonance wave functions in a reactive process may be applied, which is a direct extension of the standard TDWP method for describing a reaction scattering process. For a reactive scattering of a triatomic A + BC reaction with the initial incoming wave function \(\varPsi _{v_{0}j_{0}l_{0}}^{\mathit{JM}\epsilon }(t\! =\! 0)\) for an initial state \((v_{0},j_{0},l_{0})\), the dynamical resonance wave function at certain collision energy E n can be obtained with a Fourier transform of the time evolved incoming wave function as
The last step is reached by using the fact that before time zero the incoming wave contributes nothing to the interaction region. Thus the calculated resonance wave function is rigorous in the whole grid region and can be safely used to analyze the reactive process. The dynamical resonance wave function must have relatively large amplitude in the interaction region and pure incoming and outgoing tails with relatively small amplitude, and exhibits features of a quasi-bound state. And we can use this evidence to justify if the calculated wave function at specified collision energies corresponds to a dynamic resonance state. In contrast to the spectral quantization method, the wave function in resonance region may not be so clear since it is not overemphasized.
After the extraction of the reactive resonance wave function in certain convenient coordinates used in the propagation, one may need to transform it into another optimal coordinates to facilitate the observation of its resonance quantization structure, such as normal mode near the transition state region or product/reactant Jacobi coordinates or hyperspherical coordinates. In this way, the dynamics origin of the reactive resonance wave functions may be clarified to us.
4.4 Applications
4.4.1 Resonances in F Plus H2 and Its Isotopes
The reactive resonances reveal the quasi-bound levels of the reaction complex with unique clarity and they do exist. Identification of the reactive resonances can help us with understanding how elementary chemical processes take place at a single quantum state level. F + H2 and its isotopic analogs are the most beautiful examples.
Interest in the F + H2 reaction was largely due to Lee’s benchmark molecular beam studies [105] and early chemiluminescence and chemical laser work [98]. This work led to the early QCT studies of Muckerman [88], Blais and Truhlar [13], and Polanyi and Schreiber [97], using the PES but with serious flaws. A series of surface by Truhlar and his coworkers [17, 84, 122, 135] led to gradual improvement, and then Stark and Werner developed surfaces (SW PES) [121] from multireference configuration interaction calculations that resolved many of the earlier issues, even some problems remain. Very recently, Zhang and his coworkers developed several versions of the PES for the F + H2 reaction using icMRCI [100] and CCSDT method [40, 102], whose ultimate version has been proved to be of spectroscopy accuracy.
Early the QCT [106] and collinear quantum reactive scattering studies [113] revealed their distinct difference for predicting the F + H2 reaction, especially for the F + HD reaction where reactive resonances played a big role. Subsequent 3D quantum scattering calculations by Wyatt and coworkers [77, 78] and a variety of 3D quantum models confirmed the existence of the resonance, thereby stimulating further experiments on F + H2 and its isotopic analogs and finally leading to the molecular beam studies of Neumark and coworkers [91–94] which proved important hints that resonances play a role in this reaction.
However, the following theoretical work on the SW PES argued that the forward scattering of the F + H2 reaction results from the tunneling-induced reactivity at high impact parameters which do not need the formation of resonance [20]. And the QCT work by Aoiz et al. [9] yielded angular distributions with forward components that were consistent with the experiments, suggesting that the quantum effects, especially resonance effects, are relatively unimportant.
In 2000, the work on the F + HD reaction of Dong et al. [31] discovered the existence of reactive resonances in crossed beam experiments, where a resonance-enhanced step in the excitation function was observed, as shown in Fig. 4.4. Subsequent IR work by Nesbitt [48] confirmed this results and theoretical calculations have been presented to interpret the dynamics using SW PES [116, 117].
The excitation functions for F + HD → HF + D. The experimental results are shown with solid dots, the QCT simulations with a blue line, and the QM results with a red line. The resonance contribution is depicted with a dotted red line, and the direct reaction contribution with a dashed red line. A multisurface factor of 1/2 has been used to scale the ICS
Experimental (a) and theoretical (b) 3D contour plots for the product translational energy and angle distributions for the F(2 P 3∕2) + \(\rm H_{2}(j_{0} = 0\) ) reaction at the collision energy of 0.52 kcal/mol. The different circles represent different HF product ro-vibrational states. The forward-scattering direction for HF is defined along the F atom beam direction
In 2006, the work of Qiu et al. [100] presented the evidence for the resonances in the F + H2 reaction, with both theory and experiment exhibiting consistent behavior on XXZ PES, as shown in Fig. 4.5. The appearance of this report is catalyzed by the developments on quantum scattering method development, ab initio method and crossed-molecular beam combined with high resolution H-Rydberg state tagging technique [147]. The sharp forward peak at collision energy of 0.52 kcal/mol actually results from the interference between the first two Feshbach resonances. For total angular momentum J = 0, there are two resonance states at collision energy of 0.26 and 0.46 kcal/mol. With increasing J, the resonance energy will shift to higher collision energy. The three-dimensional (3D) scattering wave function at the collision energy of 0.26 kcal/mol shows the existence of three nodes along the H-F coordinate (correlating to the HF product) in the HF-H′ complex with no node along the reaction coordinate. The projection of the J = 0 scattering wave function at 0.26 kcal/mol to the HF vibrational states shows that the main character in this wave function is HF(v′ = 3) with the outgoing waves mostly on HF(v′ = 2). This implies that the resonance state at 0.26 kcal/mol is the ground resonance state, (003), trapped in the HF(v′ = 3)-H′ vibrational adiabatic potential (VAP) well. The 3D scattering wave function for J = 0 at the collision energy of 0.46 kcal/mol shows the existence of three nodes along the HF coordinate (correlating to the HF product) in the HF-H′ complex with one node along the reaction coordinate. The projection of the J = 0 scattering wave function at 0.46 kcal/mol to the HF vibrational states shows the main character in this wave function is predominantly HF(v′ = 3) with the outgoing waves also mostly on HF(v′ = 2). This suggests that the resonance state at 0.46 kcal/mol is the excited reaction resonance state trapped in the HF(v′ = 3)-H′ VAP well. This resonance state can be assigned to the (103) resonance state with one-quantum vibration along the reaction coordinate, zero-quantum vibration on the bending motion (or hindered rotation), and three-quanta vibration along the HF stretching. The resonance schemes were shown in Fig. 4.6.
Schematic diagram showing the resonance-mediated reaction mechanism for the F + H2 reaction with two resonance states trapped in the peculiar HF(v′ = 3)-H′ VAP well. The 1D wave functions of the two resonance states are also shown. The (003) state is the ground resonance state; the (103) resonance is the first excited resonance state. Calculated van der Waals states for the lower VAPs are also shown. OP, overtone pumping; E b, barrier height; E c, collision energy
Their subsequent work at higher collision energy (0.94 kcal/mol) demonstrated the tunneling and shape resonance effects [139], other than Feschbash resonance for arising the forward scattering in the reaction of F + H2, which suggested that the reactive resonances played quite different roles in the same reaction but at different collision energies [139].
In 2008, Ren et al. [102] measured the DCSs at several collision energies, which showed strong variation as a function of collision energies, as shown in Fig. 4.7, due to the existence of strong reactive resonance state. The theoretical DCSs on the new version PES by Zhang and his coworkers (FXZ PES) agree with the experimental observation very well, as shown in Fig. 4.8 which demonstrated that the F + H2 reaction is the first reaction which can be studied at spectroscopy accuracy, besides the H + H2 reaction.
To have a better feeling about the resonance state, the ground reactive resonance state wave function of the F + HD → HF + D, along with the 2D minimal potential, which is optimized along the angle degree of freedom, is given in Fig. 4.9. It is observed there that the wave function exhibits well features of a semi-bound state. The outgoing part, which corresponds to the HF (v′ = 2) product, has two nodes of structure but the inside peak has three nodes, which corresponds to an excited vibrational state of v′ = 3.
The most exciting chapter on detecting the reactive resonances in the F + H2 reaction and its isotopic analogs is the observation of the partial wave resonance in the F + HD by Dong et al. in 2010 [32]. The reactive resonance, as we know, which commonly is considered as being elusive and smeared by summation of many partial waves, was observed individually by Dong et al. at three different rotational quantum states of the temporarily trapped FHD complex, as shown in Fig. 4.10. This is different from the work in 2000 by Dong et al. [31] where the resonance in F + HD was identified by observing the averaged contribution from a sequence of the resonances in the cross sections. Dong et al. are, however, in 2010 the first to pick out individual resonances from this series [32].
Experimental and theoretical DCS of the HF(v = 2, j = 6) product of the F(2 P 3∕2) + HD(j 0 = 0) reaction in the backward scattering direction. The solid circles are experimental data; the red curve, the result of full quantum dynamics calculations convoluted with the experimental resolution and shifted 0.03 kcal/mol lower in energy. The error bars in the experimental data are the estimated measurement errors (1σ) for the HF(v = 2, j = 6) product peak intensity in the collision energy scan. The three peaks are assigned to the partial wave Feshbach resonances of J = 12, 13, and 14 in the F + HD → HF + D reaction, as explained in the text. The three-dimensional DCS shown was measured at 1.285 kcal/mol, with F and B indicating the forward- and backward-scattering, respectively, directions for HF with respect to the F-atom beam direction
Recent quantum reactive scattering studies of F + H2 and Cl + H2 have included spin-orbit effects and multiple surfaces within both the framework of hyperspherical coordinate coupled channel and TDWP calculations [2, 129, 140]. These works help us with better understanding the role of the spin-orbit effects in reactions.
From above discussion, we have seen a close interplay between theory and experiment which is extremely helpful with revealing the reaction dynamics mechanism. Theory and experiment verify and reinforce each other, develop side by side through mutual cross-fertilization. We can expect even more success through a close interplay between them.
4.4.2 Non-statistical Effects in H + O2 Reaction
The H + O2 → HO + O reaction and its reverse are of fundamental importance to combustion chemistry. This reaction proceeds via the formation of an intermediate complex in a deep well of 2.4 eV which is relatively stable with no barrier to dissociation. There have been many theoretical and experimental studies on this reaction, particularly on the concern about the non-statistical effects. Statistical modeling based on the statistical adiabatic channel model (SCAM) is able to account for the observed forward and reverse thermal rate constants overall a wide range of temperature, implying that the reaction is statistical. However, QCT studies find that there is significant recrossing of reasonably chosen dividing surfaces after the HO2 complex is formed in the HO + O reaction, suggesting the existence of the important non-statistical effects in this reaction. Rigorous quantum reactive scattering calculations and more accurate potentials are required to settle down this issue. However, this reaction presents obvious challenges for quantum scattering calculations, on account of the heavy masses and the deep HO2 well.
Using DMBE IV potential, Meijer and coworkers carried out wavepacket calculations of the initial state selected total cross sections for the H + O2, including partial waves up to J = 35. All of the projections of J onto the intermolecular axis have been incorporated in the calculations. They found that the calculated cross sections are lower than the experiment, which indicated the deficiencies in the DMBE IV potentials. In 2005, Xu et al. constructed a new potential (XXZLG PES) for this reaction at the internally contracted multireference configuration interaction plus the Davidson correction level with the augmented correlation consistent polarized valence quadruple zeta (aug-cc-pVQZ) basis set. It has been shown that there is remarkable improvement over the previous DMBE IV potential. Based upon this new potential and using the recent developed RCB quantum wave packet method, Sun et al. calculated state-to-state DCS and ICS of the H + O2 reaction up to 1.5 eV.
By comparing the QM rotational state distribution with the statistical limit represented by the phase space theory (PST), which assumes that the formation and decay of the reaction intermediate are separate events and the decay probability is proportional to the number of open channels. As shown in Fig. 4.11, the shape of the PST distribution is similar to that of the QM counterpart; namely, it increases with j until the highest accessible rotational state. However, the statistical model severely overestimates the QM distribution. Even when comparing with the normalized PST distribution, as shown in the same figure, the QM distribution typically overpopulates at large j values and underpopulates at small j values. Similar differences exist in other collision energies.
The deviation of the QM rotational state distribution from the statistical limit is a convincing piece of evidence in support of the argument that the title reaction has a significant non-statistical component despite its complex-forming nature. In other words, the dynamics plays a non-negligible role in the reaction. This is contrast with the conventional wisdom: usually it is assumed that the deep well in the PES which creates the long-lifetime intermediate complex will smear out all of the dynamics effect thus leads to statistical limit. This conclusion is consistent with the slight forward–backward asymmetry of the calculated DCSs reported here and the non-statistical decay of the HO2 complex observed in QCT studies. The origin of the non-statistical behavior can presumably be attributed to the relatively short lifetime of the HO2 intermediate which has not enough time to fully relax the internal energy into all degrees of the freedom in a statistical way.
The atmospherically important reaction O + O2 with three heavy atoms and deep potential well has also been studied at the state-to-state DCS level by quantum wave packet method. It reveals the failure of the statisical model from the calculated strong non-statistical effects and some quantum effects in the reaction [128].
4.4.3 H2 + OH
The H2 + OH → H + H2O reaction is a prototype reaction for H atom abstraction by an OH radical to form water as a product. Moreover, it is important in combustion chemistry and interstellar chemistry [85, 142]. Consequently, it has attracted extensive experimental and theoretical studies. Crossed-molecular beam experiments on the isotopically substituted D2 + OH → D + HOD reaction revealed that the product was strongly backward-scattered, with the majority of the available energy channeled into HOD internal excitation and the newly formed OD bond in the HOD molecule preferentially excited to the ν = 2 state [123]. The reverse reaction has also been studied widely as a prototype system for mode specific chemistry, in which different vibrational modes in the reactants can play an important role in the reaction dynamic. As three of the four atoms in this system are hydrogen isotopes, it has been straightforward to pursue both high-quality ab initio calculation of a PES and accurate quantum dynamics calculations. As a result, this reaction has become a benchmark system for four-atom reactions, in much the same role that the H + H2 reaction played for three-atom reactions.
Comparison between the experimental and theoretical integral cross sections for the H + D2O → D + HOD reaction. The dashed line is the experimental excitation function. The shaded area reflects the statistical uncertainty (1σ) of the global least squares fit procedure used to determine the optimum excitation function
In 1993, the first TDWP calculation was reported for the H2 + OH → H2O + H reaction with the total angular momentum J = 0 by using diatom–diatom Jacobi coordinates with only the spectator OH bond length frozen [158]. It was quickly extended to include all degrees of freedom for a four-atom reaction without any dynamical approximate on the same reaction system [159]. In 1996, the TDWP method was applied to study the H + H2O → H2 + OH reaction in full dimensions on the atom–triatom Jacobi coordinates [161]. Then, the method was extended to study four-atom reactions for the total angular momentum J > 0 in one set of Jacobi coordinates, with the full converged integral cross sections reported for the H2 + OH → H2O + H reaction [155] in 1999, for the H + D2O → D + HOD and H2O + H → H2 + OH reactions in 2000 [162, 164].
Figure 4.12 compares theoretical integral cross sections for the H + D2O → D + HOD exchange reaction with the experimental results [18, 19, 162]: the absolute cross sections at a relative translational energy of 1.5 and 2.2 eV and the excitation function of the reaction in the line-of-center functional model. The first-principles theoretical results agree excellently with the experiments in all respects. We note that the experimental result is thermally averaged over the initial rotation of D2O, whereas the theoretical result is for initial non-rotating D2O (preliminary calculations showed that rotational excitation of the triatomic reactant has no substantial effect on the integral cross section).
Despite the significant progress in initial state selected level, the accurate quantum calculation of the state-to-state DCSs for four-atom reactions remained a challenge for many years. State-to-state reaction probabilities for the total angular momentum J = 0 were reported for the H2 + OH → H2O + H reaction by using both the diatom–diatom and atom–triatom Jacobi coordinates [165]. Following that, the state-to-state integral and DCSs were reported for the H + H2O → H2 + OH reaction in five dimensions with the spectator OH bond length fixed, in 2002 [163] and 2005 [154], respectively. In the past few years, Althorpe and coworkers used quantum wave packet method to obtain the state-to-state reaction probability for the H2 + OH → H2O + H reaction in five and fully six dimensions [27–29]. All of these state-to-state calculations were using the reduced dimensionality method or limited to total angular momentum J = 0.
Recently, TDWP method was developed to compute DCSs for four-atom reactions and applied to the prototypical HD + OH → H2O + D [70, 145] and D2 + OH → HOD + D reactions [69]. Excellent agreements were achieved for the first time for a four-atom reaction between the full-dimensional DCS and high-resolution crossed-molecular beam experimental results on the HD + OH → H2O + D reaction [145]. Figure 4.13 compares the theoretical energy dependence of DCSs in the backward direction with the experimental result. The agreement between theory and experiment is remarkable. It also reveals that the theoretical reaction barrier of 5.4 kcal/mol on the PES they used is very accurate, and the quantum tunneling effect for the hydrogen transfer reaction is quite strong, since the reaction threshold is apparently much lower than the barrier height 5.4 kcal/mol.
Experimental and theoretical DCSs of the HD + OH → H2O + D reaction in the backward scattering direction. The experimental data, measured in relative values, are scaled to the theoretical DCS value at the collision energy (E c) of 6.15 kcal/mol. In the experiment, the DCSs at the backward scattering direction were measured by scanning the collision energy back and forth 15 times. Error bars in the experimental data indicate the estimated errors ( ± 1σ) for the DCS signal at the backward direction from the 15 scans of the collision energy
4.4.4 OH + CO
After simple four-atom reactions have been solved, however, huge challenges still persist in rigorous quantum scattering studies of complex-forming four-atom reactions with more than one heavy atoms, such as the OH + CO → H + CO2. Because of its crucial role in the conversion of CO to CO2, the OH + CO → H + CO2 reaction is important to both atmospheric [39] and combustion chemistry [86]. Due to the presence of two deep wells along the reaction path which support long-lived collision complex HOCO in both trans and cis configurations, the reaction dominated by pronounced resonances has become a prototype recently for complex-forming four-atom reactions, just as H2 + OH → H + H2O is for direct four-atom reactions.
Considerable experimental studies have been carried out on this reaction and its reverse [1, 61, 103]. Theoretically, in 1987 the first global analytic PES was constructed by Schatz, Fitzcharles, and Harding (denoted as SFH) based on the many-body expansion approach [114]. Following that, a number of global analytic [58, 59, 150] and numerical [25, 63] PES have been constructed to study the reaction more accurately, and many dynamics calculations have been performed by using quasiclassical trajectory method [59, 79]. We would like to note here that there is more detailed discussion about this reaction in the chapter by Guo et al. in this book.
The OH + CO reaction presents a huge challenge to quantum dynamics. The combination of a relatively long-lived collision complex and three heavy atoms in this reaction makes the rigorous quantum scattering calculations difficult. Kroes and coworkers obtained the first 6D total reaction probabilities for this reaction. Very large basis sets had to be used to ensure converged results [138]. Recently, Zhang and coworkers gave some preliminary full-dimensional (6D) quantum state-to-state results for this reaction on the LTSH PES. It is the first such a calculation for a four-atom reaction other than the H2 + OH \(\leftrightarrow\) H2O + H and its isotopically substituted reactions. The calculation is carried out by the RPD method. The results presented are limited to total angular momentum J = 0 for the ground initial ro-vibrational state. Advancing from J = 0 to J > 0 is extremely difficult due to the rapid increase of the rotational basis functions needed in calculation [68].
Figure 4.14 shows the CO2 product vibrational state distributions at four collision energies. For CO2, because the symmetric stretching vibrational frequency \(\nu _{1}\) is very close to the double of the bending frequency \(\nu _{2}\), it is extremely hard to make a complete assignment of all the vibrational states, and they only managed to assign some of the vibrational states with low excitation energies. The total reaction probability exhibits a pronounced peak at E c = 0. 158 eV and a dip at E c = 0. 174 eV. Although the total and, therefore the CO2 vibrational state-specific reaction probabilities at 0.158 eV are much larger than at 0.174 eV, the population structures for the two collision energies are quite similar. The (000) state has large population, but the majority of the population are contributed by the bending excited states. Figure 4.3c, d present the CO2 vibrational population at E c = 0. 1 and 0.4 eV, to show the effect of collision energy on product vibrational state distribution.
4.5 Conclusion
After persistent endeavors of decades, the quantum wave packet method has been well developed and currently it is quite mature for calculating product state-resolved different cross sections of triatomic and tetra-atomic reactive scatterings. However, due to numerical scaling of a quantum calculation, in order to study more complicated systems, developments of more efficient numerical methods are still very important in the future, such as the search and develop more efficient grid representation for angular degree of freedom and more compact Hamiltonian forms etc.
MCTDH method has been proven being efficient and memory-saving for dealing with polyatomic molecular dynamics. Theoretical methods for approximately extracting state-to-state differential cross section using MCTDH method would be worth more investigating, particularly for the reaction H + CH4 and its isotopic analogs.
Resonances in triatomic reactive scattering from the reactants in ground vibrational state have been identified and characterized, which help us to deepen the understanding of the chemical reaction dynamics at a single quantum state level. Reactive resonances in a polyatomic reaction and reaction starting with initial states other than ground vibrational states will receive more interest, along with the experimental techniques development [141]. This in turn stimulates the theoretical endeavors for more efficient theoretical methods. In a cold chemical reaction, similar resonance would, in principle, easier to be experimentally observed since there are only very limited partial waves involved. The techniques developed in this chapter can be applied to study the resonance in a cold chemical reaction straightforward.
References
Messiah A (1962) Quantum mechanics, vol 1. Wiley, New York
Cohen-Tannoudji C, Diu B, Laloe F (1992) Quantum mechanics. Wiley, New York
Basdevant J-L, Dalibard J (2005) Quantum mechanics. Springer, Heidelberg
Tannor DJ (2007) Introduction to Quantum Dynamics: A Time-Dependent Perspective. University Science Books, Sausalito, CA
Fox M (2006) Quantum optics: An introduction. Oxford University Press, Oxford
Cohen-Tannoudji C, Grynberg G, Aspect A, Fabre C (2010) Introduction to quantum optics: From the semi-classical approach to quantized light. Cambridge University Press, Cambridge
Haroche S, Raimond J-M (2006) Exploring the quantum: Atoms, cavities, and photons. Oxford University Press, Oxford
Pauling L, Wilson EB (1985) Introduction to quantum mechanics with applications to chemistry. Dover Publications, New York
Smith VH, Schaefer HF, Morokuma K (eds) (1986) Applied quantum chemistry. Springer, Heidelberg
Marcus RA (1952) Unimolecular dissociations and free radical recombination reactions. J Chem Phys 20:359
Marcus RA (1965) On the theory of electron-transfer reactions. VI. Unified treatment for homogeneous and electrode reactions. J Chem Phys 43:679
Marcus RA (1993) Electron transfer reactions in chemistry. Theory and experiment. Rev Mod Phys 65:599
Griebel M, Knapek S, Zumbusch G (2007) Numerical simulation in molecular dynamics. Springer, Heidelberg
Onuhic JN, Wolynes PG (1988) Classical and quantum pictures of reaction dynamics in condensed matter: Resonances, dephasing, and all that. J Phys Chem 92:6495
Herzberg G (1992) Molecular spectra and molecular structure. Krieger, Malabar
Miller WH (2006) Including quantum effects in the dynamics of complex (i.e., large) molecular systems. J Chem Phys 125:132305
Zuev PS, Sheridan RS, Albu TV, Truhlar DG, Hrovat DA, Borden WT (2003) Carbon tunneling from a single quantum state. Science 299:867
McMahon RJ (2003) Chemical reactions involving quantum tunneling. Science 299:833
Espinosa-García J, Corchado JC, Truhlar DG (1997) The importance of quantum effects for C-H bond activation reactions. J Am Chem Soc 119:9891
Wonchoba SE, Hu W-P, Truhlar DG (1995) Surface diffusion of H on Ni(100). Interpretation of the transition temperature. Phys Rev B 51:9985
Hiraoka K, Sato T, Takayama T (2001) Tunneling reactions in interstellar ices. Science 292:869
Cha Y, Murray CJ, Klinman JP (1989) Hydrogen tunneling in enzyme-reaction. Science 243:1325
Kohen A, Cannio R, Bartolucci S, Klinman JP (1999) Enzyme dynamics and hydrogen tunnelling in a thermophilic alcohol dehydrogenase. Nature 399:496
Truhlar DG, Gao J, Alhambra C, Garcia-Viloca M, Corchado J, Sánchez ML, Villà J (2002) The incorporation of quantum effects in enzyme kinetics modeling. Acc Chem Res 35:341
Truhlar DG, Gao J, Alhambra C, Garcia-Viloca M, Corchado J, Sánchez ML, Villà J (2004) Ensemble-averaged variational transition state theory with optimized multidimensional tunneling for enzyme kinetics and other condensed-phase reactions. Int J Quant Chem 100:1136
Hammer-Schiffer S (2002) Impact of enzyme motion on activity. Biochemistry 41:13335
Antoniou D, Caratzoulas S, Mincer J, Schwartz SD (2002) Barrier passage and protein dynamics in enzymatically catalyzed reactions. Eur J Biochem 269:3103
Domcke W, Yarkony DR, Köppel H (eds) (2004) Conical intersections, electronic strucutre, dynamics and spectroscopy. World Scientific, New Jersey
Domcke W, Yarkony DR, Köppel H (eds) (2004) Conical intersections, theory, computation and experiment. World Scientific, New Jersey
Worth GA, Cederbaum LS (2001) Mediation of ultrafast electron transfer in biological systems by conical intersections. Chem Phys Lett 338:219–223
González-Luque M, Garavelli M, Bernardi F, Mechán M, Robb MA, Olivucci M (2010) Computational. Proc Natl Acad Sci USA 97:9379
Polli D, Altoè P, Weingart O, Spillane KM, Manzoni C, Brida D, Tomasello G, Orlandi G, Kukura P, Mathies RA, Garavelli M, Cerullo G (2010) Conical intersection dynamics of the primary photoisomerization event in vision. Nature 467:440
Lan Z, Frutos LM, Sobolewski AL, Domcke W (2008) Photochemistry of hydrogen-bonded aromatic pairs: quantum dynamical calculations for the pyrrole-pyridine complex. Proc Natl Acad Sci USA 105:12707
Schultz T, Samoylova E, Radloff W, Hertel IV, Sobolewski AL, Domcke W (2004) Efficient deactivation of a model base pair via excited-state hydrogen transfer. Science 306:1765
Wolynes PG (2009) Some quantum weirdness in physiology. Proc Natl Acad Sci USA 106:17247–17248
Engel GS, Calhoun TR, Read EL, Ahn T-K, Mancal T, Cheng Y-C, Blankenship RE, Fleming GR (2007) Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446:782–786
Lee H, Cheng Y-C, Fleming GR (2007) Coherence dynamics in photosynthesis: Protein protection of excitonic coherence. Science 316:1462
Collini E, Wong CY, Wilk KE, Curmi PMG, Brumer P, Scholes GD (2010) Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 463:644
Wang Q, Schoenlein RW, Peteanu LA, Shank RA (1994) Vibrationnaly coherent photochemistry in the femtosecond primary event of vision. Science 266:422–424
Brumer P, Shapiro M (2012) Molecular response in one-photon absorption via natural thermal light vs. pulsed laser excitation. Proc Natl Acad Sci USA 109:19575
Gross A, Scheffer M (1998) Ab initio quantum and molecular dynamics of the dissociative adsorption on Pd(100). Phys Rev B 57:2493
Marx D, Parrinello M (1996) The effect of quantum and thermal fluctuations on the structure of the floppy molecule C2H3 +. Science 271:179
Arndt M, Nairz O, Voss-Andreae J, Keller C, van der Zouw G, Zeillinger A (1999) Wave-particle duality of c60 molecules. Nature 401:680
Gerlich S, Eibenberger S, Tomand M, Nimmrichter S, Hornberger K, Fagan PJ, Tüxen J, Mayor M, Arndt M (2011) Quantum interference of large organic molecules. Nat Phys 2:263
Chatzidimitriou-Dreismann A, Arndt M (2004) Quantum mechanics and chemistry: The relevance of nonlocality and entanglement for molecules. Angew Chem Int Ed 335:144
Chergui M (ed) (1996) Femtochemistry. World Scientific, Singapore
Zewail AH (1994) Femtochemistry: ultrafast dynamics of the chemical bond. World Scientific, Singapore
Ihee H, Lobastov V, Gomez U, Goodson B, Srinivasan R, Ruan C-Y, Zewail AH (2001) Science 291:385
Drescher M, Hentschel M, Kienberger R, Uiberacker M, Scrinzi A, Westerwalbesloh T, Kleineberg U, Heinzmann U, Krausz F (2002) Time-resolved atomic inner-shell spectroscopy. Nature 419:803
Goulielmakis E, Loh Z-H, Wirth A, Santra R, Rohringer N, Yakovlev VS, Zherebtsov S, Pfeifero T, Azzeer AM, Kling MF, Leone SR, Krausz F (2010) Real-time observation of valence electron motion. Nature 466:739
Krausz F, Ivanov M (2009) Attosecond physics. Rev Mod Phys 81:163–234
Kling MF, Siedschlag C, Verhoef AJ, Khan JI, Schultze M, Uphues T, Ni Y, Uiberacker M, Drescher M, Krausz F, Vrakking MJJ (2006) Control of electron localization in molecular dissociation. Science 312:246
Niikura H, Légaré F, Hasbani R, Bandrauk AD, Ivanov MY, Villeneuve DM, Corkum PB (2002) Sub-laser-cycle electron pulse for probing molecular dynamics. Nature 417:917
Stolow A, Jonas DM (2004) Muldimensional snapshots of chemical dynamics. Science 305:1575
Kahra S, Leschhorn G, Kowalewski M, Schiffrin A, Bothschafter E, Fuss W, de Vivie-Riedle R, Ernstorfer R, Krausz F, Kienberger R, Schaetz T (2012) Controlled delivery of single molecules into ultra-short laser pulses: a molecular conveyor belt. Nat Phys 8:238
Asssion A, Baumert T, Bergt M, Brixner T, Kiefer B, Seyfried V, Strehle M, Gerber G (1998) Control of chemical reactions by feedback-optimized phase-shaped femtocecond laser pulses. Science 282:919
Brixner T, Damreuer NH, Niklaus P, Gerber G (2001) Photoselective adaptative femtosecond quantum control in the liquid phase. Nature 414:57
Herek JL, Wohlleben W, Cogdell RJ, Zeidler D, Motzus M (2002) Quantum control of energy flow in light harvesting. Nature 417:533
Levis RJ, Menkir GM, Rabitz H (2001) Selective bond dissociation and rearrangement with optimally tailored, strong-field laser pulses. Science 292:709
Daems D, Guérin S, Hertz E, Jauslin HR, Lavorel B, Faucher O (2005) Field-free two-direction alignement alternation of linear molecules by elliptic laser pulses. Phys Rev Lett 95:063005
Madsen CB, Madsen LB, Viftrup SS, Johansson MP, Poulsen TB, Holmegaard L, Kumarappan V, Jorgensen KA, Stapelfeldt H (2009) Manipulating the torsion of molecules by strong laser pulses. Phys Rev Lett 102:073007
Holmegaard L, Hansen JL, Kalhøj L, Kragh SL, Stapelfeldt H, Filsinger F, Küpper J, Meijer G, Dimitrovski D, Martiny C, Madsen LB (2010) Photoelectron angular distributions from strong-field ionization of oriented molecules. Nat Phys 6:428
Bisgaard CZ, Clarkin OJ, Wu G, Lee AMD, Gessner O, Hayden CC, Stolow A (2009) Time-resolved molecular frame dynamics of fixed-in-space CS2 molecules. Science 323:1464
Bethlem HL, Berden G, Crompvoets FM, Jongma RT, van Roij AJA, Meijer G (2000) Electrostatic trapping of ammonia molecules. Nature 406:491
Kreckel H, Bruhns H,
 M, Glover SCO, Miller KA, Urbain X, Savin DW (2010) Experimental results for H2 formation from H− and H and implications for first star formation. Science 329:69
M, Glover SCO, Miller KA, Urbain X, Savin DW (2010) Experimental results for H2 formation from H− and H and implications for first star formation. Science 329:69Clary DC (1998) Quantum theory of chemical reaction dynamics. Science 279:1879
Schnieder L, Seekamp-Rahn K, Borkowski J, Wrede E, Welge KH, Aoiz FJ, Bañares L, D’Mello MJ, Herrero VJ, Rábanos VS, Wyatt RE (1995) Experimental studies and theoretical predictions for the H + D2 → HD + D reaction. Science 269:207
Qui M, Ren Z, Che L, Dai D, Harich SA, Wang X, Yang X, Xu C, Xie D, Gustafsson M, Skodje RT, Sun Z, Zhang DH (2006) Observation of Feshbach resonances in the F + H2 → HF + H reaction. Science 311:1440
Dong W, Xiao C, Wang T, Dai D, Yang X, Zhang DH (2010) Transition-state spectroscopy of partial wave resonances in the F + HD. Science 327:1501
Dyke TR, Howard BJ, Klemperer W. Radiofrequency and microwave spectrum of the hydrogen fluoride dimer; a nonrigid molecule. J Chem Phys 56:2442
Howard BJ, Dyke TR, Klemperer W (1984) The molecular beam spectrum and the structure of the hydrogen fluoride dimer. J Chem Phys 81:5417
Fellers RS, Leforestier C, Braly LB, Brown MG, Saykally RJ (1999) Spectroscopic Determination of the Water Pair Potential. Science 284:945
Saykally RJ, Blake GA (1993) Molecular interactions and hydrogen bond tunneling dynamics: Some new perspectives. Science 259:1570
Miller WH (1974) Quantum mechanical transition state theory and a new semiclassical model for reaction rate constants. J Chem Phys 61:1823–1834
Miller WH (1993) Beyond transition-state theory: a rigorous quantum theory of chemical reaction rates. Acc Chem Res 26(4):174
Thoss M, Miller WH, Stock G (2000) Semiclassical description of nonadiabatic quantum dynamics: Application to the S1 – S2 conical intersection in pyrazine. J Chem Phys 112:10282–10292
Wang HB, Thoss M, Sorge KL, Gelabert R, Gimenez X, Miller WH (2001) Semiclassical description of quantum coherence effects and their quenching: A forward-backward initial value representation study. J Chem Phys 114:2562–2571
Bowman JM, Carrington Jr. T, Meyer H-D (2008) Variational quantum approaches for computing vibrational energies of polyatomic molecules. Mol Phys 106:2145–2182
Zhang JZH (1999) Theory and application of uantum molecular dynamics. World Scientific, Singapore
McCullough EA, Wyatt RE (1969) Quantum dynamics of the collinear (H,H2) reaction. J Chem Phys 51:1253
Whitehead RJ, Handy NC (1975) J Mol Spec 55:356
Schatz GC, Kuppermann A (1976) Quantum mechanical reactive scattering for three-dimensional atom plus diatom systems. I. Theory. J Chem Phys 65:4642
Schatz GC, Kuppermann A (1976) Quantum mechanical reactive scattering for three-dimensional atom plus diatom systems. II. Accurate cross sections for H + H2. J Chem Phys 65:4668–4692
Carter S, Handy NC (1986) An efficient procedure for the calculation of the vibrational energy levels of any triatomic molecule. Mol Phys 57:175
 Z, Light JC (1986) Highly excited vibrational levels of “floppy” triatomic molecules: A discrete variable representation – Distributed Gaussian approach. J Chem Phys 85:4594
Z, Light JC (1986) Highly excited vibrational levels of “floppy” triatomic molecules: A discrete variable representation – Distributed Gaussian approach. J Chem Phys 85:4594 Z, Light JC (1987) Accurate localized and delocalized vibrational states of HCN/HNC. J Chem Phys 86:3065
Z, Light JC (1987) Accurate localized and delocalized vibrational states of HCN/HNC. J Chem Phys 86:3065Köppel H, Cederbaum LS, Domcke W (1982) Strong nonadiabatic effects and conical intersections in molecular spectroscopy and unimolecular decay: C2H4 +. J Chem Phys 77:2014
Nauts A, Wyatt RE (1983) New approach to many-state quantum dynamics: the recursive-residue-generation method. Phys Rev Lett 51:2238
Sibert EL (1990) Variational and perturbative descriptions of highly vibrationally excited molecules. Int Rev Phys Chem 9:1
Heller EJ. Time-dependent variational approach to semiclassical dynamics. J Chem Phys 64:63
Heller EJ () Wigner phase space method: Analysis for semiclassical applications. J Chem Phys 65:1289
Leforestier C, Bisseling RH, Cerjan C, Feit MD, Friesner R, Guldenberg A, Hammerich A, Jolicard G, Karrlein W, Meyer HD, Lipkin N, Roncero O, Kosloff R (1991) A comparison of different propagation schemes for the time dependent Schrödinger equation. J Comput Phys 94:59
Kosloff R (1988) Time-dependent quantum-mechanical methods for molecular dynamics. J Phys Chem 92:2087
Kosloff D, Kosloff R (1983) A Fourier-method solution for the time-dependent Schrödinger equation as a tool in molecular dynamics. J Comput Phys 52:35
Wang X-G, Carrington Jr T (2003) A contracted basis-Lanczos calculation of vibrational levels of methane: Solving the Schrödinger equation in nine dimensions. J Chem Phys 119:101
Wang X-G, Carrington Jr T (2004) Contracted basis lanczos methods for computing numerically exact rovibrational levels of methane. J Chem Phys 121(7):2937–2954
Tremblay JC, Carrington Jr T (2006) Calculating vibrational energies and wave functions of vinylidene using a contracted basis with a locally reorthogonalized coupled two-term lanczos eigensolver. J Chem Phys 125:094311
Wang X, Carrington Jr T (2008) Vibrational energy levels of CH5 +. J Chem Phys 129:234102
Norris LS, Ratner MA, Roitberg AE, Gerber RB (1996) Moller-plesset perturbation theory applied to vibrational problems. J Chem Phys 105:11261
Christiansen O (2003) Moller-plesset perturbation theory for vibrational wave functions. J Chem Phys 119:5773
Christiansen O (2004) Vibrational coupled cluster theory. J Chem Phys 120:2149
Christiansen O, Luis J (2005) Beyond vibrational self-consistent-field methods: Benchmark calculations for the fundamental vibrations of ethylene. Int J Quant Chem 104:667
Scribano Y, Benoit D (2007) J Chem Phys 127:164118
Barone V (2005) Anharmonic vibrational properties by a fully automated second-order perturbative aproach. J Chem Phys 122:014108
Bowman J (1978) Self-consistent field energies and wavefunctions for coupled oscillators. J Chem Phys 68:608
Bowman J, Christoffel K, Tobin F. Application of SCF-SI theory to vibrational motion in polyatomic molecules. J Phys Chem 83:905
Bégué D, Gohaud N, Pouchan C, Cassam-Chenaï P, Liévin J (2007) A comparison of two methods for selecting vibrational configuration interaction spaces on a heptatomic system: Ethylene oxide. J Chem Phys 127:164115
Carter S, Bowman JM, Handy NC (1998) Extensions and tests of “multimodes”: a code to obtain accurate vibration/rotation energies of many-mode molecules. Theor Chem Acc 100:191
Bowman JM (2000) Chemistry—beyond platonic molecules. Science 290:724
Culot F, Laruelle F, Liévin J (1995) A vibrational CASSCF study of stretch-bend interactions and their influence on infrared intensities in the water molecule. Theor Chem Acc 92:211
Heislbetz S, Rauhut G (2010) Vibrational multiconfiguration self-consistent field theory: Implementation and test calculations. J Chem Phys 132:124102
Meyer H-D, Le Quéré F, Léonard C, Gatti F (2006) Calculation and selective population of vibrational levels with the Multiconfiguration Time-Dependent Hartree (MCTDH) algorithm. Chem Phys 329:179–192
Joubert Doriol L, Gatti F, Iung C, Meyer H-D (2008) Computation of vibrational energy levels and eigenstates of fluoroform using the multiconfiguration time-dependent Hartree method. J Chem Phys 129:224109
Gerber RB, Buch V, Ratner MA (1982) Time-dependent self-consistent field approximation for intramolecular energy transfer. I. Formulation and application to dissociation of van der Waals molecules. J Chem Phys 77:3022
Gerber RB, Ratner MA (1988) Self-consistent-field methods for vibrational excitations in polyatomic systems. Adv Chem Phys 70:97
Makri N, Miller WH (1987) Time-dependent self-consistent (TDSCF) approximation for a reaction coordinate coupled to a harmonic bath: Single and multiconfiguration treatments. J Chem Phys 87:5781
Kotler Z, Nitzan A, Kosloff R (1988) Multiconfiguration time-dependent self-consistent field approximation for curve crossing in presence of a bath. A Fast Fourier Transform study. Chem Phys Lett 153:483
Meyer H-D, Manthe U, Cederbaum LS (1990) The multi-configurational time-dependent Hartree approach. Chem Phys Lett 165:73–78
Manthe U, Meyer H-D, Cederbaum LS (1992) Wave-packet dynamics within the multiconfiguration Hartree framework: General aspects and application to NOCl. J Chem Phys 97:3199–3213
Beck MH, Jäckle A, Worth GA, Meyer H-D (2000) The multi-configuration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wave packets. Phys Rep 324:1–105
Meyer H-D, Gatti F, Worth GA (eds) (2009) Multidimensional quantum dynamics: MCTDH theory and applications. Wiley, Weinheim
Worth GA, Beck MH, Jäckle A, Meyer H-D (2007) The MCTDH Package, Version 8.2, (2000). Meyer HD, Version 8.3 (2002), Version 8.4 (2007). See http://mctdh.uni-hd.de/
Jolicard G, Austin E (1985) Optical potential stabilisation method for predicting resonance level. Chem Phys Lett 121:106
Jolicard G, Austin E (1986) Optical potential method of caculating resonance energies and widths. Chem Phys 103:295
Riss UV, Meyer H-D (1993) Calculation of resonance energies and widths using the complex absorbing potential method. J Phys B 26:4503
Riss UV, Meyer H-D (1996) Investigation on the reflection and transmission properties of complex absorbing potentials. J Chem Phys 105:1409
Moiseyev N (1998) Quantum theory of resonances: calculating energies, widths and cross-sections by complex scaling. Phys Rep 302:211
Moiseyev N (2011) Non-Hermitian quantum mechanics. Cambridge University Press, Cambridge, UK
Thompson KC, Jordan MJT, Collins MA (1998) Polyatomic molecular potential energy surfaces by interpolation in local internal coordinates. J Chem Phys 108:8302–8316
Varandas AJC (2004) Modeling and interpolation of global multi-sheeted potential energy surfaces. In: Domcke W, Yarkony DR, Köppel H (eds), Conical Intersections. World Scientific, Singapore p 205
Huang X, Braams BJ, Bowman JM (2005) Ab initio potential energy and dipole moment surfaces for H5O2 +. J Chem Phys 122:044308
Miller WH, Handy NC, Adams JE (1980) Reaction path hamiltonian for polyatomic molecules. J Chem Phys 72:99
Ruf BA, Miller WH (1988) A new (cartesian) reaction-path mode for dynamics in polyatomic systems, with application to h-atom transfer in malonaldehyde. J Chem Soc Faraday Trans 84:1523
Tew D, Handy N, Carter S (2003) A reaction surface hamiltonian study of malonaldehyde. J Chem Phys 125:084313
Lauvergnat D, Nauts A, Justum Y, Chapuisat X (2001) A harmonic adiabatic approximation to calculate highly excited vibrational levels of “floppy molecules”. J Chem Phys 114:6592
Lauvergnat D, Nauts A (2004) A harmonic adiabatic approximation to calculate vibrational states of ammonia. Chem Phys 305:105
Gromov EV, Trofimov AB, Gatti F, Köppel H (2010) Theoretical study of photoinduced ring-opening in furan. J Chem Phys 133:164309
Gromov EV, Leveque C, Gatti F, Burghardt I, Köppel H (2011) Ab initio quantum dynamical study of photoinduced ring-opening in furan. J Chem Phys 135:164305
Köppel H, Domcke W, Cederbaum LS (1984) Multimode molecular dynamics beyond the Born-Oppenheimer approximation. Adv Chem Phys 57:59
Brocks G, Avoird AVD, Sutcliffe BT, Tennyson J (1983) Mol Phys 50:1025
Nauts A, Chapuisat X (1985) Momentum, quasi-momentum and hamiltonian operators in terms of arbitrary curvilinear coordinates, with special emphasis on molecular hamiltonians. Mol Phys 55:1287
Sutcliffe BT, Tennyson J (1986) A generalized approach to the calculation of ro-vibrational spectra of triatomic molecules. Mol Phys 58:1053–1066
Handy NC (1987) The derivation of vibration-rotation kinetic energy operators, in internal coordinates. Mol Phys 61:207
Lauvergnat D, Nauts A (2002) Exact numerical computation of a kinetic energy operator in curvilinear coordinates. J Chem Phys 116:8560
Ndong M, Joubert Doriol L, Meyer H-D, Nauts A, Gatti F, Lauvergnat D (2012) Automatic computer procedure for generating exact and analytical kinetic energy operators based on the polyspherical approach. J Chem Phys 136:034107
Gatti F, Iung C, Menou M, Justum Y, Nauts A, Chapuisat X (1998) Vector parametrization of the n-atom problem in quantum mechanics. I. Jacobi vectors. J Chem Phys 108:8804
Gatti F, Iung C (2009) Exact and constrained kinetic energy operators for polyatomic molecules: The polyspherical approach. Phys Rep 484:1–69
Yu H-G (2004) Full-dimensional quantum calculations of vibrational spectra of six-atom molecules. i. theory and numerical results. J Chem Phys 120:2270
Vendrell O, Gatti F, Meyer H-D. Dynamics and infrared spectroscopy of the protonated water dimer. Angew Chem Int Ed 46:6918–6921
Vendrell O, Gatti F, Meyer H-D. Strong isotope effects in the infrared spectrum of the zundel cation. Angew Chem Int Ed 48:352–355
Raab A, Worth G, Meyer H-D, Cederbaum LS. Molecular dynamics of pyrazine after excitation to the S2 electronic state using a realistic 24-mode model Hamiltonian. J Chem Phys 110:936–946
Hammer T, Manthe U (2011) Intramolecular proton transfer in malonaldehyde: Accurate multilayer multi-configurational time-dependent Hartree calculations. J Chem Phys 134:224305
Huarte-Larrañaga F, Manthe U (2000) Full dimensional quantum calculations of the CH4 + H → CH3 + H2 reaction rate. J Chem Phys 113:5115
Makri N (2008) Equilibrium and dynamical path integral methods in bacterial photosynthesis. In: Aartsma TJ, Matysik J (eds) Biophysical techniques in photosynthesis. Series advances in photosynthesis and respiration, vol 2. Springer, Dordrecht
Polyansky OL, Zobob NF, Viti S, Tennyson J, Bernath PF, Wallace L (1997) Water on the sun. Science 277:346
Callegari A, Theulé P, Muenter JS, Tolchenov RN, Zobov NF, Polyansky OL, Tennyson J, Rizzo TR (2002) Dipole moments of higly vibrationnally excited water. Science 297:993
Polyansky OL, Cászár AG, Shririn SV, Zobob NF, Barletta P, Tennyson J, Schenke DW, Knowles PJ (2003) High-accuracy ab initio rotation-vibration transitions for water. Science 299:539
Ndengué SA, Gatti F, Schinke R, Meyer H-D, Jost R (2010) Absorption cross section of ozone Isotopologues calculated with the multiconfiguration time-dependent Hartree (MCTDH) method: I. The Hartley and Huggins bands. J Phys Chem A 114:9855–9863
Ndengué SA, Schinke R, Gatti F, Meyer H-D, Jost R (2012) Comparison of the Huggins band for six ozone isotopologues: vibrational levels and Absorption Cross Section. J Phys Chem A 116:12260
Ndengué SA, Schinke R, Gatti F, Meyer H-D, Jost R (2012) Ozone photodissociation: isotopic and electronic branching ratios for asymmetric isotopologues. J Phys Chem A 116:12271
Schinke R (2011) Photodissociation of N2O: Potential energy surfaces and absorption spectrum. J Chem Phys 134:064313
Gatti F, Iung C, Leforestier C, Chapuisat X (1999) Fully coupled 6D calculations of the ammonia vibration-inversion-tunneling states with a split hamiltonian pseudospectral approach. J Chem Phys 111:7236–7243
Acknowledgments
We acknowledge X.M. Yang (DICP), H. Guo (UNM), D.Q. Xie (NJU), M. Alexander (UM), Soo-Y. Lee for helpful discussion and cooperated work. Funding supports from Chinese Academy of Sciences and NSFS (Grant No. 21222308, 21103187, 21133006) are acknowledged.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Sun, Z., Zhao, B., Liu, S., Zhang, DH. (2014). Reactive Scattering and Resonance. In: Gatti, F. (eds) Molecular Quantum Dynamics. Physical Chemistry in Action. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-45290-1_4
Download citation
DOI: https://doi.org/10.1007/978-3-642-45290-1_4
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-45289-5
Online ISBN: 978-3-642-45290-1
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)



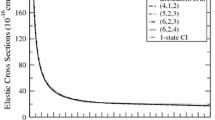














 M, Glover SCO, Miller KA, Urbain X, Savin DW (2010) Experimental results for H2 formation from H− and H and implications for first star formation. Science 329:69
M, Glover SCO, Miller KA, Urbain X, Savin DW (2010) Experimental results for H2 formation from H− and H and implications for first star formation. Science 329:69 Z, Light JC (1986) Highly excited vibrational levels of “floppy” triatomic molecules: A discrete variable representation – Distributed Gaussian approach. J Chem Phys 85:4594
Z, Light JC (1986) Highly excited vibrational levels of “floppy” triatomic molecules: A discrete variable representation – Distributed Gaussian approach. J Chem Phys 85:4594