Keywords

1 Introduction

The deformation signals of GPS permanent stations are usually extracted from their observed noisy series. For the observations of regional network, there exist not only the white, flicker and random walk noises, but also the spatial correlated Common Mode Components (CMC). The regional spatial filtering approaches, consisting typically of the “stacking” (Wdowinski et al. 1997) that has also been extended to “weighted stacking” (Nikolaidis 2002) and the principal component analysis (PCA) (Dong et al. 2006), were used to pick up CMC from the position time series of regional stations. They have been successfully applied in processing various station position time series (Marquez-Azua and Demets 2003; Wdowinski et al. 2004). The stacking filtering works well only for the limited regional network, since it is based on the assumption of CMC being spatially uniform. However, this assumption may not hold true because the spatial response of CMC can be different from the different stations. The PCA approach reveals the spatial characteristics of CMC directly by the observation series themselves. Therefore the PCA approach would work better than the stacking in larger regional network.

It is known that the observation series includes the white noise, flicker noise, random walk noise and other kinds of noises besides the trend signals. If one computes the velocity of permanent station using the pure white noise model, the estimated accuracy will be too optimistic with the factor of 3–6 (Zhang et al. 1997) or even 5–11 (Mao et al. 1999). Therefore, all of these noise components must be properly identified to recover the optimal estimates. The Maximum Likelihood Estimation (MLE) method has been frequently used to separate these noise components (Zhang et al. 1997; Langbein and Johnson 1997; Mao et al. 1999; Williams et al. 2004; Langbein 2004), and it was also used to compute the noise components of GPS/DORIS co-located stations (Williams and Willis 2006). Recently, Amiri-Simkooei et al. (2007) and Amiri-Simkooei (2009) used LS-VCE (least squares variance component estimation) to assess the noise characteristics of the daily GPS position time series. The MINQUE method as one of the classic VCE (Variance Covariance Estimation) methods proposed by Rao (1971) is popularly used in estimating the variance and covariance components for linear observation model. In this paper, we will employ the MINQUE method in estimating the white, flicker and random walk noise components of the station position time series.

In this paper, we first extract CMC from GPS station position time series of 24 permanent stations in China using PCA. Then, the further analysis suggests that the Unmodeled Common Signals (UCS) and Common Noises (CN) indeed exist in CMC. We also address the noise components of CN using MINQUE. After removing CMC from GPS station position time series, the periodic signals are extracted, followed by estimating the different noise components of the filtered series.

2 Mathematical Model

The time series of a GPS permanent station in each direction can be expressed as (Nikolaidis 2002)

$$\begin{array}{lllllll} y({t_i})&={y_0}+r{t_i}+\sum\limits_{f=1}^2 {({c_f}\sin (2\pi f{t_i})+{d_f}\cos (2\pi f{t_i}))} \nonumber \\ &\ \ \ \ \ +\sum\limits_{j=1}^{{{n_g}}} {{g_j}H({t_i}-{T_{\mathit{gj} }})} +{\varepsilon_i} \end{array}$$
(1)

where y(t i ) (i = 1, 2,…,m) is the time series observation at epoch t i in unit of year, y 0 and r are the position and velocity parameters, c f and d f are the periodic motion parameters (f = 1 for the annual motion while f = 2 for the semi-annual motion); \( \sum\nolimits_{j = 1}^{{{n_{\mathrm{g}}}}} {{g_j}H\left( {{t_i}-{T_{\mathit{gj} }}} \right)} \) are the offset correction terms with magnitudes g j at epochs T gj and H is the Heaviside step function. Equation (1) can be understood as the linear form of parameters x = [y 0 r c 1 d 1 c 2 d 2 g 1 g 2 g 3 …] T, and then it is reformulated as

$$ \boldsymbol{y}=\boldsymbol{Ax}+\boldsymbol{\varepsilon} $$
(2)

where A is the design matrix, \( \boldsymbol{\varepsilon} \) is the noise of y including the white, flicker and random walk noise components. The covariance matrix of \( \boldsymbol{\varepsilon} \) is equal to that of y, which is denoted with Σ y .

2.1 Principle Component Analysis

The PCA approach that was employed by Dong et al. (2006) to analyse time series allows non-uniform response to CMC. For a regional daily station position time series with n stations and spanning m days (without loss of generality m ≥ n), we can construct an m × n matrix X (t i , x j ) (i = 1, 2…m; j = 1, 2…n) for each coordinate component [N (north), E (east) and U (upward)] of the stations in a regional network. The column of X represents the coordinate components of one station for all epochs, while the row the coordinate components of a given epoch for all stations. It should be mentioned here that the coordinate components are detrended and demeaned first. The matrix X can be decomposed as (Dong et al. 2006)

$$ \boldsymbol{X}({t_i},{x_j})=\sum\limits_{k=1}^n {{{\boldsymbol{a}}_k}({t_i}){{\boldsymbol{v}}_k}({x_j})}, \kern0.5em (j=1,2\cdots n)$$
(3)
$$ {{\boldsymbol{a}}_k}({t_i})=\sum\limits_{j=1}^n {\boldsymbol{X}({t_i},{x_j})}\;{{\boldsymbol{v}}_k}({x_j}),\ (k=1,2\cdots n) $$
(4)

where a k is the k-th mode. v k is the k-th eigenvector of the covariance matrix B with element B(i, j) at the i-th row and j-th column is

$$ B(i,j)=\frac{1}{m-1}\sum\limits_{k=1}^m {\boldsymbol{X}({t_k},{x_i})\boldsymbol{X}({t_k},{x_j})} $$
(5)

If the eigenvalues of B are arranged in descending order, that is, λ 1 ≥ λ 2 ≥ … ≥ λ n . The first principal component corresponds to the largest eigenvalue λ 1, and the elements of its eigenvector v 1 are close to each other if the CMC exist in the regional network. Thus the mode a 1(t i ) accounts for the most of the variances of the station position time series with almost the same spatial response. The CMC of station j at epoch i is defined

$$ {{\boldsymbol{p}}_j}({t_i})={{\boldsymbol{a}}_1}({t_i}){{\boldsymbol{v}}_1}({x_j}) $$
(6)

p j (t i ) are also close with each other for the different station j.

According to Dong et al. (2006), the CMC contains both UCS and CN; it is thus further decomposed as

$$ {{\boldsymbol{a}}_1}({t_i})=\boldsymbol{a}_1^s({t_i})+\boldsymbol{a}_1^e({t_i}) $$
(7)

where \( \boldsymbol{a}_1^s({t_i}) \) and \( \boldsymbol{a}_1^e({t_i}) \) are with respect to UCS and CN. The significance of UCS can be tested via F-test as shown in Huang (1983). The null hypothesis is that the CMC time series are completely detrended and contaminated only by the Gaussian noises, whilst the alternative hypothesis is that one periodic signal still exists in this time series. The correspondent statistic of F-test is

$$ \frac{{(m-3)\sigma_k^2}}{{2({\sigma^2}-\sigma_k^2)}}\sim {F_{\alpha }}\left( {2,m-3} \right) $$
(8)

where \( {\sigma^2}=\frac{1}{m}\sum\nolimits_{i = 1}^m {{{{({\boldsymbol{a}_1}\left( {{t_{\mathrm{i}}}} \right)-{{{\bar{\boldsymbol{a}}}}_1})}}^2}}; \sigma_{\mathrm{k}}^2=\frac{1}{2}\left( {c_k^2 + d_k^2\ } \right) \) is the power of the k-th signal, and α is the significance level. \( {{\bar{\boldsymbol{a}}}_1} \) is the mean value of a 1. If more than two periodic signals are detected, their corresponding variance quantities should be removed from σ2 and the freedom is accordingly changed. Then we use the recalculated variance to carry out F-test iteratively, and the test procedure is stopped until detected signals are same. If we detect K terms of significant signals, the power spectrum of UCS (or \( \sigma_{\mathrm{CS}}^2 \)) is

$$ \sigma_{\mathit{CS}}^2=\frac{1}{2}\sum\limits_{k=1}^K {(c_k^2+d_k^2)} $$
(9)

and the power spectrum of CN (or \( \sigma_{\mathrm{CN}}^2 \)) is

$$ \sigma_{\mathit{CN}}^2={\sigma^2}-\sigma_{\mathit{CS}}^2 $$
(10)

2.2 Noise Components Estimation

The fundamental matrix equation for the iterative VCE is (Li et al. 2011)

$$ {{\boldsymbol{R}}_0}{{\boldsymbol{\Sigma}}_{\boldsymbol{y}}}{{\boldsymbol{R}}_0}^T={{\boldsymbol{v}}_0}{{\boldsymbol{v}}_0}^T $$
(11)

where \( {{\boldsymbol{R}}_0}={{\boldsymbol{I}}_m}-\boldsymbol{A}{{({{\boldsymbol{A}}^T}{\Sigma}_0^{-1}\boldsymbol{A})}^{-1 }}{{\boldsymbol{A}}^T}{\Sigma}_0^{-1 } \), \( {{\boldsymbol{v}}_0}={{\boldsymbol{R}}_0}\boldsymbol{y} \). Σ 0 is the initial value of Σ y . The other symbols are the same as those in Eq. (3). The general structure of Σ y is

$$ {{{\Sigma}}_{\boldsymbol{y}}}=\sum\limits_{i=1}^3 {{{\boldsymbol{U}}_i}} {\theta_i} $$
(12)

where θ i is the i-th unknown variance or covariance component and U i is its cofactor matrix of the component, with \( i=1,2,3 \) for white noise, flicker noise and random walk noise, respectively. \( {{\boldsymbol{U}}_1} \) is an identity matrix, the i-th row, j-th column element \( {u_2}_{ij } \) of \( {{\boldsymbol{U}}_2} \) is (Mao et al. 1999)

$$ {u_2}_{ij }{\,=\,}\left\{ \begin{array}{c} {{(\dfrac{3}{4})}^2}\times 2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i=j\; \hfill \\[15pt] {{(\dfrac{3}{4})}^2}\times (2-\dfrac{{{\log_{10 }}\left| {{t_i}-{t_j}} \right|/{\log_{10 }}2+2}}{12 })\;\;\;\;\;\;i\ne j \end{array} \right. $$
(13)

and

$$ {{\boldsymbol{U}}_3}={f_s}^{-1}\left[ {\begin{array}{*{20}{c}} 1 & 1 & 1 & \cdots & 1 \\ 1 & 2 & 2 & \cdots & 2 \\ 1 & 2 & 3 & \cdots & 3 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 2 & 3 & \cdots & m \\ \end{array}} \right]\;\;\;\;\;\;{f_s} = \frac{m-1 }{T}$$
(14)

where f s is the sampling frequency in 1/year (yr is the abbreviation of year), T is the observation span, m is the number of measurements. The noise component for an arbitrary power index can also be computed by using the arbitrary power-law noise covariance matrix derived by Williams (2003).

Fig. 1
figure 00301

Spatial eigenvectors in N, E and U directions from left to right

Full size image
Fig. 2
figure 00302

CMC and UCS in N, E and U directions from left to right

Full size image
Fig. 3
figure 00303

Power spectrum of CMC in N, E and U directions from left to right

Full size image

The VCE equation of MINQUE by Rao (1971) is as follows,

$$ \boldsymbol{N}\hat{{\theta}} =\boldsymbol{q} $$
(15)

The elements n ij of normal matrix N and q i of vector q are

$$ {n_{\mathit{ij} }}=\mathit{tr}({{\boldsymbol{W}}_0}{{\boldsymbol{U}}_i}{{\boldsymbol{W}}_0}{{\boldsymbol{U}}_j}) $$
$$ {q_i}=\boldsymbol{v}_0^T{{\boldsymbol{W}}_0}{{\boldsymbol{U}}_i}{{\boldsymbol{W}}_0}{{\boldsymbol{v}}_0} $$

where \( {{\boldsymbol{W}}_0}=\boldsymbol{R}_0^T{\Sigma}_0^{-1 }{{\boldsymbol{R}}_0}={\Sigma}_0^{-1 }{{\boldsymbol{R}}_0}=\boldsymbol{R}_0^T{\Sigma}_0^{-1 } \). The Eq. (15) needs the iterative computation with from initial value Σ 0.

3 Analysis of GPS Permanent Stations in China

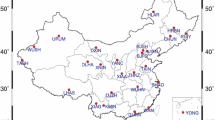
We analyze the 7-year (from 2003 to 2009) coordinate time series of 24 GPS permanent stations from the CMONOC (Crustal Movement Observation Network of China) in China, which are mainly used to monitor the tectonic deformation in China. The deployment and normalized spatial eigenvectors of 24 permanent stations in N (north), E (east) and U (up) directions are showed in Fig. 1. Their corresponding CMC are shown in Fig. 2, which account for 38.8 %, 39.1 % and 32.7 % of the total variance in N, E and U directions, respectively. Therefore, the first mode is dominant for the nationwide station network as large as in China.

The power spectrum of CMC series are shown in Fig. 3, which demonstrates that there clearly exist low frequency signals in the CMC series, i.e., the UCS signals. Therefore, we use F-test in Eq. (8) to test the significance of the UCS with significant level α = 5 %. The results are presented in Table 1. The first dominant periods for N, E and U directions are 792 days, 594 days, 792 days, and the second dominant periods are 396 days, 264 days and 170 days, respectively. The reconstructed UCS from the periods of Table 1 is plotted in Fig. 2 in red line.

Table 1 Significant periods in N, E, U (days)
Full size table
Fig. 4
figure 00304

CN in N, E and U directions from left to right

Full size image
Fig. 5
figure 00305

Power spectrum of LHAS station

Full size image

After removing the UCS from CMC, the CN is shown in Fig. 4. The power spectrums of UCS and CN are 0.017 mm2, 0.038 mm2, 0.65 mm2 and 0.48 mm2, 0.88 mm2, 10.19 mm2 in N, E and U directions, respectively. Therefore, CN is the dominant part of CMC. We use MINQUE to estimate the noises components of CN. The results are listed in Table 2, in which flicker noise is slightly larger than white noise, and random walk noise is very small. The letter “–” in the table denotes the component failed to be estimated.

Table 2 Noise components of CN in N, E, U direction
Full size table

After removing the CMC from station position time series, we get the filtered series for all stations. We further analyse the filtered series according to the power spectrum. The result suggests that the filtered series contains the significant signals, especially the annual signals in the U direction, as shown in Fig. 5 for the LHAS station as example.

Table 3 Noise components of each station’s time series in N, E, U direction
Full size table

We estimate white, flicker and random walk noise components of the filtered series with Eq. (15) using MINQUE. The results for 24 stations (Table 3) show that flicker noise is also slightly larger than white noise. The random walk noise is apparent in most stations and even larger than white or flicker noise in some stations.

4 Conclusions

From the above results and analysis we can draw the following conclusions.

  1. 1.

    The CMC obviously exist in the GNSS station position time series of nationwide stations as large as that in China, which account for 38.8 %, 39.1 % and 32.7 % of the total variance in N, E and U directions, respectively. We separate CMC into UCS and CN and find that the power spectrums of UCS and CN are 0.017 mm2, 0.038 mm2, 0.65 mm2 and 0.48 mm2, 0.88 mm2, 10.19 mm2 in N, E and U directions, respectively. Only a few evident UCS have been detected. However, the filtered series contain significant signals, especially the annual signals in up direction.

  2. 2.

    MINQUE is successfully used to estimate the white, flicker and random walk noises for CN and filtered series of each station. The results show that flicker noise is slightly larger than white noise in both CN and filtered series. And the random walk noise is significantly large for most stations.

  3. 3.

    As a result, the regional spatial filtering approaches are needed for processing the station position time series for nationwide stations. The flicker noise is even larger than white noise, if it is neglected, the precision of estimated parameters will be too optimistic, which is coincided with Williams et al. (2004).