Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

With the increasing number of new structural materials, the problem of stability analysis for bodies with a microstructure becomes important. One example of such materials is a porous material. Engineering structures made of porous materials, especially metal and polymer foams, have different applications in the last decades [2–4, 6, 9]. The foams are cellular structures consisting of a solid metal (for example aluminium, steel, copper, etc.), or polymer (polyurethane, polyisocyanurate, polystyrene, etc.) and containing a large volume fraction of gas-filled pores. There are two types of foams. One is the closed-cell foam, while the second one is the open-cell foam. The defining characteristic of metal and polymer foams are the very high porosity: typically, well over 80 %, 90 % and even 98 % of the volume consists of void spaces.

Constructions made of porous materials are widely used in modern industries with airspace or automotive applications among others. The reason for this is the advantages of such materials: better density-stiffness ratios in comparison with classical structural materials, the possibility to absorb energy, etc. As a rule, these constructions have a functionally graded structure. For example, the porous core is quite often covered by hard and stiff shell, which can be necessary for corrosion or thermal protection, and optimization of mechanical properties in the process of loading.

2 Initial Strain State of Inhomogeneous Plate

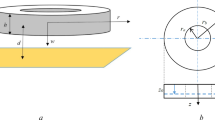
We consider the circular plate of radius \(r_1\) and thickness \(H\), and made of functionally graded material. The behavior of the plate is described by the model of micropolar elastic body [1, 5, 8, 10, 13, 19]. For the radial compression (extension) of the plate, the position of a particle in the strained state is given by the radius vector \({\varvec{R}}\) [12, 20]:

$$\begin{aligned} {R=\alpha r}\text{, } {\qquad }&{0\leqslant r\leqslant r_1}, \nonumber \\ {\Phi =\varphi }, {\qquad }&{0\leqslant \varphi \leqslant 2\pi }, \\ {Z=f(z),} {\qquad }&{\left| z \right| \leqslant H/2}, \nonumber \end{aligned}$$
(1)
$$\begin{aligned} {\varvec{R}}=\alpha r {\varvec{e}}_R +f\left( z \right) {\varvec{e}}_Z. \end{aligned}$$
(2)

Here \(r,\,\varphi ,\,z\) are cylindrical coordinates in the reference configuration (Lagrangian coordinates), \(R,\,\Phi ,\,Z\) are Eulerian cylindrical coordinates, \(\left\{ {{\varvec{e}}_r,\,{\varvec{e}}_\varphi ,\, {\varvec{e}}_z } \right\} \) and \(\left\{ {{\varvec{e}}_R,\, {\varvec{}}{\varvec{e}}_\Phi ,\, {\varvec{e}}_Z } \right\} \) are orthonormal vector bases of Lagrangian and Eulerian coordinates, respectively, \(\alpha \) is the radial compression ratio, \(f(z)\) is some unknown function, which describe the strain in the thickness direction of the inhomogeneous plate.

In addition, a proper orthogonal tensor of microrotation \({\mathbf{\mathsf{{H}} }}\) is given, which characterizes the rotation of the micropolar medium particle and for the considered strain has the form

$$\begin{aligned} \mathbf{\mathsf{{H}} }={\varvec{e}}_r \otimes {\varvec{e}}_R +{\varvec{e}}_\varphi \otimes {\varvec{e}}_\Phi +{\varvec{e}}_z \otimes {\varvec{e}}_Z. \end{aligned}$$
(3)

According to expressions (1) and (2), the deformation gradient \({\mathbf{\mathsf{{C}} }}\) is (hereinafter  \(^\prime \) denotes the derivative with respect to \(z\)):

$$\begin{aligned} {\mathbf{\mathsf{{C}} }}=\mathrm{grad}\;{\varvec{R}}=\alpha \left( {\varvec{e}}_r \otimes {\varvec{e}}_R +{\varvec{e}}_\varphi \otimes {\varvec{e}}_\Phi \right) +{f}^{\prime } {\varvec{e}}_z \otimes {\varvec{e}}_Z, \end{aligned}$$
(4)

where \(\mathrm{grad}\) is the gradient in Lagrangian coordinates. It follows from relations (3) and (4) that the wryness tensor \({\mathbf{\mathsf{{L}} }}\) is equal to zero [14, 15]

$$\begin{aligned} {\mathbf{\mathsf{{L}} }}\times {\mathbf{\mathsf{{E}} }}=-\left( {\mathrm{grad}\,{\mathbf{\mathsf{{H}} }}} \right) \cdot {\mathbf{\mathsf{{H}} }}^\mathrm{T}=0 \end{aligned}$$

and the stretch tensor \({\mathbf{\mathsf{{Y}} }}\) is expressed as follows

$$\begin{aligned} {\mathbf{\mathsf{{Y}} }}={\mathbf{\mathsf{{C}} }}\cdot {\mathbf{\mathsf{{H}} }}^\mathrm{T}=\alpha \left( {\varvec{e}}_r \otimes {\varvec{e}}_r + {\varvec{e}}_\varphi \otimes {\varvec{e}}_\varphi \right) +{f}^{\prime } {\varvec{e}}_z \otimes {\varvec{e}}_z. \end{aligned}$$
(5)

We assume that the elastic properties of the plate vary through the thickness, and they are described by the model of physically linear micropolar material, whose specific strain energy is a quadratic form of the tensors \({\mathbf{\mathsf{{Y}} }}-{\mathbf{\mathsf{{E}} }}\) and \({\mathbf{\mathsf{{L}} }}\) [7, 11]:

$$\begin{aligned} \displaystyle W\left( {{\mathbf{\mathsf{{Y}} }},{\mathbf{\mathsf{{L}} }}} \right)&=\displaystyle \frac{1}{2}\lambda (z) \mathrm{tr}^2 \left( {{\mathbf{\mathsf{{Y}} }}-{\mathbf{\mathsf{{E}} }}} \right) +\frac{1}{2}\left( {\mu (z) +\kappa (z) } \right) \mathrm{tr}\left( {\left( {{\mathbf{\mathsf{{Y}} }}-{\mathbf{\mathsf{{E}} }}} \right) \cdot \left( {{\mathbf{\mathsf{{Y}} }}-{\mathbf{\mathsf{{E}} }}} \right) ^\mathrm{T}} \right) \nonumber \\&\quad +\displaystyle \frac{1}{2}\mu (z) \mathrm{tr}\left( {{\mathbf{\mathsf{{Y}} }}-{\mathbf{\mathsf{{E}} }}} \right) ^2 \!+\frac{1}{2}\gamma _1(z) \mathrm{tr}^2 {\mathbf{\mathsf{{L}} }}\!+\!\frac{1}{2}\gamma _2(z) \mathrm{tr}\left( {{\mathbf{\mathsf{{L}} }}\cdot {\mathbf{\mathsf{{L}} }}^\mathrm{T}} \right) \!+\frac{1}{2}\gamma _3(z) \mathrm{tr}\;{\mathbf{\mathsf{{L}} }}^2. \end{aligned}$$
(6)

Here \(\lambda (z)\), \(\mu (z) \) are functions describing the change in the Lamé parameters, \(\kappa (z)\), \(\gamma _1(z)\), \(\gamma _2(z)\), \(\gamma _3(z) \) are micropolar elastic parameters changing with the thickness coordinate, \({\mathbf{\mathsf{{E}} }}\) is the unit tensor.

It follows from expressions (3), (5) and (6) that the Piola-type couple stress tensor \({\mathbf{\mathsf{{G}} }}\) is equal to zero for the deformation of radial compression (1)–(3) of the circular plate

$$\begin{aligned} {\mathbf{\mathsf{{G}} }}=\frac{\partial W}{\partial {\mathbf{\mathsf{{L}} }}}\cdot {\mathbf{\mathsf{{H}} }}=\left( {\gamma _1 \left( {\mathrm{tr}\,{\mathbf{\mathsf{{L}} }}} \right) {\mathbf{\mathsf{{E}} }}+\gamma _2 {\mathbf{\mathsf{{L}} }}+\gamma _3 {\mathbf{\mathsf{{L}} }}^\mathrm{T}} \right) \cdot {\mathbf{\mathsf{{H}} }}=0 \end{aligned}$$

and Piola-type stress tensor \({\mathbf{\mathsf{{D}} }}\) is

$$\begin{aligned} \displaystyle {\mathbf{\mathsf{{D}} }}&=\displaystyle \frac{\partial W}{\partial {\mathbf{\mathsf{{Y}} }}}\cdot {\mathbf{\mathsf{{H}} }}=\left( {\lambda \mathrm{tr}\left( {{\mathbf{\mathsf{{Y}} }}-{\mathbf{\mathsf{{E}} }}} \right) {\mathbf{\mathsf{{E}} }}+\mu \left( {{\mathbf{\mathsf{{Y}} }}^\mathrm{T}-{\mathbf{\mathsf{{E}} }}} \right) +\left( {\mu +\kappa } \right) \left( {{\mathbf{\mathsf{{Y}} }}-{\mathbf{\mathsf{{E}} }}} \right) } \right) \cdot {\mathbf{\mathsf{{H}} }} \nonumber \\&=\displaystyle \left( {\lambda s+\chi \left( {\alpha -1} \right) } \right) \left( {\varvec{e}}_r \otimes {\varvec{e}}_R + {\varvec{e}}_\varphi \otimes {\varvec{e}}_\Phi \right) +\left( {\lambda s+\chi \left( {{f}^{\prime } -1} \right) } \right) {\varvec{e}}_z \otimes {\varvec{e}}_Z, \end{aligned}$$
(7)
$$\begin{aligned} s=2\alpha +{f}^{\prime }-3,\qquad \chi =2\mu +\kappa . \end{aligned}$$

The equilibrium equations of nonlinear micropolar elasticity in absence of mass forces and moments are written as follows [7, 20]

$$\begin{aligned} \mathrm{div}{\mathbf{\mathsf{{D}} }}=0,\quad \quad \quad \mathrm{div}{\mathbf{\mathsf{{G}} }}+\left( {{\mathbf{\mathsf{{C}} }}^\mathrm{T}\cdot {\mathbf{\mathsf{{D}} }}} \right) _\times =0, \end{aligned}$$
(8)

where \(\mathrm{div}\) is the divergence in the Lagrangian coordinates. The symbol \(_\times \) represents the vector invariant of a second-order tensor:

$$\begin{aligned} {\mathbf{\mathsf{{K}} }}_\times =\left( {K_{mn} {\varvec{e}}_m \otimes {\varvec{e}}_n } \right) _\times =K_{mn} {\varvec{e}}_m \times {\varvec{e}}_n \end{aligned}$$

We assume that there are no external loads on the faces of the plate \((z=\pm H/2)\), and there is no vertical displacement on the middle surface \(z=0\):

$$\begin{aligned} \left. {\varvec{e}}_z \cdot {{\mathbf{\mathsf{{D}} }}} \right| _{z=\pm \frac{H}{2}} =0,\qquad f\left( 0 \right) =0 \end{aligned}$$
(9)

By solving the boundary problem (8), (9) while taking into account the relations (7) we found the unknown function \(f\left( z \right) \):

$$\begin{aligned} f\left( z \right) =\int \limits _0^z{\frac{2 (1-\alpha )\lambda (x)}{\lambda (x)+2\mu (x)+\kappa (x)}}dx+z \end{aligned}$$

In the special case, when the pattern of variation for elastic parameters \(\lambda ,\,\mu ,\,\kappa \) is the same

$$\begin{aligned} \lambda (z)=\lambda _0\xi (z), \qquad \mu (z)=\mu _0\xi (z), \qquad \kappa (z)=\kappa _0\xi (z) \end{aligned}$$

the expression for the function \(f(z)\) is quite simple:

$$\begin{aligned} f\left( z \right) =\alpha _3 z,\qquad \alpha _3 = 1+\frac{2\lambda _0 (1-\alpha )}{\lambda _0+2\mu _0+\kappa _0} \end{aligned}$$

3 Equilibrium Bifurcation for Inhomogeneous Plate

We assume that in addition to the above-described state of equilibrium for the inhomogeneous plate, there is an infinitely close equilibrium state under the same external loads, which is determined by the radius vector \({\varvec{R}}+\eta {\varvec{v}}\) and microrotation tensor \({\mathbf{\mathsf{{H}} }}-\eta {\mathbf{\mathsf{{H}} }}\times {\varvec{\upomega }}\). Here \(\eta \) is a small parameter, \({\varvec{v}}\) is the vector of additional displacements, \({\varvec{\upomega }}\) is a linear incremental rotation vector, which characterizes the small rotation of the micropolar medium particles, measured from the initial strain state.

The perturbed state of equilibrium for the micropolar medium is described by the equations [7]:

$$\begin{aligned} \mathrm{div}{\mathbf{\mathsf{{D}} }}^\bullet =0,\quad \quad \mathrm{div}{\mathbf{\mathsf{{G}} }}^\bullet +\left[ {\mathrm{grad}{\varvec{v}}^\mathrm{T}\cdot {\mathbf{\mathsf{{D}} }}+{\mathbf{\mathsf{{C}} }}^\mathrm{T}\cdot {\mathbf{\mathsf{{D}} }}^\bullet } \right] _\times =0, \end{aligned}$$
(10)

where \({\mathbf{\mathsf{{D}} }}^\bullet \) and \({\mathbf{\mathsf{{G}} }}^\bullet \) are the linearized Piola-type stress and couple stress tensors. In the case of physically linear micropolar material (6), the following relations are valid for these tensors [17, 18]:

$$\begin{aligned} \displaystyle {\mathbf{\mathsf{{D}} }}^\bullet&=\displaystyle \left( {\frac{\partial W}{\partial {\mathbf{\mathsf{{Y}} }}}} \right) ^\bullet \cdot {\mathbf{\mathsf{{H}} }}+\frac{\partial W}{\partial {\mathbf{\mathsf{{Y}} }}}\cdot {\mathbf{\mathsf{{H}} }}^\bullet =\left( {\lambda \left( {\mathrm{tr}\,{\mathbf{\mathsf{{Y}} }}^\bullet } \right) {\mathbf{\mathsf{{E}} }}+\left( {\mu +\kappa } \right) {\mathbf{\mathsf{{Y}} }}^\bullet + \mu {\mathbf{\mathsf{{Y}} }}^{\bullet \mathrm T}} \right) \cdot {\mathbf{\mathsf{{H}} }} \nonumber \\ \displaystyle&\quad \;-\displaystyle \left( {\lambda \mathrm{tr}\left( {{\mathbf{\mathsf{{Y}} }}-{\mathbf{\mathsf{{E}} }}} \right) {\mathbf{\mathsf{{E}} }}+\mu \left( {{\mathbf{\mathsf{{Y}} }}^\mathrm{T}-{\mathbf{\mathsf{{E}} }}} \right) +\left( {\mu +\kappa } \right) \left( {{\mathbf{\mathsf{{Y}} }}-{\mathbf{\mathsf{{E}} }}} \right) } \right) \cdot {\mathbf{\mathsf{{H}} }}\times {\varvec{\upomega }}, \end{aligned}$$
(11)
$$\begin{aligned} \displaystyle {\mathbf{\mathsf{{G}} }}^\bullet&=\displaystyle \left( {\frac{\partial W}{\partial {\mathbf{\mathsf{{L}} }}}} \right) ^\bullet \cdot {\mathbf{\mathsf{{H}} }}+\frac{\partial W}{\partial {\mathbf{\mathsf{{L}} }}}\cdot {\mathbf{\mathsf{{H}} }}^\bullet \nonumber \\&\!=\!\displaystyle \left( {\gamma _1 \left( {\mathrm{tr}\,{\mathbf{\mathsf{{L}} }}^\bullet } \right) {\mathbf{\mathsf{{E}} }}\!+\!\gamma _2 {\mathbf{\mathsf{{L}} }}^\bullet +\gamma _3 {\mathbf{\mathsf{{L}} }}^{\bullet \mathrm{T}}} \right) \cdot {\mathbf{\mathsf{{H}} }}- \left( {\gamma _1 \left( {\mathrm{tr}\,{\mathbf{\mathsf{{L}} }}} \right) {\mathbf{\mathsf{{E}} }}+\gamma _2 {\mathbf{\mathsf{{L}} }}+\gamma _3 {\mathbf{\mathsf{{L}} }}^\mathrm{T}} \right) \cdot {\mathbf{\mathsf{{H}} }}\times {\varvec{\upomega }}, \end{aligned}$$
(12)
$$\begin{aligned} {\mathbf{\mathsf{{Y}} }}^\bullet =\left( {\mathrm{grad}{\varvec{v}}+{\mathbf{\mathsf{{C}} }}\times {\varvec{\upomega }}} \right) \cdot {\mathbf{\mathsf{{H}} }}^\mathrm{T},\qquad {\mathbf{\mathsf{{L}} }}^\bullet =\mathrm{grad}\;{\varvec{\upomega }}\cdot {\mathbf{\mathsf{{H}} }}^\mathrm{T}. \end{aligned}$$

Here \({\mathbf{\mathsf{{Y}} }}^\bullet \) is the linearized stretch tensor, \({\mathbf{\mathsf{{L}} }}^\bullet \) is the linearized wryness tensor. Linearized boundary conditions on the faces of the plate \(\left( z=\pm H/2 \right) \) are written as follows:

$$\begin{aligned} \left. {\varvec{e}}_z \cdot {{\mathbf{\mathsf{{D}} }}^\bullet } \right| _{z=\pm \frac{H}{2}} =0,\qquad \left. {\varvec{e}}_z \cdot {{\mathbf{\mathsf{{G}} }}^\bullet } \right| _{z=\pm \frac{H}{2}} =0. \end{aligned}$$
(13)

We assume that there is no friction at the edge of the plate \(\left( r=r_1 \right) \), and constant normal displacement is given. This leads to the following linearized boundary conditions:

$$\begin{aligned} \displaystyle \left. {{\varvec{e}}_r \cdot {\mathbf{\mathsf{{D}} }}^\bullet \cdot {\varvec{e}}_\Phi } \right| _{r=r_1} =\left. {{\varvec{e}}_r\cdot {\mathbf{\mathsf{{D}} }}^\bullet \cdot {\varvec{e}}_Z } \right| _{r=r_1} ={\varvec{e}}_r\cdot \left. {\varvec{v}} \right| _{r=r_1}&=0, \nonumber \\ \displaystyle \left. {{\varvec{e}}_r\cdot {\mathbf{\mathsf{{G}} }}^\bullet \cdot {\varvec{e}}_R} \right| _{r=r_1} ={\varvec{e}}_\varphi \cdot \left. {\varvec{\upomega }} \right| _{r=r_1} ={\varvec{e}}_z \cdot \left. {\varvec{\upomega }} \right| _{r=r_1}&=0. \end{aligned}$$
(14)

We write the vector of additional displacements \({\varvec{v}}\) and vector of incremental rotation \({\varvec{\upomega }}\) in the basis of Eulerian cylindrical coordinates:

$$\begin{aligned} {\varvec{v}}=v_R {\varvec{e}}_R +v_\Phi {\varvec{e}}_\Phi +v_Z {\varvec{e}}_Z, \qquad {\varvec{\upomega }}=\omega _{\,R} {\varvec{e}}_R +\omega _{\,\Phi } {\varvec{e}}_\Phi +\omega _{\,Z} {\varvec{e}}_Z. \end{aligned}$$
(15)

With respect to representation (15), the expressions for the linearized stretch tensor \({\mathbf{\mathsf{{Y}} }}^\bullet \) and wryness tensor \({\mathbf{\mathsf{{L}} }}^\bullet \) have the form:

$$\begin{aligned} \displaystyle {{\mathbf{\mathsf{{Y}} }}}^\bullet&=\displaystyle \left( {\frac{\partial v_\Phi }{\partial r}-\alpha \omega _Z } \right) {\varvec{e}}_r \otimes {\varvec{e}}_\varphi + \frac{1}{r}\left( {\frac{\partial v_R }{\partial \varphi }-v_\Phi +\alpha r \omega _Z } \right) {\varvec{e}}_\varphi \otimes {\varvec{e}}_r \nonumber \\ \displaystyle \displaystyle&\quad \;+\displaystyle \left( {\frac{\partial v_Z }{\partial r}+\alpha \omega _\Phi } \right) {\varvec{e}}_r \otimes {\varvec{e}}_z + \left( {\frac{\partial v_R }{\partial z}-{f}^{\prime } \omega _\Phi } \right) {\varvec{e}}_z \otimes {\varvec{e}}_r \nonumber \\ \displaystyle \displaystyle&\quad \;+\displaystyle \frac{1}{r}\left( {\frac{\partial v_Z }{\partial \varphi }-\alpha r \omega _R } \right) {\varvec{e}}_\varphi \otimes {\varvec{e}}_z + \left( {\frac{\partial v_\Phi }{\partial z}+{f}^{\prime } \omega _R } \right) {\varvec{e}}_z \otimes {\varvec{e}}_\varphi \\ \displaystyle \displaystyle&\quad \; +\displaystyle \frac{\partial v_R }{\partial r}{\varvec{e}}_r \otimes {\varvec{e}}_r +\frac{1}{r}\left( {\frac{\partial v_\Phi }{\partial \varphi }+v_R } \right) {\varvec{e}}_\varphi \otimes {\varvec{e}}_\varphi +\frac{\partial v_Z }{\partial z}{\varvec{e}}_z \otimes {\varvec{e}}_z,\nonumber \end{aligned}$$
(16)
$$\begin{aligned} {{\mathbf{\mathsf{{L}} }}}^\bullet&=\displaystyle \frac{\partial \omega _R }{\partial r}{\varvec{e}}_r \otimes {\varvec{e}}_r + \frac{1}{r}\left( {\frac{\partial \omega _\Phi }{\partial \varphi }+\omega _R } \right) {\varvec{e}}_\varphi \otimes {\varvec{e}}_\varphi +\frac{\partial \omega _Z }{\partial z}{\varvec{e}}_z \otimes {\varvec{e}}_z \nonumber \\&\quad \;+\displaystyle \frac{\partial \omega _\Phi }{\partial r}{\varvec{e}}_r \otimes {\varvec{e}}_\varphi +\frac{1}{r}\left( {\frac{\partial \omega _R }{\partial \varphi }-\omega _\Phi } \right) {\varvec{e}}_\varphi \otimes {\varvec{e}}_r + \frac{\partial \omega _Z }{\partial r}{\varvec{e}}_r \otimes {\varvec{e}}_z \\&\quad \;+\displaystyle \frac{\partial \omega _R }{\partial z}{\varvec{e}}_z \otimes {\varvec{e}}_r +\frac{1}{r}\frac{\partial \omega _Z }{\partial \varphi }{\varvec{e}}_\varphi \otimes {\varvec{e}}_z +\frac{\partial \omega _\Phi }{\partial z}{\varvec{e}}_z \otimes {\varvec{e}}_\varphi . \nonumber \end{aligned}$$
(17)

According to relations (3)–(5), (11), (12), (15)–(17), the components of the linearized Piola-type stress tensor \({\mathbf{\mathsf{{D}} }}^\bullet \) and couple stress tensor \({\mathbf{\mathsf{{G}} }}^\bullet \) are written as follows:

$$\begin{aligned} {\varvec{e}}_r \cdot {{\mathbf{\mathsf{{D}} }}}^\bullet \cdot {\varvec{e}}_R&=\displaystyle \left( {\lambda +\chi } \right) \frac{\partial v_R }{\partial r}\,\,+\frac{\lambda }{r}\left( {\frac{\partial v_\Phi }{\partial \varphi }+v_R } \right) +\lambda \frac{\partial v_Z }{\partial z}, \nonumber \\ {\varvec{e}}_r \cdot {{\mathbf{\mathsf{{D}} }}}^\bullet \cdot {\varvec{e}}_\Phi&=\displaystyle \left( {\mu +\kappa } \right) \frac{\partial v_\Phi }{\partial r}+\frac{\mu }{r}\left( {\frac{\partial v_R }{\partial \varphi }-v_\Phi }\right) +\left( {\lambda s+2 \mu \alpha -\chi } \right) \omega _Z, \nonumber \\ {\varvec{e}}_r \cdot {{\mathbf{\mathsf{{D}} }}}^\bullet \cdot {\varvec{e}}_Z&=\displaystyle \left( {\mu +\kappa } \right) \frac{\partial v_Z }{\partial r}+\mu \frac{\partial v_R }{\partial z}-\left( {\lambda s+\mu \left( {{f}^{\prime }+\alpha } \right) -\chi } \right) \omega _\Phi , \nonumber \\ {\varvec{e}}_\varphi \cdot {{\mathbf{\mathsf{{D}} }}}^\bullet \cdot {\varvec{e}}_R&=\displaystyle \frac{\mu +\kappa }{r}\left( {\frac{\partial v_R }{\partial \varphi }-v_\Phi } \right) +\mu \frac{\partial v_\Phi }{\partial r}-\left( {\lambda s+2 \mu \alpha -\chi } \right) \omega _Z, \nonumber \\ {\varvec{e}}_\varphi \cdot {{\mathbf{\mathsf{{D}} }}}^\bullet \cdot {\varvec{e}}_\Phi&=\displaystyle \lambda \frac{\partial v_R }{\partial r}\,\,+\frac{\lambda +\chi }{r}\left( {\frac{\partial v_\Phi }{\partial \varphi }+v_R } \right) +\lambda \frac{\partial v_Z }{\partial z}, \nonumber \\ {\varvec{e}}_\varphi \cdot {{\mathbf{\mathsf{{D}} }}}^\bullet \cdot {\varvec{e}}_Z&=\displaystyle \frac{\mu +\kappa }{r}\frac{\partial v_Z }{\partial \varphi }+\mu \frac{\partial v_\Phi }{\partial z}+\left( {\lambda s+\mu \left( {{f}^{\prime }+\alpha } \right) -\chi } \right) \omega _Rz,\nonumber \\ {\varvec{e}}_z \cdot {{\mathbf{\mathsf{{D}} }}}^\bullet \cdot {\varvec{e}}_R&=\displaystyle \left( {\mu +\kappa } \right) \frac{\partial v_R }{\partial z}+\mu \frac{\partial v_Z }{\partial r}+\left( {\lambda s+\mu \left( {{f}^{\prime }+\alpha } \right) -\chi } \right) \omega _Pi, \nonumber \\ {\varvec{e}}_z \cdot {{\mathbf{\mathsf{{D}} }}}^\bullet \cdot {\varvec{e}}_\Phi&=\displaystyle \left( {\mu +\kappa } \right) \frac{\partial v_\Phi }{\partial z}+\frac{\mu }{r}\frac{\partial v_Z }{\partial \varphi }-\left( {\lambda s+\mu \left( {{f}^{\prime }+\alpha } \right) -\chi } \right) \omega _R, \nonumber \\ {\varvec{e}}_z \cdot {{\mathbf{\mathsf{{D}} }}}^\bullet \cdot {\varvec{e}}_Z&=\displaystyle \lambda \frac{\partial v_R }{\partial r}\,\,+\frac{\lambda }{r}\left( {\frac{\partial v_\Phi }{\partial \varphi }+v_R } \right) +\left( {\lambda +\chi } \right) \frac{\partial v_Z }{\partial z}, \\ {\varvec{e}}_r \cdot {{\mathbf{\mathsf{{G}} }}}^\bullet \cdot {\varvec{e}}_R&=\displaystyle \left( {\gamma _1 +\gamma _2 +\gamma _3 } \right) \frac{\partial \omega _R }{\partial r}\,\,+\frac{\gamma _1 }{r}\left( {\frac{\partial \omega _\Phi }{\partial \varphi }+\omega _R } \right) +\gamma _1 \frac{\partial \omega _Z }{\partial z}, \nonumber \\ {\varvec{e}}_r \cdot {{\mathbf{\mathsf{{G}} }}}^\bullet \cdot {\varvec{e}}_\Phi&=\displaystyle \gamma _2 \frac{\partial \omega _\Phi }{\partial r}+\frac{\gamma _3 }{r}\left( {\frac{\partial \omega _R }{\partial \varphi }-\omega _\Phi } \right) , \nonumber \\ {\varvec{e}}_\varphi \cdot {{\mathbf{\mathsf{{G}} }}}^\bullet \cdot {\varvec{e}}_R&=\displaystyle \frac{\gamma _2 }{r}\left( {\frac{\partial \omega _R }{\partial \varphi }-\omega _\Phi } \right) +\gamma _3 \frac{\partial \omega _\Phi }{\partial r}, \nonumber \\ {\varvec{e}}_r \cdot {{\mathbf{\mathsf{{G}} }}}^\bullet \cdot {\varvec{e}}_Z&=\displaystyle \gamma _2 \frac{\partial \omega _Z }{\partial r}+\gamma _3 \frac{\partial \omega _R }{\partial z}, \nonumber \\ {\varvec{e}}_z \cdot {{\mathbf{\mathsf{{G}} }}}^\bullet \cdot {\varvec{e}}_R&=\displaystyle \gamma _2 \frac{\partial \omega _R }{\partial z}+\gamma _3 \frac{\partial \omega _Z }{\partial r}, \nonumber \\ {\varvec{e}}_\varphi \cdot {{\mathbf{\mathsf{{G}} }}}^\bullet \cdot {\varvec{e}}_\Phi&=\displaystyle \gamma _1 \frac{\partial \omega _R }{\partial r}\,\,+\frac{\gamma _1 +\gamma _2 +\gamma _3 }{r}\left( {\frac{\partial \omega _\Phi }{\partial \varphi }+\omega _R } \right) +\gamma _1 \frac{\partial \omega _Z }{\partial z}, \nonumber \\ {\varvec{e}}_\varphi \cdot {{\mathbf{\mathsf{{G}} }}}^\bullet \cdot {\varvec{e}}_Z&=\displaystyle \frac{\gamma _2 }{r}\frac{\partial \omega _Z }{\partial \varphi }+\gamma _3 \frac{\partial \omega _\Phi }{\partial z}, \nonumber \\ {\varvec{e}}_z \cdot {{\mathbf{\mathsf{{G}} }}}^\bullet \cdot {\varvec{e}}_\Phi&=\displaystyle \gamma _2 \frac{\partial \omega _\Phi }{\partial z}+\frac{\gamma _3 }{r}\frac{\partial \omega _Z }{\partial \varphi }, \nonumber \\ {\varvec{e}}_z \cdot {{\mathbf{\mathsf{{G}} }}}^\bullet \cdot {\varvec{e}}_Z&=\displaystyle \gamma _1 \frac{\partial \omega _R }{\partial r}\,\,+\frac{\gamma _1 }{r}\left( \!\! {\frac{\partial \omega _\Phi }{\partial \varphi }+\omega _R }\!\! \right) +\left( {\gamma _1 +\gamma _2 +\gamma _3 } \right) \frac{\partial \omega _Z }{\partial z}. \nonumber \end{aligned}$$
(18)

Using expressions (4), (5), (7) and (15), (18), we write the equations of the neutral equilibrium (10) for the inhomogeneous plate in scalar form:

$$\begin{aligned} \left( {\mu + \kappa } \right) \left( {\frac{1}{{r^2 }}\frac{{\partial ^2 v_R }}{{\partial \varphi ^2 }} + \frac{{\partial ^2 v_R }}{{\partial z^2 }} - \frac{1}{{r^2 }}\frac{{\partial v_\Phi }}{{\partial \varphi }}} \right) + \left( {\lambda + \mu } \right) \left( {\frac{1}{r}\frac{{\partial ^2 v_\Phi }}{{\partial r\partial \varphi }} + \frac{{\partial ^2 v_Z }}{{\partial r\partial z}} } \right)&\\ + \left( {\lambda + \chi } \right) \left( {\frac{{\partial ^2 v_R }}{{\partial r^2 }} + \frac{1}{r}\frac{{\partial v_R }}{{\partial r}} - \frac{1}{{r^2 }}v_R - \frac{1}{{r^2 }}\frac{{\partial v_\Phi }}{{\partial \varphi }}} \right) + \left( {\mu ^{\prime } + \kappa ^{\prime }} \right) \frac{{\partial v_R }}{{\partial z}} + \mu ^{\prime }\frac{{\partial v_Z }}{{\partial r}}&\\ + \xi \frac{{\partial \omega _\Phi }}{{\partial z}} + \xi ^{\prime }\omega _\Phi - \frac{1}{r}\left( {\lambda s + 2\mu \alpha - \chi } \right) \frac{{\partial \omega _Z }}{{\partial \varphi }}&= 0, \end{aligned}$$
$$\begin{aligned} \frac{{\lambda + \chi }}{{r^2 }}\left( {\frac{{\partial ^2 v_\Phi }}{{\partial \varphi ^2 }} + \frac{{\partial v_R }}{{\partial \varphi }}} \right) + \frac{{\lambda + \mu }}{r}\left( {\frac{{\partial ^2 v_R }}{{\partial r\partial \varphi }} + \frac{{\partial ^2 v_Z }}{{\partial \varphi \partial z}}} \right) + \left( {\mu ^{\prime } + \kappa ^{\prime }} \right) \frac{{\partial v_\Phi }}{{\partial z}}&\\ + \left( {\mu + \kappa } \right) \left( {\frac{{\partial ^2 v_\Phi }}{{\partial r^2 }} + \frac{1}{r}\frac{{\partial v_\Phi }}{{\partial r}} - \frac{1}{{r^2 }}v_\Phi + \frac{1}{{r^2 }}\frac{{\partial v_R }}{{\partial \varphi }} + \frac{{\partial ^2 v_\Phi }}{{\partial z^2 }}} \right) + \frac{{\mu ^{\prime }}}{r}\frac{{\partial v_Z }}{{\partial \varphi }}&\\ -\xi \frac{{\partial \omega _R }}{{\partial z}} - \xi ^{\prime }\omega _R + \left( {\lambda s + 2\mu \alpha - \chi } \right) \frac{{\partial \omega _Z }}{{\partial r}}&= 0, \end{aligned}$$
$$\begin{aligned} \left( {\lambda + \chi } \right) \frac{{\partial ^2 v_Z }}{{\partial z^2 }} + \left( {\mu + \kappa } \right) \left( {\frac{{\partial ^2 v_Z }}{{\partial r^2 }} + \frac{1}{r}\frac{{\partial v_Z }}{{\partial r}} + \frac{1}{{r^2 }}\frac{{\partial ^2 v_Z }}{{\partial \varphi ^2 }}} \right)&\\ +\left( {\lambda + \mu } \right) \left( {\frac{{\partial ^2 v_R }}{{\partial r\partial z}} + \frac{1}{r}\frac{{\partial v_R }}{{\partial z}} + \frac{1}{r}\frac{{\partial ^2 v_\Phi }}{{\partial \varphi \partial z}}} \right) + \lambda ^{\prime }\frac{{\partial v_R }}{{\partial r}}{} {} + \frac{{\lambda ^{\prime }}}{r}\left( {\frac{{\partial v_\Phi }}{{\partial \varphi }} + v_R } \right)&\\ +\left( {\lambda ^{\prime } + \chi ^{\prime }} \right) \frac{{\partial v_Z }}{{\partial z}} + \xi \left( {\frac{1}{r}\frac{{\partial \omega _R }}{{\partial \varphi }} - \frac{{\partial \omega _\Phi }}{{\partial r}} - \frac{1}{r}\omega _\Phi } \right)&= 0, \end{aligned}$$
$$\begin{aligned} \left( {\gamma _1 + \gamma _2 + \gamma _3 } \right) \left( {\frac{{\partial ^2 \omega _R }}{{\partial r^2 }} + \frac{1}{r}\frac{{\partial \omega _R }}{{\partial r}} - \frac{1}{{r^2 }}\frac{{\partial \omega _\Phi }}{{\partial \varphi }} - \frac{1}{{r^2 }}\omega _R } \right)&\nonumber \\ +\left( {\gamma _1 + \gamma _3 } \right) \left( {\frac{1}{r}\frac{{\partial ^2 \omega _\Phi }}{{\partial r\partial \varphi }} + \frac{{\partial ^2 \omega _Z }}{{\partial r\partial z}}} \right) + \gamma _2 \left( {\frac{1}{{r^2 }}\frac{{\partial ^2 \omega _R }}{{\partial \varphi ^2 }} + \frac{{\partial ^2 \omega _R }}{{\partial z^2 }} - \frac{1}{{r^2 }}\frac{{\partial \omega _\Phi }}{{\partial \varphi }}} \right)&\\ +\gamma ^{\prime }_2 \frac{{\partial \omega _R }}{{\partial z}} + \gamma ^{\prime }_3 \frac{{\partial \omega _Z }}{{\partial r}} + \xi \left( {\frac{{\partial v_\Phi }}{{\partial z}} - \frac{1}{r}\frac{{\partial v_Z }}{{\partial \varphi }} + \left( {\alpha + f^{\prime }} \right) \omega _R } \right)&= 0, \nonumber \end{aligned}$$
(19)
$$\begin{aligned} \frac{{\gamma _1 + \gamma _2 + \gamma _3 }}{{r^2 }} \left( {\frac{{\partial ^2 \omega _\Phi }}{{\partial \varphi ^2 }} + \frac{{\partial \omega _R }}{{\partial \varphi }}} \right) +\frac{{\gamma _1 + \gamma _3 }}{r}\left( {\frac{{\partial ^2 \omega _R }}{{\partial r\partial \varphi }} + \frac{{\partial ^2 \omega _Z }}{{\partial \varphi \partial z}}} \right) + \gamma ^{\prime }_2 \frac{{\partial \omega _\Phi }}{{\partial z}} \\ + \gamma _2 \left( {\frac{1}{{r^2 }}\frac{{\partial \omega _R }}{{\partial \varphi }} + \frac{{\partial ^2 \omega _\Phi }}{{\partial r^2 }} + \frac{1}{r}\frac{{\partial \omega _\Phi }}{{\partial r}} + \frac{{\partial ^2 \omega _\Phi }}{{\partial z^2 }} - \frac{1}{{r^2 }}\omega _\Phi } \right) + \frac{{\gamma ^{\prime }_3 }}{r}\frac{{\partial \omega _Z }}{{\partial \varphi }}\\ + \xi \left( {\frac{{\partial v_Z }}{{\partial r}} \!-\! \frac{{\partial v_R }}{{\partial z}} \!+\! \left( {\alpha + f^{\prime }} \right) \omega _\Phi } \right) = 0 \end{aligned}$$
$$\begin{aligned} \left( {\gamma _1 + \gamma _3 } \right) \left( {\frac{{\partial ^2 \omega _R }}{{\partial r\partial z}} + \frac{1}{r}\frac{{\partial \omega _R }}{{\partial z}} + \frac{1}{r}\frac{{\partial ^2 \omega _\Phi }}{{\partial \varphi \partial z}}} \right) + \gamma _2 \left( {\frac{{\partial ^2 \omega _Z }}{{\partial r^2 }} + \frac{1}{r}\frac{{\partial \omega _Z }}{{\partial r}} + \frac{1}{{r^2 }}\frac{{\partial ^2 \omega _Z }}{{\partial \varphi ^2 }}} \right)&\\ + \left( {\gamma _1 + \gamma _2 + \gamma _3 } \right) \frac{{\partial ^2 \omega _Z }}{{\partial z^2 }} + \gamma ^{\prime }_1 \frac{{\partial \omega _R }}{{\partial r}} + \frac{{\gamma ^{\prime }_1 }}{r}\frac{{\partial \omega _\Phi }}{{\partial \varphi }} + \frac{{\gamma ^{\prime }_1 }}{r}\omega _R + \left( {\gamma ^{\prime }_1 + \gamma ^{\prime }_2 + \gamma ^{\prime }3 } \right) \frac{{\partial \omega _Z }}{{\partial z}}&\\ +\left( {\lambda s + 2\mu \alpha - \chi } \right) \left( {\frac{1}{r}\frac{{\partial v_R }}{{\partial \varphi }} - \frac{1}{r}v_\Phi - \frac{{\partial v_\Phi }}{{\partial r}} + 2\alpha \omega _Z } \right) = 0.&\end{aligned}$$

Substitution

$$\begin{aligned} v_R&=V_R \left( r,z \right) \cos n\varphi , \quad v_\Phi =V_\Phi \left( r,z \right) \sin n\varphi , \qquad v_Z =V_Z \left( r,z \right) \cos n\varphi , \\ \omega _R&=\Omega _R \left( r,z \right) \sin n\varphi , \quad \omega _\Phi =\Omega _\Phi \left( r,z \right) \cos n\varphi , \quad \omega _Z =\Omega _Z \left( r,z \right) \sin n\varphi , \end{aligned}$$
$$\begin{aligned} n=0,\ 1,\ 2,... \end{aligned}$$

allows us to separate the variable \(\varphi \) in these equations, reducing the stability analysis to the solution of homogeneous boundary problem (13), (14) and (19) for a system of six partial differential equations in the six unknown functions of two variables \(r,\ z\).

4 Axisymmetric Buckling Modes

In the special case of axisymmetric perturbations \((n=0)\) the use of substitution

$$\begin{aligned} \begin{array}{lcr} \displaystyle v_R =V_R \left( z \right) J_1\left( \beta r \right) , &{} \quad v_\Phi =0, &{} \quad v_Z =V_Z \left( z \right) J_0\left( \beta r \right) , \\ \omega _R =0, &{} \quad \omega _\Phi =\Omega _\Phi \left( z \right) J_1\left( \beta r \right) , &{} \quad \omega _Z =0, \end{array} \end{aligned}$$
(20)
$$\begin{aligned} \beta =\zeta _m/r_1, \qquad J_1\left( \zeta _m \right) =0, \qquad m=1,2,... \end{aligned}$$

leads to the separation of variable \(r\) in the equations of neutral equilibrium and allows to satisfy the linearized boundary conditions (14) at the edge of the plate.

By taking into account the relations (20), the linearized equilibrium equations (19) are written as follows:

$$\begin{aligned} \left( {\mu + \kappa } \right) V^{\prime \prime }_R + \left( {\mu ^{\prime } + \kappa ^{\prime }} \right) V^{\prime }_R&- \left( {\lambda + \chi } \right) \beta ^2 V_R - \left( {\lambda + \mu } \right) \beta V^{\prime }_Z - \\&- \beta \mu ^{\prime }V_Z + \theta \Omega ^{\prime }_\Phi + \theta ^{\prime }\Omega _\Phi = 0, \end{aligned}$$
$$\begin{aligned} \left( {\lambda + \chi } \right) V^{\prime \prime }_Z + \left( {\lambda ^{\prime } + \chi ^{\prime }} \right) V^{\prime }_Z - \left( {\mu + \kappa } \right)&\beta ^2 V_Z + \left( {\lambda + \mu } \right) \beta V^{\prime }_R + \\&+ \beta \lambda ^{\prime }V_R - \theta \beta \Omega _\Phi = 0, \nonumber \end{aligned}$$
(21)
$$\begin{aligned} \gamma _2 \Omega ^{\prime \prime }_\Phi + \gamma ^{\prime }_2 \Omega ^{\prime }_\Phi + \left[ {\left( {\alpha + f^{\prime }} \right) \theta - \gamma _2 \beta ^2 } \right] \Omega _\Phi - \theta V^{\prime }_R - \beta \theta V_Z = 0. \end{aligned}$$

Here we use the following notation

$$\begin{aligned} \theta = \lambda s + \mu \left( {\alpha + f^{\prime }} \right) - \chi . \end{aligned}$$

The linearized boundary conditions on the faces of the plate (13) take the form:

$$\begin{aligned} \left( {\mu + \kappa } \right) V^{\prime }_R - \mu \beta V_Z + \theta \Omega _\Phi = 0, \,\,\, \beta \lambda V_R + \left( {\lambda + \chi } \right) V^{\prime }_Z = 0, \,\,\, \Omega ^{\prime }_\Phi = 0. \end{aligned}$$
(22)

Thus, in the case of axisymmetric perturbations, the stability analysis of the inhomogeneous circular plate is reduced to solving a linear homogeneous boundary-value problem (21) and (22) for a system of three ordinary differential equations.

5 Symmetric Plate

It is easy to show that if the functions describing the change in the elastic parameters of the plate through the thickness are even, i.e. \(\lambda (z)=\lambda (-z)\), \(\mu (z)~=~\mu (-z)\), \({\kappa (z)=\kappa (-z)}\), \(\gamma _1(z)=\gamma _1(-z)\), \(\gamma _2(z)=\gamma _2(-z)\), \(\gamma _3(z)=\gamma _3(-z)\), then the boundary-value problem (21), (22) has two independent sets of solutions [16, 18].

The First set is formed by solutions for which the deflection of a plate is an odd function of \(z\) (symmetric buckling):

$$\begin{aligned} V_R (z) = V_R ( - z), \qquad V_Z (z) = - V_Z ( - z), \qquad \Omega _\Phi (z) = - \Omega _\Phi ( - z). \end{aligned}$$

For the Second set of solutions, on the contrary, the deflection is an even function of \(z\) (bending buckling):

$$\begin{aligned} V_R (z) = - V_R ( - z), \qquad V_Z (z) = V_Z ( - z), \qquad \Omega _\Phi (z) = \Omega _\Phi ( - z). \end{aligned}$$

Due to this property of boundary-value problem (21) and (22), for the study of stability it is sufficient to consider only the upper half of the inhomogeneous plate \((0\leqslant z \leqslant H/2)\). The boundary conditions at \(z=0\) follows from the evenness and oddness of the unknown functions \(V_R, \ V_Z,\ \Omega _\Phi \):

  1. (a)

    for the First set of solutions:

    $$\begin{aligned} {V}^{\prime }_R (0)=V_Z (0)=\Omega _\Phi (0)=0, \end{aligned}$$
    (23)
  2. (b)

    for the Second set of solutions:

    $$\begin{aligned} {V}_R (0)=V^{\prime }_Z (0)=\Omega ^{\prime }_\Phi (0)=0. \end{aligned}$$
    (24)

Thus, in the case of symmetric inhomogeneous plate, the stability analysis is reduced to solving two linear homogeneous boundary-value problems—(21), (22), (23) and (21), (22), (24)—for a system of three ordinary differential equations.

6 Conclusion

In the framework of bifurcation approach, the stability of an inhomogeneous circular plate subjected to radial compression and composed of a micropolar material is studied. For the physically linear micropolar material, a system of linearized equilibrium equations (19) is derived, which describes the behavior of the inhomogeneous plate in a perturbed state. Using special substitution (20) this equations are simplified and the linearized boundary-value problem is formulated for the case of an axisymmetric perturbations. Namely, the stability analysis is reduced to solving a linear homogeneous boundary problem (21) and (22) for a system of three ordinary differential equations.

It was also shown that, if the inhomogeneous plate is symmetric with respect to the middle surface \(z=0\), then the stability analysis is reduced to solving two independent linear homogeneous boundary-value problems for the half-plate—(21), (22), (23) and (21), (22), (24).

For specific micropolar materials all formulated boundary-value problems can be solved numerically using the same method as in [17] and [18].