Recent Advances in Nonsingular Terminal Sliding Mode Control Method

Abstract

The terminal sliding mode (TSM) control method has become a hot topic in recent years due to its special merit on finite-time convergence and good robustness. One critical issue is how to balance the singularity of control law and the fast convergence of closed-loop system. The chapter reviews the research history of the singularity and introduces the recent advance on nonsingular and fast terminal sliding mode (NFTSM) control method. The synthesis of NFTSM controller synthesis is based on a newly proposed nonsingular fast terminal function and a terminal attractor with nonnegative exponential coefficient. Both theoretical analyses and computer simulations have proved its effectiveness under the condition that plant uncertainties are bounded.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

4.1 Introduction

The Sliding Mode Control (SMC) method has been widely recognized for its good robustness to certain parameter variations and external disturbances [1, 2]. The SMC family has many variants, e.g., discrete-time SMC [3], adaptive SMC [4], dynamic SMC [5], backstepping SMC [6, 7], et al., due to its easy-to-use property and relatively simple structure. The terminal sliding mode (TSM) control method is also one of the most famous variants in recent years. The closed-loop system of SMC often has two modes, i.e., reaching mode and sliding mode. The former is to enable the state trajectory to converge to the sliding hyperplane, and the latter is to force the state to converge to the equilibrium point. The design of sliding mode controller accordingly contains two tasks: one is to design a suitable reaching law for the reaching mode, and the other is to choose an appropriate sliding function for the sliding mode. In TSM, a terminal attractor is employed as its reaching law and a terminal function is selected as its sliding function. This novel design generates special merits on system performance, such as finite-time convergence, good robustness to uncertainties, and small steady-state errors [8–11].

The terminal function plays a central role in designing TSM controllers. Its finite-time convergence property is the major merit of the TSM control method. This type of function may have other names, e.g., terminal attractor or terminal sliders, depending on their application, but actually possesses similar mathematical forms. To our knowledge, Venkataraman and Gulati [8] from California Institute of Technology were the first researchers to introduce terminal function to sliding mode control field [8]. Considering a second-order robotic system, an earlier terminal function (TF) is selected as

$$\begin{aligned} s = \dot{x} + \alpha \cdot x^{p/q}. \end{aligned}$$

(4.1)

In Eq. (4.1), $x \in \mathbb {R}$ is the system state, $\alpha \in \mathbb {R}^{+}$ and $p, q \in N$, satisfying $p < q$. One of its critical features is that the exponent $p/q$ is on state $x$ instead of on the derivative. It is well known that a linear sliding function generates exponential stability, and the state will infinitely approach, but never exactly equal the equilibrium point. On the contrary, the terminal sliding function enables a finite-time convergence property and the state can reach the equilibrium point in a discontinuous behavior. For multi-input multi-output (MIMO) systems, Man and Yu [12] extended this type of terminal function to high-dimensional situations [12]. The following research also proved its finite-time convergence property for some cascading systems [13]. This control method was applied to n-link rigid robotic manipulators and its good robustness to large uncertain dynamics was also observed [14].

Compared with linear sliding function, earlier terminal function might have slow convergence speed although it can still converge in finite time. The reason is as follows: since $p < q$ in Eq. (4.1), the exponent of state $x$ is smaller than 1. Thus, when far away from equilibrium point, i.e., $x \gg 1$, the derivative $\dot{x}$ in sliding mode will be much smaller than that in a similar linear sliding function, which thus largely slows down the convergence process. To address this issue, Yu and Man et al. [15] proposed a terminal function with fast convergence characteristics [15], called fast terminal function (FTF)

$$\begin{aligned} s = \dot{x} + \alpha \cdot x^{\gamma } + \beta \cdot x^{\rho }. \end{aligned}$$

(4.2)

In Eq. (4.2), $0 < \gamma < 1 ,\rho > 1, \gamma , \rho \in \mathbb {R}^{+}$. Compared with Eq. (4.1), Eq. (4.2) contains a polynomial term of order higher than 1. When $x \ll 1$, the high-order term is negligible, and hence Eq. (4.2) can be approximated by Eq. (4.1). When $x \gg 1$, the high-order term is able to strengthen control inputs, forcing Eq. (4.2) to converge faster than any linear sliding function. Yu and Guo et al. [16] obtained its global description and applied it to design both reaching law and sliding function [16]. This method can be easily extended by introducing new types of mathematical functions, e.g., Kang and Xi et al [17]:

$$\begin{aligned} s = \dot{x} + \frac{\alpha }{k} \left( e^{kx} - 1 \right) ^{q/p} x^{-kx}. \end{aligned}$$

(4.3)

In Eq. (4.3), $0 < k < 1$ and all other parameters are similar to those in Eq. (4.1). The theoretical analysis shows that on the sliding hyperplane the system is asymptotically stable and system state converges faster than Eq. (4.1).

One major drawback of TSM control is the singularity issue. When the system state is close to zero, the negative exponent of state in the control law will generate infinite values, not able to be implemented by actual actuators. This phenomenon is named the singularity of controllers. To resolve this issue, Yu and Man et al. [15] first modified the high-order fast terminal function and pointed out that the control input will be bounded in mathematics if some parameters satisfy the following inequality [15]:

$$\begin{aligned} \rho _{k+1} > \gamma _{k+1} > \frac{n - k - 1}{n - k}, 0 \le k \le n - 1, \end{aligned}$$

(4.4)

where $\rho , \gamma$ are the same as Eq. (4.2), n is the dimension of state, $k$ represents the k-th state. With this inequality condition, [18] and [19] designed a terminal sliding mode control law for a nonlinear dynamic system. Simulation showed that the accompanying coefficient of state approaches zero at a higher speed than state itself, thus eliminating the singular phenomenon.

However, for actual plants, the coefficient of state may not be exactly equal to zero when close to equilibrium points. The instantaneous singularity still exists because of parameter perturbations, external disturbances, and measurement errors. To obtain a truly nonsingular control law, Feng et al. [20] developed a nonsingular terminal function (NTF), realizing that the state converges in finite time during the sliding mode and the control law has no negative exponential term [20], shown as follows:

$$\begin{aligned} s = \frac{1}{\beta } \dot{x}^{p/q} + x. \end{aligned}$$

(4.5)

In Eq. (4.5), $p > 0, q >0, q$ is integer, and $1 < p/q < 2$. Combined with the global reaching conditions, a nonsingular terminal sliding mode (NTSM) control law can be designed [21, 22]. But this kind of terminal function has slow convergence speed in the region far away from equilibrium point. Moreover, a switching term inevitably exists in the control law, causing the commonly known chattering problem (another famous issue in sliding mode control). This largely limits its application in engineering practice. Zhang et al. [23] used the hysteresis layer to weaken chattering to some extent [23]. Hu et al. [24] developed an adaptive TSM control method. The method estimates the boundary of plant uncertainties and adjusts the control gain in a real-time manner [24]. The method can somewhat reduce the chattering issue in the condition of small uncertainties by avoiding using unnecessary large gain.

The designing method of terminal attractor is similar to the terminal function. By replacing state x with sliding mode variable s, all of the abovementioned terminal functions can be transferred to terminal attractors. In general, for the sake of simplicity, there are two commonly used terminal attractors, derived from Eqs. (4.1) and (4.2):

$$\begin{aligned}&\dot{s} + \alpha \cdot s^{p/q} = 0 \nonumber \\&\dot{s} + \alpha \cdot s^{\gamma } + \beta \cdot s^{\rho } = 0 \end{aligned}$$

(4.6)

In summary, the rapidity and singularity are the two key concerns in terminal sliding mode control. The fast terminal function or attractor can be used to improve convergence. The singularity is more difficult to handle in reality. The solutions up to now include the inequality constraint method and nonsingular terminal function. In real-world applications, the former still has singularity due to unexpected plant uncertainties; the latter avoid this difficulty, but might cause other issues such as slow convergence and chattering phenomenon. These shortcomings limit their application in practice.

To comprehensively deal with singularity, chattering, and slow convergence, this chapter introduces a nonsingular and fast terminal sliding mode control method. The remainder of this chapter is structured as follows. Section 4.2 reviews the conventional TSM control method. Section 4.3 introduces a newly proposed nonsingular fast terminal function and its corresponding terminal attractor, followed by how to synthesize the control law. Section 4.4 proves the convergence characteristics in both sliding and reaching modes, and the global existence of the sliding hyperplane. Section 4.5 demonstrates the success of this method. Section 4.6 concludes this chapter.

4.2 Problem Description

Consider a second-order SISO nonlinear system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{1} = x_{2}\\ \dot{x}_{2} = f (x, t) + u,\\ \end{array} \right. \end{aligned}$$

(4.7)

where $x = \left[ x_{1},x_{2} \right] ^{T} \in \mathbb {R}^{2}, u \in \mathbb {R}, f : \left( \mathbb {R}^{2}, \mathbb {R} \right) \rightarrow \mathbb {R}$. The conventional nonsingular terminal function (NTF) is defined for the sliding hyperplane [20]

$$\begin{aligned} s = x_{1} + \frac{1}{\beta } x_{2}^{p/q} , \end{aligned}$$

(4.8)

where $\bar{\beta } \in \mathbb {R}^{+}, \eta \in \mathbb {R}^{+}$ and $p, q$ are odds, satisfying $1 < p/q < 2$. The corresponding nonsingular terminal sliding mode (NTSM) control law is [20]

$$\begin{aligned} u = -f (x, t) - \frac{\bar{\beta }q}{p} x_{2}^{2-p/q} - \eta \mathrm{sgn} (s). \end{aligned}$$

(4.9)

In Eq.(4.9), the exponent of $x_{2}$ is always larger than zero, and therefore the control law completely avoids singularity. When the system is in sliding mode, we have $s = 0$ and

$$\begin{aligned} \dot{x}_{1} = - \bar{\beta }^{q/p} \cdot x_{1}^{q/p} \end{aligned}$$

(4.10)

However, the exponent of $x_{1}$ is smaller than 1 in Eq. (4.10). This is the reason causing slow convergence in large region. Another inherent shortcoming accompanying the NTSM controller is that Eq. (4.9) has a switching structure, resulting in unavoidable chattering issue. It is undesirable for precise tracking control. Even worse, it might be able to excite high-order unmodeled dynamics and cause instability.

4.3 Nonsingular and Fast TSM Control

As discussed before, the main reason for slow convergence is due to the exponent of state. Intuitively, if Eq. (4.10) has a polynomial term of degree higher than 1, the derivative of state will be increased in large region and consequently conquer this problem. Hence, we proposed a nonsingular fast terminal function (NFTF) with non-integer exponents for the sliding mode [25]

$$\begin{aligned} s = x_{1} + \frac{1}{\alpha } x_{1}^{g/h} + \frac{1}{\beta } x_{2}^{p/q} , \end{aligned}$$

(4.11)

where $\alpha \in \mathbb {R}^{+},\beta \in \mathbb {R}^{+}, p,q,g,h \in N^{+}$ are odds, satisfying

$$\begin{aligned} \begin{array}{l} 1 < p/q < 2 ,\\ g/h > p/q. \end{array} \end{aligned}$$

(4.12)

The reaching law is then defined as a terminal attractor with nonnegative exponential coefficient [25]

$$\begin{aligned} \dot{s}=\left( {-\phi s-\gamma s^{m/n}} \right) x_2^{p/q-1}, \end{aligned}$$

(4.13)

where $\phi \in \mathbb {R}^{+}, \gamma \in \mathbb {R}^{+},m, n \in N^{+}$ are odds, satisfying

$$\begin{aligned} 1 < m/n < 2. \end{aligned}$$

(4.14)

Substituting Eq. (4.11) and Eq. (4.13) into Eq. (4.7), we have a nonsingular fast terminal sliding mode (NFTSM) control law [25]

$$\begin{aligned} u=-f(x,t)-\frac{\beta q}{p}\left( {\phi s+\gamma s^{m/n}} \right) -\frac{\beta q}{p}x_2^{2-p/q} \left( {1+\frac{g}{\alpha h}x_1^{g/h-1} } \right) . \end{aligned}$$

(4.15)

The merit of NFTSM control method lies in the special structure of functions used in defining sliding mode (4.11) and reaching law (4.13). In sliding status, the sliding mode function dominates the closed-loop performance. Compared with other sliding functions, e.g., NTF, the NFTF contains a high-order exponential term of $x_{1}$. It has the ability to increase control gain when far away from equilibrium points, thus increasing the convergence speed in large region. Outside of sliding status, the terminal attractor in reaching law is used to match the specially designed NFTF. The synthesized control law eliminates any potential singularity in control inputs while not using any switching functions, thus no chattering issue.

4.4 Performance Analysis

4.4.1 Convergence Analysis for Sliding Mode

In the sliding mode, i.e., $s = 0$, the system dynamic is characterized by the sliding hyperplane. The qualitative analysis in Sect. 4.3 points out that NFTF has finite convergence time and converges faster than conventional NTF. In this section, we rigorously prove the convergence property of NFTF and NTF using the Lyapunov method. Then, we use computer simulations to compare the convergence speeds of NFTF and NTF. Before presenting the main proof we introduce a useful lemma below.

Lemma 1:

Consider a Gauss hyper-geometric function

$$\begin{aligned} F\left( {A,B,C,z} \right) =\sum _{k=0}^{+\infty } {\frac{\left( A \right) _k \left( B \right) _k}{\left( C \right) _k k!}} z^{k}. \end{aligned}$$

If $A, B, C \in \mathbb {R}^{+}$ and $C - A - B > 0$, then the function $F(A, B, C, z)$ converges for any $z < 0$. (The proof is given in [25])

Theorem 1:

For system (4.7), any state, lying on the NFTF hyperplane (4.11), converges to zero in finite time T. The convergence time T is given by

$$\begin{aligned} T=2\tau _1 ^{-q/p}\frac{p}{p-q}V\left( 0 \right) ^{\frac{p-q}{2p}}F\left( {A,B,C,-\frac{\tau _2 }{\tau _1 }V\left( 0 \right) ^{\frac{g-h}{2h}}} \right) \!, \end{aligned}$$

(4.16)

where $\tau _{1} = 2^{\frac{p+q}{2q}} \beta , \quad \tau _{2} =^{\frac{p}{2q} + \frac{g}{2h}} \frac{\beta }{\alpha ^{\prime }} \quad A= \frac{q}{p^{\prime }} \quad B = \frac{(p - q)h}{p (g-h)^{\prime }} \quad C = \frac{pg-qh}{p(g-h)^{\prime }} \quad V(t) = \frac{1}{2} x_{1}^{2}(t)$ and $F(\cdot )$ is the Gauss hyper-geometric function.

Proof:

When the system state lies on the sliding hyperplane, we have $s = 0$. Substituting $s = 0$ into Eq. (4.11), we obtain

$$\begin{aligned} \dot{x}_1^{p/q} =-\beta x_1 -\frac{\beta }{\alpha }x_1^{g/h} . \end{aligned}$$

(4.17)

Define a Lyapunov function

$$\begin{aligned} V (t) = 0.5x_{1}^{2} (t), \end{aligned}$$

(4.18)

and obtain its derivative as

$$\begin{aligned} \dot{V}^{\frac{p}{q}}=-\beta x_1^{\frac{p+q}{q}} -\frac{\beta }{\alpha }x_1^{\frac{p}{q}+\frac{g}{h}} . \end{aligned}$$

(4.19)

Note that p, q, g, and h are all odds. Thus $\dot{V} < 0$ for any $x \ne 0$. Using the Lyapunov theory of stability, we know that the closed-loop system is stable in the sliding mode, and the state at least asymptotically converges to the equilibrium point. Using Eq. (4.17), we find that the equilibrium point is unique, i.e., $x = 0$. To solve for the convergence time, we substitute $x_{1}^{2} = 2V$ into Eq. (4.19) and obtain

$$\begin{aligned} \dot{V}^{\frac{p}{q}}=-2^{\frac{p+q}{2q}} \beta V^{\frac{p+q}{2q}} -2^{\frac{p}{2q}+\frac{g}{2h}} \frac{\beta }{\alpha }V^{\frac{p}{2q}+\frac{g}{2h}} . \end{aligned}$$

(4.20)

Using $\dot{V} = dV/dt$ to Eq. (4.20), we have

$$\begin{aligned} \mathrm{d}t=-\left( {2^{\frac{p+q}{2q}} \beta V^{\frac{p+q}{2q}} +2^{\frac{p}{2q}+\frac{g}{2h}} \frac{\beta }{\alpha }V^{\frac{p}{2q}+\frac{g}{2h}} } \right) ^{-q/p} \mathrm{d}V. \end{aligned}$$

(4.21)

Let us define $\tau _{1} = 2^{\frac{p+q}{2q}} \beta$, $\tau _{2} = 2^{\frac{p}{2q}+\frac{g}{2h}} \frac{\beta }{\alpha }$, $A = \frac{q}{p}$, $B = \frac{(p-q)h}{p (g-h)}$, $C = \frac{pg - qh}{p(g - h)}$. Integrating both sides of Eq. (4.21), we obtain the convergence time T as

$$\begin{aligned} T=-\left. {2\tau _1 ^{-q/p}\frac{p}{p-q}V^{\frac{p-q}{2p}}F\left( {A,B,C,-\frac{\tau _2 }{\tau _1 }V^{\frac{g-h}{2h}}} \right) } \right| _{V(0)}^{V(T)} . \end{aligned}$$

(4.22)

It is clear that the system in sliding mode converges to the equilibrium point, i.e.,$x=0$, and thus we have $V (T) = 0$. According to the property of Gauss hyper-geometric function, we know that $F(\cdot , \cdot , \cdot , 0) = 1$. Substituting $V (T) = 0$ and $F(\cdot , \cdot , \cdot , 0) = 1$ into Eq. (4.22), we obtain Eq. (4.16).

Moreover, considering $q < p$ and $h < g$, we have $A > 0, B > , C> 0$, and $C - A - B > 0$. Using Lemma 1 and the fact that $V (0) > 0$ , we know that $F(A, B, C - \frac{\tau _{2}}{\tau _{1}} V (0)^{\frac{g - h}{2h}})$ is bounded. Thus, the convergence time T is finite, which implies that on the sliding mode hyperplane the system state converges to the equilibrium point in finite time. (End of Proof)

As discussed in Sect. 4.3, NFTF has faster convergence speed than NTF due to the high-order terms of $x_{1}$. To verify this observation, we use simulations to compare their convergence speeds in the sliding stage. When system lies on the NFTF sliding hyperplane, we have $s = 0$. By combing Eq. (4.7) and Eq. (4.11), we cancel $x_{2}$ and obtain sliding equation (4.17). Similarly, we can obtain the sliding equation (4.10) for the system lying on the NTF sliding hyperplane. To quantitatively verify the convergence speed of NFTF and NTF, we assume that the two controllers have comparable coefficients except the factor g / $h$. Note that by setting $g/h = 1$, Eq. (4.17) reduces to the form of Eq. (4.10)

$$\begin{aligned} \dot{x}_1 =- \left( {\beta +\frac{\beta }{\alpha }} \right) ^{q/p}x_1 ^{q/p}. \end{aligned}$$

To ensure that Eqs. (4.17) and (4.10) have comparable coefficients, it is required that

$$\begin{aligned} \bar{{\beta }}=\beta +\frac{\beta }{\alpha }. \end{aligned}$$

Hence, we select the following parameters for NFTF and NTF, as shown in Table 4.1.

Table 4.1 Selected parameters of NFTF and NTF

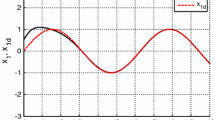
We simulate the sliding Eqs. (4.10) and (4.17) using identical initial condition $x_{1} = 9$. The state response curve of $x_{1}$ is depicted in Fig. 4.1. As shown in Fig. 4.1 (a), NFTF and NTF have the same initial states in the sliding stage. Note that NFTF is delayed by $\delta = 0.44~s$ to start compared to NTF, but both converge to zeros around $t = 3.7~s$. The state response curve of $x_{2}$, i.e., the derivative of $x_{1}$, is depicted in Fig. 4.1 (b). We observe that NFTF has larger state derivatives in magnitude than NTF when $x_{1} \gg 1$ and almost same derivatives when $x_{1} < 1$. This means that with the same parameters NFTF has faster convergence speed in sliding stage, which is consistent with the qualitative analysis presented before.

Fig. 4.1

Convergent speed comparison between NFTF and NTF a Response curve of state $x_{1}$ b Response curve of state $x_{2}$.

4.4.2 Convergence Analysis for Reaching Law

When the system is in the reaching stage, the convergence speed of the sliding mode s depends on the terminal attractor. It is proved in the following that terminal attractor (4.13) does not affect the existence of NFTF hyperplane and guarantees at least asymptotical convergence for the reaching stage. The proof is given below.

Theorem 2:

For the system (4.7) with NFTSM control law (4.15), the sliding mode hyperplane (4.11) globally exists, and the system state asymptotically reaches the sliding mode hyperplane from any initial point.

Proof:

Define a Lyapunov function

$$\begin{aligned} V=0.5\cdot s^{2}. \end{aligned}$$

(4.23)

Then,

$$\begin{aligned} \dot{V}=s\cdot \dot{s}=-\left( {\phi s^{2}+\gamma s^{m/n+1}} \right) x_2^{p/q-1} . \end{aligned}$$

(4.24)

Divide the $x_{1} - x_{2}$ phase plane into two regions

$$\begin{aligned} \begin{array}{l} D = \{ {{\varvec{x}}}|x_{1} \ne 0, x_{2} \ne 0 \},\\ \bar{D} = \{ {{\varvec{x}}}|x_{1} \ne 0, x_{2} = 0 \}. \end{array} \end{aligned}$$

(4.25)

For any ${\varvec{x}} \in \mathrm{D}$, since p, q, m, and n are all odds, we have $x_{2}^{p/q-1} > 0$ and $s^{m/n+1} > 0$, which implies that $\dot{V} < 0$. According to the Lyapunov theory of stability, the sliding mode s asymptotically converges in region D, and the sliding mode hyperplane exists for the NFTSM control law. To prove that s still converges for $x \in \bar{\mathrm{D}}$, we substitute the control law (4.13) into the system equation (4.7) and obtain

$$\begin{aligned} \dot{x}_1 =x_2 , \end{aligned}$$

(4.26)

$$\begin{aligned} \dot{x}_2 =-\frac{\beta q}{p}\left[ {\left( {\phi s+\gamma s^{m/n}} \right) +x_2^{2-p/q} \left( {1+\frac{g}{\alpha h}x_1^{g/h-1} } \right) } \right] . \end{aligned}$$

(4.27)

On the $x_{1} - x_{2}$ phase plane, we obtain the gradient equation of the state trajectory using Eq. (4.26) and Eq. (4.27)

$$\begin{aligned} \frac{{\text {d}}x_2 }{{\text {d}}x_1 }=\frac{\dot{x}_2 }{\dot{x}_1 }=\frac{-\frac{\beta q}{p}\left[ {\left( {\phi s+\gamma s^{m/n}} \right) +x_2^{2-p/q} \left( {1+\frac{g}{\alpha h}x_1^{g/h-1} } \right) } \right] }{x_2 }. \end{aligned}$$

(4.28)

Note that $p/q < 2$, and p, q, g, h, m, n are all odds. For $x_{1} > 0$ and $x_{2} = 0$, we have

$$\begin{aligned} \frac{{\text {d}}x_2 }{{\text {d}}x_1 }=-\infty , \quad \dot{x}_2 =-\frac{\beta q}{p}\left[ {\phi \left( {x_1 +\frac{1}{\alpha }x_1^{g/h} } \right) +\gamma \left( {x_1 +\frac{1}{\alpha }x_1^{g/h} } \right) ^{m/n}} \right] <0. \end{aligned}$$

(4.29)

It is observed from Eq. (4.29) that, on the $x_{1}$-positive-axis, the state trajectory is perpendicular to the $x_{1}$-axis and the state trajectory points to negative. Moreover, the velocity of the state x is not zero. Similarly, on the $x_{1}$-negative-axis, the state trajectory is perpendicular to the $x_{1}$-axis and the state trajectory points to positive. The velocity of the state x is not zero. Figure 4.2 is the illustration of the state trajectory in the reaching stage. The thick dashed line indicates the NFTF hyperplane, the thin dashed lines with arrows indicate the direction of state trajectory on $\bar{D}$, $x_{\text {init}}$ denotes the initial state, and the solid line denotes state trajectory starting from $x_{\text {init}}$.

It is observed from Fig. 4.2 that the state trajectory is symmetric for NFTSM control system. Without loss of generality, we only consider the situations when the initial state lies on the upper side of the sliding hyperplane. We discuss the different situations based on the location of the initial state:

• (1) Suppose $x_{\text {init}} \in \mathrm{IV}^{\mathrm{Top}}$. Since the state trajectory points to the negative direction on the $x_{1}$-positive-axis, the system state will not enter region I from $\mathrm{IV}^{\mathrm{Top}}$ by passing through the $x_{1}$-positive-axis. Thus, we have $x \in D$ and the sliding mode s asymptotically converges in the reaching stage;

• (2) Suppose $x_{\text {init}} \in \Pi ^{\mathrm{Top}} \cup \mathrm{I}$ and the state trajectory passes through the $x_{1}$-positive-axis. Since the state trajectory points to the negative direction on the $x_{1}$-positive-axis and the velocity is not zero, the state trajectory will not stay on the $x_{1}$-positive-axis and must enter region $\mathrm{IV}^{\mathrm{Top}}$ by passing through the axis. Thus, the sliding mode s converges to zero finally;

• (3) Suppose $x_{\text {init}} \in \Pi ^{\mathrm{Top}} \cup \mathrm{I}$ and the state trajectory does not pass through the $x_{1}$-positive-axis. Thus, we have $x \in D$ and the sliding mode s asymptotically converges in the reaching stage.

In summary, the state trajectory starting from arbitrary starting point either directly reaches the sliding hyperplane, or first passes through $\bar{D}$ and then reaches the sliding hyperplane. In both cases, the state trajectory does not stay in the region $\bar{D}$, and thus NFTF hyperplane globally exists. In conclusion, the system state at least asymptotically converges to the sliding hyperplane from arbitrary initial point. (End of Proof)

4.4.3 Effect of Stagnation

The nonnegative exponential efficient of state $x_{2}$ in the terminal attractor (4.13) is necessary to match the newly proposed NFTF for comprehensive performance enhancement. However, it also has a potential drawback if considering the whole closed-loop system, called “effect of stagnation. ” This is because state $x_{2}$ may approach zero before the sliding mode s converges to zero. In such cases, even though the state can still converge in finite time, yet its convergence speed could be very slow. The following phenomenon is observed when the effect of stagnation occurs: (4.1) state $x_{1}$ converges slowly, and $x_{2}$ is quite small compared to $x_{1}$; (4.2) state $x_{2}$ is close to a constant and its derivative is almost zero. In the following, we will analyze this effect and try to find corresponding solutions.

Fig. 4.2

State trajectory in reaching mode

When the effect of stagnation occurs, the derivative of $x_{2}$ is approximately equal to zero. Substituting $\dot{x}_{2} \thickapprox 0$ into Eq. (4.27), we have

$$\begin{aligned} \left( {\phi s+\gamma s^{m/n}} \right) +x_2^{2-p/q} \left( {1+\frac{g}{\alpha h}x_1^{g/h-1} } \right) \approx 0. \end{aligned}$$

(4.30)

We consider two situations here: One is for the situation when the system state is close to the equilibrium point, and the other is for the situation when the system state is far away from the equilibrium point. We obtain two approximations of Eq. (4.30):

• (1) When the system state is close to the equilibrium point, we have $x_{1},x_{2} \ll 1$. Then $(\phi s\,+\,\gamma s^{m/n}) \approx \gamma x_{1}^{m/n}$ and $1\,+\,\frac{g}{ah} x_{1}^{g/h-1} \approx 1$ . The Eq. (4.30) is reduced to

  $$\begin{aligned} \dot{x}_1 \approx -\gamma ^{\frac{q}{2q-p}}x_1 ^{\frac{qm}{\left( {2q-p} \right) n}}. \end{aligned}$$

  (4.31)

• (2) When the system state is far away from the equilibrium point, we have $x_{1}, x_{2} \gg 1$. Then, $(\phi s + \gamma s^{m/n}) \approx \phi x_{1}^{g/h}$ and $1 + \frac{g}{ah} x_{1}^{g/h-1} \approx \frac{g}{ah} x_{1}^{g/h-1}$. Eq. (4.30) is reduced to

  $$\begin{aligned} \dot{x}_1 \approx -\left( {\frac{\phi \alpha h}{g}} \right) ^{\frac{q}{2q-p}}x_1^{\frac{g}{g-h}\cdot \frac{q}{2q-p}}. \end{aligned}$$

  (4.32)

According to Eq. (4.31) and (4.32), even if the condition $q < p < 2q$ is satisfied, the term $2q - p$ may be still smaller than q for some choices of q and p. In such cases, if in addition $\gamma < 1$ and $\phi ah/g < 1$, then the coefficients on the right-hand side of Eqs. (4.31) and (4.32) will be very small. This will largely decrease the convergence speed of the state $x_{1}$, which is the major cause of the effect of stagnation. On the contrary, to avoid the effect of stagnation, we need to increase the coefficients on the right-hand side of Eq. (4.31) and Eq. (4.32). This means that we need to choose control parameters to satisfy one of the following conditions:

• (1) One can choose suitable $\phi$ and $\gamma$ to make $\gamma < 1$ and $\phi ah/g > 1$;

• (2) If the condition (4.1) is not satisfied, one can choose suitable p and q to make $q/(2q-p)$ very close to 1.

4.4.4 System Robustness

In practice, due to the modeling errors and external disturbances, the system convergence speed might be reduced [26–28]. In some cases, the system can even not converge to the equilibrium point, and the steady-state tracking trajectory can only reach a neighborhood region of the equilibrium point. Thus, the robustness of the control algorithm largely affects its effectiveness in practice. For control law (4.15), to analyze its robustness to model uncertainty and ability to external disturbance, we consider the following second-order nonlinear and uncertain SISO system:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 \\ \dot{x}_2 =f(x)+\Delta f(x)+u+d(t) \\ \end{array}} \right. , \end{aligned}$$

(4.33)

where $f({\varvec{x}})$ and $\Delta f ({\varvec{x}})$ are $C^{1}$ vector field, $f({\varvec{x}})$ and $d(t)$ are modeling error and external disturbance, satisfying $| \Delta f({\varvec{x}}) + d (t)| < L$.

Theorem 3:

For the uncertain system (4.33), if the control law is (4.15), then system state reaches the region $\Pi$ in a finite time and the convergence speed is not smaller than the dynamics defined by Eq. (4.34):

$$\begin{aligned} \dot{s}\cdot sgn(s)=-\varPsi x_2^{p/q-1} , \end{aligned}$$

(4.34)

where

$$\begin{aligned} \begin{array}{c} \varPsi = \phi \left| s \right| +\gamma \left| s \right| ^{m/n}-\frac{pL}{\beta q},\\ \Pi = \left\{ {x:\phi \left| s \right| +\gamma \left| s \right| ^{m/n}\le \frac{pL}{\beta q}} \right\} . \end{array} \end{aligned}$$

(4.35)

Proof:

Note that the system (4.33) contains the terms with uncertainty. We substitute the control law (4.15) into Eq. (4.33), yielding

$$\begin{aligned} \dot{x}_2 =&-\frac{\beta q}{p}\left[ {\left( {\phi s+\gamma s^{m/n}} \right) +x_2^{2-p/q} \left( {1+\frac{g}{\alpha h}x_1^{g/h-1} } \right) } \right] \nonumber \\&+\Delta f(x)+{\text {d}}(t). \end{aligned}$$

(4.36)

Differentiate Eq. (4.11) and arrange the results as

$$\begin{aligned} \dot{x}_2 =\frac{\beta q}{p}x_2^{1-p/q} \dot{s}-\frac{\beta q}{p}x_2^{2-p/q} \left( {1+\frac{g}{\alpha h}x_1^{g/h-1} } \right) \!. \end{aligned}$$

(4.37)

Combining Eq. (4.36) and Eq. (4.37), we obtain

$$\begin{aligned} \dot{s}=-\left( {\phi s+\gamma s^{m/n}-\frac{p}{\beta q}\left[ {\Delta f(x)+d(t)} \right] } \right) x_2^{p/q-1} . \end{aligned}$$

(4.38)

Since $| \Delta f({\varvec{x}}) + {\text {d}}(t)| < L$, we have

$$\begin{aligned} \dot{s}\cdot sgn(s)<-\left( {\phi \left| s \right| +\gamma \left| s \right| ^{m/n}-\frac{pL}{\beta q}} \right) x_2^{p/q-1} =-\varPsi x_2^{p/q-1} . \end{aligned}$$

(4.39)

If $\varPsi > 0$, using Theorem 2, we know that sliding mode s asymptotically converges and convergence speed is not smaller than the dynamics defined by Eq. (4.34). If $\varPsi \le 0$, sliding mode s might not continuously converge to equilibrium point, but at least reach the region confined by $\varPsi \le 0$, i.e., region $\Pi$ here. (End of Proof)

Generally, we can assume that both modeling errors and external disturbances are bounded. According to Theorem 3 and the fact that the factor $m/n > 1$ in the definition of $\Pi$, we know that the steady-state error of sliding mode s is less than the steady-state error of control system designed based on linear attractor. By choosing large enough $\phi ,\gamma$ and $n/m > 1$, we can make the convergence region of sliding mode small enough. Then, the control system has good robustness to the modeling errors and external disturbances.

4.5 Simulation Verification

Consider a nonlinear and uncertain SISO system

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 \\ \dot{x}_2 =2x_1^2 +x_2^2 +\Delta f(x)+u+{\text {d}}(t) \\ \end{array}} \right. , \end{aligned}$$

where $\Delta f ({\varvec{x}}) = 2 \cos (x_{1} + x_{2})$ and $d (t) = 2\sin (3t)$. We design the control law using the method described in this chapter. We choose the parameters for terminal sliding hyperplane as shown in Table 4.1. Other parameters are taken as $m = 1, n=3, \phi = 1.2$, and $\gamma = 1.2$. In the following, we will use simulation to demonstrate some critical properties of NFTSM, e.g., finite-time convergence, nonsingularity, non-chattering, effect of stagnation and closed-loop robustness. By tuning some control parameters, we choose the following settings of simulation conditions as shown in Table 4.2.

Table 4.2 Settings of simulation conditions

Fig. 4.3

State response in A and B

Fig. 4.4

State response in C and D

Fig. 4.5

Control input in C and D

Conditions A and B are used to demonstrate the finite-time convergence characteristics of the NFTSM control method and NTSM control method, respectively. The state response curves are shown in Fig. 4.3. The solid line is for simulation condition A and the dashed line is for simulation condition B. We observed from Fig. 4.3 that simulation condition A has faster convergence speed than B, which is because NFTSM has fast convergence characteristics. This implies that the NFTSM control method has better convergence performance than the NTSM method in a large region of state space.

Conditions C and D are used to demonstrate the nonsingularity and non-chattering characteristics of the NFTSM control method. The simulation results are shown in Figs. 4.4 and 4.5. Figure 4.4 shows the state response curves of the closed-loop system. The solid line is for the simulation condition C and the dashed line is for the simulation condition D. If there is no modeling error and no external disturbance, system state converges in finite time to the equilibrium point, as shown in solid lines. If modeling errors and external disturbances exist, the system convergence speed decreases but the system can still converge to a neighborhood region of the equilibrium point, as shown by dashed lines. The control inputs are shown in Fig. 4.4. We observe that the control inputs are both bounded and continuous in time around the equilibrium points, thus completely avoiding the singularity or chattering problems.

Conditions E and F are used to analyze how the selection of terminator parameters $\phi$ and $\gamma$ affect the effect of stagnation. The state response curves are shown in Fig. 4.6. The solid line is for the simulation condition E and the dashed line is for the simulation condition F. As shown by the dashed lines, if $\phi , \gamma < 1$, the state $x_{2}$ is much smaller than $x_{1}$ and $x_{2}$ is almost a constant. This causes the slow convergence of $x_{1}$ and the effect of stagnation occurs in the system. As shown by the solid lines, if $\phi , \gamma < 1$, the effect of stagnation disappears and the system state converges to the equilibrium point in finite time, which is consistent with the analysis results in Sect. 4.4.3.

Conditions G, H, and I are used to demonstrate the steady-state convergence characteristics of the NFTSM method. The simulation results are shown in Figs. 4.7, 4.8, and 4.9. Simulation conditions G, H, and I correspond to dot lines, dashed lines, and solid lines. According to Figs. 4.7 and 4.8, we find that the steady-state errors of state $x_{1}$ and $x_{2 }$ decrease as the parameter $\gamma$ increases. According to Fig. 4.9, the steady-state errors of the sliding mode s are less than 0.20, 0.053, and 0.018, respectively. Using Theorem 3, we can calculate the steady-state errors as 0.31, 0.064, and 0.021, which are quite close to the simulated error values. This implies that the estimation method presented in Theorem 3 works very well to estimate the steady-state errors of the closed-loop system.

Fig. 4.6

State response in E and F

Fig. 4.7

State $x_{1}$ response in G, H, and I

Fig. 4.8

State $x_{2}$ response in G, H, and I

Fig. 4.9

Sliding mode response in G, H, and I

Based on the above simulation results, we know that the NFTSM control proposed in this chapter has no singularity or chattering problems. By properly choosing parameters for the control system, we can guarantee the fast convergence of the closed-loop system, and provide good robustness to modeling errors and external disturbances.

4.6 Conclusions

To resolve the singularity and chattering problems associated with the existing TSM control method, this chapter proposed an NFTSM control method for the second-order nonlinear and uncertain system. The NFTSM control is nonsingular, time-continuous, and has faster convergence speed. The theoretical analysis and simulation experiments show that:

• (1) The proposed NFTF has finite-time convergence property, and has faster convergence speed than the NTF in the region far away from the equilibrium point. The terminal attractor with negative exponential coefficient guarantees the global existence of the sliding hyperplane, and enables the asymptotical convergence of system state to the sliding hyperplane from arbitrary starting point.

• (2) The designed NSTSM controller has no state negative exponents, thus completely eliminating the singularity phenomenon from the TSM control. Moreover, the NFTSM control is time continuous, thus eliminating the chattering phenomenon.

• (3) By properly choosing control parameters, the closed-loop system can avoid the effect of stagnation. If the modeling errors and external disturbances are bounded, then system state asymptotically converges to the neighborhood region of equilibrium point, still having good convergence speed and tracking performance.