Beam Width Performance of the Adaptive Beam Former Based on Pseudo-Interference Technique

Abstract

In this paper, we examine the beam width performance of the recently addressed robust Capon beam formers (RCB). This adaptive array employs the estimated steering vector, injected noise, and pseudo-interference to provide robustness against direction mismatch. With the generalized side lobe canceller (GSC) as the underlying structure, we first derive the effect of angular mismatch on the estimated interference correlation matrix. Then, a simple approximate expression is presented for output signal-to-interference-plus-noise-ratio (SINR) of this new beam former. Based on this expression, the angular beam width of this robust beam former is investigated. Simulation results verify the analytically predicted performance.

1 Introduction

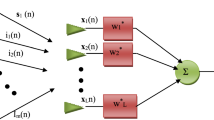
Adaptive beam former [1] is a widespread tool to suppress the interfering signals and steer the array to the direction of the desired signal. Consider a linear antenna array of N sensors with uniform half-wavelength spacing. The array steering vector a ($\theta$), where $\theta$ denotes the arrival angle, is a $N \times 1$ vector. Let $x(k)$ represent the received vector derived from this narrowband array, which is assumed to comprise a single desired signal and J interferers, expressed as follows:

$$ x(k) = s_{s} \left( k \right)a_{s} + \sum\limits_{j = 1}^{J} {s_{j} (k)} \pm a_{j} + n(k) $$

(85.1)

where $s_{s} \left( k \right)$ is the complex amplitude of the desired signal with power $\sigma_{s}^{2}$, $a_{s} = a\left( {\theta_{s} } \right)$ denotes the steering vector of the desired signal with arrival angle $\theta_{s} ,a_{j} \, = \,a\left( {\theta_{j} } \right)$ denotes the steering vector of the jth interferer with arrival angle $\theta_{j} , \, s_{j} \left( k \right)$ is the complex amplitude of the jth interfering signal with power $\sigma_{j2}$, $\sigma_{ 1 2} \geqq \sigma_{ 2 2} \geqq \cdots \geqq \sigma_{J 2}$, and $n(k)$ is the additive white noise with power σ ² _n .

The adaptive array uses a weight vector w for processing $x(k)$ to suppress the interferers and receive the desired signal. The array output y (k) is defined as

$$ y(k) = w^{H} x(k) $$

(85.2)

where the superscript $( \, \cdot \, )^{H}$ denotes the Hermit and transpose for a standard Capon beam former (SCB) [2], the weight vector w is chosen to minimize the output power with unit gain on the assumed steering vector a ₀, where a ₀ = a ($\theta$ ₀) with $\theta$ ₀ = 0o being the assumed arrived angle of the desired signal. This beam former is devised under the assumption that a ₀ is known.

But in practice, the exact $\theta$ ₀ is unavailable. Recently [3], considers steering vector estimation, interference null constraint, and power minimization techniques for designing diagonally loaded Capon beam former [4]. Since the equivalent interference-to-noise ratio (INR) in the adaptive processing can be improved, it provides more robust capabilities than the previous robust Capon beam former (RCB) [5]. The angular beam width of adaptive array is defined as the spatial interval over which the desired signal remains within a given value. In this paper, we examine the beam width of this beam former to predict the acceptable angular mismatch.

This paper is organized as follows. In Sect. 85.2, we review this pseudo-interference algorithm. In Sect. 85.3, we derive the output SINR of this beam former. The main-lobe width is also investigated. Simulation results are presented in Sect. 85.4 to validate the proposed approach. Section 85.5 concludes the entire paper.

2 Review of the Pseudo-Interference Techniques

In [3], the uncertainty constraint addressed in [5] is used to estimate the steering vector as. Let $R$ be the correlation matrix of the received vector $x(k)$, and λ _n and U _N , n = 1, 2…N, be the ordered eigenvalues and the corresponding eigenvectors of R, respectively. The estimated steering vector is given by

$$ \hat{a} = [I + \beta^{ - 1} R^{ - 1} ]^{ - 1} UU^{H} \;a_{0} $$

(85.3)

where $U = \left[ {u_{1} ,u_{2} \ldots u_{J + 1} } \right]$ is the signal-plus-interference subspace eigenvectors of R, and $\beta = 0.5\tau \lambda_{1}^{ - 1} + 0.5\,\hbox{min}$,$\left\{ {\tau \lambda_{{_{J + 1} }}^{{^{ - 1} }} ,\left[ {\sum\nolimits_{n = 1}^{J + 1} {|u_{n}^{H} UU^{H} a_{0} |^{2} \,(\varepsilon \lambda_{n}^{2} )^{ - 1} } } \right]^{0.5} } \right\}$, with $\tau = (1/\sqrt \varepsilon )(||UU^{H} a_{0} || - \sqrt \varepsilon )$, $||a_{0} - UU^{H} a_{0} ||^{2}$. To mitigate the effect of mismatch between us and $\hat{a}$, the diagonally loaded constraint $\hat{a}$ is added, where $\alpha$ a constant is. Moreover, the pseudo-interference algorithm also chooses $w$ to minimize the output interference power w ^H R _i w to achieve high interference suppression with $R_{i}$ being the interference correlation matrix. It can be expressed by the following optimization problem:

Min $w^{H} Rw$, subject to $w^{H} \hat{a} = 1$, $w^{H} w = \alpha$ and $w^{H} R_{i} w = 0$

The solution of (85.2) is

$$ w^{H} R_{i} w = 0 $$

(85.4)

where $\mu = 1/(\hat{a}^{H} Q^{ - 1} \hat{a})$, and $Q = R + \delta_{1} I + \delta_{2} R_{i}$ with δ ₁ and δ ₂ being Lagrange multipliers.

To improve the robustness, we would like to choose the Lagrange multipliers to maximize the output SINR. It is shown in [3] that the close-form solution is

$$ \delta_{1} = \hbox{max} \left\{ {0,2N\sigma_{s}^{2} - \sigma_{n}^{2} } \right\}\,{\text{and}}\,\delta_{2} = \delta_{1} /\sigma_{n}^{2} $$

(85.5)

The interference correlation matrix R _i in Q can be estimated from the following processes: First, divide the N-element array into two sub arrays. The desired signal in two sub arrays will be blocked by an (S−1)-order blocking matrix [6]. Each sub array consists of (N + J)/2 + S elements. Let T _k be the sample correlation matrix of the kth sub array, where k = 1, 2, and B be the (S−1)-order blocking matrix. Then, the signal-free correlation matrix corresponding to kth sub array can be expressed as BHTkB. Second, perform the subspace reconstruction procedure as discussed in [7]. Third, evaluate R _i from the eigenvectors of BHTkB.

3 Beam Width Properties

In the previous section, we have assumed that the interference correlation matrix is accurately estimated. When the direction mismatch θ _s−θ ₀ is large, the blocking matrix $B$ does not properly block out the desired signal and then the subspace reconstruction method cannot estimate R _i accurately. In this section, we will derive an analytic expression of the output SINR of this beam former. The angular beam width is then examined.

3.1 Output SINR When B Nulls Out A _s

We first consider the case that the direction mismatch is small. To obtain the output signal power P _s, interference-plus-noise power P _n, and corresponding SINR P _s/P _n, we decompose the weight vector w into two parts: a fixed weight vector $d = \hat{a}/N$ and an adaptive weight vector $- F(F^{H} QF)^{ - 1} F^{H} Q^{H} d$, where F is an $N \times (N - 1)$ matrix which satisfies $d^{H} F = 0$ and ${\text{rank}}(F)\, = \,N - 1$. With this GSC as the underlying structure, w can be represented as

$$ w = d - F(F^{H} QF)^{ - 1} F^{H} Q^{H} d $$

(85.6)

Using the matrix inversion lemma, $(F^{H} QF)^{ - 1}$ in $w$ can be represented as: $\left[ {(F^{H} F)^{ - 1} - \left( {1 + \zeta_{s} \gamma_{s} } \right)^{ - 1} Ma_{s} a_{s}^{H} M^{H} - \sum\nolimits_{j = 1}^{J} {\zeta_{j} } \left( {1 + \zeta_{j} \gamma_{j} } \right)^{ - 1} Ma_{j} a_{j}^{H} M^{H} } \right]$, $(F^{H} QF)^{ - 1} \approx \frac{1}{{\sigma_{e}^{2} }}$ where $\zeta_{s} = \sigma_{s}^{2} /\sigma_{e}^{2}$ denotes the equivalent signal-to-noise ratio (SNR) with $\sigma_{e}^{ 2} = \sigma_{n}^{ 2} + \delta_{ 1}$ being the equivalent noise power, $\zeta_{j} \, = \left( { 1+ \delta_{ 2} } \right)\sigma_{j}^{ 2} /\sigma_{e}^{ 2}$ denotes the equivalent jth INR, $\gamma_{s} , \, \gamma_{j} ,$ and M are defined as γ _s  = a ^H _s $F(F^{H} F)^{ - 1} F^{H}$as, $\gamma_{j} = a_{j}^{H} \;\;F(F^{H} F)^{ - 1} F^{H} \;\;a_{j} \; ,\;M = (F^{H} F)^{ - 1} F^{H}$, respectively, and we have neglected the cross-terms between a _s and a _j . Then, the output signal power, P _s = σ ² _s |w ^H a _s |², can be approximated by

$$ P_{\text{s}} = \sigma_{s}^{2} \left( {1 + \zeta_{s} \gamma_{s} } \right)^{ - 2} \left| {d^{H} a_{s} } \right|^{2} $$

(85.7)

Similarly, the output interference-plus-noise power, $P_{\text{n}} \, = \,\sigma_{n}^{ 2} \left| {\left| { \, w \, } \right|} \right|^{ 2} + j_{ 2} \left| { \, w^{H} a_{j} \, } \right|^{ 2}$, is given by

$$ P_{\text{n}} + \sigma_{n}^{ 2} \eta_{j} + \zeta_{j}^{2} \gamma_{j} )\left( {1 + \zeta_{j} \gamma_{j} } \right)^{ - 2} \left| {d^{H} a_{j} } \right|^{2} $$

(85.8)

where $\eta_{j} = \sigma_{j}^{2} /\sigma_{n}^{2}$ denotes the jth INR. Using (85.3) $\gamma_{j} \approx N$, and $\left| {d^{H} a_{j} } \right|^{2} \le 1$, the interference term in P _n can be neglected. We have

$$ P_{\text{n}} \; \approx \;\frac{{\sigma_{n}^{2} }}{N} $$

(85.9)

3.2 Output SINR When ${\user2{R}}_{i}$ Cannot Be Properly Estimated

In this case, the desired signal is wrongly considered as interference. After processing the interference subspace reconstruction procedure, the blocking matrix acts similarly as a high pass filter in the spatial domain. Let E $\in C^{N \times N}$ be the transform matrix corresponding to this filtering. Assume that the interferers are located at high pass region in the spatial domain, we have Ea _j  = a _j .

When $\theta_{\text{s}}$ and $\sigma_{\text{s}}^{ 2}$ are large, i.e $\sigma_{s}^{ 2} \left| {\left| {Ea_{s} } \right|} \right|^{ 2} /N > \sigma_{J}^{ 2}$, the estimated interference correlation matrix can be expressed as

$$ \hat{R}_{i} = \sum\limits_{j = 1}^{J - 1} {\sigma_{j}^{2} } /\sigma_{e}^{2} \gamma_{j} = a_{j}^{H} a_{j} $$

(85.10)

Then, the weight vector can be represented as

$$ \tilde{w} = d - F(F^{H} \tilde{Q}F)^{ - 1} F^{H} \tilde{Q}^{H} d $$

(85.11)

where $\tilde{Q} = Q - \delta_{2} \sigma_{J}^{2} a_{J} a_{J}^{H} \, + \,\delta_{2} \sigma_{s}^{2} Ea_{s} a_{s}^{H} E^{H}$ using the matrix inversion lemma, the output signal power, $\tilde{P}_{\text{s}} = \sigma_{s}^{2} \tilde{w}^{H} |a_{s} |^{2}$ can be approximated by

$$ \tilde{P}_{\text{s}} = \sigma_{s}^{2} |\left( {1 + \zeta_{s} \gamma_{s} } \right)^{ - 1} d^{H} a_{s} - \delta_{2} \zeta_{s} \gamma_{\text{es}} [\left( {1 + \zeta_{s} \gamma_{s} } \right)^{ - 1} - \delta_{2} \zeta_{s} \gamma_{e} \left( {1 + \delta_{2} \zeta_{s} \gamma_{e} } \right)^{ - 1} ]d^{H} Ea_{s} |^{2} $$

(85.12)

where $\gamma_{e} {\text{ and }}\gamma_{\text{se}}$ are defined as $\gamma_{e} = a_{s}^{H}$ E ^H $F(F^{H} F)^{ - 1} F^{H}$ Ea_s and $\gamma_{\text{es}} = a_{\text{s}}$ ^H E ^H $F(F^{H} F)^{ - 1} F^{H}$ as, respectively. In (85.6), we have used $\left( 1 \right. + \zeta_{s} \gamma_{s} ) \approx 1, \, \left| {\gamma_{\text{es}} } \right| < < 1,{\text{ and }}\zeta_{s} \left| {\gamma_{\text{es}} } \right| 2/\gamma_{e} \zeta_{s} \left| {\gamma_{\text{es}} } \right|\left| {\gamma_{\text{es}} } \right|/\left( { 2N} \right) \ll 1$. Similarly, the interference-plus-noise power $\tilde{P}_{\text{n}}$ can be approximated by

$$ P_{\text{n}} \approx \frac{{\sigma_{n}^{2} }}{N} \, + \,\sigma_{n}^{2} \gamma_{J} \sigma_{J}^{4} \sigma_{e}^{ - 4} \left( {1 + \sigma_{e}^{ - 2} \sigma_{J}^{2} \gamma_{J} } \right)^{ - 2} \,|d^{H} a_{J} |^{2} $$

(85.13)

3.3 Angular Beam Width

Based on the discussions in the above two subsection, we fist derive the overall output SINR. From (85.4) and (85.6), we can observe that $\gamma_{e} , \, \gamma_{es}$, and d ^H Ea _s are unwanted factors but appear in (85.6) due to as passing through the blocking matrix. When the direction mismatch is small, these factors are approximately equal to zero, and then (85.6) reduces to the same expression of (85.4). Therefore, the overall output signal power can be approximated by (85.6). Consider the case when $\sigma_{J}^{2} /\sigma_{e}^{2} > 1,{\text{ using }}\gamma_{J} \approx N {\text{and }}\left| {d^{H} a_{J} } \right|^{2} < < 1$, we have

$$ \frac{{\sigma_{n}^{2} }}{N} > > \, \Upsigma_{n}^{2} \gamma_{J} \sigma_{J}^{4} \sigma_{e}^{ - 4} \, \left( {1 + \sigma_{e}^{ - 2} \sigma_{J}^{2} \gamma_{J} } \right)^{ - 2} |d^{H} a_{J} |^{2} $$

(85.14)

Then, (85.7) can be approximated by $\tilde{P}_{\text{n}} \approx \sigma_{n}^{ 2} /N$ as in (85.5). Consequently the overall output SINR can be approximated by

$$ {\text{SINR}} \approx \;\;\frac{{N\tilde{P}_{\text{s}} }}{{\sigma_{n}^{2} }} $$

(85.15)

Using $\left( { 1+ \zeta_{s} \gamma_{s} } \right) \approx 1$, it can be verified that the dominant term in $\tilde{P}_{\text{s}} \,{\text{is}}\,\sigma_{s}^{2} |d^{H} a_{s} - \delta_{2} \zeta_{s} \gamma_{\text{es}} d^{H} Ea_{s} |^{2}$. For large value of $\eta_{s}$, where $\eta_{s} = \sigma_{n}^{ 2} /\sigma_{n}^{ 2}$ denotes input SNR, it can be shown that $\delta_{ 2} \zeta_{s} \approx \eta_{s}$ Since $\gamma_{\text{es}}$ and |d ^H Ea _s |² increase as direction mismatch increases, according to (85.6), (85.8) and $\delta_{ 2} \zeta_{s} \approx \eta_{s}$ the SINR and beam width decrease as input SNR increases. Since $B$ form a high pass filter in the spatial domain, a large value of S will provide a wider null in the direction $\theta_{0}$ [6]. Therefore, the beam width increases as S increases.

4 Simulation Results

The array in the simulations is composed of equispaced N = 32. The received data vector is as that of (85.1). Two interfering signals with $\left\{ {\theta_{ 1} ,\eta_{ 1} } \right\} = \{ 25^{\text{o}} , \, 10{\text{dB}}\}$ and $\left\{ {\theta_{ 2} ,\eta_{ 2} } \right\} = \{ 45^{\text{o}} , \, 20{\text{dB}}\}$ are impinging on the array.

Figure 85.1 shows the output SINR versus direction mismatch θ _s for a fixed $S = \, 3$. We can observe from this figure that the output SINR of the adaptive array decreases rapidly as θ _s increases for large SNR. By comparing the approximations of SINR computed from (85.8) with the simulation results, we see that the analytical results are close to the simulation results.

Fig. 85.1

Output SINR versus θs S = 3

Figure 85.2 shows the output SINR versus direction mismatch $\theta_{s}$ for a fixed $S = \, 5$. For comparison, the analytical results of output SINR using (85.8) are also plotted. Again, the analytical results are close to the simulation results. Comparing the results of Fig. 85.1 with the corresponding results shown in Fig. 85.2, we see that the beam width of these beam former increases as S increases.

Fig. 85.2

Output SINR versus θs. S = 5

5 Conclusion

We derive the effect of angular mismatch on the recently addressed (RCB). This beam former employs the derivative constraints to obtain the interference correlation matrix. Then, the pseudo-interference is injected into the RCB to provide robustness against direction mismatch. With the GSC as the underlying structure, the output SINR is investigated. It shows that the angular beam width increases as the order of the derivative constraints increases. Simulation results are furnished as well to justify this new approach.