Studying Two-Stage Vehicle Scheduling at Distribution Center Based on Cross-Docking Model

Abstract

The reasonable arrangement of the time of inbound trucks’ arrival at the distribute center was very important to ensure the smooth circulation of goods and cost reduction. The course of unloading and sorting were regarded as two stage flow shop in the Cross-docking (CD) environment including only one door and one conveyor, applying the Johnson algorithm to solve the problem of minimizing working hour of goods (work piece). Finally, according to a distribution center’ order data, the minimum time required for sorting all the batch of goods was calculated, and the optimum sequence of inbound trucks was obtained, which can provide guidance for CD practice.

Introduction

Putting effective control on information and physical flow on the supply chain has been two key tasks of supply chain management (Wen Shi and Xue Ding 2009). In many areas, Cross-docking model has gained successful applying, such as JIT manufacturing industry (McEvoy 1997), EDI (Ross 1997), mail system (Forger 1995; Yonghui et al. 2006). Retailing industry realizes the goals of improving the efficiency of two flows’ management, reducing related costs and enhancing the customers’ satisfaction level successfully by means of Cross-docking model. Wal-Mart is a typical case (Stalk et al. 1992). It requires a synchronization and coordination of inbound and outbound trucks to make sure that transport time and temporary inventory at the distribution center (DC) are kept as low as possible.

With successful application of Cross-docking model in management practice, many scholars have spent much time in studying Cross-docking vehicle scheduling problem (Nils Boysen 2010; Wooyeon Yu and Egbelu 2008). Among them, someone regarded it as a two-stage problem to analysis. For example, Dong-yan MA and Feng CHEN abstracted the inbound/outbound trucks and goods needed to sort as two machines and work pieces respectively, established constrains on “work pieces” according to orders, and then solved this scheduling problem with Dynamic Programming Method (Dong-yan Ma and Feng Chen 2007). Dong-yan MA calculated it further with simulated annealing algorithm afterwards (Dong-yan Ma 2008). Jie CHEN and Feng CHEN discussed a kind of two-stage problem in the case of uncertain processing time (Jie Chen and Feng Chen 2010).

Kai-lei SONG has raised two-stage Cross-docking trucks scheduling problem based on direct transport and milk project in condition of different supplier/customer’s goods supply/demand (Kai-lei 2008). By testing with numerical example and practical proof, two-stage research method is a good method for solving Cross-docking scheduling problem. The papers using Johnson algorithm to solve this kind of problem are less at present. Gang WANG made a tentative research in his M.A. theses, putting forward the idea of utilizing the improved Johnson algorithm to Two-Stage Flexible Flow Shop Scheduling Problem in order to optimize arrangement of tasks in distribution center (Gang Wang 2008).

This paper’s research springboard is to see this problem as a Two-Stage Flow Shop Problem, which is solved by Modulo-Matrix multiplications based on Johnson algorithm (Yu-ai Qin 2009). On the basis of constructing Cross-docking implementing basic environment, making Cross-docking vehicle scheduling analysis factor-products relevant to elements of Johnson algorithm-work pieces, setting up the objective function of minimizing trucks’ staying time in DC is to get the optimal arrival consequence of inbound trucks and offer a proposal in Cross-docking practice.

Problem Descriptions

DC Layout

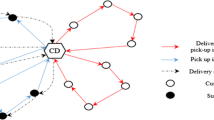
Cross-docking environment described in detail is shown in Fig. 30.1:

Fig. 30.1

Distribution center layout diagram

Only one unloading location, the inbound truck must wait until the former unloads all of goods;

Just one convey belt, whose rate is known and fixed;

Platforms on both sides of convey belt; when all of goods on one platform according to order is collected, the relevant outbound truck will load the goods and leave;

No temporary storage area, all of goods can be distributed to platforms.

Basic Ideas

In this paper, the course of goods going through the DC is regarded as a kind of flow shop problem concerning manufacturing “work pieces” on order on two machines. The object is to minimize the total time spent on the two machines by all the work pieces, obtain the best sequence of inbound trucks accordingly.

Set two machines M₁ and M₂: M₁ expresses the course of unloading goods on the convey belt from inbound truck; M₂ expresses the process between falling on the convey belt and arriving at each platform;

There is a one-to-one correspondence between every inbound truck and one supplier;

Only one kind and different goods is loaded on a truck, unloaded at once, being counted as a “work piece” of J₁, J₂… J_n;

Each work piece passes the machine M₁ and M₂ in order; the length of stay on them is marked as T_1,1, T_1,2,… T_1,i,…T_1,n and T_2,1,T_2,2,…T_2,i,…T_2,n separately and is known.

Two-Machine Flow Shop

Work Schedule

Table 30.1 is a two-machine work schedule, T_1,i and T_2,i means respectively the time of “work piece i” staying on machine M₁ and M₂ (i = 1,…,n). The assumptions are as follows: for each time point, one machine can only process a work piece uninterruptedly; after processed on machine M₁, the work piece can enter the machine M₂ if M₂ is available; work pieces are processed one by one with no stop between them.

Table 30.1 Two machines work schedule

Time Data’s Implication and Abstracting

In cross-docking scheduling management practice, the time in the work schedule is given a specific meaning.

• T_1,1 T_1,2 T_1,3 … T_1,i … T_1,n

T_1,i: time of unloading all goods from one inbound truck to convey belt.

• T_2,1 T_2,2 T_2,3 … T_2,i … T_2,n

This paper supposes that each platform corresponds to one delivery route carried out by one outbound truck. Unless there is a large fluctuation in the number of orders (including store and goods), DC will fix every delivery route, assigning fixed driver to finish the task by experience. When stores distributed to each platform is determined, all the goods information of each platform can be obtained according to customer order information table (Table 30.2). Then if the location of each platform and the running speed of convey belt are known, the time T_2,i spent on the convey belt is known accordingly.

Table 30.2 Customer order information table

Johnson Algorithm for Optimal Solution

• 1. Formulation describing: Work piece set G₁ = {J₁,J₂,… J_n} performs flow shop on two machines, supposing G₁ has a feasible solution ω₁. T_1,i and T_2,i are processing time of J_i on machine M₁ and M₂. The work piece J_j is behind J_i. when the sequence of work pieces in front of J_i is denoted as S, and the one behind J_i is denoted as S^′, so: ω₁ = SJ_iJ_j S^′.

  • A(S): the Modulo-Matrix’ multiplication formula of S;

  • A(S^′): the Modulo-Matrix’ multiplication formula of S^′;

  So, the time span of ω₁:

  A(ω₁) = A(S) $\otimes$ A(J_i) $\otimes$ A(J_j) $\otimes$ A(S^′);

  Exchange the position of J_i and J_j, the new feasible solution ω₂ and its time span:

  A(ω₂) = A(S) $\otimes$ A(J_j) $\otimes$ A(J_i) $\otimes$ A(S^′).

  Where: A (J_i) $\otimes$ A(J_j) = $\left[ {\begin{array} {llllllllllll}{\mathrm{ T}\text{1,}\mathrm{ i}\otimes \mathrm{ T}\text{1,}\mathrm{ j}} & {\mathrm{ H}(\mathrm{ i}\text{,}\mathrm{ j})} \\{} & {\mathrm{ T}\text{2,}\mathrm{ i}\otimes \mathrm{ T}\text{2,}\mathrm{ j}} \\ \end{array}} \right]$;

  A(J_j) $\otimes$ A(J_i) = $\left[ {\begin{array}{lllllllllll} {\mathrm{ T}\text{1,}\mathrm{ j}\otimes \mathrm{ T}\text{1,}\mathrm{ i}} & {\mathrm{ H}(\mathrm{ j}\text{,}\mathrm{ i})} \\{} & {\mathrm{ T}\text{2,}\mathrm{ j}\otimes \mathrm{ T}\text{2,}\mathrm{ i}} \\ \end{array}} \right]$;

  H(i,j) = T_1,i $\otimes$ T_1,j $\otimes$ T_2,j $\oplus$ T_1,i $\otimes$ T_2,i $\otimes$ T_2,j

  H(j,i) = T_1,j $\otimes$ T_1,i $\otimes$ T_2,i $\oplus$ T_1,j $\otimes$ T_2,j $\otimes$ T_2,i

  Suppose real number H(i,j) $\leq$ H(j,i);

  So, T_1,i $\otimes$ T_1,j $\otimes$ T_2,j $\oplus$ T_1,i $\otimes$ T_2,i $\otimes$ T_2,j $\leq$

  $$ {{\mathrm{ T}}_{{1,\mathrm{ j}}}} \otimes {{\mathrm{ T}}_{{1,\mathrm{ i}}}} \otimes {{\mathrm{ T}}_{{2,\mathrm{ i}}}} \otimes {{\mathrm{ T}}_{{1,\mathrm{ j}}}} \otimes {{\mathrm{ T}}_{{2,\mathrm{ j}}}} \otimes {{\mathrm{ T}}_{{2,\mathrm{ i}}}} $$

  (30.1)

  Change (30.1) into inequality:

  max{T_1,i + T_1,j + T_2,j,T_1,i + T_2,i + T_2,j}

  $\quad\quad\quad\quad\quad\quad\leq$ max{T_1,j + T_1,i + T_2,i,T_1,j + T_2,j + T_2,i}

  $$ \min \left\{ {{{\mathrm{ T}}_{{1,\mathrm{ i}}}},{{\mathrm{ T}}_{{2,\mathrm{ j}}}}} \right\}\leq\ \min \left\{ {{{\mathrm{ T}}_{{1,\mathrm{ j}}}},{{\mathrm{ T}}_{{2,\mathrm{ i}}}}} \right\} $$

  (30.2)

  When inequality (30.2) holds, A(ω₁) $\leq$ A(ω₂)

  Inequality (30.2) is Johnson formula.

• 2. Algorithm application: For work scheduling T, Johnson algorithm coming from Johnson formula can get optimal solution (Liu-tao Yang 2010); the specific methods are as follows:

  Step1: take minimum value in T, then if it is at the first row, put the related “work piece” in the first place, otherwise if it is at the second row, put the related “work piece” in the last place;

  Step2: eliminate this “work piece” stated in Step1, go back to Step1 until all piece work are sorted.

Case Analysis

A third party logistics company adopts cross-docking management model to provide distribution service for community supermarkets. There are seven suppliers, supplying 15 stores with 7 different goods such as rolls and steamed bread and so on (Table 30.3). The object is making trucks scheduling plan to minimum the time span of all goods going through unloading and sorting course.

Table 30.3 Customer order information table

According experience, four routine lines corresponding to four platforms are utilized. The stores concluded on each line are as follows: L₁:1-5-7-9; L₂:2-3-4-13; L₃: 6-8-10-15; L₄: 11-12-14. By means of calculation, all goods concluded on one line can be loaded on to an outbound truck. After fixing the platform location, the time of seven kinds of goods staying on the convey belt can be known. Every good is regarded as a work piece, and the course of unloading and transmitting to appointed platform is regarded as two stages according to the thought of two-stage flow shop. Considering the unloading time next, two machines work schedule of this case is obtained (Table 30.4).

Table 30.4 Two machines work schedule (unit: minutes)

Two-machine flow shop’s “mifang diagram” (Fig. 30.2):

Fig. 30.2

Two machines flow shop “mifang” diagram

Change into Modulo-Matrix form:

$$ \begin{array}{lllllll} & A(0)=\left[ {\begin{array}{lllllll} 0 & 0 \\ \end{array}} \right];\quad\;\;\;A(1)=\left[ \begin{array}{lllllll} \begin{array}{llllll} 3 & 8 \\ \end{array} \hfill \\ \begin{array}{lllll} z & 5 \\ \end{array} \hfill \\ \end{array}\right];\quad\;\;\;A(2)=\left[ \begin{array}{lllll} \begin{array}{llll} 6 & {14} \\ \end{array} \hfill \\ \begin{array}{llll} z & 8 \\ \end{array} \hfill \\ \end{array} \right] \\& A(3)=\left[ \begin{array}{llll} \begin{array}{lllll} 9 & {16} \\ \end{array} \hfill \\ \begin{array}{lllll} z & 7 \\ \end{array} \hfill \\ \end{array} \right];\quad A(4)=\left[ \begin{array}{llll} \begin{array}{llllll} 4 & {11} \end{array} \hfill \\ \begin{array}{lllll} z & 7 \\ \end{array} \hfill \\ \end{array} \right];\quad\;\;A(5)=\left[ \begin{array}{lll} \hfill \begin{array}{llllll} {12} & {30} \\ \end{array} \\ \hfill \begin{array}{lll}z & {18} \\ \end{array} \\ \end{array} \right] \\& A(6)=\left[ \begin{array}{llllll} \hfill \begin{array}{llll} {15} & {35} \\ \end{array} \\ \hfill \begin{array}{lll} z & {20} \\ \end{array} \\ \end{array} \right];\quad A(7)=\left[ \begin{array}{lll} \begin{array}{lll} {10} & {17} \\ \end{array} \\ \begin{array} {lllll}z & 7 \\ \end{array} \\ \end{array} \right];\quad A(8)=\left[ {\begin{array}{lllll} 0 \\0 \\ \end{array}} \right]\end{array} $$

According to Johnson algorithm, optimal schedule has two results as follows:

• 1. J₁-J₄-J₂-J₅-J₆-J₃-J₇

• 2. J₁-J₄-J₂-J₅-J₆-J₇-J₃

By calculating the Modulo-Matrix’ multiplication formula On the basis of maximal Quasi-Fields (R, max, +) combining with the two schedule results, time span T is as follow:

• T = A(0) $\otimes$ A(1) $\otimes$ A(2) $\otimes$ A(3) $\otimes$ A(4) $\otimes$ A(5) $\otimes$ A(6) $\otimes$ A(7) $\otimes$ A(8)

The minimal time span is 77 min. That means the minimal time of all goods spent on the two courses is 77 min, and the best sequence of inbound truck arriving at DC is known too.

Conclusion

This paper analyses the whole course from unloading to sorting in DC. Regarding goods in each inbound truck as a “work piece”, the minimal time span, as a index of calculating the total time spent in above process, can be known by means of two-stage flow shop theory. That means the inbound trucks’ arriving sequence can be determined in meeting the minimal time span. This study belongs to a part of vehicle scheduling. Abstracting useful information by excel is highly workable policy, and the Johnson algorithm can solve this kind of problem easily and effectively. This paper’s disadvantages are: first, lack of vehicle scheduling programming for outbound trucks; second, the data of stores included in each route line and the platforms’ exact location has effect on the final result. In theory, for above two elements changing, all the possible situations need to be calculated and compared to obtain the best result.

This case study shows calculating the optimal result by hand applies only to small-scale problem. For large-scale problem, creating new program is an effective method to extend the application scope of Johnson algorithm theory in cross-docking. As a starting point combining the study of cross-docking vehicle scheduling and practice, searching the new algorithm, the improvement of Johnson algorithm, and the breaking point of this area will be focus in future research.