Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Nomenclature

\(a,\bar{a}, \bar{a}_{0}, a_{\max},\bar{a}_{\max}\): Contact radius, mean contact radius, macroscale value of mean contact radius, maximum contact radius, mean value of maximum contact radius

A a, A r, A ra, A re, A re0, A rp, A rp0, A ds, A dp: Apparent area of contact, real area of contact, real area of contact during adhesion, real area of elastic contact, macroscale value of real area of elastic contact, real area of plastic contact, macroscale value of real area of plastic contact, real area of contact during asperity summit deformation, area of contact with particles

b: Burgers vector

c: Constant, specified by crystal structure

C 0: Constant required for normalization of p(d)

\(d,d_{\rm e}, d_{\rm n}, d_{\ln}, \bar{d}, d_{0}\): Particle diameter, minimum for exponential distribution, mean for normal distribution, exponential of mean of ln (d) for log-normal distribution, mean trapped particles diameter, macroscale value of mean trapped particles diameter

D: Interface zone thickness

E 1, E 2, E *: Elastic moduli of contacting bodies, effective elastic modulus

F, F a, F d, F ae, F ap, F a, F ds, F dp, F m, F m0: Friction force, friction force due to adhesion, friction force due to deformation, friction force during elastic adhesional contact, plastic adhesional contact, summit deformation, particles deformation respectively, meniscus force for wet contact, macroscale value of meniscus force

G: Elastic shear modulus

h: Indentation depth

h f: Liquid film thickness

H, H 0: Hardness, hardness in absence of strain gradient

k, k 0: Wear coefficient, macroscale value of wear coefficient

l s, l d: Material-specific characteristic length parameters

L, L lwl, L lc, L s, L d: Length of the nominal contact zone, long wavelength limit for roughness parameters, long wavelength limit for contact parameters, length parameters related to l s and l d

L p: Peclet number

m, n: Indices of exponents for scale-dependence of σ and β *

n tr: Number of trapped particles divided by the total number of particles

p a, p ac: Apparent pressure, critical apparent pressure

p(d), p tr(d): Probability density function for particle size distribution, probability density function for trapped particle size distribution

P(d): Cumulative probability distribution for particle size

\(R,\ R_{\rm p}, \overline{R}_{\rm p}, \overline{R}_{\rm p0}\): Effective radius of summit tips, radius of summit tip, mean radius of summit tips, macroscale value of the mean radius of summit tips

R(τ): Autocorrelation function

s: Spacing between slip steps on the indentation surface

s d: Separation distance between reference planes of two surfaces in contact

N, N 0: Total number of contacts, macroscale value of total number of contacts

T, T 0: Maximum flash temperature rise, macroscale value of temperature rise

x: Sliding distance

v: Volume of worn material

V: Sliding velocity

W: Normal load

z, z min, z max: Random variable, minimum and maximum value of z

α: Probability for a particle in the border zone to leave the contact region

β *, β * 0: Correlation length, macroscale value of correlation length

γ: Surface tension

Γ: Gamma function

ε: Strain

η: Density of particles per apparent area of contact

η int, η cr: Density of dislocation lines per interface area, critical density of dislocation lines per interface area

κ: Curvature

κ t: Thermal diffusivity

θ: Contact angle between the liquid and surface

θ i: Indentation angle

θ r: Roughness angle

μ, μ a, μ ae, μ ae0, μ ap, μ ap0, μ d, μ ds, μ ds0, μ dp, μ dp0, μ r, μ r0, μ re, μ re0, μ rp, μ rp0, μ wet: Coefficient of friction, coefficient of adhesional friction, coefficient of adhesional elastic friction, macroscale value of coefficient of adhesional elastic friction, coefficient of adhesional plastic friction, macroscale value of coefficient of adhesional plastic friction, coefficient of deformation friction, coefficient of summits deformation friction, macroscale value of coefficient of summits deformation friction, coefficient of particles deformation friction, macroscale value of coefficient of particles deformation friction, ratchet component of the coefficient of friction, macroscale value of ratchet component of the coefficient of friction, ratchet component of the coefficient of elastic friction, macroscale value of ratchet component of the coefficient of elastic friction, ratchet component of the coefficient of plastic friction, macroscale value of ratchet component of the coefficient of plastic friction, and coefficient of wet friction

ν 1, ν 2: Poisson’s ratios of contacting bodies

ρc p : Volumetric specific heat

σ, σ 0, σ e, σ n, σ ln: Standard deviation of rough surface profile height, macroscale value of standard deviation of rough surface profile height, standard deviation for the exponential distribution, standard deviation for the normal distributions, standard deviation for ln (d) of the log normal distribution

ρ, ρ G, ρ S: Total density of dislocation lines per volume, density of GND per volume, density of SSD per volume

φ, φ 0: Transition index, macroscale value of transition index

τ, τ 0: Spatial parameter, value at which the autocorrelation function decays

τ a, τ a0, τ Y, τ Y0, τ ds, τ ds0, τ dp, τ dp0, τ p: Adhesional shear strength during sliding, macroscale value of adhesional shear strength, shear yield strength, shear yield strength in absence of strain gradient, shear strength during summits deformation, macroscale value of shear strength during summits deformation, shear strength during particles deformation, macroscale value of shear strength during particles deformation, Peierls stress.

2 Introduction

Microscale and nanoscale measurements of tribological properties, which became possible due to the development of the surface force apparatus (SFA), atomic force microscope (AFM), and friction force microscope (FFM) demonstrate scale dependence of adhesion, friction, and wear as well as mechanical properties including hardness [1–4]. Advances of micro-/nanoelectromechanical systems (MEMS/NEMS) technology in the past decade make understanding of scale effects in adhesion, friction, and wear especially important, since surface to volume ratio grows with miniaturization and surface phenomena dominate. Dimensions of MEMS/NEMS devices range from ≈1 mm to few nm.

Experimental studies of scale dependence of tribological phenomena have been conducted recently. AFM experiments provide data on nanoscale [5, 6, 7, 8, 9, 10] whereas microtriboapparatus [11, 12] and SFA [13] provide data on microscale. Experimental data indicate that wear mechanisms and wear rates are different at macro- and micro-/nanoscales [14, 15]. During sliding, the effect of operating conditions such as load and velocity on friction and wear are frequently manifestations of the effect of temperature rise on the variable under study. The overall interface temperature rise is a cumulative result of numerous flash temperature rises at individual asperity contacts. The temperature rise at each contact is expected to be scale dependent, since it depends on contact size, which is scale dependent.

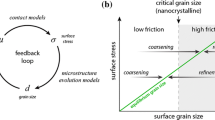
Friction is a complex phenomenon, which involves asperity interactions involving adhesion and deformation (plowing) (Fig. 16.1). Adhesion and plastic deformation imply energy dissipation, which is responsible for friction. A contact between two bodies takes place on high asperities, and the real area of contact (A r) is a small fraction of the apparent area of contact [16]. During contact of two asperities, a lateral force may be required for asperities of a given slope to climb against each other. This mechanism is known as ratchet mechanism, and it also contributes to the friction. Wear and contaminant particles present at the interface, referred as the third body, also contribute to friction (Fig. 16.2a). In addition, during contact, even at low humidity, a meniscus is formed. Generally, any liquid that wets or has a small contact angle on surfaces will condense from vapor into cracks and pores on surfaces as bulk liquid and in the form of annular-shaped capillary condensate in the contact zone. Figure 16.2b shows a random rough surface in contact with a smooth surface with a continuous liquid film on the smooth surface. The presence of the liquid film of the condensate or preexisting film of the liquid can significantly increase the adhesion between the solid bodies [16]. The effect of meniscus is scale-dependent.

Fig. 16.1
figure 1

(a) A block diagram showing friction mechanisms and generation and propagation of dislocations during sliding, (b) a block diagram of rough contact models

Full size image
Fig. 16.2
figure 2

Schematics of (a) two-bodies and three-bodies during dry contact of rough surfaces, (b) formation of menisci during wet contact

Full size image

A quantitative theory of scale effects in friction should consider scale effect on physical properties relevant to these contributions. However, conventional theories of contact and friction lack characteristic length parameters, which would be responsible for scale effects. The linear elasticity and conventional plasticity theories are scale-invariant and do not include any material length scales. A strain gradient plasticity theory has been developed, for microscale deformations, by Fleck et al. [17], Nix and Gao [18] and Hutchinson [19]. Their theory predicts a dependence of mechanical properties on the strain gradient, which is scale dependent: the smaller is the size of the deformed region, the greater is the gradient of plastic strain, and, the greater is the yield strength and hardness.

A comprehensive model of scale effect in friction including adhesion, two- and three-body deformations and the ratchet mechanism, has recently been proposed by Bhushan and Nosonovsky [20, 21, 22] and Nosonovsky and Bhushan [23]. The model for adhesional friction during single and multiple asperity contact was developed by Bhushan and Nosonovsky [20] and is based on the strain gradient plasticity and dislocation assisted sliding (gliding dislocations at the interface or microslip). The model for the two-body and three-body deformation was proposed by Bhushan and Nosonovsky [21] and for the ratchet mechanism by Nosonovsky and Bhushan [23]. The model has been extended for wet contacts, wear and interface temperature by Bhushan and Nosonovsky [22]. The detailed model is presented in this chapter.

The chapter is organized as follows. In the next section of this chapter, the scale effect in mechanical properties is considered, including yield strength and hardness based on the strain gradient plasticity and shear strength at the interface based on the dislocation assisted sliding (microslip). In the fourth section, scale effect in surface roughness and contact parameters is considered, including the real area of contact, number of contacts, and mean size of contact. Load dependence of contact parameters is also studied in this section. In the fifth section, scale effect in friction is considered, including adhesion, two- and three-body deformation, ratchet mechanism, meniscus analysis, total value of the coefficient of friction and comparison with the experimental data. In the sixth and seventh sections, scale effects in wear and interface temperature are analyzed, respectively.

3 Scale Effect in Mechanical Properties

In this section, scale dependence of hardness and shear strength at the interface is considered. A strain gradient plasticity theory has been developed, for microscale deformations, by Fleck et al. [17], Nix and Gao [18], Hutchinson [19], and others, which is based on statistically stored and geometrically necessary dislocations (to be described later). Their theory predicts a dependence of mechanical properties on the strain gradient, which is scale dependent: the smaller is the size of the deformed region, the greater is the gradient of plastic strain, and, the greater is the yield strength and hardness. Gao et al. [24] and Huang et al. [25] proposed a mechanism-based strain gradient (MSG) plasticity theory, which is based on a multiscale framework, linking the microscale (10–100 nm) notion of statistically stored and geometrically necessary dislocations to the mesoscale (1–10 μm) notion of plastic strain and strain gradient. Bazant [26] analyzed scale effect based on the MSG plasticity theory in the limit of small scale, and found that corresponding nominal stresses in geometrically similar structures of different sizes depend on the size according to a power exponent law.

It was recently suggested also, that relative motion of two contacting bodies during sliding takes place due to dislocation-assisted sliding (microslip), which results in scale-dependent shear strength at the interface [20]. Scale effects in mechanical properties (yield strength, hardness, and shear strength at the interface) based on the strain gradient plasticity and dislocation-assisted sliding models are considered in this section.

3.1 Yield Strength and Hardness

Plastic deformation occurs during asperity contacts because a small real area of contact results in high contact stresses, which are often beyond the limits of the elasticity. As stated earlier, during loading, generation and propagation of dislocations is responsible for plastic deformation. Because dislocation motion is irreversible, plastic deformation provides a mechanism for energy dissipation during friction. The strain gradient plasticity theories [17, 18, 19] consider two types of dislocations: randomly created statistically stored dislocations (SSD) and geometrically necessary dislocations (GND). The GND are required for strain compatibility reasons. Randomly created SSD during shear and GND during bending are presented in Fig. 16.3a. The density of the GND (total length of dislocation lines per volume) during bending is proportional to the curvature κ and to the strain gradient

$$\rho_{\rm G} = \frac{\kappa}{b} = \frac{1}{b}\frac{\partial{\varepsilon}}{\partial{z}}\propto\nabla{\varepsilon},$$
(16.1)

where ε is strain, b is the Burgers vector, and ∇ε is the strain gradient.

Fig. 16.3
figure 3

(a) Illustration of statistically stored dislocations during shear and geometrically necessary dislocations during bending, (b) geometrically necessary dislocations during indentation

Full size image

The GND during indentation (Fig. 16.3b) are located in a certain sub-surface volume. The large strain gradients in small indentations require GND to account for the large slope at the indented surface. SSD, not shown here, also would be created and would contribute to deformation resistance, and are function of strain rather than strain gradient. According to Nix and Gao [18], we assume that indentation is accommodated by circular loops of GND with Burgers vector normal to the plane of the surface. If we think of the individual dislocation loops being spaced equally along the surface of the indentation, then the surface slope

$$ \tan\theta_{\rm i} = \frac{h}{a} = \frac{b}{s}, $$
(16.2)

where θ i is the angle between the surface of the conical indenter and the plane of the surface, a is the contact radius, h is the indentation depth, b is the Burgers vector, and s is the spacing between individual slip steps on the indentation surface (Fig. 16.3b). They reported that for geometrical (strain compatibility) considerations, the density of the GND is

$$ \rho_{\rm G} = \frac{3}{2\mathit{bh}}\tan^{2}\theta_{\rm i} = \frac{3}{2b}\left(\frac{\tan\theta_{\rm i}}{a}\right) = \frac{3}{2b}\nabla{\varepsilon}. $$
(16.3)

Thus ρ G is proportional to strain gradient (scale dependent) whereas the density of SSD, ρ S is dependent upon the average strain in the indentation, which is related to the slope of the indenter (tan θ i). Based on experimental observations, ρ S is approximately proportional to strain [17].

According to the Taylor model of plasticity [30], dislocations are emitted from Frank–Read sources. Due to interaction with each other, the dislocations may become stuck in what is called the Taylor network, but when externally applied stress reaches the order of Peierls stress for the dislocations, they start to move and the plastic yield is initiated. The magnitude of the Peierls stress τ p is proportional to the dislocation’s Burgers vector b divided by a distance between dislocation lines s [27, 28]

$$\tau_{\rm p} = \mathit{Gb}/(2\pi s),$$
(16.4)

where G is the elastic shear modulus. An approximate relation of the shear yield strength τ Y to the dislocations density at a moment when yield is initiated is given by [27]

$$\tau_{\rm Y0} = \mathit{cGb}/s = \mathit{cGb}\sqrt{\rho},$$
(16.5)

where c is a constant on the order of unity, specified by the crystal structure and ρ is the total length of dislocation lines per volume, which is a complicated function of strain ε and strain gradient (∇ɛ)

$$\rho = \rho_{\rm S}(\varepsilon)+\rho_{\rm G}(\nabla{\varepsilon}).$$
(16.6)

The shear yield strength τ Y can be written now as a function of SSD and GND densities [30]

$$\tau_{\rm Y} = \mathit{cGb}\sqrt{\rho_{\rm S}+\rho_{\rm G}} = \tau_{\rm Y0}\sqrt{1+(\rho_{\rm G}/\rho_{\rm S}}),$$
(16.7)

where

$$\tau_{\rm Y0} = \mathit{cGb}\sqrt{\rho_{\rm S}}$$
(16.8)

is the shear yield strength value in the limit of small ρ G/ρ S ratio (large scale) that would arise from the SSD, in the absence of GND. Note that the ratio of the two densities is defined by the problem geometry and is scale dependent. Based on the relationships for ρ G (16.3) and ρ S, the ratio ρ G/ρ S is inversely proportional to a and (16.7) reduces to

$$\tau_{\rm Y} = \tau_{\rm Y0}\sqrt{1+(l_{\rm d}/a)},$$
(16.9)

where l d is a plastic deformation length that characterizes depth dependence on shear yield strength. According to Hutchinson [19], this length is physically related to an average distance a dislocation travels, which was experimentally determined to be between 0.2 and 5 μm for copper and nickel. Note that l d is a function of the material and the asperity geometry and is dependent on SSD.

Using von Mises yield criterion, hardness \(H = 3\sqrt{3}\tau_{\rm Y}\). From (16.9) the hardness is also scale-dependent [18]

$$H = H_{0}\sqrt{1+(l_{\rm d}/a)},$$
(16.10)

where H 0 is hardness in absence of strain gradient. Equation (16.9) provides dependence of the resistance force to deformation upon the scale in a general case of plastic deformation [20].

Scale dependence of yield strength and hardness has been well established experimentally. Bhushan and Koinkar [29] and Bhushan et al. [30] measured hardness of single-crystal silicon(100) up to a peak load of 500 μN. Kulkarni and Bhushan [31] measured hardness of single crystal aluminum(100) up to 2000 μN and Nix and Gao [18] presented data for single crystal copper; using a three-sided pyramidal (Berkovich) diamond tip. The hardness on nanoscale is found to be higher than on microscale (Fig. 16.4). Similar results have been reported in other tests, including indentation tests for other materials [32, 33, 34], torsion and tension experiments on copper wires [17, 19], and bending experiments on silicon and silica beams [35].

Fig. 16.4
figure 4

Indentation hardness as a function of residual indentation depth for Si(100) [30], Al(100) [31], Cu(111) [32]

Full size image

3.2 Shear Strength at the Interface

Mechanism of slip involves motion of large number of dislocations, which is responsible for plastic deformation during sliding. Dislocations are generated and stored in the body and propagate under load. There are two modes of possible line (or edge) dislocation motion: gliding, when dislocation moves in the direction of its Burgers vector b by a unit step of its magnitude, and climbing, when dislocation moves in a direction, perpendicular to its Burgers vector (Fig. 16.5a). Motion of dislocations can take place in the bulk of the body or at the interface. Due to periodicity of the lattice, a gliding dislocation experiences a periodic force, known as the Peierls force [31]. The Peierls force is responsible for keeping the dislocation at a central position between symmetric lattice lines and it opposes dislocation’s gliding (Fig. 16.5b). Therefore, an external force should be applied to overcome Peierls force resistance against dislocation’s motion. Weertman [36] showed that a dislocation or a group of dislocations can glide uniformly along an interface between two bodies of different elastic properties. In continuum elasticity formulation, this motion is equivalent to a propagating interface slip pulse, however the physical nature of this deformation is plastic, because dislocation motion is irreversible. The local plastic deformation can occur at the interface due to concentration of dislocations even in the predominantly elastic contacts. Gliding of a dislocation along the interface results in a relative displacement of the bodies for a distance equal to the Burgers vector of the dislocation, whereas a propagating set of dislocations effectively results in dislocation-assisted sliding, or microslip (Fig. 16.6).

Fig. 16.5
figure 5

(a) Schematics of gliding and climbing dislocations motion by a unit step of Burgers vector b. (b) Origin of the periodic force acting upon a gliding dislocation (Peierls force). Gliding dislocation passes locations of high and low potential energy

Full size image
Fig. 16.6
figure 6

Schematic showing microslip due to gliding dislocations at the interface

Full size image

Several types of microslip are known in the tribology literature [16], the dislocation-assisted sliding is one type of microslip, which propagates along the interface. Conventional mechanism of sliding is considered to be concurrent slip with simultaneous breaking of all adhesive bonds. Based on Johnson [37] and Bhushan and Nosonovsky [20], for contact sizes on the order of few nm to few μm, dislocation-assisted sliding is more energetically profitable than a concurrent slip. Their argument is based on the fact that experimental measurements with the SFA demonstrated that, for mica, frictional stress is of the same order as Peierls stress, which is required for gliding of dislocations.

Polonsky and Keer [38] considered the preexisting dislocation sources and carried out a numerical microcontact simulation based on contact plastic deformation representation in terms of discrete dislocations. They found that when the asperity size decreases and becomes comparable with the characteristic length of materials microstructure (distance between dislocation sources), resistance to plastic deformation increases, which supports conclusions drawn from strain gradient plasticity. Deshpande et al. [39] conducted discrete plasticity modeling of cracks in single crystals and considered dislocation nucleation from Frank–Read sources distributed randomly in the material. Pre-existing sources of dislocations, considered by all of these authors, are believed to be a more realistic reason for increasing number of dislocations during loading, rather than newly nucleated dislocations [30]. In general, dislocations are emitted under loads from preexisting sources and propagate along slip lines (Fig. 16.7). As shown in the figure, in regions of higher loads, number of emitted dislocations is higher. Their approach was limited to numerical analysis of special cases.

Fig. 16.7
figure 7

Generation of dislocations from sources (*) during plowing due to plastic deformation

Full size image

Bhushan and Nosonovsky [20] considered a sliding contact between two bodies. Slip along the contact interface is an important special case of plastic deformation. The local dislocation-assisted microslip can exist even if the contact is predominantly elastic due to concentration of dislocations at the interface. Due to these dislocations, the stress at which yield occurs at the interface is lower than shear yield strength in the bulk. This means that average shear strength at the interface is lower than in the bulk.

An assumption that all dislocations produced by externally applied forces are distributed randomly throughout the volume would result in vanishing small probability for a dislocation to be exactly at the interface. However, many traveling (gliding and climbing) dislocations will be stuck at the interface as soon as they reach it. As a result of this, a certain number of dislocations will be located at the interface. In order to account for a finite dislocation density at the interface, Bhushan and Nosonovsky [20] assumed, that the interface zone has a finite thickness D. Dislocations within the interface zone may reach the contact surface due to climbing and contribute into the microslip. In the case of a small contact radius a, compared to interface zone thickness D, which is scale dependent, and is approximately equal to a. However, in the case of a large contact radius, the interface zone thickness is approximately equal to the average distance dislocations can climb l s. An illustration of this is provided in Fig. 16.8. The depth of the subsurface volume, from which dislocations have a high chance to reach the interface is limited by l s and by a, respectively, for the two cases considered here. Based on these geometrical considerations, an approximate relation can be written as

$$D = \frac{\mathit{al}_{\rm s}}{l_{\rm s}+a}.$$
(16.11)

The interface density of dislocations (total length of dislocation lines per interface area) is related to the volume density as

$$\eta_{\rm int} = \rho\,D = \rho\left(\frac{\mathit{al}_{\rm s}}{l_{\rm s}+a}\right).$$
(16.12)
Fig. 16.8
figure 8

Gliding dislocations at the interface generated from sources (*). Only dislocations generated within the interface zone can reach the interface. (a) For a large contact radius a, thickness of this zone D is approximately equal to an average distance dislocations climb l s. (b) For small contact radius a, the thickness of the interface zone is approximately equal to a

Full size image

During sliding, dislocations must be generated at the interface with a certain critical density η int =  η cr. The corresponding shear strength during sliding can be written following (16.9) as

$$\tau_{\rm a} = \tau_{\rm a0}\sqrt{1+(l_{\rm s}/a)},$$
(16.13)

where

$$\tau_{\rm a0} = \mathit{cGb}\sqrt{\frac{\eta_{\rm cr}}{l_{\rm s}}}$$
(16.14)

is the shear strength during sliding in the limit of a ≫ l s.

Equation (16.13) gives scale-dependence of the shear strength at the interface and is based on the following assumptions. First, it is assumed that only dislocations in the interface zone of thickness D, given by (16.11), contribute into sliding. Second, it is assumed, that a critical density of dislocations at the interface η cr is required for sliding. Third, the shear strength is equal to the Peierls stress, which is related to the volume density of the dislocations ρ =  η/D according to (16.4), with the typical distance between dislocations \(s = 1/\sqrt{\rho}\). It is noted, that proposed scaling rule for the dislocation assisted sliding mechanism (16.13) has a similar form to that for the yield strength (16.9), since both results are consequences of scale dependent generation and propagation of dislocations under load [20].

4 Scale Effect in Surface Roughness and Contact Parameters

During multiple-asperity contact, scale dependence of surface roughness is a factor which contributes to scale dependence of the real area of contact. Roughness parameters are known to be scale dependent [16], which results, during the contact of two bodies, in scale dependence of the real area of contact, number of contacts and mean contact size. The contact parameters also depend on the normal load, and the load dependence is similar to the scale dependence [23]. Both effects are analyzed in this section.

4.1 Scale Dependence of Roughness and Contact Parameters

A random rough surface with Gaussian height distribution is characterized by the standard deviation of surface height σ and the correlation length β * [16]. The correlation length is a measure of how quickly a random event decays and it is equal to the length, over which the autocorrelation function drops to a small fraction of the value at the origin. The correlation length can be considered as a distance, at which two points on a surface have just reached the condition where they can be regarded as being statistically independent. Thus, σ is a measure of height distribution and β * is a measure of spatial distribution.

A surface is composed of a large number of length scales of roughness that are superimposed on each other. According to AFM measurements on glass-ceramic disk surface, both σ and β * initially increase with the scan size and then approach a constant value, at certain scan size (Fig. 16.9). This result suggests that disk roughness has a long wavelength limit, L lwl, which is equal to the scan size at which the roughness values approach a constant value [16]. It can be assumed that σ and β * depend on the scan size according to an empirical power rule

$$\begin{array}{ll}&\;\;\,\sigma = \sigma_{0}\left(\frac{L}{L_{\rm lwl}}\right)^{\!\!n},\qquad L, L_{\rm lwl},\\&\beta^{\ast} = \beta_{0}^{\ast}\left(\frac{L}{L_{\rm lwl}}\right)^{\!\!m},\qquad L, L_{\rm lwl},\end{array}$$
(16.15)

where n and m are indices of corresponding exponents and σ 0 and β * 0 are macroscale values [20]. Based on the data, presented in Fig. 16.9, it is noted that for glass-ceramic disk, long-wavelength limit for σ and β * is ≈17 and 23 μm, respectively. The difference is expected to be due to measurement errors. An average value L lwl = 20 μm is taken here for calculations. The values of the indices are found as m = 0.5, n = 0.2, and the macroscale values are σ 0 = 5.3 nm, β 0 * = 0.37 μm [23].

Fig. 16.9
figure 9

Roughness parameters as a function of scan size for a glass-ceramic disk measured using AFM [16]

Full size image

For two random surfaces in contact, the length of the nominal contact size L defines the characteristic length scale of the problem. The contact problem can be simplified by considering a rough surface with composite roughness parameters in contact with a flat surface. The composite roughness parameters σ and β * can be obtained based on individual values for the two surfaces [16]. For Gaussian surfaces, the contact parameters of interest, to be discussed later, are the real area of contact A r, number of contacts N, and mean contact radius \(\bar{a}\). The long wavelength limit for scale dependence of the contact parameters L lc, which is not necessarily equal to that of the roughness L lwl will be used for normalization of length parameters. The scale dependence of the contact parameters exists if L < L lc [23].

The mean of surface height distribution corresponds to so-called reference plane of the surface. Separation s d is a distance between reference planes of two surfaces in contact, normalized by σ. For a given s d and statistical distribution of surface heights, the total real area of contact (A r), number of contacts (N), and elastic normal load W e can be found, using statistical analysis of contacts. The real area of contact, number of contacts and elastic normal load are related to the separation distance s d [40]

$$\begin{array}{ll}&A_{\rm r}\,\propto\,F_{\rm A}(s_{\rm d}),\\&\,N\,\propto\frac{1}{(\beta^{\ast})^{2}}F_{\rm N}(s_{\rm d}),\\&W_{\rm e}\propto\frac{E^{\ast}\sigma}{\beta^{\ast}}F_{\rm W}(s_{\rm d}),\end{array}$$
(16.16)

where F A(s d), F N(s d), and F W(s d), are integral functions defined by Onions and Archard [40]. It should be noted, that A r and N as functions of s d are prescribed by the contact geometry (σ, β *) and do not depend on whether the contact is elastic or plastic. Based on Onions and Archard data, it is observed that the ratio F W/F A is almost constant for moderate s d <1.4 and increases slightly for s d > 1.4. The ratio F A/F N decreases rapidly with s d and becomes almost constant for s d > 2.0. For moderate loads, the contact is expected to occur on the upper parts of the asperities (s d >2.0), and a linear proportionality of F A(s d), F N(s d), and F W(s d) can be assumed [20].

Based on (16.16) and the observation that F W/F A is almost constant, for moderate loads, A re (the real area of elastic contact), N, and \(\bar{a}\) are related to the roughness, based on the parameter L lc, as

$$A_{\rm re}\propto \frac{\beta^{\ast}}{\sigma E^{\ast}}W = A_{\rm re0}\left(\frac{L}{L_{{\rm lc}}} \right)^{\!\!m-n}, \quad L, L_{\rm lc},$$
(16.17)
$$\;N\propto \frac{W}{\beta^{*}\sigma E^{\ast}} = N_{0}\left(\frac{L}{L_{\rm lc}} \right)^{\!\!-m-n}, \quad L, L_{\rm lc},$$
(16.18)
$$\;\overline{a}\propto \beta^{\ast} = \sqrt{\frac{A_{{\rm r}}}{N}} = \overline{a}_{0}\left(\frac{L}{L_{\rm lc}} \right)^{\!\!m},\quad L, L_{\rm lc}.$$
(16.19)

The mean radius of summit tips \(\overline{R}_{{\rm p}}\) is given, according to Whitehouse and Archard [41]

$$\overline{R}_{\rm p}\propto\frac{(\beta^{\ast})^{2}}{\sigma} = \overline{R}_{{\rm p}0}\left(\frac{L}{L_{{\rm lwl}}} \right)^{\!\! 2m-n},\quad L \,<\, L_{\rm lwl},$$
(16.20)

where \(\overline{a}_0\), N 0 and \(\overline{R}_{\rm p0}\) are macroscale values, E * is the effective elastic modulus of contacting bodies [22], which is related to the elastic moduli E 1, E 2 and Poisson’s ratios ν 1, ν 2 of the two bodies as \(1/E^{\ast} = \left(1-v_1^2\right)/E_1+\left(1-v_2^2\right)/E_2\) and which is known to be scale independent, and variables with the subscript 0 are corresponding macroscale values (for L ≥ L lc).

Dependence of the real area of plastic contact A rp on the load is given by

$$A_{\rm rp} = \frac{W}{H},$$
(16.21)

where H is hardness. According to the strain gradient plasticity model [17, 18], the yield strength τ Y is given by (16.9) and hardness H is given by (16.10). In the case of plastic contact, the mean contact radius can be determined from (16.19), which is based on the contact geometry and independent of load [20]. Assuming the contact radius as its mean value from (16.19) based on elastic analysis, and combining (16.10), (16.19) and (16.21), the real area of plastic contact is given as

$$\begin{array}{ll}&{\rm A}_{\rm rp} = \frac{W}{H_0\sqrt{1+(l_{\rm d}/\bar{a})}}\\&\qquad = \frac{W}{H_0\sqrt{1+(L_{\rm d}/L)^m}},\quad L, L_{\rm lc},\end{array}$$
(16.22)

where L d is a characteristic length parameter related to l d, \(\bar{a}\), and L lc [20]

$$L_{\rm d} = L_{\rm lc}\left(\frac{l_{\rm d}}{\bar{a}_0}\right)^{\!\! l/m}.$$
(16.23)

The scale dependence of A re, N, and \(\bar{a}\) is presented in Fig. 16.10.

Fig. 16.10
figure 10

Scale length dependence of normalized contact parameters (m = 0.5, n = 0.2) (a) real area of contact, (b) number of contacts, and (c) mean contact radius

Full size image

4.2 Dependence of Contact Parameters on Load

The effect of short and long wavelength details of rough surfaces on contact parameters also depends on the normal load. For low loads, the ratio of real to apparent areas of contact A r/A a, is small, contact spots are small, and long wavelength details are irrelevant. For higher A r/A a, long wavelength details become important, whereas small wavelength details of the surface geometry become irrelevant. The effect of increased load is similar to the effect of increased scale length [23].

In the preceding subsections, it was assumed that the roughness parameters are scale-dependent for L < L lwl, whereas the contact parameters are scale-dependent for L < L lc. The upper limit of scale dependence for the contact parameters L lc depends on the normal load, and it is reasonable to assume that L lc is a function of A r/A a, and the contact parameters are scale-dependent when A r/A a is below a certain critical value. It is convenient to consider the apparent pressure p a, which is equal to the normal load divided by the apparent area of contact [23].

For elastic contact, based on (16.15) and (16.17), this condition can be written as

$$\frac{A_{\rm re}}{A_{\rm a}}\propto\frac{\beta^{\ast}p_{\rm a}}{\sigma} = p_{\rm a}\frac{\beta_0^{\ast}}{\sigma_0}\left(\frac{L}{L_{\rm lwl}}\right)^{m-n}, p_{\rm ac},$$
(16.24)

where p ac is a critical apparent pressure, below which the scale dependence occurs [23]. From (16.24) one can find

$$L, L_{\rm lwl}\left(\frac{\beta_0^{\ast}}{\sigma_0}\frac{p_{\rm a}}{p_{\rm ac}}\right)^{\!\!1/(n-m)}.$$
(16.25)

The right-hand expression in (16.24) is defined as L lc

$$L_{\rm lc} = L_{\rm lwl}\left(\frac{\beta_0^{\ast}}{\sigma_0}\frac{p_{\rm a}}{p_{\rm ac}}\right)^{\!\!1/(n-m)}.$$
(16.26)

For plastic contact, based on (16.22)

$$\frac{A_{\rm rp}}{A_{\rm a}}\propto\frac{p_{\rm a}}{\sqrt{1+(L_{\rm d}/L)^m}}, p_{\rm ac}.$$
(16.27)

In a similar manner to the elastic case, (16.27) yields [23]

$$L_{\rm lc} = L_{\rm d}\left[\left(\frac{p_{\rm a}}{p_{\rm ac}}\right)^{\!\!2}-1\right]^{-1/m}.$$
(16.28)

Load dependence of the long wavelength limit for contact parameters, L lc is presented in Fig. 16.11 for an elastic contact based on (16.28), and for a plastic contact based on (16.28), for m = 0.5, n = 0.2 [23]. The load (apparent pressure) is normalized by β * 0/(p ac σ 0) for the elastic contact and by p ac for the plastic contact. In the case of elastic contact, it is observed, that the long wavelength limit decreases with increasing load. For a problem, characterized by a given scale length L, increase of load will result in decrease of L lc and, eventually, the condition L < L lc will be violated; thus the contact parameters, including the coefficient of friction, will reach the macroscale values. Decrease of L lc with increasing load is also observed in the case of plastic contact, the data presented for p a/p ac > 1.

Fig. 16.11
figure 11

Dependence of the normalized long wavelength limit for contact parameters on load (normalized apparent pressure) for elastic and plastic contacts (m = 0.5, n = 0.2)

Full size image

5 Scale Effect in Friction

According to the adhesion and deformation model of friction [16], the coefficient of dry friction μ can be presented as a sum of adhesion component μ a and deformation (plowing) component μ d. The later, in the presence of particles, is a sum of asperity summits deformation component μ ds and particles deformation component μ dp, so that the total coefficient of friction is [21]

$$\begin{array}{ll}\mu = \mu_{\rm a}+\mu_{\rm ds}+\mu_{\rm dp} = \frac{F_{\rm a}+F_{\rm ds}+F_{\rm dp}}{W} = \frac{A_{\rm ra}\tau_{\rm a}+A_{\rm ds}\tau_{\rm ds}+A_{\rm dp}\tau_{\rm dp}}{W},\end{array}$$
(16.29)

where W is the normal load, F is the friction force, A ra, A ds, A dp are the real areas of contact during adhesion, two body deformation and with particles, respectively, and τ is the shear strength. The subscripts a, ds, and dp correspond to adhesion, summit deformation and particle deformation.

In the presence of meniscus, the friction force is given by

$$F = \mu(W+F_{\rm m}),$$
(16.30)

where F m is the meniscus force [16]. The coefficient of friction in the presence of the meniscus force, μ wet, is calculated using only the applied normal load, as normally measured in the experiments [22]

$$\begin{array}{ll}\mu_{\rm wet} = \mu\left(1+\frac{F_{\rm m}}{W}\right)\\ = \frac{A_{\rm ra}\tau_{\rm a}+A_{\rm ds}\tau_{\rm ds}+A_{\rm dp}\tau_{\rm dp}}{W}\left(1+\frac{F_{\rm m}}{W}\right).\end{array}$$
(16.31)

Equation (16.31) shows that μ wet > μ, because F m is not taken into account for calculation of the normal load in the wet contact.

It was shown by Greenwood and Williamson [42] and by subsequent modifications of their model, that for contacting surfaces with common statistical distributions of asperity heights, the real area of contact is almost linearly proportional to the normal load. This linear dependence, along with (16.29), result in linear dependence of the friction force on the normal load, or coefficient of friction being independent of the normal load. For a review of the numerical analysis of rough surface contacts, see Bhushan [43, 44] and Bhushan and Peng [45]. The statistical and numerical theories of contact involve roughness parameters – e.g. the standard deviation of asperity heights and the correlation length [16]. The roughness parameters are scale dependent. In contrast to this, the theory of self-similar (fractal) surfaces solid contact developed by Majumdar and Bhushan [46] does not include length parameters and are scale-invariant in principle. The shear strength of the contacts in (16.29) is also scale dependent. In addition to the adhesional contribution to friction, elastic and plastic deformation on nano- to macroscale contributes to friction [16]. The deformations are also scale dependent.

5.1 Adhesional Friction

The adhesional component of friction depends on the real area of contact and adhesion shear strength. Here we derive expressions for scale dependence of adhesional friction during single-asperity and multiple-asperity contacts.

5.1.1 Single-Asperity Contact

The scale length during single-asperity contact is the nominal contact length, which is equal to the contact diameter 2a. In the case of predominantly elastic contacts, the real area of contact A re depends on the load according to the Hertz analysis [47]

$$A_{\rm re} = \pi a^2,$$
(16.32)

and

$$a = \left(\frac{3WR}{4E^{\ast}}\right)^{\!\!\!1/3},$$
(16.33)

where R is effective radius of curvature of summit tips, and E * is the effective elastic modulus of the two bodies. In the case of predominantly plastic contact, the real area of contact A rp is given by (16.21), whereas the hardness is given by (16.10).

Combining (16.10), (16.13), (16.29), and (16.32), the adhesional component of the coefficient of friction can be determined for the predominantly elastic contact as

$$\mu_{\rm ae} = \mu_{\rm ae0}\sqrt{1+(l_{\rm s}/a)}$$
(16.34)

and for the predominantly plastic contact as

$$\mu_{\rm ap} = \mu_{\rm ap0}\sqrt{\frac{1+(l_{\rm s}/a)}{1+(l_{\rm d}/a)}},$$
(16.35)

where μ ae0 and μ ap0 are corresponding values at the macroscale [20].

The scale dependence of adhesional friction in single-asperity contact is presented in Fig. 16.12a. In the case of single asperity elastic contact, the coefficient of friction increases with decreasing scale (contact diameter), because of an increase in the adhesion strength, according to (16.34). In the case of single asperity plastic contact, the coefficient of friction can increase or decrease with decreasing scale, because of an increased hardness or increase in adhesional strength. The competition of these two factors is governed by l d/l s, according to (16.35). There is no direct way to measure l d and l s. We will see later, from experimental data, that the coefficient of friction tends to decrease with decreasing scale, therefore, it must be assumed that l d/l s > 1 for the data reported in the paper [20].

Fig. 16.12
figure 12

Normalized results for the adhesional component of the coefficient of friction, as a function of scale (a/l s for single asperity contact and L/L lc for multi-asperity contact). In the case of single asperity plastic contact, data are presented for two values of l d/l s. In the case of multi-asperity contact, data are presented for m = 0.5, n = 0.2. For multi-asperity elastic contact, data are presented for three values of L S/L lc. For multi-asperity plastic contact, data are presented for two values of L d/L s

Full size image

5.1.2 Multiple-Asperity Contact

The adhesional component of friction depends on the real area of contact and adhesion shear strength. Scale dependence of the real area of contact was considered in the preceding section. Here we derive expressions for scale-dependence of the shear strength at the interface during adhesional friction. It is suggested by Bhushan and Nosonovsky [20] that, for many materials, dislocation-assisted sliding (microslip) is the main mechanism, which is responsible for the shear strength. They considered dislocation assisted sliding based on the assumption, that contributing dislocations are located in a subsurface volume. The thickness of this volume is limited by the distance which dislocations can climb l s (material parameter) and by the radius of contact a. They showed that τ a is scale dependent according to (16.13). Assuming the contact radii equal to the mean value given by (16.19)

$$\tau_{\rm a} = \tau_{\rm a0}\sqrt{1+(L_{\rm s}/L)^m},\quad L \,<\, L_{\rm lc},$$
(16.36)

where

$$L_{\rm s} = L_{\rm lc}\left(\frac{l_{\rm s}}{\bar{a}_0}\right)^{\!\!\!1/m}.$$
(16.37)

In the case of absence of the microslip (e.g., for an amorphous material), it should be assumed in (16.34–16.36), L s =  l s =  0.

Based on (16.9, 16.17, 16.24, 16.29, 16.36, 16.37), the adhesional component of the coefficient of friction in the case of elastic contact μ ae and in the case of plastic contact μ ap, is given as [20]

$$\begin{array}{ll}\mu_{\rm ae} = \frac{\tau_{\rm a}A_{\rm re}}{W} = \frac{\tau_{\rm a0}A_{\rm re0}}{W}\left(\frac{L}{L_{\rm lc}}\right)^{m-n}\sqrt{1+(L_{\rm s}/L)^m} = \frac{\mu_{\rm ae0}}{\sqrt{1+(l_{\rm s}/\bar{a}_0)}}\left(\frac{L}{L_{\rm lc}}\right)^{m-n}\\ \quad\times\sqrt{1+(L_{\rm s}/L)^m},\quad L, L_{\rm lc};\end{array}$$
(16.38)
$$\begin{array}{ll}\mu_{\rm ap} = \frac{\tau_{\rm a0}}{H_0}\sqrt{\frac{1+(L_{\rm s}/L)^m}{1+(L_{\rm d}/L)^m}} = \mu_{\rm ap0}\sqrt{\frac{1+(l_{\rm d}/\bar{a}_0)}{1+(l_{\rm s}/\bar{a}_0)}}\sqrt{\frac{1+(L_{\rm s}/L)^m}{1+(L_{\rm d}/L)^m}},\;\; L, L_{\rm lc},\end{array}$$
(16.39)

where μ ae0 and μ ap0 are values of the coefficient of friction at macroscale (L ≥ L lc).

The scale dependence of adhesional friction in multiple-asperity elastic contact is presented in Fig. 16.12b, which is based on (16.38), for various values of L s/L lc. The change of scale length L affects the coefficient of friction in two different ways: through the change of A re (16.17) and τ a (16.36) below L lc. Further, τ a is controlled by the ratio L s/L. Based on (16.36), for small ratio of L s/L lc, scale effects on τ a is insignificant for L/L lc > 0. As it is seen from Fig. 16.12b by comparison of the curve with L s/L lc =  0 (insignificant scale effect on τ a), L s/L lc =  1, and L s/L lc = 1000 (significant scale effect on τ a), the results for the normalized coefficient of friction are close, thus, the main contribution to the scaling effect is due to change of A re. In the case of multiple-asperity plastic contact, the results, based on (16.39), are presented in Fig. 16.12b for L d/L s = 0.25, L d/L s =  5 and L d/L lc =  1 and L d/L lc = 1,000. The change of scale affects the coefficient of friction through the change of A rp (16.34), which is controlled by L d, and τ a (16.36), which is controlled by L s. It can be observed from Fig. 16.12b, that for L d > L s, the change of A rp prevails over the change of τ a, with decreasing scale, and the coefficient of friction decreases. For L d < L s, the change of τ a prevails, with decreasing scale, and the coefficient of friction increases [20]. Expressions for the coefficient of adhesional friction are presented in Table 16.1.

Table 16.1 Scaling factors for the coefficient of adhesional friction [20]
Full size table

5.2 Two-Body Deformation

Based on the assumption that multiple asperities of two rough surfaces in contact have conical shape, the two-body deformation component of friction can be determined as

$$\mu_{\rm ds} = \frac{2\tan\theta_{\rm r}}{\pi},$$
(16.40)

where θ r is the roughness angle (or attack angle) of a conical asperity [16, 48]. Mechanical properties affect the real area of contact and shear strength and these cancel out in (16.29).

The roughness angle is scale-dependent and is related to the roughness parameters [41]. Based on statistical analysis of a random Gaussian surface,

$$\tan\theta_{\rm r}\propto\frac{\sigma}{\beta^{\ast}}.$$
(16.41)

From (16.40) it can be interpreted that stretching the rough surface in the vertical direction (increasing vertical scale parameter σ) increases tan θ r, and stretching in the horizontal direction (increasing vertical scale parameter β *) decreases tan θ r.

Using (16.40) and (16.41), the scale dependence of the two-body deformation component of the coefficient of friction is given as [21]

$$\begin{array}{ll}\mu_{\rm ds} = \frac{2\sigma_0}{\pi\beta^{\ast}}\left(\frac{L}{L_{\rm lc}}\right)^{\!\!n-m} = \mu_{\rm ds0}\left(\frac{L}{L_{\rm lc}}\right)^{\!\!n-m},\quad L, L_{\rm lc},\end{array}$$
(16.42)

where μ ds0 is the value of the coefficient of summits deformation component of the coefficient of friction at macroscale (L ≥ L lc).

The scale dependence for the two-body deformation component of the coefficient of friction is presented in Fig. 16.13 for m = 0.5, n = 0.2. The coefficient of friction increases with decreasing scale, according to (16.42). This effect is a consequence of increasing average slope or roughness angle.

Fig. 16.13
figure 13

Normalized results for the two-body deformation component of the coefficient of friction

Full size image

5.3 Three-Body Deformation Friction

In this sections of the paper, size distribution of particles will be idealized according to the exponential, normal, and log normal density functions, since these distributions are the most common in nature and industrial applications (See Appendix). The probability for a particle of a given size to be trapped at the interface depends on the size of the contact region. Particles at the edge of the region of contact are likely to leave the contact area, whereas those in the middle are likely to be trapped. The ratio of the edge region area to the total apparent area of contact increases with decreasing scale size. Therefore, the probability for a particle to be trapped decreases, as well as the three-body component of the coefficient of friction [21].

Let us consider a square region of contact of two rough surfaces with a length L (relevant scale length), with the density of debris of η particles per unit area (Fig. 16.14). We assume that the particles have the spherical form and that p(d) is the probability density function of particles size. It is also assumed that, for a given diameter, particles at the border region of the contact zone of the width d/2 are likely to leave the contact zone, with a certain probability α, whereas particles at the center of the contact region are likely to be trapped. It should be noted, that particles in the corners of the contact region can leave in two different directions, therefore, for them the probability to leave is 2α. The total nominal contact area is equal to L 2, the area of the border region, without the corners, is equal to 4(L − d)d/2, and the area of the corners is equal to d 2.

Fig. 16.14
figure 14

Schematics of debris at the contact zone and at its border region. A particle of diameter d in the border region of d/2 is likely to leave the contact zone

Full size image

The probability density of size distribution for the trapped particles p tr(d) can be calculated by multiplying p(d) by one minus the probability of a particle with diameter d to leave; the later is equal to the ratio of the border region area, multiplied by a corresponding probability of the particle to leave, divided by the total contact area [21]

$$\begin{array}{ll}p_{\rm tr}(d) = p(d)\left(1-\frac{2\alpha(L-d)d+2\alpha d^2}{L^2}\right)= p(d)\left(1-\frac{2\alpha d}{L}\right),\quad d \frac{L}{2\alpha}.\end{array}$$
(16.43)

The ratio of the number of trapped particles to the total number of particles, average radius of a trapped particle \(\bar{d}\), and average square of trapped particles \(\overline{d^2}\), as functions of L, can be calculated as

$$\begin{array}{ll}&n_{\rm tr} = \frac{\int\nolimits_{0}^{L/2}p_{\rm tr}(d){\rm d}d}{\int\nolimits_{0}^{\infty}p(d){\rm d}d} = \frac{\int\nolimits_{0}^{L/2}p(d)\left(1-\frac{2\alpha d}{L}\right){\rm d}d}{\int\nolimits_{0}^{\infty}p(d){\rm d}d},\\&\;\;\,\bar{d} = \frac{\int\nolimits_{0}^{L/2}dp_{\rm tr}(d){\rm d}d}{\int\nolimits_{0}^{L/2}p_{\rm tr}(d){\rm d}d},\\&\;\overline{d^2} = \frac{\int\nolimits_{0}^{L/2}d^2p_{\rm tr}(d){\rm d}d}{\int\nolimits_{0}^{L/2}p_{\rm tr}(d){\rm d}d}.\end{array}$$
(16.44)

Let us assume an exponential distribution of particles’ size (16.A7) with d e = 0. Substituting (16.A7) into (16.44) and integrating yields for the ratio of trapped particles [21]

$$\begin{array}{ll}n_{\rm tr} = \frac{\int\nolimits_0^{L/(\alpha 2)}\frac{1}{\sigma_{\rm e}}\exp\left(-\frac{d}{\sigma_{\rm e}}\right)\left(1-\frac{2\alpha d}{L}\right){\rm d}d}{\int_0^{\infty}\frac{1}{\sigma_{\rm e}}\exp\left(-\frac{d}{\sigma_{\rm e}}\right){\rm d}d} = \exp\left(-\frac{d}{\sigma_{\rm e}}\right)\left.\frac{\sigma_{\rm e}-L/(2\alpha)+d}{L/(2\alpha)}\right|_{0}^{L/(2\alpha)}\cr = \frac{2\alpha\sigma_{\rm e}}{L}\left[\exp\left(-\frac{L}{2\alpha\sigma_{\rm e}}\right)-1\right]+1,\end{array}$$
(16.45)

whereas the mean diameter of the trapped particles is

$$\begin{array}{ll}\bar{d} = \frac{\int\nolimits_0^{L/(\alpha 2)}d\exp\left(-\frac{d}{\sigma_{\rm e}}\right)\left(1-\frac{2\alpha d}{L}\right){\rm d}d}{\int\nolimits_0^{L/(2\alpha)}\exp\left(-\frac{d}{\sigma_{\rm e}}\right)\left(1-\frac{2\alpha d}{L}\right){\rm d}d}= \sigma_{\rm e}\frac{\exp\left(-\frac{L}{2\alpha\sigma_{\rm e}}\right)\left(1+\frac{4\alpha\sigma_{\rm e}}{L}\right)+1-\frac{4\alpha\sigma_{\rm e}}{L}}{\frac{2\alpha\sigma_{\rm e}}{L}\left[\exp\left(-\frac{L}{2\alpha\sigma_{\rm e}}\right)-1\right]+1}\end{array}$$
(16.46)

and the mean square radius of the trapped particles is

$$\begin{array}{ll}\overline{d^2} = \frac{\int\nolimits_0^{L/(2\alpha)}d^2\exp\left(-\frac{d}{\sigma_{\rm e}}\right)\left(1-\frac{2\alpha d}{L}\right){\rm d}d}{\int\nolimits_0^{L/(2\alpha)}\exp\left(-\frac{d}{\sigma_{\rm e}}\right)\left(1-\frac{2\alpha d}{L}\right){\rm d}d}\\ = \sigma_{\rm e}^2\frac{\exp\left(-\frac{L}{2\alpha\sigma_{\rm e}}\right)\left(\frac{L}{2\alpha\sigma_{\rm e}}+4+\frac{12\alpha\sigma_{\rm e}}{L}\right)+2-\frac{12\alpha\sigma_{\rm e}}{L}}{\frac{2\alpha\sigma_{\rm e}}{L}\left(\exp\left(-\frac{L}{2\alpha\sigma_{\rm e}}\right)-1\right)+1}.\end{array}$$
(16.47)

For the normal and log normal distributions, similar calculations can be conducted numerically.

The area, supported by particles can be found as the number of trapped particles ηL 2 n tr multiplied by average particle contact area

$$A_{\rm dp} = \eta L^2n_{\rm tr}\frac{\pi\overline{d^2}}{4},$$
(16.48)

where \(\overline{d^2}\) is mean square of particle diameter, η is particle density per apparent area of contact (L 2) and n tr is a number of trapped particles divided by the total number of particles [21].

The plowing deformation is plastic and, assuming that particles are harder than the bodies, the shear strength τ dp is equal to the shear yield strength of the softer body τ Y which is given by the (16.9) with \(a = \bar{d}/2\). Combining (16.29) with (16.9) and (16.48)

$$\begin{array}{ll}\mu_{\rm dp} = \frac{A_{\rm dp}\tau_{\rm dp}}{W} = \eta\frac{L^2}{W}\frac{\pi\overline{d^2}}{4}n_{\rm tr}\tau_{\rm Y0}\sqrt{1+2l_{\rm d}/\bar{d}}\\ = \mu_{\rm dp0}n_{\rm tr}\frac{\overline{d^2}}{\overline{d_0^2}}\frac{\sqrt{1+2l_{\rm d}/\overline{d}}}{\sqrt{1+2l_{\rm d}/\overline{d_0}}},\end{array}$$
(16.49)

where \(\bar{d}\) is mean particle diameter, \(\overline{d_0}\) is the macroscale value of mean particle diameter, and μ dp0 is macroscale (L →∞, n tr → 1) value of the third-body deformation component of the coefficient of friction given as

$$\mu_{\rm dp0} = \eta\frac{L^2}{W}\frac{\pi\overline{d_0^2}}{4}\tau_{\rm Y0}\sqrt{1+2l_{\rm d}/\bar{d}_0}.$$
(16.50)

Scale dependence of the three-body deformation component of the coefficient of friction is presented in Fig. 16.15, based on (16.49). The number of trapped particles divided by the total number of particles, as well as the three-body deformation component of the coefficient of friction, are presented as a function of scale size divided by α for the exponential, normal, and log normal distributions. The dependence of μ d/μ d0 is shown as a function of L/(ασ e) for the exponential distribution and normal distribution, for d n =  d e =  2σ e and l d/σ e =  1, whereas for the log normal distribution the results are presented as a function of L/α, for (ln d ln) =  2, σ ln =  1, and l d/σ ln =  1. This component of the coefficient of friction decreases for all of the three distributions. The results are shown for l d/σ ln =  1, however, variation of l d/σ ln in the range between 0.1 and 10 does not change significantly the shape of the curve. The decrease of the three-body deformation friction force with decreasing scale results with this component being small at the nanoscale.

Fig. 16.15
figure 15

The number of trapped particles divided by the total number of particles and three-body deformation component of the coefficient of friction, normalized by the macroscale value, for three different distributions of debris size: (a) exponential, (b) normal, and (c) log-normal distributions

Full size image

5.4 Ratchet Mechanism

Surface roughness can have an appreciable influence on friction during adhesion. If one of the contacting surfaces has asperities of much smaller lateral size, such that a small tip slides over an asperity, having the average angle θ r (so called ratchet mechanism), the corresponding component of the coefficient of friction is given by

$$\mu_{\rm r} = \mu_{\rm a}\tan^2\theta_{\rm r},$$
(16.51)

where μ r is the ratchet mechanism component of friction [16]. Combining (16.15, 16.41, 16.38, 16.39) yields for the scale dependence of the ratchet component of the coefficient of friction in the case of elastic μ re and plastic contact μ rp

$$\begin{array}{ll}\mu_{\rm re} = \mu_{\rm ae}\left[\frac{2\sigma_0}{\pi\beta_0^{\ast}}\left(\frac{L}{L_{\rm lc}}\right)^{\!\!\!n-m}\right]^2= \frac{\mu_{\rm re0}}{\sqrt{1+(l_{\rm s}/\bar{a}_0)}}\left(\frac{L}{L_{\rm lc}}\right)^{\!\!\!n-m}\\ \quad\times\sqrt{1+(L_{\rm s}/L)^m},\quad L, L_{\rm lc},\end{array}$$
(16.52)
$$\begin{array}{ll}\mu_{\rm rp} = \mu_{\rm ap}\left[\frac{2\sigma_0}{\pi\beta_0^{\ast}}\left(\frac{L}{L_{\rm lc}}\right)^{\!\!\!n-m}\right]^2 = \mu_{\rm rp0}\left(\frac{L}{L_{\rm lc}}\right)^{\!\!\!2(n-m)}\sqrt{\frac{1+(l_{\rm d}/\bar{a}_0)}{1+(l_{\rm s}/\bar{a}_0)}}\\ \quad\times\sqrt{\frac{1+(L_{\rm s}/L)^m}{{1+(L_{\rm d}/L)^m}}},\quad L, L_{\rm lc},\end{array}$$
(16.53)

where μ re0 and μ rp0 are the macroscale values of the ratchet component of the coefficient of friction for elastic and plastic contact correspondingly [23].

Scale dependence of the ratchet component of the coefficient of friction, normalized by the macroscale value, is presented in Fig. 16.16, for scale independent adhesional shear strength, τ a = const , (L s =  0) and for scale dependent τ a (L s = 10L d), based on (16.51) and (16.53). The ratchet component during adhesional elastic friction μ re is presented in Fig. 16.16a. It is observed, that, with decreasing scale, μ re increases. The ratchet component during adhesional plastic friction μ rp is presented in Fig. 16.16b. It is observed, that, for L s =  0, with decreasing scale, μ rp increases [23].

Fig. 16.16
figure 16

Normalized results for the ratchet component of the coefficient of friction, as a function of scale, for scale independent (L s =  0) and scale dependent (L s =  10L lc) shear strength (m = 0.5, n = 0.2). (a) contact, (b) plastic contact (L d =  10L lc)

Full size image

5.5 Meniscus Analysis

During contact, if a liquid is introduced at the point of asperity contact, the surface tension results in a pressure difference across a meniscus surface, referred to as capillary pressure or Laplace pressure. The attractive force for a sphere in contact with a plane surface is proportional to the sphere radius R p, for a sphere close to a surface with separation s or for a sphere close to a surface with continuous liquid film [16]

$$F_m\propto R_{\rm p}.$$
(16.54)

The case of multiple-asperity contact is shown in Fig. 16.1b. Note, that both contacting and near-contacting asperities wetted by the liquid film contribute to the total meniscus force. A statistical approach can be used to model the contact. In general, given the interplanar separation s d, the mean peak radius \(\overline{R}_{\rm p}\), the thickness of liquid film h f, the surface tension γ, liquid contact angle between the liquid and surface θ, and the total number of summits in the nominal contact area N,

$$F_m = 2\pi\overline{R}_{\rm p}\gamma(1+\cos\theta)N.$$
(16.55)

In (16.54), γ and θ are material properties, which are not expected to depend on scale, whereas \(\overline{R}_{\rm p}\) and N depend on surface topography, and are scale-dependent, according to (16.18) and (16.20).

$$F_m\propto \overline{R}_{\rm p}N = F_{\rm m0}\left(\frac{L}{L_{\rm lwl}}\right)^{m-2n},\quad L, L_{\rm lwl},$$
(16.56)

where F m0 is the macroscale value of the meniscus force (L ≥ L lwl).

Scale dependence of the meniscus force is presented in Fig. 16.17, based on (16.56) for m = 0.5, n = 0.2. It may be observed that, depending on the value of D, the meniscus force may increase or decrease with decreasing scale size.

Fig. 16.17
figure 17

Meniscus force for m = 0.5, n = 0.2

Full size image

5.6 Total Value of Coefficient of Friction and Transition from Elastic to Plastic Regime

During transition from elastic to plastic regime, contribution of each of the three components of the coefficient of friction in (16.29) changes. In the elastic regime, the dominant contribution is expected to be adhesion involving elastic deformation, and in the plastic regime the dominant contribution is expected to be deformation. Therefore, in order to study transition from elastic to plastic regime, the ratios of deformation to adhesion component should be considered. The expression for the total value of the coefficient of friction, which includes meniscus force contribution, based on (16.29) and (16.31) can be rewritten as [21]

$$\mu_{\rm wet} = \mu_{\rm a}\left(1+\frac{\mu_{\rm ds}}{\mu_{\rm a}}+\frac{\mu_{\rm dp}}{\mu_{\rm a}}\right)\left(1+\frac{F_{\rm m}}{W}\right).$$
(16.57)

The ratchet mechanism component is ignored here since it is present only in special cases. Results in the preceding subsection provide us with data about the adhesion and two-body and three-body deformation components of the coefficient of friction, normalized by their values at the macroscale. However, that analysis does not provide any information about their relation to each other or about transition from the elastic to plastic regime. In order to analyze the transition from pure adhesion involving elastic deformation to plastic deformation, a transition index φ can be considered [21]. The transition index is equal to the ratio of average pressure in the elastic regime (normal load per real area of elastic contact) to hardness or simply the ratio of the real area of plastic contact divided by the real area of elastic contact

$$\phi = \frac{W}{A_{\rm re}H} = \frac{A_{\rm rp}}{A_{\rm re}}.$$
(16.58)

Using (16.17) and (16.22), the scale-dependence of φ is

$$\begin{array}{ll}\phi = \frac{W}{A_{\rm re0}(L/L_{\rm lc})^{m-n}H_0\sqrt{1+(L_{\rm s}/L)^m}} = \phi_0\frac{\sqrt{1+(l_{\rm s}/\bar{a})}(L/L_{\rm lc})^{n-m}}{\sqrt{1+(L_{\rm s}/L)^m}},\quad L, L_{\rm lc},\end{array}$$
(16.59)

where φ 0 is the macroscale value of the transition index [21].

With a low value of φ close to zero, the contacts are mostly elastic and only adhesion contributes to the coefficient of friction involving elastic deformation. Whereas with increasing φ approaching unity, the contacts become predominantly plastic and deformation becomes a dominant contributor. It can be argued that A ds/A re and A dp/A re will also be a direct function of φ, and in the paper these will be assumed to have linear relationship.

Next, the ratio of adhesion and deformation components of the coefficient of friction in terms of φ is obtained. In this relationship, τ ds and τ dp are equal to the shear yield strength, which is proportional to hardness and can be obtained from (16.9), using (16.19) and (16.36)

$$\begin{array}{ll}\frac{\mu_{\rm ds}}{\mu_{\rm ae}} = \frac{A_{\rm ds}\tau_{\rm ds}}{A_{\rm re}\tau_{\rm a}} \propto\phi\frac{\tau_{\rm ds}}{\tau_{\rm a}} = \phi\frac{\tau_{\rm ds0}\sqrt{1+(L_{\rm d}/L)^m}}{\tau_{\rm a0}\sqrt{1+(L_{\rm s}/L)^m}},\quad L, L_{\rm lc},\end{array}$$
(16.60)
$$\begin{array}{ll}\frac{\mu_{\rm dp}}{\mu_{\rm ae}} = \frac{A_{\rm dp}\tau_{\rm dp}}{A_{\rm re}\tau_{\rm a}} \propto\phi\frac{\tau_{\rm dp}}{\tau_{\rm a}} = \phi\frac{\tau_{\rm Y0}\sqrt{1+2l_{\rm d}/\bar{d}}}{\tau_{\rm a0}\sqrt{1+(L_{\rm s}/L)^m}},\quad L, L_{\rm lc},\end{array}$$
(16.61)

The sum of adhesion and deformation components [21]

$$\begin{array}{ll}\mu_{\rm wet}&\, = \mu_{\rm ae}\left[1+\phi\left(\frac{\tau_{\rm ds0}\sqrt{1+(L_{\rm d}/L)^m}}{\tau_{\rm a0}\sqrt{1+(L_{\rm s}/L)^m}}+\frac{\tau_{\rm Y0}\sqrt{1+2l_{\rm d}/\bar{d}}}{\tau_{\rm a0}\sqrt{1+(L_{\rm s}/L)^m}}\right)\right]\\&\quad\times\left[1+\frac{F_{\rm m0}}{W}\left(\frac{L}{L_{\rm lwl}}\right)^{\!\!\!m-2n}\right],\quad L, L_{\rm lc}.\end{array}$$
(16.62)

Note that φ itself is a complicated function of L, according to (16.59).

Scale dependence of the transition index, normalized by the macroscale value, is presented in Fig. 16.18, based on (16.59). It is observed that, for L s =  0, the transition index decreases with increasing scale. For L s =  10 L lc, the same trend is observed for m > 2n, but, in the case m < 2n, φ decreases. An increase of the transition index means that the ratio of plastic to elastic real areas of contact increases. With decreasing scale, the mean radius of contact decreases, causing hardness enhancement and decrease of the plastic area of contact. Based on this, the model may predict an increase or decrease of the transition index, depending on whether elastic or plastic area decreases faster.

Fig. 16.18
figure 18

The transition index as a function of scale. Presented for m = 0.5, n = 0.2 and m = 0.5, n = 0.4

Full size image

The dependence of the coefficient of friction on φ is illustrated in Fig. 16.19, based on (16.62). It is assumed in the figure that the slope for the dependence of μ dp on φ is greater than the slope for the dependence of μ ds on φ. For φ close to zero, the contact is predominantly elastic, whereas for φ approaching unity the contact is predominantly plastic.

Fig. 16.19
figure 19

The coefficient of friction (dry contact) as a function of the transition index for given scale length L. With increasing φ and onset of plastic deformation, both μ ds and μ dp grow, as a result of this, the total coefficient of friction μ grows as well

Full size image

5.7 Comparison with the Experimental Data

Experimental data on friction at micro- and nanoscale are presented in this subsection and compared with the model. First, a single-asperity predominantly elastic contact is considered [20], then transition to plastic deformation involving multiple asperity contacts is analyzed [23].

5.7.1 Single-Asperity Predominantly-Elastic Contact

Nanoscale dependence of friction force upon the normal load was studied for Pt-coated AFM tip versus mica in ultra-high vacuum (UHV) by Carpick et al. [7], for Si tip versus diamond and amorphous carbon by Schwarz et al. [8] and for Si3N4 tip on Si, SiO2, and diamond by Bhushanand Kulkarni [6] (Fig. 16.20a). Homola et al. [13] conducted SFA experiments with mica rolls with a single contact zone (before onset of wear) (Fig. 16.21b). Contacts relevant in these experiments can be considered as single-asperity, predominantly elastic in all of these cases. For a single-asperity elastic contact of radius a, expression for μ is given by (16.17). For the limit of a small contact radius a ≪ l s, the (16.13) combined with the Hertzian dependence of the contact area upon the normal load (16.33) yields

$$F_{\rm e}\approx\pi a^2\tau_0\sqrt{l_{\rm s}/a}^{3/2}\propto W^{1/2}.$$
(16.63)

If an adhesive pull-off force W 0 is large, (16.63) can be modified as

$$F_{\rm e} = C_0\sqrt{W+W_0},$$
(16.64)

where C 0 is a constant. Friction force increases with square root of the normal load, opposed to the two third exponent in scale independent analysis.

Fig. 16.20
figure 20

Summary of (a) AFM data (upper: Pt-coated tip on mica in UHV [7], middle: Si tip on DLC and diamond in UHV [8], lower: Si3N4 tip on various materials [6]) and (b) SFA data (on mica versus mica in dry air [13]) for friction force as a function of normal load

Full size image
Fig. 16.21
figure 21

Shear stress as a function of contact radius. Microscale and nanoscale data compared with the model for l s = 1 μm and l s = 10 μm

Full size image

The results in Fig. 16.20 demonstrate a reasonable agreement of the experimental data with the model. The platinum-coated tip versus mica [7] has a relatively high pull-off force and the data fit with C 0 = 23.7 (nN)1/2 and W 0 = 170 nN. For the silicon tip versus amorphous carbon and natural diamond, the fit is given by C 0 = 8.0, 19.3 (nN)1/2 and small W 0. For the virgin Si(111), SiO2, and natural diamond sliding versus Si3N4 tip [8], the fit is given by C 0 = 0.40, 0.76, 0.86 (nN)1/2 for Si(111), SiO2, and diamond, respectively and small W 0. For two mica rolls [13], the fit is given by C 0 = 10 N1/2 and W 0 = 0.5 N [20].

AFM experiments provide data on nanoscale, whereas SFA experiments provide data on microscale. Next we study scale dependence on the shear strength based on these data. In the AFM measurements by Carpick et al. [7], the average shear strength during sliding for Pt–mica interface was reported as 0.86 GPa, whereas the pull-off contact radius was reported as 7 nm. In the SFA measurements by Homola et al. [13], the average shear strength during sliding for mica–mica interface was reported as 25 MPa, whereas the contact area during high loads was on the order of 10−8 m2, which corresponds to a contact radius on the order 100 μm. To normalize shear strength, we need shear modulus. The shear modulus for mica is G mica = 25.7 GPa [49] and for Pt is G Pt = 63.7 GPa [50]. For mica–Pt interface, the effective shear modulus is

$$G = 2G_{\rm mica}G_{\rm Pt}/(G_{\rm mica}+G_{\rm Pt}) = 36.6\,{\rm GPa}.$$
(16.65)

This yields the value of the shear stress normalized by the shear modulus τ a/G = 2.35×10−2 for Carpick et al. [7] AFM data and 9.73×10−4 for the SFA data. These values are presented in the Fig. 16.21 together with the values predicted by the model for assumed values of l s = 1 and 10 μm. It can be seen that the model (16.13) provides an explanation of adhesional shear strength increase with a scale decrease [20].

5.7.2 Transition to Predominantly Plastic Deformation Involving Multiple Asperity Contacts

Next, we analyze the effect of transition from predominantly elastic adhesion to predominantly plastic deformation involving multiple asperity contacts [23]. The data on nano- and microscale friction for various materials, are presented in Table 16.2, based on Ruan and Bhushan [5], Liu and Bhushan [11], and Bhushan et al. [12], for Si(100), graphite (HOPG), natural diamond, and diamond-like carbon (DLC). There are several factors responsible for the differences in the coefficients of friction at micro- and nanoscale. Among them are the contributions from ratchet mechanism, meniscus effect, wear and contamination particles, and transition from elasticity to plasticity. The ratchet mechanism and meniscus effect result in an increase of friction with decreasing scale and cannot explain the decrease of friction found in the experiments. The contribution of wear and contamination particles is more significant at macro/microscale because of larger number of trapped particles (Fig. 16.15). It can be argued, that for the nanoscale AFM experiments the contacts are predominantly elastic and adhesion is the main contribution to the friction, whereas for the microscale experiments the contacts are predominantly plastic and deformation is an important factor. Therefore, transition from elastic contacts in nanoscale contacts to plastic deformation in microscale contacts is an important effect [23].

Table 16.2 Micro- and nanoscale values of the coefficient of friction, typical physical properties of specimens, and calculated apparent contact radii and apparent contact pressures at loads used in micro- and nanoscale measurements. For calculation purposes it is assumed that contacts on micro- and nanoscale are single-asperity elastic contacts [23]
Full size table

According to (16.29), the friction force depends on the shear strength and a relevant real area of contact. For calculation of contact radii and contact pressures, the elastic modulus, Poisson’s ratio, and hardness for various samples, are required and presented in Table 16.2 [50, 51, 52, 53, 54, 55]. In the nanoscale AFM experiments a sharp tip was slid against a flat sample. The apparent contact size and mean contact pressures are calculated based on the assumption, that the contacts are single asperity, elastic contacts (contact pressures are small compared to hardness). Based on the Hertz equation [47], for spherical asperity of radius R in contact with a flat surface, with an effective elastic modulus E *, under normal load W, the contact radius a and mean apparent contact pressure p a are given by

$$a = \left(\frac{3WR}{4E^{\ast}}\right)^{\!\!\!1/3},$$
(16.66)
$$p_{\rm a} = \frac{W}{\pi a^2}.$$
(16.67)

The surface energy effect [16] was neglected in (16.66) and (16.67), because the experimental value of the normal adhesion force was small, compared to W [5]. The calculated values of a and p a for the relevant normal load are presented in Table 16.2 [23].

In the microscale experiments, a ball was slid against a nominally flat surface. The contact in this case is multiple-asperity contact due to the roughness, and the contact pressure of the asperity contacts is higher than the apparent pressure. For calculation of a characteristic scale length for the multiple asperity contacts, which is equal to the apparent length of contact, (16.66) was also used. Apparent radius and mean apparent contact pressure for microscale contacts at relevant load ranges are also presented in Table 16.2 [23].

A quantitative estimate of the effect of the shear strength and the real area of contact on friction is presented in Table 16.3. The friction force at mean load (average of maximum and minimum loads) is shown, based on the experimental data presented in Table 16.2. For microscale data, the real area of contact was estimated based on the assumption that the contacts are plastic and based on (16.33) for mean loads given in Table 16.2. For nanoscale data, the apparent area of contact was on the order of several square nanometers, and it was assumed that the real area of contact is comparable with the mean apparent area of contact, which can be calculated for the mean apparent contact radius, given in Table 16.2. The estimate provides with the upper limit of the real area of contact. The lower limit of the shear strength is calculated as friction force, divided by the upper limit of the real area of contact, and presented in Table 16.3 [23]. Based on the data in Table 16.3, for Si(100), natural diamond and DLC film, the microscale value of shear strength is about two orders of magnitude higher, than the nanoscale value, which indicates, that transition from adhesion to deformation mechanism of friction and the third-body effect are responsible for an increase of friction at microscale. For graphite, this effect is less pronounced due to molecularly smooth structure of the graphite surface [23].

Table 16.3 Mean friction force, the real area of contact and lower limit of shear strength [23]
Full size table

Based on data available in the literature [6], load dependence of friction at nano-/microscale as a function of normal load is presented in Fig. 16.22. Coefficient of friction was measured for Si3N4 tip versus Si, SiO2, and natural diamond using an AFM. They reported that for low loads the coefficient of friction is independent of load and increases with increasing load after a certain load. It is noted that the critical value of loads for Si and SiO2 corresponds to stresses equal to their hardness values, which suggests that transition to plasticity plays a role in this effect. The friction values at higher loads for Si and SiO2 approach to that of macroscale values. This result is consistent with predictions of the model for plastic contact (Fig. 16.11), which states that, with increasing normal load, the long wavelength limit for the contact parameters decreases. This decrease results in violation of the condition L < L lc, and the contact parameters and the coefficient of friction reach the macroscale values, as was discussed earlier. It must be noted, that the values of m = 0.5 and n = 0.2 are taken based on available data for the glass-ceramic disk (Fig. 16.9), these parameters depend on material and on surface preparation and may be different for Si, SiO2, and natural diamond, however, no experimental data on scale dependence of roughness parameters for the materials of interest are available.

Fig. 16.22
figure 22

Coefficient of friction as a function of normal load [6]

Full size image

6 Scale Effect in Wear

The amount of wear during adhesive or abrasive wear involving plastic deformation is proportional to the load and sliding distance x, divided by hardness [16]

$$v = k_0\frac{W_x}{H},$$
(16.68)

where v is volume of worn material and k 0 is a nondimensional wear coefficient. Using (16.10) and (16.19), the relationships can be obtained for scale dependence of the coefficient of wear in the case of the fractal surface and power-law dependence of roughness parameters

$$v = k\frac{W_x}{H_0}$$
(16.69)

and

$$k = \frac{k_0}{\sqrt{1+(l_{\rm d}/\bar{a})}} = \frac{k_0}{\sqrt{1+(L_{\rm d}/L)^m}},\quad L \,< \,L_{\rm lwl},$$
(16.70)

where k is scale-dependent wear coefficient, and k 0 corresponds to the macroscale limit of the value of k [22].

Scale dependence of the wear coefficient is presented in Fig. 16.23 for m = 0.5 and n = 0.2, based on (16.70). It is observed, that the wear coefficient decreases with decreasing scale; this is due to the fact that the hardness increases with decreasing mean contact size.

Fig. 16.23
figure 23

The wear coefficient as a function of scale, presented for m = 0.5, n = 0.2

Full size image

7 Scale Effect in Interface Temperature

Frictional sliding is a dissipative process, and frictional energy is dissipated as heat over asperity contacts. Therefore, a high amount of heat per unit area is generated during sliding. A contact is formed and destroyed as one asperity passes the other at a given velocity. When an asperity comes into contact with another asperity, the real area of contact starts to grow, when the asperities are directly above each other, the area is at maximum, as they move away from each other, the area starts to get smaller. There are number of contacts at a given time during sliding. For each individual asperity contact, a flash temperature rise can be calculated. High temperature rise affects mechanical and physical properties of contacting bodies.

For thermal analysis, a dimensionless Peclet number is used

$$L_{\rm p} = \frac{6Va_{\max}}{16\kappa_{\rm t}},$$
(16.71)

where V is sliding velocity, a max is maximum radius of contact for a given contact spot, and κ t is thermal diffusivity. This parameter indicates whether the sliding is high-speed or low-speed. If L p > 10, the contact falls into the category of high speed; if L p < 0.5, it falls into the category of low speed; if 0.5 ≤ L p ≤ 10, a transition regime should be considered [16]. For high L p, there is not enough time for the heat to flow to the sides during the lifetime of the contact and the heat flows only in the direction, perpendicular to the sliding surface. Based on the numerical calculations for flash temperature rise of as asperity contact for adhesional contact [16], the following relation holds for the maximum temperature rise T, normalized by the rate at which heat is generated q, divided by the volumetric specific heat ρc p

$$\begin{array}{ll}&\frac{T\rho c_{\rm p}V}{q} = 0.95\left(\frac{2Va_{\max}}{\kappa_{\rm t}}\right)^{\!\!\!1/2}\!\!\!\!\!,\quad\ \ \ \ L_{\rm p}, 10\\&\qquad\ \ \,= 0.33\left(\frac{2Va_{\max}}{\kappa_{\rm t}}\right),\qquad L_{\rm p}, 0.5.\end{array}$$
(16.72)

The rate at which heat generated per time per unit area depends on the coefficient of friction μ, sliding velocity V, apparent normal pressure p a, and ratio of the apparent to real areas of contact (A a/A r)

$$q = \mu p_{\rm a}V\frac{A_{\rm a}}{A_{\rm r}}.$$
(16.73)

Based on (16.72) and (16.73),

$$\begin{array}{ll}&\frac{T\rho c_{\rm p}}{p_{\rm a}} = 0.95\frac{A_{\rm c}}{A_{\rm a}}\mu\left(\frac{2Va_{\max}}{\kappa_{\rm t}}\right)^{\!\!\!1/2}\!\!\!\!\!\!\!,\ \ \ \ \ \ \quad L_{\rm p}, 10\\&\qquad\; = 0.33\frac{A_{\rm r}}{A_{\rm a}}\mu\left(\frac{2Va_{\max}}{\kappa_{\rm t}}\right),\qquad\; L_{\rm p}, 0.5.\end{array}$$
(16.74)

For a multiple asperity contact, mean temperature in terms of average of maximum contact size can be written as

$$\begin{array}{ll}&\frac{{\bar T}\rho c_{\rm p}}{p_{\rm a}} = 0.95\frac{A_{\rm r}}{A_{\rm a}}\mu\left(\frac{2V\bar{a}_{\max}}{\kappa_{\rm t}}\right)^{\!\!\!1/2},\quad \quad \, L_{\rm p}, 10\\&\qquad\; = 0.33\frac{A_{\rm r}}{A_{\rm a}}\mu\left(\frac{2V\bar{a}_{\max}}{\kappa_{\rm t}}\right),\qquad L_{\rm p}, 0.5.\end{array}$$
(16.75)

In (16.75) \(\bar{a}_{\max}\), μ and A a/A r are scale dependent parameters. During adhesional contact, the maximum radius \(\bar{a}_{\max}\) is proportional to the contact radius \(\bar{a}\), and the scale dependence for \(\bar{a}_{\max}\) is given by (16.19), for μ by (16.38–16.39), and for A re and A rp by (16.17) and (16.21). The scale dependence of q, involving μ and A r, and \(\bar{a}_{\max}\) in (16.72) can be considered separately and then combined. For the sake of simplicity, we only consider the scale dependence of \(\bar{a}_{\max}\). For the empirical rule dependence of surface roughness parameters and the fractal model, in the case of high and low velocity, (16.75) yields [22]

$${\frac{\bar {T}\rho c_{\rm p}V}{q} =0.95\left(\frac{ 2VC_{\rm A}L^{m}}{\kappa}\right)^{\!\!\!1/2},\qquad L\,< \,L_{\rm lwl},\ L_{\rm p}\,>\,10 \\ =0.33\left(\frac{ 2VC_{\rm A}L^{m}}{\kappa}\right),\qquad L\,< \,L_{\rm lwl},\ L_{\rm p}\,<\,0.5.}$$
(16.76)

Scale dependence for the ratio of the flash temperature rise to the amount of heat generated per unit time per unit area, for a given sliding velocity, as a function of scale, is presented in Fig. 16.24, based on (16.76), for the high-speed and low-speed cases. For the empirical rule dependence of roughness parameters, the results are shown for m = 0.5, n = 0.2.

Fig. 16.24
figure 24

Ratio of the flash temperature rise to the amount of heat generated per unit time per unit area, for a given sliding velocity, as a function of scale. Presented for m = 0.5, n = 0.2

Full size image

8 Closure

A model, which explains scale effects in mechanical properties (yield strength, hardness, and shear strength at the interface) and tribology (surface roughness, contact parameters, friction, wear, and interface temperature), has been presented in this chapter.

Both mechanical properties and roughness parameters are scale-dependent. According to the strain gradient plasticity, the scale dependence of the so-called geometrically necessary dislocations causes enhanced yield strength and hardness with decreasing scale. The shear strength at the interface is scale dependent due to the effect of dislocation-assisted sliding. An empirical rule for scale dependence of the roughness parameters has been proposed, namely, it was assumed, that the standard deviation of surface height and autocorrelation length depend on scale according to a power law when scale is less than the long wavelength limit value.

Both single asperity and multiple asperity contacts were considered. For multiple asperity contacts, based on the empirical power-rule for scale dependence of roughness, contact parameters were calculated. The effect of load on the contact parameters was also studied. The effect of increasing load is similar to that of increasing scale because it results in increased relevance of longer wavelength details of roughness of surfaces in contact.

During sliding, adhesion and two- and three-body deformation, as well as ratchet mechanism, contribute to the friction force. These components of the friction force depend on the relevant real areas of contact (dependent on roughness, mechanical properties, and load), average asperity slope, number of trapped particles, and relevant shear strength during sliding. The relevant scaling length is the nominal contact length – contact diameter (2a) for a single-asperity contact, only considered in adhesion, and scan length (L) for multiple-asperity contacts, considered in adhesion and deformation.

For the adhesional component of the coefficient of friction, the shear yield strength and hardness increase with decreasing scale. In the case of elastic contact, the real area of contact is scale independent for single-asperity contact, and may increase or decrease depending on roughness parameters, for multiple-asperity contact. In the case of plastic contact, enhanced hardness results in a decrease in the real area of contact. The adhesional shear strength at the interface may remain constant or increase with decreasing scale, due to dislocation-assisted sliding (or microslip). The model predicts that the adhesional component of the coefficient of friction may increase or decrease with scale, depending on the material parameters and roughness. The coefficient of friction during two-body deformation and the ratchet component depend on the average slope of the rough surface. The average slope increases with scale due to scale dependence of the roughness parameters. As a result, the two-body deformation component of the coefficient of friction increases with decreasing scale. The three-body component of the coefficient of friction depends on the concentrations of particles, trapped at the interface, which decreases with decreasing scale.

The transition index, which is responsible for transition from predominantly elastic adhesional friction to plastic deformation was proposed and was found to change with scale, due to scale dependence of roughness parameters. For the transition index close to zero, the contact is predominantly elastic and the dominant contribution to friction is adhesion involving elastic deformation. The increase of the transition index leads to an increase in plastic deformation with increasing contribution of the deformation component of friction, which results in larger value of the total coefficient of friction.

In presence of the meniscus force, the measured value of the coefficient of friction is greater than the value of the coefficient of dry friction. The difference is especially important for small loads, when the normal load is comparable with the meniscus force. The meniscus force depends on peak radii and may either increase or decrease with scale, depending on the surface parameters.

The wear coefficient and the ratio of the maximum flash temperature rise to the amount of heat generated per unit time per unit area, for a given sliding velocity, as a function of scale, decrease with decreasing scale due to decrease in the mean contact size.

The proposed model is used to explain the trends in the experimental data for various materials at nanoscale and microscale, which indicate that nanoscale values of coefficient of friction are lower than the microscale values (Tables 16.2 and 16.3). The two factors responsible for this trend are the increase of the three-body deformation and transition from elastic adhesive contact to plastic deformation. Experimental data show that the coefficient of friction increases with increasing load after a certain load and reaches the macroscale value. This is due to the onset of plastic deformation with increasing load and the effect of load on contact parameters, which affect the coefficient of friction.

9 Statistics of Particle Size Distribution

9.1 Statistical Models of Particle Size Distribution

Particle size analysis is an important field for different areas of engineering, environmental, and biomedical studies. In general, size distribution of particles depends on how the particles were formed and sorted. Several statistical distributions, which govern distribution of random variables including particle size, have been suggested (Fig. 16.25), [56, 57, 58, 59, 60]. Statistical distributions commonly used are either the probability density (or frequency) function (PDF) p(z) or cumulative distribution function (CDF) P(h). P(h) associated with random variable z(x), which can take any value between −∞ and +∞ or z min  and z max , is defined as the probability of the event z(x) ≤ z′ and is written as [61]

$$P(z) = {\rm Prob}(z\leq z^{\prime})$$
(16.77)

with P(−∞) =  0 and P(∞) =  1.

Fig. 16.25
figure 25

Common statistical distributions of particle size. (a) Probability density distributions. (b) Cumulative distributions

Full size image

The PDF is the slope of the CDF given by its derivative

$$p(z) = \frac{{\rm d}P(z)}{{\rm d}z}$$
(16.78)

or

$$P(z\leq z^{\prime}) = P(z^{\prime}) = \int\limits_{-\infty}^{z^{\prime}}(z){\rm d}z.$$
(16.79)

Furthermore, the total area under the probability density function must be unity; that is, it is certain that the value of z at any x must fall somewhere between plus and minus infinity or z min  and z max . The definition of p(z) is phrased as that the random variable z(x) is distributed as p(z).

The probability density (or frequency) function, p(d), in the exponential form is the simplest distribution mathematically

$$p(d) = \frac{1}{\sigma_{\rm e}}\exp\left(-\frac{d-d_{\rm e}}{\sigma_{\rm e}}\right),\quad d\geq d_0,$$
(16.80)

where d is particle diameter, σ e is standard deviation, and d e is minimum value (for this distribution). For convenience, the density function can be normalized by σ e in terms of a normalized variable d * equal to (d − d e)/σ e

$$p(d^{\ast}) = \exp(-d^{\ast}),\quad d^{\ast}\geq 0,$$
(16.81)

which has zero minimum and unity standard deviation. The cumulative distribution function P(d′) is given as

$$P_(d^{\prime}) = P(d^{\ast}\leq d^{\prime}) = 1-\exp(-d^{\prime}).$$
(16.82)

The Gaussian or normal distribution is used to represent data for a wide collection of random physical phenomena in practice such as surface roughness. The probability density and cumulative distribution functions are given as

$$\begin{array}{ll}&p(d) = \frac{1}{\sqrt{2\pi}\sigma_{\rm n}}\exp\left(-\frac{(d-d_{\rm n})^2}{2\sigma_{\rm n}^2}\right), \quad-\infty \,< \,d \,< \,\infty,-\infty\, < \,d_{\rm n} \,<\, \infty,\sigma_{\rm e} \,>\, 0,\end{array}$$
(16.83)

where d n is the mean value. The integral of p(d) in the interval −∞< d <∞ is equal to 1. In terms of the normalized variables, (16.82) reduces to

$$p(d^{\ast}) = \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{d^{\ast2}}{2}\right)$$
(16.84)

and

$$\begin{array}{ll}&p(d^{\prime}) = P(d^{\ast}\leq d^{\prime})\\&\qquad\; = \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{d^{\prime}}\exp[-(d^{\ast})^2/2{\rm d \it d^{\ast} = {\rm erf}(d^{\prime})},\end{array}$$
(16.85)

where erf(d′) is called the error function and its values are listed in most statistical handbooks. The pdf is bell-shaped and the CDF is S-shaped.

For particle size distribution, of interest here, the diameter cannot be less than zero. For this condition, (16.83) must be modified by using a constant on the right side

$$p(d) = \frac{C_0}{\sqrt{2\pi}\sigma_{\rm e}}\exp\left(-\frac{(d-d_{\rm n})^2}{2\sigma_{\rm e}^2}\right),\quad0\leq d, \infty,$$
(16.86)

where

$$C_0 = \left[\frac{1}{\sqrt{2\pi}}\int\limits_{-d_0/\sigma}^{\infty}\exp\left(-\frac{t^2}{2}\right)\,{\rm d}t\right]^{-1}.$$

The constant is calculated by integrating p(d) in the interval 0 ≤ d ≤∞ and equating to one

$$\int\limits_{0}^{\infty}p(d){\rm d}d = 1.$$
(16.87)

The log-normal distribution is commonly used to describe particle size distribution. A variable d is log-normally distributed if ln d is normally distributed. Log-normal probability density function for variable d, for which ln (d) has a Gaussian distribution with a mean ln (d)ln) and standard deviation σ ln, is given as

$$\begin{array}{ll}&p(d) = \frac{1}{\sqrt{2\pi}\sigma_{\ln}}\left(\frac{1}{d}\right)\exp\left\{-\frac{[\ln(d/d_{\ln})]^2}{2\sigma_{\ln}^2}\right\}, \quad0 \,< \,d \,<\, \infty.\end{array}$$
(16.88)

The mean of the log-normal distribution is exp (ln d ln+ σ ln 2/2), the standard deviation is exp (2 ln d ln + σ ln 2)× [exp (σ ln 2) − 1], the skewness is [exp (σ ln)2 + 2] [exp (σ ln 2)− 1]1/2, and kurtosis is exp [4(σ ln)2] + 2 exp [3(σ ln)2] + 3 exp [2(σ ln)2] − 3 [58]. The case where d ln =  0 is called the standard log-normal distribution. The density function can be normalized by σ ln in terns of a normalized variable d * =  (ln d − d ln)/σ ln

$$p(d^{\ast}) = \frac{1}{\sqrt{2\pi}}\left(\frac{1}{d^{\ast}}\right)\exp\left(-\frac{(d^{\ast})^2}{2}\right)$$
(16.89)

and

$$P(d^{\prime}) = P(d^{\ast}\leq d^{\prime}) = \frac{1}{2}\left[1+{\rm erf}\left(\frac{d^{\prime}}{\sqrt{2}}\right)\right].$$
(16.90)

The log-normal distribution of particle size occurs when the dispersion is attained by comminution (milling, grinding, crushing). The size distribution of pulverized silica, granite, calcite, limestone, quartz, soda, ash, alumina, clay, as well as of wear particles is often governed by the log-normal distribution [62]. A size distribution is usually presented either as probability density or frequency p(d), or as cumulative percent (percent of particles greater than given size) P(d), or as cumulative mass versus particle size. All these presentations are interrelated [62].

9.2 Typical Particle Size Distribution Data

Typical experimental data for size distributions of atmospheric (dust), sand, and abrasive diamond particles are presented in Fig. 16.26a. It can be seen, that the atmospheric particles [63] follow the normal distribution function. The dune sand is low in heavy mineral content, so the curve is concaved downward. Micaceous dune sand is sorted by gravity slide on a sharp mountain slope and appears to follow log-normal distribution, as many distributions of sediments, which are sorted by gravity. Whereas beach sand distribution curve is concaved upward, due to richness in smaller size component [62]. The abrasive diamond particles follow the log-normal distribution [64].

Fig. 16.26
figure 26

(a) Experimental data for atmospheric [63], sand [62], and abrasive diamond [64] particle size distribution. (b) Experimental data for wear particle size distribution (steel–steel [65], steel–diamond [66], steel–polyethylene [67]). (c) Change with time of wear debris production rate during lubricated sliding as a function of particle size [68]

Full size image

Size distribution of wear particles has been studied actively since 1970s, when the ferrography was introduced [69, 70]. The data for wear particles is presented in Fig. 16.26b. Xuan et al. [65] studied the size distribution of submicrometer particles during sliding of steel–steel using a Falex 3, pin-on-disk machine, using a laser particle counter for various sliding distances. They found a distribution, which is close to the log-normal function. Mizumoto and Kato [66] studied size distribution of particles generated during pin-on-disk test, for diamond, sapphire, silicon carbide, and tungsten carbide pins versus steel disk, using a laser particle counter. They found that the probability density function is exponential for particles greater than 1 μm diameter, however for smaller particles a linear law was assumed. Shanbhag et al. [67] studied wear particles for ultrahigh molecular weight polyethylene (UHMWPE) versus titanium in biomedical applications (total knee replacement) using a scanning electron microscope. They found that the distribution is close to that of the normal distribution. Numerous data for wear particles are presented by Anderson[71]. Hunt [68] discusses various techniques of debris measurement and analysis in lubricants. A typical change in wear debris generation rate, which occurs with time, is presented in Fig. 16.26c. Change in the size distribution of wear particles in lubricant indicates an onset of mechanical failure.