Keywords

4.1 Introduction

Signal transduction plays a crucial role in the complex dynamics of living cells to the extent that it is considered a fundamental information processing mechanism in living systems. The recent availability of data on signal transduction has the potential for the creation of artificial systems conducting computation and communication using its inherent mechanisms. It also promises to give inspiration on building computation and communication systems in our world, which are based on novel principles only used in biological organisms till date.

It is yet unknown what advantages can be gained from using biologically inspired mechanisms in the application to information processing systems, but given the high efficiency by which biological organisms function, it makes sense to study them, especially in the framework of an information processing paradigm. The boundary conditions of the processes in biological systems tend to be quite different from what we are normally used to in our daily lives. Noise, for example, is large compared to signal levels. Mechanisms to cope with it in traditional systems include error-correcting codes, and it is an interesting issue to investigate whether and to what extent such techniques are applicable in biological systems. To investigate issues like these, it is important to have a formal model describing biological signal transduction. The most commonly used model is the network, which has topological features such as hubs in a scale-free network [1]. This suggests the exploration of efficient ways to systematically understand the robustness of networks in terms of graphs, where the building block of the signal transduction networks that are treated as complex systems called network motif in [2] are defined. Based on the technology of networks, we can model the dynamics of signal transduction networks and find a quantitative description of its signaling mechanism that sustains the robustness of the corresponding cellular signaling processes, which have been widely reported in the signal transduction networks for chemotaxis, heat shock response, ultrasensitivity, and cell cycle control [3].

In this chapter, we formulate a model of signal transduction in terms of graph theory to increase our understanding of its information processing role in biological systems. A graph is a set of nodes named as vertexes with relations between them called edges. In the framework of a communication network, for example, the edges represent the communication channels that exist and through which communication takes place between the nodes. Applied to biological systems, we obtain a formulation of the structure of signaling pathways of signal transduction. We illustrate our concepts through a particular protein called MAPK (Mitogen-Activating Protein Kinase), which plays an important role in intracellular communications processes. We then add concepts related to error-correcting codes to study how robustness of the above processes can be improved, as well as a new concept of fixed points in biological systems, which serve to restore signals through nonlinear dynamics with feedback.

This chapter is focused on computational aspects of signal transduction in cells. In Sect. 4.2, based on the biochemistry features of signal transduction processes, the data structure of graph is presented to formulate the signaling pathway of signal transduction, in which MAPK is discussed as an instance of pathways for describing the dynamic processes of signal transduction networks. In Sect. 4.3, a fixed point phenomenon is studied as well as the robustness factor for developing molecular communication systems. In Sect. 4.4, the molecular codes for error correction are designed from the network level of signal transduction.

4.2 Cellular Signal Transduction Networks and their Formal Model

Signal transduction in cells is a biochemical process that is of fundamental importance for their functioning. In living cells, signal transduction is carried out by series of biochemical reactions that are regulated by genetic factors. The signals used in signal transduction are usually quantified by concentrations of the corresponding chemicals.

4.2.1 Some Preliminaries of the Biochemistry of Signal Transduction

Cellular signal transduction is defined as a phenomenon, process, or mechanism that realizes a series of biochemical reactions in cells in response to stimuli of chemical signals outside the cells; this function includes the so-called cell communication.

Cell communication is the term used for the communication processes in cells that take the form of chemical signals and that is realized by the biochemical reactions in cells through cellular signal transduction. Cell communication can be distinguished into intercellular and intracellular communications.

Inter-cell communication describes how cells interact with each other. An important mechanism in inter-cell communication is formed by signaling molecules, which are also known as first messengers. Intercell communication has four types [5,12]: (1) contact-dependent signaling, in which cells have direct membrane-to-membrane contact to exchange signals, (2) paracrine signaling, in which cells release signals into the extracellular space to act locally on neighboring cells, (3) synaptic signaling, in which neuronal cells transmit signals electrically along their axons and release neurotransmitters at synapses, and (4) endocrine signaling, in which hormonal signals are secreted into the blood stream to be distributed on a wide scale throughout an organism’s body.

Intra-cell communication concerns the communication within cells. When an incoming first messenger molecule reaches a cell, it cannot directly pass the cell membrane, but is bound by specific receptors that effectuate the activation of certain signaling molecule proteins within the cell. Referred to as secondary messengers, these signals are relayed by a chemical reaction process through a signaling cascade, which relays the signals to the nucleus of the cell. In this chapter, we will mainly discuss about intra-cell communication. Important signaling molecules in cells are proteins. We will be especially interested in proteins that can bind to a phosphate molecule. Such proteins are called phospho-proteins. When a phosphate is attached to a protein, it becomes phosphorylized through a phosphorylation process; when it becomes detached, it becomes dephosphorylized through a dephosphorylation process. To switch between the two states, special enzymes are required. The enzyme that realizes phosphorylation is called kinase, the enzyme that realizes dephosphorylation is called phosphatase.

The phosphorylation/dephosphorylation state of a protein will be used in the following to encode the binary state of a variable. This state can be detected by immunofluorescence analysis, which provides us with a possible tool to read out such a variable.

The signaling pathway in cells is a series of biochemical reactions, which have specific biological functions.

4.2.2 Graphic Representation for Signal Transduction

The reactions in a signaling pathway will be described by a directed graph with input and output. By the graphic representation, we can get the information form of the signal transduction network, from which we can investigate the structure, encoding, and networks of signal transduction in cells.

To study the structural relations concerning the transduction of signals, we define transduction in a spatial form as a graph. Let a molecule be represented by a vertex (node) in a graph and let a biochemical reaction be represented by an edge (link), then we obtain a graph.

$$ {{G}} = \langle {{V}},{{E}}\rangle, $$

where the vertex set is defined as the set V = {V 1, V 2,…,V n}, and the edge set is defined as E = E(V i , V j ) (V i , V j  ∈ V). Any parameters of a biochemical reaction represented by an edge are depicted as labels to that edge.

The direction of a biochemical reaction is represented in this formalism by a directed edge in the graph, which is graphically depicted as an arrow from one vertex to another vertex. In case a biochemical reaction is bidirectional, the corresponding edge is also bidirectional, and it will be depicted as merely a line between its vertices. Figure 4.1 shows a graph representing a pathway from a substrate vertex to a product vertex.

Fig. 4.1
figure 1

A pathway: a graph versus signals

Full size image

The actual phosphorylation process follows the so-called Michaelis–Menten equation [6], which appears in the graph as a label on the edge between the substrate-vertex and the product-vertex. The Michaelis–Menten equation is described as follows. Let the reactant denote the input to the pathway, then the product is calculated by the Michaelis–Menten equation as

$${\text{d/d}}t\left({\text{product(\it t)}}\right)=k_{3}*{\text{enzyme}}*{\text{substrate(\it t)}}/\left({{\text{substrate(\it t)}} + k_m} \right) $$

where product(t) is the product concentration at time t, substrate(t) is the substrate concentration, enzyme is the enzyme concentration, and k 1, k 2, and k 3 are the coefficients of the biochemical reaction, wherein k m = k 2/k 1(k 3 ≪ k 2).

The above formalism is used for describing an individual pathway (Cf. Fig. 4.2). If a pathway cannot be divided into any other pathways, then the pathway is called indivisible or atomic. Atomic pathways are the building blocks from which more complex pathway networks are constructed. Such complex pathways are called interacted pathways. The entire pathway network will be constructed by these building blocks. In case of phosphorylation and dephosphorylation states, for example, it is possible to switch between these states via the interacted pathways that are regulated by kinases and phosphatases.

Fig. 4.2
figure 2

The concept of pathway as a system

Full size image

The interaction of different states needs to be investigated considering their influence on biological functions of cells. MAPK cascade is one of the important pathways with such features.

4.2.5 Example of Pathway: The MAPK Cascade

A MAPK cascade is an important pathway that is at the base of many biological functions in cells, such as in a phosphorylation process. Involved in a MAPK cascade is a number of kinases with the following names:

MAPK::

Mitogen activating protein kinase,

MAPKK::

Mitogen activating protein kinase kinase,

MAPKKK::

Mitogen activating protein kinase kinase kinase,

MAPKKKK::

Mitogen activating protein kinase kinase kinase kinase,

The resulting pathway is called k-layered, with k being an integer denoting the number of stages in the cascade. The structure of MAPK cascade is illustrated in Fig. 4.3. From top to down in the order going from upstream to down stream, MAPKKKK phosphorylates MAPKKK, MAPKKK phosphorylates MAPKK, MAPKK phosphorylates MAPK, which effectuates a phosphorylated protein as output to the process.

Fig. 4.3
figure 3

The hierarchical structure of MAPK cascade

Full size image

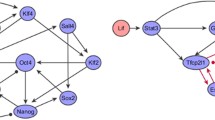
When building information models of signal transduction, it is important to structurally analyze the functionality of a signaling pathway network. As an example of a structural model, we show the MAPP cascade of budding yeast in Fig. 4.4, which involves the kinases Ste20, Ste11, Ste7, Kss1/Fus3, and Far1/Ste12. In this cascade, MAPKKKK is Ste20, MAPKKK is Ste11, MAPKK is Ste7, and there are two MAPK factors, Kss1 and Fus3. Furthermore, there are proteins at the bottom of the MAPK cascade, called Far1 and Ste12; these proteins, which form the output of the cascade, play an active role in the reproduction of cells. In technical terms, Far1 is a CDK (Cyclin-dependent Kinase) inhibitor, and Ste2 is a TF (Transcription Factor) Ste12. Other examples of signal pathways can be found in KEGG [7].

Fig. 4.4
figure 4

An example of a MAPK cascade

Full size image

Up to now, we have witnessed that the objects—nodes and links of pathway networks—can be represented by the vertexes and edges of graphs. Based on these, the dynamic features of networks can be investigated based on the computational formulation given above.

4.3 Dynamical Analysis of Signal Transduction Networks

4.3.1 Temporal Dynamics of Signal Transduction Networks

Based on the graphic structure, we formulated in previous sections, we will discuss the dynamics features of signal transduction networks to systematically understand their information processing mechanism. Basically, the dynamics of signal transduction can be investigated by two major aspects: spatial dynamics and temporal dynamics of signal transduction. In signal transduction, the spatial dynamics is mainly reflected in diffusion processes. Kholodenko’s review article [8] on spatial dynamics uses the diffusion equation with polar coordinates to formulate the concentration values of kinases in the MAPK cascade constrained by the distance of diffusion.

This chapter focuses mostly on the information processing aspect of signal transduction networks, which clearly have a temporal character, and so we limit our discussion to the temporal dynamics of signal transduction. Such dynamics is usually formulated by differential equations, among which the Michaelis–Menten equation mentioned in Sect. 4.2 is the most fundamental. The Michaelis–Menten equation describes the biochemical reaction among molecules used for signaling in cells:

A substrate X is the input to the pathway under the regulation of an enzyme E, and product Y is the output of the pathway. The enzyme plays the role of catalyzer, which triggers the biochemical reaction and transforms the initial substrate into the resulting product.

$$ {\text{S}} + {\text{E}}\mathop{\longrightarrow}\limits^{k_{1}}{\text{S}} \cdot {\text{E}}\mathop{\longrightarrow}\limits^{k_{3}}{\text{P}} + {\text{E}} $$
$$ {\text{S}} \cdot {\text{E}}\mathop{\longrightarrow}\limits^{k_{2}}{\text{S}} + {\text{E}} $$

The parameters k 1, k 2, and k 3 describe the conversion rates and

$$ k_{\text{m}} = \left( {k_{2} + k_{3} } \right)/k_{1} $$

which is called the Michaelis constant. In the following, we will denote the concentration of any chemical X as [X], describing the number of molecules per unit volume.

We can obtain a simple differential equation system for the kinetic dynamics of the product P, where E0 is the total concentration of the enzyme.

$$ {\text{d/dt}}\left[ {\text{P}} \right] = k_{3} \left[ {{\text{E}}_{0} } \right]*\left[ {\text{X}} \right]/\left( {k_{\text{m}} + \left[ {\text{X}} \right]} \right). $$

The above formulation, however, is only valid under quasi steady-state conditions, i.e., conditions in which the concentration of the substrate-bound enzyme changes at a much slower rate than those of the product and substrate. This allows the enzyme to be treated as constant, which is E0 in the formula.

A question arising naturally from here is how to use the above form to explain the MAPK cascade we already mentioned before. Therefore, we reformulate it as a set of coupled differential equations in which each stage in the cascade corresponds to one equation:

$$ {\text{d/dt}}\left[ {\text{MAPKKK}} \right] = k_{3} \left( {\text{MAPKKK}} \right)\left[ {{\text{MAPKKKK}}\left( 0 \right)} \right]*\left[ {\text{MAPKKK}} \right]/\left( {k_{\text{m}} \left( {\text{MAPKKK}} \right) + \left[ {\text{MAPKKK}} \right]} \right), $$
$$ {\text{d/dt}}\left[ {\text{MAPKK}} \right] = k_{3} \left( {\text{MAPKK}} \right)\left[ {{\text{MAPKKK}}\left( 0 \right)} \right]*\left[ {\text{MAPKK}} \right]/\left( {k_{\text{m}} \left( {\text{MAPKK}} \right) + \left[ {\text{MAPKK}} \right]} \right), $$
$$ {\text{d/dt}}\left[ {\text{MAPK}} \right] = k_{3} \left( {\text{MAPK}} \right)\left[ {{\text{MAPKK}}\left( 0 \right)} \right]*\left[ {\text{MAPK}} \right]/\left( {k_{\text{m}} \left( {\text{MAPK}} \right) + \left[ {\text{MAPK}} \right]} \right), $$
$${\text{d/dt}}\left[ {\text{output-of-MAPKcascade}} \right] = k_{3} \left( {\text{output-of-MAPKcascade}} \right)\left[ {{\text{MAPK}}\left( 0 \right)} \right]* \\ \left[ {\text{output-of-MAPKcascade}} \right]/\left( {k_{\text{m}} \left({\text{output-of-MAPKcascade}} \right) + \left[{\text{output-of-MAPKcascade}} \right]} \right), $$

With the appropriate parameters, usually obtained from empirical observations, the system MAPK cascade can be numerically calculated. Basically, the general behavior can be described as an amplification of the initial substrate concentration S(0), resulting in an enhanced signal with higher concentration of the resulting product P(final moment).

One of the well-known functions of the MAPK cascade in cellular signal transduction networks is to act as an amplifier for intracellular signaling processes. However, an unexpected phenomenon—a fixed point that occurs at a four-layered MAPK cascade where a feedback is embedded—is observed by simulation [9], which shows that in theory the second messengers’ signals can be kept at a constant value during their relay processes within cells.

4.3.2 Fixed Point for Pathways with Feedbacks

Nonlinear dynamics features, such as bifurcation [3], have been reported in signal transduction networks. In order to study the computational and communication capacity of signal transduction networks, it is necessary to make sure to analyze how the cellular signals are controlled so that the information flow can be quantitatively measured. This framework forms the basis of the architectural design and performance analysis of engineered ICT systems inspired by signal transduction networks in cells. In this section, we take the fixed-point phenomena as an instance to demonstrate the nonlinear phenomena of signal transduction networks, as reported in [9].

4.3.2.1 The Model for the Simulation

As shown in Figs. 4.5 and 4.6, the structure of a MAPK cascade is layered, with feedback being embedded into each layer.

Fig. 4.5
figure 5

Three-layered MAPK cascade with feedback

Full size image
Fig. 4.6
figure 6

Four-layered MAPK cascade with feedback

Full size image

The set of coupled differential equations, in case feedback is present, then becomes

$${\text{d/dt}}\left[ {\text{phosphor-protein in MAPKKK layer}} \right] = - k_{3} \left[ {\text{MAPKKK}} \right]\left[ {{\text{MAPKKKK}}\left( 0 \right)} \right]* \\ \left[ {\text{MAPKKK}} \right]/\left( {k_{\text{m}} \left( {\text{MAPKKK}} \right) + \left[ {\text{MAPKKK}} \right]} \right) - \int {\left[ {\text{MAPKK}} \right]{\text{dt}}} ,$$
$${\text{d/dt}}\left[ {\text{phosphor-protein in MAPKK layer}} \right] =-k_{3} \left( {\text{MAPKK}} \right)\left[ {{\text{MAPKKK}}\left( 0 \right)} \right]* \\ \left[ {\text{MAPKK}} \right]/\left( {k_{\text{m}} \left( {\text{MAPKK}} \right) + \left[ {\text{MAPKK}} \right]} \right)-\int {\left[ {\text{MAPK}} \right]{\text{dt}}},$$
$$ {\text{d/dt}}\left[ {\text{phosphor-protein in MAPK layer}} \right] =-k_{3} \left( {\text{MAPK}} \right)\left[ {{\text{MAPKK}}\left( 0 \right)} \right]* \\ \left[ {\text{MAPK}} \right]/\left( {k_{\text{m}} \left( {\text{MAPK}} \right) + \left[ {\text{MAPK}} \right]} \right)-\int {\left[ {\text{output-of-MAPK-cascade}} \right]{\text{dt}}}, $$
$$ {\text{d/dt}}\left[ {\text{MAPKKK}} \right] = k_{3} \left( {\text{MAPKKK}} \right)\left[ {{\text{MAPKKKK}}\left( 0 \right)} \right]*\left[ {\text{MAPKKK}} \right]/\left( {k_{\text{m}} \left( {\text{MAPKKK}} \right) + \left[ {\text{MAPKKK}} \right]} \right), $$
$$ {\text{d/dt}}\left[ {\text{MAPKK}} \right] = k_{3} \left( {\text{MAPKK}} \right)\left[ {{\text{MAPKKK}}\left( 0 \right)} \right]*\left[ {\text{MAPKK}} \right]/\left( {k_{\text{m}} \left( {\text{MAPKK}} \right) + \left[ {\text{MAPKK}} \right]} \right), $$
$$ {\text{d/dt}}\left[ {\text{MAPK}} \right] = k_{3} \left( {\text{MAPK}} \right)\left[ {{\text{MAPKK}}\left( 0 \right)} \right]*\left[ {\text{MAPK}} \right]/\left( {k_{\text{m}} \left( {\text{MAPK}} \right) + \left[ {\text{MAPK}} \right]} \right), $$
$$ \begin{gathered} {\text{d/dt}}\left[ {\text{output-of-MAPKcascade}} \right] = k_{3} \left( {\text{output-of-MAPKcascade}} \right)\left[ {{\text{MAPKK}}\left( 0 \right)} \right]* \hfill \\ \left[ {\text{output-of-MAPKcascade}} \right]/\left( {k_{\text{m}} \left( {\text{output-of-MAPKcascade}} \right) + \left[ {\text{output-of-MAPKcascade}} \right]} \right), \hfill \\ \end{gathered} $$

where the integral part is calculated from initial time 0 to the current time t.

4.3.2.2 Simulation

Because the essential process of intracellular communication exhibits nonlinear dynamics behaviors in a biochemistry framework in the model above, it is possible to figure out what kind of parameters of Michaelis–Menten kinetics behind the fixed-point phenomena is used by the molecular mechanism of signal transduction networks through the MAPK cascade.

The conditions are set as follows:

  • The initial concentration of the enzyme = 0.45.

  • In the MAPKKKK, MAPKKK, MAPKK, MAPK layer, the product acts as the kinase for the succeeding MAPKKK, MAPKK, MAPK layers and output of the entire MAPK cascade at its bottom.

  • In each layer of MAPK cascade k m = 0.1 and k 3 = 0.01.

  • The initial concentration of substrates (phospho-proteins) in all the pathway-like units is set as 0.45.

  • The step/sample number is 10.

  • The initial concentration of product is set as 0.001.

Now follows a simulation of a four-layered MAPK cascade.

Let y = f(x) denote the signaling process from MAPK denoted as x to protein of the entire MAPK cascade y; we observed that

$$ {\text{\it f}}\left( {0.0001030} \right) = 0.0001030. $$

where x = y = 0.0001030.

This is a fixed-point-like phenomenon. The value 0.0001030 determines the crucial point of phase transition between the monotonic decreasing mode and the fixed-point-like mode.

4.3.4 Robustness

At the system level of a pathway network, dynamics features of pathway networks are the key to understand the cellular signaling mechanism. One of the most important dynamics features of pathway networks is robustness. The robustness of a pathway network can be investigated through different means: for example, stability analysis is an efficient one in the case of the Mos-p MAPK cascade pathway, where Mos-p is a kinase/protein that is in the phosphorylation state, whereas Mos is the same protein in the dephosphorylation state.

The cell has high robustness against external disturbances. As Kitano [10] points out, cancer is an example of robustness in the cell. In contrast with the robustness of pathway networks in the cell, the communication network is very fragile: for example, the Achelles’ heel phenomenon in internet networks occurs when failures occur. This contrast motivates us to quantitatively describe the biological robustness [11] of pathway networks to investigate the possibility of applying the knowledge of the biological robustness in pathway networks to the design of information networks in the future.

In the previous sections, we discussed the graphic structure that is usual in computer science. It is obvious that the robustness of cellular signaling processes described in terms of nonlinear dynamics is tightly connected with the “dynamical” graphic structure of pathway networks. In general, the parameters of the differential equations that describe the biochemical reactions of pathway networks can be defined as labels that correspond to the graph, where the vertices and edges of the graph are defined for the pathway network in previous section. These topics belong to the field called Dynamical Networks, which refers to the integration of nonlinear dynamics and graph theory. In this section, we define nonlinear dynamics systems in a matrix formulation that corresponds to the graph of the pathway network.

Based on these schemes, we formulate the robustness mechanism of cellular signaling pathway networks.

4.3.4.1 Basic Concepts

The concept of robustness is defined as follows.

Definition of Robustness. Robustness refers to a mechanism that can guarantee and realize the state transition of a (usually dynamic) system from vulnerable and unstable states to sustainable (stable) states when the system suffers from disturbance that is outside the environment and that is unexpected in most cases [12].

Let us define a nonlinear system W for describing the cellular signaling mechanism in cells:

$$ W(X,S,U,Y,Q)$$

where X is the input to the system, Y the output of the system, S the state of the system, U the feedback, and Q parameter vector.

The system description is given as follows:

$${\text{d}}/{\text{d}}t(X)=AX+BS$$
$$Y=CS$$

where A, B, are C are matrices.

All the above-mentioned variables are vectors.

We focus on the definition of robustness in terms of the system state. Then, we define the robustness by the function G(·) satisfying the condition that

$$S=G(S,E)$$

when the system suffered disturbance E.

The robustness feature of pathway is expressed in several aspects of pathway network. The stability is one among them. The above-mentioned formulation makes it possible to use the states of the system for describing the robustness where the robustness mechanism is interpreted as the mechanism for providing the steady states. The Mos-p MAPK pathway [13] is an example explaining/analyzing the pathway stability for the robustness of the corresponding pathway network. In this pathway, the term “stable steady states” denoted as SS is used to describe the state transition of the pathway network within the certain domain [13]. The Mos-p MAPK pathway includes a MAPK cascade. As Huang et al. [14] reported, the nonlinear dynamics feature of different phosphorylation processes in a MAPK cascade varies, i.e., the phosphorylation concentration versus time curve is different for each layer of a MAPK cascade. The significance of this phenomenon is obvious if we reveal the fixed point of the MAPK cascade presented in the previous section.

4.3.4.2 Stability Analysis: From an Example of the Mos-p MAPK Pathway for Explanation of Stability

The Mos-p MAPK pathway that demonstrates the transition between the stable/unstable steady states in cells is reported in [13]. In order to make the formulation of the corresponding model, we need the Hill coefficient and the Hill equation.

The Hill equation is given as

$$ \delta = \left( {\left[ {{L}} \right]^{{n}} } \right)/\left( {{{K}}_{\text{d}} + \left[ {{L}} \right]^{{n}} } \right) = \left[ {{L}} \right]^{{n}} /\left( {{{K}}_{{\rm A}}^{{n}} + \left[ {{L}} \right]^{{n}} } \right), $$

where δ is the concentration of the phosphorylated protein, [L] the ligand concentration, K d the equilibrium dissociation constant, K A is the ligand concentration occupying half of the binding sites, and n is the Hill coefficient describing the cooperativity of binding.

The cooperativity means the degree of the biochemical reactions for binding the substrate and enzyme. Here, ligand means an enzyme protein that can bind with another molecule. In Mos-p MAPK pathway, Mos-p is the ligand.

The coefficient n mentioned above is normally denoted as n Hill; n Hill = 1 refers to the case of Michaelis–Menten kinetics, which corresponds to the case of completely independent binding, regardless of how many additional ligands are already bound, n Hill ≥ 1 shows the case of positive cooperativity and n Hill ≤1 shows the case of negative cooperativity.

The Hill coefficient describes the nonlinear degree of the product’s response to the ligand.

By this way, the SS state can be quantitatively described. When the SS state is achieved, the activation degree (concentration) of Mos-p can be formulated as a fixed point of the following form:

$$ {\text{Mos-p}} = {{f}}\left( {\text{Mos-p}} \right), $$

where f(·) refers to the Mos-p MAPK cascade pathway.

This shows the steady state of Mos-p, which is consistent with the phenomena reported by Ferrell et al. [13].

Based on the ultrasensitivity quantization, we have a closer look at the Mos-p MAPK pathway from two viewpoints.

A Brief Look at the System. We consider the input of the system as the proteins Mos-P and malE-Mos, and the output as the protein MAPK. Here, two signals concerning MAPK are involved—activated MAPK and phosphorylated MAPK (phos·MAPK for short).

Based on the results from the experiment reported in [13], we can use the Michaelis–Menten equation to obtain that the response of Mek is monotonic to Mos-P, to malE-Mos, or to Mos-P and malE-Mos. In addition, the response of activate·MAPK or phos·MAPK is monotonic to the systems’ inputs Mos-P or to malE-Mos or to Mos-P and malE-Mos, under the condition that there is no feedback in the pathway networks, which are branched at the routes from Mos-P and malE-Mos to Mek. The phosphorylation effect can be witnessed at Mek, MAPK, and Mos-P.

A graphic description for this pathway network is given in Fig. 4.7.

Fig. 4.7
figure 7

Cascade without feedback and with feedback

Full size image

Modeling the Temporal Dynamics of the System. Considering the robustness again, we realize that we need the feedback (Cf. Fig. 4.7) and related nonlinear cellular signaling mechanism to help us understand the robustness within this pathway network.

Let us use the Hill-coefficient-based formula to describe the temporal behavior of cellular signaling. Assuming the time series of malE-Mos as

$$ {\text{d/d}}t\left[ {{\text{moleE-}} {\text{Mos}}} \right] = {{f}}_1\left( {\left[ {{\text{molE-}}{\text{Mos}}} \right],\;{\text{coefficients}}} \right) $$

where f 1( ) takes the form of a monotonic function with a decreasing order,

we obtain

$$ \left[ {{\text{moleE-}} {\text{Mos}}} \right]\left( {{{n}} + 1} \right) - \left[ {{\text{molE-}}{\text{Mos}}} \right]\left( {{n}} \right) = {\text{coefficient}}\left[ {{\text{molE-}}{\text{Mos}}} \right]\left( {{t}} \right) $$

This is the time difference equation used for numerical calculation.

Let m denote the step, where m is an integer, and the [molE-Mos] is set as 0.

Then, we obtain

$$ \begin{aligned} \left[ {\text{active MAPK tot}} \right]\left( {{{m}} + 1} \right) & = \left( {\left[ {{\text{Mos-}}{\text{P}}} \right]\left( {{m}} \right) + 1000} \right)^{{H}} \\ & \quad /\left( {{\text{EC}}50^{\text{H}} + \left( {\left[ {{\text{Mos-}}{\text{P}}} \right]\left( {{m}} \right) + 1000} \right)^{\text{H}} } \right) \\ \end{aligned} $$

where H refers to the Hill coefficient n H = 5, EC50 = 20 (nM), [molE-Mos](t = 0) is set as 1,000.

Then

$$ \begin{aligned} \left[ {{\text{Mos-}}{\text{P}}} \right]\left( {{{m}} + 2} \right) & = 0.5*\left[ {\text{active MAPK}} \right]\left( {{{m}} + 1} \right) \\ & = 0.5*\left[ {{\text{MAPK}}\left( {\text{tot}} \right)} \right]\left( {\left[ {{\text{Mos-}}{\text{P}}} \right]\left( {{m}} \right) + 1000} \right)^{\text{H}} \\ & \quad /\left( {{\text{EC}}50^{\text{H}} + \left( {\left[ {{\text{Mos-}}{\text{P}}} \right]\left( {{m}} \right) + 1000} \right)^{\text{H}} } \right) \\ \end{aligned} $$

Now assume that [Mos-P](m + 3) = [Mos-P](m + 2) + [Mos-P](m). Let the moment n + 1 correspond to m + 3, n correspond to m when we set the time reference of Mos-P according to the initial time of going through the pathway and the final time. The moments of m + 1 and m + 2 refer to the internal states of the pathway network as a system. Consequently, we have

$$ \begin{aligned} \left[ {{\text{Mos-}}{\text{P}}} \right]\left( {{{n}} + 1} \right) & = 0.5*\left( {\left[ {{\text{Mos-}}{\text{P}}} \right]\left( {{n}} \right) + 1000} \right)^{\text{H}} \\ & \quad /\left( {{\text{EC}}50^{\text{H}} + \left( {\left[ {{\text{Mos-}}{\text{P}}} \right]\left( {{n}} \right) + 1000} \right)^{\text{H}} } \right) \\ & \quad + \left[ {{\text{Mos-}}{\text{P}}} \right]\left( {{n}} \right) \\ \end{aligned} $$

The Mos-P MAPK pathway derived computing process then becomes

$$ \begin{aligned} \left[ {{{x}}\left( {{{n}} + 1} \right)} \right] - \left[ {{{x}}\left( {{n}} \right)} \right] & = 0.5*\left( {\left[ {{{x}}\left( {{n}} \right)} \right] + 1000} \right)^{5} \\ & \quad /\left( {20^{5} + \, \left( {\left[ {x\left( n \right)} \right] \, + \, 1000} \right)^{5} } \right) - \left[ {x\left( n \right)} \right] \\ \end{aligned} $$

where x is an integer ≥ 0 and [x(0)] is set as 5.

$${\text{Let}}\;f(\left({x\left(t\right)}\right)=0.5*\left({{{x}}\left({{t}} \right) + 1000} \right)^{5}/\left( {20^{5} + \left({{{x}}\left( {{t}} \right) + 1000} \right)^{5} } \right) - {{x}}\left( {{t}} \right)$$
$$ {\text{d}}/{\text{d}}t\left( {{{x}}\left( {\text{\it t}} \right)} \right) = {{x}}\left( {{{t}} + 1} \right) - {{x}}\left( t \right) = {{f}}(\left( {{{x}}\left( {{t}} \right)} \right) $$

We define a function in general:

$$ {\text{d}}/{\text{d}}t\left( {{{x}}\left( {{t}} \right)} \right) = {{f}}(\left( {{{x}}\left( {{t}} \right)} \right) $$

when [molE-Mos] is treated as a constant.

It is obvious that the above system is still nonlinear even though the control input [molE-Mos] is a constant.

Considering the dynamics feature of control input [molE-Mos], we can have that

$$ \begin{aligned} {\text{d}}/{\text{d}}t\left( {{{x}}\left( {{t}} \right)} \right) & = 0.5*\left( {{{x}}\left( {{t}} \right) + {{u}}\left( {{t}} \right)} \right)^{5} \\ & \quad /\left( {20^{5} + \left( {{{x}}\left( {{t}} \right) + {{u}}\left( {{t}} \right)} \right)^{5} } \right) - {{x}}\left( {{t}} \right) \\ \end{aligned} $$

where x(t) = Mos-p that refers to the state of the system, and u(t) = [molE-Mos] that refers to the control input.

Since this is a coupled system, it is necessary to decouple the different signals to efficiently control the system.

The description of the pathway network as a system is normally established by a differential equation. Denote the system by the following equations:

$$ {\text{d}}\left[ {{{X}}\left( {{t}} \right)} \right]/{\text{d}}t = {{f}}\left( {{{t}},{{X}}\left( {{t}} \right),{{U}}\left( {{t}} \right)} \right) $$
$$ {{X}}\left( {{t}} \right) = {{g}}\left( {{{t}},{{X}}\left( {{t}} \right)} \right) $$

where t is time, U(t) is the input, X(t) is the state, and Y(t) is the output.

This is a general form that includes the case of nonlinear systems.

Based on the instance of Mos-p MAPK pathway we discussed before, the cellular pathway network is modeled as a controller-centered system where feedback is embedded. Different constraints can be used to formulate specific objects in applications, e.g., a matrix-based representation could be

$$ {\text{d}}X\left( {{t}} \right)/{\text{d}}t= {{A}}\left( {{t}} \right){{X}}\left( {{t}} \right) + {{B}}\left( {{t}} \right){{U}}\left( {{t}} \right) $$
$$ {{Y}}\left( {{t}} \right) = {{C}}\left( {{t}} \right){{X}}\left( {{t}} \right) $$

where A(t), B(t), and C(t) are matrices.

In this instance, the variable is one-dimensional, and a nonlinear relation exists between state transitions. Therefore, we have that

$$ {\text{d}}/{\text{d}}t\left( {{{x}}\left( {{t}} \right)} \right) = {{f}}\left( {{{x}}\left( {{t}} \right),{{u}}\left( {{t}} \right)} \right) $$

where x(t) = [Mos-p]—this is the state; u(t) = [molE-Mos]—this is the control input; this equation is established under the steady states of the Mos-p MAPK pathway.

The output for detecting the signals of phosphorylation is given as follows:

$$ {{y}}\left( {{t}} \right) = {\text{phos}} \cdot \left[ {\text{MAPK}} \right] = {{g}}(\left( {{{x}}\left( {{t}} \right),{{u}}\left( {{t}} \right)} \right) $$

where

$$ \begin{aligned} {{g}}(\left( {{{x}}\left( {{t}} \right),{{u}}\left( {{t}} \right)} \right) & = 0.5*\left( {{{x}}\left( {{t}} \right) + {{u}}\left( {{t}} \right)} \right)^{3} \\ & \quad /\left( {20^{5} + \left( {{{x}}\left( {{t}} \right) + {{u}}\left( {{t}} \right)} \right)^{3} } \right) \\ \end{aligned} $$

under the condition that the Mos-p MAPK pathway is with the steady state.

From the above discussion of pathway systems, we have presented a dynamics-based representation for formulating the robustness of a dynamic system, which is motivated by the biological robustness in cellular pathway networks, but which can be modified and extended to any abstract dynamic system where feedback is embedded.

4.4 Error-Correcting Codes for Cellular Signaling Pathways

How can we carry out reliable information processing by pathway networks with dynamics features? An important element underlying cellular signaling is the robustness of molecular pathways. Mechanisms such as those resembling error-correcting codes may play an essential role in this framework.

4.4.2 Molecular Coding from Molecular Communication

A reversible molecular switch is the basis of information representation in cellular informatics. Two kinds of reversible molecular switches exist in cells.

Fig. 4.9
figure 9

Molecular switch for binary codes (bits)

Full size image

The molecular switch of phosphorylation and dephosphorylation The phosphorylation state of a signaling protein is defined as 1, whereas the dephosphorylation state of a signaling protein is defined as 0. The phosphorylation process is regulated by kinase, while the dephosphorylation process is regulated by phosphatase.

The switch of GTP-bound and GDP-bound states As shown in Fig. 4.9, the GTP-bound state of GTPase set by the so-called GEF and GEF pathway is defined as 1 and the GDP-bound state of GTPase set by the so-called GAP and GAP pathway is defined as 0.

The MAPK cascade consists of several phosphorylation processes. Therefore. multiple binary codes can be generated, e.g., four bits generated by four-layered MAPK cascade (see Fig. 4.10).

Fig. 4.10
figure 10

Four bits generated from a MAPK cascade

Full size image

The above molecular switches allow us to formulate a mathematical model for information processing based on an abstraction of the data structure corresponding to the signaling pathways.

The above framework only involves switches, and it does not include the redundancy typically associated with error-correcting codes. If we intend to include such codes, then the resulting mechanisms should be compatible with the mechanisms encountered in cell communication.

4.4.3 LDPC Coding for Pathways

Error-correcting codes are mathematical constructs, and their design involves a different philosophy from the way in which biological mechanisms have evolved, which includes an element of randomness. Fortunately, there is an error-correcting code, of which the design—though mathematically well founded—involves a random element as well. Called Low Density Parity Code (LDPC), this code is, surprisingly, very efficient, in the sense that it allows transmission of information at rates very close to the theoretical maximum. These codes were developed in 1960 by Gallager, and they had been long forgotten due to the perception of them being impractical, only to be rediscovered by MacKay in 1996. Ironically, the randomness in LDPC codes is very attractive in the framework of biologic systems, and this is the reason why we describe them in more detail.

The LDPC code is defined by a partite graph BG = 〈V, E〉, where the vertex set V = V 1 ∪ V 2. V 1 is an ordered set of nodes, each of which is labeled by a binary number. The set V 1 thus denotes a binary code word. V 2 is a set of which each node is labeled by a binary number equaling the parity value of the sum of the labels of the nodes in V 1 that are connected to the node in V 2 by an edge in E.

As shown in Fig. 4.11, at first, let V 12 be 1 and V 21 be 0, so that the parity summation should be 0, and V 11 should accordingly be assigned the value 1. This is the encoding scheme. The decoding is carried out in a reverse way, as shown in Fig. 4.12.

Fig. 4.11
figure 11

A simple example of an LDPC encoding

Full size image
Fig. 4.12
figure 12

A simple example of an LDPC decoding

Full size image

Assume that V 11 is lost during information transmission, then to restore the value of V 11, we need to use the information of V 12 and V 21. Because V 12 is 1 and the parity summation is 0, we can infer that V 11 should be 1.

Figure 4.13 gives the encoding process of 5 bits in V 1 (labeled as L 1), where the known bits are put into the condition part of an “IF THEN” rule and the unknown bits are put into the conclusion part of this rule.

Fig. 4.13
figure 13

The rules for generating words

Full size image

The nodes in V 1 are called L 1-units and the ones in V 2 are called L 2-units, owing to the fact that they are described by two separated vertex sets in a bipartite graph.

Within the signal transduction model followed in this chapter, the two bipartite parts associated with the generation of an LDPC can be designed as shown in Fig. 4.14, where the information processing units corresponding to the phosphorylation/dephosphorylation pathway and GEF/GAP pathway are denoted as L 1-unit and L 2-unit, respectively.

Fig. 4.14
figure 14

An example of a pathway that is mapped to the model in Fig. 4.12

Full size image

As shown in the above figure, the bipartite graph to encode an LDPC code is mapped from a pathway whose input is V 12 when in the phosphorylation state and V 21 when in the GTP-bound state and whose output is 11 when in the phosphorylation state. This pathway corresponds to the graph in Figs. 4.11 and 4.12 for encoding and decoding an LDPC code.

The above model allows us to encode phosphorylation pathways and the dephosphorylation pathways in terms of an LDPC code, which is capable of approaching the Shannon limit. The derived encoding/decoding model is bidirectional, symmetrical and “implicitly binary” (i.e., its binary form can be formulated in terms of n bits of the L1-units of the model), which differs from the previous model given in [15] that is one-directional, asymmetrical (from phosphorylation/dephosphorylation to GTP-bound/GDP-bound states) and “explicitly binary” (i.e., the phosphorylation/dephosphorylation mechanism directly encodes the code z).

4.5 Summary

In this chapter, we have described pathways in biological organisms that behave de-facto like communication systems on cellular scales. The robustness of biological communication systems offers an important lesson for the design of man-made communication systems: key concepts in this context are parallelism, adaptability, and structural stability. We have also described LDPC codes, which have much in common—due to their randomness—with the unstructured character of biological systems. This may suggest that LDPC codes form an important avenue of research in the realization of communication systems that include the above key concepts. Cellular signal transduction networks form a rich source of inspiration in the design of next-generation communication systems, which will have greater robustness, greater capacity, and greater adaptability, but which will also be less visible to its users, forming a transparent ever-present environment, such as the overlay-network in [16].