Keywords

1 Introduction

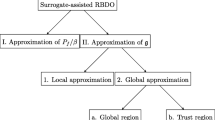
Over a period of many years an in-house toolbox named MetaBox for metamodel-based simulations and optimization with and without uncertainties has been develop during different research projects. Today, the toolbox contains several approaches for DoE, a bunch of metamodels packed together as an ensemble of metamodels, and methods for simulations and optmizations with uncertainties such as Monte Carlo, FORM, SORM and RBDO. This paper presents the current status of the toolbox concerning metamodel-based RBDO. An overview of available options in MetaBox is given in Fig. 1.

The project of MetaBox was initiated by simulating rotary draw bending using artificial neural networks (ANN) [1]. It was concluded that several hidden layers are needed in order to get satisfactory results. Shortly after, we started to develop a successive response surface methodology using ANN [2, 3]. This approach has proven to be very efficient for screening and generating proper DoEs. Methods for DoE of non-regular spaces were developed in [4, 5]. In particular, the S-optimal DoE presented in this paper has proven to be very useful. Work on metamodel-based simulations with uncertainties was initiated in [6]. Then, work on metamodel-based optimization with uncertainties was started, during several years [7,8,9,10] a framework for metamodel-based RBDO was developed. Meanwhile, several metamodels were also implemented in MetaBox such as Kriging, RBFN [11,12,13], polynomial chaos expansion (PCE), SVM [14] and SVR.

The outline of the paper is as follows: in Sect. 2 a short overview of implemented metamodels in MetaBox is given, in Sect. 3 the main ideas of FORM- and SORM-based RBDO as well as our implemented SQP-based RBDO algorithm are presented, in Sect. 4 a well-known benchmark is studied using different choices of DoEs and metamodels with and without uncertainties. Finally, some concluding remarks are given.

Fig. 1.
figure 1

Available options in MetaBox (www.oru.se).

Full size image

2 Metamodels

Let us assume that we have a set of sampling data \(\{\hat{\varvec{x}}^i,\hat{f}^i\}\) obtained from design of experiments. We would like to represent this set of data with a function, which we call a response surface, a surrogate model or a metamodel. One choice of such a function is the regression model given by

$$\begin{aligned} f=f({\varvec{x}})={\varvec{\xi }}({\varvec{x}})^T{\varvec{\beta }}, \end{aligned}$$
(1)

where \({\varvec{\xi }}={\varvec{\xi }}({\varvec{x}})\) is a vector of polynomials of \({\varvec{x}}\) and \({\varvec{\beta }}\) contains regression coefficients. By minimizing the sum of squared errors, i.e.

$$\begin{aligned} \min _{{\varvec{\beta }}} \,\sum _{i=1}^{N} \left( X_{ij} \beta _j -\hat{f}^i \right) ^2, \end{aligned}$$
(2)

where \(X_{ij}= \xi _j(\hat{\varvec{x}}^i)\) and N is the number of sampling points, then we obtain optimal regression coefficients from the normal equation according to

$$\begin{aligned} {\varvec{\beta }}^*=\left( {\varvec{X}}^T{\varvec{X}}\right) ^{-1}{\varvec{X}}^T\hat{\varvec{f}}. \end{aligned}$$
(3)

Examples of other useful metamodels are Kriging, radial basis functions, polynomial chaos expansion, support vector machines and support vector regression. The basic equations of these models as implemented in MetaBox are presented in the following.

2.1 Kriging

The Kriging model is given by

$$\begin{aligned} {f}({\varvec{x}}) = {\varvec{\xi }}({\varvec{x}})^T{\varvec{\beta }}^* + {\varvec{r}}({\varvec{x}})^T{\varvec{R}}^{-1}({\varvec{\theta }}^*)\left( \hat{\varvec{f}}-{\varvec{X}}{\varvec{\beta }}^*\right) , \end{aligned}$$
(4)

where the first term represents the global behavior by a linear or quadratic regression model and the second term ensures that the sample data is fitted exactly. \({\varvec{R}}={\varvec{R}}({\varvec{\theta }})=[R_{ij}]\), where

$$\begin{aligned} R_{ij}=R_{ij}({\varvec{\theta }},\hat{\varvec{x}}^i,\hat{\varvec{x}}^j)=\exp \left( -\sum _{k=1}^N \theta _k(\hat{x}^i_k-\hat{x}^i_k)^2 \right) . \end{aligned}$$
(5)

Furthermore, \({\varvec{\theta }}^*\) is obtained by maximizing the following likelihood function:

$$\begin{aligned} \frac{1}{\sigma ^N\sqrt{\det ({\varvec{R}})(2\pi )^N}}\exp \left( -\frac{({\varvec{X}}{\varvec{\beta }}-\hat{{\varvec{f}}})^T {\varvec{R}}^{-1}({\varvec{X}}{\varvec{\beta }}-\hat{{\varvec{f}}})}{2\sigma ^2} \right) \end{aligned}$$
(6)

and

$$\begin{aligned} {\varvec{\beta }}^* =\left( {\varvec{X}}^T{\varvec{R}}^{-1}({\varvec{\theta }}^*){\varvec{X}}\right) ^{-1} {\varvec{X}}^T {\varvec{R}}^{-1}({\varvec{\theta }}^*) \hat{\varvec{f}}. \end{aligned}$$
(7)

2.2 Radial Basis Function Networks

For a particular signal \(\hat{\varvec{x}}^k\) the outcome of the radial basis function network can be written as

$$\begin{aligned} f^k=f(\hat{\varvec{x}}^k) = \sum _{i=1}^{N_{\varPhi }} A_{ki} \alpha _i +\sum _{i=1}^{N_{\beta }} B_{ki}\beta _i, \end{aligned}$$
(8)

where \(N_{\varPhi }\) is the number of radial basis functions, \(N_{\beta }\) is the number of regression coefficients in the bias,

$$\begin{aligned} \begin{array}{ccc} A_{ki}=\varPhi _i(\hat{\varvec{x}}^k)&\text {and}&B_{ki}=\xi _i(\hat{\varvec{x}}^k). \end{array} \end{aligned}$$
(9)

Both linear and quadratic regression models are used as bias. Furthermore, \(\varPhi _i=\varPhi _i(\hat{\varvec{x}}^k)\) represents the radial basis function.

Thus, for a set of signals, the corresponding outgoing responses \({\varvec{f}}=\{f^i\}\) of the network can be formulated compactly as

$$\begin{aligned} {\varvec{f}}= {\varvec{A}}{\varvec{\alpha }} + {\varvec{B}}{\varvec{\beta }}, \end{aligned}$$
(10)

where \({\varvec{\alpha }} = \{\alpha _i\}\), \({\varvec{\beta }}=\{\beta _i\}\), \({\varvec{A}}=[A_{ij}]\) and \({\varvec{B}}=[B_{ij}]\). If we let \({\varvec{\beta }}\) be given a priori by the normal equation as

$$\begin{aligned} {\varvec{\beta }}=\left( {\varvec{B}}^T{\varvec{B}}\right) ^{-1}{\varvec{B}}^T\hat{\varvec{f}}, \end{aligned}$$
(11)

then

$$\begin{aligned} {\varvec{\alpha }}={\varvec{A}}^{-1}\left( \hat{\varvec{f}}-{\varvec{B}}\hat{\varvec{\beta }}\right) . \end{aligned}$$
(12)

Otherwise, \({\varvec{\alpha }}\) and \({\varvec{\beta }}\) are established by solving

$$\begin{aligned} \left[ \begin{array}{ccc} {\varvec{A}} &{} {\varvec{B}} \\ {\varvec{B}}^T &{} {\varvec{0}} \end{array}\right] \left\{ \begin{array}{c} {\varvec{\alpha }} \\ {\varvec{\beta }} \\ \end{array}\right\} = \left\{ \begin{array}{c} \hat{\varvec{f}} \\ {\varvec{0}} \end{array} \right\} . \end{aligned}$$
(13)

2.3 Polynomial Chaos Expansion

Polynomial chaos expansion by using the Hermite polynomials \(\varphi _n=\varphi _n(y)\) can be written as

$$\begin{aligned} f({\varvec{x}}) = \sum _{i=0}^{M}c_i \prod _{j=1}^{N_{\text{ VAR }}}\varphi _i(x_j), \end{aligned}$$
(14)

where \(M+1\) is the number of terms and constant coefficients \(c_i\), and \(N_{\text{ VAR }}\) is the number of variables \(x_i\). The Hermite polynomials are defined by

$$\begin{aligned} \varphi _n=\varphi _n(y)=(-1)^n\exp \left( \dfrac{x^2}{2}\right) \dfrac{\mathrm {d}^n}{\mathrm {d}x^n}\left( \exp \left( -\dfrac{x^2}{2}\right) \right) . \end{aligned}$$
(15)

For instance, one has

$$\begin{aligned} \varphi _0= 1, \\ \end{aligned}$$
(16a)
$$\begin{aligned} \varphi _1=y,\\ \end{aligned}$$
(16b)
$$\begin{aligned} \varphi _2=y^2-1,\\ \end{aligned}$$
(16c)
$$\begin{aligned} \varphi _3=y^3-3y, \\ \end{aligned}$$
(16d)
$$\begin{aligned} \varphi _4=y^4-6y2+3,\\ \end{aligned}$$
(16e)
$$\begin{aligned} \varphi _5=y^5-10y^3+15y,\\ \end{aligned}$$
(16f)
$$\begin{aligned} \varphi _6=y^6-15y^4+45y^2-15,\\ \end{aligned}$$
(16g)
$$\begin{aligned} \varphi _7=y^7-21y^5+105y^3-105y. \end{aligned}$$
(16h)

The unknown constants \(c_i\) are then established by using the normal equation. A nice feature of the polynomial chaos expansion is that the mean of \(f({\varvec{X}})\) in (14) for uncorrelated standard normal distributed variables \(X_i\) is simply given by

$$\begin{aligned} \mathrm {E}[f({\varvec{X}})]=c_0. \end{aligned}$$
(17)

2.4 Support Vector Machines

Let us classify the sampling data in the following manner:

$$\begin{aligned} y^i=\left\{ \begin{array}{ll} 1 &{} \hat{f}^i\ge \tilde{f}, \\ -1 &{} \text{ otherwise }, \end{array}\right. \end{aligned}$$
(18)

where \(\tilde{f}\) is a threshold value. The soft non-linear support vector machine separate sampling data of different classes by a hyper-surface on the following format:

$$\begin{aligned} \sum _{i=1}^{N} \lambda ^{*}_i y^ik({\varvec{x}}^i,{\varvec{x}}) + b^*=0, \end{aligned}$$
(19)

where \(k({\varvec{x}}^i,{\varvec{x}})\) is a kernel function, and \(\lambda ^{*}_i\) and \(b^*\) are obtained by solving

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle { \min _{{\varvec{\lambda }}}} \, \dfrac{1}{2}\sum _{i=1}^N\sum _{j=1}^N \lambda _i\lambda _jy^iy^jk({\varvec{x}}^i,{\varvec{x}}^j)-\sum _{i=1}^N\lambda _i\\ \text{ s.t. } \left\{ \begin{array}{l} \displaystyle {\sum _{i=1}^{N}}\lambda _iy^i=0, \\ 0 \le \lambda _i \le C, i=1,\ldots ,N. \end{array}\right. \end{array}\right. \end{aligned}$$
(20)

The least-square support vector machine is established by solving

$$\begin{aligned} \left[ \begin{array}{cc} 0 &{} -{\varvec{y}}^T \\ {\varvec{y}} &{} {\varvec{A}} + \gamma {\varvec{I}} \end{array} \right] \left\{ \begin{array}{c} b \\ {\varvec{\lambda }} \end{array} \right\} = \left\{ \begin{array}{c} 0 \\ {\varvec{1}} \end{array} \right\} , \end{aligned}$$
(21)

where \({\varvec{y}}=\{y^1;\ldots ;y^N\}\), \(\gamma =1/C\), \({\varvec{1}}=\{1;\ldots ;1\}\) and

$$\begin{aligned} {\varvec{A}}=[A_{ij}], A_{ij}=y^iy^j k({\varvec{x}}^i,{\varvec{x}}^j). \end{aligned}$$
(22)

2.5 Support Vector Regression

The soft non-linear support vector regression model reads

$$\begin{aligned} f({\varvec{x}}) = \sum _{i=1}^N \lambda ^ik({\varvec{x}}^i, {\varvec{x}})- \sum _{i=1}^N \hat{\lambda }^ik({\varvec{x}}^i, {\varvec{x}})+b^*, \end{aligned}$$
(23)

where \(\lambda ^i\), \(\hat{\lambda }^i\) and \(b^*\) are established by solving

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle { \min _{({\varvec{\lambda }},\hat{\varvec{\lambda }})} \, \dfrac{1}{2} \sum _{i=1}^N \sum _{j=1}^N (\lambda ^i-\hat{\lambda }^i)(\lambda ^j-\hat{\lambda }^j)k({\varvec{x}}^i, {\varvec{x}}^j) +\sum _{j=1}^N (\hat{\lambda }^i-\lambda ^i)\hat{f}^i + \delta \sum _{j=1}^N( \lambda ^i+\hat{\lambda }^i)}\\ \text{ s.t. } \left\{ \begin{array}{l} \displaystyle { \sum _{j=1}^N (\lambda ^i-\hat{\lambda }^i)=0}, \\ 0\le \lambda ^i,\hat{\lambda }^i\le C, i=1,\ldots ,N. \end{array}\right. \end{array}\right. \end{aligned}$$
(24)

Finally, the corresponding least square support vector regression model is established by solving

$$\begin{aligned} \left[ \begin{array}{ccc} 0 &{} -{\varvec{1}}^T &{} {\varvec{1}} \\ {\varvec{1}} &{} {\varvec{B}}+\gamma {\varvec{I}} &{} -{\varvec{B}} \\ -{\varvec{1}} &{} -{\varvec{B}} &{} {\varvec{B}} + \gamma {\varvec{I}} \end{array} \right] \left\{ \begin{array}{c} b \\ {\varvec{\lambda }} \\ \hat{\varvec{\lambda }} \end{array} \right\} = \left\{ \begin{array}{c} 0 \\ \hat{\varvec{f}}-\delta {\varvec{1}} \\ -\hat{\varvec{f}}-\delta {\varvec{1}} \end{array} \right\} , \end{aligned}$$
(25)

where \(\gamma =1/C\), \({\varvec{1}}=\{1;\ldots ;1\}\) and

$$\begin{aligned} {\varvec{B}}=[B_{ij}], B_{i,j}=\varphi ({\varvec{x}}^i)\varphi ({\varvec{x}}^j)=k({\varvec{x}}^i,{\varvec{x}}^j) \end{aligned}$$
(26)

is a matrix containing kernel values.

3 Reliability Based Design Optimization

By using the metamodels presented in the previous section it is straight-forward to set up any design optimization problem as

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle { \min _{{\varvec{x}}} f({\varvec{x}})} \\ \text{ s.t. } g({\varvec{x}}) \le 0. \end{array} \right. \end{aligned}$$
(27)

For instance the metamodel \(f=f({\varvec{x}})\) might represent the mass of a design and \(g=g({\varvec{x}})\) is a metamodel-based limit surface for the stresses obtained by finite element analysis.

A possible draw-back with the formulation in (27) is that it is not obvious how to include a margin of safety. For instance, what is the optimal safety factor to be included in g? An alternative formulation that includes a margin of safety is

$$\begin{aligned} \left\{ \begin{array}{l} \underset{\varvec{\mu }}{\min }\quad \mathrm {E}[f({\varvec{X}})] \\ \mathrm {s.t.} \quad \mathrm {Pr}[g({\varvec{X}}) \le 0] \ge P_s, \end{array} \right. \end{aligned}$$
(28)

where \({\varvec{X}}\) now is treated as a random variable, \(\mathrm {E}[\cdot ]\) designates the expected value of the function f, and \(\mathrm {Pr}[\cdot ]\) is the probability that the constraint \(g\le 0\) being true. \(P_s\) is the target of reliability that must be satisfied.

3.1 FORM

An established invariant approach for estimating the reliability is the first order reliability method (FORM) suggested by Hasofer and Lind. The basic idea is to transform the reliability constraint from the physical space to a space of uncorrelated standard Gaussian variables and then find the closest point to the limit surface from the origin. This point is known as the most probable point (MPP) of failure. The distance from the origin to the MPP defines the Hasofer-Lind reliability index \(\beta _{\text{ HL }}\), which in turn is used to approximate the probability of failure as

$$\begin{aligned} \mathrm {Pr}[g\le 0] \approx \varPhi (-\beta _{\text{ HL }}). \end{aligned}$$
(29)

Assuming that \({\varvec{X}}\) is normal distributed with means collected in \({\varvec{\mu }}\) and \({\varvec{\sigma }}\) containing standard deviations, the MPP is obtained by solving

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\underset{{\varvec{x}}}{\min }} \, \beta _{\text{ HL }}=\sqrt{\displaystyle {\sum _{i=1}^{N}} \left( \dfrac{x_i-\mu _i}{\sigma _i}\right) ^2} \\ \text{ s.t. } g({\varvec{x}})=0. \end{array}\right. \end{aligned}$$
(30)

3.2 SORM

The approximation in (29) is derived by performing a first order Taylor expansion at the MPP and then evaluating the probability. Second order reliability methods (SORM) is obtained by also including the second order terms in the Taylor expansion. Based on these higher order terms the FORM approximation of the reliability is corrected.

For instance, by letting \(\lambda _i\) denoting the principle curvatures of a second order Taylor expansion of g, we can correct (29) by using e.g. Tvedt’s formula, i.e.

(31)

3.3 SQP-based RBDO Approach

Recently, a FORM-based SQP approach for RBDO with SORM corrections was proposed in [10]. For non-Gaussian variables, we derive the following FORM-based QP-problem in the standard normal space:

$$\begin{aligned} \left\{ \begin{array}{l} \underset{\eta _i}{\min }\quad f({\varvec{\eta }})\\ \mathrm {s.t.} \quad \left\{ \begin{array}{l} \mu _{\tilde{g}}\le - \beta _t \sigma _{\tilde{g}}, \\ -\epsilon \le \eta _i \le \epsilon , \end{array} \right. \end{array} \right. \end{aligned}$$
(32)

where

(33)

Here, \(\beta _t=\varPhi ^{-1}(P_s)\) is the target reliability index which can be corrected by a SORM approach as presented above or any Monte Carlo approach. The optimal solution to (32), denoted \(\eta _i^*\), is mapped back from the standard normal space to the physical space using

$$ \mu _i^{k+1} \approx \mu _i^k+\dfrac{\varPhi (Y_i^k)}{\rho _i(\mu _i^k;{\varvec{\theta }}_i^k)}\eta _i^*. $$

Then, a new QP-problem is generated around \({\varvec{\mu }}^{k+1}\) and this procedure continues in sequence until convergence is obtained. The QP-problem in (32) is solved using quadprog.m in Matlab.

Fig. 2.
figure 2

Different design of experiments.

Full size image
Table 1. Deterministic solutions for different DoEs and metamodels.
Full size table

4 Numerical Examples

In order to demonstrate the metamodel-based RBDO approach presented above, we consider the following well-known benchmark:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle { \underset{\small \mu _i}{\min }\quad \left( \mu _{1}+\mu _{2}\right) ^2 }\\ \text{ s.t. } \left\{ \begin{array}{l} \mathrm {Pr}[g_1=20-X_{1}^2X_{2} \le 0]\ge \varPhi (3), \\ \mathrm {Pr}\left[ \begin{array}{l} g_2=1 -\displaystyle {\frac{(X_{1}+X_{2}-5)^2}{30} } \\ \displaystyle {-\frac{(X_{1}-X_{2}-12)^2}{120}} \le 0 \end{array} \right] \ge \varPhi (3), \\ \mathrm {Pr}[g_3=X_{1}^2+8X_{2} -75 \le 0] \ge \varPhi (3),\\ 1\le \mu _i\le 7, \end{array} \right. \\ \end{array}\right. \end{aligned}$$
(34)

where \(\mathrm {VAR}[X_i]=0.3^2\). A small modification of the original problem is done by taking the square of the objective function. This problem was recently considered in [10] by solving (32) sequentially. The example was in that work also generalized to 50 variables and 75 constraints for five different distributions simultaneously (normal, lognormal, Gumbel, gamma and Weibull). The analytical solution for two variables with normal distribution is obtained to be (3.4525, 3.2758) 45.2702 with our RBDO algorithm. The corresponding deterministic solution is (3.1139, 2.0626) 26.7965.

Now, we will consider (34) to be a “black-box”, which we treat by setting up design of experiments and metamodels. The quality of the metamodel is dependent on the choice of DoE. Figure 2 presents four useful strategies of DoEs. In Fig. 2a we adopt successive screening to set up the DoE, in Fig. 2b we use space-filling with a genetic algorithm by maximizing the distance to the closest point, and in the other two figures we apply Halton and Hammersley sampling. For these four sets of sampling data, we set up 12 different metamodels automatically and then find the deterministic solution for each metamodel-based problem of our “black-box”. The solutions are presented in Table 1. One concludes that the solutions depend on the choice of DoE and metamodel. For many combinations the corresponding “black-box” solution is very close to the analytical one.

Fig. 3.
figure 3

Left: successive screening using Halton sampling, right: adaptive sampling using MPP and SVM.

Full size image
Table 2. RBDO solutions for different DoEs and metamodels.
Full size table

The choices of DoE strategy and metamodel is even more pronounced when we perform metamodel-based RBDO. In Fig. 3, we set up the DoE for RBDO by first performing successive screening with Halton sampling, then this DoE is augmented by adding the sampling points (green dots) based on the optimal solutions (deterministic and RBDO solution) and the active most probable points as well as points (red dots) along the limits surface based on a global SVM [14]. The corresponding metamodel-based RBDO solutions are presented in Table 2 as well as the corresponding solutions for the successive factorial DoE presented in Table 1. One concludes that the choices of augmented successive Halton sampling and RBFN, PCE or SVR produce the best performance. For these choices the metamodel-based “black-box” solution is close to the analytical one.

5 Concluding Remarks

A framework for metamodel-based RBDO has been developed and implemented in MetaBox. Several options of DoEs, metamodels and optimization approaches are possible. In a near future, optimal ensemble of metamodels will also be available as an option.