A Novel Variable-Gain Rectilinear or Circular Formation Algorithm for Unicycle Type Vehicles

Abstract

In this paper, we propose a novel variable-gain formation algorithm to steer a group of unicycle type vehicles moving in straight lines or circular orbits with three types of phase configurations (synchronized, balanced and stabilization of the average linear momentum). The algorithm design is carried out from the viewpoint of optimization theory to guarantee that control gains are variable. Specifically, a step length search algorithm used in optimization methods is employed to update the control gain at each iteration. The implementation details of the rectilinear/circular formation algorithm are given to show that the three types of phase configurations can be reached by utilizing corresponding well-designed objective functions. Furthermore, global convergence properties of the formation algorithm are analyzed. Both the results of simulations and experiments show good performance of the proposed formation algorithm.

1 Introduction

A team of mobile robots moving in rectilinear and circular formation have been widely used in both military and civilian scenarios such as ground cleaning, battlefield surveillance and source seeking [1,2,3]. In recent years, those formation control problems have been investigated with various robot models, among which unicycle models are frequently used in describing Unmanned Aerial Vehicles (UAVs) and Wheeled Mobile Robots (WMRs) [4].

A brief review of formation control of unicycle type robots is provided as below. In [5], the authors assume that both the orientation and the speed of each unicycle can be controlled, which increases the complexity of controlling robots. In [6], oscillatory control is applied to control constant-speed unicycle robots. However, the speeds of all the robots are required to be identical. Ref. [7] focuses on the patterns of formation. Several final formation patterns are generated by a centralized Hungarian algorithm for optimizing the robots’ goal positions. The disadvantage of it is that all the robots can not keep moving with the final formation patterns. A more complex formation control problem is discussed in [8,9,10,11,12], where all the robots not only move in desired circular orbits, but also maintain a particular phase configuration. [8, 9] focus on achieving synchronized and balanced phase configuration for a group of robots with all-to-all and limited communication, respectively. In synchronized phase configuration, all the robots move in a common direction, while in balanced phase configuration, the sum of the phasors of all the robots is zero. In [10, 11], the authors propose suitable feedback control laws for achieving particular type of circular formation with synchronized or balanced phase configuration. It should be noted that all the methods proposed in refs. [6, 8,9,10,11] are based on the assumption that the speeds of all the robots are identical. Under this assumption, many practical formation patterns can not be achieved for a group of robots with identical angular frequencies such as concentric circular formation with different radii. This assumption is removed in [12] and another phase configuration is defined as the stabilization of the average linear momentum, which means that the average position of all the robots stabilize on a fixed point. However, the control gains designed in all of the above-mentioned control schemes are fixed, which decreases the usability of these methods since selecting appropriate control gains manually is very time-consuming.

From the above discussion, we know that both the identical speeds and fixed control gains have many limitations in practice. Motivated by these facts, it is more realistic to propose a variable-gain formation algorithm for multiple unicycle type mobile robots with nonidentical speeds. In this paper, we design a variable-gain Rectilinear/Circular Formation Algorithm (RCFA) based on Broyden-Fletcher-Goldfarb-Shanno (BFGS) method [13], in which all the robots are required to move in straight lines or circles with three types of phase configurations (synchronized, balanced and stabilization of the average linear momentum). Those formation patterns have several potential applications such as crops harvesting and spying work in adversarial areas. The main contributions of this paper are listed as follows:

• 1. Unlike these existing control methods, we solve the rectilinear and circular formation control problems from the viewpoint of optimization theory. In this case, three types of phase configurations can be reached by solving corresponding optimization problems and the rectilinear/circular motion of robots can be achieved by utilizing particular control laws. In particular, we introduce a step length search algorithm into RCFA to update the control gain at each iteration. Thus, the formation algorithm proposed in this paper has variable control gains.

• 2. The control input designed in this paper contains only the angular frequency and there is no requirements for the speeds of robots. Thus, RCFA acquires more flexibility than other methods. Furthermore, global convergence of RCFA can be ensured while subject to some mild assumptions.

The remainder of this paper is organized as follows. Section 2 describes the system model used in this paper. RCFA and global convergence of it are presented in Sect. 3. In Sect. 4, the algorithms are illustrated by simulations and experiments. Finally, Sect. 5 concludes the paper.

2 Preliminaries

2.1 System Model

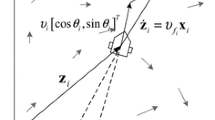
In this section, we represent the kinematic model of the unicycle type mobile robots in the form of discrete-time integration [14]. Consider a group of N unicycle robots, the kinematic model of the robot m is described by

$$\begin{aligned} x_{m,k+1}&=x_{m,k} + v_m \cos \theta _{m,k}\varDelta t \end{aligned}$$

(1a)

$$\begin{aligned} y_{m,k+1}&=y_{m,k} + v_m \sin \theta _{m,k}\varDelta t \end{aligned}$$

(1b)

$$\begin{aligned} \theta _{m,k+1}&=\theta _{m,k} + u_{m,k} \varDelta t \end{aligned}$$

(1c)

where k denotes the kth iteration and $\theta _m$ is the orientation of robot m and $x_m,y_m\in \mathcal {R}$ are the coordinates in the plane, for $m=1,\ldots ,N$. The robot m has a positive constant speed $v_m>0$ and $u_m \in \mathcal {R}$ is the control input (angular frequency). Note that $\varDelta t$ is the sampling interval and it will be neglected in the following analysis without loss of generality.

2.2 Problem Formulation

In this paper, we investigate the rectilinear and circular formation control problems from the viewpoint of optimization theory. In particular, a novel variable-gain formation algorithm are proposed to make a group of robots keep moving in rectilinear/circular formation with three types of phase configurations. There are two major issues to be tackled in the design of the formation algorithm. The first issue is that how to make the phase angles of robots reach a desired phase configuration, and the other is that how to make all the robots keep moving in straight lines or circles with one of the three types of phase configurations.

3 Main Results

3.1 Achieving Rectilinear/Circular Formation with Synchronized and Balanced Phase Configuration

For the synchronized and balanced phase configuration, there is a so-called order parameter defined as

$$\begin{aligned} p_\theta =\frac{1}{N}\sum _{m=1}^{N}e^{i\theta _m}. \end{aligned}$$

(2)

to measure the synchrony in the networks of N coupled oscillators [15]. When all phase angles of robots are synchronized, all the robots have a common phase angle. We have $|p_\theta |=1$. The balanced phase configuration means that the sum of the phasors of N coupled robots is zero, i.e., $|p_\theta |=0$.

We solve the first issue by defining the corresponding objective functions. In order to make a group of N robots reach the synchronized or balanced phase configuration, the objective function $f_{p_\theta }(\varvec{\theta }):\mathcal {R}^N \rightarrow \mathcal {R}$ is defined as

$$\begin{aligned} f_{p_\theta }(\varvec{\theta })=\gamma \frac{N}{2}|p_\theta |^2 \end{aligned}$$

(3)

where $\varvec{\theta }=[\theta _1,\ldots ,\theta _N]^T$ and $\gamma =\pm 1$. Each element of $\varvec{\theta }$ is the phase angle of each robot. From the definitions of the synchronized and balanced phase configuration we know that $f_{p_\theta }(\varvec{\theta })$ reaches its unique minimum when all phase angles of robots are synchronized (for $\gamma =-1$) or balanced (for $\gamma =1$). Thus, the phase control problem is successfully transformed into an unconstrained nonlinear optimization problem by defining the above objective function, i.e., the synchronized and balanced phase configuration can be achieved by minimizing $f_{p_\theta }$.

The second issue can be tackled by utilizing particular control laws in RCFA. RCFA is designed based on BFGS method to minimize the predefined objective function. BFGS is an iterative method for solving unconstrained nonlinear optimization problem. It begins with an initial state of the parameter $\varvec{\theta }$ and generates a sequence of improved estimates along descent direction. Finally, they will stop iterating when the minimum of the objective function is found. Thus, the main work of us is that designing appropriate descent directions, control laws and the rule of updating step length according to the principles of the general optimization methods.

The descent direction of the BFGS method at the kth iteration is defined as

$$\begin{aligned} \varvec{d}_k= - \varvec{B}_k^{-1} \varvec{g}_k \end{aligned}$$

(4)

where $\varvec{B}_k$ is an approximation of the true Hessian $\varvec{H}_k$ of the objective function and is a symmetric positive definite matrix and $\varvec{g}_k$ is the gradient of $f_{p_\theta }(\varvec{\theta }_k)$. ${\varvec{d}}_k$ is a descent direction ($\varvec{g}_k^T\varvec{d}_k<0$). $\varvec{B}_k$ will be updated at every iteration by the following

$$\begin{aligned} \varvec{B}_{k+1}=\varvec{B}_k - \frac{\varvec{B}_k\varvec{s}_k{\varvec{s}_k}^T\varvec{B}_k}{{\varvec{s}_k}^T\varvec{B}_k\varvec{s}_k} + \frac{\varvec{y}_k{\varvec{y}_k}^T}{{\varvec{y}_k}^T\varvec{s}_k} \end{aligned}$$

(5)

where $\varvec{s}_k = \varvec{\theta }_{k+1} - \varvec{\theta }_k$, $\varvec{y}_k = \varvec{g}_{k+1} - \varvec{g}_k$.

In order to achieve rectilinear formation with synchronized and balanced phase configuration, the control law is designed as

$$\begin{aligned} \varvec{u}_k= \alpha _k \varvec{d}_k \end{aligned}$$

(6)

where $\alpha _k$ is the step length (control gain). Thus, when the objective function $f_{p_\theta }$ reaches its unique minimum, the control inputs will be zero, i.e., all the robots will move in straight lines and meanwhile synchronized and balanced phase configuration can be achieved by setting $f_{p_\theta }$ with $\gamma =-1$ and $\gamma =1$, respectively.

For the circular formation pattern, we change the control law into

$$\begin{aligned} \varvec{u}_k= \alpha _k \widetilde{\varvec{d}}_k=\alpha _k \varvec{d}_k + \mathbbm {1}_{(-\infty ,0]}(\Vert \varvec{g}_k\Vert )\varvec{\omega }_d \end{aligned}$$

(7)

where $\mathbbm {1}_\varOmega (x)$ is the indicator function, i.e., $\mathbbm {1}_\varOmega (x)=1$ if $x \in \varOmega$, and $\mathbbm {1}_\varOmega (x)=0$, otherwise. $\varvec{\omega }_d = [\omega _1,\ldots ,\omega _N]^T$, the elements of $\varvec{\omega _d}$ denote desired angular frequencies of the robots and are constant values. It is not difficult to show that $\widetilde{\varvec{d}}_k$ is always a descent direction. When $f_{p_\theta }$ reaches its unique minimum, we have $\varvec{u}_k =\varvec{\omega }_0$, i.e., all of the robots will move in circles with synchronized (for $\gamma =-1$) and balanced (for $\gamma =1$) phase configuration.

3.2 Achieving Rectilinear/Circular Formation with Stabilization of the Average Linear Momentum

The average linear momentum is needed to measure the average position of the robots, which is defined as

$$\begin{aligned} \dot{Z}=\frac{1}{N}\sum _{m=1}^{N}v_me^{i\theta _m}. \end{aligned}$$

(8)

Apparently, the average position of all the robots stabilize on a fixed point if and only if $\dot{Z}=0$.

In order to make a group of N robots stabilize on a fixed average position, the objective function $f_{\dot{Z}}(\varvec{\theta }): \mathcal {R}^N \rightarrow \mathcal {R}$ is given by

$$\begin{aligned} f_{\dot{Z}}(\varvec{\theta }) = \frac{ N}{2}|\dot{Z}|^2. \end{aligned}$$

(9)

Thus, $f_{\dot{Z}}(\varvec{\theta })$ reaches its unique minimum when the stabilization of the average linear momentum is achieved.

Based on the same principles described in Sect. 3.1, the control laws (6) and (7) can also be utilized to achieve the rectilinear and circular formation with stabilization of the average linear momentum.

Remark 1:

If all the robots have a common unit speeds, all three types of phase configurations can be achieved by utilizing the order parameter, since $p_\theta$ can be interpreted as the derivative of the average position $Z=\frac{1}{N}\sum _{m=1}^{N}x_m+iy_m$. However, we assume that all the robots have nonidentical constant speeds so that $p_\theta$ and $\dot{Z}$ are treated separately in this paper. Note that synchronized phase configuration can also be reached by maximizing $f_{\dot{Z}}$.

3.3 RCFA: Rectilinear/Circular Formation Algorithm

Based on the discussion above, all the robots can move in straight lines or circular orbits with three types of phase configurations by minimizing the corresponding objective functions with particular control laws. The implementation details of the RCFA are presented in the Algorithm 1.

In order to make the control input acquires variable control gains. The control gain is searched by using the following Algorithm 2. Note that two types of descent directions $\varvec{d}_k$ and $\widetilde{\varvec{d}}_k$ are denoted by $\mathbf d _k$ in this algorithm.

To obtain global convergence of RCFA, the angle $\widetilde{\theta }_k$ between $\mathbf d _k$ and $-\varvec{g}_k$ is needed, which is defined by

$$\begin{aligned} \cos \widetilde{\theta }_k = \frac{-\varvec{g}_k^T \mathbf d _k}{\Vert \varvec{g}_k\Vert \Vert \mathbf d _k\Vert }. \end{aligned}$$

(10)

We first show the convergence of Algorithm 2 in the RCFA by the following lemma.

Lemma 1

Suppose that $\{\varvec{\theta }_k\}$ is a sequence generated by (6) or (7) with Algorithm 1, and $f(\varvec{\theta }_k)$ is bounded below in $\mathcal {R}^N$. Assume also that the gradient $\varvec{g}_k$ of $f(\varvec{\theta }_k)$ exists and is uniformly continuous in the level set

$$\begin{aligned} \mathcal {L}(\varvec{\theta }_0)=\{ \varvec{\theta }_k \in \mathcal {R}^N|f(\varvec{\theta }_k) \le f(\varvec{\theta }_0) \} \end{aligned}$$

(11)

for an arbitrary staring point $\varvec{\theta }_0 \in \mathcal {R}^N$. If the descent direction $\mathbf d _k$ satisfies that

$$\begin{aligned} 0 \le \widetilde{\theta }_k \le \frac{\pi }{2}-\eta , \quad \eta \in (0, \frac{\pi }{2}), \end{aligned}$$

(12)

we have $\Vert \varvec{g}(\varvec{\theta }^*)\Vert =0$ for any limit point $\varvec{\theta }^*$ of the sequence $\{\varvec{\theta }_k\}$.

Proof

We prove this lemma by contradiction and suppose that $\varvec{\theta }^*$ is a limit point of the sequence $\{\varvec{\theta }_k\}$ and $\Vert \varvec{g}(\varvec{\theta }^*)\Vert \ne 0$. Since $\mathbf d _k$ is a descent direction, $\{ f(\varvec{\theta }_k) \}$ is monotonically decreasing. Also because $f(\varvec{\theta }_k)$ is bounded below, the limit of $f(\varvec{\theta }_k)$ exists and we obtain that $f(\varvec{\theta }_k) - f(\varvec{\theta }_{k+1}) \rightarrow 0, \quad f(\varvec{\theta }_k) \rightarrow f(\varvec{\theta }^*)$. From Algorithm 2, we have that $-a_1\varvec{g}_k^T\varvec{\widetilde{s}}_k \rightarrow 0, \varvec{g}_k^T\widetilde{\varvec{s}}_k \rightarrow 0$ where $\varvec{\widetilde{s}}_k=\alpha ^j\mathbf d _k$. In addition, we can also show that $\cos \widetilde{\theta }_k = \frac{-\varvec{g}_k^T\widetilde{\varvec{s}}_k}{\Vert \varvec{g}_k\Vert \Vert \widetilde{\varvec{s}}_k\Vert },$ and since $\cos \widetilde{\theta }_k >0$ according to (12), we have $\Vert \widetilde{\varvec{s}}_k\Vert \rightarrow 0$.

The parameter j used in Algorithm 2 is the least nonnegative integer which makes the inequality true. Thus for $\alpha ^{j-1}=\alpha ^j/\alpha$, we have

$$\begin{aligned} f(\varvec{\theta }_k+\alpha ^{j-1}{} \mathbf d _k) - f(\varvec{\theta }_k) > a_1 \alpha ^{j-1}\varvec{g}_k^T\mathbf d _k. \end{aligned}$$

(13)

Note that $\alpha ^{j-1}{} \mathbf d _k = \varvec{\widetilde{s}}_k/\alpha$, we can rewrite (13) as

$$\begin{aligned} f(\varvec{\theta }_k+\frac{\varvec{\widetilde{s}}_k}{\alpha }) - f(\varvec{\theta }_k) > a_1 \varvec{g}_k^T\frac{\varvec{\widetilde{s}}_k}{\alpha }. \end{aligned}$$

(14)

Let $\varvec{p}_k = \frac{\varvec{\widetilde{s}}_k}{\Vert \varvec{\widetilde{s}}_k \Vert }$, then $\frac{\varvec{\widetilde{s}}_k}{\alpha } = \frac{\Vert \varvec{\widetilde{s}}_k\Vert }{\alpha }\varvec{p}_k$. According to $\Vert \widetilde{\varvec{s}}_k\Vert \rightarrow 0$, we have that $\alpha _k' = \frac{\Vert \varvec{\widetilde{s}}_k\Vert }{\alpha } \rightarrow 0$ and (14) can be rewritten as

$$\begin{aligned} \frac{f(\varvec{\theta }_k+ \alpha _k'\varvec{p}_k) - f(\varvec{\theta }_k)}{\alpha _k'} > a_1 \varvec{g}_k^T\varvec{p}_k. \end{aligned}$$

(15)

On the one hand, since $\Vert \varvec{p}_k\Vert =1$, $\{\Vert \varvec{p}_k\Vert \}$ is bounded. Therefore, there exists a convergent subsequence $\{\Vert \varvec{p}_k\Vert \}$ and $\{\Vert \varvec{p}_k\Vert \} \rightarrow \Vert p^*\Vert =1$. By taking the limit on both sides of (15), we obtain that $\varvec{g}^T(\varvec{\theta }^*)p^* \ge a_1 \varvec{g}^T(\varvec{\theta }^*)p^*$. Thus,

$$\begin{aligned} \varvec{g}^T(\varvec{\theta }^*)p^* \ge 0. \end{aligned}$$

(16)

On the other hand, $\varvec{p}_k = \frac{\varvec{\widetilde{s}}_k}{\Vert \varvec{\widetilde{s}}_k \Vert } = \frac{\mathbf {d}_k}{\Vert \mathbf {d}_k\Vert }$, we have

$$\begin{aligned} -\varvec{g}_k^T\varvec{p}_k = -\varvec{g}_k^T(\frac{\mathbf {d}_k}{\Vert \mathbf {d}_k \Vert }) = \Vert \varvec{g}_k\Vert \cos \widetilde{\theta }_k \ge \Vert \varvec{g}_k\Vert \sin \eta . \end{aligned}$$

(17)

By taking the limit of (17), we have $-\varvec{g}(\varvec{\theta }^*)^T\varvec{p}^* \ge \Vert \varvec{g}(\varvec{\theta }^*)\Vert \sin \eta >0$, i.e.,

$$\begin{aligned} \varvec{g}(\varvec{\theta }^*)^T\varvec{p}^* < 0, \end{aligned}$$

(18)

which gives a contradiction to (16). Therefore, $\Vert \varvec{g}(\varvec{\theta }^*)\Vert = 0$.   $\blacksquare$

In the end, the global convergence of RCFA is presented in the following theorem.

Theorem 1

Let $\varvec{B}_0$ be any symmetric positive definite initial matrix, and let $\varvec{\theta }_0$ be a staring point for which Assumption 6.1 proposed in [13] is satisfied. Then the sequence $\{\varvec{\theta }_k\}$ generated by the RCFA converges to the minimizer $\varvec{\theta }^*$ of $f_{p_\theta }$.

Proof

The theorem follows from the results of Theorem 6.5 in [13] and its proof is omitted here.   $\blacksquare$

4 Simulations and Experiments

In this section, simulations and experiments are performed on a group of WMRs to verify the feasibility and effectiveness of RCFA.

4.1 Simulation Results

First, a group of five robots modeled by (1) are configured with speeds $v_1=0.7,v_2=0.5,v_3=0.5,v_4=0.3$ and $v_5=0.3$. The initial phase angles are shown in Figs. 1(a) and 2(a), in which $\theta _1=0,\theta _2=-\pi /4,\theta _3=\pi /4,\theta _4=-\pi /2$ and $\theta _5=\pi /2$. If we set the objective function as $f_{p_\theta }$ (with $\gamma =-1$), rectilinear formation with synchronized phase configuration is achieved by utilizing RCFA with the control law (6). If we set the objective function to $f_{\dot{Z}}$, as expected, all the robots can keep moving in rectilinear formation with a fixed average position. The motion of robots in the two simulations are shown in Figs. 1(b) and 2(b) (the average position of robots is marked by $\oplus$), respectively.

Fig. 1.

Rectilinear formation with synchronized phase configuration

Fig. 2.

Rectilinear formation with stabilization of the average linear momentum

Then, a group of three robots are configured with speeds $v_1=1.5,v_2=1$ and $v_3=0.8$ to achieve the circular formation pattern by using RCFA with the control law (7). The initial phase angles are shown in Figs. 3(a) and 4(a), in which $\theta _1=3\pi /4,\theta _2=\pi /2$ and $\theta _3=\pi /4$. By setting $f_{p_\theta }$ as the objective function with $\gamma =-1$ and $\gamma =1$, circular formation with synchronized and balanced phase configurations are achieved, respectively. The motion of the robots are shown in Figs. 3(b) and 4(b).

4.2 Experimental Results

Two typical formation experiments are carried out on a group of two PIONEER 3DX mobile robots installed with the Robot Operating System (ROS). The PIONEER 3DX is equipped with two processors, a laptop (2.2-GHz CPU and 8-GB memory) for running the algorithm and communicating with other robots via WIFI, and a 32-bit microprocessor (44.2368 MHz) for motion control. The position of each robot is estimated by using its on-board motor encoder. The updating frequency of the algorithm is set as 10 Hz. In the first experiment, we initialize the phase angles of the two robots to 0 and $\pi /2$, respectively. Similarly, we set the initial phase angles of the two robots to 0 and $\pi /4$ in the second experiment, respectively. Rectilinear and circular formation with synchronized phase configuration are shown in Figs. 5(a) and 6(a), respectively. The complete moving trajectories of the two robots are recorded in an odometer log and plotted in Figs. 5(b) and 6(b).

Fig. 3.

Circular formation with synchronized phase configuration

Fig. 4.

Circular formation with balanced phase configuration

Fig. 5.

The snapshots and trajectories of the rectilinear formation with synchronized phase for a group of two robots.

Fig. 6.

The snapshots and trajectories of the circular formation with synchronized phase for a group of two robots.

5 Conclusion and Future Work

This paper studies rectilinear and circular formation control problems for multiple unicycle type vehicles. A novel variable-gain RCFA is proposed based on BFGS method and global convergence properties can be guaranteed under some mild assumptions. Furthermore, the control inputs in present paper contain only the orientations of the robots and the speeds of the robots can be nonidentical. Simulation and experiment results verified the feasibility and effectiveness of the proposed algorithm.

In our future work, we aim to investigate another formation pattern, in which all the robots are required to move in concentric circular formation (a common circle or different circles around a common center) with phase synchronization/balancing. This type of formation control problem is more complicated since it requires both circular orbit control and phase control.