Improved Input-to-State Stability Analysis of Discrete-Time Time-Varying Systems

Abstract

This note is concerned with input-to-state stability analysis of discrete-time switched nonlinear time-varying (DSNTV) systems. Some sufficient conditions are derived for testing input-to-state stability (ISS) of discrete-time nonlinear time-varying (DNTV) systems. ISS of DSNTV systems is further studied. The main feature of these obtained results is that the time-difference of Lyapunov functions of subsystems is allowed to be indefinite. Globally uniformly asymptotically stability (GUAS) and globally uniformly exponentially stability (GUES) concepts are utilized for analysis stability of general DNTV and DSNTV systems. An numerical example demonstrate the effectiveness of the proposed approaches.

The authors would like to thank Professor Bin Zhou for fruitful suggestions.

1 Introduction

Switched systems are a class of important systems composed of many subsystems, which have received extensive attention from researchers in the past decades. The application of the switched systems are very extensive, such as artificial intelligence systems, power systems, and economic systems. Because switching is widespread in practical systems, switched systems have received great attention in the control community and a large number of results have been reported (see [3, 6, 10, 17, 18, 20, 21] and the reference therein). Particularly, stability analysis of switched system is the most important and fundamental problem in these results. Various stability concepts such as asymptotic stability [23], input-to-state stability (ISS) [13], and finite time stability have been thoroughly investigated for both continuous and discrete systems by exploiting Lyapunov’s second method. For this stability analysis method, unlike the well-established time-invariant system stability theory, stability analysis of time-varying systems is full of challenges. This is also true for discrete nonlinear time-varying (DNTV) systems and discrete switched nonlinear time-varying (DSNTV) systems.

ISS means that the bound of the system response can be determined by the bounds of disturbance input and system initial state. ISS has proved to be very effective in describing the external disturbance input of the control system, and has attracted more and more attention of researchers since the pioneering result [15]. As mentioned earlier, ISS analysis can be applied on both continuous-time and discrete-time systems. For continuous-time systems, ISS analysis was studied in [15, 16, 19]. However, when $V(t,x)\ge \rho (|u|)$, the time derivative of Lyapunov functions along the trajectories of the considered system in these documents must be negative. Recently, an improved ISS analysis method based on Lyapunov function is studied in [3, 12, 14, 22, 24], which allows the time derivative of Lyapunov functions to be indefinite. For discrete-time systems, ISS analysis was studied in [6, 8, 10, 11]. Whereas, the time-shift of the ISS-Lyapunov function needs to be negative under some additional condition on u. [7] improved these results, and proposed two methods.The advantage of this method is that the time-difference of the Lyapunov functions are allowed to be indefinite. Inspired by these existing work, in this paper, we continue to extend the method in [3, 7, 22, 24] to the ISS analysis of DNTV and DSNTV systems.

Lyapunov’s second method has been recognized as a very powerful tool in stability theory, especially the time-invariant systems. However, stability analysis for time-varying systems is more challenging than time-invariant systems. Therefore, stability analysis methods for time-varying systems still need to be further studied. For both continuous systems and discrete systems, the classical Lyapunov stability analysis method requires the derivative or difference of the Lyapunov function to be negative (see [2, 4, 5] and the reference therein). Recently, we have established a stability analysis method for several kinds of time-varying systems in [22,23,24,25] that allows the time derivative (time difference) of Lyapunov functions to be indefinite. Meanwhile, a similar stability analysis method was also used in the ISS analysis for continuous nonlinear time-delay systems by Ning et al. [13] and switched systems by Chen and Yang [3], respectively.

The main purpose of this paper is to establish stability theorems to discrete-time time-varying systems by using improved Lyapunov functions developed in [3, 24]. The main contributions of this paper are highlighted as follows: (1). With the help of the scalar stable function [23, 25] and an improved comparison lemma, some sufficient conditions are derived for testing ISS of DNTV systems. (2). Extend the results from Item 1 to DSNTV systems. (3). Studied the globally uniformly asymptotically stability (GUAS) and globally uniformly exponentially stability (GUES) of the previous two kinds of systems. The time-difference of Lyapunov functions in all these methods is allowed to be indefinite under some additional condition, which is more easily satisfied than the conditions in [6, 8].

Notation: In this paper, $\mathbf {R}$, $\mathbf {R}^{+}$, and $\mathbf {R}^{n}$ denote the set of real numbers, nonnegative real numbers, and n-dimensional Euclidean space respectively. For p, $q\in J$ with $p\le q$, $\mathbf {I}[p,q]\$is the set $\{p,p+1,\ldots ,q\}$ and $\mathbf {I}[p,\infty )$ is the set $\{p,p+1,\ldots \}$. Let $J=\mathbf {I}[0,\infty )$ and $\varPi _{j=k_{0}}^{k}H(k)=I_{n}$, $\forall k<k_{0}$, $k_{0}\in J$. Denote $l_{\infty }^{m}=\{f(k):J\rightarrow \mathbf {R}^{m},|\sup _{k\in J} \{|f(k)|\}<\infty \}$. For a, $b\in J$, and a function f, we denote $\vert f\vert _{\mathbf {I}[a,b]}=\sup \{ \vert f(s)\vert ,s\in \mathbf {I}[a,b]\}$. The function $\psi :\mathbf {R}^{+}\rightarrow \mathbf {R}^{+}$ is a $\mathcal {K}$ function, if $\psi$ is continuous and strictly increasing and $\psi (0)=0$. If $\psi \in \mathcal {K}$ and moreover $\lim _{s\rightarrow \infty }\psi (s)=\infty$, then it is denoted by $\psi \in \mathcal {K}_{\infty }$. The function $\psi (s,k):\mathbf {R}^{+} \times \mathbf {R}^{+}\rightarrow \mathbf {R}^{+}$ is a $\mathcal {KL}$ function, if $\psi (\cdot ,k)\in \mathcal {K}$ for a fixed k, and $\psi (s,\cdot )$ is decreasing with $\lim _{k\rightarrow \infty }\psi (s,k)=0$ for a fixed s. For a positive constant x,the function $\left\lfloor x\right\rfloor$ denotes the largest integer not greater than x.

2 Problem Formulation and Preliminaries

2.1 Systems Description

We first consider the following discrete nonlinear time-varying system (DNTV)

$$\begin{aligned} x\left( k+1\right) =f\left( k,x(k),u\left( k\right) \right) ,x(k_{0})=x_{0},k\ge k_{0}, \end{aligned}$$

(1)

where initial time $k_{0}\in J$, the state of the system $x\left( k\right) :J\rightarrow \mathbf {R}^{n}$, the input $u(k):J\rightarrow \mathbf {R}^{m}$ is assumed to be locally essentially bounded. We also assume that $f:\mathbf {R} ^{+}\times \mathbf {R}^{n}\times \mathbf {R}^{m}\rightarrow \mathbf {R}^{n}$ is locally essentially bounded with $f(k,0,0)=0$.

For futher use, we introduce the following definition, which characterize several stability notions for system (1).

Definition 1

The system (1) is said to be:

• 1. Input-to-state stable (ISS) if there exist a $\mathcal {KL}$-function $\sigma$ and a $\mathcal {K}$-function $\gamma$ such that, for each $u\in l_{\infty }^{m}$, and $k\ge k_{0}$, $k_{0}\in J$, (see [8])

  $$ \vert x(k) \vert \le \sigma (\vert x_{0}\vert ,k-k_{0}) +\gamma (\vert u \vert _{\mathbf {I}[ k_{0},k-1]}); $$

• 2. Globally uniformly asymptotically stable (GUAS) (with $u\equiv 0$), if there exists a $\mathcal {KL}$-function $\sigma$ such that, for any $k\ge k_{0}$, $k_{0}\in J$, (see [1, 9])

  $$ \vert x( k) \vert \le \sigma (\vert x_{0}\vert ,k-k_{0}) ; $$

• 3. Globally uniformly exponentially stable (GUES) (with $u\equiv 0$), if there exist two positive constants $\alpha$ and $\beta <1$ such that, for any $k\ge k_{0}$, $k_{0}\in J$, (see [1, 9])

  $$ \vert x( k) \vert \le \alpha \beta ^{k-k_{0}}\vert x_{0}\vert . $$

We next consider the following discrete-time switched nonlinear time-varying (DSNTV) systems:

$$\begin{aligned} x\left( k+1\right) =f_{\vartheta \left( k\right) }\left( k,x(k),u\left( k\right) \right) ,x(k_{0})=x_{0},k\ge k_{0}, \end{aligned}$$

(2)

where initial time $k_{0}\in J$, the state of the system $x(k)\in \mathbf {R}^{n}$, the input $u(k)\in \mathbf {R}^{m}$ is assumed to be locally essentially bounded, and switching signal $\vartheta :J\rightarrow Q=\{1,2,\ldots ,q\}$. Let $k_{1}<k_{2}<\cdots <k_{t}$, $t\ge 1$, denote the switching instants of $\vartheta (\tau )$ for $k_{0}< \tau <k$ and $\{x(k_{0}): (i_{0},k_{0}),(i_{1},k_{1}),\ldots ,(i_{t},k_{t}),\ldots ,|i_{t}\in Q,t\in J\}$ denote the switching sequence. When $k\in [k_{j},k_{j+1})$, the $i_{j}$th subsystem is active. For each $i\in Q$, $f_{i}:\mathbf {R}^{+}\times \mathbf {R}^{n} \times \mathbf {R}^{m}\rightarrow \mathbf {R}^{n}$ is locally essentially bounded with $f_{i}(k,0,0)=0$. Moreover, system (1) and system (2) have the same stability definition. Let $\varkappa (a,b)$ denote the number of switches occurring in the interval $\mathbf {I}[a,b]$. Throughout this paper, we assume that x(k) is a single-valued function.

2.2 Scalar Stable Functions and Comparison Lemma

To build our results, we need the following basic concepts recalled from [23, 25].

Consider the following scalar discrete linear time-varying (DLTV) system

$$\begin{aligned} y\left( k+1\right) =\mu \left( k\right) y\left( k\right) ,k\in J, \end{aligned}$$

(3)

where $\mu \left( k\right) :J\rightarrow \mathbf {R}^{+}$ and $y\in \mathbf {R}$.

Definition 2

[23, 25] The function $\mu \left( k\right)$ is a uniformly stable (US) function if system (3) is US, a asymptotically stable (AS) function if system (3) is AS, and a uniformly asymptotically stable (UAS) function if system (3) is UAS.

By noting that the state transition matrix $\phi _1(k,k_{0})$ for system (3) is [23, 25]

$$\begin{aligned} \phi _1 \left( k,k_{0}\right) =\prod \limits _{i=k_{0}}^{k-1}\mu \left( i\right) ,\forall k\ge k_{0},k_{0}\in J . \end{aligned}$$

(4)

We have the following result.

Lemma 1

[23, 25] The function $\mu \left( k\right) :J\rightarrow \mathbf {R}^{+}$ is

• 1. US if and only if there exists a number $\chi \ge 1$ such that, for any $k\ge k_{0},k_{0}\in J$, $\phi _1 ( k,k_{0}) \le \chi$ is satisfied;

• 2. AS if and only if $\lim _{k\rightarrow \infty }\phi _1 \left( k,k_{0}\right) =0;$

• 3. UAS if and only if there exist two numbers $\chi \ge 1$ and $\lambda \in (0,1)$ such that

  $$\begin{aligned} \phi _1 \left( k,k_{0}\right) \le \chi \lambda ^{k-k_{0}},\forall k\ge k_{0},k_{0}\in J. \end{aligned}$$

  (5)

To obtain the ISS stability theorem, we need the following comparison lemma.

Lemma 2

Let y(k) be a function satisfying

$$\begin{aligned} y\left( k+1\right) \le \mu \left( k\right) y\left( k\right) ,\text { whenever }y\left( k+1\right) \ge \psi \left( k\right) , \end{aligned}$$

(6)

where $\mu (k)$ is a US function and $\psi (k):J\rightarrow \mathbf {R}$ is a sequence (which can be dependent on y). Then, the following inequality is established

$$\begin{aligned} y\left( k\right) \le \max \left\{ \phi _1 \left( k,k_{0}\right) y\left( k_{0}\right) ,\chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}\right\} . \end{aligned}$$

(7)

Proof

We consider the following inequality in two cases,

$$\begin{aligned} y\left( s+1\right) \ge \psi \left( s\right) . \end{aligned}$$

(8)

Case 1: For all $s\in \mathbf {I} [k_{0},k-1]$, (8) holds. By using (4), (6) and Gronwall inequality, we have

$$\begin{aligned} y\left( k\right) \le \phi _1 \left( k,k_{0}\right) y\left( k_{0}\right) . \end{aligned}$$

(9)

Case 2: For some $s\in \mathbf {I}[k_{0},k-1]$, (8) does not hold true. Let $k^{*}\in \mathbf {I}[k_{0},k-1]$ be the maximal number such that $y\left( k^{*}+1\right) <\psi \left( k^{*}\right)$. Then we have either $k^{*}<k-1$ or $k^{*}=k-1$. If $k^{*}<k-1$, then (8) holds for all $s\in \mathbf {I}[k^{*}+1,k-1]$, which implies $y\left( s+1\right) \le \mu \left( s\right) y\left( s\right)$, and thus

$$\begin{aligned} y\left( k\right)&\le \phi _1 \left( k,k^{*}+1\right) y\left( k^{*}+1\right) <\chi \psi \left( k^{*}\right) \le \chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}. \end{aligned}$$

(10)

If $k^{*}=k-1$, then by the definition of $k^{*}$ and (6), we have

$$\begin{aligned} y\left( k\right)&=y\left( k^{*}+1\right) <\psi \left( k^{*}\right) \le \chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}. \end{aligned}$$

(11)

Now, combining (9), (10) and (11), we conclude that (7) is true.

3 Main Results

3.1 Improved ISS Analysis for DNTV Systems

We first establish an improved ISS analysis for DNTV system (1).

Theorem 1

Assume that there exist two functions $u_{1},u_{2}\in \mathcal {K} _{\infty }$, a function $\rho \in \mathcal {K}$, a AS and US function $\mu (k)$, and a function $V(k,x):J\times \mathbf {R}^{n}\rightarrow \mathbf {R}$, such that, for all $k\in J$ and $x\in \mathbf {R}^{n}$, the following conditions hold:

$$\begin{aligned} \mathrm {(A).} \quad&u_{1}(\left| x\right| )\le V(k,x(k))\le u_{2} (\left| x\right| ).\\ \mathrm {(B).} \quad&V\left( k+1,x(k+1)\right) \le \mu \left( k\right) V\left( k,x(k)\right) \text { if } V\left( k+1,x(k+1)\right) \ge \rho \left( \left| u\left( k\right) \right| \right) . \end{aligned}$$

Then the DNTV system (1) is ISS.

Proof

We choose $y(k)=V(k,x(k))=\left| y(k)\right|$, $\psi (k)=\rho \left( \left| u\left( k\right) \right| \right)$. Then (B) is just in the form of (6) and it follows from Lemma 2 that, for any $k\ge k_{0}\in J$,

$$\begin{aligned} y\left( k\right)&\le \max \left\{ \varTheta (k),\chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}\right\} \le \varTheta (k)+\chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}, \end{aligned}$$

where $\varTheta (k)=\phi _1 ( k,k_{0})y(k_{0})$. Hence, by using $\alpha (a+b)\le \alpha (2a)+\alpha (2b), \alpha \in \mathcal {K}, a\ge 0, b\ge 0$ and condition (A), we get, for any $k,k_{0}\in J$, with $k\ge k_{0}$,

$$\begin{aligned} \left| x(k)\right|&\le u_{1}^{-1}\left( y\left( k\right) \right) \le u_{1}^{-1}\left( 2\varTheta (k)\right) +u_{1}^{-1}\left( 2\chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}\right) . \end{aligned}$$

(12)

We next construct a $\mathcal {KL}$-function $\sigma _{1}(\left| x_{0}\right| ,k-k_{0})$ satisfying $2\varTheta (k)\le \sigma _{1}(\vert x_{0}\vert ,k-k_{0})$. Since $\mu (k)$ is AS, namely, $\lim _{k\rightarrow \infty }\phi _1 ( k,k_{0})=0$, there exists a sequence $\{k_{i}\}$, satisfying, for $k,i\in J$, $k_{i}\rightarrow \infty ,i\rightarrow \infty$, such that $2\varTheta (k)\le \frac{2\chi y(k_{0})}{i+1}\le \frac{2\chi u_{2}(\left| x_{0}\right| )}{i+1},k\ge k_{i}$. Then $\mathcal {KL}$-function $\sigma _{1}$ is defined as, for all $j\ge 1$,

$$ \sigma _{1}=\left\{ \begin{array} [c]{ll} \frac{2\chi u_{2}(\left| x_{0}\right| )}{j}\left( 1-\frac{k-k_{j} }{\left( j+1\right) \left( k_{j+1}-k_{j}\right) }\right) &{} ,k\in \mathbf {I}\left[ k_{j},k_{j+1}\right) ,\\ 2\chi u_{2}(\left| x_{0}\right| ) &{} ,k\in \mathbf {I}\left[ k_{0} ,k_{1}\right) . \end{array} \right. $$

From which and (12), we have

$$ \left| x(k)\right| \le u_{1}^{-1}\left( \sigma _{1}(\left| x_{0}\right| ,k-k_{0})\right) +u_{1}^{-1}\left( 2\chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}\right) , $$

which shows that the system (1) is ISS. The proof is finished.

From Example 1 in [23], it is easy to know that we can find a scalar stable function $\mu (k)$ that is US and AS but is not UAS. But, if scalar stable function $\mu (k)$ is UAS, then it is a AS and US function. Therefore, we can get the following corollary, which seems more concise.

Corollary 1

[7] Assume that there exist two functions $u_{1},u_{2}\in \mathcal {K} _{\infty }$, a function $\rho \in \mathcal {K}$, a UAS function $\mu (k)$, and a function $V(k,x):J\times \mathbf {R} ^{n}\rightarrow \mathbf {R}$, such that, for all $k\in J$ and $x\in \mathbf {R}^{n}$, (A) and (B) are satisfied, then the DNTV system (1) is ISS.

We mention that Theorem 1 and Corollary 1 can be viewed as the discretization of Theorem 2 in [3] and Theorem 3 in [24] respectively. In addition, Theorem 1 and Corollary 1 are an extension of Lemma 3.5 in [8]. Because, under condition $V( k+1,x(k+1)) \ge \rho ( \vert u( k) \vert )$, the time-shift of Lyapunov functions can take both negative and positive values. DLTV (researched in [z]) is a special case of DNTV.

3.2 Improved ISS Analysis for DSNTV Systems

We then can provide the following ISS stability theorems for system (2).

Theorem 2

Assume that there exist two functions $u_{1},u_{2}\in \mathcal {K} _{\infty }$, a function $\rho \in \mathcal {K}$, a US function $\mu _{i}(k)$, two positive constants $b\ge 1,B$, and a function $V_{i}(k,x):J\times \mathbf {R} ^{n}\rightarrow \mathbf {R}$, such that, for all $k\in J$ and $x\in \mathbf {R}^{n}$,

$$\begin{aligned} \mathrm {(C)} \quad&u_{1}(\left| x\right| )\le V_{i_{j}}(k,x(k))\le u_{2} (\left| x\right| ).\\ \mathrm {(D)} \quad&V_{i_{j}}( k+1,x(k+1)) \le \mu _{i_{j}}( k) V_{i_{j}}( k,x(k))\text { if } V_{i_{j}}( k+1,x(k+1)) \ge \rho ( \vert u( k) \vert ).\\ \mathrm {(E)} \quad&V_{i_{j+1}}\left( k,x(k)\right) \le bV_{i_{j}}\left( k,x(k)\right) ,\forall i_{j}\in Q.\\ \mathrm {(F)} \quad&\lim _{k\rightarrow \infty }m(k)=0 \text { and } n(k)<B, \end{aligned}$$

where $m(k)=b^{\varkappa (k_{0},k)}\phi _2(k,k_{0})$ and $n(k)=\Sigma _{k_{0}<k_{s}<k}(b^{\varkappa (k_{s},k)}\phi _2(k,k_{s} ))$. Then the system (2) is ISS.

Proof

We also choose $y_{i_{j}}(k)=V_{i_{j}}(k,x(k))=|y_{i_{j}}(k)|$, $\psi (k)=\rho \left( \left| u\left( k\right) \right| \right)$. The state transition matrix for $\mu _{i}(k)$, denoted by $\phi _2(k,k_{0})$, is given by

$$\begin{aligned} \phi _2\left( k,k_{0}\right) =\prod \limits _{s=k_{0}}^{k-1}\mu _{\vartheta \left( s\right) }\left( s\right) ,\forall k\ge k_{0},k_{0}\in J. \end{aligned}$$

(13)

Meanwhile, Lemma 1 and Lemma 2 remains true for $\phi _2$. By using Lemma 2 agian, we have, for any $k\in \mathbf {I}[k_{j}+1,k_{j+1}]$, $j\in J$,

$$\begin{aligned} y_{i_{j}}\left( k\right) \le \phi _2\left( k,k_{j}\right) y_{i_{j} }\left( k_{j}\right) +\chi \left| \psi \right| _{\mathbf {I}[k_{j},k-1]}. \end{aligned}$$

(14)

Now, for proving ISS, we need to prove that, for all $k\ge k_{0}$,

$$\begin{aligned} y_{\vartheta ( k) }( k)\le & {} m(k)y_{i_{0} }\left( k_{0}\right) +\left( 1+n(k)\right) \chi \vert \psi \vert _{\mathbf {I}[k_{0},k-1]}. \end{aligned}$$

(15)

We prove this by mathematical induction. For $k\in \mathbf {I}[k_{0}+1,k_{1}]$, (15) follows from (14), namely,

$$ y_{i_{0}}\left( k\right) \le b\phi _2\left( k,k_{0}\right) y_{i_{0} }\left( k_{0}\right) +\chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}. $$

We now assume that (15) is true for $k\in \mathbf {I}[k_{j}+1,k_{j+1}]$, namely,

$$\begin{aligned} y_{i_{j}}( k)\le & {} m(k)y_{i_{0} }\left( k_{0}\right) +\left( 1+n(k) \right) \chi \vert \psi \vert _{\mathbf {I}[k_{0},k-1]}, \end{aligned}$$

(16)

and want to show that (15) is still satisfied for $k\in \mathbf {I}[k_{j+1}+1 ,k_{j+2}]$. By using (E), (14), and (16), we have

$$\begin{aligned} y_{i_{j+1}}\left( k\right) \le \,&\phi _2\left( k,k_{j+1}\right) y_{i_{j+1}}\left( k_{j+1}\right) +\chi \left| \psi \right| _{\mathbf {I}[k_{j+1},k-1]}\\ \le \,&b\phi _2\left( k,k_{j+1}\right) y_{i_{j}}\left( k_{j+1}\right) +\chi \left| \psi \right| _{\mathbf {I}[k_{j+1},k-1]}\\ \le \,&b\phi _2\left( k,k_{j+1} \right) \left( m(k_{j+1}) y_{i_{0}}\left( k_{0}\right) +\left( 1+n(k_{j+1}) \right) \chi \left| \psi \right| _{\mathbf {I}[k_{0},k_{j+1} -1]}\right) \\&+\chi \left| \psi \right| _{\mathbf {I}[k_{j+1},k-1]}\\ \le \,&b^{\varkappa \left( k_{0},k\right) }\phi _2\left( k,k_{0}\right) y_{i_{0}}\left( k_{0}\right) + \chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}\\&\times \left( 1+b\phi _2\left( k,k_{j+1}\right) +\sum _{k_{0}<k_{s}<k_{j+1}} \left( b^{\varkappa \left( k_{s},k\right) }\phi _2\left( k,k_{s}\right) \right) \right) \\ = \,&m(k)y_{i_{0}}\left( k_{0}\right) +\left( 1+n(k) \right) \chi \vert \psi \vert _{\mathbf {I}[k_{0},k-1]}. \end{aligned}$$

Therefore, (15) is satisfied for all $k\ge k_{0},k_{0}\in J$. Then, by using $\alpha (a+b)\le \alpha (2a)+\alpha (2b), \alpha \in \mathcal {K}, a\ge 0, b\ge 0$, (C), and (15), we get, for all $k\ge k_{0}$

$$\begin{aligned} \left| x\left( k\right) \right| \le \,&u_{1}^{-1}\left( 2u_{2}\left( \left| x_{0}\right| \right) m\left( k\right) \right) +u_{1}^{-1}\left( 2\left( 1+n\left( k\right) \right) \chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}\right) \\ \le \,&u_{1}^{-1}\left( 2u_{2}\left( \left| x_{0}\right| \right) m\left( k\right) \right) +u_{1}^{-1}\left( 2\left( 1+B\right) \chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}\right) . \end{aligned}$$

Since $\lim _{k\rightarrow \infty }m(k)=0$, using a similar method in Theorem 1, we can construct a $\mathcal {KL}$-function $\sigma _{2}$ such that, for all $k\in J$, $2u_{2}\left( \left| x_{0}\right| \right) m\left( k\right) \le \sigma _{2}(\left| x_{0}\right| ,k-k_{0})$. Hence, the system (2) is ISS. The proof is finished.

Corollary 2

Assume that there exist an integer $m\ge 1$ and a constant $\bar{\delta }_{1}$ satisfying $\delta _{j}\triangleq k_{j+1}-k_{j}\ge \bar{\delta }_{1},\forall j\ge m$, with $j\in J$, two functions $u_{1},u_{2}\in \mathcal {K}_{\infty }$, a function $\rho \in \mathcal {K}$, a UAS function $\mu _{i}(k)$, a positive constant $b\ge 1$ and a function $V_{i}(k,x):J\times \mathbf {R}^{n} \rightarrow \mathbf {R}$, such that, for all $k\in J$ and $x\in \mathbf {R}^{n}$, (C), (D), (E) and

$$\begin{aligned} \root \bar{\delta }_{1} \of {b}\lambda <1, \end{aligned}$$

(17)

are satisfied. Then the system (2) is ISS.

Proof

We also choose $y_{i_{j}}(k)=V_{i_{j}}(k,x(k))=\left| y_{i_{j} }(k)\right|$, $\psi (k)=\rho \left( \left| u\left( k\right) \right| \right)$. Moreover, the state transition matrix for $\mu _{i}(k)$ is defined in (13). According to the analysis of the Theorem 2, we have, for all $k\ge k_{0}$

$$\begin{aligned} \left| x\left( k\right) \right| \le u_{1}^{-1}\left( 2u_{2}\left( \left| x_{0}\right| \right) m\left( k\right) \right) +u_{1} ^{-1}\left( 2\left( 1+n\left( k\right) \right) \chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}\right) , \end{aligned}$$

(18)

where $m(k)=b^{\varkappa (k_{0},k)}\phi _2(k,k_{0})$ and $n(k)=\Sigma _{k_{0}<k_{s}<k}(b^{\varkappa (k_{s},k)}\phi _2(k,k_{s} ))$. We consider two cases:

Case 1: A finite number of switching for system (2).

Case 2: An infinite number of switching for system (2).

In Case 1, there exist an integer q and a constant $n_{1}$ such that the q-th subsystem is active on $\mathbf {I}[k_{q},\infty )$, and

$$\begin{aligned} m(k)&=b^{\varkappa (k_{0},k)}\phi _2(k,k_{0})\le b^{q+1} \chi \lambda ^{k-k_{0}},\\ n(k)&=\sum _{k_{0}<k_{s}<k}\left( b^{\varkappa (k_{s},k)}\phi _2\left( k,k_{s}\right) \right) =n_{1}<\infty , \end{aligned}$$

from which and (18) it follows that, for all $k\ge k_{0}$,

$$ \left| x\left( k\right) \right| \le u_{1}^{-1}\left( m_{1} u_{2}\left( \left| x_{0}\right| \right) \lambda ^{k-k_{0}}\right) +u_{1}^{-1}\left( 2(1+ n_{1})\chi \left| \psi \right| _{\mathbf {I}[k_{0},k-1]}\right) , $$

where $m_{1}=2\chi b^{q+1}$. Hence, system (2) is ISS in Case 1.

Now consider Case 2. Let $k\in \mathbf {I}[k_{t}+1,k_{t+1}],t\in J$. Then we have either $t\ge m$ or $t<m$. If $t<m$, then we have system (2) is ISS by using the same approach as Case 1. If $t\ge m$, then we have,

$$\begin{aligned} \varkappa (k_{0},k)&=m+\sum _{j=m}^{t}\frac{k_{j+1}-k_{j}}{\delta _{j}} \le \frac{1}{\bar{\delta }_{1}}\sum _{j=0}^{t-1}( k_{j+1}-k_{j}) +2m \le \frac{1}{\bar{\delta }_{1}}( k-k_{0}) +2m, \end{aligned}$$

from which and condition (17) it follows that, for all $k\ge k_{0}$

$$\begin{aligned} m(k)&=b^{\varkappa (k_{0},k)}\phi _2(k,k_{0}) \le \chi b^{2m}\left( \root \bar{\delta }_{1} \of {b}\lambda \right) ^{k-k_{0}},\\ n(k)&=\sum _{k_{0}<k_{s}<k}( b^{\varkappa (k_{s},k)}\phi _2( k,k_{s}) ) \le \sum _{k_{0}<k_{s}<k}\left( b^{\varkappa (k_{s},k)}\chi \lambda ^{k-k_{s} }\right) \\&=n_{2}+\sum _{k_{m}\le k_{s}<k}( b^{\varkappa (k_{s},k)}\chi \lambda ^{k-k_{s} }) \le n_{2} + \frac{b\chi }{1-b\lambda ^{\bar{\delta }_{1}}}, \end{aligned}$$

where $n_{2}=\Sigma _{k_{0}<k_{s}<k_{m}}(b^{\varkappa (k_{s},k)}\chi \lambda ^{k-k_{s} })$ . Hence, all the conditions in Theorem 2 are satisfied, the system (2) is ISS. The proof is finished.

Theorem 3

Assume that system (2) has an infinite number of switching. Assume that there exist two functions $u_{1},u_{2}\in \mathcal {K}_{\infty }$, a function $\rho \in \mathcal {K}$, a US function $\mu _{i}(k)$, a positive constant $b\ge 1$, a positive integer p, a constant $\bar{\lambda }\in (0,1)$ and a function $V_{i}(k,x):J\times \mathbf {R}^{n}\rightarrow \mathbf {R}$, such that, for all $k\in J$ and $x\in \mathbf {R}^{n}$, (C), (D), (E) and

$$\begin{aligned} b^{p}\phi _2\left( k_{p(j+1)},k_{pj}\right) \le \bar{\lambda }<1 \end{aligned}$$

(19)

are satisfied. Then the system (2) is ISS.

Proof

According to the analysis of the Theorem 2, we also have, for all $k\ge k_{0}$, (18) holds, where $\psi (k),m(k)$ and n(k) are given in Theorem 2 and Corollary 2. By using (D), (E) and (19), we have $\lim _{k\rightarrow \infty }m(k) =\lim _{k\rightarrow \infty }b^{\varkappa (k_{0},k)}\phi _2(k,k_{0})\le \lim _{k,z\rightarrow \infty }b^{p( z+1) }\phi _2(k,k_{pz})\phi _2(k_{pz},k_{0}) \le \lim _{z\rightarrow \infty }\chi b^{p}\bar{\lambda }^{z}=0,$ where $z=\lfloor \varkappa (k_{0},$ $k)/p \rfloor$. Next, we claim that there exists a constant L such that,

$$\begin{aligned} n(k)\le \chi \left( 1+\frac{b^{p}\chi }{1-\bar{\lambda }}\right) \sum _{s=0}^{p-1}b^{s}=L<\infty . \end{aligned}$$

(20)

For all $k\ge k_{0}$, there exist two positive integers j and l, such that $k\in \mathbf {I}[k_{j}+1,k_{j+1}]\subseteq \mathbf {I}[k_{lp}+1,k_{(l+1)p}]$. Similarly to the proof of Theorem 5 in [3], we next consider two cases.

Case 1: $l=0$. In this case, we have

$$\begin{aligned} n(k)&=\sum _{k_{0}<k_{s}<k}\left( b^{\varkappa (k_{s},k)}\phi _2\left( k,k_{s}\right) \right) \le \chi \sum _{s=1}^{p-1}b^{s}. \end{aligned}$$

(21)

Case 2: $l>0$. In this case, we have

$$\begin{aligned} n(k)&=\sum _{k_{0}<k_{s}<k}\left( b^{\varkappa (k_{s},k)}\phi _2\left( k,k_{s}\right) \right) \nonumber \\&\le \chi \sum _{s=1}^{p-1}b^{s}+b^{\varkappa (k_{lp},k)}\chi ^{2}\sum _{s=0}^{p-1}b^{s}\sum _{i=0}^{l-1}\bar{\lambda }^{i}\nonumber \\&\le \chi \left( 1+\frac{b^{p}\chi }{1-\bar{\lambda }}\right) \sum _{s=0} ^{p-1}b^{s}. \end{aligned}$$

(22)

Combining (21) and (22), we can get (20) and n(k) is bounded. Hence, the system (2) is ISS.

3.3 Asymptotic Stability Analysis

We finally introduce some crateria for system (1) and (2) with $u\equiv 0$.

Corollary 3

[25] Then the system (1) with $u\equiv 0$ is:

• 1. GUAS if there exist two functions $u_{1},u_{2}\in \mathcal {K}_{\infty }$, a UAS function $\mu (k)$ and a function $V(k,x):J\times \mathbf {R}^{n}\rightarrow \mathbf {R}$ such that, for all $x\in \mathbf {R}^{n}$, (A), and

  $$\begin{aligned} V\left( k+1,x(k+1)\right) \le \mu \left( k\right) V\left( k,x(k)\right) , \forall k\in J, \end{aligned}$$

  (23)

  are satisfied.

• 2. GUES if there exist three positive constants $u_{1},u_{2},\pi$, a UAS function $\mu (k)$ and a function $V(k,x):J\times \mathbf {R}^{n}\rightarrow \mathbf {R}$ such that, for all $k\in J$ and $x\in \mathbf {R}^{n}$, $u_{1}\left| x\right| ^{\pi }\le V(k,x(k))\le u_{2}\left| x\right| ^{\pi }$, and (23) are satisfied.

Corollary 4

The assumption of $\delta$, b, $\mu _{i}(k)$ and $V_{i}(k,x):J\times \mathbf {R}^{n}\rightarrow \mathbf {R}$ in Corollary 2 is still valid. Then the system (2) with $u\equiv 0$ is:

• 1. GUAS if there exist two functions $u_{1},u_{2}\in \mathcal {K}_{\infty }$ such that, for all $k\in J$ and $x\in \mathbf {R}^{n}$, (C), (E), (17), and

  $$\begin{aligned} V_{i}\left( k+1,x(k+1)\right) \le \mu _{i}\left( k\right) V_{i}\left( k,x(k)\right) , \end{aligned}$$

  (24)

  are satisfied.

• 2. GUES if there exist three positive constants $u_{1},u_{2},\pi$, such that, for all $k\in J$ and $x\in \mathbf {R}^{n}$, $u_{1}\left| x\right| ^{\pi }\le V_{i}(k,x(k))\le u_{2}\left| x\right| ^{\pi },$ (E), (17), and (24) are satisfied.

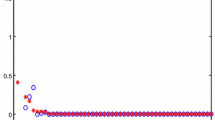
4 An Numerical Example

Consider system (2) with $x(k)\in \mathbf {R}^{2}$, $u(k)\in \mathbf {R}$, $\sigma \left( k\right) \in Q=\{1,2\}$, and

$$\begin{aligned} f_{1}\left( k,x(k),u(k)\right)&=\left( 2.1-2M(k)\right) x(k)+u(k),\\ f_{2}\left( k,x(k),u(k)\right)&=\left( 1.3+M(k)\right) x(k)+u(k). \end{aligned}$$

where $M(k)=\cos \left( k\pi /10\right)$. Let $V_{1}(k,x(k))=V_{2}(k,x(k))=|x(k)|$, then we have $V_{1}(k+1,x(k+1))\le (2.2-2M(k))V_{1}(k,x(k))$, $V_{2}(k+1,x(k+1))\le (1.4+M(k))V_{2}(k,x(k))$, for $V_{i}(k,x(k))\ge 100|u(k)|^{2},i=1,2$. Let $\mu _{1}(k)=(2.2-2M(k))$, $\mu _{2}(k)=(1.4+M(k))$, $\rho (s)=100s^{2}$, $u_{1}(|x(k)|)=u_{2}(|x(k)|)=|x(k)|$, and $b=1$, we can verify that (C), (D) and (E) are satisfied. Since the equations $\mu _{1}(k)$ and $\mu _{2}(k)$ are periodic functions with period 20, we have, for $k\in \mathbf {I}[0, 19]$,

$$ \left\{ \begin{array} [c]{ll} \mu _{2}(k)\le \mu _{1}(k), &{} k\in \mathbf {I}[5, 15],\\ \mu _{1}(k)<\mu _{2}(k), &{} otherwise. \end{array} \right. $$

Assume that $\vartheta ( k)=2$ over $\mathbf {I}[20m+5,20m+16], \forall m\in J$ and $\vartheta ( k)=1$ in other case, then $\mu _{i}(k)$ is UAS, which implies $\root \bar{\delta }_{1} \of {b}\lambda <1$. Hence the system is ISS.

5 Conclusion

This paper has studied the input-to-state (ISS) stability analysis of discrete-time switched nonlinear time-varying (DSNTV) systems by using Lyapunov’s second method. The existing ISS approaches were improved and some sufficient conditions have been proposed to analyze the ISS of discrete-time nonlinear time-varying (DNTV) systems with the help of the concept of scalar stable function and an improved comparison lemma. The improved input-to-state stability analysis approache was applied on a class of DSNTV systems and some criteria are obtained. The advantage of the conditions obtained is that the time-difference of improved Lyapunov functions are allowed to be indefinite. Finally, globally uniformly asymptotically stability (GUAS) and globally uniformly exponentially stability (GUES) concepts were considered for analysis stability of general DNTV and DSNTV systems.