Throughput Analysis for Energy Harvesting Cognitive Radio Networks with Unslotted Users

Abstract

Considering a cognitive radio network (CRN) with the energy harvesting (EH) capability, we design a sensing-based flexible timeslot structure for a secondary transmitter (ST). This structure focuses on an unslotted transmission mode between two primary users (PUs). In this structure, the ST can decide whether to transmit data or to harvest energy based on the sensing results. Aiming to maximize the long-term average achievable throughput of the secondary system, we study an optimal policy, including the optimal energy harvesting time as well as the optimal transmit power. To reduce the computational complexity, we also derive an effective suboptimal policy by maximizing the upper bound on the throughput. Finally, simulation results demonstrate that the proposed flexible timeslot structure outperforms the conventional fixed timeslot structure in terms of average achievable throughput.

1 Introduction

A cognitive radio network (CRN) with energy harvesting (EH) is expected as a promising solution for green communications [1, 2]. Different from energy-efficient protocol designs [3,4,5], the EH technology may increase the battery life of wireless devices by replenishing energy from various energy sources [6, 7], while CRNs can improve the spectral efficiency by opportunistic access schemes. In view of the inherent “harvesting-sensing-throughput” tradeoff in EH CRNs [8, 9], it is crucial for an EH secondary user (SU) to effectively utilize energy (i.e., charging or discharging) to improve system performance and spectral efficiency [10, 11].

Existing studies focused on the optimal energy management and spectrum sensing policies in EH CRNs with time-slotted PUs. In this scenario, the channel of a PU remains idle or busy invariably in one slot while changes with a certain probability in another. Also, SUs need to synchronize with the PUs’ slot to achieve cooperative communications. In particular, the authors presented a saving-sensing-transmitting timeslot division strategy for an EH secondary transmitter (ST) to maximize its expected achievable throughput in [8]. In [12] the authors analyzed impacts of sensing and access probabilities as well as the energy queue capacity on the maximum achievable throughput in a multi-user EH CRN. The authors of [13] investigated the optimal energy-efficient resource allocation schemes for the EH CRNs. Moreover, information-energy cooperative strategies in [14, 15] are investigated to further improve the energy efficiency.

Yet, PUs may send signals in an unslotted manner during actual transmission [16, 17]. PUs and SUs may be hard to be synchronized because of incompatible communication protocols. As a result, it is urgent to study novel spectrum access strategies and/or power allocation schemes for SUs with unslotted primary systems. To the best of our knowledge, little has been done to improve the achievable throughput of an SU in the unslotted EH CRNs. Our exploration of this uncharted area requires addressing the following challenging questions: (i) How to formulate a primary traffic model in the unslotted scenario? (ii) How to design an unslotted data transmit policy of an SU with energy constraint?

Considering these questions, the authors formulated the duration of either an idle state or a busy one as an exponential distributed random variable in [16,17,18]. They calculated the prior probability of channel being idle using the mean durations of these two states. Similarly, [19, 20] employed the channel’s state transition matrix to derive stationary probabilities of channel states. Then, several solutions were proposed for the conventional CRNs without EH. The authors first derived the optimal frame duration and transmit power for energy-unconstrained SUs in [17]. Then, they studied the optimal power control policy in [16] to maximize SUs’ energy efficiency in the presence of unslotted PUs and sensing errors. In [19], the authors designed two data transmit policies with idle and busy sensing results to fully utilize unslotted channels. Also, the authors of [20] elaborated an optimal dual sensing-interval policy to maximize ST’s spectrum utilization to achieve opportunistic energy harvesting for primary signals.

By adopting the same assumption of [20], we present a novel sensing-based flexible timeslot structure for the unslotted EH CRN in this article. Instead of achieving SU’s optimal spectrum utilization, we intend to maximize its achievable throughput. Moreover, we assume that an ST may harvest energy from the ambient environment. After that, it employs a part of the stored energy to sense the primary channel. If the channel is sensed as idle, the ST will send data via the channel; otherwise, it should continue to harvest energy then re-sense the channel after energy harvesting. The main contributions are as follows:

• Considering an EH CRN with an unslotted primary system, we propose a novel sensing-based flexible timeslot structure for the EH ST to maximize its long-term average achievable throughput.

• For the throughput maximization problem, we employ a differential evolution (DE) algorithm to derive the optimal policy, including the optimal harvesting time and the optimal transmit power.

• To reduce the computational complexity, we also derive an effective suboptimal policy by maximizing the upper bound on the achievable throughput.

The remainder of this paper is organized as follows. An EH CRN architecture including primary and secondary systems is described in Sect. 2. In Sect. 3, we formulate and solve the achievable throughput maximization problem of the secondary system. Section 4 demonstrates the throughput performance of our flexible timeslot structure. Finally, we conclude this paper in Sect. 5.

2 System Model

Figure 1 is an EH CRN with Rayleigh fading channels. Channel power gains $|h_{pp}|^2$, $|h_{sp}|^2$ and $|h_{ss}|^2$ of PT-PR, ST-PR and ST-SR links are exponentially distributed variables with unit mean. Moreover, noise power is assumed to be $N_{0}$ for all users.

Fig. 1.

System model of an EH CRN.

2.1 Primary System Model

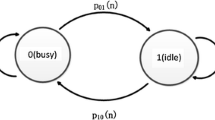
A PT sends signals to its PR in an unslotted mode¹ with a fixed transmit power $P_{p}$. The corresponding channel state alternatively transfers between busy and idle with random durations. Similar to [17, 19, 20], busy and idle durations can be modeled as independent exponentially distributed random variables with mean $E_1=\frac{1}{\lambda _1}$ and $E_0=\frac{1}{\lambda _0}$.² Thus, the busy and idle probabilities are defined as

$$\begin{aligned} {p_1} = \Pr \{ S(t) = 1\} = \frac{{{\lambda _0}}}{{{\lambda _0} + {\lambda _1}}} , \text {and} \ {p_0} = \Pr \{ S(t) = 0\} = \frac{{{\lambda _1}}}{{{\lambda _0} + {\lambda _1}}}. \end{aligned}$$

(1)

where $S(t)=1$ (or $S(t)=0$) indicates the channel is busy (or idle) at time t. And the primary communication is successful only when the received SINR at the PR is higher than a predefined threshold $\beta$ [21].

2.2 Secondary System Model

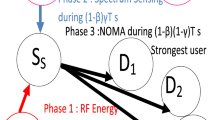
In the secondary system, an EH-enabled ST completely depends on the energy harvested from the ambient environment to communicate with its energy-unconstrained secondary receiver (SR) when the channel is idle. Here, we propose a novel sensing-based flexible timeslot structure for ST to realize effective transmissions, shown as Fig. 2. This structure includes three processes, i.e., energy harvesting, spectrum sensing, and data transmission, with durations of $T_{eh}$, $T_{se}$, and $T_{tr}$, respectively. Due to hardware duplex limitations [8, 22], we assume that the ST can perform only one process at any time.

Fig. 2.

The sensing-based flexible timeslot structure.

Energy Harvesting. In this process, the ST harvests energy from the ambient environment. The energy flows follow an i.i.d random process with mean $P_{eh}$, thus the average harvested energy is $e_h=P_{eh}T_{eh}$ during $T_{eh}$. These energy is stored in the battery and the battery capacity is assumed to be infinite. Note that the energy loss caused by harvesting is negligible in this paper.

Spectrum Sensing. After energy harvesting, the ST carries out spectrum sensing with an energy detector. Since $T_{se}$ is much smaller than $E_1$ and $E_0$, it is reasonable to think that the channel state remains unchanged during $T_{se}$ [19]. If the channel is sensed as idle, the ST transmits; otherwise, it converts to energy harvesting process immediately. The sensing accuracy is measured by the detection probability $P_d$ and the false alarm probability $P_f$. For a target detection probability $P_{d}^{*}$, the false alarm probability $P_{f}$ can be written as

$$\begin{aligned} {P_{f}}=Q\left( {\sqrt{2{\gamma _{ST}} + 1} \cdot {Q^{ - 1}}(P_d^{*}) + {\gamma _{ST}} \sqrt{{T_{se}} \cdot {f_s}}} \right) , \end{aligned}$$

(2)

where is a Q-function, $f_s$ is the ST’s sampling frequency to primary signals and $\gamma _{ST}$ is the received SNR of primary signals at the ST.

For analysis simplicity, we assume the energy consumption for spectrum sensing $e_s$ is proportional to $T_{se}$, i.e., $e_s=P_{se}T_{se}$, where $P_{se}$ is the power consumption per unit of sensing time.

Data Transmission. It is assumed that the ST has perfect information of $h_{ss}$ but only knows the distributions of $h_{pp}$ and $h_{sp}$. When the channel is sensed as idle, the ST will exhaust all its residual energy $E_r$ to transmit [8]. The transmit power, $P_{tr}$, is consistent during transmission and the transmit time ${T_{tr}} = \frac{{{E_r}}}{{{P_{tr}}}}$ varies with different $E_r$.

3 Problem Formulation

In this section, we first formulate the long-term achievable throughput of the secondary system, then derive a differential evolution based optimal policy to maximize this throughput. Finally, we further develop a suboptimal policy to reduce the computational complexity by maximizing the upper bound on the average achievable throughput.

3.1 Formulation of the Average Achievable Throughput

According to whether it transmits data after spectrum sensing, we classify ST’s successive operations into Case A and Case B, as shown in Fig. 2.

Case A: The ST harvests energy and senses the channel, but not transmits data. Case A happens when the channel is sensed as busy (no matter what the exact channel state is) with the probability of ${P_A}={p_1}{P_d^{*}}+{p_0}{P_f}$, where ${p_1}{P_d^{*}}$ is the probability that the channel is correctly sensed as busy and ${p_0}{P_f}$ is the probability that ST wrongly senses the idle channel as busy.

Case B: After the channel is sensed as idle, the ST performs a data transmission. Here, Case B can be further divided into Scenario 1 and Scenario 2 according to the real channel state:

• 1. Scenario 1: It happens when the channel is really idle and no false alarm is generated with the probability of ${P_{B1}} = {p_0}(1 - {P_f})$.

• 2. Scenario 2: It happens when the channel is actually busy but wrongly sensed as idle by the ST with the probability of ${P_{B2}} = {p_1}(1 - {P_d^{*}})$.

In an unslotted primary system, PUs can start or stop transmitting at any time. Thus in Scenario 1, the PT might occupy the channel when ST is transmitting. This inevitably leads to interference between two systems, i.e., collisions. ST’s maximum instantaneous transmit rate under the idle channel is ${r(P_{tr})} = {\log _2}\left( {1 + \alpha P_{tr}}\right)$, where $\alpha =\frac{|h_{ss}|^2}{N_{0}}$. While a collision happens, secondary transmission fails and $r(P_{tr})$ reduces to zero for $P_p$ is much higher than $P_{tr}$. And the outage probability of PUs is

$$\begin{aligned} P_{out}=\Pr [\frac{{|h_{pp}|^2{P_p}}}{{{|h_{sp}|^2}{P_{tr}} + {N_0}}} < \beta ]=1-\frac{P_pe^{-\frac{\beta N_0}{P_p}}}{\beta P_{tr}+P_p}. \end{aligned}$$

(3)

According to [20, 23], given $S(t)=0$, the channel’s expected idle time during $[t,t+T_{tr}]$ is a function of $P_{tr}$, i.e.,

$$\begin{aligned} {T_0^0{(P_{tr})}} = \frac{E_{r}}{P_{tr}} -C_{0}(P_{tr}), \end{aligned}$$

(4)

where

$$\begin{aligned} C_{0}(P_{tr})=\frac{{{E_r}}}{{{P_{tr}}}}{p_1} +\frac{{{{\mathop {\mathrm {e}}\nolimits } ^{\left( {\frac{{ - ({\lambda _1} + {\lambda _0}){E_r}}}{{{P_{tr}}}}} \right) }} - 1}}{{{\lambda _1} + {\lambda _0}}}{p_1} \end{aligned}$$

(5)

is the average collision time and has been illustrated in Fig. 2.

For Scenario 2, the ST might have opportunities to enable successful transmission after the current primary transmission is finished. And the expected idle time during $[t,t+T_{tr}]$ provided that $S(t)=1$ is

$$\begin{aligned} {T_0^1{(P_{tr})}} = \frac{E_{r}}{P_{tr}} -C_{1}(P_{tr}), \end{aligned}$$

(6)

where

$$\begin{aligned} C_{1}(P_{tr})=\frac{{{E_r}}}{{{P_{tr}}}}{p_1} - \frac{{{{\mathop {\mathrm {e}}\nolimits } ^{\left( {\frac{{ - ({\lambda _1} + {\lambda _0}){E_r}}}{{{P_{tr}}}}} \right) }} - 1}}{{{\lambda _1} + {\lambda _0}}}{p_0}. \end{aligned}$$

(7)

The ST may go through Case A k times before going through Scenario 1 or Scenario 2 of Case B with the probability $P_{B1}{P_A}^k$ or $P_{B2}{P_A}^k$, respectively. And the residual energy $E_r$ for each condition is $E_r(T_{eh})=(1+k)(T_{eh}P_{eh}-T_{se}P_{se} )$. Therefore the average achievable throughput of the secondary system for a long-term period can be written as

$$\begin{aligned} R(T_{eh},P_{tr}) = \sum \limits _{k = 0}^\infty \frac{ r(P_{tr}) \varDelta (P_{tr})P_{tr} }{{T(T_{eh})P_{tr} + E_{r}(T_{eh})}} \cdot {{P_A}^k}, \end{aligned}$$

(8)

where $\varDelta (P_{tr})={{P_{B1}} T_0^0({P_{tr}}) + {P_{B2}} T_0^1({P_{tr}})}$ is ST’s average effective transmit time, and $T(T_{eh})= (1 + k)({T_{eh}} + {T_{se}})$.

3.2 Average Achievable Throughput Maximization

We formulate the maximization problem of the long-term average achievable throughput as

$$\begin{aligned} \mathbf {P1:} \quad \mathop {\max }\limits _{{T_{eh}},{P_{tr}}}&\quad R(T_{eh}, P_{tr}) \end{aligned}$$

(9a)

$$\begin{aligned} s.t.&\quad P_{tr}\ge 0 \end{aligned}$$

(9b)

$$\begin{aligned}&\quad {e_{h}} \ge {e_{s}} \end{aligned}$$

(9c)

$$\begin{aligned}&\quad P_{out} \le P_{out}^{max} \end{aligned}$$

(9d)

$$\begin{aligned}&\quad 0 \le T_{eh}\le T_{eh}^U . \end{aligned}$$

(9e)

In P1, (9c) refers to the average energy causality constraint. $P_{out}^{max}$ in (9d) is the outage probability threshold of the primary system. And $T_{eh}^U$ in (9e) is the maximum allowed energy harvesting time.

Substituting the expressions of $e_h$ and $e_s$ into (9c), we obtain

$$\begin{aligned} {T_{eh}} \ge T_{eh}^L, \ \text {where} \ {T_{eh}^L = \frac{{{P_{se}}{T_{se}}}}{{{P_{eh}}}}}. \end{aligned}$$

(10)

And according to (9d), we can get

$$\begin{aligned} {P_{tr}} \le P_{tr}^U, \ \text {where} \ P_{tr}^U=\frac{1}{\beta }(\frac{P_pe^{-\frac{\beta N_0}{P_p}}}{1-P_{out}^{max}}-P_p). \end{aligned}$$

(11)

Then P1 can be rewritten as

$$\begin{aligned} \mathbf {P2:} \quad \mathop {\max }\limits _{{T_{eh}},{P_{tr}}}&\quad R(T_{eh},P_{tr}) \nonumber \\ s.t.&\quad T_{eh}^L \le {T_{eh}} \le T_{eh}^U \\&\quad 0 \le {P_{tr}} \le P_{tr}^U \nonumber . \end{aligned}$$

(12)

Here, P2 is a non-trivial problem. We employ the differential evolution (DE) algorithm [24] to solve it. The optimal policy derivation is detailed in Algorithm 1, where the population size $N_p$, mutation factor F, crossover constant $C_r$ and the maximum number of generation $G_{max}$ are set to be 30, 0.85, 0.7 and 100, respectively. The total time complexity of Algorithm 1 is $O(2N_pG_{max})$.

3.3 Suboptimal Solution Derivation

Since the optimal policy of Algorithm 1 has a relatively high computational complexity, we next propose a suboptimal but effective policy as below.

Theorem 1

The average achievable throughput of the secondary system $R(T_{eh},P_{tr})$ is upper bounded by

$$\begin{aligned} R_U(T_{eh},P_{tr})= \frac{{{p_0}(1 - {P_f})r({P_{tr}}){\phi _1(T_{eh})}}}{{{\phi _1(T_{eh})}{P_{tr}} + {\phi _2(T_{eh})}}}\cdot \frac{1}{1-P_A}, \end{aligned}$$

(13)

where $\phi _1(T_{eh})=T_{eh}P_{eh}-T_{se}P_{se}$, $\phi _2(T_{eh})=T_{eh}+T_{se}$.

Proof

Since Q(x) is a monotonously decreasing function, ${P_f} \le P_d^*$ holds according to (2). Then we have

$$\begin{aligned} \varDelta (P_{tr}) \le (1-P_f)(p_0T_0^0({P_{tr}})+P_1T_0^1({P_{tr}})). \end{aligned}$$

(14)

Substituting (4) and (6) into (14), we can further derive that $\varDelta (P_{tr})\le \frac{p_0(1-P_f)E_r}{P_{tr}}$. Additionally, $\sum _{k = 0}^\infty {P_A^k}=\frac{1}{1-P_A}$. Therefore,

$$\begin{aligned} R(T_{eh},P_{tr})\le \frac{{{p_0}(1 - {P_f})r({P_{tr}}){\phi _1(T_{eh})}}}{{{\phi _1(T_{eh})}{P_{tr}} + {\phi _2(T_{eh})}}}\cdot \frac{1}{1-P_A}. \end{aligned}$$

(15)

This completes the proof of Theorem 1.

Then we discard the constant components in $R_U(T_{eh},P_{tr})$ and maximize it under the same constraints with P2, i.e.,

$$\begin{aligned} \mathbf {P3:} \quad \mathop {\max }\limits _{{T_{eh}},{P_{tr}}}&\quad \frac{{r({P_{tr}}){\phi _1(T_{eh})}}}{{{\phi _1(T_{eh})}{P_{tr}} + {\phi _2(T_{eh})}}} \nonumber \\ s.t.&\quad T_{eh}^L \le {T_{eh}} \le T_{eh}^U \\&\quad 0 \le {P_{tr}} \le P_{tr}^U \nonumber . \end{aligned}$$

(16)

To solve P3, we present the following Theorem 2.

Theorem 2

For P3, the optimal energy harvesting time $T_{eh}^{'}$ is $T_{eh}^U$ and the optimal transmit time $P_{tr}^{'}$ is given as

$$\begin{aligned} P_{tr}^{'}= \min \{ P_{tr}^U,\frac{\varphi }{{\alpha \cdot W\left( {\frac{\varphi }{e}} \right) }} - \frac{1}{\alpha } \}, \end{aligned}$$

(17)

where $W(\cdot )$ refers to the Lambert W function and $\varphi = \frac{{\alpha ({T_{eh}^{U}P_{eh}-T_{se}P_{se}})}}{{{T_{eh}^{U}+T_{se}}}} - 1$.

Proof

We first define a function

$$\begin{aligned} f(T_{eh},P_{tr})\triangleq \frac{{r({P_{tr}}){\phi _1(T_{eh})}}}{{{\phi _1(T_{eh})}{P_{tr}} + {\phi _2(T_{eh})}}}. \end{aligned}$$

(18)

It can be easily proved that the first order partial derivative of $f(T_{eh},P_{tr})$ with respect to $T_{eh}$ is positive for any ${T_{eh}} \in [T_{eh}^L,T_{eh}^U]$. Therefore, $f(T_{eh},P_{tr})$ is a monotonically increasing function for $T_{eh}$ and the optimal harvesting time $T_{eh}^{'}$ of P3 is obtained at $T_{eh}^U$.

Substituting $T_{eh}^{'}=T_{eh}^U$ into (18), we have $f(P_{tr})= \frac{{r({P_{tr}}){\phi _3}}}{{{\phi _4}{P_{tr}} + {\phi _3}}}$, where $\phi _3=T_{eh}^{U}P_{eh}-T_{se}P_{se}$ and $\phi _4=T_{eh}^{U}+T_{se}$. We denote the stationary point of $f(P_{tr})$ by $P_{tr}^{s}$ and it can be derived as

$$\begin{aligned}&{\left. {\frac{{\partial f(P_{tr})}}{{\partial {P_{tr}}}}} \right| _{{P_{tr}} = P_{tr}^s}} = 0 \Rightarrow \alpha {\phi _4}{P_{tr}} + {\phi _3} - {\phi _4}(1 + \alpha {P_{tr}})ln(1 + \alpha {P_{tr}}) = 0 \nonumber \\&\Rightarrow P_{tr}^{s}=\frac{\varphi }{{\alpha \cdot W\left( {\frac{\varphi }{e}} \right) }} - \frac{1}{\alpha }, \end{aligned}$$

(19)

where $W(\cdot )$ refers to the Lambert W function and $\varphi = \frac{{\alpha {\phi _4}}}{{{\phi _3}}} - 1$. Since $\frac{{\partial f({P_{tr}})}}{{\partial {P_{tr}}}}\ge 0$ when $0\le P_{tr}\le P_{tr}^{s}$ and $\frac{{\partial f({P_{tr}})}}{{\partial {P_{tr}}}}\le 0$ when $P_{tr}\ge P_{tr}^{s}$, the optimal transmit power of P3 is $P_{tr}^{'}= \min \{ P_{tr}^U,P_{tr}^{s} \}$. This completes the proof of Theorem 2.

Now, we can derive $(T_{eh}^{'},P_{tr}^{'})$ as a suboptimal policy to maximize the average achievable throughput by using Theorem 2. Next, we will evaluate its performance in Sect. 4.

4 Simulation Results

In this section, simulation results are presented to evaluate the performance of our proposed sensing-based flexible timeslot structure. Unless mentioned explicitly, simulation parameters (mainly referred to [21, 25]) are set as Table 1.

Table 1. Simulation parameters

Firstly, we present the impacts of average idle duration $E_0$ and average busy duration $E_1$ on the maximum average achievable throughput of the optimal policy, as shown in Fig. 3. The target detection probability $P_d^{*}$ and $P_{eh}$ are set to be 0.9 and 20 mW, respectively. As we can see, the maximum average achievable throughput increases with $E_0$ for a given $E_1$. The reasons come from two aspects. One is that the increase of $E_0$ results in a higher $p_0$ and a lower $P_A$ when $E_1$ is kept constant. And the decreased $P_A$ provides the ST with more spectrum access opportunities. The other is that the increase of $E_0$ prolongs ST’s average effective transmit time and finally leads to a throughput improvement. In addition, it can be seen that the maximum average achievable throughput raises up with a slow-down tendency, due to $p_0$ converges to 1 as $E_0$ enlarges. These also explain the throughput decline resulting from the increase of $E_1$ for a fixed $E_0$. In the case of the same $p_0$ (i.e., $E_0=0.1$ s with $E_1=0.2$ s and $E_0=0.2$ s with $E_1=0.4$ s), the throughput is absolutely dominated by $E_0$ thus a higher $E_0$ gains a better throughput performance.

Next, we analyze the impact of the target detection probability $P_d^{*}$ on the maximum average achievable throughput of the optimal policy in Fig. 4. Here, $E_0$ and $E_1$ are set to be 0.05 s and 0.1 s, respectively. As shown in Fig. 4, the maximum average achievable throughput grows significantly with the growth of $P_d^{*}$. Since $P_A$ monotonically increases with $P_d^{*}$, the ST has fewer spectrum access opportunities. To take full advantages of these rare opportunities, the ST may reduce $T_{eh}$ to sense the spectrum more frequently and then improve $P_{tr}$ to acquire a higher instantaneous transmit rate. The decrease of $T_{eh}$ and the increase of $P_{tr}$ jointly result in a higher maximum average achievable throughput.

4.1 Impacts of Key Parameters on the Optimal Policy

Fig. 3.

R versus $E_0$.

Fig. 4.

R versus $P_d$.

Fig. 5.

Throughput.

Finally, we discuss the impact of $P_{eh}$ on the throughput performance. From Fig. 4 we can observe that a higher average achievable throughput can be achieved by employing a higher $P_{eh}$. But the higher $P_{eh}$ is, the smaller the throughput gain is obtained. This implies that blindly promoting energy harvesting performance is not always desirable. The reason is that the increment of harvesting rate could not lead to a proportional throughput gain as we expected.

4.2 Analysis of the Average Achievable Throughput

In this subsection, we compare the maximum average achievable throughput of the optimal policy and suboptimal policy of our proposed flexible timeslot structure in Fig. 5. A conventional fixed timeslot structure proposed in [8] is introduced as our reference. Note the difference of throughput between the optimal and suboptimal policies is quite small, which indicates that our suboptimal policy can provide a proper approximation to the optimal policy. In addition, the average available throughput grows gradually when the growth of $E_0$. The reason is that the larger $E_0$ can provide more spectrum access opportunities for an ST. Accordingly, the results in Fig. 5 illustrate that our policies (including the optimal policy and suboptimal policy) outperform the conventional one both in achievable throughput. This demonstrates that our proposed flexible structure has more freedom to harvest and sense than a fixed timeslot structure.

5 Conclusion

In this paper, we propose a flexible timeslot structure for an EH CRN. The ST with the energy harvesting capability in this structure can share the same spectrum with an unslotted primary system without degrading primary transmission. To achieve this goal, we formulate an optimal policy derivation problem to maximize the long-term average achievable throughput of the secondary system under energy causality constraint and the SINR requirement of the primary system. Then, we design a DE-based optimal policy derivation to find the optimal solution and further provide a relative suboptimal policy to reduce the computational complexity. Numerical results demonstrate that our flexible timeslot structure is superior to the conventional fixed one. These results also indicate that it is necessary to design this flexible structure for the secondary system when PUs communicate with each other in the unslotted mode.