Abstract
We compute the corrections to the Schwarzschild metric necessary to reproduce the Hawking temperature derived from a Generalized Uncertainty Principle (GUP), so that the GUP deformation parameter is directly linked to the deformation of the metric. Using this modified Schwarzschild metric, we compute corrections to the standard General Relativistic predictions for the perihelion precession for planets in the solar system. This analysis allows us to set bounds for the GUP deformation parameter from well-known astronomical measurements.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Research on generalizations of the uncertainty principle of quantum mechanics has nowadays a long history [1]. One of the main lines of investigation focuses on understanding how the Heisenberg Uncertainty Principle (HUP) should be modified once gravity is taken into account. Given the pivotal rôle played by gravitation in these arguments, it is not surprising that the most relevant modifications to the HUP have been proposed in string theory, loop quantum gravity, deformed special relativity, and studies of black hole physics [2,3,4,5,6,7], just to mention some of the most notable frameworks.
Studies that aim at putting bounds on the dimensionless deforming parameter of the GUP, heretofore denoted by \(\beta \), date back at least to Brau [8], and can be roughly divided into three different categories (actually, only two, as we will see). In the first group one finds papers such as those of Brau [8], Vagenas [9], Nozari [10], which use a specific (in general, non linear) representation of the operators in the deformed fundamental commutatorFootnote 1 \( \left[ \hat{X},\hat{P}\right] = i\,\hbar (1 + \beta \, \hat{P}^2/m_{\mathrm{p}}^2)\,\) in order to compute corrections to quantum mechanical predictions, such as energy shifts in the spectrum of the hydrogen atom, or to the Lamb shift, the Landau levels, Scanning Tunneling Microscope, charmonium levels, etc. The bounds so obtained on \(\beta \) are quite stringent, but the drawback of this approach is a potentially strong dependence of the expected shifts on the specific (non linear) representation chosen for the operators \(\hat{X}\) and \(\hat{P}\) in the fundamental commutator.
In the second group, we can find the works of, e.g., Chang [11], Nozari and Pedram [12], where a deformation of classical Newtonian mechanics is introduced by modifying the standard Poisson brackets in a way that resembles the quantum commutator, \( \left[ \hat{x},\hat{p}\right] = i\,\hbar \left( 1 + \beta _0\, \hat{p}^2\right) \quad \Rightarrow \quad \{X,P\} = \left( 1 + \beta _0\, P^2\right) \ , \) where \(\beta _0=\beta /m_{\mathrm{p}}^2\). In particular, Chang in [11] computes the precession of the perihelion of Mercury directly from this GUP-deformed Newtonian mechanics, and interprets it as an extra contribution to the well known precession of 43”/century due to General Relativity (GR). He then compares this global result with the observational data, and the very accurate agreement between the GR prediction and observations leaves Chang not much room for possible extra contributions to the precession. In fact, he obtains the tremendously small bound \(\beta \lesssim 10^{-66}\). A problem with this approach is that a GUP-deformed Newtonian mechanics is simply superposed linearly to the usual GR theory. One may argue that a modification of GR at order \(\beta \) should likewise be considered, but this is however omitted in [11]. In other words, it is not clear why the two structures, GR and GUP-modified Newtonian mechanics, should coexist independently, and why the two different precession errors add into a final single precession angle. Most important, as a matter of fact, in the limit \(\beta \rightarrow 0\), [11] recovers only the Newtonian mechanics but not GR, and GR corrections must be added as an extra structure. Clearly, the physical relevance of this approach and the bound that follows for \(\beta \), remain therefore questionable.
Finally, a third group of works on the evaluation of \(\beta \) contains, for example, papers by Ghosh [13] and Pramanik [14]. They use a covariant formalism, first defined in Minkowski space, with the metric \(\eta _{\mu \nu }=\mathrm{diag}(1,-1,-1,-1)\), which can be easily generalized to curved space-times via the standard procedure \(\eta _{\mu \nu } \rightarrow g_{\mu \nu }\). These papers should however be considered as belonging to the second group. In fact, a closer look reveals that they also start from a deformation of classical Poisson brackets, although posited in covariant form. From the deformed covariant Poisson brackets, they obtain interesting consequences, like a \(\beta \)-deformed geodesic equation, which leads to a violation of the Equivalence Principle. They do not deform the field equations or the metric. In [15], however, we show that this violation of the Equivalence Principle is completely due to the postulate of deformed Poisson brackets, and has nothing to do with the covariant formalism, or with a deformation of the GR field equations or solutions, or of the geodesic equation. Nonetheless, the Ghosh–Pramanik formalism remains covariant when \(\beta \rightarrow 0\) and reproduces standard GR results in the limit \(\beta \rightarrow 0\) (this differs, in general, from the results obtained by papers in the second group).
The novelties of our approach, when compared with the previous ones, are many and various. The main point is to start directly from a quantum mechanical effect, the Hawking evaporation, for which the GUP is necessarily relevant, rather than postulating specific representations of canonical operators or modifications of the classical equations of motion. We connect the deformation of the Schwarzschild metric directly to the uncertainty relation, without relying on a specific representation of commutators. We leave the Poisson brackets and classical Newtonian mechanics untouched, and recover GR, and standard quantum mechanics, in the limit \(\beta \rightarrow 0\). In particular, we preserve the Equivalence Principle, and the equation of motion of a test particle is still given by the standard geodesic equation. In the present work, this is obtained by deforming a specific solution of the standard GR field equations, namely the Schwarzschild metric.
2 Deforming the Schwarzschild Metric
In this section, we start from a known way of deriving the Hawking temperature directly from the metric of a black hole, and then show how the GUP modifies the Hawking temperature. These two steps will pave the road to a deformation of the Schwarzschild metric, constructed so as to reproduce the GUP-modified Hawking temperature. We consider here a space-time with a metric that locally has the form
where \(\mathrm{d}\Omega ^2 = \mathrm{d}\theta ^2+\sin ^2\theta \,\mathrm{d}\phi ^2\). The horizons (if any), are located at the positive zeros of the function F(r) (see, for example, [16]).
We loosely follow a standard derivation, as for example that in [17]. Suppose \(r=r_\mathrm{H}\) is an horizon, so that \(F(r_\mathrm{H})=0\), and consider \(r \ge r_\mathrm{H}\). Then, a quantized scalar field outside the horizon lives in a heat bath with temperature
Therefore the temperature of the black hole horizon as seen by a distant observer is in general given by formula (17.2). In particular, for a Schwarzschild black hole the function F(r) is given by \((1-2 G_{\mathrm{N}}M/r)\), the horizon is at \(r_H = 2\,G_{\mathrm{N}}\,M\), and we get \( T_\mathrm{H} = \hbar /(8\pi \, G_{\mathrm{N}}\,M) \ , \) which is the well-known Hawking temperature.
We now give here a derivation of the mass-temperature relation starting directly from the uncertainty relations. The most common form of deformation of the Heisenberg uncertainty relation (and the form of GUP that we are going to study in this paper) is without doubt the following
The dimensionless parameter \(\beta \) is usually assumed to be of order one, in the most common quantum gravity formulations. Following the arguments of [18,19,20,21,22,23], we promptly arrive to translate relation (17.3) into a mass-temperature relation for a Schwarzschild black hole
To zero order in \(\beta \), we recover the usual Hawking formula. Let us note that in this work we assume that the correction induced by the GUP has a thermal character, and therefore it can be cast in the form of a shift of the Hawking temperature. Of course, there are also different approaches (see e.g. [24]), where the corrections do not respect the exact thermality of the spectrum, and thus need not be reducible to a simple shift of the temperature.
We can legitimately wonder what kind of (deformed) metric would predict a Hawking temperature like the one inferred from the GUP relation (17.4), for a given \(\beta \). Since we are interested only in small corrections to the Hawking formula, we can consider a deformation of the Schwarzschild metric of the kind
and we shall look for the lowest order correction in \(\varepsilon \). We see that (17.5) is actually the simplest mathematical form, if one supposes that the metric can be expanded in powers of 1 / r. This is nothing else than the well known Eddington–Robertson expansion of a spherically symmetric metric. Note however that, since \(R_{\mathrm{H}}/r\sim 10^{-5}\) on the surface of the Sun, the term proportional to \(\varepsilon \) can still be considered small even if \(\varepsilon \) is relatively large. The temperature predicted by this deformed Schwarzschild metric is
which must coincides with the temperature \(T(\beta )\) predicted by (17.4), for any given \(\beta \). This yields a relation between \(\beta \) and \(\varepsilon \),
For \(|\varepsilon | \ll 1\), to the lowest order in \(\varepsilon \), we thus get \( \beta = - \pi ^2 M^2 \varepsilon ^2/(4\,m_{\mathrm{p}}^2)\,\) where we notice that both \(\beta \) and \(\varepsilon \) are dimensionless. It is now of great interest to observe that (17.7) forces us to admit that \(\beta < 0\), since \(\varepsilon \le 1\). Although quite unexpected, this might be a suggestion of fundamental importance. It seems that a metric is able to reproduce the GUP-deformed Hawking temperature only if the deforming parameter \(\beta \) is negative. We already encountered a situation like this when we studied the uncertainty relation formulated on a crystal lattice [25]. This could be a further hint that the physical space-time has actually a lattice or granular structure at the level of the Planck scale.
3 Perihelion Precession by Deformed Schwarzschild Metric
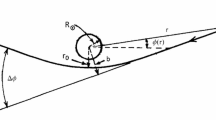
Having established a connection between the GUP parameter \(\beta \) and the deformation \(\varepsilon \) of the Schwarzschild metric, we are now in a position to compute the physical (possible observable) consequences of such a deformed metric. Here, we consider a particle bound in a orbit around a massive body, typically a planet around the Sun. Again, we roughly follow the treatment of [26]. The relevant geometrical parameters for an elliptic orbit in a polar coordinates system, with the radial coordinate r which at aphelia and perihelia takes, respectively, the maximum value \(r_+\) and minimum value \(r_-\), are the eccentricity e, the semi-major axis a, and the semilatus rectum L. These geometrical parameters are related by \( r_\pm = (1\pm e)\, a\), \(L = (1 - e^2)\,a\), \(\frac{2}{L} = \frac{1}{r_+} + \frac{1}{r_-} \ . \) The angle swept out by the position vector when it increases from \(r_-\) to r is then given by the integral
The total change in \(\phi \) at every lap is just twice the change as r increases from \(r_-\) to \(r_+\). This would equal \(2\pi \) if the orbit were a closed ellipse, so the total orbital precession in each revolution is given by \( \Delta \phi = 2 \left| \phi (r_+) - \phi (r_-)\right| - 2\pi \ . \) We expand the integrand before integrating, and the small parameter is given by \(R_{\mathrm{H}}/r_-\), or better \(R_{\mathrm{H}}/L\). Finally the total precession after a single lap, to first order in \(R_{\mathrm{H}}/L\), is given by
which, of course, reproduces the usual GR prediction in the limit \(\varepsilon \rightarrow 0\). This relation should now be compared with known observational data.
The perihelion precession for Mercury is by far the best known and measured GR precession in the Solar system. Referring to [27] for the latest most accurate and comprehensive data, we can report the relation
where \(\langle \dot{\omega }\rangle \) is the measured perihelion shift, \(J_2\) a dimensionless measure of the quadrupole moment of the Sun, and \(\gamma \) and \(\bar{\beta }\) are the usual Eddington–Robertson expansion parameters. The latest data from helioseismology give \(J_2=(2.2\pm 0.1) \cdot 10^{-7}\). The measured perihelion shift of Mercury is known to about \(0.1\%\) from radar observations of Mercury between 1966 and 1990 [28]. The solar oblateness effect due to the quadrupole moment is then smaller than the observational error, so it can be neglected. Substituting standard orbital elements and physical constants for Mercury and the Sun, we obtain
where we can place a bound of \(|2\,\gamma - \bar{\beta } -1| \lesssim 3 \cdot 10^{-3}\). Comparing with \(\Delta \phi \) from (17.9), we get \( |\varepsilon | \lesssim 6\cdot 10^{-3}\,\) which, replaced in (17.7), yields the lower bound
We can also consider the most recent data from the Messenger spacecraft [29], which orbited Mercury in 2011–2013, and improved very much the knowledge of its orbit. Then we can push this bound even lower, to \(|2\gamma - \bar{\beta } -1| \lesssim 7.8 \cdot 10^{-5}\), although the knowledge of \(J_2\) would have to improve simultaneously. If just the error in \(|2\gamma - \bar{\beta } -1|\) were taken into account, this would imply \( |\varepsilon | = 2\,\left| 2\gamma - \bar{\beta } -1\right| \lesssim 1.56 \cdot 10^{-4} \) and therefore
But of course this limit should not be considered completely reliable in this contest, since the less accurate bound on \(J_2\) cannot be brutally neglected, at least in principle. Once again the perihelion shift appears to be one of the most precise tests of GR, a true GR effect not present at all in Newtonian gravity (as it is well known).
4 Conclusions
We have shown that a suitable deformation of the Schwarz-schild metric can reproduce the Hawking temperature for a black hole, when this is computed from a Generalized Uncertainty Principle. We have found in this way an analytic relation between the deformation parameter of the metric \(\varepsilon \) and the usual GUP deformation parameter \(\beta \). In particular, when \(\beta \rightarrow 0\), we correctly recover GR, and standard quantum mechanics. Neither the geodesic equation, nor the equivalence principle are violated, for any value of \(\beta \) or \(\varepsilon \). Well-known astronomical measurements, in the Solar system as well as in binary pulsar systems, allowed us to put constraints on the parameter \(\beta \). This direction seems to point towards promising research: at present we just deformed the Schwarzschild solution, but a future possibility is to deform the full field equations of GR, in order to get, among other things, a more stringent bound on the GUP parameter \(\beta \). We would like to conclude by emphasizing once again that, although in the existing literature one can find bounds on \(\beta \) much tighter than those obtained in this paper, they seem to depend, at least partially, either on a specific (non linear) representation of the deformed commutator, or on the hypothesis of a deformation of Poisson brackets, which implies a violation of the equivalence principle. The line of reasoning presented in this paper avoids these possible difficulties.
Notes
- 1.
We shall work with \(c=k_B=1\), but explicitly show the Newton constant \(G_{\mathrm{N}}\) and Planck constant \(\hbar \). We also recall that the Planck length is defined as \(\ell _{\mathrm{p}}^2=G_{\mathrm{N}}\,\hbar /c^3\), the Planck energy as \(\mathscr {E}_{\mathrm{p}}\,\ell _{\mathrm{p}}= \hbar \, c /2\), and the Planck mass as \(m_{\mathrm{p}}=\mathscr {E}_{\mathrm{p}}/c^2\), so that \(G_{\mathrm{N}}=\ell _{\mathrm{p}}/2\,m_{\mathrm{p}}\) and \(\hbar =2\,\ell _{\mathrm{p}}\,m_{\mathrm{p}}\).
References
H.S. Snyder, Phys. Rev. 71, 38 (1947); C.N. Yang, Phys. Rev. 72, 874 (1947); C.A. Mead, Phys. Rev. 135, B 849 (1964); F. Karolyhazy. Nuovo Cimento A 42, 390 (1966)
D. Amati, M. Ciafaloni, G. Veneziano, Phys. Lett. B 197, 81 (1987); D.J. Gross, P.F. Mende. Phys. Lett. B 197, 129 (1987)
M. Maggiore, Phys. Lett. B 304, 65 (1993)
A. Kempf, G. Mangano, R.B. Mann, Phys. Rev. D 52, 1108 (1995)
F. Scardigli, Phys. Lett. B 452, 39 (1999)
R.J. Adler, D.I. Santiago, Mod. Phys. Lett. A 14, 1371 (1999)
F. Scardigli, R. Casadio, Class. Quantum Gravity 20, 3915 (2003)
F. Brau, J. Phys. A 32, 7691 (1999)
S. Das, E. Vagenas, Phys. Rev. Lett. 101, 221301 (2008)
P. Pedram, K. Nozari, S.H. Taheri, JHEP 1103, 093 (2011)
L.N. Chang, D. Minic, N. Okamura, T. Takeuchi, Phys. Rev. D 66, 026003 (2002)
K. Nozari, S. Akhshabi, Chaos Solitons Fractals 37, 324 (2008)
S. Ghosh, Class. Quantum Gravity 31, 025025 (2014)
S. Pramanik, S. Ghosh, Int. J. Mod. Phys. A 28(27), 1350131 (2013)
F. Scardigli, R. Casadio, Eur. Phys. J. C 75, 425 (2015)
M. Walker, J. Math. Phys. (N.Y.) 11, 2280 (1970)
A. Zee, Quantum Field Theory in a Nutshell (Princeton University Press, Princeton, 2003)
F. Scardigli, Nuovo Cimento B 110, 1029 (1995)
R.J. Adler, P. Chen, D.I. Santiago, Gen. Relativ. Gravity 33, 2101 (2001)
M. Cavaglia, S. Das, R. Maartens, Class. Quantum Gravity 20, L205 (2003)
L. Susskind, J. Lindesay, An Introduction to Black Holes, Information, and the String Theory Revolution (World Scientific, Singapore, 2005). See chapter 10
K. Nouicer, Class. Quantum Gravity 24, 5917 (2007)
F. Scardigli, Glimpses on the Micro Black Hole Planck Phase, arXiv:0809.1832
G. Dvali, C. Gomez, Black Hole’s Quantum N-Portrait, arXiv:1112.3359
P. Jizba, H. Kleinert, F. Scardigli, Phys. Rev. D 81, 084030 (2010)
S. Weinberg, Gravitation and Cosmology (Wiley, New York, 1972)
C.M. Will, Living Rev. Relativ. 9, 3 (2006). Update in arXiv:1403.7377v1
I.I. Shapiro, Solar system tests of general relativity: recent results and present plans, in Proceedings of the 12th International Conference on General Relativity and Gravity, ed. by N. Ashby, D.F. Bartlett, W. Wyss, Boulder, 1989, (Cambridge University Press, Cambridge, U.K., New York, U.S.A., 1990)
A.K. Verma, J. Laskar, Astron. Astrophys. 561, A115 (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Scardigli, F., Casadio, R. (2018). Perihelion Precession and Generalized Uncertainty Principle. In: Nicolini, P., Kaminski, M., Mureika, J., Bleicher, M. (eds) 2nd Karl Schwarzschild Meeting on Gravitational Physics. Springer Proceedings in Physics, vol 208. Springer, Cham. https://doi.org/10.1007/978-3-319-94256-8_17
Download citation
DOI: https://doi.org/10.1007/978-3-319-94256-8_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94255-1
Online ISBN: 978-3-319-94256-8
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)