9.1 Introduction

In their classic work, Eigen and Schuster (1977) point out, in a single breath, two apparently defining properties of living matter, genetic information and homochirality. The origin of these two properties has spurred many productive lines of research. However, these two subfields have remained fairly distinct from one another, as experimental systems differ substantially. We have recently reviewed elsewhere the recent progress that has been made by adopting a synthetic and mechanistic perspective to these questions, shifting the focus from the specific origin of life on Earth to the mechanisms that could give rise to life more generally (Pressman et al. 2015). This shift is timely given the developing picture of the universe as being quite rich in exoplanets that might have conditions favorable for life. While mathematical models may lack the baroque beauty and realism of experimental science, they can be powerful in revealing general principles and mechanisms that may apply widely. In the spirit of searching for generalizable mechanisms, we review here mathematical models describing the prebiotic evolution of genetic information and the emergence of homochirality. A comparison of these models reveals an underlying commonality that connects the evolutionary dynamics of prebiotic replicators to the amplification dynamics of chiral molecules.

In this discussion, we will assume for convenience that genetic evolution took place in the RNA world in which RNA stored genetic information and catalyzed chemical reactions (Bartel and Szostak 1993; Crick 1968; Orgel 1968; Woese et al. 1966). The RNA world probably included other molecules, such as lipids and simple peptides, but genetic inheritance would have been based on RNA. At some point, the presence of other chemical cycles would have been necessary to generate the compounds needed for RNA replication. However, we will focus on replicator scenarios, taking the simplistic perspective that these chemical cycles are considered only insofar as they may affect RNA fitness. While RNA is used for the sake of discussion, the mathematical models are relatively agnostic regarding the identity of the genetic polymer.

In the absence of any chiral polarization, the synthesis of chiral molecules from achiral starting materials generally results in the formation of mixtures containing equal amounts of both enantiomers (i.e., racemic mixtures). For example, this is the case for the formation of amino acids in the prebiotic synthesis experiments carried out by Miller (1953). In stark contrast, molecules that form the building blocks of life (e.g., amino acids and sugars) essentially exist as a single enantiomer in biology. Empirically, biological systems are homochiral, having a nearly complete chiral imbalance (mirror symmetry breaking), raising the question of how biological homochirality arises (Guijarro and Yus 2009; Blackmond 2010; Cintas 2016).

Several theories have been proposed to explain the origins of biomolecular homochirality (Guijarro and Yus 2009). Proposed mechanisms are either deterministic (i.e., a specific chiral field or influence causes the breaking of mirror symmetry) or random (i.e., the direction of symmetry breaking is random). In deterministic theories, the enantiomer imbalance is created due to an external chiral field or influence. Deterministic mechanisms can also be either local in space or universal, i.e., applying everywhere. Some examples of local deterministic mechanisms are circularly polarized light (CPL), β-Radiolysis, or the magnetochiral effect (Barron 1981, 1986). This mechanism does not have to occur on Earth, but instead may occur elsewhere with the enantiomeric imbalance of organic molecules being delivered to Earth by meteorites and comets (Myrgorodska et al. 2015). On the other hand, the most accepted universal deterministic theory is based on the electroweak interaction. The theory of electroweak interactions predicts a parity violating energy difference (PVED) between the two enantiomers of chiral molecules of 10−13–10−21 eV; however, no conclusive energy difference has been reported so far (Bargueno et al. 2011). In comparison, chance or random theories are based on the knowledge that a perfect racemic mixture is statistically exceedingly improbable for a molecular system of any reasonable size (Mislow 2003). That is, an initial enantiomeric excess is virtually inescapable due to stochastic fluctuations within a racemic system.

Regardless of the type of theory, biological homochirality is believed to arise through the same three sequential stages: (1) the symmetry is broken, either by a chiral field or influence or by random chance on a microscopic scale; (2) once any kind of imbalance has been created, the initial imbalance is amplified; and (3) once a significant enantiomeric enrichment has been produced, the chiral imbalance is transferred through the entire system (e.g., from monomers to polymers); this step is referred to as “transmission.”

Although every theory follows the three same steps, the relevance of each step is different for each type of theory. For a deterministic mechanism, the method by which an initial enantiomeric excess is made is important (step 1). In a chance mechanism, by contrast, the source of the initial imbalance is not as important as the need to amplify the initial imbalance through an efficient mechanism; the key process in this case is chiral amplification (step 2). While chance theories obviate the need to invoke chiral physical fields and support the idea that homochirality is a “stereochemical imperative” of molecular evolution (Siegel 1998), both chance and deterministic theories, regardless of the chiral field or force involved, would still require an effective amplification mechanism. Therefore, for mathematical models of the evolution of biological homochirality, the focus of the model is not on the source of the initial enantiomeric imbalance but on the ability of the model to amplify a tiny initial enantiomeric imbalance, such as by autocatalytic reactions.

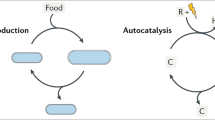
The chemical reactions involved in the evolution of genetic information and the emergence of homochirality can be translated readily into mathematical models (Fig. 9.1). The purpose of this chapter is to review some models of early evolutionary dynamics and illustrate their relationships with models describing possible amplification mechanisms leading to homochirality in the prebiotic world.

Fig. 9.1
figure 1

Relationships among models considered

Full size image

9.2 Polymerization and Replication in “Prelife” Models

A crucial question regarding the origin and chemical evolution of RNA is how chemical kinetics become evolutionary dynamics (Chen and Nowak 2012). That is, how does evolution get started before RNA exhibits specific functions, particularly replication? We review the models by Nowak et al. on the emergence of replication in the simplest possible population dynamics that can produce information and complexity.

We consider a prebiotic scenario of polymers that grow by monomer addition, in which the monomers come in two types (a binary alphabet). In this case, the polymers carry information, and different sequences may or may not differ in their rates of growth by polymerization. For example, we imagine a prebiotic chemistry that produces a binary “soup” of activated monomers, denoted by 0* and 1*, which can either become deactivated (0∗ → 0 and 1∗ → 1) or form random polymers (binary sequences) of any length via the chemical reactions i + 0∗ → i0 and i + 1∗ → i1. Following this scheme, each binary string, i, has only one possible predecessor, i′, and two possible descendants, i0 and i1. This system has been named “prelife” and the associated dynamics “prevolution” (Nowak and Ohtsuki 2008; Ohtsuki and Nowak 2009). If we denote the abundance of each binary sequence i as xi, then the chemical kinetics of prelife can be described by the following system of differential equations:

$$ {\dot{x}}_i={a}_i{x}_{i^{\prime }}-\left(d+{a}_{i0}+{a}_{i1}\right){x}_i, $$
(9.1)

where ai is the rate constant of monomer addition (i.e., i′ → i) and includes the concentration of activated monomers, which are assumed to be at steady state, and d is the decay rate. If we consider that every sequence of the same length grows at the same rate (a0 = a1 and ai = a for all other i), then all sequences with the same length are found to have the same abundance at equilibrium and the longer sequences are found to be exponentially less abundant. If by contrast, different sequences of the same length grow at different rates (e.g., some reactions occur at a rate, ai = 1 + s, while the other reactions occur at a slower rate ai = 1), then the equilibrium distribution of all sequences depends on the rate difference s. As s increases, the equilibrium abundance of some sequences becomes higher than that of other sequences of the same length. Thus, differences in reaction rate can create downstream asymmetries that are essentially a chemical analog of natural selection.

As Eigen demonstrated earlier for his model of replicators, prelife also exhibits an “error threshold,” i.e., a limit to the degree of mutation that can be tolerated while preserving genetic information. In analogy to Eigen’s model, we can consider a “master sequence” of length n, which is more fit and abundant than all other sequences of the same length (this situation can be depicted as a “single-peak” fitness landscape). The master sequence is defined by the fact that the reactions leading to it are faster than the other reactions taking place in the system. If every reaction leading to the master sequence makes mistakes by incorporating the wrong monomer with probability w, then the master sequence is selected only if w < 1/n. That is, there is an error threshold for the emergence of the master sequence, namely, that the mutation rate is inversely proportional to the length of the master sequence. In other words, for a certain polymerization accuracy, there is a maximum value for the sequence length over which the master sequence is not preserved anymore and the informational content is destroyed by the mistakes made in polymerization.

To introduce replication to prelife, assuming the parameters are adequate for selection of the master sequence, some sequences are allowed to act as templates for replication (enzymatic or chemical). The system is then described by a set of differential equations based on Eq. (9.1) for prevolutionary dynamics, except with an extra term which represents replication (see Sect. 9.3.1):

$$ {\dot{x}}_i={a}_i{x}_{i^{\prime }}-\left(d+{a}_{i0}+{a}_{i1}\right){x}_i+{rx}_i\left({f}_i-\phi \right). $$
(9.2)

In this case, fi is the fitness of sequence i, ϕ = ∑ifixi / ∑ixi is the average fitness (this term ensures that the total population in the system remains constant), and the parameter r represents a scale factor between the rates of template-directed replication (“life”) and template-independent sequence growth (“prelife”). For small values of r, the dynamics are dominated by prevolution, that is, the abundance of potential replicators is not high enough to affect the equilibrium structure of prelife, dominated by non-templated polymerization. However, there is a critical value for r, over which those sequences that replicate at a faster rate dominate the population, whereas all other sequences that replicate slower are depleted.Footnote 1 This critical value, rc, which evidences a well-defined phase transition between prelife and life, can be obtained by solving for the condition that the net reproductive rate of replicator i, defined as gi = r(fi − ϕ) − (d + ai0 + ai1), is positive.

If sequences incorporate mutations (errors) when replicating with probability u, then the net reproductive rate of the master sequence is gi = r(fiq − ϕ) − (d + ai0 + ai1), where q = (1 − u)n represents the replication accuracy (i.e., the probability of error-free replication). The master sequence will be selected only if the replication accuracy exceeds a certain minimum value, q > (d + ai0 + ai1)/rfi. In other words, life (replicators) is selected over prelife (polymerization) only if the mutation rate, u, is less than a critical value. Therefore, imperfect replication imposes an error threshold for the emergence of life-like growth dynamics that depends on the length of the potential replicators, the relative fitness of the master sequence, and the balance between the rate of polymerization and the rate of replication.

These models clarify that a kind of natural (chemical) selection can precede replicators per se and may be a mechanism for favoring a master sequence. In addition, the mere presence of the mechanism of replication is not enough to favor replicators, as replicating sequences in the system do not always attain much higher abundances than non-replicating sequences of the same length. Interestingly, in prelife scenarios without replication, small differences in growth rates result in small differences in abundances, reflecting the expected chemical kinetics. On the other hand, in prelife scenarios with replication, small differences in replication rates can lead to large differences in abundance, reflecting the dynamics seen in evolution.

Although the prelife models use a binary alphabet for the monomers, similar dynamics are expected in a quaternary system (Sievers and Von Kiedrowski 1994). Prelife models, although abstract in some aspects, are a straightforward approach to modeling that could be applied to non-templated nucleic acid polymerization (Ertem and Ferris 1996; Ferris and Ertem 1992, 1993; Ferris et al. 1996; Rajamani et al. 2008; Monnard and Deamer 2001, 2002) and template-directed polymerization (Sawai and Orgel 1975; Orgel 1992; Manapat et al. 2009; Ohtsuki and Nowak 2009) in different scenarios.

9.3 Models of Replication and Mutation

9.3.1 The Replicator, Replicator-Mutator, and Quasispecies Models

The dynamics of a system composed of self-replicating entities is described by the replicator equation (Hofbauer and Sigmund 1998; Hofbauer et al. 1979; Maynard Smith 1982). An important feature that is captured in the replicator equation is frequency-dependent selection, i.e., that the fitness of a particular sequence depends on the frequency of the other sequences in the population. The replicator equation that describes evolutionary game dynamics of discrete phenotypes reads as follows:

$$ {\dot{x}}_i={x}_i\left[{f}_i\left(\boldsymbol{x}\right)-\overline{f}\right], $$
(9.3)

where xi is the frequency of sequence i; fi is the fitness of xi and is a function of the distribution of the population, given by the vector x = (x1, …, xn); and \( \overline{f} \) represents the average fitness, \( \overline{f}={\sum}_{j=1}^n{x}_j{f}_j\left(\boldsymbol{x}\right) \). Note that ∑ixi = 1 by definition. In Eq. (9.3), the fitness function depends on the distribution of the population types, so that the replicator equation can capture the frequency-dependence of fitness. This key feature is the reason why the replicator equation is useful in several different fields [such as population genetics (Hadeler 1981), autocatalytic reaction networks (Stadler and Schuster 1992), game theory (Bomze and Burger 1995), or language evolution (Nowak et al. 2001)]. However, with respect to early evolution, a major caveat is that the replicator equation does not account for the effect of mutations and so does not model the invention of new types. A generalization of the replicator equation which incorporates mutation is given by the replicator-mutator equation:

$$ {\dot{x}}_i=\sum \limits_{j=1}^n{x}_j{f}_j\left(\boldsymbol{x}\right){q}_{ji}-{x}_i\overline{f}, $$
(9.4)

where qij is the probability that replication of sequence i gives rise to sequence j. The replicator equation (Eq. 9.3) is clearly a particular case of the replicator-mutator equation (Eq. 9.4), in which the fitness of each xi is a function of the distribution of the population x, but there is no mutation. Presumably the different replicators eventually established cooperation (e.g., increased fitness of i with increased abundance of j) during early evolution.

While the replicator-mutator equation describes a system in which fitness depends on the frequency of other types, the quasispecies model describes a system in which mutations are allowed but the fitness of any sequence does not depend on the fitness of other sequences. The quasispecies can be visualized as a family of closely related sequences (or genotypes) that exist in a scenario in which there is replication and mutations (that is, mistakes can be made when replicating sequences). Consider a master sequence, xm, whose fitness is much higher than all competing sequences, such that its abundance persists at a level higher than that of all other sequences. With every round of replication, xm will generate a population of mutants closely related to itself, making it impossible for xm to completely eliminate its competitors (members of its own quasispecies). Since the replicator equation does not include mutation, the quasispecies model may be a more adequate formalism to study early evolution. For a detailed discussion on the mathematical equivalences between these replicator models, or for other uses of the models, see Page and Nowak (2002).

9.3.2 Lotka-Volterra Equations of Interacting Species

The Lotka-Volterra equations (Lotka 1920; Volterra 1926) (also commonly known as the predator-prey equations) are frequently used in ecology to describe the interactions among n different species. The model can be described by the following differential equation for each species:

$$ {\dot{y}}_i={y}_i\ {f}_i\left(\boldsymbol{y}\right), $$
(9.5)

where yi is the abundance of species i and fi is the fitness (or reproductive rate) of each species, which is a function of the distribution of the population abundance, given by the vector y = (y1, …, yn). One may see that these equations describe frequency-dependent selection, like the replicator models discussed above. Interestingly, as Hofbauer et al. pointed out almost two decades ago (Hofbauer and Sigmund 1998), using the barycentric transformation xi = yi/(1 + y) for i = 1, …, n − 1, and xn = 1/(1 + y), where y is defined as \( y={\sum}_{i=1}^{n-1}{y}_i \), it is readily shown that the replicator equation for n phenotypes (Eq. 9.3) is equivalent to the Lotka-Volterra equations for n − 1 species (Eq. 9.5).

One of the simplest forms of the Lotka-Volterra model considers only reproduction and mutual antagonism effects, and two different species, N1 and N2, which have net rates of increase (birth minus death) ε1 and ε2. The change of N1 and N2 population numbers over time can be described by the following pair of differential equations (Lotka 1925, 1932):

$$ {\dot{N}}_1={\varepsilon}_1\ {N}_1+{\mu}_1\ {N}_2\ {N}_{1,} $$
(9.6)
$$ {\dot{N}}_2={\varepsilon}_2\ {N}_2+{\mu}_2\ {N}_1\ {N}_2. $$
(9.7)

The signs of μ1 and μ2 describe the interaction between the two species. If μ1 or μ2 is negative, the interaction is unfavorable and antagonistic for that species; if μ1 or μ2 is positive, the interaction is favorable for that species; and if μ1 and μ2 are 0, the interaction is neutral for that species. When the interaction between species is mutually unfavorable (μ1 < 0 and μ2 < 0), and assuming that the rates of reproduction are both positive (ε1 > 0 and ε2 > 0), the system is found to have a saddle point about which the slightest variation leads to the complete extinction of one of the two species. Thus, if initial conditions are such that N1 > N2 (or N2 > N1), the system evolves toward an asymptotic solution, in which only one of the two species survives (competitive exclusion). This feature is reminiscent of chiral amplification, in which an initially small imbalance in numbers is amplified to total enantiomeric excess. We examine models of homochirality to address this similarity in detail.

9.4 Models of Absolute Asymmetric Synthesis

9.4.1 Frank Model of Homochirality

In a footnote, Volterra specified that he did not consider the degenerate case (equal rates and parameters for both species; in this case ε1 = ε2 and μ1 = μ2) because such a situation is of “infinitesimally small probability” (Volterra 1926; English Translation in Chapman 1931). However, as it was recently noted by Ribo and Hochberg (2015), this special case of the Lotka-Volterra two-species competitive exclusion model for two distinguishable but degenerate species is identical to the degenerate case of enantiomerism that was later considered by Frank in a model for spontaneous asymmetric synthesis in chemical systems (Frank 1953).

In an attempt to explain the origin of biological homochirality, Frank proposed a simple model in which two chemical substances, n1 and n2, which are enantiomers of each other, act as autocatalysts for their own production (with rate ka > 0) and as inhibitors for the production of their optical enantiomer (with rate kb > 0). The system is described by the following pair of differential equations (where concentration brackets are omitted in the notation for simplicity):

$$ {\dot{n}}_1={k}_a\ {n}_1-{k}_b\ {n}_2\ {n}_1, $$
(9.8)
$$ {\dot{n}}_2={k}_a\ {n}_2-{k}_b\ {n}_1\ {n}_2. $$
(9.9)

As in the Lotka-Volterra model, the analytical solutions for Eqs. (9.8) and (9.9) show that every starting condition different from [n1]0 = [n2]0 will lead to one of the asymptotes [n1] = 0 or [n2] = 0. Thus, the equality of [n1]0 and [n2]0 represents a condition of unstable equilibrium. With this in mind, the ecological competitive exclusion principle, originally derived from the Lotka-Volterra two-species model, can be regarded as a consequence of sufficiently antagonistic interactions between two (biological) species that are competing for common, finite resources. In the Frank model—and generally in the literature on absolute asymmetric synthesis—this antagonistic interaction between (chemical) species is usually referred to as mutual inhibition.

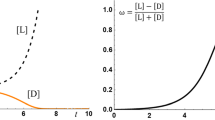
Figure 9.2 shows how the autocatalytic production of enantiomers n1 and n2, coupled with a step of mutual inhibition, in which n1 and n2 interact with each other in such a way that results in the removal of both from the system, can propagate and amplify an initial imbalance of one of the enantiomers present in the system [Eqs. (9.8)–(9.9)]. In this sense, this antagonistic interaction (represented by the mutual inhibition between enantiomers) essentially decreases the racemic content in the system, making the enantiomeric imbalance more evident. For low concentrations of monomers, the mutual inhibition between enantiomers will remove the monomers from the system before a significant enrichment can be observed. However, if the concentration of enantiomers is large enough, the amplification process can be sustained and the enantioselective autocatalysis of one of the enantiomers (n1 in the example of Fig. 9.2) will eventually dominate the system.

Fig. 9.2
figure 2

Homochirality emerging according to the Frank model, based on autocatalytic replication and mutual inhibition of enantiomers. Adapted from Blackmond (2010)

Full size image

9.4.2 A Realistic Model of Homochirality

The original Frank model did not account for reversibility, as it should do for realistic chemical scenarios. A more realistic version of the model was later proposed (Kondepudi and Nelson 1983), in which the autocatalytic species are derived from an achiral precursor, and all steps, including the formation of the mutual inhibition complex, are reversible. This model can be described by the following set of chemical reactionsFootnote 2:

  1. 1.

    Production of chiral compound:

$$ A\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}{n}_1,\kern1em A\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}{n}_2. $$
(9.10)
  1. 2.

    Autocatalytic production:

$$ A+{n}_1\underset{k_{-2}}{\overset{k_2}{\rightleftharpoons }}{n}_1+{n}_1,\kern1em A+{n}_2\underset{k_{-2}}{\overset{k_2}{\rightleftharpoons }}{n}_2+{n}_2. $$
(9.11)
  1. 3.

    Hetero-dimerization:

$$ {n}_1+{n}_2\underset{k_{-3}}{\overset{k_3}{\rightleftharpoons }}{n}_1{n}_2. $$
(9.12)

Equation (9.10) represents the formation of chiral product from achiral precursors. Equation (9.11) corresponds to the (first order) autocatalytic reaction described by the first term in Eqs. (9.8) and (9.9). Finally, Eq. (9.12) corresponds to the mutual inhibition of the two species described by the second term in Eq. (9.8–9.9). This mutual inhibition can be expressed as a reaction in which the interaction of the two chiral species produces an achiral product that is usually removed from the system or converted back to chiral monomers through reversible reactions (Eq. 9.12). The elimination of the heterodimer can be neglected if the mutual inhibition is irreversible. However, under realistic chemical conditions, including reversibility in the system, some thermodynamic constraints must be considered and fulfilled (Blackmond and Matar 2008). The equilibrium constants for the direct production and the autocatalytic reactions in Eqs. (9.10)–(9.12) are given by:

$$ {K}_1=\frac{k_1}{k_{-1}}=\frac{\left[{n}_1\right]}{\left[A\right]}=\frac{\left[{n}_2\right]}{\left[A\right]},\kern1.25em {K}_2=\frac{\left[{k}_2\right]}{\left[{k}_{-2}\right]}=\frac{{\left[{n}_1\right]}^2}{\left[A\right]\left[{n}_1\right]}=\frac{{\left[{n}_2\right]}^2}{\left[A\right]\left[{n}_2\right]}, $$

and therefore the system must satisfy the interesting constraint that k1/k−1 = k2/k−2.

The Lotka-Volterra and Frank models are both described by the same general differential equations. However, distinctions can be seen in the more realistic version of the Frank model. In contrast to biological transformations, chemical reactions are reversible, and the constraints on the reaction rate constants are required to fulfill the principle of micro-reversibility. In addition, several versions of Frank’s original model have been proposed during the last decades: considering only one achiral precursor (A), as in Eq. (9.10) (Plasson et al. 2007; Saito and Hyuga 2005), or two achiral precursors (A and B) (Kondepudi and Nelson 1983), neglecting the reaction in Eq. (9.10) compared with the autocatalytic reaction in Eq. (9.11) (Frank 1953; Saito and Hyuga 2004; Iwamoto 2003), or using the direct continuous elimination of both chiral compounds L and D from the system to model the mutual inhibition in Equation (9.12) and the removal of the achiral heterodimer from the system (Iwamoto 2003). These models differ in detail but all exhibit the basic property of mutual inhibition (or antagonism) which leads to all-or-nothing selection of one chemical (or biological) species.

For a system of reversible reactions under conditions that allow a chemical thermodynamic equilibrium to be reached (i.e., a closed system with uniform matter, temperature, and energy distributions), the racemic state is the state of maximum entropy. Homochirality therefore appears as the result of a temporary asymmetric amplification [i.e., a chiral excursion (Blanco et al. (2011)], which may be kinetically trapped. In this case, the system described by Eqs. (9.10)–(9.12) is capable of amplifying an initially tiny statistical enantiomeric excess, from ee ∼10−8% to practically 100%, leading to a long duration chiral excursion at nearly 100% ee, before someday approaching the lowest energy racemic state at thermodynamic equilibrium. On the other hand, in a system with a nonuniform energy distribution (e.g., energy absorption by only some of the species of the system, or open to matter exchange with the surroundings), depending on the conditions, the final stable stationary state may be chiral. To describe this, a key parameter is used, defined as g = k−2/k3; and the chiral state is found to be stable if g < gc ≤ 1, where \( {g}_c=\left(\sqrt{1+16h}-1\right)/8h \) and h = (k1 k3[A]/(k2[A] − k−1)2. Thus, a necessary but not sufficient condition to achieve a final stable chiral state is k3 > k−2. That is, the chiral state is stable if and only if the heterochiral complex forms more quickly than the homochiral reversion to the achiral precursor (Crusats et al. 2009), or in different words, if the racemic content of the system decreases faster than the decay of the homochiral state.

Frank stated in his 1953 paper that “A laboratory demonstration may not be impossible” and he was right. More than 40 years after Frank proposed his original model, the first experimental demonstration of absolute asymmetric synthesis was made when Soai and coworkers reported spontaneous generation of enantiomeric excess in the autocatalytic addition of diisopropylzinc to prochiral pyrimidine carbaldehydes (Soai et al. 1995). Furthermore, and as Frank predicted, this reaction was shown to yield the autocatalytic product in very high enantiomeric excess (over 90%) even if starting from a very low enantiomeric excess (2%) in the original catalyst. Shortly after the initial discovery, Soai’s group reported enantiomeric excesses as high as 85% for a reaction initiated with an enantiomeric excess of 0.1% (Shibata et al. 1998). This intriguing behavior stands out not only as a paradigm of absolute asymmetric synthesis (Avalos et al. 1998; Feringa and Van Delden 1999) but also as an experimental proof of concept for the abiotic emergence of biological homochirality (Weissbuch et al. 2005).

The kinetic schemes derived from the Frank model reproduce the mirror-symmetry-breaking behavior of the Soai reaction. More importantly, from the kinetic viewpoint, the enantioselective autocatalysis at the monomer level seems to be consistent with all reported experimental results of the Soai reaction (Islas et al. 2005). More recently, Mauksch, Tsogoeva, and coworkers have found experimental evidence for both asymmetric autocatalysis (Mauksch et al. 2007a; Amedjkouh and Brandberg 2008) and for spontaneous mirror symmetry breaking (SMSB) (Mauksch et al. 2007b) in the organocatalytic Mannich reaction, a process that takes place in conditions much closer to equilibrium than those of the mostly irreversible Soai dialkylzinc addition.

9.4.3 Limited Enantioselectivity (LES)

In a Frank-like chemical reaction network, a necessary (but not sufficient) condition to achieve a final stable chiral state is that the heterochiral interaction between products and catalysts is favored compared to the homochiral interaction [k3 > k−2 in Eqs. (9.10)–(9.12)]. This seems to be the case in the majority of chiral organic compounds (following the high number of chiral compounds that crystallize as racemic crystals, compared to those yielding a racemic mixture of enantiopure crystals or racemic conglomerates) (Collet et al. 1981). However, this is not the case for some significant compounds in prebiotic chemistry, as, for example, several amino acids. To explain the emergence of chirality in enantioselective autocatalysis for compounds which do not follow Frank-like schemes, the limited enantioselectivity (LES) model (Avetisov and Goldanskii 1996) was proposed as a mechanism for SMSB. The basic model is composed of coupled enantioselective and non-enantioselective autocatalysis and is described by the following chemical transformations:

  1. 1.

    Production of chiral compound:

$$ A\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}{n}_1,\kern1em A\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}{n}_2. $$
(9.13)
  1. 2.

    Autocatalytic production:

$$ A+{n}_1\underset{k_{-2}}{\overset{k_2}{\rightleftharpoons }}{n}_1+{n}_1,\kern1em A+{n}_2\underset{k_{-2}}{\overset{k_2}{\rightleftharpoons }}{n}_2+{n}_2. $$
(9.14)
  1. 3.

    Limited enantioselectivity:

$$ A+{n}_1\underset{k_{-3}}{\overset{k_3}{\rightleftharpoons }}{n}_1+{n}_2,\kern1em A+{n}_2\underset{k_{-3}}{\overset{k_3}{\rightleftharpoons }}{n}_1+{n}_2. $$
(9.15)

Equations (9.10) and (9.11) in the Frank model are identical to Eqs. (9.13) and (9.14) in the LES model. However, the catalytic production of the opposite enantiomeric product (cross-catalysis rather than autocatalysis) in LES (in Eq. 9.15) substitutes for the mutual inhibition reaction in the Frank model (in Eq. 9.12). In both models (Frank and LES), the enantioselective autocatalysis (Eqs. 9.11 and 9.14) is coupled to a reaction that leads to the decrease of the racemic composition of chiral catalysts. In Frank, this decrease is achieved through the “mutual inhibition” between enantiomers in Eq. (9.12) (with rate k3) and in LES through the inverse reaction of the non-enantioselective autocatalysis in Eq. (9.15) (with rate k−3). Both reactions lead to the same mathematical terms.

The equilibrium constants for the direct production and the autocatalytic reactions in this case are given by:

$$ {\displaystyle \begin{array}{ll}{K}_1& =\frac{k_1}{k_{-1}}=\frac{\left[{n}_1\right]}{\left[A\right]}=\frac{\left[{n}_2\right]}{\left[A\right]},\kern0.5em {K}_2=\frac{\left[{k}_2\right]}{\left[{k}_{-2}\right]}=\frac{{\left[{n}_1\right]}^2}{\left[A\right]\left[{n}_1\right]}\\ {}& =\frac{{\left[{n}_2\right]}^2}{\left[A\right]\left[{n}_2\right]},\kern0.5em {K}_3=\frac{\left[{k}_3\right]}{\left[{k}_{-3}\right]}=\frac{\left[{n}_1\right]\left[{n}_2\right]}{\left[A\right]\left[{n}_1\right]}=\frac{\left[{n}_2\right]\left[{n}_1\right]}{\left[A\right]\left[{n}_2\right]},\end{array}} $$

so the system is under the thermodynamic constraint k1/k−1 = k2/k−2 = k3/k−3.

A linear stability study reveals that in this case, the key parameter can be approximated to g = k−2/k−3; and the chiral state is found to be stable if g < gc ≤ 1, where gc ≈ (1 − k3/k2)/(1 + 3k3/k2) (Ribo and Hochberg 2008). However, this cannot be achieved when the thermodynamic constraint is fulfilled. Previous reports had claimed SMSB in this model; however, as Blackmond et al. already pointed out in the past (Blackmond and Matar 2008; Blackmond 2009), contradictory reports concerning this were the consequence of the use of a set of reaction rate constants which do not fulfill the thermodynamic constraint mentioned above.

For a system to be maintained in a chiral stationary state, final conditions must be those of constant energy exchange with the surroundings and maximum entropy. Thus, although the thermodynamic constraint forbids any SMSB from occurring in this model (in either closed or open systems), it has been suggested that this can occur in the presence of additional reagents (Blanco et al. 2013a) or in temperature gradients if the autocatalysis and limited enantioselective catalysis are compartmentalized within regions of low and high temperature, respectively (Blanco et al. 2013b)—in such a way that the thermodynamic constraints become compatible with conditions for a final stable chiral state.

We note that the inverse reaction of the non-enantioselective autocatalysis (\( {n}_1+{n}_2\overset{k_{-3}}{\to }A+{n}_1 \) and \( {n}_1+{n}_2\overset{k_{-3}}{\to }A+{n}_2 \)), can be regarded as a predator-prey interaction, in which, interestingly, both species play the role of prey and predator at the same time. This dual role reflects the fact that n1 and n2 correspond to the two enantiomeric species of the same molecule, so this case must correspond to a completely symmetrical situation. Thus, although LES cannot explain SMSB, it may be interesting to study its properties to understand mutual predator-prey interactions.

9.5 Conclusion

Some new scenarios for the emergence of SMSB in compounds that do not follow a Frank-like scheme have arisen during the last years. These scenarios correspond to the deracemization of racemic mixtures of crystals (Noorduin et al. 2008, 2009; Viedma 2005) and the crystallization from boiling solutions (Viedma and Cintas 2011; El-Hachemi et al. 2011). Furthermore, a recent example on sublimations suggests that the same principle is probably also applicable to other phase transitions (Viedma et al. 2011). All these experiments, as well as both the Frank model and the LES model, correspond to cases of SMSB in bifurcation scenarios, where the racemic state is metastable and the more stable final state corresponds to a stationary chiral state. In all cases, small statistical fluctuations about the ideal racemic composition are amplified, taking the system out of the metastable racemic state and driving it into one of the two degenerate stationary chiral states. In the absence of any external polarization dictating the sign of the outcome, the sign of the chiral final state follows a stochastic distribution, as is the case in all the abovementioned experiments.

Although the replicator equation, the LV equations, and the Frank model are used for different purposes and may appear to have little resemblance to each other, it is interesting to note that the three models have equivalent mathematical descriptions. In particular, winner-take-all outcomes prevail in certain parameter regimes in these scenarios. As with the prelife models, these sharp transitions seem to characterize living systems, whether they consist of biological or chemical species.