DTI Segmentation Using Anisotropy Preserving Quaternion Based Distance Measure

Abstract

In brain research, the second order tensor model of the diffusion tensor imaging (DTI) encodes diffusion of water molecules in micro-structures of tissues. These tensors are real matrices lying in a non-linear space enjoying the Riemannian symmetric space structure. Thus, there are natural intrinsic metrics there, together with their extrinsic approximations. The effective implementations are based on the extrinsic ones employing their vector space structure. In processing DTI, the Log-Euclidean (LogE) metric is most popular, though very far from optimal. The spectral decomposition approach yields the distance measures which respect the anisotropy much better. In the present work, we propose to use the spherical linear interpolation (slerp-SQ) which performs much better than the LogE one and provides better interpolation of geodesics than the spectral-quaternion one. We have implemented the localized active contour segmentation method for these metrics, providing much better handling of the inhomogeneity of the data than global counterpart.

Sumit Kaushik has been supported by the grant MUNI/A/1138/2017 of Masaryk University, Jan Slovak gratefully acknowledges support from the Grant Agency of the Czech Republic, grant Nr. GA17-01171S.

1 Introduction

The non-invasive DW-MRI method can quantify the degree of diffusion of water molecules in the brain. The second order diffusion model was introduced in [13]. In this model, the tensors encoding diffusion are 3$\,\times \,$3 symmetric positive definite matrices with six degrees of freedom, lying in the $\mathbb {S}^{+}(3)$ space. The anisotropic tensors in DTI represent white matter micro-structures which allow more diffusion oriented along axons. The segmentation of white matter structures has relevance in diagnosis and clinical studies of patients with multiple sclerosis, stroke, and brain-connectivity issues. For segmentation, the deformable models were long been used for intensity images in earlier works, called snakes, cf. [9]. These contours are guided by an energy function which deals with topological changes while evolving. For example, [14, 15] used edge based function but had disadvantage because of inability to deal with noise and it required initial curve to be placed near to the boundary of the object of interest. The level sets (geometrically known as implicit curves in hypersurface) were exploited in [2] to deal with topological changes of the evolving curve. In their remarkable paper [3], Chan-Vese incorporated region based energy model based on Mumford-Shah formulation [1]. The method was based on minimization of global energy which was formulated as a variational problem. This resolved the problem with edge based methods, but such global methods fail to segment the objects whose parts have non-homogenous statistics. To resolve this issue, localized curve model was introduced by Lankton et al. in [11] and subsequently was used by them in [12] for fibre bundle segmentation. Further, they advocated that the efficiency of the method relies upon the choice of distance measure or metric. This is one of the motivation for current work.

The space of tensors in DTI is well studied and known as a non-Euclidean Riemannian symmetric space. The work [16] provided a Riemann framework for computing. Affine invariant metrics on the homogenous space $\mathbb {S}^{+}$ are well known in differential geometry texts [17], while in statistics, they are known as Fisher information metrics [18]. The use of the latter technique for DTI was advocated in [20].

In the current work, we implement the localized segmentation method for DTI based on the so called slerp-SQ metric and we have chosen the widely used Log-Euclidean metric, introduced in [21], for comparison. This spherical linear interpolation of quaternion slerp-SQ distance measure is an extension of the spectral-quaternion (SQ) measure for curve evolution. We provide arguments why is this metric better in providing smooth interpolation of geodesics. We achieved very fast and effective segmentation of white matter structure as compared to the Log Euclidean metric for 2D cross section. It works very well for structures with quickly varying curvatures (e.g. corpus collasum). At the same time, it enables the segmentation curve to deal with the heterogeneity of the tensors in the underlying image, which is due to variation in the orientation and eigen-values. Results on both synthetic images and on real human brain images are shown.

2 Localization of Global Energy Formulation

In early works for scalar images, deformable models were called snakes. Kass et al. [9] introduced an energy function to evolve the curve which was fast but had difficulty in handling topological changes. The evolution of curves is guided by the curvature motion and edge function: $g(|\nabla u_{0}|)=(1+|\nabla (G_{\sigma }\star u_{0})|)^{-1}$. Here, $u_{0}$ is image, $G_{\sigma }$ is the Gaussian function and $\star$ is the convolution operation.

In [14, 15] g acts as evolving and a stopping term for the curve as its value is zero near the boundaries of object. The disadvantage of these edge based methods is their inability to deal with noise because in the process of smoothing noise, Gaussian also smoothes the boundaries. Another shortcoming is that the initial curve needs to be placed near the boundary of object of interest. Osher and Sethian in [10] used level-sets to deal the topological changes during curve evolution, the evolving curve is embedded in high dimensional surface. Further, based on Mumford Shah model [1], as a special case, Chan-Vese [3] model evolved the curve without requiring edges as stopping condition, they used energy formulation based on first moments of energy distribution in the interior and exterior regions of the curve. Minimization of the energy converges the evolving curve to boundary of the object. It enables to segment the objects with or without discontinuous boundaries, and it is robust to noise. Let $\phi$ be the surface embedding the curve, i.e. $\partial \phi /\partial t =F|\nabla \phi |$. Various choices of the function F exist in literature. Region based techniques works well for the objects with uniform features but fails where sub-region of the object has non-uniformity i.e. the statistics of the object’s (local) region has variation. Authors in [5] incorporated local statistics into variational framework to deal heterogeneity. [6,7,8, 11] are some works in this direction.

In the current work, we are using [11] energy functional which they used in followed up paper [12] for fibre bundle segmentation for 3D DTI. They used Log-Euclidean metric and advocated the improvement under a better similarity measures/metric. A bounding ball mask ${\mathcal B}(x,y)$ is selected with a fixed radius r across the length of contour, with value 1 inside and zero outside. The reader is referred to [11] for details on the variational setup. The iterative optimization of the energy is implemented with the help of the Euler-Lagrange equation

$$ \textstyle \frac{\partial \phi }{\partial t}(x) =\delta \phi (x)\int _{\varOmega _{y}}{\mathcal B}(x,y) \cdot \nabla _{\phi (y)}F(I(y),\phi (y))\,dy\,+\,\lambda \delta \phi (x)\, \mathrm{div}\frac{\nabla \phi (x)}{\vert \nabla \phi (x)\vert } .$$

3 Distance Measures for Second Order Tensors

These tensors can be considered to lie either in a Euclidean space (extrinsically) or the embedded space (intrinsically). With Euclidean space approach, the advantage is that it is a vector space and all statistics are easily performed but at the cost of accuracy and closure property. Embedded space has inherent non-scalar curvature. However, advantage is that it reduces the dimension of the problem and under proper metric promises accurate results. Computational speed is an issue in this case when it involves enormous data (e.g. DTI). The symmetric positive definite (SPD) matrices forms a manifold called Riemann symmetric space. Geometrically, these matrices forms a cone (because of positive definite constraint) in $\mathbb {R}{}^{n}$. Euclidean space approach in [24] gives a unique mean but smoothing operations may result in negative or null eigenvalues, which are non-physical for diffusion process. Further, it gives rise to problems like the swelling effect.

3.1 State of the Art

Notice, the matrix exponential is a diffeomorphism from the embedding space $\mathbb {R}^{6}$ of the symmetric 3 by 3 matrices to the tensor space $\mathbb {S}^{+}$ (the manifold of the positive definite ones).

Log-Euclidean Metric: The latter mathematical observation was exploited by the authors in [21] and gave a Lie group structure to the tensor space. With this structure computations become easy in three steps: Take $\log$ of the tensor space, process the vector data (symmetric matrices), use $\exp$ to map the data back to the manifold. This is a popular metric for DTI processing. The composition operation is not the usual matrix multiplication (under which it is not a Lie group). It is given by:

$$\begin{aligned} p_{1}\bullet p{}_{2}&=\exp (\log (p_{1})+\log (p_{2}))\end{aligned}$$

(1)

$$\begin{aligned} \text{ dist }^{2}(p_{1},\,p_{2})&={\text {trace}}((\log (p_{1})-\log (p_{2}))^{2} \end{aligned}$$

(2)

and the interpolation curve between two tensors $p_{1}$ and $p_{2}$ is

$$\begin{aligned} p(t)=\exp (1-t)\log (p_{1})\,+\,t\log (p_{2}). \end{aligned}$$

(3)

This extrinsic metric is an approximation of intrinsic affine invariant metric. They are very close to each other near to the identity. It is invariant with respect to the similarity transformations (rotation or scaling). Log Euclidean interpolation curve provides a closed-form mean for two or more tensors.

Spectral Metric: For the first time, [19] used spectral treatment for regularization of noisy diffusion tensors. The key idea is to treat eigenvalues and eigenvectors separately. An interpolation curve between any two tensors $u_{1}$ and $u_{2}$ is given by:

$$\begin{aligned} p(t)&=u(t)\varLambda (t) u^{T}(t)\end{aligned}$$

(4)

$$\begin{aligned} u(t)&=u_{1}\exp (t\log (u_{1}^{T}u_{2}))\end{aligned}$$

(5)

$$\begin{aligned} \varLambda (t)&=\exp (1-t)\,\log (\varLambda _{1})\,+\,t\,\log (\varLambda _{2}) \end{aligned}$$

(6)

where $u_{1}$, $u_{2}\in \mathbb {SO}(3)$ (the rotational group) and $\varLambda _{1}$ and $\varLambda _{2}$ are diagonal matrices with eigen values entries. This interpolation curve is a geodesic in the product of Lie groups $\mathbb {SO}(3)\,\times \,\mathbb {D}^{+}(3)$, where $\mathbb {D}^{+}(3)$ is the group of diagonal matrices with positive elements. This Lie group is a four-fold covering of $\mathbb {S}^{+}(3)$. The tensor has four distinct orientations, determined by rotations of principle axes by $\pi$, and one due to identity. Let G be one such four-tuple of $u_{2}$. Then distance between the any two rotations $u_{1}$ and $u_{2}$:

$$\begin{aligned} \text{ dist }(u_{1},\,u_{2})={{\arg }}\,\,\mathop {{\min }}\limits _{u\in G}\text{ dist }(u_{1}\,,\,u)\,={{\arg }}\,\,{\min }||{{\log }}(u_{1}u_{2}^{T})||_{2} \end{aligned}$$

(7)

The calculations here require four matrix $\exp$ and $\log$ operations. To reduce the number of computations, rotation is performed in the quaternion space in [22]. We have extended the spectral quaternion metric which is based on Lerp (linear interpolation) and we use inner-product based metric for the rotation space.

Fig. 1.

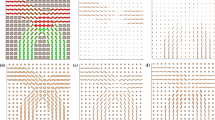
Comparison of smoothness of the interpolation curves depicted by angular difference in principle eigenvectors. Blue curve is for slerp-SQ and red for SQ in (a) with $n=4$ tensors, (b) $n=10$. Green is for LogE in (c). Mean diffusivity (MD) evolves monotonically better in slerp-SQ than SQ but not with LogE metric. In (d) the Hilbert anisotropy evolves similar in both slerpSQ and SQ, in comparison to LogE. In (e), the determinant evolves similar in all three cases. In (f), the fractional anisotropy evolves similar in both slerpSQ and SQ, in comparison to LogE. (Color figure online)

3.2 Slerp-SQ

We propose to use the spherical version of the linear interpolation spectral quaternion distance measure. The Hopf-Rinow-De Rham theorem indicates that among all possible geodesics between any two points on a complete manifold there exists at least one geodesic with minimum length which can be considered as distance between two points. We exploit spherical linear interpolation (Slerp) of quaternions. Slerp produces smoother curves in quaternion space and resulting geodesic is thus closer to the geodesic distance in the Lie group $\mathbb {SO}(3)\,\mathbf{x}\,\mathbb {D}^{+}(3)$.

The slerp interpolation between two quaternions $q_{1}$ and $q_{2}$ is

$$\begin{aligned} q_{m}(q_{1,}q_{2},t)=\frac{sin[(1-t){\theta }]}{sin{{\theta }}}q_{1}+\frac{sin[t{{\theta }}]}{sin{{\theta }}}q_{2} \end{aligned}$$

(8)

where $\theta ={\mathrm{arccos}(|q_{1}.q_{2}}|)$. Notice, $\theta$ is a metric and we shall denote it $d_{slerpSQ}$.

This seems to be a better choice than the metric

$$\begin{aligned} d_{SQ}&=1-{{\cos }({d_{slerpSQ}})} \end{aligned}$$

used in [22]. Notice, $d_{SQ}$ metric is an chordal distance approximation in $S^{3}$ quaternion space. Further, it converges to 0 at a slower rate and not bounded equivalent to other metrics [23] for rotation space.

Anisotropy carries useful information and requires to be preserved during processing of DTI tensors. The Eq. 4 for the interpolation curve between tensors is valid for those with distinct eigenvalues. To account for the tensors with same eigenvalues (2 or more), a smooth transition function f(x) (keeping $\beta =0.6$) is used in [22],

$$\begin{aligned} f(x)=\frac{(\beta x)^{4}}{1+(\beta x)^{4}} \end{aligned}$$

(9)

This function gets low value in case of isotropic tensors and high value for anisotropic ones. The true distance between two tensor is given by a weighted sum of $d_\lambda + \alpha d_{slerpSQ}$. The coefficient $\alpha$ is given as

$$\begin{aligned} \alpha (HA_{1,}HA_{2})=f(\min (HA_{1,}HA_{2})), \end{aligned}$$

(10)

where Hilbert anisotropy $HA=\log \frac{\lambda _{max}}{\lambda _{min}}$ with $\lambda _{i}$ being eigenvalues of the tensors. This similarity measure is not a distance between two tensors but it provides an approximation according to anisotropy. The latter approach lead to the following algorithms.

The Fig. 1 indicates that the evolution of scalar anisotropies, i.e., mean diffusitivity and fractional anisotropy, is much closer to linear in SQ and Slerp-SQ than in LogE cases. Moreover, Slerp-SQ behaves better than SQ. As the number of tensors increases, Slerp-SQ converges to SQ (Fig. 2).

3.3 The Algorithms

We present the computation of the means and distance measures now.

Fig. 2.

In (a), slerp-SQ is faster (both curves shown at 521 iterative step, both are able to segment the object). In (b), LogE fails to evolve after 50th iteration, whereas slerp-SQ continued segmenting the whole object. Segmentation inside region of interest (roi) shown with ellipse, localization radius = 20, z-slice = 86, data size = 191$\,\times \,$236$\,\times \,$171. In (c), LogE fails to deal with heterogeneity present in roi, while in (d), slerp-SQ is able to discern the heterogeneous data present within roi.

4 Results

We used two 2D structures, parabola and circle, having high and constant curvature respectively. Background is kept uniform and various degree of heterogeneity in structures is obtained by inducing randomness in eigenvalues and eigenvectors. Curve with slerp-SQ distance measure is shown in green and that of LogE in black color in the figures. A slice of the human brain image is chosen¹ and algorithm is run to segment an arbitrary region, where heterogeneity is visible. LogE fails to discern the non-homogenous region (encircled). Results are overlapped on image with darker region showing the white matter presence.

5 Conclusion

The choice of distance measure in localized curve evolution is crucial in extracting white matter structure effectively. Decoupling of eigenvalues and rotations is important for preserving anisotropy and representation of Rotational space with Quaternion space not only reduces computations but also maintains anisotropy preservation. Introducing spherical linear interpolation for quaternions produces smooth curves in quaternion space and in turn in tensor space. It guarantees the geodesic distance to be closer approximation of metric with correct segmentation is achieved. Next part of our work will be to extract white matter structure in 3D and reduce the computations required for localized contour evolution.