The Reflection of Cylindrical Shock Wave Segments on Cylindrical Wall Segments

Abstract

The reflection of a two-dimensional cylindrical shock wave segment on a concave-cylindrical wall segment was investigated from an experimental and numerical perspective. The images obtained from experiment show no qualitative difference between cylindrical shock behavior and how a plane shock would behave in terms of the features developed. The length of the shock’s Mach stem was plotted against subtending angle. Two limits are highlighted, one where the shock’s radius is much larger than the wall’s radius and another where the wall has the larger radius: the former being akin to a plane shock interacting with a cylindrical wall segment. The increase in initial shock Mach number was observed to affect the type of Mach reflection that is formed as well as the transition point to a transitioned Mach reflection.

1 Introduction

In this paper, we investigate the reflection of cylindrical shock wave segments on concave-cylindrical wall segments. Similar work on the reflection of plane shocks on concave and cylindrical walls has been done before [1,2,3]—in this case, the emphasis is on the curvature of the shock with the cylindrical shock serving as a specific example. This investigation is carried out in a two-dimensional domain.

Introducing curvature to the shock changes the shock’s dynamics. While a plane shock (two dimensional) maintains a uniform shock strength (for as long as it does not encounter obstacles), a cylindrical shock’s strength depends on the shock’s radius. An expression defining this relationship was derived by Guderley [4]. In addition to variable shock strength, the curvature of the shock introduces an implicit spatial constraint. A plane shock can be imagined to extend indefinitely in space, with any limitation to that extension being entirely arbitrary.

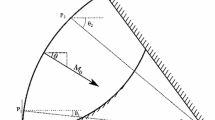
Consider Fig. 1; the angle (θ _span) determines the region of space occupied by the shock. It follows, therefore, that the maximum circumference of any converging cylindrical shock is 2πr, where r is the shock’s radius. Another difference between plane and curved shocks is shock orientation. Whereas a plane shock’s orientation (θ) is constant, for as long as the shock does not encounter an obstacle, a cylindrical shock’s orientation varies along the shock.

Fig. 1

Interaction of a two-dimensional cylindrical shock with a concave-cylindrical wall segment

The factors cited above are the motivation behind this work. As will be shown, the qualitative behavior of both plane and cylindrical shocks remains the same albeit, with quantitative differences. The study was carried out from an experimental and numerical perspective. In all cases considered (unless specified otherwise), the shock has an initial radius of 165 mm and a span of 55°; numerical studies were carried out using ANSYS Fluent.

2 Experimental Facility

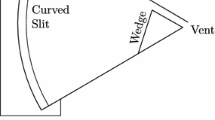
Two-dimensional cylindrical shock waves were produced by the use of the annular method [5]; this involves transforming a two-dimensional plane shock into a cylindrical shock by passing the former through a cylindrical circular slit. The cylindrical shock, so produced, then interacts with the cylindrical wall segment—shown in Fig. 2.

Fig. 2

Test section for investigating the reflection of cylindrical shock waves on cylindrical walls for a shock propagating from left to right. (a) Schematic of test section where the shock and the cylindrical wall interact. (b) A picture of the test section as constructed

Four wall radii were considered (Fig. 3) for the bottom wall, and the upper wall was left perpendicular to the shock wave. This is hardly exhaustive of the combinations that can be made between a shock of some radius r and walls of specific radius. Thus, the ratio between shock radius and wall radius (r _s/r _w) was found useful in reporting the data gathered. The leading edge of the cylindrical wall was designed to be perpendicular to the shock. Thus, this study investigates only one aspect of shock reflection; further work is required for cases where the shock and the wall are not initially perpendicular.

Fig. 3

Sketches of concave-cylindrical wall segments. (a) 82 mm radius. (b) 100 mm radius. (c) 140 mm radius. (d) 180 mm radius

3 Observations

Similar to Ben-Dor and Takayama’s work [6], on encountering the concave-cylindrical wall, a Mach reflection (MR) forms on the shock’s front and later transforms into a transitioned regular reflection (TRR). Compression waves propagate up along the shock, before the formation of the MR; it is their coalescence that results in an MR. Figures 4 and 5 show images of the evolution of such a shock. In Fig. 5, owing to the roughness of the wall, disturbances can be seen emanating from the wall. The first such disturbance does not contribute to the formation of the MR—as expected from what is known about plane shocks [6].

Fig. 4

A 165 mm shock wave segment with initial Mach number of 1.32 propagating up a 180 mm radius wall. These are typical of all cases observed. (a) Time = 10 μs, (b) time = 70 μs, (c) time =110 μs, (d) time = 170 μs, (e) time = 180 μs, (f) time = 190 μs, (g) time = 210 μs, (h) time = 230 μs

Fig. 5

A 165 mm shock wave segment with initial Mach number of 1.43 propagating up a 140 mm radius wall. (a) Time = 10 μs, (b) time = 50 μs, (c) time = 90 μs, (d) time = 110 μs, (e) time = 130 μs, (f) time = 150 μs, (g) time = 160 μs, (h) time = 170 μs

A critical parameter is the moment when (or position where) the shock first transitions into an MR. That parameter could not, however, be located owing to limitations in camera resolution and frame rate. In Fig. 4, for example, one can deduce that the MR formation position is between Fig. 4c, d. A similar weakness exists for the transition to TRR; the exact moment cannot be accurately captured by experiment. Fortunately, by extrapolation an estimate to this transition point can be determined. This is done by defining the transition point as the point where the Mach stem’s length vanishes; thus, the Mach stem length is measured in all frames and extrapolated to the vanishing point.

Figure 6 shows the numerical results for a shock reflecting on a 33 mm wall. Again, this is a typical result for all simulation run. Again, the qualitative behavior is similar to that observed in experiments.

Fig. 6

Numerical schlieren images of a shock-wall ratio equal to 5 and initial Mach number 2. (a) Time = 10 μs, (b) time = 15 μs, (c) time = 20 μs, (d) time = 25 μs, (e) time = 28 μs, (f) time = 32 μs, (g) time = 38 μs, (h) time = 43 μs

4 Discussion

Figure 7 shows the Mach stem length measured on a 180 mm radius wall compared to CFD data. The angle subtended at the center of the wall by the Mach stem—produced toward the wall’s center—is used to label the x-axis. The precision of the experimental data points was low owing to the low resolution of the images obtained combined with the closeness of the shock strengths. However, we see that CFD data is representative of the trend; therefore, it will be used further to illustrate more trends.

Fig. 7

Variation of Mach stem length on a 180 mm radius wall segment compared with CFD data. (a) Angle of formation, (b) Mach stem trend, with a line of best fit $(h=-0.0059(\theta_F+\phi)^2-0.1354(\theta_F+\phi)+12.7276)$ on experimental data

Figure 8 shows variations in Mach stem length classified by initial shock strength and shock-wall ratios. The last of the series of figures shows a justification for using the shock-wall ratio as the independent variable. Mach stem lengths from two shocks with different radii but similar shock-wall ratios are compared, and the resulting—nondimensionalized—stem lengths correspond well. In Fig. 8a, b, the concept of extrapolating to the vanishing Mach stem length is illustrated.

Fig. 8

CFD stem length data compared by shock-wall ratios and Mach number. (a) Initial Mach number, 1.5; (b) initial Mach number, 2.5; (c) initial Mach number, 3; (d) comparing two different shocks with equal wall ratios (R _s/R _w = 0.92)

Extrapolation to the vanishing length must be carried out with care. It is not always the case that the MR transitions to TRR. Consider the sketch in Fig. 7a; depending on the shock’s span and wall radius, the bottom and top wall may meet before the shock makes the transition. That being the case, an extrapolation to vanishing length of the Mach stem will give misleading results.

In each of the figures (Fig. 8), the nonlinear behavior of the shock is evident. Consider the transition to TRR (vanishing stem length); an increase in shock-wall ratio is not accompanied by a uniform increase in the transition angle (φ). As the shock-wall ratio increases, the stem curves converge and cluster together. This is indicative of an approach toward a limit, i.e., the case where a plane shock interacts with a cylindrical wall segment (R _s≫R _w). Thus, a corresponding conjecture can be made that when the wall radius is much greater than the shock radius, then another limit exists akin to a cylindrical shock segment interacting with a plane wedge. This, however, is not supported by the data presented here.

As would be expected, increasing the shock’s initial strength allows the MR to persist much further up along the cylindrical wall segment. It cannot, however, be claimed that a similar increase allows the MR to form at smaller angles although such a conclusion is intuitive. In this case, this is a result of limitations in computational capabilities much like weaknesses in camera resolution.

There are three different types of MR, two of which are illustrated by the data in Fig. 8. The different types relate to how the Mach stem length varies: when the length increases (direct Mach reflection (diMR)), when the length decreases (inverse Mach reflection (inMR)), and when the length is constant (stationary Mach reflection (stMR)). In Fig. 8, we see that as the shock strength increases, the curves’ curvature tends to increase. In Fig. 8a, all profiles illustrate a decreasing stem length, while in Fig. 8c, we see a marked tendency to start off in the stationary regime.

It is argued, here, that increasing the cylindrical shock segment’s Mach number affects the type of MR that is formed. A question thus arises: How do we classify the type of reflection that will occur by shock strength? Moreover, will a further increase in shock strength lead to the initial MR being a diMR? It must be borne in mind though that increasing shock strength might make the effects of viscosity and ionization more pronounced, effects which were assumed to be negligible in this study.

5 Conclusion

The reflection of a cylindrical shock wave segment on a cylindrical wall segment was studied. Reflection patterns formed were similar to those that are known to occur with plane shocks on cylindrical wall segments. A comparison was made between CFD simulations and experimental images, of which no qualitative or quantitative differences were observed. For quantitative analysis, it was found useful to use the shock-wall ratio (R _s/R _w) for the study. The variation in Mach stem length formed by the shock was classified by shock-wall ratio and by Mach number.

From the data, it was argued that a limit exists where the shock radius is much larger than the wall radius: this limit being the case where a plane shock interacts with a cylindrical wall. By the same token, another limit was postulated to exist when the shock’s radius is the smaller. The effect of shock strength was shown to be the variation in Mach reflection type—whether it is a diMR, inMR, or stMR. Finally, from the data gathered, it was highlighted that it is impossible to identify the initial point when (where) the MR first forms.