Keywords

1 Introduction

Trees have long been used to represent species relationships [1,2,3]. The leaves of a phylogenetic tree correspond to current species while its branchings indicate past speciation events. However, complex evolutionary events, such as genetic reassortments or hybrid speciations, do not fit into this elementary framework. Such non-tree-like events play an important role in the evolution of viruses, bacteria and plants. This issue has led to the development of various notions of phylogenetic networks [4].

A natural generalization of phylogenetic trees is obtained by representing them as split networks, that is, collections of bipartitions over the species set. On a tree whose leaves are labeled by species names, each edge can be thought of as a bipartition over the species: removing the edge produces exactly two connected components. In this representation, trees are characterized by the fact that their splits have a certain compatibility property [5]. More generally, circular networks relax this compatibility property, while retaining enough structure to be useful as representations of evolutionary history [6]. Such networks are widely used in practice. Although they do not explicitly model specific evolutionary events (see, e.g., [7] for a discussion), their straightforward visualization and fast reconstruction have made them a popular exploratory tool to detect network-like evolution in genetic datasets [8]. They are also useful in cases where data is insufficient to single out a unique tree-like history, but instead supports many possible evolutionary scenarios.

Standard reconstruction methods for circular networks, such as the Neighbor-Net algorithm introduced in [9], rely on a metric on the species set. Such a metric, which quantifies how far apart species are in the Tree of Life, is estimated from genetic data. Very roughly, it counts how many mutations separate any two species. This leads to a key difficulty: under standard stochastic models of DNA evolution, distantly related sequences are known to produce statistically unreliable distance estimates [10, 11]. This is problematic for Neighbor-Net, in particular, as it is based on the popular tree reconstruction method Neighbor-Joining, whose sensitivity to distance estimation errors is well established theoretically [12].

In the tree case, more robust reconstruction methods were developed using the notion of a distorted metric which captures the dependence of the error in the distance through a radius of accuracy [13, 14]. A key insight to come out of this line of work, starting with the seminal results of [10, 11], is that a phylogenetic tree can be reconstructed using only a subset of the pairwise distances—those less than roughly the chord depth of the tree. Here the chord depth of an edge is the shortest path between two leaves passing through that edge and the chord depth of the tree is the maximum depth among its edges. This result is remarkable because, in general, the depth can be significantly smaller than the diameter. As a consequence, a number of results have been obtained showing that, under common stochastic models of sequence evolution, a polynomial amount of data suffices to reconstruct a phylogenetic tree with bounded branch lengths. See e.g. [15,16,17,18]. This approach has also inspired practical reconstruction methods [19, 20].

Here we design the first reconstruction method for circular networks based on distorted metrics. In addition to generalizing the chord depth, we show that, unlike the tree case, pairwise distances within the chord depth do not in general suffice to reconstruct these networks. We introduce the notion of maximum incompatibility, a measure of the extent to which the network differs from a tree, to obtain a tight (up to a constant) bound on the required radius of accuracy. Before stating our main results, we provide some background on split networks.

2 Background

We start with some basic definitions. See [4] for an in-depth exposition.

Definition 1

(Split networks [6]). A split \(S = (S_1, S_2)\) on a set of taxa \(\mathcal {X}\) is an unordered bipartition of \(\mathcal {X}\) into two non-empty, disjoint sets: \(S_1, S_2 \in \mathcal {X}\), \(S_1\cap S_2 =\emptyset \), \(S_1\cup S_2 = \mathcal {X}\). We say that \(\mathcal {N}= (\mathcal {X},\mathcal {S}, w)\) is a weighted split network (or split network for short) on a set of \(\mathcal {X}\) if \(\mathcal {S}\) is a set of splits on \(\mathcal {X}\) and \(w: \mathcal {S}\rightarrow (0,\infty )\) is a positive split weight function. We assume that any two splits \(S^{(1)} = \{S^{(1)}_1, S^{(1)}_2\}\), \(S^{(2)} = \{S^{(2)}_1, S^{(2)}_2\}\) in \(\mathcal {S}\) are distinct, that is, \(S^{(1)}_1 \ne S^{(2)}_1, S^{(2)}_2\).

For any \(x, y \in \mathcal {X}\), we let \(\mathcal {S}|_{x,y}\) be the collection of splits in \(\mathcal {S}\) separating x and y, that is,

$$ \mathcal {S}|_{x,y} = \{S \in \mathcal {S}\,:\, \delta _S(x,y) = 1\}, $$

where \(\delta _S(x,y)\), known as the split metric, is the indicator of whether \(S = (S_1, S_2)\) separates x and y

(1)

For a split \(S \in \mathcal {S}|_{x,y}\), we write \(S = \{S_x, S_y\}\) where \(x \in S_x\) and \(y \in S_y\). For simplicity, we assume that \(\mathcal {S}|_{x,y} \ne \emptyset \) for all \(x,y \in \mathcal {X}\). (Taxa not separated by a split can be identified.)

Let \(T = (V,E)\) be a binary tree with leaf set \(\mathcal {X}\) and non-negative edge weight function \(w : E \rightarrow [0,+\infty )\). We refer to \(\mathcal {T}= ( \mathcal {X}, V, E, w)\) as a phylogenetic tree. Any phylogenetic tree can be represented as a weighted split network. For each edge \(e \in E\), define a split on \(\mathcal {X}\) as follows: after deleting e, the vertices of \(\mathcal {T}\) form two disjoint connected components with corresponding leaf sets \(S^1\) and \(S^2\); we let \(S_e = \{S^1, S^2\}\) be the split generated by e in this way. Conversely, one may ask: given a split network \(\mathcal {N}= (\mathcal {X}, \mathcal {S}, w)\), is there a phylogenetic tree \(\mathcal {T}= ( \mathcal {X}, V, E, w)\) such that \(\mathcal {S}= \{S_e: e\in E\}\) (with \(w(S_e) = w(e)\))? To answer this question, we need the concept of compatibility.

Definition 2

(Compatibility [21]). Two splits \(S^{(1)} = \{S^{(1)}_1, S^{(1)}_2\}\) and \(S^{(2)} = \{S^{(2)}_1, S^{(2)}_2\}\) are called compatible, if at least one of the following intersections is empty:

$$\begin{aligned} S_1^{(1)}\cap S_1^{(2)}, \quad S_1^{(1)}\cap S_2^{(2)}, \quad S_2^{(1)}\cap S_1^{(2)}, \quad S_2^{(1)}\cap S_2^{(2)}. \end{aligned}$$

We write \(S^{(1)} \sim S^{(2)}\) to indicate that \(S^{(1)}\) and \(S^{(2)}\) are compatible. Otherwise, we say that the two splits are incompatible. A set of splits \(\mathcal {S}\) is called compatible if all pairs of splits in \(\mathcal {S}\) are compatible.

In words, for any two splits, there is one side of one and one side of the other that are disjoint. The following result was first proved in [21]. Given a split network \(\mathcal {N}= (\mathcal {X}, \mathcal {S}, w)\), there is a phylogenetic tree \(\mathcal {T} = ( \mathcal {X}, V, E, w)\) such that \(\mathcal {S}= \{S_e: e\in E\}\) if and only if \(\mathcal {S}\) is compatible. For a collection of splits \(S^{(1)}, \ldots , S^{(\ell )}\) on \(\mathcal {X}\), we let

$$\begin{aligned} \mathscr {C}_\mathcal {N}(S^{(1)}, \ldots , S^{(\ell )}) = \{S \in \mathcal {S}\,:\, S \sim S^{(i)}, \forall i\}, \end{aligned}$$
(2)

be the set of splits of \(\mathcal {N}\) compatible with all splits in \(S^{(1)}, \ldots , S^{(\ell )}\), and we let

$$\begin{aligned} \mathscr {I}_\mathcal {N}(S^{(1)}, \ldots , S^{(\ell )}) = \{S \in \mathcal {S}\,:\, \exists i, S \not \sim S^{(i)}\}, \end{aligned}$$
(3)

be the set of splits of \(\mathcal {N}\) incompatible with at least one split in \(S^{(1)}, \ldots , S^{(\ell )}\). We drop the subscript \(\mathcal {N}\) when the network is clear from context.

Most split networks cannot be realized as phylogenetic trees. The following is an important special class of more general split networks.

Definition 3

(Circular networks [6]). A collection of splits \(\mathcal {S}\) on \(\mathcal {X}\) is called circular if there exists a linear ordering \((x_1, \dots , x_n)\) of the elements of \(\mathcal {X}\) for \(\mathcal {S}\) such that each split \(S\in \mathcal {S}\) has the form:

$$\begin{aligned} S = \{\, \{x_{p}, \dots , x_{q}\}\,, \,\mathcal {X}- \{x_{p}, \dots , x_{q}\}\,\} \end{aligned}$$

for \(1 < p \le q \le n\). We say that a split network \(\mathcal {N}= \{\mathcal {X}, \mathcal {S}, w\}\) is a circular network if \(\mathcal {S}\) is circular.

Phylogenetic trees, seen as split networks, are special cases of circular networks (e.g. [4]). Circular networks have the appealing feature that they cannot contain too many splits. Indeed, let \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) be a circular network with \(|\mathcal {X}| = n\). Then \(|\mathcal {S}| = O(n^2)\) [6]. In general, circular networks are harder to interpret than trees are. In fact, they are not meant to represent explicit evolutionary events. However, they admit an appealing visualization in the form of an outer-labeled (i.e., the taxa are on the outside) planar graph that gives some insight into how “close to a tree” the network is. As such, they are popular exploratory analysis tools. We will not describe this visualization and how it is used here, as it is quite involved. See, e.g., [4, Chap. 5] for a formal definition and [8] for examples of applications.

Split networks are naturally associated with a metric. We refer to a function \(d:\mathcal {X}\,\times \,\mathcal {X}\rightarrow [0,+\infty ]\) as a dissimilarity over \(\mathcal {X}\) if it is symmetric and \(d(x,x) = 0\) for all x.

Definition 4

(Metric associated to a split network). Let \(\mathcal {N}= (\mathcal {X}, \mathcal {S},w)\) be a split network. The dissimilarity \(d:\mathcal {X}\,\times \,\mathcal {X}\rightarrow [0,\infty )\) defined as follows

$$\begin{aligned} d(x,y)=\sum _{S\in \mathcal {S}|_{x,y}} w(S), \end{aligned}$$

for all \(x,y \in \mathcal {X}\), is referred to as the metric associated to \(\mathcal {N}\). (It can be shown that d is indeed a metric. In particular, it satisfies the triangle inequality.)

The metric associated with a circular network can be used to reconstruct it.

Definition 5

(d-splits). Let \(d:\mathcal {X}\,\times \,\mathcal {X}\rightarrow [0,\infty )\) be a dissimilarity. The isolation index \(\alpha _d(S)\) of a split \(S = \{S_1, S_2\}\) over \(\mathcal {X}\) is given by

$$\begin{aligned} \alpha _d(S)=\min \{\tilde{\alpha }_d(x_1,y_1|x_2,y_2)\,:\, x_1,y_1\in S_1, x_2,y_2\in S_2\}, \end{aligned}$$

where

$$\begin{aligned} \tilde{\alpha }_d(x_1,y_1|x_2,y_2)= & {} \frac{1}{2}(\max \{d(x_1,y_1)+d(x_2,y_2), d(x_1,x_2)+d(y_1,y_2), \\&\qquad \qquad d(x_1,y_2)+d(y_1,x_2)\}-d(x_1,y_1)-d(x_2,y_2)). \end{aligned}$$

(Note that the latter is always non-negative.) We say that S is a d -split if \(\alpha _d(S) > 0\).

The following result establishes that circular networks can be reconstructed from their associated metric.

Lemma 1

(d-splits and circular networks [6]). Let \(\mathcal {X}\) be a set of n taxa and let \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) be a circular network with associated metric d. Then \(\mathcal {S}\) coincides with the set of all d-splits of \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\). Further the isolation index \(\alpha _d(S)\) equals w(S) for all \(S\in \mathcal {S}\).

The split decomposition method reconstructs \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) from d in polynomial time. When \(\mathcal {N}\) is compatible, d is an additive metric. See e.g. [2, 5].

In practice one obtains an estimate \(\hat{d}\) of d, called the distance matrix, from DNA sequences, e.g., through the Jukes-Cantor formula [22] or the log-det distance [23]. The accuracy of this estimate depends on the amount of data used [10, 11]. In previous work in the context of tree reconstruction, distorted metrics were used to encode the fact that large d-values typically produce unreliable \(\hat{d}\)-estimates.

Definition 6

(Distorted metrics [13, 14]). Suppose \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) is a split network with associated metric d. Let \(\tau , R>0\). We say that a dissimilarity \(\hat{d}: \mathcal {X}\times \mathcal {X}\rightarrow [0,+\infty ]\) is a \((\tau ,R)\)-distorted metric of \(\mathcal {N}\) if \(\hat{d}\) is accurate on “short” distances, that is, for all \(x,y\in \mathcal {X}\)

$$\begin{aligned} d(x,y)<R+\tau \quad \text {or}\quad \hat{d}(x,y)<R+\tau \quad \implies \quad |d(x,y)-\hat{d}(x,y)|<\tau . \end{aligned}$$

We refer to \(\tau \) and R as the tolerance and accuracy radius of \(\hat{d}\) respectively.

Distorted metrics have previously been motivated by analyzing Markov models on trees that are commonly used to model the evolution of DNA sequences [10, 11]. Such models have also been extended to split networks [24].

3 Main Results

By the reconstruction result mentioned above, any circular network \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) with associated metric d can be reconstructed from a \((\tau ,R)\)-distorted metric where \(\tau \) is 0 and R is greater or equal than the diameter \(\max \{d(x,y)\,:\, x,y \in \mathcal {X}\}\) of \(\mathcal {N}\). In the tree case, it has been shown that a much smaller R suffice [10, 11, 14, 17]. Here we establish such results for circular networks.

Chord depth and maximum incompatibility. To bound the tolerance and accuracy radius needed to reconstruct a circular network from a distorted metric, we introduce several structural parameters. The first two parameters generalize naturally from the tree context.

Definition 7

(Minimum weight). Let \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) be a split network. The minimum weight of \(\mathcal {N}\) is given by

$$ \epsilon _\mathcal {N}= \min \{w(S)\,:\,S \in \mathcal {S}\}. $$

Let \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) be a split network with associated metric d. For a subset of splits \(\mathcal {A} \subseteq \mathcal {S}\), we let

$$\begin{aligned} d(x,y;\mathcal {A}) = \sum _{S \in \mathcal {S}|_{x,y} \cap \mathcal {A}} w(S), \end{aligned}$$
(4)

be the distance between x and y restricted to those splits in \(\mathcal {A}\).

Definition 8

(Chord depth). Let \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) be a split network with associated metric d. The chord depth of a split \(S \in \mathcal {S}\) is

$$\begin{aligned} \varDelta _\mathcal {N}(S) = \min \left\{ d(x,y;\mathscr {C}_\mathcal {N}(S)) \,:\, x,y\in \mathcal {X}\text { such that } S \in \mathcal {S}|_{x,y} \right\} , \end{aligned}$$

and the chord depth of \(\mathcal {N}\) is the largest chord depth among all of its splits

$$\begin{aligned} \varDelta _\mathcal {N}= \max \left\{ \varDelta _\mathcal {N}(S): S\in \mathcal {S}\right\} . \end{aligned}$$

It was shown in [17, Corollary 1] that, if \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) is compatible, then a \((\tau , R)\)-distorted metric with \(\tau < \frac{1}{4} \epsilon _\mathcal {N}\) and \(R > 2 \varDelta _\mathcal {N}+ \frac{5}{4}\epsilon _\mathcal {N}\) suffice to reconstruct \(\mathcal {N}\) in polynomial time (among compatible networks).

For more general circular networks, the minimum weight and chord depth are not sufficient to characterize the tolerance and accuracy radius required for reconstructibility; see Example 1 below. For that purpose, we introduce a new notion that, roughly speaking, measures the extent to which a split network differs from a tree.

Definition 9

(Maximum incompatibility). Let \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) be a split network. The incompatible weight of a split \(S\in \mathcal {S}\) is

$$\begin{aligned} \varOmega _\mathcal {N}(S) = \sum _{S' \in \mathscr {I}(S)} w(S'), \end{aligned}$$

and the maximum incompatibility of \(\mathcal {N}\) is the largest incompatible weight among all of its splits

$$\begin{aligned} \varOmega _\mathcal {N}= \max \{\varOmega _\mathcal {N}(S): S\in \mathcal {S}\}. \end{aligned}$$

We drop the subscript in \(\epsilon _\mathcal {N}\), \(\varDelta _\mathcal {N}\) and \(\varOmega _\mathcal {N}\) when the \(\mathcal {N}\) is clear from context.

Statement of results. We now state our main result.

Theorem 1

NetworkReconstruction Suppose \(\mathcal {N} = (\mathcal {X}, \mathcal {S}, w)\) is a circular network. Given a \((\tau ,R)\)-distorted metric with \(\tau < \frac{1}{4}\epsilon _\mathcal {N}\) and \(R > 3\varDelta _\mathcal {N}+ 7 \varOmega _\mathcal {N}+ \frac{5}{2} \epsilon _\mathcal {N}\), the split set \(\mathcal {S}\) can be reconstructed in polynomial time together with weight estimates \(\hat{w} \,:\, \mathcal {S}\rightarrow (0,+\infty )\) satisfying \(|\hat{w}(S)-w(S)| < 2\tau \).

Establishing robustness to noise of circular network reconstruction algorithms is important given that, as explained above, such networks are used in practice to tentatively diagnose deviations from tree-like evolution. Errors due to noise can confound such analyses. See e.g. [8] for a discussion of these issues.

In [17, Sect. 4], it was shown that in the tree case the accuracy radius must depend linearly on the depth. The following example shows that the accuracy radius must also depend linearly on the maximum incompatibility.

Fig. 1.
figure 1

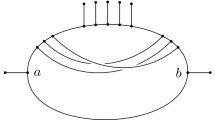
Two circular networks indistinguishable from a distorted metric with sublinear dependence on the maximum incompatibility. Here the taxa are ordered on a circle and lines indicate splits. For instance, in (A), the leftmost vertical line is the split with \(\{z_0, x_1, x_2\}\) on one side and all other taxa on the other. In both networks, \(\mathcal {X}= \{x_1, x_2, y_1, y_2\} \cup \{z_0, z_1,\ldots ,z_n\}\), and the n vertical lines, the horizontal line, and the two arcs are splits of weight 1.

Full size image

Example 1

(Depth is insufficient; linear dependence in maximum incompatibility is needed). Consider the two circular networks in Fig. 1. In both networks, \(\mathcal {X}= \{x_1, x_2, y_1, y_2\} \cup \{z_0,z_1,\ldots ,z_n\}\), and the n vertical lines, the horizontal line, and the two arcs are splits of weight 1. The chord depth of both networks is 1 while their maximum incompatibility is n. In both networks

  • \(d(z_i, x_j) = i +1\), \(0\le i \le n\), \(1\le j \le 2\),

  • \(d(z_i, y_j) = n-i+1\), \(0\le i \le n\), \(1\le j \le 2\),

  • \(d(x_1, x_2) = d(y_1,y_2) = 2\),

  • \(d(x_1,y_2) = d(x_2, y_1) = n+2\).

The only difference is that, in graph (A), \(d(x_1, y_1) = n+2\) and \(d(x_2, y_2) = n\) while, in graph (B), \(d(x_2, y_2) = n + 2\) and \(d(x_1, y_1) = n\). If we choose the distance matrix \(\hat{d}\) as follows:

  • \(\hat{d}(x_1, y_1) = \hat{d}(x_2,y_2) = n+1\),

  • \(\hat{d} = d\) for all other pairs,

then \(\hat{d}\) is a \((\tau , n-1)\)-distorted metric of both networks for any \(\tau \in (0,1)\). Hence, these two circular networks are indistinguishable from \(\hat{d}\). Observe that the chord depth is 1 for any n, but the maximum incompatibility can be made arbitrary large. (Note that the claim still holds if we replace the chord depth with the “full chord depth” \(\max \{\min \{d(x,y)\,:\,x,y \in \mathcal {X}, S \in \mathcal {S}|_{x,y}\}\,:\, S \in \mathcal {S}\}\), which also includes weights of incompatible splits separating x and y.)

Proof idea. Our proof of Theorem 1 is based on a divide-and-conquer approach of [17], first introduced in [14] and also related to the seminal work of [10, 11] on short quartet methods and the decomposition methods of [19, 20]. More specifically, we first reconstruct sub-networks in regions of small diameter. We then extend the bipartitions to the full taxon set by hopping back from each taxon to this small region and recording which side of the split is reached first. However, the work of [17] relies heavily on the tree structure, which simplifies many arguments. Our novel contributions here are twofold:

  • We define the notion of maximum incompatibility and highlight its key role in the reconstruction of circular networks, as we discussed above.

  • We extend the effective divide-and-conquer methodology developed in [10, 11, 14, 17, 19, 20] to circular networks. The analysis of this more general class of split networks is more involved than the tree case. In particular, we introduce the notion of a compatible chain—an analogue of paths in graphs—which may be of independent interest in the study of split networks.

Details are provided in [25].