Benefits and Application of Tree Structures in Gaussian Process Models to Optimize Magnetic Field Shaping Problems

Abstract

Recent years have witnessed the development of powerful numerical methods to emulate realistic physical systems and their integration into the industrial product development process. Today, finite element simulations have become a standard tool to help with the design of technical products. However, when it comes to multivariate optimization, the computation power requirements of such tools can often not be met when working with classical algorithms. As a result, a lot of attention is currently given to the design of computer experiments approach. One goal of this work is the development of a sophisticated optimization process for simulation based models. Within many possible choices, Gaussian process models are most widely used as modeling approach for the simulation data. However, these models are strongly based on stationary assumptions that are often not satisfied in the underlying system. In this work, treed Gaussian process models are investigated for dealing with non-stationarities and compared to the usual modeling approach. The method is developed for and applied to the specific physical problem of the optimization of 1D magnetic linear position detection.

1 Introduction

Gaussian process (GP) models have been widely used as emulators for time-consuming computer models, where the most common approach is adopted from spatial statistics and named Kriging [13]. This refers to a linear model with a systematic departure realized as a stationary Gaussian random function. A major problem with this approach is the strong assumption of stationarity and homoscedasticity of the GPs, which is firstly difficult to verify and secondly often not valid. An efficient way to deal with this problem is to partition the input parameter space into regions and to fit individual, stationary GPs in each region. This method is referred to as treed Gaussian process modeling [6].

It is the ultimate goal of this work to develop an emulator based on GPs to model and optimize realistic physical systems using FEM data. This is done in the context of magnetic linear position detection where the magnetic field of a permanent magnet is emulated in the magneto-static limit. In such systems, a magnet moves relative to a magnetic sensor and the state of the magnet is determined from the field that is seen by the sensor. The advantages are wear-free measurements, high resolutions, low power requirements, and an excellent robustness against temperature and dirt with multiple applications in modern industries, e.g., in the detection of shifting shafts, flexible arm mechanisms, gearboxes or lift systems, [16]. To improve the signal stability while retaining cost-effectiveness, it is proposed in [9] to shape the magnetic field at the sensor by designing a compound magnet. However, even when dealing with a small number of constituents, the compound features multiple degrees of freedom which makes the modeling and optimization process difficult.

This work is intended to be a preliminary study for emphasizing advantages and also possible disadvantages of the treed GP models in comparison to the usual GPs. Thus, emulators of the magnetic field are constructed and investigated for both modeling approaches. To that end, the sample points for the construction of the models are generated from an analytical description for the magnetic field. Furthermore, at this early stage, the compound consists only of a single rectangular magnet, considerably reducing the number of parameters to better understand the potential and the difficulties of this method.

2 Magnetic Linear Position Detection

Magnetic position and orientation detection systems play an important role in modern industrial applications. Their features include contact-free measurement, low power requirements, and high resolutions combined with an excellent robustness against oil, grease, and dirt without the need for airtight seals or other environmental contamination control in harsh environments. Long life times up to decades and cost-effectiveness are especially interesting for the cost-driven automotive sector where magnetic sensors are increasingly used for gear shift detection, gas pedals, speed sensors, and many other applications.

Fig. 11.1

a shows a sketch of a linear position detection system. A rectangular magnet with magnetization $\mathbf {M}$ oriented in the z-direction moves along the stroke $s \in [-S, S]$ in x-direction and generates a magnetic field with components $B_{x}$ and $B_{z}$. The sensor is positioned on the positive z-axis at a distance $\varDelta$ from the magnet called the airgap. b shows the magnetic field components detected by the sensor as a function of the position of the magnet for a typical setup with a cubical magnet with side length 10mm, a remanence field of one Tesla and an airgap of 5mm

State-of-the-art magnetic linear position detection systems feature a magnet that moves relative to a magnetic sensor which detects the magnetic field to determine the position of the magnet; see Fig. 11.1a. The magnetic field is generally not a linear function of the position of the magnet but typically features an even and an odd component; see Fig. 11.1b. It can be a sensitive task to find a bijective map that relates the magnetic field to the position of the magnet. Distinction is essentially made between 1D and 2D magnetic position detection systems, where the former picks up both components of the magnetic field applying a 2D sensor, while the latter just detects the odd component with a simple 1D probe. For 1D position sensing, the linear range of the odd field component about the origin is used; see Fig. 11.1b. When compared to their 2D counterparts, 1D systems have a lot of shortcomings like small measurement ranges and an even smaller linear region as well as airgap instability. Despite these critical disadvantages, 1D systems are still used in modern industrial applications, solely due to their cost-effectiveness, as 1D sensors are much cheaper than 2D ones.

It is proposed in [9] to improve 1D magnetic position detection systems by designing a compound magnet which features a highly linear odd field component $B_{x}$ along a given stroke while minimizing the magnet volume at the same time to reduce costs. The multiple shape parameters of the compound make the optimization a very time-consuming process when calculating the magnetic field by FEM means. In the following sections, a design of computer experiments approach is developed.

3 Gaussian Process Models

The statistical approach for computer experiments consists of two parts—experimental design and modeling. The designing refers to finding a set $D_{n}$ of n points in the experimental domain T that optimally represents the entire domain; for further information, see [1, 5, 14, 15]. Then, data is collected based on the optimal design $D_{n}$ and the relationship between the input variables $\mathbf {x_{i}}=(x_{1},\ldots ,x_{s})^{T}$, $i=1,\ldots ,n$, and the output is modeled.

3.1 Kriging Setup

Among many different modeling approaches (see, e.g., [5]), especially Gaussian process models, also called Kriging models, are of main interest for computer experiments. Here, the response $Y(\mathbf {x})$ is treated as a realization of a stochastic process, i.e.,

$$\begin{aligned} Y(\mathbf {x})= \mu (\mathbf {x})+ Z(\mathbf {x}), \end{aligned}$$

(11.1)

where $\mu (\mathbf {x})$ is the trend function and $Z(\mathbf {x})$ is a primarily stationary Gaussian process with zero mean. There are different types of Kriging based on the definition of the trend function. The most general form is known as universal Kriging, where the trend function is specified by $\mu (\mathbf {x})=\mathbf {f}(\mathbf {x})^{T}\mathbf {\beta }$, i.e., as a regression model. Here, the function vector $\mathbf {f}$ is fixed, and the parameter vector $\mathbf {\beta }$ needs to be estimated. The ordinary Kriging approach defines a slightly simpler model, which has an unknown but constant trend, i.e., $\mu (\mathbf {x})= \mu$. The covariance matrix of the Gaussian process $Z(\mathbf {x})$ is given by

$$\begin{aligned} Cov(Z(\mathbf {x_{i}}), Z(\mathbf {x_{j}}))=\sigma ^{2}R(\mathbf {x_{i}},\mathbf {x_{j}}), \end{aligned}$$

(11.2)

where $R(\mathbf {x_{i}},\mathbf {x_{j}})=Corr(Z(\mathbf {x_{i}}),Z(\mathbf {x_{j}}))$ is a given correlation function, scaled by the process variance $\sigma ^{2}$ and $\mathbf {x_{i}}$, $\mathbf {x_{j}} \in D_{n}$. Most of the time, it is assumed that the stochastic process is stationary, i.e., $R(\mathbf {x_{i}},\mathbf {x_{j}})=R(\mathbf {x_{i}}-\mathbf {x_{j}}) = R(\mathbf {h})$. Among many possible correlation functions (see [11]), the Matérn class is of great importance and is given by

$$\begin{aligned} R(h) = \frac{2^{1-\nu }}{\varGamma (\nu )}\left( \frac{\sqrt{2\nu }h}{\theta }\right) ^{\nu }K_{\nu }\left( \frac{\sqrt{2\nu }h}{\theta }\right) , \end{aligned}$$

(11.3)

where $\varGamma$ is the gamma function, $K_{\nu }$ is a modified Bessel function, $h=|x_{i}-x_{j}|$, and $\nu , \theta$ are positive parameters. The sample paths of a GP with the Matérn correlation function are $\lfloor \nu -1\rfloor$ times differentiable. Note, that, in general, the product correlation rule is used for multivariate input variables in computer experiments, i.e., $R(\mathbf {x_{i}},\mathbf {x_{j}})= \prod \limits _{k=1}^{s}R_{j}(x_{ik}-x_{jk})$, see [3]. Usually, the parameters $\mathbf {\beta },\sigma ^{2}, \nu$, and $\theta$ are unknown and hence need to be estimated, e.g., by maximum likelihood estimation (MLE); see [5] for further details. When the parameters are specified, the model can be used to make predictions $Y(\mathbf {x_{0}})$ at untried points $\mathbf {x_{0}} \notin D_{n}$. Let $\mathbf {x_{1}},\ldots ,\mathbf {x_{n}} \in D_{n}$ be the set of design points and $\mathbf {y_{D}}=(y(\mathbf {x_{1}}),\ldots ,y(\mathbf {x_{n}}))^{T}$ the corresponding data, then a linear predictor of $y(\mathbf {x_{0}})$ is given by

$$\begin{aligned} \hat{Y}(\mathbf {x_{0}})=\mathbf {\lambda }^{T}(\mathbf {x_{0}})\mathbf {y_{D}}. \end{aligned}$$

(11.4)

Among all linear predictors, the best linear unbiased predictor (BLUP) is a common choice for prediction at untried points. This predictor minimizes the mean squared error (MSE)

$$\begin{aligned} \text{ MSE }\left( \hat{Y}(\mathbf {x_{0}})\right) =\mathbb {E}\left( \mathbf {\lambda }^{T}\mathbf {y_{D}} - \hat{Y}(\mathbf {x_{0}})\right) ^{2}, \end{aligned}$$

(11.5)

with respect to $\mathbf {\lambda }$ under the unbiased-constraint

$$\begin{aligned} \mathbb {E}\left( \mathbf {\lambda }^{T}\mathbf {Y_{D}}\right) =\mathbb {E}\left( Y(\mathbf {x_{0}})\right) . \end{aligned}$$

(11.6)

Solving this optimization problem defines the BLUP as

$$\begin{aligned} \hat{Y}(\mathbf {x_{0}})=\mathbf {f}^{T}{\hat{\beta }}+\mathbf {k}K_{D}^{-1}(\mathbf {y_{D}}-F{\hat{\beta }}), \end{aligned}$$

(11.7)

where $\mathbf {f}=\left( f_{1}(\mathbf {x_{0}}),\ldots ,f_{k}(\mathbf {x_{0}})\right) ^{T}$, $K_{D}=\sigma ^{2}R_{D}$, $\mathbf {k}=\left( R(\mathbf {x_{1}},\mathbf {x_{0}}),\ldots ,R(\mathbf {x_{n}},\mathbf {x_{0}})\right)$, ${\hat{\beta }}$ is the least squares estimator of $\mathbf {\beta }$ and F the design matrix, [13].

3.2 The Curse of Stationarity

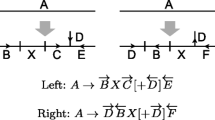
A lot of research has been done concerning GPs and complex computer code modeling with a lot of examples and case studies where this approach was successfully demonstrated; see, e.g., [3]. Nevertheless, it has also been shown that especially the strong assumption of stationarity of the process can lead to problems, as many physical models exhibit a clear non-stationary behavior. To deal with this problem, non-stationary correlation functions can be used; see [10]; however, fitting fully non-stationary models quickly becomes difficult and computationally intractable. Another approach uses treed Gaussian process models (TGP); see, e.g., [6]. Here, the main idea is to divide the parameter space by making binary splits on single variables, i.e., a tree partition and fitting an independent GP model in each leaf; see Fig. 11.2.

Fig. 11.2

Tree partitioning: division of the input space by binary splits. The two splits result in three leafs, i.e., three data sets—for ${ GP1}$, all data points with $x_{1} \le c_{1}$ are used, ${ GP2}$ contains all data points with $x_{1} > c_{1}$ and $x_{2} \le c_{2}$, and ${ GP3}$ includes the remaining data. An independent GP model is fitted in each of the three leafs

This method has the advantage of a comparatively simple modeling of non-stationarity and an easier covariance matrix inversion as a result of data reduction in each leaf. It is also more likely that the trend functions in each leaf can be assumed to be simple functions or even just constants without losing information, making parameter estimation easier and reducing the risk of over-fitting. Furthermore, the partitioning yields perfect conditions for multi-core computing, which may further reduce computation time.

4 Case Study: Magnetic Field Shaping

In this section, different GP models are tested to describe the odd component $B_x$ of the magnetic field along the stroke $s\in$[−10, 10] mm of a rectangular magnet with sides 2a, 2b, and 2c aligned in x-,y-, and z-direction and a magnetization of $\mathbf {M} = (0,0,x)$. In this first case study, the magnet volume V and side a are fixed to known, and realistic values and boundaries are given for the other parameters; see Table 11.1. The resulting GP model is then used to find the optimal values for c and x where the deviation of $B_x$ along the stroke from a linear function with a slope of one millitesla per millimeter is minimal.

Table 11.1 Assumptions and constraints for the involved parameters

A CL$_{2}$-optimal latin hypercube design (see [5]) with $n=50$ points for the parameters c and x with respective ten regularly spaced points along the stroke s is used to generate the data, a total of 500 points (c,x,s), of the final design. It is important to notice that the FEM simulation environment would always model the magnetic field along the entire stroke providing an arbitrary number of sample points for s and thus limiting the number of evaluations only for the parameters c and x. Without loss of generality, the data is generated using an analytical description of the magnetic field for ideal permanent magnets for testing the validity of the GP model, see [2]. A constant trend function and Matérn correlation function with $\nu =\frac{3}{2}$ are assumed for the GP models, and the DIviding RECTangles (DIRECT) algorithm is used for global optimization; see [7, 8]. The algorithms are implemented in R, making use of the packages DiceKriging, DiceDesign, nloptr ([4, 7, 12]).

It is known that for the parameter c, the stationarity assumption does not hold. For small values of c, the magnetic field varies strongly, while it is quite flat for larger values; see Fig. 11.3. Therefore, several GP models are investigated based on different splits for c and compared due to their ability to obtain the optimal values for c and x, which can be determined from the analytical model to be $c=10.264815$ and $x=997.9207$. The results are summarized in Table 11.2 and represented graphically in Fig. 11.4.

Fig. 11.3

Influence of the parameter c on the magnetic field $B_{x}$. The red point refers to the optimal value for c based on optimization of the analytical function, and the two red lines divide c into the parts used in the trees. The x-axis refers to the interval [0.1, 50] mapped onto [0, 1]

Table 11.2 Different GP models, based on the splits defined by c border and the related optimized parameter values

Fig. 11.4

The left-hand figures show real versus predicted outputs for 5000 arbitrary parameter combinations. The right-hand figures show the optimization solution based on the analytical equation and the models. The dashed line refers to the solution where the parameters obtained by the model with two splits are inserted into the analytical equation and the red line refers to a line with slope one in all pictures

It can be seen from Table 11.2 and Fig. 11.4 that the TGP approach can really yield improvements and give an almost perfect fit despite the stationarity assumption, especially when using two splits on c. However, solutions can also get worse by bad splitting, where especially the last and extreme case in Table 11.2, i.e., when the border is drawn almost directly at the optimal value, emphasizes one of the major drawbacks of treed structures. In this case, the estimated optimal values for c and x are far from being an acceptable solution. The reason for this lies in inaccuracies near the borders that occur due to the natural behavior of treed processes: at the border two processes, with probably completely different structures, melt together. This means that unless there is an sample point directly at the border, the two processes may not even meet at the same point leading to discontinuities. Assuming that there are enough border sample points, there remains the problem that differentiability of the process at the border will be never guaranteed, but rather very unlikely; see Fig. 11.5. However, the assumption of differentiability is crucial for many physical systems and hence should be also held in belonging models.

Fig. 11.5

It is shown how the magnetic field $B_{x}$ changes along the parameter c. The red dotted line refers to the border which at the same time is the solution for the optimal c. The processes do melt together at the same point because there is a sample point directly at the border, however, the undesirable bend, and hence non-differentiability, is obvious

5 Conclusion and Outlook

It has been shown that treed Gaussian process models can be a powerful tool for the design of computer experiments, but great care must be taken with respect to the partitioning of the tree. Especially, predictions near borders can exhibit large errors and bad functional attributes. For optimization, it is crucial to grant good fitting of the GP model, especially near the optimum. However, it can never be guaranteed that the optimum is not located near or even directly at a border. Thus, actual research is strongly concerned with the construction of border processes that yield at least once continuously differentiable borders. Furthermore, also systematic and reasonable partitioning is currently under investigation, which should be achieved using an adapted genetic algorithm. From a physical point of view, more complex compound magnets with considerably more parameters will be implemented based on realistic, noisy FEM data to improve real-world magnetic linear position detection systems moving beyond the analytic description.