Weight-Improved K-Means-Based Consensus Clustering

Abstract

Many consensus clustering methods ensemble all the basic partitionings (BPs) with the same weight and without considering their contribution to consensus result. We use the Normalized Mutual Information (NMI) theory to design weight for BPs that participate in the integration, which highlights the contribution of the most diverse BPs. Then an efficient approach K-means is used for consensus clustering, which effectively improves the efficiency of combinatorics learning. Experiment on UCI dataset iris demonstrates the effective of the proposed algorithm in terms of clustering quality.

1 Introduction

There is no single clustering algorithm can performs best for all data sets [1], and can discover all types of cluster shapes and structures [2]. Consensus clustering approached are able to integrate multiple clustering solutions obtained from different data sources into a unified solution, and provide a more robust, stable and accurate final result [3]. However, the previous research still has some limitations.

Firstly, high quality BPs are beneficial to the performance of consensus clustering yet the partitions with poor quality will lead to worse consensus result. But most studies tend to integrate all BPs, and they do not filter poor BPs. Secondly, the diversity between BPs also have great impact on consensus clustering, diverse BPs which means the BP that has different mutual information with other BPs will have different contribution to the consensus result. However, there are few references explore impact of the number of BPs to consensus clustering neither did they take into account the diversity of BPs into the integration process.

We proposed weight-improved K-means-based consensus clustering (WIKCC). Firstly, we design weight for each BP participating in the integration. Specifically, we generate multiple BPs and measure the quality of each BP using normalized Rand index $R_{n}$ [6], and sort the BPs in the increasing order of $R_{n}$, then we explore the influence of the number of BPs on consensus clustering, based on the above exploration we can choose an appropriate number of better BPs for consensus clustering, which can minimize the number of BPs in quality assurance. After that we construct the co-occurrence matrix with the selected BPs, and calculate the similarity of two BPs with Normalized Mutual Information (NMI) method [4] according to the co-occurrence matrix. Then weight of each BP is designed according to NMI values which reflect a single BP to overall BPs’ similarity. K-means-based method [2] make special attention for its simplicity and high efficiency. So we transform consensus clustering to K-means clustering.

2 Weight Design Based on the Normalized Mutual Information

Mutual information is used to measure the shared information of the two distributions. We compute the NMI between two BPs, and the greater the value of NMI means the lower difference, which will result in lower ${\text{w}}_{\text{i}}$.

Given two BPs results $\uppi_{\text{i}}$ with ${\text{K}}_{\text{i}}$ clusters, $\uppi_{\text{i}} = \left\{ {{\text{C}}_{1}^{{\left( {\text{i}} \right)}} ,{\text{C}}_{2}^{{\left( {\text{i}} \right)}} , \ldots ,{\text{C}}_{{{\text{K}}_{\text{i}} }}^{{\left( {\text{i}} \right)}} } \right\}$ and $\uppi_{\text{j}}$ with ${\text{K}}_{\text{j}}$ clusters, $\uppi_{\text{j}} = \left\{ {{\text{C}}_{1}^{{\left( {\text{j}} \right)}} ,{\text{C}}_{2}^{{\left( {\text{j}} \right)}} , \ldots {\text{C}}_{{{\text{K}}_{\text{j}} }}^{{\left( {\text{j}} \right)}} } \right\}$ the mutual information between two results is defined as follows:

$$ {\text{NMI}}\left( {\uppi_{\text{i}} ,\uppi_{\text{j}} } \right) = \frac{{2{\text{I}}_{1} \left( {\uppi_{\text{i}} ,\uppi_{\text{j}} } \right)}}{{{\text{I}}_{2} \left( {\uppi_{\text{i}} } \right) + {\text{I}}_{2} \left( {\uppi_{\text{j}} } \right)}} $$

(1)

$$ I_{1} \left( {\uppi_{i} ,\uppi_{j} } \right) = \sum\nolimits_{h} {\sum\nolimits_{l} {\frac{{\left| {C_{h}^{\left( i \right)} \cap C_{l}^{\left( j \right)} } \right|}}{n}} } \log \frac{{n\left| {C_{h}^{\left( i \right)} \cap C_{l}^{\left( j \right)} } \right|}}{{\left| {C_{h}^{\left( i \right)} } \right||C_{l}^{\left( j \right)} |}} $$

(2)

$$ I_{2} \left( {\uppi_{i} } \right) = - \sum\nolimits_{h} {\frac{{|C_{h}^{\left( i \right)} |}}{n}} \log \frac{{|C_{h}^{\left( i \right)} |}}{n} $$

(3)

$$ I_{2} \left( {\uppi_{j} } \right) = - \sum\nolimits_{l} {\frac{{|C_{l}^{\left( j \right)} |}}{n}} \log \frac{{|C_{l}^{\left( j \right)} |}}{n} $$

(4)

For a single BP the average mutual information can be defined as:

$$ {\text{H}}\left( {\pi_{i} } \right) = \frac{1}{r - 1}\sum\nolimits_{k = 1,k \ne i}^{r} {NMI\left( {\pi_{i} ,\pi_{k} } \right),\left( {i = 1,2, \ldots r} \right)} $$

(5)

Where ${\text{h}} \in \left\{ {1,2, \ldots ,{\text{k}}_{\text{i}} } \right\}$, ${\text{l}} \in \left\{ {1,2, \ldots ,{\text{k}}_{\text{j}} } \right\}$ is one of the cluster result label of $\uppi_{\text{i}}$ and $\uppi_{\text{j}}$, $\left| {{\text{C}}_{\text{h}}^{{\left( {\text{i}} \right)}} } \right|$, $\left| {{\text{C}}_{\text{l}}^{{\left( {\text{j}} \right)}} } \right|$ respectively represent the number of the data set belong to cluster ${\text{C}}_{\text{h}}^{{\left( {\text{i}} \right)}}$ in $\uppi_{\text{i}}$ and ${\text{C}}_{\text{l}}^{{\left( {\text{j}} \right)}}$ in $\uppi_{\text{j}}$, $\left| { {\text{C}}_{\text{h}}^{{\left( {\text{i}} \right)}} \cap {\text{C}}_{\text{l}}^{{\left( {\text{j}} \right)}} } \right|$ is the number of the dataset belong both to ${\text{C}}_{\text{h}}^{{\left( {\text{i}} \right)}}$ and ${\text{C}}_{\text{l}}^{{\left( {\text{j}} \right)}}$, r is the number of the BPs.

The greater $H\left( {\pi_{i} } \right)$ indicate that cluster member $\pi_{i}$ share more information with other cluster members. The weight is defined as:

$$ w_{m}^{,} = \frac{1}{{H\left( {\pi_{i} } \right)}} $$

(6)

The normalized form is defined as:

$$ w_{m} = \frac{{w_{m}^{,} }}{{\mathop \sum \nolimits_{m = 1}^{r} w_{m}^{,} }} $$

(7)

The weight is bigger as the greater diversity between two base clustering.

3 The Weight-Improved K-Means-Based Consensus Clustering

In this section, we first introduce the co-occurrence matrix which is used for records the situation of sharing dataset between two BPs. Table 1 shows an example.

Table 1. The co-occurrence matrix

In Table 1, BPs: $\pi^{*}$ and $\pi_{i}$ contain k and $k_{i}$ clusters respectively, $n_{{KK_{i} }}^{\left( i \right)}$ represents the number of the objects that belongs to both $C_{K}$ and $C_{{K_{i} }}^{\left( i \right)}$, then let $n_{{k_{ + } }} = \sum\nolimits_{j = 1}^{{K_{i} }} {n_{kj}^{\left( i \right)} } ,1 \le j \le K_{i} ,1 \le k \le K,P_{kj}^{\left( i \right)} = n_{kj}^{\left( i \right)} /n,p_{k + } = n_{k + } /n ,and \,p_{ + j}^{\left( i \right)} = n_{ + j}^{\left( i \right)} /n$. We can obtain a normalized co-occurrence matrix (NCM), based on which we can compute the centroid of the K-means clustering.

K-means algorithm cannot directly run on the co-occurrence matrix, so a binary data set is introduced to represent the result of r BPs. The binary data set $X_{l}^{\left( b \right)} = \{ x_{l}^{\left( b \right)} |1 \le l \le n\}$ as follows:

$$ x_{l}^{\left( b \right)} = \left\langle {x_{l,1}^{\left( b \right)} , \ldots ,x_{l,i}^{\left( b \right)} , \ldots ,x_{l,r}^{\left( b \right)} } \right\rangle , \;{\text{with}}\; $$

(8)

$$ x_{l,i}^{\left( b \right)} = \left\langle {x_{l,i1}^{\left( b \right)} , \ldots ,x_{l,ij}^{\left( b \right)} , \ldots x_{l,iKi}^{\left( b \right)} } \right\rangle ,\;{\text{and}}\; $$

(9)

$$ x_{l,ij}^{\left( b \right)} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {if\;object\;l\;belongs\;to\;the\;cluster\;C_{j} \;in\;\pi_{i} } \hfill \\ {0,} \hfill & {otherwise} \hfill \\ \end{array} } \right., $$

(10)

Where $x_{l}^{\left( b \right)}$ is an n $\times \sum\nolimits_{i = 1}^{r} {K_{i} }$ binary data set matrix with $\left| {x_{l,i}^{\left( b \right)} } \right| = 1$.

We use the K-means algorithm to integrate the BPs, suppose r BPs are integrated to a result $\pi^{*}$, $m_{k}$ represent the centroid of the $C_{k} \;in\;\pi^{*}$ as follows:

$$ m_{k} = \left\langle {m_{k,1} , \ldots ,m_{k,i} , \ldots ,m_{k,r} } \right\rangle ,with $$

(11)

$$ m_{{{\text{k}},{\text{i}}}} = \left\langle {m_{k,i1} , \ldots ,m_{k,ij} , \ldots ,m_{{k,iK_{i} }} } \right\rangle , $$

(12)

The centroids of the K-means on $X^{b}$ are represented as follows:

$$ m_{k,i} = \left\langle {\frac{{p_{k1}^{\left( i \right)} }}{{p_{k + } }}, \ldots ,\frac{{p_{kj}^{\left( i \right)} }}{{p_{k + } }}, \ldots ,\frac{{p_{{kK_{i} }}^{\left( i \right)} }}{{p_{k + } }}} \right\rangle ,\forall k,i. $$

(13)

The centroids can be computed by the Co- occurrence matrix, and $m_{k}$ is a vector of $\sum\nolimits_{i = 1}^{r} {k_{i} }$ dimension. The element in the vector is computed by the number of shared data set between current cluster and all of the clusters of BPs.

By using the co-occurrence matrix and the binary data set the consensus clustering are transformed to the K-means clustering, that is:

$$ { \hbox{max} }\sum\nolimits_{i = 1}^{r} {w_{i} U\left( {\pi ,\pi^{*} } \right)} = min\sum\nolimits_{k = 1}^{k} {\sum\nolimits_{{xl \in C_{k} }} {f\left( {x_{l}^{\left( b \right)} ,m_{k} } \right)} } $$

(14)

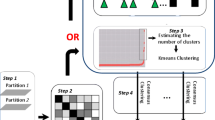
As shown in Fig. 1. In BPs generation phase, classic partition clustering method K-means is used, different initial number of cluster k, to generate diversified BPs. In consensus clustering phase, after generating the BPs and computing the weight for each clustering member, we can obtain the weighted co-occurrence matrix, and then we can get the weighted binary dataset $X^{\left( b \right)\prime }$, by running K-means on weighted binary dataset $X^{\left( b \right)\prime }$, we can get final consensus result $\pi^{*}$.

Fig. 1.

Algorithm WIKCC

4 Experimental Results

We present experiment on UCI dataset iris. The normalized Rand index (${\text{R}}_{\text{n}}$) [6] is adopted. Its value usually range between [0,1]. The higher value, indicate that the higher quality of clustering. We demonstrate the cluster validity of WIKCC by comparing it with two well-known consensus clustering algorithms the K-means-based algorithm (KCC) [2], the hierarchical algorithm (HCC) [5].

4.1 Quality of BPs

We run K-means algorithm 100 times with the initialized number of clusters randomized within [K, $\sqrt n$] to generate 100 basic partitionings (BPs) for consensus clustering; K is the true class of data set, n is the number of the instances, the squared Euclidean distance is used for the distance function, the quality of each BPs is measured by $R_{n}$, the distribution of quality of BPs is shown as Fig. 2.

Fig. 2.

Clustering quality distribution of BPs

As can be seen in Fig. 2, the distribution of the clustering quality of the BPs show that there is a large proportion of BPs with poor quality, but only quite a small proportion of BPs with relatively high quality. This shows that the incorrect pre-specified number of classes will lead to weak clustering result.

4.2 Exploration of Impact Factors

In order to In order to determine a suitable number of BPs for WIKCC, we explore the influence of the number of BPs on consensus clustering. In the above experiment, r BPs have generated, and r = 100. We randomly select a part of BPs to obtain the subset $\prod^{\text{r}}$, with r = 10, 20, …, 90. For each r we do KCC [2] algorithm 100 times to get 100 consensus clustering result. The distribution of the quality of consensus clustering result for different subset is shown as Fig. 3.

Fig. 3.

Impact of the number of BPs to the consensus clustering

As shown in Fig. 3, when r < 50, the quality of the consensus result present increasing trend with the increase of r, but when r > 50 the result fluctuate in a mall range and nearly tend to be stable, it imply that 50 may be the appropriate number of BPs for WIKCC. Based on above exploration we chose the BPs with the quality of the top 50 BPs for WIKCC.

4.3 WIKCC versus Other Clustering Methods

We compare the WIKCC with KCC and HCC, we choose top 50 better BPs for each method and run on the iris dataset for 10 times.

We can see in Fig. 4. The WIKCC shows significantly higher than KCC, and outperforms better than the HCC in term of the quality of consensus clustering. In addition, comprising the Figs. 2 and 4, we can see that consensus clustering is much better than almost all the basic clustering result obtained by K-means, this indicates that, the consensus clustering method can find the real cluster structure more accurately than a single traditional clustering algorithm by integrating the commonality of many basic clustering results, so it can obtain a more stable and accurate clustering result by ensemble multiple weak BPS.

Fig. 4.

WIKCC versus KCC and HCC

5 Concluding Remarks

We explore the influence of the number of BPs on the consensus clustering and chose appropriate number better BPs for WIKCC. The weight is designed by the NMI method between two BPs based on co-occurrence matrix. Finally, the experiment on iris demonstrates that WIKCC outperforms the state-of-the-art well-known KCC and HCC algorithms in terms of clustering quality. In the future, we will explore the more other factors that have influence on the performance of KCC, and we will consider more other factors when designing the weights.