Outage Probability Analysis of Single Energy Constraint Relay NOMA Network

Abstract

In this paper, we investigate energy harvesting decode-and-forward relaying non-orthogonal multiple access (NOMA) networks. Specifically, one source node wishes to transmit two symbols to its two desired destinations directly and via the help of an intermediate energy constraint relay node, and the NOMA technique is applied in the transmission of both hops (from source to relay and from relay to destinations). For performance evaluation, we derive the closed-form expressions for the outage probability (OP) at $D_1$ and $D_2$. Our analysis is substantiated via Monte Carlo simulation. The effect of several parameters, such as power allocation factors in both transmissions in two hops, the power splitting ratio, the location of relay node, to the outage performances at two destinations is investigated.

1 Introduction

Due to the significantly growing number of users and wireless devices, the future 5G networks are required to support the demand for low-latency, low-cost and diversified services, yet at higher quality and a thousand-time faster data rate. In the quest for new technologies, non-orthogonal multiple access (NOMA) technique has emerged as one of the most prominent candidates in meeting these requirements. The use of NOMA can ensure a significant spectral efficiency as it takes advantage of the power domain to serve multiple users at the same time/frequency/code. In addition, compared with conventional multiple access, NOMA offers better user fairness since even users with weak channel state information (CSI) can be served in a timely manner.

NOMA in cooperative and cognitive radio networks has been pursued by research groups from Princeton University, USA (Ding et al.) and Queen Mary University of London, UK (Elkashlan et al.) with a focus on cooperative communication protocols and performance analysis of cooperative networks [1] and large-scale underlay cognitive radio networks [2] taking into account users? geographical distribution. Specifically, in [1], the authors analyzed the outage probability and diversity order under the assumption that users with better channel conditions can decode the message for the others, and proposed a cooperative NOMA transmission protocol. The work in [2] presented the closed-form expression of outage probability to evaluate the system performance by using stochastic-geometry. Also in this research stream, Men and Ge (Xidian University, China) proposed a NOMA-based downlink cooperative cellular system, where the base station communicates with two paired mobile users through the help of a half-duplex amplify-and-forward (AF) relay [3]. To investigate the performance of the considered network, a closed-form expression of outage probability was derived and ergodic sum-rate was studied. By comparing NOMA with conventional multiple access, the authors showed that NOMA can offer better spectral efficiency and user fairness since more users are served at the same time/frequency/spreading code. Furthermore, J.-B. Kim and I.-H. Lee’s research group has investigated NOMA in cooperative networks and derived exact and closed-form expressions of outage probability. The results showed that the system performance is improved significantly with NOMA. Their system model consists of one base station (BS) and two users, in which user 1 communicates directly to the BS while user 2 communicates with the BS through the help of user 1.

For NOMA with RF-EH, authors from Aristotle University have studied data rates optimization and fairness increase in NOMA systems with wireless energy harvesting based on time allocation [4]. The analytical and simulation results indicated that this proposed method is better than TDMA scheme. Moreover, the research group from Queen Mary University of London (UK) and Princeton University (USA) proposed NOMA scheme in simultaneous wireless information and power transfer (SWIPT) networks [5]. Specifically, near NOMA users that are close to the source act as energy harvesting relays to help far NOMA users. Furthermore, the authors investigated the performance of the considered systems by deriving the closed-form expressions for outage probability and system throughput under the random distribution of users’ location. Analytical and simulation results showed that selecting users can reasonably reduce the outage probability. Moreover, by carefully choosing the parameters of the network such as transmission rate or power splitting coefficient, system performance can be guaranteed even if the users do not use their own batteries to power the relay transmission.

In this paper, we investigate energy harvesting DF NOMA relaying networks, in which one source nodes want to transmit its two symbols to two destinations directly and via the help of an energy constraint relay nodes. The relay harvests the energy and decode the radio frequency (RF) signal from the source and forward the encoded signal to two destinations. In addition, the NOMA technique is considered for transmission in both hops from the source to relay and from relay to destinations with two set of power allocation factor.

Notation: The notation $\mathcal {CN}\left( {0,{N_0}} \right)$ denotes a circularly symmetric complex Gaussian random variable (RV) with zero mean and variance ${N_0}$. $\mathcal {E}\left\{ . \right\}$ denotes mathematical expectation. The functions ${f_X}\left( . \right)$ and ${F_X}\left( . \right)$ present the probability density function (PDF) and cumulative distribution function (CDF) of RV X. The function $\varGamma \left( {x,y} \right)$ is an incomplete Gamma function (Eq. 8.310.1 of [6]). $C_b^a = \frac{{b!}}{{a!\left( {b - a} \right) !}}$. Notation $\Pr [.]$ returns the probability.

2 Network and Channel Models

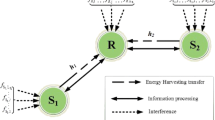
As illustrated in Fig. 1, we consider a system model of a NOMA EH DF relaying network, where a source node S want to transmit its two symbols $x_1$ and $x_2$ to two destination nodes $D_1$ and $D_2$, respectively, directly and via the help of an intermediate EH relay nodes R. All nodes are equipped with single antenna operating in half-duplex mode. In Fig. 1, $(h_1,d_1)$, $(h_2,d_2)$, $(h_3,d_3)$, $(h_4,d_4)$, and $(h_5,d_5)$ denote the Rayleigh channel coefficients over the distances for the links between S and R, R and $D_1$, R and $D_2$, S and $D_1$, and S and $D_2$, respectively. The corresponding channel gain ${g_\varOmega } \buildrel \varDelta \over = {\left| {{h_\varOmega }} \right| ^2}$ is exponential random variable (RV) with parameter ${\lambda _\varOmega } = {\left( {{d_\varOmega }} \right) ^\beta }$, with $\varOmega \in \left\{ {1,2,3,4,5} \right\}$ and $\beta$ denote path-loss exponent. The channel state information (CSI) is assumed to be known at all nodes. The corresponding probability density function (PDF) and cumulative distribution function (CDF) of each RV is ${f_{{g_\varOmega }}}\left( x \right) = {\lambda _\varOmega }{e^{ - {\lambda _\varOmega }x}}$ and ${F_{{g_\varOmega }}}\left( x \right) = 1 - {e^{ - {\lambda _\varOmega }x}}$, respectively. The power splitting architecture is apply at relay for harvesting the energy with power splitting ratio $\rho$ and $(1-\rho )$ for decoding the source information.

The channels from S to R, from R to $D_1$, and from R to $D_2$ are denoted by $h_1$, $h_2$ and $h_3$, respectively. In the first phase, the source node S broadcast its signal containing two symbols $x_1$ and $x_2$ as a form $x= \sqrt{{a_1}P} {x_1} + \sqrt{{a_2}P} {x_2}$, with $\mathcal {E}\left\{ {{{\left| {{x}} \right| }^2} = 1} \right\}$, P is a transmit power of source node, $a_1$ and $a_2$ respectively denote the power allocation coefficient for symbols $x_1$ and $x_2$, and ${a_1} + {a_2} =1$, ${a_1} \ge {a_2}$. The received signals at relay R and two destinations $D_1$ and $D_2$, respectively, given as

$$\begin{aligned} {y_1} = {h_1}({\sqrt{{a_1}P} {x_1} + \sqrt{{a_2}P} {x_2}})+ n_{1}^a \end{aligned}$$

(1)

$$\begin{aligned} {y_4} = {h_4}({\sqrt{{a_1}P} {x_1} + \sqrt{{a_2}P} {x_2}})+ n_{4}^a \end{aligned}$$

(2)

$$\begin{aligned} {y_5} = {h_5}({\sqrt{{a_1}P} {x_1} + \sqrt{{a_2}P} {x_2}})+ n_{5}^a \end{aligned}$$

(3)

where $n_{1}^a$, $n_{4}^a$, and $n_{5}^a$ $\sim \mathcal {CN}( {0,{N_0}} )$ denote the additive white Gaussian noise (AWGN) at R, $D_1$, and $D_2$, respectively.

Fig. 1.

Network model for NOMA energy constraint DF relaying.

At relay R, the received signal $y_1$ in (1) is split into two parts for energy harvesting $(y_{1,eh})$ and information decoding $(y_{1,id})$:

$$\begin{aligned} y_{1,eh} = \sqrt{\rho }y_1 = {h_1}(\sqrt{\rho {a_1}P} {x_1} + \sqrt{\rho {a_2}P} {x_2})+ \sqrt{\rho }n_{1}^a \end{aligned}$$

(4)

$$\begin{aligned} y_{1,id} = \sqrt{(1-\rho )} y_1 = {h_1}(\sqrt{(1-\rho ) {a_1}P} {x_1} + \sqrt{(1-\rho ) {a_2}P} {x_2})+ \sqrt{(1-\rho )}n_{1}^a \end{aligned}$$

(5)

The harvested power at R can be obtained from (4) as:

$$\begin{aligned} P_R = \eta \rho a_1 P |h_1|^2 + \eta \rho a_2 P |h_1|^2 = \eta \rho P |h_1|^2 = \eta \rho P g_1 \end{aligned}$$

(6)

The received RF signals is sampled by RF-to-baseband conversion units. Thus, the signals in (2), (3) and (5) are added with the noise $n^c \sim \mathcal {CN}(0,\mu N_0)$, with $\mu > 0$, as

$$\begin{aligned} y_4^c = {h_4}({\sqrt{{a_1}P} {x_1} + \sqrt{{a_2}P} {x_2}})+ n_{4}^a + n_{4}^c \end{aligned}$$

(7)

$$\begin{aligned} y_5^c = {h_5}({\sqrt{{a_1}P} {x_1} + \sqrt{{a_2}P} {x_2}})+ n_{5}^a + n_{5}^c \end{aligned}$$

(8)

$$\begin{aligned} y_{1,id}^c = {h_1}(\sqrt{(1-\rho ) {a_1}P} {x_1} + \sqrt{(1-\rho ) {a_2}P} {x_2})+ \sqrt{(1-\rho )}n_{1}^a + n_{1}^c \end{aligned}$$

(9)

First, to decode symbol $x_1$, the relay R and two destinations $D_1$ and $D_2$ treat $x_2$ as noise. We obtain the signal to interference plus noise (SINR) for $x_1$ at R, $D_1$, and $D_2$, respectively, as

$$\begin{aligned} \gamma _1^{x_1}=\frac{{{a_1}(1 - \rho )P|h_1|^2}}{{{a_2}(1 - \rho )P|h_1|^2 + (1 - \rho + \mu )N_0}}=\frac{{{a_1}(1 - \rho ){\gamma _0}{g_1}}}{{{a_2}(1 - \rho ){\gamma _0}{g_1} + (1 - \rho + \mu )}} \end{aligned}$$

(10)

$$\begin{aligned} \gamma _4^{x_1}=\frac{{{a_1}P|h_4|^2}}{{{a_2}P|h_4|^2 + \left( {1 + \mu } \right) {N_0}}} = \frac{{{a_1}{\gamma _0}{g_4}}}{{{a_2}{\gamma _0}{g_4} + 1 + \mu }} \end{aligned}$$

(11)

$$\begin{aligned} \gamma _5^{x_1}= \frac{{{a_1}P|h_5|^2}}{{{a_2}P|h_5|^2 + \left( {1 + \mu } \right) {N_0}}} = \frac{{{a_1}{\gamma _0}{g_5}}}{{{a_2}{\gamma _0}{g_5} + 1 + \mu }} \end{aligned}$$

(12)

where ${\gamma _0} \buildrel \varDelta \over = \frac{P}{N_0}$ denote the transmit signal to noise (SNR).

Second, the relay R and destination $D_2$ decode symbol $x_2$ by cancelling $x_1$ with successive interference cancellation (SIC) from (9) and (8). The received SNRs for $x_2$ at R and $D_2$ are respectively given as

$$\begin{aligned} \gamma _1^{x_2}= \frac{{a_2}(1-\rho )P|{h_1}|^2}{(1-\rho ){N_0}+\mu {N_0}}=\frac{{a_2}(1-\rho )\gamma _0 {g_1}}{1-\rho +\mu } \end{aligned}$$

(13)

$$\begin{aligned} \gamma _5^{x_2}= \frac{{a_2}P|{h_5}|^2}{(1+\mu )N_0}=\frac{{a_2}\gamma _0g_5}{1+\mu } \end{aligned}$$

(14)

In the second phase, after successfully decoded the symbols $x_1$ and $x_2$, relay R forwards them to $D_1$ and $D_2$ as a form $(\sqrt{{b_1}P_R} {x_1} + \sqrt{{b_2}P_R} {x_2})$ with the transmit power $P_R$ in (6), with $b_1$ and $b_2$ denote the power allocation coefficient ($b_1 + b_2 = 1$, $b_1 \ge b_2$). The base-band received signals at $D_1$ and $D_2$ are expressed as

$$\begin{aligned} {y_2} = {h_2}({\sqrt{{b_1}P_R} {x_1} + \sqrt{{b_2}P_R} {x_2}})+ n_{2}^a + n_{2}^c \end{aligned}$$

(15)

$$\begin{aligned} {y_3} = {h_3}({\sqrt{{b_1}P_R} {x_1} + \sqrt{{b_2}P_R} {x_2}})+ n_{3}^a + n_{3}^c \end{aligned}$$

(16)

where $n_{2}^a, n_{3}^a \sim \mathcal {CN}(0,N_0)$, $n_{2}^c, n_{3}^c \sim \mathcal {CN}(0,\mu N_0)$.

$D_1$ decode its desired symbol ($x_1$) by treating $x_2$ as noise. From (15), the SINR for decoding $x_1$ at $D_1$ is given as

$$\begin{aligned} \gamma _2^{x_1}= \frac{{{b_1}P_R|h_2|^2}}{{{b_2}P_R|h_2|^2 + \left( {1 + \mu } \right) {N_0}}} = \frac{{{b_1}\eta \rho {\gamma _0} g_1{g_2}}}{{{b_2}\eta \rho {\gamma _0}g_1{g_2} + 1 + \mu }} \end{aligned}$$

(17)

$D_2$ decode its desired symbol ($x_2$) after decoding $x_1$ (with SINR $\gamma _3^{x_1}= \frac{{{b_1}P_R{g_3}}}{{{b_2}P_R{g_3} + \left( {1 + \mu } \right) {N_0}}} = \frac{{{b_1}\eta \rho {\gamma _0} g_1{g_3}}}{{{b_2}\eta \rho {\gamma _0}g_1{g_3} + 1 + \mu }}$) and cancelling it. The SNR for decoding $x_2$ at $D_2$ is given as

$$\begin{aligned} \gamma _3^{x_2}= \frac{b_2 P_R |h_3|^2}{(1+ \mu ) N_0 } = \frac{b_2 \eta \rho \gamma _0 g_1 g_3}{1+ \mu } \end{aligned}$$

(18)

3 Outage Probability Analysis

In this paper, the receiver decodes successfully the information if its SINR or SNR satisfies the pre-defined threshold $\gamma _t$. In this section, we will derive the outage probabilities at $D_1$, $D_2$ both cases of one relay and multiple relays under relay selection scheme.

3.1 Outage Probability at $D_1$

An outage event happens when $D_1$ unsuccessfully decodes the symbol $x_1$ both from S in the first phase and from R in the second phase. The outage probability at $D_1$ can be formulated as

$$\begin{aligned} \begin{gathered} OP_{{D_1}}^{1relay} = \underbrace{\Pr \left[ {\min \left( {\gamma _1^{{x_1}},\gamma _1^{{x_2}}} \right)< {\gamma _t},\gamma _4^{{x_1}}< {\gamma _t}} \right] }_{O{P_1}} \\ + \underbrace{\Pr \left[ {\min \left( {\gamma _1^{{x_1}},\gamma _1^{{x_2}}} \right) \geqslant {\gamma _t},\max \left( {\gamma _4^{{x_1}},\gamma _2^{{x_1}}} \right) < {\gamma _t}} \right] }_{O{P_2}} \\ \end{gathered} \end{aligned}$$

(19)

Particularly, $OP_1$ is the outage event for the case that R can not decode successfully both $x_1$ and $x_2$ $\left( {\min \left( {\gamma _1^{{x_1}},\gamma _1^{{x_2}}} \right) < {\gamma _t}} \right)$, leading to R does not forward the signal $(\sqrt{{b_1}P_R} {x_1} + \sqrt{{b_2}P_R} {x_2})$ to destinations, and the destination $D_1$ can not decode successfully symbol $x_1$ directly from S in the first phase $\left( {\gamma _4^{{x_1}} < {\gamma _t}} \right)$. $OP_2$ is the outage event for the case that R decodes correctly both symbol $x_1$ and $x_2$ $\left( {\min \left( {\gamma _1^{{x_1}},\gamma _1^{{x_2}}} \right) \ge {\gamma _t}} \right)$, but $D_1$ can not decodes successfully $x_1$ both from S and R in the first and second phase, respectively $\left( {\max \left( {\gamma _4^{{x_1}},\gamma _2^{{x_1}}} \right) < {\gamma _t}} \right)$.

The term $OP_1$ and $OP_2$ can be obtain by substituting the SINRs and SNRs in (10), (13), (11) and (17) into (19) as follows

(20)

where ${\omega _1} \triangleq 1 + \mu$, ${\omega _2} \triangleq \frac{{1 - \rho + \mu }}{{1 - \rho }}$.

$$\begin{aligned} O{P_2}&= \Pr \left[ \begin{gathered} \min \left( {\frac{{{a_1}(1 - \rho ){\gamma _0}{g_1}}}{{{a_2}(1 - \rho ){\gamma _0}{g_1} + (1 - \rho + \mu )}},\frac{{{a_2}(1 - \rho ){\gamma _0}{g_1}}}{{1 - \rho + \mu }}} \right) \geqslant {\gamma _t}, \\ \max \left( {\frac{{{a_1}{\gamma _0}{g_4}}}{{{a_2}{\gamma _0}{g_4} + 1 + \mu }},\frac{{{b_1}\eta \rho {\gamma _0}{g_1}{g_2}}}{{{b_2}\eta \rho {\gamma _0}{g_1}{g_2} + 1 + \mu }}} \right)< {\gamma _t} \\ \end{gathered} \right] \nonumber \\&= \Pr \left[ {{g_4}< \frac{{\left( {1 + \mu } \right) {\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}} \right] \Pr \left[ \begin{gathered} {g_1} \geqslant \frac{{(1 - \rho + \mu ){\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) (1 - \rho ){\gamma _0}}},{g_1} \geqslant \frac{{\left( {1 - \rho + \mu } \right) {\gamma _t}}}{{{a_2}(1 - \rho ){\gamma _0}}} \\ \frac{{{b_1}\eta \rho {\gamma _0}{g_1}{g_2}}}{{{b_2}\eta \rho {\gamma _0}{g_1}{g_2} + 1 + \mu }}< {\gamma _t} \nonumber \\ \end{gathered} \right] \\&\mathop = \limits ^{\left( {21.1} \right) } \left( {1 - {e^{ - \frac{{{\lambda _4}\left( {1 + \mu } \right) {\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}}} \right) \nonumber \\&\times \left\{ \begin{gathered} \Pr \left[ {{g_1} \geqslant \frac{{(1 - \rho + \mu ){\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) (1 - \rho ){\gamma _0}}},{g_2}< \frac{{\left( {1 + \mu } \right) {\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) \eta \rho {\gamma _0}{g_1}}}} \right] \,\,\,\,\,if\,\,{a_1} - {a_2}{\gamma _t}< {a_2} \\ \Pr \left[ {{g_1} \geqslant \frac{{\left( {1 - \rho + \mu } \right) {\gamma _t}}}{{{a_2}(1 - \rho ){\gamma _0}}},{g_2}< \frac{{\left( {1 + \mu } \right) {\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) \eta \rho {\gamma _0}{g_1}}}} \right] \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\,{a_1} - {a_2}{\gamma _t} \geqslant {a_2} \nonumber \\ \end{gathered} \right. \\&\mathop = \limits ^{\left( {21.2} \right) } \left( {1 - {e^{ - \frac{{{\lambda _4}{\omega _1}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}}} \right) \nonumber \\&\times \left\{ \begin{gathered} {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}} - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}} {\left( { - \frac{{{\lambda _1}{\lambda _2}{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}}}} \right) ^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}} \right) \,\,\,\,\,if\,\,{a_1} < \left( {1 + {\gamma _t}} \right) {a_2} \\ {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}}} - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}} {\left( { - \frac{{{\lambda _1}{\lambda _2}{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}}}} \right) ^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}} \right) \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\,{a_1} \geqslant \left( {1 + {\gamma _t}} \right) {a_2} \\ \end{gathered} \right. \end{aligned}$$

(21)

where ${\omega _3} \triangleq \frac{{1 + \mu }}{{\eta \rho }}$.

where (21.2) is obtained from (21.1) by using the result in Appendix A. Note that we allocate the power coefficients $a_1$, $a_2$, $b_1$, and $b_2$ that $(a_1 - a_2 \gamma _t) > 0$ and $(b_1 - b_2 \gamma _t) > 0$ for $OP_1$ and $OP_2$ not equal to 0.

Finally, a closed-form expression for $OP_{{D_1}}^{1relay}$ is derived by substituting (20) and (21) into (19) as

(22)

3.2 Outage Probability at $D_2$

In this paper, the desired symbol for destination is $x_2$, thus $D_2$ has to successfully decode $x_1$ first then using SIC to obtain $x_2$. There are two cases for outage happening at $D_2$ that (i) both $x_1$ and $x_2$ can not be decoded successfully from S and $D_2$ in the first time slot $({\left( {\min \left( {\gamma _1^{{x_1}},\gamma _1^{{x_2}}} \right)< {\gamma _t},\min \left( {\gamma _5^{{x_1}},\gamma _5^{{x_2}}} \right) < {\gamma _t}} \right) })$, the probability for this event is denoted by $OP_5$; (ii) R detects correctly $x_1$ and $x_2$ transmitted from S in the first phase but $D_2$ does not from both S and R in the first and second phases, repsectively.

$({\Pr \left[ {\min \left( {\gamma _1^{{x_1}},\gamma _1^{{x_2}}} \right) \geqslant {\gamma _t},\min \left( {\gamma _5^{{x_1}},\gamma _5^{{x_2}}} \right)< {\gamma _t}, \min \left( {\gamma _3^{{x_1}},\gamma _3^{{x_2}}} \right) < {\gamma _t}} \right] })$ ,this probability denoted by $OP_6$. The outage probability at D can be formulated by:

$$\begin{aligned} \begin{gathered} OP_{{D_2}}^{\,1\,relay} = \underbrace{\Pr \left[ {\left( {\min \left( {\gamma _1^{{x_1}},\gamma _1^{{x_2}}} \right)< {\gamma _t},\min \left( {\gamma _5^{{x_1}},\gamma _5^{{x_2}}} \right)< {\gamma _t}} \right) } \right] }_{O{P_5}} \\ + \underbrace{\Pr \left[ {\min \left( {\gamma _1^{{x_1}},\gamma _1^{{x_2}}} \right) \geqslant {\gamma _t},\min \left( {\gamma _5^{{x_1}},\gamma _5^{{x_2}}} \right)< {\gamma _t},\min \left( {\gamma _3^{{x_1}},\gamma _3^{{x_2}}} \right) < {\gamma _t}} \right] }_{O{P_6}} \\ \end{gathered} \end{aligned}$$

(23)

The probabilities $OP_5$ and $OP_6$ can be obtained by substituting the SINRs and SINRs $\gamma _1^{x_1}$, $\gamma _1^{x_2}$, $\gamma _5^{x_1}$, $\gamma _5^{x_2}$, $\gamma _3^{x_1}$, and $\gamma _3^{x_2}$ into (23) as follows

(24)

(25)

where $OP_{5.1}$ can be obtained from $OP_1$ as

$$\begin{aligned} O{P_{5.1}} = \left\{ \begin{gathered} \left( {1 - {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}}} \right) \,\,\,\,\,if\,\,\,\,{a_1} < {a_2}\left( {1 + {\gamma _t}} \right) \\ \left( {1 - {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}}}} \right) \,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\,\,\,{a_1} \geqslant {a_2}\left( {1 + {\gamma _t}} \right) \\ \end{gathered} \right. \end{aligned}$$

(26)

$OP_{5.2}=OP_{6.1}$ is expressed as

(27)

$OP_{6.2}$ is derived from Appendix B as

$$\begin{aligned} O{P_{6.2}} = \left\{ \begin{gathered} {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}} - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}} \right) ,} \,\,\,if\,\,\left\{ \begin{gathered} {b_1}< {b_2}\left( {1 + {\gamma _t}} \right) \\ {a_1}< {a_2}\left( {1 + {\gamma _t}} \right) \\ \end{gathered} \right. \, \\ {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}} - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{{b_2}{\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}} \right) } ,\,\,\,if\,\,\left\{ \begin{gathered} {b_1} \geqslant {b_2}\left( {1 + {\gamma _t}} \right) \\ {a_1}< {a_2}\left( {1 + {\gamma _t}} \right) \\ \end{gathered} \right. \,\, \\ {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}}} - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}} \right) ,} \,\,\,if\,\,\left\{ \begin{gathered} {b_1} < {b_2}\left( {1 + {\gamma _t}} \right) \\ {a_1} \geqslant {a_2}\left( {1 + {\gamma _t}} \right) \\ \end{gathered} \right. \,\,\, \\ {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}}} - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{{b_2}{\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}} \right) } ,\,\,\,if\,\,\left\{ \begin{gathered} {b_1} \geqslant {b_2}\left( {1 + {\gamma _t}} \right) \\ {a_1} \geqslant {a_2}\left( {1 + {\gamma _t}} \right) \\ \end{gathered} \right. \, \\ \end{gathered} \right. \end{aligned}$$

(28)

The outage probability at $D_2$ in the case of one relay can be obtained by substituting the equations from (24) to (28) into (23) as

$$\begin{aligned} \begin{gathered} OP_{{D_2}}^{1\,\,relay} = \\ \left\{ \begin{gathered} \left( {1 - {e^{ - \frac{{{\lambda _5}{\omega _1}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}}} \right) \left[ {1 - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}} \right) } } \right] ,\,\,\,if\,\,\left\{ \begin{gathered} {b_1}< {b_2}\left( {1 + {\gamma _t}} \right) \\ {a_1}< {a_2}\left( {1 + {\gamma _t}} \right) \\ \end{gathered} \right. \, \\ \left( {1 - {e^{ - \frac{{{\lambda _5}{\omega _1}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}}} \right) \left[ {1 - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{{b_2}{\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}} \right) } } \right] ,\,\,if\,\,\left\{ \begin{gathered} {b_1} \geqslant {b_2}\left( {1 + {\gamma _t}} \right) \\ {a_1}< {a_2}\left( {1 + {\gamma _t}} \right) \\ \end{gathered} \right. \,\, \\ \left( {1 - {e^{ - \frac{{{\lambda _5}{\omega _1}{\gamma _t}}}{{{a_2}{\gamma _0}}}}}} \right) \left[ {1 - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}} \right) } } \right] \,,\,\,\,if\,\,\left\{ \begin{gathered} {b_1} < {b_2}\left( {1 + {\gamma _t}} \right) \\ {a_1} \geqslant {a_2}\left( {1 + {\gamma _t}} \right) \\ \end{gathered} \right. \,\,\, \\ \left( {1 - {e^{ - \frac{{{\lambda _5}{\omega _1}{\gamma _t}}}{{{a_2}{\gamma _0}}}}}} \right) \left[ {1 - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{{b_2}{\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}} \right) } } \right] \,,\,\,\,if\,\,\left\{ \begin{gathered} {b_1} \geqslant {b_2}\left( {1 + {\gamma _t}} \right) \\ {a_1} \geqslant {a_2}\left( {1 + {\gamma _t}} \right) \\ \end{gathered} \right. \,\,\, \\ \end{gathered} \right. \\ \end{gathered} \end{aligned}$$

(29)

4 Result and Disscussion

This section provide result and discussion of the outage performance at both $D_1$ and $D_2$ in both cases of one and N relays via Monte Carlo simulation and theoretical results. In a two-dimensional plane, the corrdinates of the source S, the destinations $D_1$, $D_2$, and the cluster of relays are (0, 0), (1, 0.3), $(0.8,-0.3)$, and $(x_R, 0)$, respectively. Hence, we obtain the normalize distances $d_1=|x_R|$, $d_2=\sqrt{(1-x_R)^2+0.3^2}$, $d_3=\sqrt{(0.8-x_R)^2+0.3^2}$, $d_4=\sqrt{1+0.3^2}$, $d_5=\sqrt{0.8^2+0.3^2}$. We assume that the path-loss exponent $\beta = 3$, the target $\gamma _t=1$, and $\mu =1$.

Fig. 2.

Effect of power allocation $a_1$, $a_2$, $b_1$, and $b_2$ on the outage probability at $D_1$ and $D_2$ versus $\rho$, when $x_R=0.4$, $\gamma _0= 15$ dB, $\rho =0.5$, and $\eta =0.9$.

In Fig. 2, the outage probabilities at $D_1$ and $D_2$ versus power splitting ratio $\rho \in (0.1,0.9)$ (for relay located between source and destinations) are investigated. It can be seen that at $\rho$ around 0.7, the outage performances of almost cases in this scenario are obtained the best performance because it is the optimal position for relay to decode information and harvest energy from source in the first phase and forward information to destination in the second phase. We note that $D_2$ locates nearer the source and relay than $D_1$ does, therefore the outage performance at $D_2$ is better than $D_1$ in the case of the power allocation for symbol $x_2$ and $x_1$ is nearly similar like $(a_1,a_2)=(b_1,b_2)=(0.6,0.4)$, but in the case that the power allocation for $x_1$ is much higher than that for $x_2$, the outage performance at $D_1$ is higher than that at $D_2$.

5 Conclusions

In this paper, we consider energy harvesting technique in the NOMA relaying networks. Partial relay selection scheme is applied to improve the system performance. The closed-form expressions of the outage probability are presented to evaluation and comparison of the performance at two destinations in both cases of single and multiple relays. These theoretical expressions are derived using the Monte Carlo simulation method. The theoretical results match the simulation results well.

Appendices

A Appendix A: Finding the Closed-Form of Probability $\Pr \left[ {{g_1} \geqslant {u_1},{g_2} < \frac{{{u_2}}}{{{g_1}}}} \right]$

By using the PDF of RV $g_1$ and CDF of RV $g_2$, the probability $\Pr \left[ {{g_1} \geqslant {u_1},{g_2} < \frac{{{u_2}}}{{{g_1}}}} \right]$ can be obtained as

$$\begin{aligned} \begin{gathered} \Pr \left[ {{g_1} \geqslant {u_1},{g_2} < \frac{{{u_2}}}{{{g_1}}}} \right] = \int \limits _{{u_1}}^\infty {{f_{{g_1}}}\left( x \right) } {F_{{g_2}}}\left( {\frac{{{u_2}}}{x}} \right) dx \\ = \int \limits _{{u_1}}^\infty {{\lambda _1}{e^{ - {\lambda _1}x}}\left( {1 - {e^{ - \frac{{{\lambda _2}{u_2}}}{x}}}} \right) dx} \\ = {e^{ - {\lambda _1}{u_1}}} - \underbrace{\int \limits _{{u_1}}^\infty {{\lambda _1}{e^{ - {\lambda _1}x}}{e^{ - \frac{{{\lambda _2}{u_2}}}{x}}}dx} }_{{I_1}} \\ \end{gathered} \end{aligned}$$

(A.1)

To calculate the integral $I_1$, we first apply the Eq. 1.211 of [6]: ${e^x} = \sum \limits _{k = 0}^\infty {\frac{{{x^k}}}{{k!}}}$ to the term ${{e^{ - \frac{{{\lambda _2}{u_2}}}{x}}}}$ to obtain (A.2.1), then using Eq. 3.381.3 of [6]: $\int _u^\infty {{x^{v - 1}}{e^{ - \mu x}}dx} = \frac{1}{{{\mu ^v}}}\varGamma \left( {v,\mu u} \right)$ to obtain (A.2.2) as follows

$$\begin{aligned} \begin{gathered} {I_1}\mathop = \limits ^{{\text {(A.2.1)}}} {\lambda _1}\sum \limits _{k = 0}^\infty {\frac{1}{{k!}}} {\left( { - {\lambda _2}{u_2}} \right) ^k}\int \limits _{{u_1}}^\infty {\frac{{{e^{ - {\lambda _1}x}}}}{{{{\left( x \right) }^k}}}dx} \\ \mathop = \limits ^{{\text {(A.2.2)}}} \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}} {\left( { - {\lambda _1}{\lambda _2}{u_2}} \right) ^k}\varGamma \left( {1 - k,{\lambda _1}{u_1}} \right) \\ \end{gathered} \end{aligned}$$

(A.2)

By substituting (A.3) into (A.1), we obtain:

$$\begin{aligned} \Pr \left[ {{g_1} \geqslant {u_1},{g_2} < \frac{{{u_2}}}{{{g_1}}}} \right] = {e^{ - {\lambda _1}{u_1}}} - \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}} {\left( { - {\lambda _1}{\lambda _2}{u_2}} \right) ^k}\varGamma \left( {1 - k,{\lambda _1}{u_1}} \right) \end{aligned}$$

(A.3)

B Appendix B: Proof of Eq. (28)

First, for the case of ${a_1} < {a_2}\left( {1 + {\gamma _t}} \right)$, the probability $OP_{6.2}$ in (25) can be rewritten as

$$\begin{aligned} \begin{array}{l} O{P_{6.2}}|_{{a_1}< {a_2}\left( {1 + {\gamma _t}} \right) } = \Pr \left[ \begin{array}{l} {g_1} \ge \frac{{(1 - \rho + \mu ){\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) (1 - \rho ){\gamma _0}}}\\ \min \left( {\frac{{{b_1}\eta \rho {\gamma _0}{g_1}{g_3}}}{{{b_2}\eta \rho {\gamma _0}{g_1}{g_3} + 1 + \mu }},\frac{{{b_2}\eta \rho {\gamma _0}{g_1}{g_3}}}{{1 + \mu }}} \right)< {\gamma _t} \end{array} \right] \\ = \Pr \left[ \begin{array}{l} {g_1} \ge \frac{{(1 - \rho + \mu ){\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) (1 - \rho ){\gamma _0}}}\\ \frac{{{b_1}\eta \rho {\gamma _0}{g_1}{g_3}}}{{{b_2}\eta \rho {\gamma _0}{g_1}{g_3} + 1 + \mu }}< \frac{{{b_2}\eta \rho {\gamma _0}{g_1}{g_3}}}{{1 + \mu }},\frac{{{b_1}\eta \rho {\gamma _0}{g_1}{g_3}}}{{{b_2}\eta \rho {\gamma _0}{g_1}{g_3} + 1 + \mu }}< {\gamma _t} \end{array} \right] \\ + \Pr \left[ \begin{array}{l} {g_1} \ge \frac{{(1 - \rho + \mu ){\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) (1 - \rho ){\gamma _0}}}\\ \frac{{{b_1}\eta \rho {\gamma _0}{g_1}{g_3}}}{{{b_2}\eta \rho {\gamma _0}{g_1}{g_3} + 1 + \mu }} \ge \frac{{{b_2}\eta \rho {\gamma _0}{g_1}{g_3}}}{{1 + \mu }},\frac{{{b_2}\eta \rho {\gamma _0}{g_1}{g_3}}}{{1 + \mu }}< {\gamma _t} \end{array} \right] \\ = \underbrace{\Pr \left[ \begin{array}{l} {g_1} \ge \frac{{(1 - \rho + \mu ){\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) (1 - \rho ){\gamma _0}}}\\ {g_3} > \frac{{\left( {{b_1} - {b_2}} \right) \left( {1 + \mu } \right) }}{{{{\left( {{b_2}} \right) }^2}\eta \rho {\gamma _0}{g_1}}},{g_3}< \frac{{\left( {1 + \mu } \right) {\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) \eta \rho {\gamma _0}{g_1}}} \end{array} \right] }_{O{P_{6.2.1}}} + \underbrace{\Pr \left[ \begin{array}{l} {g_1} \ge \frac{{(1 - \rho + \mu ){\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) (1 - \rho ){\gamma _0}}}\\ {g_3} \le \frac{{\left( {{b_1} - {b_2}} \right) \left( {1 + \mu } \right) }}{{{{\left( {{b_2}} \right) }^2}\eta \rho {\gamma _0}{g_1}}},{g_3} < \frac{{\left( {1 + \mu } \right) {\gamma _t}}}{{{b_2}\eta \rho {\gamma _0}{g_1}}} \end{array} \right] }_{O{P_{6.2.2}}} \end{array} \end{aligned}$$

(B.1)

where $OP_{6.2.1}$ and $OP_{6.2.2}$ are given as

$$\begin{aligned} O{P_{6.2.1}} = \left\{ \begin{array}{l} \int \limits _{\frac{{{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}^\infty {{f_{{g_1}}}\left( x \right) \left[ {{F_{{g_3}}}\left( {\frac{{{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}x}}} \right) - {F_{{g_3}}}\left( {\frac{{\left( {{b_1} - {b_2}} \right) {\omega _3}}}{{{{\left( {{b_2}} \right) }^2}{\gamma _0}x}}} \right) } \right] dx,\,\,\,\,\,\,if\,\,{b_1} < {b_2}\left( {1 + {\gamma _t}} \right) } \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\,{b_1} \ge {b_2}\left( {1 + {\gamma _t}} \right) \end{array} \right. \end{aligned}$$

(B.2)

$$\begin{aligned} \begin{array}{l} O{P_{6.2.2}} = \left\{ \begin{array}{l} \Pr \left[ \begin{array}{l} {g_1} \ge \frac{{{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}\\ {g_3} \le \frac{{\left( {{b_1} - {b_2}} \right) {\omega _3}}}{{{{\left( {{b_2}} \right) }^2}{\gamma _0}{g_1}}} \end{array} \right] \,\,\,\,if\,{b_1}< {b_2}\left( {1 + {\gamma _t}} \right) \,\\ \Pr \left[ \begin{array}{l} {g_1} \ge \frac{{{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}\\ {g_3}< \frac{{{\omega _3}{\gamma _t}}}{{{b_2}{\gamma _0}{g_1}}} \end{array} \right] \,\,\,\,if\,{b_1} \ge {b_2}\left( {1 + {\gamma _t}} \right) \, \end{array} \right. \\ = \left\{ \begin{array}{l} \int \limits _{\frac{{{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}^\infty {{f_{{g_1}}}\left( x \right) \left[ {{F_{{g_3}}}\left( {\frac{{\left( {{b_1} - {b_2}} \right) {\omega _3}}}{{{{\left( {{b_2}} \right) }^2}{\gamma _0}{g_1}}}} \right) } \right] dx,} \,\,\,\,if\,{b_1} < {b_2}\left( {1 + {\gamma _t}} \right) \,\\ \int \limits _{\frac{{{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}^\infty {{f_{{g_1}}}\left( x \right) \left[ {{F_{{g_3}}}\left( {\frac{{{\omega _3}{\gamma _t}}}{{{b_2}{\gamma _0}{g_1}}}} \right) } \right] dx,} \,\,\,\,if\,{b_1} \ge {b_2}\left( {1 + {\gamma _t}} \right) \, \end{array} \right. \end{array} \end{aligned}$$

(B.3)

By substituting (B.2) and (B.3) into (B.1), and using the result in Appendix A, we obtain

$$\begin{aligned} \begin{array}{l} {\left. {O{P_{6.2}}} \right| _{{a_1}< {a_2}\left( {1 + {\gamma _t}} \right) }} = O{P_{6.2.1}} + O{P_{6.2.2}}\\ = \left\{ \begin{array}{l} \int \limits _{\frac{{{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}^\infty {{f_{{g_1}}}\left( x \right) \left[ {{F_{{g_3}}}\left( {\frac{{{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}{g_1}}}} \right) } \right] dx,} \,\,\,\,if\,{b_1}< {b_2}\left( {1 + {\gamma _t}} \right) \,\\ \int \limits _{\frac{{{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}^\infty {{f_{{g_1}}}\left( x \right) \left[ {{F_{{g_3}}}\left( {\frac{{{\omega _3}{\gamma _t}}}{{{b_2}{\gamma _0}{g_1}}}} \right) } \right] dx,} \,\,\,\,if\,{b_1} \ge {b_2}\left( {1 + {\gamma _t}} \right) \, \end{array} \right. \\ = {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}}} - \left\{ \begin{array}{l} \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}} \right) ,} \,\,\,\,if\,{b_1} < {b_2}\left( {1 + {\gamma _t}} \right) \,\\ \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{{b_2}{\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{\left( {{a_1} - {a_2}{\gamma _t}} \right) {\gamma _0}}}} \right) } ,\,\,\,\,if\,{b_1} \ge {b_2}\left( {1 + {\gamma _t}} \right) \, \end{array} \right. \end{array} \end{aligned}$$

(B.4)

Next, we can obtain the result for $OP_{6.2}$ in the case of ${{a_1} \ge {a_2}\left( {1 + {\gamma _t}} \right) }$ from (B.4) with replacing ‘$\left( {{a_1} - {a_2}{\gamma _t}} \right)$’ by ‘$a_2$’ as

$$\begin{aligned} {\left. {O{P_{6.2}}} \right| _{{a_1} \ge {a_2}\left( {1 + {\gamma _t}} \right) }} = {e^{ - \frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}}} - \left\{ \begin{array}{l} \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{\left( {{b_1} - {b_2}{\gamma _t}} \right) {\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}} \right) ,} \,\,\,\,if\,{b_1} < {b_2}\left( {1 + {\gamma _t}} \right) \,\\ \sum \limits _{k = 0}^\infty {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda _1}{\lambda _3}{\omega _3}{\gamma _t}}}{{{b_2}{\gamma _0}}}} \right) }^k}\varGamma \left( {1 - k,\frac{{{\lambda _1}{\omega _2}{\gamma _t}}}{{{a_2}{\gamma _0}}}} \right) } ,\,\,\,\,if\,{b_1} \ge {b_2}\left( {1 + {\gamma _t}} \right) \, \end{array} \right. \end{aligned}$$

(B.5)

By combining (B.4) and (B.5), we finish the proof for Eq. (28).