Abstract
We present in this paper a generic framework for the analysis of multi-threaded programs with recursive procedure calls, synchronisation by rendez-vous between parallel threads, and dynamic creation of new threads. To this end, we consider a model called Synchronized Dynamic Pushdown Networks (SDPNs) that can be seen as a network of pushdown processes executing synchronized transitions, spawning new pushdown processes, and performing internal pushdown actions. The reachability problem for this model is unfortunately undecidable. Therefore, we tackle this problem by introducing an abstraction framework based on Kleene algebras in order to compute an abstraction of the execution paths between two regular sets of configurations. We combine an automata theoretic saturation procedure with constraint solving in a finite domain. We then apply this framework to a Counter-Example Guided Abstraction Refinement (CEGAR) scheme, using multiple abstractions of increasing complexity and precision.
This work was partially funded by the FUI project FREENIVI.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The use of parallel programs has grown in popularity in the past fifteen years, but these remain nonetheless fickle and vulnerable to specific issues such as race conditions or deadlocks. Static analysis methods for this class of programs remain therefore more relevant than ever.
Pushdown Systems (PDSs) are a natural model for programs with sequential, recursive procedure calls, as shown by Esparza et al. in [6]. Thus, networks of pushdown systems can be used to model multithreaded programs, where each PDS in the network models a sequential component of the whole program. In this context, Dynamic Pushdown Networks (DPNs) were introduced by Bouajjani et al. in [4].
Intuitively, this class of automata consists of a network of pushdown systems running independently in parallel. Each member of a DPN can, after a transition, spawn a new PDS which is then introduced as a new member of the network. Thus, DPNs can be used to represent a network of threads where each thread can recursively call procedures, perform internal actions, or spawn a new thread.
However, this model cannot represent synchronization between threads or parallel components. In order to handle communication in multithreaded programs, Bouajjani et al. introduced in [2] Communicating Pushdown Systems (CPDSs), a model which consists of a tuple of pushdown systems synchronized by rendez-vous on execution paths. However, CPDSs have a constant number of processes and cannot therefore handle dynamic creation of new threads.
Hence, we introduce in this paper a more accurate model, namely, Synchronized Dynamic Pushdown Networks (SDPNs) that combines DPNs with CPDSs in order to handle dynamic thread creation and communication at the same time. A SDPN can be seen as a DPN where PDS processes can synchronize via rendez-vous by sending and receiving messages. In a SDPN, pushdown processes can apply internal actions labelled by a letter \(\tau \) without synchronization, just like a DPN, but can also synchronize through channels. To do so, we represent each channel by a pair of letters, as an example a and \(\overline{a}\), that can be used to label transitions. If one thread can execute an action labelled with a signal a, and another thread another action labelled with \(\overline{a}\), then both threads can synchronize and execute their respective transitions simultaneously, in a single step labelled by \(\tau \).
We consider the reachability problem for SDPNs, that is, finding if a critical configuration can be reached from the set of starting configurations of the program. An equivalent problem is to compute the set \(Paths ( \mathcal {C}, \mathcal {C'} )\) of execution paths leading from a configuration in \(\mathcal {C}\) to a configuration in \(C'\) and check if it is empty. This problem unfortunately remains undecidable for synchronized systems, as proven by Ramalingam in [10].
Therefore, the set of execution paths \(Paths ( C, C' )\) cannot be computed in an exact manner. To overcome this problem, we proceed as in [2]: our approach is based on the computation of an abstraction \(\alpha ( Paths ( \mathcal {C}, \mathcal {C'} ) )\) of the execution paths language. To this aim, we propose techniques based on:
-
the representation of regular sets of configurations of SDPNs with finite word automata;
-
the use of these automata to determine a set of constraints whose least fixpoint characterizes the set of execution paths of the program; to compute this set of constraints, (1) we consider a relaxed semantics on SDPNs that allows partially synchronized runs, (2) we abstract sets of execution paths as functions in a Kleene algebra, instead of simple elements of the abstract domain, and (3) we use a shuffle product on abstract path expressions to represent the interleaving and potential synchronization of parallel executions;
-
the resolution of this set of constraints in an abstract domain; we consider in particular the case where the abstract domain is finite; the set of constraints can then be solved using an iterative fixpoint computation.
Note that the main contribution of our approach w.r.t. to [2, 12] is the introduction of functions to represent sets of abstracted path expressions and the use of a shuffle product to model the interleaving of threads. The abstraction framework as defined in these papers cannot be applied to SDPNs due to the presence of dynamic thread creation, hence, the need for functions and shuffling.
We can then apply this abstraction framework for the reachability problem to a Counter-Example Guided Abstraction Refinement (CEGAR) scheme inspired by the work of Chaki et al. in [5]. The idea is the following: (1) we do a reachability analysis of the program, using a finite domain abstraction of order n in our abstraction framework; if the target set of configurations is not reachable by the abstract paths, it is not reachable by actual execution paths either; otherwise, we obtain a counter-example; (2) we check if the counter-example can be matched to an actual execution of the program; (3) if it does, then we have shown that the target set of configurations is actually reachable; (4) otherwise, we refine our abstraction and use instead a finite domain abstraction of order \(n + 1\) in step (2). This CEGAR scheme is then used to prove that a Windows driver first presented in [9] can reach an erroneous configuration, using an abstraction of the original program. An updated version of this driver is then shown to be error-free.
Related Work. Wenner introduced in [13] a model of Weighted Dynamic Pushdown Networks (WDPNs), extending the work of Reps et al. on Weighted Pushdown Systems in [11] to DPNs. WDPNs share some similarities with our abstraction framework on SDPNs: each transition is labelled by a weight in a bounded idempotent semiring, these weights can be composed along execution paths, and the sum of the weights of all execution paths between two sets of configurations can be computed, provided that a simple extension of the original semiring to an abstract set of execution hedges can be found. WDPNs, however, do not feature simultaneous, synchronized actions between pushdown processes. Moreover, in order to be efficient, the extensions of the abstract domain have to be chosen on a case-by-case basis in order to label tree automata, whereas our framework works for every finite-domain abstraction and only uses finite state automata.
Multi-Stack Pushdown Systems (MPDSs) are pushdown systems with two or more stacks, and can be used to model synchronized parallel programs. Qadeer et al. introduced in [8] the notion of context, that is, a part of an execution path during which only one stack of the automaton can be modified. The reachability problem within a bounded number of context switches is decidable for MPDSs. However, MPDSs have a bounded number of stacks and, unlike SDPNs, cannot therefore handle the dynamic creation of new threads.
Bouajjani et al. introduced in [1] Asynchronous Dynamic Pushdown Networks, or ADPNs. This model extends DPNs by adding a global control state to the whole network as a mean of communication between processes; each pushdown process can then apply rules either by reading its own local state or the global state of the network. The reachability problem within a bounded number of context switches is decidable for ADPNs, where a context here stands for a part of an execution path during which transitions altering global variables are all executed by the same process. This is an underapproximation of the actual reachability problem for synchronized parallel programs, whereas we compute in this paper an overapproximation of the same problem. The former can be used to find errors in a program but, unlike the latter, does not allow one to check that a program is free from errors.
Extensions of the Kleene algebra framework of [2] were defined in [3, 12] to compute abstractions of execution paths of multithreaded recursive programs communicating via rendez-vous. However, unlike SDPNs, the models considered in these articles cannot describe thread spawns, where the father of a new thread can resume its execution independently of its children.
Paper Outline. In Sect. 2 of this paper, we define Synchronized Dynamic Pushdown Networks (SDPNs). We study in Sect. 3 the reachability problem for this class of automata. We present in Sect. 4 an abstraction framework based on Kleene algebras that allows us to overapproximate the set of execution paths between two sets of configurations C and \(C'\) of a SDPN. In Sect. 5, we define structures to represent this abstraction. This framework relies on an algorithm computing the set of abstract paths leading to a set of configurations C of a SDPN, which is explained in Sect. 6. Finally, in Sect. 7, we present a CounterExample Guided Abstraction Refinement scheme that relies on our abstraction framework and apply it to a model of an actual program in Sect. 8.
2 Synchronized Dynamic Pushdown Networks
2.1 The Model and Its Semantics
Definition 1
(Synchronized Dynamic Pushdown Networks). A Synchronized Dynamic Pushdown Network (SDPN) is a quadruplet \(M = ( Act, P, \varGamma , \varDelta )\) where Act is a finite set of actions, P a finite set of control states, \(\varGamma \) a finite stack alphabet disjoint from P, and \(\varDelta \subseteq ( P \varGamma \times Act \times P \varGamma ^* ) \cup ( P \varGamma \times Act \times P \varGamma ^* P \varGamma ^* )\) a finite set of transition rules.
If \(( p \gamma , a, w ) \in \varDelta \), \(p \in P\), \(\gamma \in \varGamma \), \(a \in Act\), and \(w \in P \varGamma ^* \cup P \varGamma ^* P \varGamma ^*\), we write that  . There are two types of transition rules in a SDPN:
. There are two types of transition rules in a SDPN:
-
rules of the form
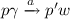 in \(P \varGamma \times Act \times P\) allow a pushdown process in the network to pop a symbol \(\gamma \) from its stack, push a word w, then move from state p to \(p'\); these rules are standard pushdown rules and model a thread calling or ending procedures while moving through its control flow;
in \(P \varGamma \times Act \times P\) allow a pushdown process in the network to pop a symbol \(\gamma \) from its stack, push a word w, then move from state p to \(p'\); these rules are standard pushdown rules and model a thread calling or ending procedures while moving through its control flow; -
rules of the form
 in \(P \varGamma \times Act \times P \varGamma ^* P \varGamma ^*\) allow a pushdown process in the network to pop a symbol \(\gamma \) from its stack, push a word w, move from state p to \(p'\), then spawn a new pushdown process in state \(p''\) and with initial stack \(w'\); these rules model dynamic creation of new threads.
in \(P \varGamma \times Act \times P \varGamma ^* P \varGamma ^*\) allow a pushdown process in the network to pop a symbol \(\gamma \) from its stack, push a word w, move from state p to \(p'\), then spawn a new pushdown process in state \(p''\) and with initial stack \(w'\); these rules model dynamic creation of new threads.
We assume that the set Act contains a letter \(\tau \) that represents internal or synchronized actions, and that other letters in \(Lab = Act \setminus \{ \tau \}\) model synchronization signals. Moreover, to each synchronization signal a in Lab, we can match an unique co-action \(\overline{a} \in Lab\), such that \(\overline{\overline{a}} = a\).
We introduce the set \(Conf_M = \left( P \varGamma ^* \right) ^*\) of configurations of a SDPN M. A configuration \(p_1 w_1 \ldots p_n w_n\) represents a network of n processes where the i-th process is in control point \(p_i\) and has stack content \(w_i\).
The Strict Semantics. We will model synchronization between threads as a form of communication by rendez-vous: two pushdown processes can synchronize if one performs a transition labelled with a and the other, a transition labelled with \(\overline{a}\). Intuitively, one thread sends a signal over a channel and the other thread waits for a signal to be received along the same channel.
To this end, we define a strict transition relation  on configurations of M according to the following strict semantics:
on configurations of M according to the following strict semantics:
- (1):
-
given a symbol \(a \in Act\), two rules
 and
and  in \(\varDelta \), and two configurations \(u = u_1 p \gamma u_2 p' \gamma ' u_3\) and \(v=u_1 w_1 u_2 w'_1 u_3\) of M, we have
in \(\varDelta \), and two configurations \(u = u_1 p \gamma u_2 p' \gamma ' u_3\) and \(v=u_1 w_1 u_2 w'_1 u_3\) of M, we have 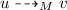 ; two synchronized processes perform a simultaneous action;
; two synchronized processes perform a simultaneous action; - (2):
-
given a rule
 in \(\varDelta \) and two configurations \(u = u_1 p \gamma u_2\) and \(v = u_1 w_1 u_2\) of M, we have
in \(\varDelta \) and two configurations \(u = u_1 p \gamma u_2\) and \(v = u_1 w_1 u_2\) of M, we have  ; a process performs an internal action.
; a process performs an internal action.
We say that v is reachable from u w.r.t. the strict semantics if  , where
, where  stands for the transitive closure of
stands for the transitive closure of  .
.
The strict semantics accurately models communication by rendez-vous. However, for technical matters, we also need to consider a relaxed semantics for SDPNs.
The Relaxed Semantics. The relaxed semantics on SDPNs allow partially synchronized executions on a SDPN: a process can perform a transition labelled with \(a \in Lab\) even if it doesn’t synchronize with a matching process executing a transition labelled with \(\overline{a}\).
We therefore introduce a relaxed transition relation  labelled in Act on configurations of M:
labelled in Act on configurations of M:
(1) & (2) given two configurations u and v of M,  if and only if
if and only if  ;
;  features rules (1) and (2) of \(\dashrightarrow _{M}\);
features rules (1) and (2) of \(\dashrightarrow _{M}\);
(3) given a rule  in \(\varDelta \), a word \(w_1 \in ( P \varGamma ^* ) \cup ( P \varGamma ^* )^2\), and two configurations \(u = u_1 p \gamma u_2\) and \(v = u_1 w_1 u_2\) of M, we have
in \(\varDelta \), a word \(w_1 \in ( P \varGamma ^* ) \cup ( P \varGamma ^* )^2\), and two configurations \(u = u_1 p \gamma u_2\) and \(v = u_1 w_1 u_2\) of M, we have  ; a process performs an action but does not synchronize.
; a process performs an action but does not synchronize.
The restriction of the relaxed semantics to rules (2) and (3) yields the DPN semantics, as defined by Bouajjani et al. in [4].
For a given word \(\sigma = a_1 \ldots a_n \in Act^*\) and two configurations c, \(c'\) of M, we write that  if there are n configurations \(c_1, \ldots , c_n\) of M such that
if there are n configurations \(c_1, \ldots , c_n\) of M such that  and \(c_n = c'\). We then say that \(c'\) is reachable from c w.r.t. the relaxed semantics. For a given set of configurations C, we introduce
and \(c_n = c'\). We then say that \(c'\) is reachable from c w.r.t. the relaxed semantics. For a given set of configurations C, we introduce  .
.
For two subsets C and \(C'\) of \(Conf_M\), we define the set  , including paths with non-synchronized actions labelled in Lab.
, including paths with non-synchronized actions labelled in Lab.
2.2 From a Program to a SDPN Model
We can assume that the program is given by a control flow graph, whose nodes represent control points of threads or procedures and whose edges are labelled by statements. These statements can be variable assignments, procedure calls or returns, spawns of new threads, or communications between threads through unidirectional point-to point channels, where a thread sends a value x through a channel c and another thread waits for this value then assigns it to a variable y.
Without loss of generality, we assume that threads share no global variables and instead can only synchronize through channels. We distinguish local variables that belong to a single procedure from thread-local variables that can be accessed by any procedure called by a given instance of a thread. We also consider that both local and global variables may only take a finite number of values.
Given a control flow graph, we define a corresponding SDPN. The set of states P is the set of possible valuations of thread-local variables. The stack alphabet \(\varGamma \) is the set of all pairs (n, l) where n is a node of the flow graph and l is a valuation of the local variables of the current procedure.
Channels can be used to send and receive values. For each channel c and value x that can be sent through c, a label (c!, x) and its co-action \(( c?, x ) = \overline{( c!, x )}\) belong to Act. The internal action \(\tau \) belongs to Act as well.
For each statement s labelling an edge of the flow graph between nodes \(n_1\) and \(n_2\), we introduce the following transition rules in the corresponding SDPN, where \(g_1\) and \(g_2\) (resp. \(l_1\) and \(l_2\)) are the valuations of thread-local (resp. procedure-local) variables before and after the execution of the statement:
-
if s is an assignment, it is represented by rules of the form
 assigning new values to variables in \(g_1\) and \(l_1\) results in new valuations \(g_2\) and \(l_2\);
assigning new values to variables in \(g_1\) and \(l_1\) results in new valuations \(g_2\) and \(l_2\); -
if s is a procedure call, rules of the form
 represent s, where \(f_0\) is the starting node of the called procedure and \(l_0\) the initial valuation of its local variables;
represent s, where \(f_0\) is the starting node of the called procedure and \(l_0\) the initial valuation of its local variables; -
if s is a procedure return, it is represented by rules of the form
 ; we simulate returns of values by introducing an additional thread-local variable and assigning the return value to it in the valuation \(g_2\);
; we simulate returns of values by introducing an additional thread-local variable and assigning the return value to it in the valuation \(g_2\); -
if s is a thread spawn, rules of the form
 represent s, where \(g_0\) and \(l_0\) are respectively the initial valuations of the thread-local and procedure-local variables of the new thread, and \(n_0\) its starting node;
represent s, where \(g_0\) and \(l_0\) are respectively the initial valuations of the thread-local and procedure-local variables of the new thread, and \(n_0\) its starting node; -
if s is an assignment of a value x carried through a channel c to a variable y, it is represented by rules of the form
 where \(g_1\) and \(g_2\) (resp. \(l_1\) and \(l_2\)) are such that assigning the value x to the variable y in \(g_1\) (resp. \(l_1\)) results in the new valuations \(g_2\) (resp. \(l_2\));
where \(g_1\) and \(g_2\) (resp. \(l_1\) and \(l_2\)) are such that assigning the value x to the variable y in \(g_1\) (resp. \(l_1\)) results in the new valuations \(g_2\) (resp. \(l_2\)); -
if s is an output through a channel c of the value x of a variable y, it is represented by rules of the form
 such that the variable y has value x in either \(g_1\) or \(l_1\).
such that the variable y has value x in either \(g_1\) or \(l_1\).
Finally, we consider the starting configuration \(g_{init} ( n_{init}, l_{init} )\) where \(g_{init}\) and \(l_{init}\) are respectively the initial valuations of the thread-local and procedure-local variables of the main thread, and \(n_{init}\) its starting node.
3 The Reachability Problem
As described previously in Sect. 2.2, we can model the behaviour of a real multi-threaded program with a SDPN. Many static analysis techniques rely on being able to determine whether a given critical state is reachable or not from the starting configuration of a program.
Since checking reachability in a real program amounts to checking reachability in its corresponding SDPN w.r.t to the strict semantics, we want to solve the following reachability problem: given a SDPN M and two sets of configuration C and \(C'\), is there a configuration in \(C'\) that is reachable from C w.r.t. the strict semantics?
It has unfortunately been proven by Ramalingam in [10] that, even if C and \(C'\) are regular, this problem is undecidable for synchronization-sensitive pushdown systems, hence, SDPNs. Therefore, we reduce this problem to an execution path analysis of SDPNs with relaxed semantics.
3.1 From the Strict to the Relaxed Semantics
It is easy to see that the following Theorem holds:
Theorem 1
Let M be a SDPN and c, \(c'\) two configurations of M;  if and only if \(\exists n \ge 0\) such that
if and only if \(\exists n \ge 0\) such that  .
.
Intuitively, an execution path w.r.t. the relaxed semantics of the form \(\tau ^n\) only uses internal actions or synchronized actions between two threads: a synchronization signal a is always paired with its co-action \(\overline{a}\). Any configuration reachable using this path can be reached w.r.t. the strict semantics as well. Such a path is said to be perfectly synchronized.
Therefore, the reachability problem amounts to determining whether:
that is, if there is an execution path from C to \(C'\) w.r.t. the relaxed semantics of the form \(\tau ^n\). Obviously, we can’t always compute \(Paths_M ( C, C' )\). Our idea is therefore to compute an abstraction (over-approximation) of \(Paths_M ( C, C' )\) and check the emptiness of its intersection with \(\tau ^*\): if it is indeed empty, then \(C'\) can’t be reached from C w.r.t. the strict semantics.
It is worth noting that a configuration \(p'_1 w'_1 p'_2 w'_2\) reachable from \(p_1 w_1 p_2 w_2\) w.r.t. the strict semantics by synchronizing two rules  and
and  using the synchronization rule (1) can obviously be reached w.r.t. the relaxed semantics by applying these two rules sequentially, using rule (3) twice, although the resulting path would obviously not be perfectly synchronized. Hence, the following Theorem holds:
using the synchronization rule (1) can obviously be reached w.r.t. the relaxed semantics by applying these two rules sequentially, using rule (3) twice, although the resulting path would obviously not be perfectly synchronized. Hence, the following Theorem holds:
Theorem 2
Let M be a SDPN and c, \(c'\) two configurations of M; \(c'\) is reachable from c w. r. t. the relaxed SDPN semantics if and only if it is reachable w. r. t. the DPN semantics.
It implies that, since we can compute \(pre^* ( M, C )\) w.r.t. the DPN semantics, we can compute it w.r.t. the relaxed SDPN semantics as well.
3.2 Representing Infinite Sets of Configurations
In order to compute an abstraction of \(Paths_M ( C, C' )\) we need to be able to finitely represent infinite sets of configurations of a SDPN M. To do so, we introduce a class of finite automata called M-automata, as defined in [4]:
Definition 2
( M -automata). Given a SDPN \(M = ( Act, P, \varGamma , \varDelta )\), an M-automaton is a finite automaton \(A = ( \Sigma , S, \delta , s_{init}, F)\) such that:
-
\(\Sigma = P \cup \varGamma \) is the input alphabet;
-
the set of states \(S = S_C \cup S_S\) can be partitioned in two disjoint sets \(S_C\) and \(S_S\);
-
\(\delta \subseteq S \times \Sigma \times S\) is the set of transitions;
-
\(\forall s \in S_C\) and \(\forall p \in P\), there is at most a single state \(s_p\) such that \(( s, p, s_p ) \in \delta \); moreover, \(s_p \in S_S\) and s is the only predecessor of \(s_p\); transitions from states in \(S_C\) are always labelled with state symbols in P and go to dedicated states in \(S_S\);
-
states in \(S_C\) do not have exiting transitions labelled with letters in \(\varGamma \);
-
states in \(S_S\) do not have exiting transitions labelled in P; transitions labelled with letters in \(\varGamma \) always go to states in \(S_S\);
-
transitions from \(S_S\) to \(S_C\) are always labelled with \(\varepsilon \); these are the only allowed \(\varepsilon \)-transitions in the M-automaton;
-
\(s_{init} \in S_C\) is the initial state;
-
\(F \subseteq S_C\) is the set of final states.
An M-automaton is designed in such a manner that every path accepting a configuration \(p_1 w_1 \ldots p_n w_n\) is a sequence of sub-paths  where \(s_i \in S_C\), \(s_{i+1} \in S_C\) and every state in the path
where \(s_i \in S_C\), \(s_{i+1} \in S_C\) and every state in the path  is in \(S_S\). Being a finite state automaton, an M-automaton accepts a regular language that is a subset of \(Conf_M\). Any regular language in \(( P \varGamma ^* )^*\) can be accepted by an M-automaton.
is in \(S_S\). Being a finite state automaton, an M-automaton accepts a regular language that is a subset of \(Conf_M\). Any regular language in \(( P \varGamma ^* )^*\) can be accepted by an M-automaton.
M-automata were introduced so that one could compute the set of predecessors of a DPN, hence, of a SDPN as well, by applying a saturation procedure to an M-automaton accepting the set of starting configurations, as shown by Bouajjani et al. in [4].
4 An Abstraction Framework for Paths
Since we can’t compute the exact set \(Paths_M (C, C' )\), we will over-approximate it. To do so, we will use the following mathematical framework, basing our technique on the approach presented by Bouajjani et al. in [2].
4.1 Abstractions and Galois Connections
Let \(\mathcal {L} = (2^{Act^*}, \subseteq , \cup , \cap , \emptyset , Act^*)\) be the complete lattice of languages on Act.
Our abstraction of \(\mathcal {L}\) requires a lattice \(E = ( D, \le , \sqcup , \sqcap , \bot , \top )\), from now on called the abstract lattice, where D is a set called the abstract domain, as well as a pair of mappings \(( \alpha , \beta )\) called a Galois connection, where \(\alpha : 2^{Act^*} \rightarrow D\) and \(\beta : D \rightarrow 2^{Act^*}\) are such that \(\forall x \in 2^{Act^*}\), \(\forall y \in D\),  .
.
\(\forall L \in \mathcal {L}\), given a Galois connection \((\alpha , \beta )\), we have \(L \subseteq \beta (\alpha ( L ))\). Hence, the Galois connection can be used to overapproximate a language, such as the set of execution paths of a SDPN.
Moreover, it is easy to see that \(\forall L_1, \forall L_2 \in \mathcal {L}\), \(\alpha ( L_1 ) \sqcap \alpha ( L_2 ) = \bot \) if and only if \(\beta (\alpha ( L )) \cap \beta (\alpha ( L )) = \emptyset \). We therefore only need to check if \(\alpha ( Paths_M ( C, C' ) ) \sqcap \alpha ( \tau ^* ) = \bot \). From then on, \(\alpha ( Paths_M ( C, C' ) )\) will be called the abstraction of \(Paths_M ( C, C' )\), although technically \(\beta ( \alpha ( Paths_M ( C, C' ) )\) is the actual overapproximation.
4.2 Kleene Algebras
We want to define abstractions of \(\mathcal {L}\) such that we can compute the abstract path language \(\alpha ( Paths_M ( C', C ) )\), assuming the sets \(C'\) and C are regular. In order to do so, we consider a special class of abstractions, called Kleene abstractions.
An idempotent semiring is a structure \(K = ( A, \oplus , \odot , \overline{0}, \overline{1} )\), where \(\oplus \) is an associative, commutative, and idempotent (\(a \oplus a = a\)) operation, and \(\odot \) is an associative operation. \(\overline{0}\) and \(\overline{1}\) are neutral elements for \(\oplus \) and \(\odot \) respectively, \(\overline{0}\) is an annihilator for \(\odot \) (\(a \odot \overline{0} = \overline{0} \odot a = \overline{0}\)) and \(\odot \) distributes over \(\oplus \).
K is an Act-semiring if it can be generated by \(\overline{0}\), \(\overline{1}\), and elements of the form \(v_{a} \in A\), \(\forall a \in Act\). A semiring is said to be closed if \(\oplus \) can be extended to an operator over countably infinite sets while keeping the same properties as \(\oplus \).
We define \(a^{0} = \overline{1}\), \(a^{n+1} = a \odot a^{n}\) and \(a^{*} = \mathop {\bigoplus } \limits _{n \ge 0} a^{n}\). Adding the \(*\) operation to an idempotent closed Act-semiring K transforms it into a Kleene algebra.
4.3 Kleene Abstractions
An abstract lattice \(E = ( D, \le , \sqcup , \sqcap , \bot , \top )\) is said to be compatible with a Kleene algebra \(K = ( A, \oplus , \odot , \overline{0}, \overline{1} )\) if \(D = A\),  , \(\bot = \overline{0}\) and \(\sqcup = \oplus \).
, \(\bot = \overline{0}\) and \(\sqcup = \oplus \).
A Kleene abstraction is an abstraction such that the abstract lattice E is compatible with the Kleene algebra and the Galois connection \(\alpha : 2^{Act^*} \rightarrow D\) and \(\beta : D\rightarrow 2^{Act^*}\) is defined by:
Intuitively, a Kleene abstraction is such that the abstract operations \(\oplus \), \(\odot \), and \(*\) can be matched to the union, the concatenation, and the Kleene closure of the languages of the lattice \(\mathcal {L}\), \(\overline{0}\) and \(\overline{1}\) to the empty language and \(\{ \varepsilon \}\), \(v_a\) to the language \(\{ a \}\), the upper bound \(\top \in K\) to \(Act^*\), and the operation \(\sqcap \) to the intersection of languages in the lattice \(\mathcal {L}\).
In order to compute \(\alpha ( L )\) for a given language L, each word \(a_{1} \ldots a_{n}\) in L is matched to its abstraction \(v_{a_1} \odot \ldots \odot v_{a_n}\), and we consider the sum of these abstractions.
We can check if \(\alpha ( Paths_M ( C, C' ) ) \sqcap \mathop {\bigoplus } \limits _{n \ge 0} v_{\tau }^n = \bot \); if it is indeed the case, then \(\beta ( \alpha ( Paths_M ( C, C' ) ) ) \cap \tau ^* = \emptyset \), and since \(\beta ( \alpha ( Paths_M ( C, C' ) ) )\) is an over-approximation \(Paths_M ( C, C' )\), it follows that \(Paths_M ( C, C' ) \cap \tau ^* = \emptyset \).
A finite-chain abstraction is an abstraction such that the lattice \(( K, \oplus )\) has no infinite ascending chains. In this paper, we rely on a particular class of finite-chain abstractions, called finite-domain abstractions, whose abstract domain K is finite, such as the following examples:
Prefix Abstractions. Let n be an integer and \(W ( n ) = \left\{ w \in Act^* \mid \left| w \right| \le n \right\} \) be the set of words of length smaller than n. We define the n-th order prefix abstraction \(\alpha ^{pref}_n\) as follows: the abstract lattice \(A = 2^{W}\) is generated by the elements \(v_a = \left\{ a \right\} \), \(a \in Act\); \(\oplus = \cup \); \(U \odot V = \{ \text {pref}_n ( uv ) \mid u \in U, v \in V \}\) where \(\text {pref}_n ( w )\) stands for the prefix of w of length n (or lower if w is of length smaller than n); \(\overline{0} = \emptyset \); and \(\overline{1} = \left\{ \varepsilon \right\} \). From there, we build an abstract lattice where \(\top = W\), \(\sqcap = \cap \), and \(\le = \subseteq \). This abstraction is accurate for the n-th first steps of a run, then approximates the other steps by \(Act^*\).
We can apply a prefix abstraction of order 2 to the example shown in Fig. 1. For ease of representation, we show a control flow graph, although we could use the procedure outlined in Sect. 2.2 to compute an equivalent SDPN. We also consider without loss of generality that spawns, calls, and returns are silent \(\varepsilon \)-transitions.
We check that, starting from an initial set of configurations C with a single thread M in state \(m_0\), the set \(C'\) where M is in state \(m_2\) can’t be reached w.r.t. the strict semantics. We have \(\alpha ^{pref}_2 ( Paths_M ( C, C' ) ) = \{ b, b \tau , b a, b \overline{a} \}\), \(\alpha ^{pref}_2 ( \tau ^* ) = \{ \varepsilon , \tau , \tau \tau \}\), and \(\alpha ^{pref}_2 ( Paths_M ( C, C' ) ) \cap \alpha ^{pref}_2 ( \tau ^* ) = \emptyset \), hence, \(C'\) can’t be reached from C w.r.t. the strict semantics. Intuitively, the transition labelled with b in thread M can’t synchronize as there isn’t any transition labelled with \(\overline{b}\) in the whole program.
Suffix Abstractions. Let W be the set of words of length smaller than n. We define the n-th order suffix abstraction \(\alpha ^{suff}_n\) as follows: the abstract lattice \(A = 2^{W}\) is generated by the elements \(v_a = \left\{ a \right\} \), \(a \in Act\); \(\oplus = \cup \); \(U \odot V = \{ \text {suff}_n ( uv ) \mid u \in U, v \in V \}\) where \(\text {suff}_n ( w )\) stands for the suffix of w of length n (or lower if w is of length smaller than n); \(\overline{0} = \emptyset \); and \(\overline{1} = \left\{ \varepsilon \right\} \). From there, we build an abstract lattice where \(\top = W\), \(\sqcap = \cap \), and \(\le = \subseteq \). This abstraction is accurate for the n-th last steps of a run, then approximates the other steps by \(Act^*\).
We apply a suffix abstraction of order 2 to the example shown in Fig. 2. We check that, starting from an initial set of configurations C with a single thread M in state \(m_0\), the set \(C'\) where M is in state \(m_2\) can’t be reached w.r.t. the strict semantics. We have \(\alpha ^{suff}_2 ( Paths_M ( C, C' ) ) = \{ b, a b, \overline{a} b, \tau b \}\), \(\alpha ^{suff}_2 ( \tau ^* ) = \{ \varepsilon , \tau , \tau \tau \}\), and \(\alpha ^{suff}_2 ( Paths_M ( C, C' ) ) \cap \alpha ^{suff}_2 ( \tau ^* ) = \emptyset \), hence, \(C'\) can’t be reached from C w.r.t. the strict semantics. Intuitively, the transition labelled with b in thread M can’t synchronize as there isn’t any transition labelled with \(\overline{b}\) in the whole program.
It is worth noting that the reachability problem in Fig. 2 can’t be solved by a prefix abstraction, no matter its order. The reason is that \(\forall n \ge 0\), there is an execution path \(\tau ^n b \in Paths_M ( C, C' )\), hence, \(\tau ^n \in \alpha ^{pref}_n ( Paths_M ( C, C' ) )\). Intuitively, the two self-pointing loops of nodes \(m_1\) and \(n_1\) can synchronize.
Conversely, we can’t use a suffix abstraction to solve the reachability problem in Fig. 1. The reason is that \(\forall n \ge 0\), there is an execution path \(b \tau ^n \in Paths_M ( C, C' )\), hence, \(\tau ^n \in \alpha ^{suff}_n ( Paths_M ( C, C' ) )\). Intuitively, the self-pointing loop of node \(m_2\) can synchronize with the self-spawning loop in thread N.
Thus, these two abstractions (prefix and suffix) complement each other.
5 Representing Abstract Path Languages
We define structures to represent \(\alpha ( Paths_M ( C, C' ) )\) and reduce their construction to a predecessor problem. To do so, we can’t use the K multi-automata introduced in [2] and must rely instead on M-automata labelled by functions in the abstract domain.
5.1 The Shuffle Product
Assuming we know the abstract path languages of two different threads, we want to compute the abstract path language of these two threads running in parallel. Intuitively, this new language will be an interleaving of the two aforementioned sets, but can feature synchronized actions between the two threads as well.
To this end, we inductively define a shuffle operation  on abstract path expressions:
on abstract path expressions:
-
 ;
; -
if
 ;
; -
 ; two synchronized actions a and \(\overline{a}\) result in an internal action \(\tau \), hence, there is a component
; two synchronized actions a and \(\overline{a}\) result in an internal action \(\tau \), hence, there is a component  of the shuffle product where the two paths synchronize.
of the shuffle product where the two paths synchronize.
We can extend the operation  to sets of path expressions.
to sets of path expressions.
5.2 K-configurations
Let \(M = ( Act, P, \varGamma , \varDelta )\) be a SDPN and \(K = ( A, \oplus , \odot , \overline{0}, \overline{1} )\) a Kleene algebra corresponding to a Kleene abstraction. We define inductively the set \(\varPi _{K}\) of path expressions as the smallest subset of K such that:
-
\(\overline{1} \in \varPi _{K}\);
-
if \(\pi \in \varPi _{K}\), then \(\forall a \in Act\), \(v_a \odot \pi \in \varPi _{K}\).
For a given path expression \(\pi \), we define its length \(\left| \pi \right| \) as the number of occurrences of simple elements of the form \(v_a\) in \(\pi \).
A K-configuration of M is a pair \((c, \pi ) \in Conf_M \times \varPi _K\). We can extend the transition relation  to K-configurations with the following semantics: \(\forall a \in Act\), if
to K-configurations with the following semantics: \(\forall a \in Act\), if  , then \(\forall \pi \in \varPi _K\),
, then \(\forall \pi \in \varPi _K\),  ; \(( c, v_{a} \odot \pi )\) is said to be an immediate K-predecessor of \(( c', \pi )\). The reachability relation \(\leadsto _{M, K}\) is the reflexive transitive closure of
; \(( c, v_{a} \odot \pi )\) is said to be an immediate K-predecessor of \(( c', \pi )\). The reachability relation \(\leadsto _{M, K}\) is the reflexive transitive closure of  .
.
For a given set of configurations C, we introduce the set \(pre_{K}^{*} ( M, C )\) of K-configurations \(( c, \pi )\) such that \(( c, \pi ) \leadsto _{M, K} ( c', \overline{1} )\) for \(c' \in C\):
As we will see later, the abstract path expression \(\pi \) is meant to be the abstraction of an actual execution path from c to \(c'\).
5.3 (K, M)-Automata
We represent potentially infinite sets of K-configurations of a SDPN M with a class of labelled M-automata, called (K, M)-automata.
Definition 3
Let \(M = ( Act, P, \varGamma , \varDelta )\) be a SDPN, a (K, M)-automaton is a finite automaton \(A = ( \Sigma , S, \delta , s_{init}, F )\) where \(\Sigma = P \cup \varGamma \) is the input alphabet, \(S = S_C \cup S_S\) is a finite set of control states with \(S_C \cap S_S = \emptyset \), \(\delta \subseteq ( S_C \times P \times S_S ) \cup ( S_S \times \varGamma \times K^{K} \times S_S ) \cup ( S_S \times \{ \varepsilon \} \times S_C )\) a finite set of transition rules (where \(K^K\) is the set of functions from K to K), \(s_{init}\) an initial state, and F a set of final states.
Moreover, A is such that, if we consider the projection \(\delta _\Sigma \) of \(\delta \) on \(S \times \Sigma ^* \times S\), ignoring labels in \(K^K\), then \(( \Sigma , S, \delta _\Sigma , s_i, F )\) is an M-automaton.
Intuitively, a (K, M)-automaton can be seen as an M-automaton whose transitions labelled by stack symbols in \(\varGamma \) have been given an additional label in \(K^K\). We can consider a simple M-automaton as a (K, M)-automaton if we label each transition in \(S_S \times \varGamma \times S_S\) with the identity function.
Before defining a proper transition relation of (K, M)-automata, we first explain the intuition behind the use of functions in \(K^K\) as labels.
The Need for Functions. The use of functions in \(K^K\) instead of simple abstract values in K as done in [2] is a novelty of this paper. Our intuition is that functions of the form  where f(x) is a monomial expression in K[x] can be used to represent and compose sets of abstract paths. The variable x stands for parts of an execution path that can later be expanded by further transitions.
where f(x) is a monomial expression in K[x] can be used to represent and compose sets of abstract paths. The variable x stands for parts of an execution path that can later be expanded by further transitions.
As an example, the set of abstract execution paths represented by the tree \(T_1\) in Fig. 3 can be modelled by the function  . If, from the node \(t_3\) of the tree, it is possible to expand the abstract paths by either \(v_a\) or \(v_\tau \), as shown in Fig. 5, then a function representing this set of abstract paths can be computed by composing \(f_1\) with the function
. If, from the node \(t_3\) of the tree, it is possible to expand the abstract paths by either \(v_a\) or \(v_\tau \), as shown in Fig. 5, then a function representing this set of abstract paths can be computed by composing \(f_1\) with the function  representing the tree \(T_2\) shown in Fig. 4.
representing the tree \(T_2\) shown in Fig. 4.
Indeed, \(f_1 \circ f_2 ( x ) = v_a \odot v_\tau \odot v_a \odot x \oplus v_a \odot v_\tau \odot v_\tau \odot x \oplus v_{\overline{a}}\). When we no longer want to expand a set of execution paths, we can get rid of the variable x by considering the element of the abstract domain \(f ( \overline{1} ) \in K\).
Had we instead represented \(T_1\) and \(T_2\) by two abstract values \(v_a \odot v_\tau \oplus v_{\overline{a}}\) and \(v_a \oplus v_{\tau }\) in K, as done in [2], the concatenation of these two values would have yielded \(v_a \odot v_\tau \odot v_a \oplus v_a \odot v_\tau \odot v_\tau \oplus v_{\overline{a}} \odot v_\tau \oplus v_{\overline{a}} \odot v_a\). But \(v_{\overline{a}} \odot v_\tau \) and \(v_{\overline{a}} \odot v_a\) obviously should not belong to the abstraction of execution paths, hence, unlike [2], we need functions in \(K^K\) that can be composed and shuffled instead of simple abstract values in K.
The Transition Relation. Let A be a (K, M)-automaton. We define a simple transition relation  according to the following semantics:
according to the following semantics:
-
if \(( s, p, s' ) \in \delta \cap ( S \times ( P \cup \{ \varepsilon \} ) \times S )\), then
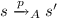 ;
; -
if \(( s, \gamma , e, s' ) \in \delta \cap ( S_S \times \varGamma \times K^{K} \times S_S )\), then
 ;
; -
if
 and
and  , then
, then  , where \(\circ \) is the composition operation on functions.
, where \(\circ \) is the composition operation on functions.
We then extend this transition relation to a full path relation  :
:
-
for each \(s \in S_S\),
 , where Id stands for the identity function;
, where Id stands for the identity function; -
if there is a sequence
 with \(s_0, \ldots , s_n \in S_S\), then
with \(s_0, \ldots , s_n \in S_S\), then  , where \(w = \gamma _{1} \ldots \gamma _{n}\) and \(e = e_{1} \circ \ldots \circ e_{n}\); this is a simple sequence of actions along a single thread;
, where \(w = \gamma _{1} \ldots \gamma _{n}\) and \(e = e_{1} \circ \ldots \circ e_{n}\); this is a simple sequence of actions along a single thread; -
if there is a sequence
 such that \(s, s'', q \in S_S\) and \(s' \in S_C\), then
such that \(s, s'', q \in S_S\) and \(s' \in S_C\), then  , where \(w = p_1 w_1 p_2 w_2\) and
, where \(w = p_1 w_1 p_2 w_2\) and  ; the automaton represents two parallel processes \(p_1 w_1\) and \(p_2 w_2\) whose abstract execution paths must be shuffled; moreover, since the first process will no longer be extended by further transitions of the automaton, we get rid of the variable x by considering \(e_1 ( \overline{1} )\) instead.
; the automaton represents two parallel processes \(p_1 w_1\) and \(p_2 w_2\) whose abstract execution paths must be shuffled; moreover, since the first process will no longer be extended by further transitions of the automaton, we get rid of the variable x by considering \(e_1 ( \overline{1} )\) instead.
A path  is said to be an execution of A if \(s_0 = s_{init}\). It is then said to be accepting if \(s_n \in F\). We then say that A accepts \(( c, \pi )\) for all \(\pi \in \varPi _K\) such that \(\pi \le e ( \overline{1} )\). This way, accepting execution paths in (K, M)-automata can be used to represent whole sets of path expressions. We define the set \(L_K ( A )\) of all K-configurations of M accepted by A.
is said to be an execution of A if \(s_0 = s_{init}\). It is then said to be accepting if \(s_n \in F\). We then say that A accepts \(( c, \pi )\) for all \(\pi \in \varPi _K\) such that \(\pi \le e ( \overline{1} )\). This way, accepting execution paths in (K, M)-automata can be used to represent whole sets of path expressions. We define the set \(L_K ( A )\) of all K-configurations of M accepted by A.
6 Computing the Abstraction
Let C and \(C'\) be two regular sets of configurations of a SDPN \(M = ( Act, P, \varGamma , \varDelta )\). We want to check if \(Paths_M ( C, C' ) \cap \tau ^* = \emptyset \). To that end, we compute an abstraction \(\alpha ( Paths_M ( C, C' ) )\), where \(\alpha \) is a finite-domain abstraction. To this aim, we will proceed as follows.
We first compute a (K, M)-automaton \(A_{pre_{K}^{*}}\) accepting \(pre_{K}^{*} ( C' )\). Our intuition is that, if \(( c', \pi ) \leadsto _{M, K} ( c, \overline{1} )\), then there is an execution path from \(c'\) to c w.r.t. the relaxed semantics whose abstraction is \(\pi \). We can then restrict \(A_{pre_{K}^{*}}\) to only accept K-configurations that are also in \(C \times \varPi _K\) by computing the product automaton \(A'\) between \(A_{pre_{K}^{*}}\) and an M-automaton accepting C.
We can then consider the following abstraction:
Without loss of generality, we suppose that \(\varDelta \subseteq ( P \times \varGamma \times Act \times P \varGamma P \varGamma ) \cup ( P \times \varGamma \times Act \times P \varGamma ^{\le 2} )\): each transition rule of M can spawn at most one new process and push at most two stack symbols.
6.1 Computing \(pre^* ( M, C )\)
Given a SDPN M and a regular set C of configurations of M accepted by an M-automaton A, we want to compute an M-automaton \(A_{pre^*}\) accepting \(pre^* ( M, C )\). Thanks to Theorem 2, we can apply the saturation procedure defined in [4] to A. Let us remind this procedure. Initially, \(A_{pre^*} = A\), then we apply the following rules until saturation to \(A_{pre^*}\):
- \(( R_1 )\) :
-
if
 and
and 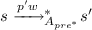 for \(s \in S_S\), \(s' \in S\), then add
for \(s \in S_S\), \(s' \in S\), then add  ;
; - \(( R_2 )\) :
-
if
 and
and  for \(s \in S_S\), \(s' \in S\), then add
for \(s \in S_S\), \(s' \in S\), then add  .
.
 stands for the transitive closure of the transition relation on the finite state automaton \(A_{pre^*}\). The initial and final states remain the same.
stands for the transitive closure of the transition relation on the finite state automaton \(A_{pre^*}\). The initial and final states remain the same.
Let us remind the intuition of these rules. We consider a subpath  . By design of an M-automaton, s should be in \(S_C\) and there should be a path
. By design of an M-automaton, s should be in \(S_C\) and there should be a path  in the automaton. If we apply the saturation rule \(( R_1 )\), we add an edge \(s_p \xrightarrow {p} s'\) to \(A_{pre^*}\) and create a subpath
in the automaton. If we apply the saturation rule \(( R_1 )\), we add an edge \(s_p \xrightarrow {p} s'\) to \(A_{pre^*}\) and create a subpath  in the automaton. Therefore, if \(A_{pre^*}\) accepts a configuration \(u_1 p' w' u_2\) with a path
in the automaton. Therefore, if \(A_{pre^*}\) accepts a configuration \(u_1 p' w' u_2\) with a path  , \(q_F \in F\), then it will accept its predecessor \(u_1 p \gamma u_2\) as well with a path
, \(q_F \in F\), then it will accept its predecessor \(u_1 p \gamma u_2\) as well with a path  . The role of \(( R_2 )\) is similar.
. The role of \(( R_2 )\) is similar.
Thus, when this saturation procedure ends, the M-automaton \(A_{pre^*}\) accepts the regular set \(pre^* ( M, C )\). Assuming the initial M-automaton A representing C is of constant size, the procedure terminates after a polynomial (in \(| \varDelta |\)) number of steps.
6.2 From \(pre^* ( M, C )\) to \(pre^*_K ( M, C )\)
Given a SDPN M and a regular set C of configurations of M accepted by an M-automaton A, we want to compute a (K, M)-automaton \(A_{pre^*_K}\) accepting \(pre^*_K ( M, C )\). To this end, we will add new labels to the M-automaton \(A_{pre^*}\). Our intuition is the following: \(A_{pre_{K}^{*}}\) should be such that if we have \(( c', \pi ) \leadsto _{M, K} ( c, \overline{1} )\), \(c \in C\), then c can be reached from \(c'\) by an execution path whose abstract representation in K is the path expression \(\pi \).
In order to compute \(A_{pre_{K}^{*}}\), we proceed as follows: we first accept configurations in C with the path expression \(\overline{1}\), then, from there, set constraints on the labelling functions of transitions of \(A_{pre^*}\) depending on the relationship between edges introduced by the previous saturation procedure. This way, we build iteratively a set of constraints whose least fixpoint can abstract the set of execution paths from \(pre^* ( M, C )\) to C.
To this end, each transition t in \(A_{pre^*}\) labelled in \(\varGamma \) is given a second label \(\lambda ( t ) \in K^K\). To do so, we compute a set of constraints whose smallest solution (according to the order \(\le \) of the Kleene algebra) will be the labels \(\lambda ( t )\). If  , then we write \(\lambda ( t ) = \lambda ( q_1, \gamma , q_2 )\).
, then we write \(\lambda ( t ) = \lambda ( q_1, \gamma , q_2 )\).
The Constraints. Let x be the variable of functions in \(K^K\). We now consider the following set of constraints on transitions of \(A_{pre^*}\) in \(S_S \times \varGamma \times S_S\):
- \(( Z_1 )\) :
-
if t belongs both to A and \(A_{pre^*}\), then for each \(x \in K\):
$$\begin{aligned} x \le \lambda ( t )( x ) \end{aligned}$$ - \(( Z_2 )\) :
-
for each rule
 , for each \(q \in Q\), for each \(s \in S_c\): $$\begin{aligned} v_{a} \odot \lambda ( s_{p'}, \gamma ', q ) \le \lambda ( s_{p}, \gamma , q ) \end{aligned}$$
, for each \(q \in Q\), for each \(s \in S_c\): $$\begin{aligned} v_{a} \odot \lambda ( s_{p'}, \gamma ', q ) \le \lambda ( s_{p}, \gamma , q ) \end{aligned}$$ - \(( Z_3 )\) :
-
for each rule
 , for each \(s \in S_c\): $$\begin{aligned} v_{a} \odot Id \le \lambda ( s_{p}, \gamma , s_{p'} ) \end{aligned}$$
, for each \(s \in S_c\): $$\begin{aligned} v_{a} \odot Id \le \lambda ( s_{p}, \gamma , s_{p'} ) \end{aligned}$$ - \(( Z_4 )\) :
-
for each rule
 , for each \(q \in Q\), for each \(s \in S_c\): $$\begin{aligned} \mathop {\bigoplus } \limits _{q' \in Q} v_{a} \odot ( \lambda ( s_{p'}, \gamma _{1}, q' ) \circ \lambda ( q', \gamma _{2}, q ) ) \le \lambda ( s_{p}, \gamma , q ) \end{aligned}$$
, for each \(q \in Q\), for each \(s \in S_c\): $$\begin{aligned} \mathop {\bigoplus } \limits _{q' \in Q} v_{a} \odot ( \lambda ( s_{p'}, \gamma _{1}, q' ) \circ \lambda ( q', \gamma _{2}, q ) ) \le \lambda ( s_{p}, \gamma , q ) \end{aligned}$$ - \(( Z_5 )\) :
-
for each rule
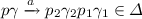 , for each \(q \in Q\), for each \(s \in S_c\):
, for each \(q \in Q\), for each \(s \in S_c\): 
We now explain intuitively the meaning of these constraints.
The Intuition. If c is a configuration of C, then \(A_{pre^*_K}\) should accept \(( c, \overline{1} )\). This is expressed by constraint \(( Z_1 )\).
Let \(c' = p' \gamma ' w \in pre^* ( M, C )\). If  and \(( c', \pi ) \in pre^*_K ( M, C )\), then \(c = p \gamma w \in pre^* ( M, C )\), \(( c, v_a \odot \pi ) \leadsto _{M, K} ( c', \pi )\), and \( ( c, v_a \odot \pi ) \in pre^*_K ( M, C )\). Hence, if \(A_{pre^*_K}\) accepts \(( c', \pi )\) and uses a transition
and \(( c', \pi ) \in pre^*_K ( M, C )\), then \(c = p \gamma w \in pre^* ( M, C )\), \(( c, v_a \odot \pi ) \leadsto _{M, K} ( c', \pi )\), and \( ( c, v_a \odot \pi ) \in pre^*_K ( M, C )\). Hence, if \(A_{pre^*_K}\) accepts \(( c', \pi )\) and uses a transition  while doing so, then it should accept \(( c, v_a \odot \pi )\) as well using a transition
while doing so, then it should accept \(( c, v_a \odot \pi )\) as well using a transition  . This is expressed by constraint \(( Z_2 )\).
. This is expressed by constraint \(( Z_2 )\).
Let \(c' = p' w \in pre^* ( M, C )\). If  and \(( c', \pi ) \in pre^*_K ( M, C )\), then \(c = p \gamma w \in pre^* ( M, C )\), \(( c, v_a \odot \pi ) \leadsto _{M, K} ( c', \pi )\), and \( ( c, v_a \odot \pi ) \in pre^*_K ( M, C )\). Hence, if \(A_{pre^*_K}\) accepts \(( c', \pi )\), then it should accept \(( c, v_a \odot \pi )\) as well using a transition
and \(( c', \pi ) \in pre^*_K ( M, C )\), then \(c = p \gamma w \in pre^* ( M, C )\), \(( c, v_a \odot \pi ) \leadsto _{M, K} ( c', \pi )\), and \( ( c, v_a \odot \pi ) \in pre^*_K ( M, C )\). Hence, if \(A_{pre^*_K}\) accepts \(( c', \pi )\), then it should accept \(( c, v_a \odot \pi )\) as well using a transition  . This is expressed by constraint \(( Z_3 )\).
. This is expressed by constraint \(( Z_3 )\).
Let \(c' = p' \gamma _1 \gamma _2 w \in pre^* ( M, C )\). If  and also \(( c', \pi ) \in pre^*_K ( M, C )\), then \(c = p \gamma w \in pre^* ( M, C )\), \(( c, v_a \odot \pi ) \leadsto _{M, K} ( c', \pi )\), and \( ( c, v_a \odot \pi ) \in pre^*_K ( M, C )\). Hence, if \(A_{pre^*_K}\) accepts \(( c', \pi )\) and uses two transition
and also \(( c', \pi ) \in pre^*_K ( M, C )\), then \(c = p \gamma w \in pre^* ( M, C )\), \(( c, v_a \odot \pi ) \leadsto _{M, K} ( c', \pi )\), and \( ( c, v_a \odot \pi ) \in pre^*_K ( M, C )\). Hence, if \(A_{pre^*_K}\) accepts \(( c', \pi )\) and uses two transition  and
and  while doing so, then it should accept \(( c, v_a \odot \pi )\) as well using a transition
while doing so, then it should accept \(( c, v_a \odot \pi )\) as well using a transition  . Moreover, there can be many possible intermediate states \(q'\) between \(s'_p\) and q such that
. Moreover, there can be many possible intermediate states \(q'\) between \(s'_p\) and q such that  and
and  . In the automaton \(A_{pre^*_K}\), the abstract path \(\pi \) should therefore be represented by the sum for all possible intermediate state \(q'\) of the concatenation of the two labelling functions \(\lambda (s_{p'}, \gamma _1, q' )\) and \(\lambda ( q', \gamma _2, q )\). This is expressed by constraint \(( Z_4 )\).
. In the automaton \(A_{pre^*_K}\), the abstract path \(\pi \) should therefore be represented by the sum for all possible intermediate state \(q'\) of the concatenation of the two labelling functions \(\lambda (s_{p'}, \gamma _1, q' )\) and \(\lambda ( q', \gamma _2, q )\). This is expressed by constraint \(( Z_4 )\).
Let \(c' = p_2 \gamma _2 p_1 \gamma _1 w \in pre^* ( M, C )\). If  and \(( c', \pi ) \in pre^*_K ( M, C )\), then \(c = p \gamma w \in pre^* ( M, C )\), \(( c, v_a \odot \pi ) \leadsto _{M, K} ( c', \pi )\), and \( ( c, v_a \odot \pi ) \in pre^*_K ( M, C )\). The two processes \(p_2 \gamma _2\) and \(p_1 \gamma _1\) are interleaved, hence, their abstract execution paths must be shuffled: if \(\pi _1\) is an execution path associated to \(p_1 \gamma _1\), and \(\pi _2\), to \(p_2 \gamma _2\), then an abstract path
and \(( c', \pi ) \in pre^*_K ( M, C )\), then \(c = p \gamma w \in pre^* ( M, C )\), \(( c, v_a \odot \pi ) \leadsto _{M, K} ( c', \pi )\), and \( ( c, v_a \odot \pi ) \in pre^*_K ( M, C )\). The two processes \(p_2 \gamma _2\) and \(p_1 \gamma _1\) are interleaved, hence, their abstract execution paths must be shuffled: if \(\pi _1\) is an execution path associated to \(p_1 \gamma _1\), and \(\pi _2\), to \(p_2 \gamma _2\), then an abstract path  should be associated to \(p_2 \gamma _2 p_1 \gamma _1\). Moreover, if we consider a path
should be associated to \(p_2 \gamma _2 p_1 \gamma _1\). Moreover, if we consider a path  in the automaton \(A_{pre^*_K}\), then no abstract path \(\pi _2\) associated to \(p_2 \gamma _2\) can be extended further, and should therefore be represented by \(( \lambda ( s_{p_2}, \gamma _{2}, s' ) ( \overline{1} ) )\). Again, we must also consider each possible intermediate state \(s''\) in the previous path, hence, a sum of functions. This is expressed by constraint \(( Z_5 )\).
in the automaton \(A_{pre^*_K}\), then no abstract path \(\pi _2\) associated to \(p_2 \gamma _2\) can be extended further, and should therefore be represented by \(( \lambda ( s_{p_2}, \gamma _{2}, s' ) ( \overline{1} ) )\). Again, we must also consider each possible intermediate state \(s''\) in the previous path, hence, a sum of functions. This is expressed by constraint \(( Z_5 )\).
Solving the Constraints. Since \(\alpha \) is a finite-domain abstraction, the set \(K^K\) of functions in K is finite as well. Let \(t_1, \ldots , t_m\) be an arbitrary numbering of the transitions of \(A_{pre_{K}^{*}}\) labelled with functions in the abstract domain and let \(k_1, \ldots , k_n\) be an enumeration of the elements of the finite domain K (\(n = | K |\)). The labelling constraints of Sect. 6.2 define a system of inequalities on \(m * n\) variables \(x_1, \ldots , x_{m n}\) such that its smallest solution is \(t_1 ( k_1 ), \ldots , t_1 ( k_n )\), \(t_2 ( k_1 ), \ldots , t_m ( k_n )\). It is worth noting that we can replace two different inequalities \(e_1 ( x ) \le t_i ( x )\) and \(e_2 ( x ) \le t_i ( x )\) by a single inequality \(e_1 ( x ) \oplus e_2 ( x ) \le t_i ( x )\). We therefore end up with a system of the form:
where the functions \(f_i\) are monomials in \(K [ x_1, \ldots , x_{m n} ]\). Finding the least solution of this system of inequalities amounts to finding the least pre-fixpoint of the monotonic and continuous function:
By Tarski’s theorem, this fixpoint exists and is equal to \(\bigoplus \limits _{i \ge 0} F^i ( \overline{0} )\).
In a finite-domain, this iterative computation always terminates in a number of steps bounded by the length l of the longest ascending chain in K. There are mn functions \(f_i\), each with a number of \(\oplus \), \(\odot \), and  operations in \(O ( |\varDelta | |Q| )\). Moreover, we know that \(m = O ( | \varDelta |^k )\) for an integer k. Each iteration step therefore features \(O ( |K| |\varDelta |^{k+1} |Q| )\) operations, and the whole procedure, \(O ( l |K| |\varDelta |^{k+1} |Q| )\) operations. For a prefix or suffix abstraction of order j, \(| K | = |Act|^j\), hence, \(O ( l |Act|^j |\varDelta |^{k+1} |Q| )\) operations
operations in \(O ( |\varDelta | |Q| )\). Moreover, we know that \(m = O ( | \varDelta |^k )\) for an integer k. Each iteration step therefore features \(O ( |K| |\varDelta |^{k+1} |Q| )\) operations, and the whole procedure, \(O ( l |K| |\varDelta |^{k+1} |Q| )\) operations. For a prefix or suffix abstraction of order j, \(| K | = |Act|^j\), hence, \(O ( l |Act|^j |\varDelta |^{k+1} |Q| )\) operations
Once \(A_{pre_{K}^{*}}\) is properly labelled, the following Theorem holds:
Theorem 3
Let M be a SDPN and A an M-automaton accepting a regular set of configurations C. Then the (K, M)-automaton \(A_{pre_{K}^{*}}\) accepts \(pre_{K}^{*} ( M, C )\).
6.3 Finding the Abstraction
We can compute an automaton \(A_{pre_{K}^{*}}\) that accepts the set \(pre_{K}^{*} ( M, C' )\). We then want to find a (K, M)-automaton \(A'\) that accepts \(pre_{K}^{*} ( M, C' ) \cap C \times \varPi _{K}\).
To do so, we define the intersection \(A' = ( \Sigma , S', \delta ', s'_{init}, F' )\) of the automaton \(A_{pre^{*}} = ( \Sigma , S, \delta , s_{init}, F )\) with an M-automaton \(A_1 = ( \Sigma , S_1, \delta _1, s_{1, init}, F_1 )\) accepting C, where \(S' = S \times S_1\), \(s'_{init} = ( s_{init}, s_{1, init} )\), \(F = F \times F_1\), and  . Moreover, we label \(A'\) with abstract functions in such a manner that \(\lambda ( ( q, q_1 ), a, ( q', q'_1 ) ) = \lambda ( q , a, q' )\).
. Moreover, we label \(A'\) with abstract functions in such a manner that \(\lambda ( ( q, q_1 ), a, ( q', q'_1 ) ) = \lambda ( q , a, q' )\).
The (K, M)-automaton \(A'\) then obviously accepts \(pre_{K}^{*} ( M, C' ) \cap C \times \varPi _{K}\). Eventually, our abstraction is \(\alpha ( Paths_M ( C, C' ) ) = \mathop {\bigoplus } \{ \pi \mid ( c, \pi ) \in L_K ( A' ) \}\).
7 Using Our Framework in a CEGAR Scheme
Following the work of Chaki et al. in [5], we propose a semi-decision procedure that, in case of termination, answers exactly whether \(Paths_M ( C, C' ) \cap \tau ^* = \emptyset \).
We first model a program as a SDPN M, as shown in Sect. 2.2, its starting configurations as a regular set C, and a set of critical configurations whose reachability we need to study as another regular set \(C'\).
We then introduce the following Counter-Example Guided Abstraction Refinement (CEGAR) scheme based on the finite-domain abstraction framework detailed previously, starting from \(n = 1\).
- Abstraction::
-
we compute abstractions \(\alpha ( Paths_M ( C, C' ) )\) of the set of executions paths for \(\alpha = \alpha ^{pref}_n\) and \(\alpha = \alpha ^{suff}_n\);
- Verification::
-
for \(\alpha = \alpha ^{pref}_n\) and \(\alpha = \alpha ^{suff}_n\), we check if \(\alpha ( Paths_M ( C, C' ) ) \sqcap \alpha ( \tau ^* ) = \bot \); if it is indeed true, then we conclude that \(C'\) can’t be reached from C using only internal or synchronized actions;
- Counter-Example Validation::
-
if there is such a path, we then check if our abstraction introduced a spurious counter-example; this can be done in a finite number of steps by checking if this counter-example can be reached within the n-th first or last execution steps of the program, depending on which abstraction (prefix or suffix) provided us with a counter-example; if the counter-example is not spurious, then we conclude that \(C'\) is reachable from C w.r.t. the strict semantics;
- Refinement::
-
if the counter-example was spurious, we go back to the first step, but use this time finite-domain abstractions of order \(n + 1\).
If this procedure ends, we can decide the reachability problem.
8 A Case Study
We use a CEGAR scheme to find an error in a Bluetooth driver for Windows NT. We consider here an abstracted version of a driver found in [9] that nonetheless keeps the erroneous trace, in a manner similar to [5, 7]. We then fix the driver by changing one of its routines, then use the CEGAR scheme to prove that this new version of the driver is correct.
We model the network of processes in the driver as a SDPN. New requests for the driver are represented by thread spawns, and the driver’s counter of active requests, by a counter on the stack, hence, a recursive process, making full use of our model’s features.
We were able to discover the bug by applying our finite-domain abstraction in a CEGAR scheme: we start from abstractions of order 1 and increment the order until we deduce that the erroneous configuration is reachable using a prefix abstraction of size 12. We then correct one of the program’s subroutines accordingly and apply our CEGAR scheme to prove it’s now error-free.
Note that this bug was also discovered in [5, 7, 9]. However, our approach is more complete and precise than these works: [9] can only discover errors, whereas our scheme can also prove that the modified version of the driver is correct; [5] does not handle dynamic thread creation, and thus had to guess the number of threads for which the error arises; and [7] models thread creation as parallel calls (not as spawns), where the father process waits for its children to terminate in order to resume its execution.
References
Bouajjani, A., Esparza, J., Schwoon, S., Strejček, J.: Reachability analysis of multithreaded software with asynchronous communication. In: Sarukkai, S., Sen, S. (eds.) FSTTCS 2005. LNCS, vol. 3821, pp. 348–359. Springer, Heidelberg (2005). https://doi.org/10.1007/11590156_28
Bouajjani, A., Esparza, J., Touili, T.: A generic approach to the static analysis of concurrent programs with procedures. In: POPL 2003 (2003)
Bouajjani, A., Esparza, J., Touili, T.: Reachability analysis of synchronized pa systems. Electron. Notes Theor. Comput. Sci. 138(3), 153–178 (2005)
Bouajjani, A., Müller-Olm, M., Touili, T.: Regular symbolic analysis of dynamic networks of pushdown systems. In: Abadi, M., de Alfaro, L. (eds.) CONCUR 2005. LNCS, vol. 3653, pp. 473–487. Springer, Heidelberg (2005). https://doi.org/10.1007/11539452_36
Chaki, S., Clarke, E., Kidd, N., Reps, T., Touili, T.: Verifying concurrent message-passing C programs with recursive calls. In: Hermanns, H., Palsberg, J. (eds.) TACAS 2006. LNCS, vol. 3920, pp. 334–349. Springer, Heidelberg (2006). https://doi.org/10.1007/11691372_22
Esparza, J., Hansel, D., Rossmanith, P., Schwoon, S.: Efficient algorithms for model checking pushdown systems. In: Emerson, E.A., Sistla, A.P. (eds.) CAV 2000. LNCS, vol. 1855, pp. 232–247. Springer, Heidelberg (2000). https://doi.org/10.1007/10722167_20
Patin, G., Sighireanu, M., Touili, T.: Spade: verification of multithreaded dynamic and recursive programs. In: Damm, W., Hermanns, H. (eds.) CAV 2007. LNCS, vol. 4590, pp. 254–257. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73368-3_28
Qadeer, S., Rehof, J.: Context-bounded model checking of concurrent software. In: Halbwachs, N., Zuck, L.D. (eds.) TACAS 2005. LNCS, vol. 3440, pp. 93–107. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31980-1_7
Qadeer, S., Wu, D.: Kiss: keep it simple and sequential. In: PLDI 2004 (2004)
Ramalingam, G.: Context-sensitive synchronization-sensitive analysis is undecidable. ACM Trans. Program. Lang. Syst. 22(2), 416–430 (2000)
Reps, T., Schwoon, S., Jha, S., Melski, D.: Weighted pushdown systems and their application to interprocedural dataflow analysis. Sci. Comput. Program. 58(1), 206–263 (2005)
Touili, T.: Dealing with communication for dynamic multithreaded recursive programs. In: VISSAS 2005 (2005)
Wenner, A.: Weighted dynamic pushdown networks. In: Gordon, A.D. (ed.) ESOP 2010. LNCS, vol. 6012, pp. 590–609. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11957-6_31
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Pommellet, A., Touili, T. (2017). Static Analysis of Multithreaded Recursive Programs Communicating via Rendez-Vous. In: Chang, BY. (eds) Programming Languages and Systems. APLAS 2017. Lecture Notes in Computer Science(), vol 10695. Springer, Cham. https://doi.org/10.1007/978-3-319-71237-6_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-71237-6_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-71236-9
Online ISBN: 978-3-319-71237-6
eBook Packages: Computer ScienceComputer Science (R0)





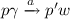 in
in  in
in  and
and  in
in 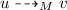 ; two synchronized processes perform a simultaneous action;
; two synchronized processes perform a simultaneous action; in
in  ; a process performs an internal action.
; a process performs an internal action. assigning new values to variables in
assigning new values to variables in  represent s, where
represent s, where  ; we simulate returns of values by introducing an additional thread-local variable and assigning the return value to it in the valuation
; we simulate returns of values by introducing an additional thread-local variable and assigning the return value to it in the valuation  represent s, where
represent s, where  where
where  such that the variable y has value x in either
such that the variable y has value x in either 

 ;
; ;
; ; two synchronized actions a and
; two synchronized actions a and  of the shuffle product where the two paths synchronize.
of the shuffle product where the two paths synchronize.


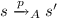 ;
; ;
; and
and  , then
, then  , where
, where  , where Id stands for the identity function;
, where Id stands for the identity function; with
with  , where
, where  such that
such that  , where
, where  ; the automaton represents two parallel processes
; the automaton represents two parallel processes  and
and 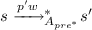 for
for  ;
; and
and  for
for  .
. , for each
, for each  , for each
, for each  , for each
, for each 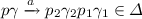 , for each
, for each 