Configurational Forces in a Phase Field Model for Dynamic Brittle Fracture

Abstract

In this work, the concept of configurational forces is proposed to enhance the post-processing of phase field simulations for dynamic brittle fracture. A local configurational force balance is derived by taking the gradient of the Lagrangian density of the phase field fracture problem. It is shown that the total configurational forces computed for a crack tip control volume are closely related to the Griffith criterion of classical fracture mechanics. Finally, the evaluation of the configurational within the finite element framework is demonstrated by two examples.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The numerical analysis of dynamic brittle fracture by so-called phase field models has gained attention in recent years, see e.g. Hofacker and Miehe [12], Borden et. al. [3], Steinke et al. [30], Li et al. [17] and Schlüter et al. [28, 29]. In phase field models for fracture, a scalar order parameter, the phase field, represents cracks in a continuous manner, i.e. there is a smooth transition zone in which the phase field varies from a value indicating undamaged material to another value that indicates completely broken material. Hence, the distribution of the phase field variable can be seen as a regularized approximation of the crack. Crack growth is governed by two coupled partial differential equations: the equation of motion and the phase field evolution equation. These are the Euler–Lagrange equations of Hamilton’s principle if, following Griffith’s [9] idea, the fracture energy is interpreted as a part of the potential energy. Phase field models for dynamic brittle fracture have been able to predict fracture phenomena like crack branching and intersonic fracture in good agreement with experiments and theoretical predictions, e.g. in Schlüter et al. [28], Borden et al. [3] and Li et al. [17]. However, often it is difficult to gain deeper insight into the computational results and some features of the computational results remain obscure.

The development of the concept of configurational forces on the other hand started with Eshelby’s pioneering work [7] and has since been extended and applied to various fields, see e.g. the textbooks of Gurtin [10], Kienzler and Herrmann [13] and Maugin [18, 19]. Configurational forces represent the change of potential energy of a body with respect to certain quantities that characterize the material configuration, i.e. the size and shape of cracks or the position of an inclusion. This energetic point of view of material changes links the concept of configurational forces to phase field models for fracture. Indeed, configurational forces in a phase field model for fracture have been studied in Kuhn and Müller [15], Kuhn [14] and Hakim and Karma [11] for the quasi-static case where inertia terms are neglected. In this case, the configurational force components acting on a crack tip are related to well-known quantities of fracture mechanics such as the path-independent ${\mathscr {J}}$-integral, see Rice [27], and the fracture resistance. In contrast to numerical strategies that rely on the configurational forces in order to model crack propagation such as in Miehe and Gürses [21] and Özenç et al. [25], the evaluation of the configurational forces is not a necessity in phase field fracture models. In the context of phase field fracture models, configurational forces should rather be understood as a post-processing tool that enhances the understanding of the simulations.

In this work, the idea to consider configurational forces for a phase field fracture model from Kuhn and Müller [15] is extended to the dynamic case. After a brief introduction of the employed phase field model for dynamic fracture, a configurational force balance is derived by considering the gradient of the Lagrangian of the fracture problem. This balance describes the energetic changes associated with a translation of a crack tip, i.e. crack growth, and is used to highlight the relation of the phase field model to the Griffith criterion of classical fracture mechanics. Lastly, two dynamic fracture problems are solved numerically. The analysis of the results relies on the computed configurational forces and reveals interesting features of the simulations.

2 A Phase Field Model for Dynamic Brittle Fracture

We consider a homogeneous body $\varOmega \subset \mathbb {R}^2$ with external boundary $\partial \varOmega$ that consists of linear elastic material with Lamé parameters $\lambda$ and $\upmu$ as well as mass density $\rho$. The speed of surface waves in this elastic medium, the Rayleigh wave speed, can be approximated by

$$\begin{aligned} c_r\approx {\dfrac{0.87+1.12\nu }{1+\nu }}\sqrt{\frac{\mu }{\rho }}, \end{aligned}$$

(1)

see Rahman and Michelitsch [26], where

$$\begin{aligned} \nu =2\dfrac{\lambda }{\lambda +\mu } \end{aligned}$$

(2)

is the Poisson’s ratio. The motion of the body is described in terms of the displacement field $\mathbf {u}\left( \mathbf {x},t\right) =u_1\mathbf {e}_1+u_2\mathbf {e}_1$, where $\mathbf {e}_1$ and $\mathbf {e}_2$ are the unit vectors in $x_1$- and $x_2$-direction of a cartesian coordinate system. Physical internal forces are represented by the Cauchy stress tensor . The fields have to satisfy Dirichlet boundary conditions

$$\begin{aligned} \mathbf {u}\left( \mathbf {x},t\right) ~=~\mathbf {u}^*\left( t\right) \end{aligned}$$

(3)

on $\partial \varOmega _{\mathbf {u}}$ and traction boundary conditions

(4)

on $\partial \varOmega _{\mathbf {t}}$, where $\mathbf {n}$ is the outward normal vector on the boundary $\partial \varOmega = \partial \varOmega _{\mathbf {u}}\cup \partial \varOmega _{\mathbf {t}}$. In addition, initial conditions

$$\begin{aligned} \mathbf {u}\left( \mathbf {x},t_0\right) =\mathbf {u}_0\left( \mathbf {x}\right) \end{aligned}$$

(5)

and

$$\begin{aligned} \dot{\mathbf {u}}\left( \mathbf {x},t_0\right) =\mathbf {v}_0\left( \mathbf {x}\right) , \end{aligned}$$

(6)

where $\dot{(*)}=\dfrac{\partial {(*)}}{\partial {t}}$ indicates the material time derivative, have to be provided. The linearized strain tensor

(7)

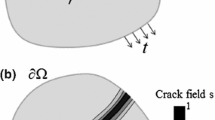
serves as a strain measure. Cracks are denoted as $\varGamma$, see Fig. 1a, and are approximated by an order parameter $s(\mathbf {x},t)\in \left[ 0,1\right]$ which varies continuously from $s=1$ in undamaged material to $s=0$ in fully broken material, as displayed in Fig. 1b. To be precise, the cracks $\varGamma$ are replaced by the zero set of s and the surface measure of $\varGamma$ is approximated by the crack surface density per unit volume which is formulated in terms of the order parameter

$$\begin{aligned} \gamma =\frac{(1-s)^2}{4{l}}+{l}{|\nabla {s}|}^2 \end{aligned}$$

(8)

as proposed in Bourdin [4]. The integral

$$\begin{aligned} \int _{\varOmega } \gamma \ \mathrm{d}V\end{aligned}$$

(9)

yields the surface measure of the crack set $\varGamma$. Initial cracks in the material are modelled by specifying initial conditions

$$\begin{aligned} s(\mathbf {x},t_0)=~0 \end{aligned}$$

(10)

for the order parameter. Following Griffith’s idea, the crack $\varGamma$ is associated with a fracture energy that is required to create the crack surface. The phase field is used to approximate this fracture energy in a regularized manner, i.e.

$$\begin{aligned} \int _{\varGamma }{{\mathscr {G}}_c \ \mathrm{d}A}\approx \int _{\varOmega }{ \psi ^{s}\mathrm{d}V}=E^{s}, \end{aligned}$$

(11)

where

$$\begin{aligned} \psi ^s={\mathscr {G}}_c\gamma \end{aligned}$$

(12)

is the fracture energy density per unit volume. The parameter ${\mathscr {G}}_c$ denotes the fracture resistance which is assumed to be a constant material parameter. The length-scale parameter l controls the width of the phase field approximated crack, i.e. an increase of l causes the width of the transition zone between broken and unbroken material to increase as well. It can be shown that the volume integral on the right-hand side of approximation (11) converges to the surface integral on the left-hand side if ${l}\rightarrow {0}$, as illustrated in Miehe et al. [23]. In order to model the degradation of stiffness in broken material, the phase field s is linked to the elastic energy of the body, i.e.

(13)

Fig. 1

a Fractured body with internal discontinuity (sharp crack) $\varGamma$ b and smooth representation of the crack by means of a phase field $s(\mathbf {x},t)$

where the strain energy density is given by

(14)

The strain energy density is decomposed in a crack driving part $\psi ^e_+$ that is affected by a degradation function g(s) and a part that is associated with compressive strain states $\psi ^e_-$. In the literature, there are several propositions to implement this decomposition, which all aim to prevent unphysical fracture behaviour in compressive load states. The model of Miehe et al. [22] proposes a split based on a spectral decomposition of whereas Strobl and Seelig [31] actually take the orientation of the phase field crack into account. The approach used in this work follows the publication of Amor et al. [1] and is based on a volumetric-deviatoric decomposition of the strain tensor . The degradation function g(s) models the loss of stiffness in broken material by reducing the strain energy accordingly, i.e. it has to satisfy $g(1)=1$ and $g(0)=0$. The compressive strain energy is not affected by g(s) which models the impenetrability of cracks during crack closure, i.e. no degradation of the compressive stress, see (16). In this work, the degradation function is chosen to be

$$\begin{aligned} g(s)=a(s^3-s^2)+3s^2-2s^3,\quad {\text {where}}\quad a=0.1 \end{aligned}$$

(15)

as proposed in Borden [2]. An additional consequence of leaving $\psi ^e_{-}$ unaffected by s is that crack growth is not driven by compressive load states, which becomes apparent in (23). The stress is

(16)

The kinetic energy of the body is assumed not to be affected by the phase field, i.e.

$$\begin{aligned} K(\dot{\mathbf {u}})=\int _{\varOmega }{k}\ \mathrm{d}V, \quad \text {where}\quad k=\dfrac{1}{2}\rho \dot{\mathbf {u}}\cdot \dot{\mathbf {u}}. \end{aligned}$$

(17)

Eventually, the dynamic fracture problem can be stated using Hamilton’s principle

$$\begin{aligned} \delta \int _{t_1}^{t_2} L\ \mathrm{d}t=0, \end{aligned}$$

(18)

for arbitrary times $t_1<t_2$. The Lagrangian is given by

$$\begin{aligned} L = \displaystyle \int _{\varOmega }{\mathscr {L}}\ \mathrm{d}V+P, \end{aligned}$$

(19)

where

$$\begin{aligned} P=\int _{\partial \varOmega _{\mathbf {t}}}{\mathbf {t}^*\cdot \mathbf {u}}\ \mathrm{d}A\end{aligned}$$

(20)

is the work of external forces - neglecting volume forces - acting on the boundary $\partial {\varOmega }_{\mathbf {t}}$ and

(21)

is the Lagrangian density per unit volume. The Euler–Lagrange equations following from (18) are the equation of motion

(22)

and the phase field equation

$$\begin{aligned} \begin{aligned} \dfrac{\partial {\psi }}{\partial {s}}-\text {div}\left( \dfrac{\partial {\psi }}{\partial \nabla {s}}\right) =0 \quad \Leftrightarrow \quad&g'(s)\psi ^{{e}}_{+}-{\mathscr {G}}_c\left[ 2{l}\Delta {s}+\frac{1-s}{2{l}}\right] =0, \end{aligned} \end{aligned}$$

(23)

with

$$\begin{aligned} \psi =\psi ^e+\psi ^s, \end{aligned}$$

(24)

as well as the traction boundary conditions

(25)

and the Neumann boundary conditions for the phase field

$$\begin{aligned} \begin{aligned} \nabla {s}\cdot \mathbf {n}=0\quad \text { on } \partial \varOmega . \end{aligned} \end{aligned}$$

(26)

The Dirichlet boundary conditions for the displacement field have to be specified as shown in (3) but do not follow directly from Hamilton’s principle. An additional constraint on the phase field s is necessary to impose the irreversibility of fracture. This is achieved by defining homogeneous Dirichlet boundary conditions

$$\begin{aligned} \begin{array}{ll} s(\mathbf {x},t>t^*_{\mathbf {x}}) = 0&\ \text { if }\ s(\mathbf {x},t^*_{\mathbf {x}})=0 \end{array} \end{aligned}$$

(27)

on the crack field. Herein, $t^*_{\mathbf {x}}$ is the time when the crack field becomes zero at the location $\mathbf {x}$ for the first time. The extension (27) allows for partial reversibility of the phase field because s is interpreted as an indicator field for cracks rather than a damage variable. Since only the zero set of s is interpreted as the crack, the extension (27) prevents unphysical crack healing. Details on the implementation in a finite element scheme can be found in Kuhn [14] whereas details on the interpretation of the phase field as a damage-like variable and the corresponding irreversibility constraint can be found in Miehe et al. [23].

3 Configurational Force Balance for a Phase Field Model for Dynamic Brittle Fracture

Crack growth corresponds to a translation of the crack tip with respect to its coordinates $\mathbf {z}$ in the reference configuration. As explained in Kienzler and Herrmann [13], a configurational force balance law that captures the energy change due to a translation of the considered defect, in our case the crack tip, can be found by taking the gradient of the Lagrangian density. In the phase field model, the evolution of the phase field is governed by the Lagrangian (19) but also by the irreversibility constraint (27). Thus, a configurational force balance law derived by taking the gradient of the Lagrangian density without incorporating the irreversibility constraint does only describe the fracture process as long as the load is high enough to sustain the cracks and the irreversibility constraint does not play a role. We still follow the gradient of the Lagrangian approach to derive the configurational force balance but discuss the neglected irreversibility condition as part of the interpretation of the computational results in Sect. 5. In order to determine the energetic driving force on a particular crack tip, the Lagrangian density ${\mathscr {L}}$ is considered to additionally be a function of the position of that crack tip $\mathbf {z}$ and the gradient

(28)

is computed. Employing Einstein’s summation convention and making use of the identities

$$\begin{aligned} \dfrac{{\partial \psi }}{\partial {s_{,i}}}{s_{,ik}}=\left( s_{,k}\dfrac{\partial {\psi }}{\partial {s_{,i}}}\right) _{,i}-\left( \dfrac{\partial \psi }{\partial {s_{,i}}}\right) _{,i}s_{,k} \end{aligned}$$

(29)

and

$$\begin{aligned} \dfrac{\partial {\psi }}{\partial {\varepsilon }_{ij}}\varepsilon _{ij,k}= \left( u_{j,k}\sigma _{ji}\right) _{,i}-u_{i,k}\sigma _{ij,j}\end{aligned}$$

(30)

the components of Eq. (28) can be rewritten as

$$\begin{aligned} \begin{aligned} -{\mathscr {L}}_{,k}=&\dfrac{\partial {\psi }}{\partial {s}}{s}_{,k}+\left( s_{,k}\dfrac{\partial {\psi }}{\partial {s_{,i}}}\right) _{,i}-\left( \dfrac{\partial \psi }{\partial {s_{,i}}}\right) _{,i}s_{,k}\\&+\left( u_{j,k}\sigma _{ji}\right) _{,i}-u_{i,k}\sigma _{ij,j}-\dfrac{\partial {k}}{\partial \dot{u}_i}\dot{u}_{i,k}-\dfrac{\partial {\mathscr {L}}}{\partial {z_i}}z_{i,k} \end{aligned} \end{aligned}$$

(31)

By means of the equation of motion (22), the evolution Eq. (23) and the definition of the linear momentum

$$\begin{aligned} \mathbf {p}=\dfrac{\partial {k}}{\partial {\dot{u}_{k}}}\mathbf {e}_k=\rho \dot{\mathbf {u}} \end{aligned}$$

(32)

we obtain

$$\begin{aligned} -\nabla {\mathscr {L}}=\left( \left( s_{,k}\dfrac{\partial {\psi }}{\partial {s_{,i}}}+u_{j,k}\sigma _{ji}\right) _{,i}-{u_{i,k}\dot{p}_{i}}-p_i\dot{u}_{i,k}-\dfrac{\partial {\mathscr {L}}}{\partial {z_i}}z_{i,k}\right) \mathbf {e}_k\end{aligned}$$

(33)

which with

$$\begin{aligned} -\nabla {\mathscr {L}}=-({\mathscr {L}}\delta _{ki})_{,i}\ \mathbf {e}_k,\quad \quad \quad \delta _{ij}={\left\{ \begin{array}{ll} 1\ \text {if}\ i=j\\ 0\ \text {else} \end{array}\right. } \quad \end{aligned}$$

(34)

can be recast in the form

$$\begin{aligned} \mathbf {g}=\text {div}{\mathsf {\Sigma }}-\dot{\varvec{\mathfrak p}}. \end{aligned}$$

(35)

Here, the configurational stress tensor

$$\begin{aligned} {\mathsf {\Sigma }}={\mathsf {\Sigma }}^{{e}}+{\mathsf {\Sigma }}^{{s}} \end{aligned}$$

(36)

consisting of the dynamic Eshelby stress tensor or elastic part of the configurational stress tensor

$$\begin{aligned} {\mathsf {\Sigma }}^e=\left( {\left( \psi ^e-k\right) }\delta _{ij}-u_{k,i}\sigma _{kj}\right) \mathbf {e}_i\otimes \mathbf {e}_j, \end{aligned}$$

(37)

and the cohesive configurational stress tensor

$$\begin{aligned} {\mathsf {\Sigma }}^s=\left( \psi ^s\delta _{ij}-s_{,i}\dfrac{\partial {\psi }}{\partial {s_{,j}}}\right) \mathbf {e}_i\otimes \mathbf {e}_j\end{aligned}$$

(38)

has been introduced. The symbol “$\otimes$” denotes the dyadic product. The expression

$$\begin{aligned} {\varvec{\mathfrak p}}=-u_{i,k}p_i\ \mathbf {e}_k=-\left( \text {grad}\mathbf {u}\right) ^T\mathbf {p} \end{aligned}$$

(39)

denotes the so-called pseudo-momentum, see e.g. Maugin and Trimarco [20], whereas the quantity

$$\begin{aligned} \mathbf {g}=-z_{i,k}\dfrac{\partial {\mathscr {L}}}{\partial {z_i}}\mathbf {e}_k \end{aligned}$$

(40)

is the local contribution of the state at $\mathbf {x}$ to the energetic driving force that acts on the crack tip $\mathbf {z}$. Alternatively, $\mathbf {g}$ might be interpreted as a measure of the change of ${\mathscr {L}}$ at $\mathbf {x}$ due to an infinitesimally small translation of the crack tip $\mathbf {z}$. By integration over a subdomain R of $\varOmega$, a global form of the configurational force balance

$$\begin{aligned} \begin{aligned} \underbrace{\int _{R}\mathbf {g}\ \mathrm{d}V}_{\mathbf {G}_R}&=\underbrace{\int _{R}\text {div}{\mathsf {\Sigma }}^e\ \mathrm{d}V}_{\mathbf {G}^e_R}+\underbrace{\int _{R}\text {div}{\mathsf {\Sigma }}^s\ \mathrm{d}V}_{\mathbf {G}^s_R}-\underbrace{\int _{R} \dot{\varvec{\mathfrak {p}}}\ \mathrm{d}V}_{-\varvec{\mathfrak {P}}_R},\\ \mathbf {G}_R&=\mathbf {G}^e_R+\mathbf {G}^s_R+{\varvec{\mathfrak {P}}}_R \end{aligned} \end{aligned}$$

(41)

is obtained. In contrast to $\mathbf {g}$, the quantity $\mathbf {G}_R$ represents the resulting configurational force on $\mathbf {z}$ of the states of all $\mathbf {x}$ inside R.

4 Discussion of the Configurational Force Balance

In this section, the configurational force balances that were established in the previous section are discussed. In particular, their role as a means to highlight the connection between phase models for dynamic brittle fracture and Griffith’s description of brittle fracture in the framework of dynamic linear elastic fracture mechanics (LEFM) is explained.

To this end, we consider a LEFM model of the crack tip and the region surrounding it, see Fig. 2a as well as the corresponding phase field representation, see Fig. 2b. In order to evaluate the relevant energetic driving forces on a particular crack tip, suitable control volumes should at least contain all particles that constitute the near tip region and no other crack tip. Hence, a disc with radius $\delta$ that is centered around the crack tip $\mathbf {z}$

$$\begin{aligned} D_{\delta }(t)=\{\mathbf {x}(t)\in \varOmega :\left||\mathbf {x}(t)-\mathbf {z}(t)\right||\le {\delta }\} \end{aligned}$$

(42)

is chosen as a control volume for the phase field problem and a $\xi$-$\eta$-coordinate system is introduced where $\mathbf {e}_{\xi }$ is tangential to the crack path at $\mathbf {z}$. The control volume for the respective LEFM problem, is bounded by the contour $\partial {D}_{\delta }'$ and the crack faces as displayed in Fig. 2a. Presume that

Fig. 2

a Crack tip region of a problem formulated in the framework of linear elastic fracture mechanics (LEFM) and b the associated phase field representation of the crack tip region

• A: the boundary conditions at the crack faces are adequately modeled by (14).

In that case,

• B: the displacements $\mathbf {u}$ in $D_{\delta }$ but outside the subset $R_s\subset {D}_{\delta }$ where the phase field is significantly different from $s=1$ are assumed to be a good approximation of the displacements $\mathbf {u}'$ that are obtained for the otherwise identical problem formulated in the framework of dynamic linear elastic fracture mechanics, see Fig. 1 a. The size of $R_{s}$ depends on the length-scale parameter l which is assumed to be small compared to $\delta$. Consequently, it is also $\partial {D_{\delta ,A\rightarrow {B}}}\approx {\partial {D}_{\delta }}$.

Assumption B is motivated by the proofs of $\varGamma$-convergence for the quasi-static phase field model, e.g. in Chambolle [5] which establish a link between the global energies and their minimizers obtained in a free-discontinuity model on the one hand and a phase field model on the other hand. Furthermore, we choose

• C: $D_{\delta }$ to be small enough compared to a typical length-scale L of the problem to ensure that the fields on $\partial {D}_{\delta }\setminus \partial {D}_{\delta ,B\rightarrow {A}}$ and $\partial {D}_{\delta }'$ are the universal crack tip fields known from linear elastic fracture mechanics.

Addtionally,

• D: it is assumed that the fields in ${D}_{\delta }$ are smooth enough to allow the gradient and divergence operations.

Assumption C justifies that for any fields $\phi \left( \mathbf {x},t\right)$ that show high gradients in the near-tip region the "transport condition of the singularity" assumption

• E:
  $$\begin{aligned} \dfrac{\partial {\phi }}{\partial {t}}\approx -\nabla {\phi }\cdot \mathbf {v}, \end{aligned}$$

  (43)

with the crack tip velocity

$$\begin{aligned} \mathbf {v}=\dfrac{\mathrm{d}}{\mathbf {z}}{\mathrm{d}t} \end{aligned}$$

(44)

is made, see Ehrlacher [6]. In particular,

$$\begin{aligned} -\dot{\mathbf {u}}\approx \left( \text {grad}\mathbf {u}\right) \mathbf {v}\quad \text {and}\quad -\ddot{\mathbf {u}}\approx \left( \text {grad}\dot{\mathbf {u}}\right) \mathbf {v} \end{aligned}$$

(45)

is used which also implies

$$\begin{aligned} \dot{k}=\rho \ddot{\mathbf {u}}\cdot \dot{\mathbf {u}}\approx -\nabla {k}\cdot {\mathbf {v}}. \end{aligned}$$

(46)

In order to find out how the configurational force balances relate to the energy release rate known from dynamic linear elastic fracture mechanics, the working of the dynamic Eshelby stress tensor and the pseudo-momentum on $D_{\delta }$ are considered. With the definition of the dynamic Eshelby stress tensor (37), of the pseudo-momentum (39), the divergence theorem, the symmetry of the stress tensor, the fact that $\mathbf {v}$ is constant in $D_{\delta }$, (45) and (46)$_1$ we obtain

(47)

Application of the gradient theorem to the kinetic energy density

$$\begin{aligned} \int _{D_{\delta }} \nabla {k}\ \mathrm{d}V= \int _{\partial {D}_{\delta }} {k}\mathbf {n}_{\delta } {\ } \mathrm{d}A, \end{aligned}$$

(48)

taking the dot product with $\mathbf {v}$ on both sides and using (46) results in

$$\begin{aligned} \int _{D_{\delta }}\dot{k}\ \mathrm{d}V\approx -\int _{\partial {D_{\delta }}}{k}\mathbf {n}_{\delta }\ \mathrm{d}A\cdot \mathbf {v}. \end{aligned}$$

(49)

Thus, we obtain from (47) and (49)

(50)

Division by the absolute value of the crack tip velocity v and making use of $\mathbf {v}\approx {v}\mathbf {e}_{\xi }$ yields

(51)

From assumptions B it follows that

(52)

where the boundary is split into two segments $\partial {D}_{\delta ,A\rightarrow {B}}$ and $\partial {D}_{\delta ,B\rightarrow {A}}$, see Fig. 2b. Herein, ($\cdot$)$'$ marks the respective quantities obtained in the otherwise identical problem formulated in the framework of linear elastic fracture mechanics. Presuming that the tip domain is indeed small, see assumption C, the integrals in (52) are path-independent and the dynamic energy release rate is

(53)

e.g. see Freund [8]. By means of (53) and the relations (51) and (52) we eventually obtain a link between the configurational forces in the phase field model and quantities from classical fracture mechanics as

$$\begin{aligned} {\mathscr {G}}\approx \left( \mathbf {G}^e_{D_{\delta }}+\varvec{\mathfrak {P}_{D_{\delta }}}\right) \cdot \mathbf {e}_{\xi }. \end{aligned}$$

(54)

In order to obtain an interpretation of the cohesive configurational stress the procedure described in Kuhn [14] is followed. Firstly, the divergence theorem is applied to the second term on the right-hand side of (41), i.e.

$$\begin{aligned} \mathbf {G}^s_{D_{\delta }}=\int _{D_{\delta }}\text {div}{\mathsf {\Sigma }}^s\ \mathrm{d}V=\int _{\partial {D}_{\delta }}{\mathsf {\Sigma }}^s\mathbf {n}_{\delta }\ \mathrm{d}A=\int _{\partial {D}_{\delta ,A\rightarrow {B}}}{\mathsf {\Sigma }}^s\mathbf {n}_{\delta }\ \mathrm{d}A+ \int _{\partial {D}_{\delta ,B\rightarrow {A}}}{\mathsf {\Sigma }}^s\mathbf {n}_{\delta }\ \mathrm{d}A. \end{aligned}$$

(55)

On the first segment $\left. {\mathsf {\Sigma }}^s\right| _{\partial {D}_{\delta ,A\rightarrow {B}}}=\mathbf {0}$ since $s\equiv {1}$. If the second segment is sufficiently far away from the crack tip, i.e. assumption B is fulfilled and the crack is straight inside $D_{\delta }$, it is reasonable to assume that the phase field has the same shape in $\eta$-direction as the 1D solution derived in Kuhn  [14],

$$\begin{aligned} \left. s(x_1,x_2)\right| _{\partial {D}_{\delta ,B\rightarrow {A}}}=1-\exp \left( -\dfrac{\left|\eta \right|}{2l}\right) . \end{aligned}$$

(56)

Thus, it is

$$\begin{aligned} \left. {\mathsf {\Sigma }}^s\right| _{\partial {D}_{\delta ,B\rightarrow {A}}}=\left( \begin{matrix} \psi ^s &{} 0 \\ 0 &{} 0 \end{matrix} \right) \end{aligned}$$

(57)

with

$$\begin{aligned} \psi ^s=\dfrac{{\mathscr {G}}_c}{2{l}}\exp \left( -\dfrac{\left|\eta \right|}{l}\right) . \end{aligned}$$

(58)

Eventually these considerations yield

$$\begin{aligned} \mathbf {G}^s_{D_{\delta }}=\int _{\partial {D}_{\delta ,B\rightarrow {A}}}{\mathsf {\Sigma }}^s\mathbf {n}\ \mathrm{d}A= \int _{\partial {D}_{\delta ,B\rightarrow {A}}}\left( \begin{matrix} -\psi ^s\\ 0 \end{matrix} \right) \mathrm{d}{\eta }=\left( \begin{matrix} -{\mathscr {G}}_c\\ 0 \end{matrix} \right) =-{\mathscr {G}}_c\mathbf {e}_{\xi }. \end{aligned}$$

(59)

Hence, with (54), (59) and (41) we find that the configurational force balance applied to an appropriately small crack tip disc $D_{\delta }$ in the form

$$\begin{aligned} \mathbf {G}_{D_{\delta }}\cdot \mathbf {e}_{\xi }=\left( \mathbf {G}^e_{D_{\delta }}+\varvec{\mathfrak {P}_{D_{\delta }}}+\mathbf {G}^s_{D_{\delta }}\right) \cdot \mathbf {e}_{\xi }=0 \end{aligned}$$

(60)

is closely related to the Griffith condition for stable crack growth

$$\begin{aligned} \quad {\mathscr {G}}={\mathscr {G}}_c. \end{aligned}$$

(61)

The Griffith condition is fulfilled if $\mathbf {G}_{D_{\delta }}=\mathbf {0}$, i.e. the crack driving forces $\mathbf {G}^e_{D_{\delta }}+\varvec{\mathfrak {P}_{D_{\delta }}}$ balance the cohesive configurational force $\mathbf {G}^s_{D_{\delta }}$.

In order to judge whether the size of the control volume $D_{\delta }$ is chosen large enough in order to comply with assumption B, we consider a second tip disc control volume R with radius $\delta _{R}>\delta$ and a third control volume $R_{\delta }=R\setminus {D_{\delta }}$ that does not include the crack tip, any other crack tip nor the regions dominated by the stress concentrations surrounding them. It is

$$\begin{aligned} \displaystyle \int _{R} \left( \varvec{\text {div}\varSigma }^e-\dot{\varvec{\mathfrak {p}}}\right) \ \mathrm{d}V= \displaystyle \int _{R_{\delta }} \left( \varvec{\text {div}\varSigma }^e-\dot{\varvec{\mathfrak {p}}}\right) \ \mathrm{d}V+ \displaystyle \int _{D_{\delta }} \left( \text {div}\varvec{\varSigma }^e-\dot{\varvec{\mathfrak {p}}}\right) \ \mathrm{d}V. \end{aligned}$$

(62)

The integral $\int _{R_{\delta }} \left( \varvec{\text {div}\varSigma }^e-\dot{\varvec{\mathfrak {p}}}\right) \ \mathrm{d}V$ represents the crack-extending energetic driving force on $\mathbf {z}$ that results from the states of all $\mathbf {x}$ inside $R_{\delta }$, see (41). Since no stress concentration is located in $R_{\delta }$, it is

$$\begin{aligned} \left|\displaystyle \int _{R_{\delta }} \left( \text {div}{{\mathsf {\Sigma }}}^e-\dot{\varvec{\mathfrak {p}}}\right) \ \mathrm{d}V\right| \ll \left|\displaystyle \int _{D_{\delta }} \left( {\text {div}{\mathsf {\Sigma }}}^e-\dot{\varvec{\mathfrak {p}}}\right) \ \mathrm{d}V\right|. \end{aligned}$$

(63)

From (62) it follows

$$\begin{aligned} \displaystyle \int _{R} \left( \text {div}{{\mathsf {\Sigma }}}^e-\dot{\varvec{\mathfrak {p}}}\right) \ \mathrm{d}V\approx \displaystyle \int _{D_{\delta }} \left( \text {div}{{\mathsf {\Sigma }}}^e-\dot{\varvec{\mathfrak {p}}}\right) \ \mathrm{d}V. \end{aligned}$$

(64)

Equation (64) implies that the value of the above integral is insensitive to a further increase of the size of the control volume if the crack tip field is sufficiently contained in $D_{\delta }$. Hence, $\delta$ is chosen large enough, if (64) is fulfilled for $\delta _R>\delta$.

By taking the dot product with $\mathbf {e}_{\xi }$ on both sides of (64), we obtain by means of (54)

$$\begin{aligned} {\mathscr {G}}\approx \displaystyle \int _{R} \left( \text {div}{{\mathsf {\Sigma }}}^e-\dot{\varvec{\mathfrak {p}}}\right) \ \mathrm{d}V\cdot \mathbf {e}_{\xi } \end{aligned}$$

(65)

Relation (59) holds for larger control volumes as well as long as the crack is straight and aligned with $\mathbf {e}_{\xi }$. Hence, under these conditions, the configurational force balance in the form (60) can be applied to a large control volume and still be related to the Griffith condition (61).

5 Numerical Examples

In order to demonstrate the significance of the derived configurational force balances for the analysis of phase field simulations of fracture, two numerical experiments are performed. The set of coupled Eqs. (22) and (23) is solved by a finite element scheme with bilinear shape functions, implicit time integration and automatic step size control, see Schlüter et al. [29] for details. The degradation function used in Schlüter et al. [29] differs from the general cubic formulation used in this work, which may raise the question whether this variation has any consequences for the numerical solution strategy. Indeed, in Kuhn et al. [16] a monolithic finite element scheme with bilinear shape functions proved to have difficulties predicting crack nucleation in previously undamaged material if a degradation function of the type (15) with $a=0$ was used. However, these difficulties are removed for $a>0$. Furthermore, crack nucleation in pristine material is not considered in this work. Consequently, the chosen numerical solution strategy is assumed to be suitable for the presented problems. The computation of the configurational forces within the finite element framework is explained in Müller et al. [24], Kuhn and Müller [15] and Kuhn [14].

Fig. 3

a Phase field s (contour), domain $D_{\delta }$ (circle), total configurational force $\underline{\mathbf {G}}_{D_{\delta }}$ in the unloaded state (arrow). b Applied load $u^*$ and crack speed v (solid lines), Rayleigh wave speed (dashed line) and the point in time (black circle) at which the convergence study displayed in Fig. 4a is performed

Fig. 4

a configurational force components evaluated at time for different radii of the control volume. b $\xi$-components of the configurational forces for a tip disc control volume with a radius of $\delta =20l$, see also the vertical black line in Fig. 4a, period of crack growth (grey area) and point in time at which Fig. 4a is recorded (vertical black line)

5.1 Crack Arrest

To begin with, a tension-loaded specimen with an initial crack as depicted in Fig. 3a is considered. The length-scale parameter is set to $l=0.02L$ and the element size h of the regular mesh is small enough to resolve the phase field crack properly, i.e. $h=2l$. The Lamé parameters of the material are $\lambda =\upmu$, i.e. the Poisson’s ratio is $\nu =\frac{1}{4}$. The applied displacement, $\mathbf {u}^*(t)=\pm \ {u}^*(t)\ \mathbf {e}_2$, is controlled such that after initial crack growth in $x_1$-direction - with crack speeds of around half the Rayleigh wave speed $c_r$- the crack arrests and the velocity drops to zero, see the magenta line in Fig. 3b. The maximum applied displacement is $u_{max}=0.8$  which causes the crack to extend from its initial size of 0.5L to its final length of 1.53L. The crack speed is calculated from a post-processing regression analysis of a series of subsequent crack tip positions. Herein, the current crack tip position $\mathbf {z}(t)$ is identified with the position of the node I that is the most advanced on the crack path and fullfills $s_I=0$. Subsequently, a polynomial is fitted to this discrete representation of the crack tip location in order to get a smoothed representation of the crack tip position as a function of t

$$\begin{aligned} \tilde{\mathbf {z}}(t)\approx \mathbf {z}(t), \end{aligned}$$

(66)

which allows to compute the crack speed as

$$\begin{aligned} \mathbf {v}={\dot{\tilde{\mathbf {z}}}} \end{aligned}$$

(67)

and the tangential vector as

$$\begin{aligned} \mathbf {e}_{\xi }=\dfrac{\mathbf {v}}{\left|\mathbf {v}\right|}, \end{aligned}$$

(68)

see also Fig. 6a.

Figure 4a shows the $\xi$-component of the configurational forces $\underline{G}^e_{\xi }+\underline{\mathfrak {P}}_{\xi }$, $\underline{G}^s_{\xi }$ and $\underline{G}_{\xi }$ evaluated at time for different sizes of the tip control volume. The index $(*)_{D_{\delta }}$ is skipped for clarity from this point on, whereas the underbar notation indicates that the respective quantities are evaluated numerically. It can be observed that control volumes with a radius smaller than $\delta =10l$ do not yield converged values of the configurational force components $\underline{G}^e_{\xi }+\underline{\mathfrak {P}}_{\xi }$ and $\underline{G}^s_{\xi }$. In this case, the tip disc is too small compared to l to include the near tip stress field or to evaluate the cohesive fracture resistance force correctly. Thus, assumption B, see the previous chapter, is violated and the computed configurational forces cannot be related in any way to the energy release rate ${\mathscr {G}}$ or the fracture resistance ${\mathscr {G}}_c$. Larger control volumes however approve that - apart from a slight overestimation of the cohesive configurational force which is typical for finite element discretizations of phase field models for fracture, see e.g. Kuhn [14] and Borden [2] - the cohesive force is $\underline{G}^s_{\xi }\approx -{\mathscr {G}}_c$. Thus, the cohesive configurational force $\underline{G}^s_{\xi }$ represents the materials resistance to crack propagation in accordance with (59). The part $\underline{G}^e_{\xi }+\underline{\mathfrak {P}}_{\xi }$ on the other hand is the crack driving component which counteracts the cohesive force $\underline{G}^s_{\xi }$. For all control volumes, the total tip configurational force is $\underline{G}_{\xi }\approx {0}$, which underlines the phase field model’s connection to the Griffith condition (61). The crack tip control volume needs to be chosen large enough such that $\underline{\mathbf {G}}^e+\varvec{\underline{\mathfrak {P}}}$ is insensitive to a further increase of the radius $\delta$, see (63). As can be observed in Fig. 4 a this is fulfilled for a size of at least $\delta =10{l}$. For further analysis, we choose $\delta =20l$ in this example, see also the vertical black line in Fig. 4a.

Figure 4b shows records of the configurational forces with respect to time for a control volume of size $\delta =20\,l$. Initially, only the cohesive configurational force is non-zero and its $\xi$-component agrees well with ${\mathscr {G}}_c$ as mentioned above. Over the course of the simulation this does not change significantly, except for a slight increase of $\vert {\underline{G}_{\xi }^s}\vert$ well before crack initiation. The elastic component of the configurational force $\underline{G}^e_{\xi }$ is the crack driving force. It is controlled by the applied displacement load, see also Fig. 3b, and decreases as soon as the displacement load is reduced. Inertial effects are present even before crack initiation at time which becomes apparent in the nonzero pseudo-momentum $\underline{\mathfrak {P}}_{\xi }$. However, up to crack initiation $\underline{\mathfrak {P}}_{\xi }$ oscillates around zero and only shows a clear trend to negative values during the period of crack propagation where it reaches peak values of around $-0.5{\mathscr {G}}_c$. Thus, in this stage of the simulation $\underline{\mathfrak {P}}_{\xi }$ represents a resistance to crack propagation which is in contrast to $\underline{G}^s_{\xi }$ due to inertial effects and not due to the cohesion of material particles. Note that the Griffith condition $\underline{G}_{\xi }\approx 0$ is fulfilled during crack growth. In the last stages of crack growth, i.e. for , positive values of $\underline{\mathfrak {P}}_{\xi }$ can be observed which imply a crack driving inertial force. It can be concluded that there is an inertial resistance to crack deceleration that keeps the crack growing although $\underline{G}_{\xi }^e$ does not provide a sufficiently large crack driving force anymore to overcome the material resistance $\underline{G}^s_{\xi }$. Eventually, $\underline{G}^e_{\xi }$ drops to the point that the Griffith condition is no longer satisfied and the crack stops. Initially, the total configurational force is $\underline{G}_{\xi } \approx - {\mathscr {G}}_c$, since the crack tip is unloaded and thus $\underline{G}_{\xi }^e=0$ and $\underline{\mathfrak {P}}_{\xi }=0$ but the material’s resistance  $\underline{G}_{\xi }^s=-{\mathscr {G}}_c$ is non-zero. A negative $\xi$-component of the total configurational force implies that the resulting energetic driving force on the crack tip favors a recession of the crack, i.e. crack healing. Hence, an according evolution of the order parameter should take place in this subcritical load state. However, such an evolution of s is prevented by the irreversibility constraint (27). The irreversibility constraint counteracts the crack closing energetic driving force $\underline{G}_{\xi }^s$ in subcritical load states but - since the antagonistic irreversibility force is not accounted for in the configurational force balances (35) and (41) - $\underline{G}_{\xi }\approx -{\mathscr {G}}_c$ follows.

This example demonstrates the main character of the different components of the crack tip configurational force. The elastic part $\underline{G}^e_{\xi }$ is the crack driving energetic force, whereas $\underline{G}^s_{\xi }$ and $\underline{\mathfrak {P}}_{\xi }$ represent the material’s and the inertial resistance to crack propagation. During crack deceleration the inertial forces may also play a crack driving role, i.e. $\underline{\mathfrak {P}}_{\xi }>0$. The fact that $\underline{G}_{\xi }\approx {0}$ during crack propagation highlights the connection of the phase field model to Griffith’s description of crack growth. Furthermore, it is found that states at which $\underline{G}_{\xi }<0$ have to be interpreted as subcritical load states where the irreversibility constraint (27) comes into effect. Additionally, it is observed that the size of the control volume needs to be large enough compared to the length-scale parameter l in order to yield useful results, e.g. $\delta >20l$. Above this critical size, the configurational force components $\underline{G}^e_{\xi }+\underline{\mathfrak {P}}_{\xi }$, $\underline{G}^s_{\xi }$ and $\underline{G}_{\xi }$ are insensitive to a further increase of the size of the control volume.

5.2 Branching

In this section, the concept of configurational forces is employed to study dynamic crack branching in the phase field model. A body with an initial crack as displayed in Fig. 5a is considered. The Lamé parameters of the material are $\lambda =\upmu$, i.e. $\nu =1/4$. Again, a regular mesh with an element size of $h=2\,l$ is used where the length-scale parameter is set to $l=0.005\,L$. The traction load $\mathbf {t}^*=\pm {t}^*\mathbf {e}_2$ is increased linearly to its maximum value of and afterwards held constant, see Fig. 5b. The crack originally propagates in $x_1$-direction and eventually branches, see the crack pattern displayed in Fig. 6a. It is not possible to unambiguously identify the moment of branching since the diffuse phase field representation of the crack surface does not allow to identify distinct crack tips in the very early stages of the branching process. Instead, branching is announced by a period A of crack widening and the formation of bulges indicating the directional instability of the crack, see Fig. 6b. Subsequently, pronounced bulging of the crack tip initiates crack branching and eventually two distinct crack tips can be identified. This branching period is denoted as B and lasts from to , see also Figs. 5b and 6b.

Fig. 5

a Setup for the branching problem and b crack speed v and applied traction load $t^*$. The period of crack branching B is indicated by the grey region

Fig. 6

a representation of the crack pattern by successive crack tip positions $\tilde{\mathbf {z}}$ (black lines), tangential vectors $\mathbf {e}_{\xi }$ for the lower (blue arrows) and upper (red arrows) branch, illustration of the $\xi$-$\eta$-coordinate system. b $\xi$-components of the configurational forces for a tip disc control volume with a radius of $\delta =15l$ (thin lines) and corresponding moving average filtered data (thick lines). The stages of branching A, B, C are indicated by regions of different shades of grey

Fig. 7

Configurational force components for different radii of the tip disc: a the elastic part $\underline{G}^e_{\xi }$ (red) and the pseudo-momentum $\underline{\mathfrak {P}}_{\xi }$ (green), b the sum of the elastic part and the pseudo-momentum $\underline{G}^e_{\xi }+\underline{\mathfrak {P}}_{\xi }$, c the cohesive configurational force $\underline{G}^s_{\xi }$ and d the total configurational force $\underline{G}_{\xi }$. The branching period B is indicated by the grey region

The crack speed - recorded for the lower branch - reaches its maximum value of $v\approx 0.56 c_r$ right after branching occurs, see the magenta line in Fig. 5b. The configurational force components acting on a control volume of size $\delta =15l$ are displayed in Fig. 6b. In addition to the computed data (thin lines) the corresponding moving average filtered data sets (thick lines) are plotted. The filtered data corresponds to the unweighted mean of the data of the last 30 time steps and the resulting lag is corrected. This post-processing step is necessary to make the strongly oscillating configurational forces more accessible to interpretation. After this smoothing step it becomes obvious that the main characteristics of the configurational force components from the previous numerical example remain the same. Again, $\underline{G}^e_{\xi }>0$ is the crack driving force whereas $\underline{G}^s_{\xi }<0$ and $\underline{\mathfrak {P}}_{\xi }<0$ represent the material and inertial resistance to crack propagation. In contrast to the previous example however, the total configurational force acting on the crack tip is slightly larger than zero in the phase of notable crack widening A, and shows peak averaged values of around $\underline{G}_{\xi }\approx 1.0 \ {\mathscr {G}}_c$ during crack branching, i.e. phase B. This suggests that the crack driving force exceeds the inertial and material resistance and thus, an additional crack tip is formed to transform sufficient amounts of energy. Period C that lasts from to denotes the period where branching already took place but the two crack tips are still located in $D_{15l}$. In this phase, domain independence of $\underline{G}^e_{\xi }+\underline{\mathfrak {P}}_{\xi }$, i.e. (63), is not valid since more than one stress concentration is contained in $D_{15l}$. Note that the cohesive configurational force $\underline{G}^s_{\xi }$ peaks significantly later than $\underline{G}_{\xi }$, i.e. at the end of C, driving the total configurational force $\underline{G}_{\xi }$ back to zero. The absolute values of the inertial configurational force before branching of $\vert \underline{\mathfrak {P}}_{\xi }\vert >1.0 {\mathscr {G}}_c$ exceed the maximum values of the previous, non-branching example.

The various components of the tip configurational force are displayed in Fig. 7 for different sizes of the crack tip control volume ranging from $\delta =10l$ to $\delta =20l$. As expected, the elastic configurational force $\underline{G}^e_{\xi }$ and the pseudo-momentum $\underline{\mathfrak {P}}_{\xi }$ for themselves are clearly dependent on the size of the control volume, since their graphs (quantitatively) vary significantly for different $\delta$, see Fig. 7a. The sum $\underline{G}^e_{\xi } + \underline{\mathfrak {P}}_{\xi }$, plotted in Fig. 7b, on the other hand is less sensitive to the size of the control volume, which is in good agreement with the considerations that led to (63), see Fig. 7b. A significant difference in the graphs of $\underline{G}^e_{\xi } + \underline{\mathfrak {P}}_{\xi }$ can however be noted directly after crack branching. This is due to the fact that the second crack tip may still be contained in a larger control volume while it is not located in a smaller control volume anymore. The quantity $\underline{G}^e_{\xi } + \underline{\mathfrak {P}}_{\xi }$ corresponds to the dynamic energy release rate, see (65), and reaches values larger than $1.3\ {\mathscr {G}}_c$ with an increasing tendency prior to branching and $\sim 2.0\ {\mathscr {G}}_c$ during the period of crack branching B.

The cohesive configurational forces show pronounced peak values. Their magnitude as well as the time of their occurrence is clearly dependent on $\delta$, see Fig. 7c. The peak occurs right before the second crack tip exits the respective control volume, i.e. at the end of period C, and is thus delayed for larger control volumes. Larger control volumes also contain a larger part of the second crack (tip) and hence the absolute value of $\underline{G}^s_{\xi }$ is larger as well. Apart from these features, the cohesive configurational force provides a resistance to crack propagation slightly larger than ${\mathscr {G}}_c$ as explained in the previous example.

The total configurational force $\underline{G}_{\xi }$ also shows a low sensitivity on $\delta$. All graphs in Fig. 7d have a significant peak during crack branching in common. Its magnitude ranges from $\underline{G}_{\xi }\approx {0.7}{\mathscr {G}}_c$ for $\delta =10\,l$ to $\underline{G}_{\xi }\approx {1.0}{\mathscr {G}}_c$ for $\delta =20\,l$. In contrast to the crack arrest simulation however, $\underline{G}_{\xi }$ is slightly larger than zero before and after crack branching. Consequently, the Griffith condition (61) is not perfectly fulfilled but the crack driving force exceeds the cohesive material resistance.

The evaluation of the configurational forces in this numerical example suggest that a critical energy release rate ${\mathscr {G}}\approx \underline{G}^e_{\xi } + \underline{\mathfrak {P}}_{\xi }$ and total configurational force $\underline{G}_{\xi }$ go along with dynamic crack branching. Furthermore, it shows that the energy release rate ${\mathscr {G}}\approx \underline{G}^e_{\xi } + \underline{\mathfrak {P}}_{\xi }$, the cohesive configurational force $\underline{G}^s_{\xi }$ and the total configurational force $\underline{G}_{\xi }$ are less sensitive to the size of the crack tip control volume than $\underline{G}^e_{\xi }$ and $\underline{\mathfrak {P}}_{\xi }$, which is in good agreement with the considerations made in Sect. 4.

6 Conclusions

In this work, the concept of configurational forces is proposed to enhance the post-processing and the interpretation of the results of phase field simulations for dynamic brittle fracture. A local configurational force balance is derived by taking the gradient of the Lagrangian density of the phase field fracture problem. It is shown that the total configurational forces computed for a crack tip control volume are closely related to the Griffith criterion of classical fracture mechanics.

The relevance of the configurational forces as a post-processing tool for dynamic phase field simulations is illustrated by means of two examples. The first example deals with a crack arrest scenario, where an initially fast growing crack stops again. Here, the inertial resistance to crack propagation at high crack speeds can be visualized by considering the pseudo-momentum of the crack tip. Furthermore, the connection to the Griffith criterion is established by noting that the total configurational force tangential to the direction of crack growth is approximately zero during crack propagation. The second numerical example deals with the phenomenon of dynamic crack branching. In this case, configurational forces yield interesting insights in the simulations. Right before branching, the absolute value of the crack driving configurational force exceeds the resistant cohesive configurational force by a factor of around two. This indicates that an additional crack tip needs to be nucleated in order to match the energy flux to the crack tip with the energy that can be dissipated during the creation of the new fracture surface. Furthermore, the observation of these critical values of the crack driving force enable the identification of crack branching even before two distinct crack tips can be observed in contour plots of the phase field variable.

It is concluded that the concept of configurational forces is indeed helpful to reveal features of phase field simulations for dynamic brittle fracture. Furthermore, the decomposition of the configurational force acting on a phase field crack tip and the interpretation of its components highlight the relation of the model to Griffith’s energetic description of brittle fracture.