Comparing MapReduce-Based k-NN Similarity Joins on Hadoop for High-Dimensional Data

Abstract

Similarity joins represent a useful operator for data mining, data analysis and data exploration applications. With the exponential growth of data to be analyzed, distributed approaches like MapReduce are required. So far, the state-of-the-art similarity join approaches based on MapReduce mainly focused on the processing of vector data with less than one hundred dimensions. In this paper, we revisit and investigate the performance of different MapReduce-based approximate k-NN similarity join approaches on Apache Hadoop for large volumes of high-dimensional vector data.

1 Introduction

The k-NN similarity joins serve as a powerful tool in many domains. In the data mining and machine learning context, k-NN joins can be employed as a preprocessing step for classification or cluster analysis. In data exploration and information retrieval, similarity joins provide a similarity graph with the most relevant entities for each object in the database. Their applications can be found for example in the image and video retrieval domain [6, 7], and in network communication analysis and malware detection frameworks [2, 10]. Because data volumes are often too large to be processed on a single machine (especially for high-dimensional data), we study the use of the distributed MapReduce environment [5] on Hadoop¹. Hadoop MapReduce is a widely adopted technology and considered an efficient and scalable solution for distributed big data processing.

Related papers [8, 14, 15] have deeply analyzed advantages, disadvantages and bottlenecks of distributed MapReduce systems Hadoop and Spark². [21]. In this paper, we study similarity join algorithms that were designed and implemented on Apache Hadoop. The comparison considers methods employing data organization/replication strategies initialized randomly as they enable convenient application and usage on different domains. Although a study tackling similarity joins have been previously published for Hadoop [18], the study focused just on two-dimensional data. The need of effective and efficient high-dimensional-data k-NN similarity joins led us to revise available MapReduce algorithms and integrate further adaptations. In the paper, we study three different approaches which offer diverse ways of approximate query processing with a promising trade-off between error and computation time (when compared to exact k-NN similarity joins).

The main contribution of this paper is a revision of similarity join algorithms and their comparison. Particularly, we report findings for high-dimensional data (200, 512 and 1000 dimensions) and show the benefits of the pivot-based approach.

The paper is structured in the following order. In Sect. 2, all essential definitions are presented. Section 3 summarizes all investigated k-NN similarity join algorithms with revisions. In Sect. 4, we examine the presented approaches in multiples experimental evaluations and discuss the results, and finally, in Sect. 5, we conclude the paper.

2 Preliminaries

In this section, we present fundamental concepts and basic definitions related to approximate k-NN similarity joins. All the definitions use the standard notations [18, 22].

2.1 Similarity Model and k-NN Joins

In this paper we address the efficiency of k-NN similarity joins of objects $o_i$ modeled by high-dimensional vectors $v_{o_i} \in \mathbb {R}^n$. In the following text, a shorter notation $v_i$ will be used instead of $v_{o_i}$. In connection with a metric distance function $\delta :\mathbb {R}^n \times \mathbb {R}^n \rightarrow \mathbb {R}^+_0$, the tuple $M = (\mathbb {R}^n, \delta )$ forms a metric space that serves as a similarity model for retrieval (low distance means high similarity and vice versa)³.

Let us suppose two sets of objects in a metric space M: database (train) objects $S \subseteq \mathbb {R}^n$ and query (test) objects $R \subseteq \mathbb {R}^n$. The similarity join task is to find the k nearest neighbors for each query object $q \in R$ from the set S employing a metric function $\delta$. Usually, the Euclidean ($L_2$) metric is employed. Formally:

$$ kNN(q, S) = \{X \subset S; |X| = k \wedge \forall x_i \in X, \forall y \in S - X: \delta (q, x_i) \le \delta (q, y)\} $$

The k-NN similarity join is defined as:

$$ R \bowtie S = \{(q, s)| q \in R, s \in kNN(q, S)\}. $$

Because of the high computational complexity of similarity joins, we focus on approximations of joins which can significantly reduce computation costs while keeping reasonable precision. Formally an approximate k-NN query for an object $q \in R$ is labeled as ${kNN_a}(q)$ and defined as $\epsilon$-approximation of exact k-NN:

$$kNN_a(q, S) = \{X \subset S; |X| = k \wedge $$

$$\max _{x_i \in kNN(q, S)} \delta (q, x_i) \le \max _{x_i \in X} \delta (q, x_i) \le \epsilon \cdot \max _{x_i \in kNN(q, S)} \delta (q, x_i)\}$$

where $\epsilon \ge 1$ is an approximation constant. The corresponding approximate k-NN similarity join is defined as:

$$ R \bowtie _a S = \{(q, s)| q \in R, s \in kNN_a(q, S)\}, $$

For high-dimensional vector representations, all the pairwise distances between dataset vectors tend to be similar and high with respect to the maximal distance (the effect of high intrinsic dimensionality [22]). The $\epsilon$ constant for such datasets and given k would have to be small to guarantee a meaningful precision with respect to exact search. At the same time, filtering methods considering small $\epsilon$ would often result in inefficient (i.e., too expensive) approximate kNN query processing. Therefore, in this work we do not consider such guarantees for the compared methods (theoretical limitations of the guarantees are out of the scope of this paper). In the experiments, we focus just on the error of the similarity join approximation. The k-NN query approximation precision (or recall with respect to the exact k-NN search) is defined as:

$$precision(k, q, S)=\frac{|kNN(q, S) \cap {kNN_a}(q, S)|}{k}$$

2.2 MapReduce Environment

Since data volumes are significantly increasing every day, centralized solutions are often intractable for large data processing. Therefore, the need for effective distributed data processing is emerging. In this paper, we have adopted the MapReduce [5] paradigm that is often used for parallel processing of big datasets. The algorithms described in Sect. 3 are implemented in the Hadoop MapReduce environment which consists of several components. Datasets are stored in the Hadoop distributed file system (HDFS), which is designed to form a big virtual file space to contain data in one place. Data files are physically stored on different data nodes across the cluster and are replicated in multiple copies (protection against a hardware failure or a data node disconnection). Name nodes manage access to data according to the distance from a request source to a data node (it finds the closest data node to a request).

In Hadoop, every program is composed of one or more MapReduce jobs. Each job consists of three main phases: a map phase, a shuffle phase and a reduce phase. In the map phase, data are loaded from the HDFS file system, split into fractions and sent to mappers where a fraction of data is parsed, transformed and prepared for further processing. The output of the map phase are ${\texttt {<key, value>}}$ pairs. In the shuffle phase, all ${\texttt {<key, value>}}$ pairs are grouped and sorted by the key attribute and all values for a specific key are sent to a target reducer. Ideally, each reducer receives the same (or similar) number of groups to equally balance a workload of the job. In the reduce phase all reducers process values for an obtained key (or multiple keys) and usually perform the main execution part of the whole job. Finally, all computed results from the reduce phase are written back to the HDFS.

3 Related k-NN Similarity Joins

In this paper we study a pivot-based approach for general metric spaces and two vector space approaches - space-filling Z-curve and locality sensitive hashing.

3.1 Pivot-Based Approach

The original version of this approximate k-NN join algorithm [2] utilizes pivot space partitioning based on a set of preselected global pivots $p_i \in P \subset S$. This approach was inspired by the Lu et al. work [11], which focused on exact similarity joins. The algorithm is composed of two main phases: the preprocessing phase and the actual k-NN join computation phase.

In the preprocessing phase, both sets of database and query objects (S and R) are distributed into Voronoi cells $C_i$ using the Voronoi space partitioning algorithm according to the preselected pivots P (a cell $C_i$ is determined by the pivot $p_i \in P$). The set of all created cells is denoted as C. Next, all distances ${d_j}_i$ from objects $o_j \in S \cup R$ to all pivots $p_i$ (${d_j}_i=\delta (o_j, p_i)$) have to be computed, and for every object $o_j$ the nearest pivot $p_n$ with the distance ${d_j}_n$ is stored within the $o_j$ data record. Also, global statistics are evaluated for every Voronoi cell $C_i$ such as the covering radius, number of objects $o_j$ and total size of all objects $o_j$ in the particular cell $C_i$. At the end of the preprocessing phase, the Voronoi cells $C_i$ are clustered into bigger groups $G_l$. Every group $G_l$ should contain objects of a similar total size to properly balance further parallel k-NN join workload.

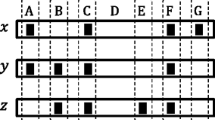
The second phase performs k-NN join of two sets S and R in a parallel MapReduce environment (one MapReduce job). Every computing unit (one reducer $red_l$) receives a subset $S_l \subset S$ of database objects and $R_l \subset R$ of query objects corresponding to a group $G_l$ precomputed in the previous phase. Because not all nearest neighbors for query objects $q_l \in R_l$ may be present in a group $G_l$ (especially for query objects near $G_l$ space boundaries), a replication heuristic is employed. Specifically, every database object located in each cell $C_j \in C$ is replicated to groups $G^m \subset G$ (and corresponding nearest cells) containing pivots $p_i$ that are within ReplicationThreshold nearest pivots to pivot $p_j$. At each reducer, metric filtering rules and additional approximate filtering (only the closest cells to the query are considered) are employed to speed up the query processing. Additional details of this algorithm can be found in the original paper [2]. The output of a reducer $red_l$ is a set of the k nearest neighbors for every query object $q_l \in R_l$. An overview of the space partitioning and replication algorithm is depicted in Fig. 1a.

Fig. 1.

An example of the Voronoi space partitioning and replication of database objects $o_n \in S$. The first part (a) depicts the replication based on distances between pivots $p_i$. For the $ReplicationThreshold=2$ only the object $o_3$ is replicated to the other group $G_1$, whereas $o_1$ and $o_2$ have the closest pivot to the corresponding pivot $p_i$ (in the cell $c_i$) in the same group. In the (b) scenario, for the $MaxRecDepth=2$ all three objects $o_n$ near groups boundaries are replicated to the other group because the second closest pivot to the objects $o_n$ lies in the other group.

Algorithm Revision. In this paper, we use a slightly modified version of the previously described algorithm. The main difference is the utilization of a repetitive (recursive) Voronoi partitioning inspired by indexing techniques in metric spaces such as M-Index [16]. Basically, every object $o_j$ is identified by a pivot permutation [3] determined by a set of closest pivots instead of a single closest pivot. The modification influences mainly the preprocessing phase and also the database objects replication heuristic. An example of the use of the revised algorithm is represented in Fig. 1b.

We define a new parameter MaxRecDepth which sets a threshold for the maximum depth of the Voronoi space partitioning. In the preprocessing phase, for every object $o_j$ ($o_j \in S \cup R$) the distances to all pivots are evaluated and the ordered list of the MaxRecDepth nearest pivots $P_j \subset P$ is stored (in the form of pivot IDs) with object $o_j$.

The replication heuristic in the beginning of the second phase utilizes directly the stored lists of nearest pivots. Specifically, every database object $o_j$ located in a cell $C_j \in C$ is replicated to groups $G_i \subset G$ that contain cells determined by pivots from $P_j$.

3.2 Space-Filling Curve Approach

A space-filling curve is a bijection which maps an object from an n-dimensional space to a one-dimensional value, trying to preserve the locality of objects with high probability. For example, the z-order curve creates values (referenced as z-values) that can be computed easily by interleaving the binary representation of coordinate values. Z-curves can be used to efficiently approximate kNN search [20]. When querying the database, the z-value of the query object is calculated and k database objects with nearest z-values are returned. To reach a more precise results, c independent copies of the database are created in the preprocessing phase, each of them shifted by a random vector $v_i \in \mathbb {R}^n$. For each database copy $C_i$, z-values of modified objects are computed and sorted in a list $L_i$. When querying the database, the query object is shifted by each $v_i$ as well, producing a vector of c z-values $z_i$. Each $z_i$ is used to query list $L_i$ for $2 \cdot k$ objects with the k nearest lower and k nearest higher z-values. Thus, up to $2 \cdot c \cdot k$ distinct candidates are collected in total, their distance to the query object is computed and the resulting k nearest candidates are returned.

The centralized solution has been adapted for the MapReduce framework [23]. To distribute the work among the nodes, the objects in each copy $C_i$ are split in n partitions, depending on their z-value. Inside each partition, each present query object is used to find $2\cdot k$ nearest database object candidates using z-values⁴ and also the distances to the candidates are evaluated. Each partition is processed by a separate reducer. Using a suitable number of partitions and having data equally distributed, the portion of data for each reducer is small enough to be stored in a node memory. Finally, the nearest objects for each query are detected by merging the candidate results obtained from all copies $C_i$. We have modified the original source code [23] to keep the partition objects in memory and to optimize the serialization of z-values.

3.3 Locality Sensitive Hashing Approach

Locality Sensitive Hashing (LSH) [4] is another technique that can be used in the context of k-NN Similarity Join algorithms. Specifically, Stupar et al. proposed RankReduce [19], a MapReduce-based approximate algorithm to simultaneously process a small number of k-NN search queries in a single MapReduce job using LSH. The key idea behind RankReduce is to use hashing to build an index that assigns similar records to the same hash table buckets. Unlike the original RankReduce method, our implementation compares only database and query objects from the same bucket. Our method is composed of two MapReduce jobs: a hashing job including k-NN evaluation and a merging job. During the map phase of the hashing job, both database S and query objects R are hashed using a set of l hash tables each containing j hash functions of the form $h_{a,B}(v)=\lfloor (a \cdot v +B)/W \rfloor$, where W is a parameter. For every input record $v \in S \cup R$ a set of output keys (buckets) $key_l$ is evaluated. One $key_l$ represents a unique string formed from j hash functions corresponding to the hash table l. The map phase emits pairs of the form $(key_l, v)$. In the reduce phase of the hashing job, local k-NN candidates are computed for a subset of queries and database objects in every bucket identified by the key $key_l$. In the second MapReduce job, all partial results are loaded, grouped by the query object IDs and global k-NN results for all queries are produced.

3.4 Exact k-NN Similarity Join Approach

In order to be able to evaluate the performance of approximate methods, an exact k-NN similarity join was also implemented. We used the pivot space approach (Subsect. 3.1) with ReplicationThreshold parameter set to the number of pivots (thus, all database objects were replicated to all reducers) and the filter parameter explained in the original paper [2] was set to the value 1 (meaning all Voronoi cells $C_i$ are processed on each reducer).

4 Experimental Evaluation

In this section, we experimentally evaluate and compare the presented MapReduce k-NN similarity join algorithms. Main emphasis is put on scalability, precision and the overall similarity join time of all solutions for high-dimensional data. First, we describe the test datasets and the evaluation platform, then we investigate parameters for all the methods and, finally, we compare the performance of all the approaches in multiple testing scenarios.

4.1 Description of Datasets and Test Platform

In the experiments, we perform k-NN similarity joins on three vector datasets with various number of dimensions: 200, 512 and 1000. The 200 and 1000-dimensional datasets contain histogram vectors which were formed from a few key features located in HTTPS proxy logs collected by the Cisco cloud. Features were transformed into vectors using two techniques. The dataset with 200 dimensions was created by uniform feature mapping into a 4-dimensional hypercube [9]. In the dataset with 1000 dimensions, each HTTPS communication feature was assigned to the closest pre-trained Gaussian utilizing a well known density estimation technique called Gaussian Mixture Model (GMM) [12]. The resulting vectors are histograms of occurrences of each Gaussian. These feature extraction algorithms are also implemented in the MapReduce framework. Our implementation is inspired by works [2, 9, 13]. The algorithm processes all HTTPS communication features in parallel, groups them by a given key and applies a specific feature transformation strategy to produce final descriptors (vectors).

The last dataset consists of 335944 officially provided key frames from the TRECVid IACC.3 video dataset [1]. The descriptors for each key frame were extracted from the last fully connected layer of the pretrained VGG deep neural network [17] and further reduced to 512 dimensions using PCA.

All datasets are divided into the database S and query points R. The number of database objects ranges from about $|S|=$150 000 to 450 000 objects. The size of the query part ranges from about $|R|=$180 000 to 320 000 objects in every dataset. Every object contains an ID and a vector of values stored in the space saving format presented in the paper [2]. The size of datasets vary according to the number of dimensions from 0.5GB to 3GB of data in the sparse text format. We employ the Euclidean ($L_2$) distance metric as the similarity measure.

The experiments ran on a virtualized Hadoop 2.6.0 cluster with 20 worker nodes, each having 6 GB RAM and 2 core CPU (Intel(R) Xeon(R) running at 2.20 GHz) and were implemented in Java 1.7.

4.2 Fine Tuning of Experimental Methods

In this subsection, we investigate parameters for every tested algorithm. Note that all time values include not only the running time of the k-NN similarity join but also the preprocessing time. The parameter tuning tests ran on the 1000-dimensional dataset and the k value was set to 5.

Fig. 2.

Pivot-based approach parameters tuning

Fig. 3.

Z-curve approach number of shifts tuning

Fig. 4.

LSH approach W parameter tuning

In Fig. 2, we compare the ReplicationThreshold and MaxRecDepth parameters for related and revised pivot-based (Voronoi) approaches described in Sect. 3.1. Although lower parameter values run faster, they do not achieve convincing accuracy. For the rest of the experiments, we fixed MaxRecDepth parameter to the value 10 which promises a competitive precision and running time trade off. In the following experiments, we do not consider the original version with ReplicationThreshold. In general, the Voronoi space partitioning approach used 2000 randomly preselected pivots, Voronoi cells $C_i$ were grouped into 18 distinct groups $G_l$ and the filter parameter explained in the original paper [2] was set to the value 0.05.

You may notice that the total running time for some lower parameter values is longer than for following higher values, e.g. $ReplicationThreshold=3$ and 5 or $MaxRecDepth=1$ and 3. Despite more replications, a shorter k-NN evaluation time is caused by the efficient candidate processing in the actual algorithm evaluation on each reducer where parent filtering and lower bound filtering techniques in a metric space are utilized [2, 22]. Note that closer k objects to many queries appear in their group and so the ranges of k-NN queries get tighter. Hence, more candidates are filtered out by the triangle inequality and the total number of actual distance computations is lower.

Figure 3 displays the precision and overall time for the Z-curve approach for growing number of random vector shifts presented in Sect. 3.2. We may observe that more shifts slightly increases approximation precision, but running time is prolonged significantly. In other experiments, we fixed the number of shifts to value 5. We used 40 partitions, in order to fit the number of reducers. The Z-curve parameter $\epsilon$ was set to 0.128 which provided reasonably balanced size of partitions while keeping shorter pre-processing time. Notice that in the paper [23], different $\epsilon$ values did not affect the precision.

In Fig. 4, we examine the influence of the parameter W on the performance of the LSH method described in Sect. 3.3. With growing W, both precision and time increase substantially. Longer running time for higher W values is mainly caused by hashing objects into bigger buckets (more objects fall into the same bucket). However, this parameter heavily depends on the specific dataset. For other experiments, we fixed $W=1$ for the 200-dimensional dataset, $W=100$ for the 512-dimensional TrecVid dataset and $W=20$ for the 1000-dimensional dataset. Generally, we used 10 hash tables each containing 20 hash functions.

4.3 Comparison of Methods

We propose multiple testing scenarios designed to test the main aspects of each k-NN approximate similarity join algorithm.

Size-Dependent Computation. Each of the datasets, both train and test vectors, were sampled in order to create subsets containing $\frac{1}{4}$, $\frac{1}{2}$, $\frac{3}{4}$ and all of the original data. The methods were tested on each sample. The graphs 5, 6 and 7 show that the running time generally increases with higher dimensionality and dataset size. Surprisingly, the Z-curve method is sometimes slower than the exact algorithm, due to the high index initialization costs. The revised pivot space method shows to have the best approximation precision/speed tradeoff across all datasets.

As we can see in the Figs. 8, 9 and 10, the approximation precision of the methods does not significantly change with the size when each dataset is considered separately. In all cases, the precision of the pivot space method is clearly the highest, ranging from 73% for the 200-dimensional dataset up to 88% for the 1000-dimensional dataset.

Fig. 5.

200-dimensional dataset: computation time

Fig. 6.

512-dimensional dataset: computation time

Fig. 7.

1000-dimensional dataset: computation time

Fig. 8.

200-dimensional dataset: precision

Fig. 9.

512-dimensional dataset: precision

Fig. 10.

1000-dimensional dataset: precision

K-Dependent Computation. In the graphs 11 and 12, we investigate the influence of increasing the parameter k (from the k nearest neighbors) on the precision and total similarity join time. All the presented experiments were performed on the 1000-dimensional dataset. The precision stays the same or slowly decreases for the pivot space and LSH methods, whereas time complexity is gradually increasing, but the difference is only marginal. On the other hand, the growing k increases the precision and time complexity for the Z-curve approach. This observation could be explained by more database objects replications to neighboring partitions caused by higher k (this property comes from the original distributed Z-curve design described in the paper [23]). The results of all the methods follow trends identified in the previous graphs. The pivot space approach outperforms other algorithms in the precision/speed tradeoff.

Fig. 11.

k-dependent computation: precision

Fig. 12.

k-dependent computation: time

4.4 Discussion

In the experiments, three related approximate MapReduce-based k-NN similarity joins on Hadoop were investigated using settings recommended in the original papers. Note that the Z-curve and LSH (RankReduce) related methods used primarily low-dimensional datasets during the design of the approaches (30 dimensions in [23], 32 an 64 dimensions in [19]). In the experiments, the pivot-based approach using the repetitive Voronoi partitioning significantly outperformed the other two methods in the precision/efficiency tradeoff. Our hypothesis is that for high-dimensional data the Z-curve and LSH methods suffer from the random shifts and hash functions that do not reflect data distributions. We verified this hypothesis on our synthetic 10-dimensional dataset in which all three methods provided expected behavior, as presented in the original papers. Note that specific subsets of the dataset could potentially reside in low-dimensional manifolds. Hence, finetuning specific parameters of the two methods (number of shifts in Fig. 3 and W in Fig. 4) do not provide a significant performance boost.

On the other hand, the pivot-based approach uses representatives from the data distribution and employs pairwise distances to determine data replication strategies. As demonstrated also by metric access methods for k-NN search [16, 22], it seems that the distance-based approach can be also directly used as a robust and intuitive method for approximate k-NN similarity joins in high-dimensional spaces.

5 Conclusions

In this paper, we focused on approximate k-NN similarity joins in the MapReduce environment on Hadoop. Although comparative studies have been proposed for the considered approaches, the studies focused mainly on data with less than one hundred dimensions. According to our findings, the dimensionality affects the conclusions about the compared approaches. Two out of three methods previously tested for low-dimensional data did not perform well under their original recommended design and settings.

In the future, we plan to thoroughly analyze and track the bottlenecks of all the methods and try to provide a theoretically sound explanation about the performance limits and approximation errors of all the tested approaches. For similarity joins, we plan to employ other approaches for MapReduce based approximate kNN search using LSH, for example [24] that performed well on 128 dimensional data. We also plan to consider implementing algorithms in other MapReduce frameworks such as Spark and study performance differences. Findings in a very recent paper [8] promise improvements.