Mobile Radio Tomography: Agent-Based Imaging

Abstract

Mobile radio tomography applies moving agents that perform wireless signal strength measurements in order to reconstruct an image of objects inside an area of interest. We propose a toolchain to facilitate automated agent planning, data collection, and dynamic tomographic reconstruction. Preliminary experiments show that the approach is feasible and results in smooth images that clearly depict objects at the expected locations when using missions that sufficiently cover the area of interest.

1 Introduction

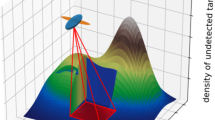
Radio tomography is a technique for measuring the signal strength of low-frequency radio waves exchanged between sensors around an area, and reconstructing information about objects in that area. We send a signal between a source and target sensor of a bidirectional link. The signal passes through objects that attenuate it, resulting in a detectably weaker signal at the receiving end. This phenomenon makes it possible to determine where objects are located. The typical setup for radio tomography is illustrated in Fig. 1(left), in which the sensors are situated on the boundaries in an evenly distributed manner. Gray lines represent unobstructed links and red lines indicate links attenuated by the object.

Fig. 1.

The sensor network and the physical realization of a vehicle.

Radio tomography has several benefits over other detection techniques. We can see through walls, smoke or other obstacles. The technique does not require objects to carry sensor devices. The radio waves are non-intrusive, with no permanent effects on people. The technique is less privacy-invasive than optical cameras as the possible level of detail is inherently limited due to the nature of the radio waves. It is not possible to accurately identify a person, but we do aim for reconstructed objects that we recognize as such.

A static sensor network with a large number of affordable sensors, placed around an area of interest, can be used to reconstruct and visualize a smooth image in real time [15]. The drawbacks of a static network are the requirement of a large number of sensors and the inability to resolve gaps in the sensor coverage or to react to information obtained through the reconstruction.

One way to resolve these issues is to move the sensors around using agents, which are realized as autonomous vehicles as pictured in Fig. 1(right). We position them along a grid which defines discrete and precise sensor positions. These positions produce a matrix of coordinate-based pixels in the reconstructed image. In comparison to the static setup, we require fewer sensors and less prior knowledge about the area. We may adapt the coverage dynamically, for example by zooming in on a part of the area. We name this concept mobile radio tomography, which includes both the agent-based measurement collection and the dynamic reconstruction approach.

In this paper, we present our toolchain for mobile radio tomography using intelligent agents, as an engineering effort that builds upon and combines several techniques. In Sect. 2 we describe the key challenges for mobile radio tomography and the components in our toolchain that address them. We then cover two such challenges in greater detail: (i) planning the paths of the agents in Sect. 3, and (ii) reconstructing an image from the measurements in Sect. 4. Results for real-world experiments are presented in Sect. 5, followed by conclusions and further research in Sect. 6. This paper is based on two master’s theses on the subject of mobile radio tomography [10, 14].

2 Toolchain

Compared to existing localization and mapping techniques that use statically positioned sensors [11, 15], radio tomographic imaging with dynamically positioned agents leads to several new challenges. In particular, routes must be planned for each agent such that they obtain isotropic sampling of the network while also shortening the total scanning time and ensuring collision-free movement. Images must be reconstructed from the measurements in real time, requiring algorithms and models that work with a restricted set of data that is potentially incomplete and certainly noisy. Synchronization between the agents must be interleaved with data acquisition using a robust communication protocol.

To deal with these challenges, we developed an open-source, component-based toolchain. The toolchain is mainly written in Python, with low-level hardware components written in C. The diagram in Fig. 2 shows the toolchain’s components.

Fig. 2.

Diagram of components in the toolchain.

The planning components generate missions for signal strength measurements, as discussed in Sect. 3. The problem of devising a set of link positions to measure is solved by an evolutionary multiobjective algorithm that simulates reconstruction models to ensure that the links cover the entire network. Next, a waypoint assignment algorithm distributes the sensor positions for each link over the vehicles. A path graph search algorithm prevents the vehicles from clashing.

Execution of the mission is taken care of by the vehicle control components. The monitor oversees the process and tracks auxiliary sensors on the vehicles, such as distance sensors for obstacle detection. It makes the RF (radio frequency) sensor perform the signal strength measurements and it may use the search algorithm for collision avoidance during a mission. The mission consists of the waypoints for the vehicle and provides instructions to the vehicle controller. During a mission, this causes the vehicle to move toward the next waypoint.

The reconstruction component converts the signal strength measurements to a two-dimensional visualization of the area of interest. We describe this process in detail in Sect. 4. The weight matrix determines which pixels are intersected by a link, and a weighting model describes how the contents of pixels contribute to a measured signal strength.

3 Missions

We instruct the autonomous vehicles to travel to specific locations around the area of interest, that two-by-two correspond to the positions where sensor measurements must be performed. A vehicle executes its mission, which consists of waypoints denoting locations to be visited in order. We wish to plan the mission algorithmically instead of assigning waypoints by hand. The vehicles perform measurements together while traversing short and safe paths that do not conflict with concurrent routes. This problem is related to various multi-agent vehicle routing problems with synchronization constraints [6, 9, 13]. We propose a two-stage algorithm, and describe both parts in text as well as pseudocode.

We assume that we know which links we measure for collecting tomographic data; later on we generate these links using an evolutionary algorithm. To measure a link, sensors must be placed at two positions at the same time. We distribute these tasks over the vehicles. Our assignment algorithm is given as input a set

$$\begin{aligned} P = \{(p_{1,1}, p_{1,2}), (p_{2,1}, p_{2,2}), \ldots , (p_{\omega ,1}, p_{\omega ,2})\} \end{aligned}$$

(1)

with $\omega$ location pairs of coordinate tuples (two-dimensional vectors), and a set $V = \{v_1, v_2, \ldots , v_\eta \}$ of $\eta \ge 2$ vehicles, initially located at coordinate tuples $S_1, S_2, \ldots , S_\eta$. Now define $U = \{(u,v) \, | \, u \in V, v \in V, u \ne v\}$, the pairwise unique permutations of the vehicles, e.g., with two vehicles, this is $U = \{(v_1, v_2), (v_2, v_1)\}$.

Our greedy assignment in Algorithm 1 then works as follows: for each vehicle pair $\vartheta = (v_a, v_b) \in U$ and each sensor pair $\rho = (p_{c,1}, p_{c,2}) \in P$, determine the distances $d_1(\vartheta , \rho ) = \left\| S_a - p_{c,1}\right\| _1$ and $d_2(\vartheta , \rho ) = \left\| S_b - p_{c,2}\right\| _1$. We use the $L^1$ norm $\left\| \cdot \right\| _1$ to only move in cardinal directions on a grid; in other applications we may use the $L^2$ norm $\left\| \cdot \right\| _2$. Next, take the maximal distance (since one agent must wait for the other to perform a measurement), and finally select the overall minimal pair combination, i.e., solve the following optimization problem:

$$\begin{aligned} \mathop {\mathrm {\arg \,\min }}_{(\vartheta ,\rho ) \, \in \>\! U \times P} \Bigl (\max (d_1(\vartheta ,\rho ), d_2(\vartheta ,\rho ))\Bigr ) \end{aligned}$$

(2)

The selected positions are then assigned to the chosen vehicle pair, and removed from P. Additionally, $S_a$ becomes the first position and $S_b$ becomes the second sensor position. The greedy algorithm then continues with the next step, until P is empty, thus providing a complete assignment for each vehicle.

Secondly, we design a straightforward collision avoidance algorithm that searches for routes between waypoints that do not conflict with any concurrent route of another vehicle; see Algorithm 2. The algorithm is kept simple in order to incorporate it into an evolutionary algorithm (see [7, 12] for more intricate methods which result in optimized routes). We use a path graph search algorithm to find a safe route that crosses no other routes. Once a vehicle performs a measurement involving another vehicle, their prior routes no longer conflict.

Let $v_p$ be the vehicle that we currently assign the position $N_p$ to, and $v_q$ the vehicle that will visit the other sensor position. We also initialize sets $W_1, W_2, \ldots , W_\eta$, where each $W_i$ indicates with which other vehicles the given vehicle $v_i$ has recently performed a measurement. We assume that the search algorithm is given as input a graph G, start point $S_p$ and end point $N_p$, and outputs a route of intermediate points $R^*$, or an empty sequence if there is no safe path.

We use the collision avoidance algorithm every time the waypoint assignment algorithm assigns a position to a vehicle, so twice per step. Thus, we detect problematic situations as they occur, which are either solved via detours (although the vehicle might also search for a faster safe path while the mission takes place), or by rejecting the entire assignment. The resulting assignments should be collision-free, assuming that all vehicles follow their assigned route and wait for each other at synchronization points, where they also perform their signal strength measurements.

In order to supply the waypoint assignment algorithms with a non-static set of sensor positions P (see (1)), we utilize an evolutionary multiobjective algorithm [8]. The iterative algorithm generates a set of positions and alters it in such a way that it theoretically converges toward an optimal assignment. We keep a population $(X_1, X_2, \ldots , X_\mu )$ of multiple individuals, each of which contains variables that encode the positions in an adequate form. After a random initialization, the algorithm performs iterations in which it selects a random individual $X_i$ and slightly mutates it to form a new individual [2].

In our situation, the variables of an individual encode coordinates for positions around the area of interest, and possibly inside of it as well. Define $m^{(i)}$ as the number of pairs of positions that are correctly placed, such that the link between the positions intersects the network. Using these positions, we can deduce other information, such as a weight matrix $A^{(i)}$ (containing link influence on pixels; see Sect. 4), for each individual $X_i$. The algorithm then removes an individual that is infeasible according to the domain of the variable or due to the constraints in (3) and (4), such as a minimum number of valid links $\zeta$. The constraints are wrapped into a combined feasibility value in (5):

$$\begin{aligned} Q_1^{(i)}&: \exists j: \forall k: A^{(i)}_{j,k} \ne 0 \end{aligned}$$

(3)

$$\begin{aligned} Q_2^{(i)}&: m^{(i)} \ge \zeta \end{aligned}$$

(4)

$$\begin{aligned} f_i&= {\left\{ \begin{array}{ll} 0 &{} \text {if}~\lnot Q_1^{(i)} \vee \lnot Q_2^{(i)} \\ 1 &{} \text {if}~Q_1^{(i)} \wedge Q_2^{(i)} \end{array}\right. } \end{aligned}$$

(5)

In the case that all constraints and domain restrictions are met by each individual, the multiobjective algorithm uses a different selection procedure based on the objective functions. We remove an individual if its objective values are strictly higher than those of one dominating individual in the population. If none of the individuals are dominated, we remove the one with the minimum crowding distance [5]. The crowding distance is defined as the area around the individual within the objective space. We can place the objective values in this space as a plotted function, which is known as the Pareto front.

We provide two objective functions that the evolutionary multiobjective algorithm should minimize. Certain parts of the algorithm favor two over more than two objectives, which is why we combine related functions as terms of one overarching objective. Maximization problems, such as achieving optimal coverage area with the generated links, are converted to minimization objectives by negating them. The objective functions in (6) and (7) describe desirable properties for intersecting links and minimized distances, respectively:

$$\begin{aligned} g_1(X_i)&= -\sum _{j = 1}^{m^{(i)}} \sum _{k = 1}^{n} A^{(i)}_{j,k} \end{aligned}$$

(6)

$$\begin{aligned} g_2(X_i)&= \delta \cdot \left( \sum _{j = 1}^{m^{(i)}} \left\| p_{j,1}^{(i)} - p_{j,2}^{(i)}\right\| _2\right) + (1 - \delta ) \cdot T^{(i)} \end{aligned}$$

(7)

In the entire selection step of the evolutionary algorithm, we use the reconstruction, waypoint assignment and collision avoidance algorithms to check that a new individual adheres to the constraints and to calculate the objective values. Aside from the link weight matrix $A^{(i)}$ for one individual $X_i$, we calculate the pairwise $L^2$ norms between sensor positions, and $T^{(i)}$, the sum of minimized route distances (2), weighted by a factor $\delta$. These algorithms generate missions that provide sufficient network coverage. When we stop the evolutionary multiobjective algorithm, we can manually select one of the individuals and use the mission it generates, using the Pareto front as a reference for balanced objective values [5].

4 Reconstruction

The reconstruction phase takes care of converting a sequence of signal strength measurements to a two-dimensional image of size $m \times n$ pixels that may be visualized. Let $M = \{(s_1, t_1, r_1), \ldots , (s_k, t_k, r_k)\}$ be the input, in which $s_i$ and $t_i$ are pairs of integers indicating the x and y coordinates on the grid for the source and target sensor i, respectively, $r_i$ is the received signal strength indicator (RSSI) and k is the total number of measurements. We express the conversion problem algebraically as $A{\varvec{x}} = {\varvec{b}}$. Here, ${\varvec{b}}$ is a column vector of RSSI values $(r_1, r_2, \ldots , r_k)^T$, ${\varvec{x}}$ is a column vector of $m \cdot n$ pixel values (in row-major order) and A is a weight matrix that describes how the RSSI values are to be distributed over the pixels that are intersected by the link, according to a weighting model.

In general, signal strength measurements contain a large amount of noise due to multipath interference. The wireless sensors send signals in all directions, and thus more signals than those traveling in the line-of-sight path may reach the target sensor, causing interference. This phenomenon is especially problematic in indoor environments due to reflection of signals. Although techniques exist to include an estimate of the contribution of noise inside the model [15], we suppress noise outside the model using calibration measurements and regularization algorithms. The difficulty lies in the fact that the reconstruction problem is an ill-posed inverse problem, which we have to solve for highly noisy and unstable measurements.

The weight matrix A defines the mapping between the input ${\varvec{b}}$ and the output ${\varvec{x}}$. If and only if the contents of a pixel with index i attenuate a link with index $\ell$, then the weight $w_{\ell , i}$ in row $\ell$ and column i is nonzero. Given a link $\ell$, a weighting model determines which pixels have an influence on this link and are thus assigned nonzero weights. The weights may be normalized using the link length $d_\ell$ to favor shorter links [16]. The variable $d_{\ell ,i}$ is the sum of distances from the center of pixel i to the two endpoints of link $\ell$.

The line model in (8) assumes that the signal strength is determined by objects on the line-of-sight path, as shown in Fig. 3a; the ellipse model in (9) is based on the definition of Fresnel zones:

$$\begin{aligned} w_{\ell , i} = {\left\{ \begin{array}{ll} 1 &{} \text {if link}~\ell ~\text {intersects pixel}~i\\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(8)

$$\begin{aligned} w_{\ell , i} = {\left\{ \begin{array}{ll} 1/\sqrt{d_{\ell }} &{} \text {if}~d_{\ell , i} < d_{\ell } + \lambda \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(9)

$$\begin{aligned} w_{\ell , i} = e^{-{\left( d_{\ell , i} - d_{\ell }\right) }^2 / 2\sigma ^2} \end{aligned}$$

(10)

Fresnel zones, used to describe path loss in communication theory, are ellipsoidal regions with focal points at the endpoints of the link and a minor axis diameter $\lambda$. Only pixels inside this region are assigned a nonzero weight, as seen in Fig. 3b.

Fig. 3.

Illustration of weight assignment for a link from (0, 0) to (16, 16) by the weighting models.

Moreover, we introduce a new Gaussian model in (10). This model is based on the assumption that the distribution of noise conforms to a Gaussian distribution. The log-distance path loss model is a signal propagation model that describes this assumption as well [1].

The general Gaussian function is defined as $f(x) = \alpha \,e^{-{\left( x - \mu \right) }^2 / 2\sigma ^2}$. In this equation $\alpha$ is the height of the curve’s peak, $\mu$ is the location of the peak’s center and $\sigma$ is the standard deviation that controls the width of the top of the curve. The Gaussian model uses the Gaussian function to assign weights for the pixels. Most weight is assigned to pixels on the line-of-sight path and less weight is assigned to pixels that are farther away, depending on their distance from the line-of-sight path ($d_{\ell , i} - d_{\ell }$). We specifically use a Gaussian function with $\alpha = 1$ and $\mu = 0$ since this ensures that pixels on the line-of-sight path get the highest weight, as depicted in Fig. 3c. The parameter $\sigma$ may be tuned as in practice there appears to be a wide range of suitable values.

Due to the ill-posed nature of the problem, in general there exists no exact solution for $A{\varvec{x}} = {\varvec{b}}$ because A is not invertible. Instead, we attempt to find a solution ${\varvec{x}}_{ min }$ that minimizes the error using least squares approximation [3] as defined in (11), where R(x) is a regularization term:

$$\begin{aligned} {\varvec{x}}_{ min } = \underset{{\varvec{x}}}{\mathop {\mathrm {\arg \,\min }}}\left( \,\left\| A\,{\varvec{x}} - {\varvec{b}}\,\right\| ^{\,2}_2 + R({\varvec{x}})\right) \end{aligned}$$

(11)

The singular value decomposition (SVD) of A may be used to solve this and is defined as $A = U \varSigma V^T$, in which U and V are orthogonal matrices and $\varSigma$ is a diagonal matrix with singular values [16]. If we use the exact variant of singular value decomposition which does not apply any regularization, then we have the regularization term $R({\varvec{x}}) = 0$. Truncated singular value decomposition (TSVD) is a regularization method that only keeps the $\tau$ largest singular values in the SVD and is defined as $A = U_\tau \varSigma _\tau V^T_\tau$ [16]. Small singular values have low significance for the solution and become erratic when taking the reciprocals for $\varSigma$. Moreover, the truncated singular value decomposition is faster to compute, which is an important property for reconstructing images in real time.

While the dimensionality reduction from TSVD does stabilize the solution, the resulting images may still contain unstable spots. Iterative regularization methods incorporate desired characteristics of the reconstructed images. Total variation minimization (TV, see [16]) enforces that the reconstructed images are smooth, i.e., that the differences between neighboring pixels are as small as possible, by favoring solutions that minimize variability in the resulting image. The gradient $\nabla {\varvec{x}}$ of ${\varvec{x}}$ is a measure of the variability of the solution. The regularization term in (11) is set to $R({\varvec{x}}) = \alpha \sum _{i=0}^{\xi -1} \sqrt{{(\nabla {\varvec{x}})}^{\,2}_i + \beta }$, in which $\xi$ is the number of elements in $\nabla {\varvec{x}}$. The parameter $\alpha$ indicates the importance of a smooth solution and leads to a trade-off as a high value indicates more noise suppression, but less correspondence to the actual measurements. The term is not squared, so we need an optimization algorithm for the minimization. The parameter $\beta$ is a small value that prevents discontinuity in the derivative when ${\varvec{x}} = 0$, as that generally needs to be supplied to optimization algorithms.

Finally, let us consider another measure of variability. Maximum entropy minimization (ME) smoothens the solution by minimizing its entropy. Entropy is a concept in thermodynamics that provides a measure of the amount of disorder in a structure. The Shannon entropy is defined as $H = -\sum _{i=0}^{\gamma -1} q_i \log _2(q_i)$, in which $\gamma$ is the number of unique gray levels in the solution and $q_i$ is the probability that gray level i occurs in the solution. Low entropy indicates a low variation in gray levels (which we observe as noise). While this regularization technique is well-known [4], we have found no previous work discussing its application to radio tomographic imaging. The regularization term in (11) is set to $R({\varvec{x}}) = \alpha H$. We calculate a numerical approximation of the derivative. The described reconstruction methods and weighting models allow us to obtain a clear image of the area.

5 Experiments

To study the effectiveness of our approach, we perform a series of experiments. Two vehicles drive around on the boundaries of a $20 \times 20$ grid in an otherwise empty experiment room. We use hand-made missions that apply common patterns used in tomography, such as fan beams. With this setup we create a dataset with two persons standing in the middle of the left side and in the bottom right corner of the network, and a dataset with one person standing in the top right corner of the network. A separate dataset is used for calibration.

The first experiment compares all combinations of regularization methods and weighting models to determine which pair yields the most accurate reconstructions. We use the dataset with the two persons, so both must be clearly visible. The outcomes of this experiment are presented in Fig. 4, in which darker pixels indicate low attenuation and brighter pixels indicate high attenuation.

Fig. 4.

Reconstructions combining regularization methods and weighting models (two persons dataset).

The first observation is that SVD indeed leads to major instabilities because of the lack of regularization. Noise is amplified to an extent that the images do not provide any information about the positions of the persons. TSVD, while being a relatively simple regularization method, provides more stable resulting images that clearly show the positions of the two persons. The ellipse model and the new Gaussian model yield similar clear results, whereas using the line model leads to slightly more noise compared to the former two. Even though TV and ME use different variation measures, the reconstructions are visually the same and equally clear.

Besides providing a clear indication of where the persons are located inside the network, it is important that the reconstructed images are smooth. The second experiment studies the smoothening effects of the regularization methods using 3D surface plots of the raw grayscale images, i.e., without any additional coloring steps applied. The only difference between the experiment runs are the regularization method, so any other parameters remain the same, such as the Gaussian weighting model and the precollected dataset with the two persons that we use as input. The results for this experiment are shown in Fig. 5.

Fig. 5.

3D surface plots of the reconstructions for each regularization method (two persons dataset).

The ideal surface plot consists of a flat surface with two spikes exactly at the positions of the persons. The surface plot for SVD is highly irregular, which leads to noticeable noise in the image due to a high variance in pixel values. In contrast, the surface plot for TSVD is smooth and the two spikes are clearly distinguishable. However, there are still some small unstable spots. The surface plots for TV and ME are, again, practically the same and have even fewer instabilities.

With regard to the algorithmically generated missions discussed in Sect. 3, we perform a parameter optimization by comparing the average objective values of the resulting individuals in multiple runs of the evolutionary algorithm. The twelve parameters influence the sensitivity and scale of the optimization algorithm, as well as the waypoint assignment and collision avoidance algorithms. Certain features, such as a mutation operator specially designed to optimize link positions, can be enabled and disabled this way as well. We provide 350 unique combinations of values to these parameters, and repeat each experiment five times.

We find that some of these variables influence the performance in terms of stability, convergence speed and finding optimized positions. For example, the specialized mutation operator finds individuals that have better objective values, but result in chaotic populations over time. The population size hardly affects the algorithm’s effectiveness nor speed. Other parameters produce missions which are applicable only if we change the dimensions of the area of interest.

For the final experiment, we generate a mission for a $20 \times 20$ grid using the evolutionary multiobjective algorithm, and compare it to a hand-made mission used previously. The algorithm is tuned to place sensors for at least 320 and up to 400 valid links to be measured during the mission. The results of the parameter optimization are applied as well. At 7000 iterations, we end the generation run and pick a knee point solution that optimizes both objectives in the resulting Pareto front. A manual check using the collision avoidance algorithm determines that this assignment is safe. In Fig. 6, we show the images resulting from the tomographic reconstruction of the dataset with one person.

Fig. 6.

Reconstructions for algorithmically planned and hand-made missions (one person dataset).

The reconstruction, which is run in real time during the collection of signal strength measurements, uses TV and the Gaussian model. We can track the time it takes before a mission provides a smooth and correct result, in terms of quality and realism. In Fig. 6a, we are around halfway through the planned mission, with 204 out of 382 measurements collected. The reconstructed image clearly shows the person standing in the top right corner. Figure 6b shows the reconstructed image provided by the hand-made mission after 413 out of 800 measurements. Although this mission’s movements are less erratic (and more measurements per time unit are made), it is not stable enough to clearly show one person while it develops. Figure 6c shows the end result, where the hand-made mission does provide an acceptable reconstructed image. The planned mission does not diverge from its initial smooth image and we can stop the mission early.

6 Conclusions and Further Research

We propose a mobile radio tomography toolchain that collects wireless signal strength measurements using dynamic agents, which are autonomous vehicles that move around with sensors. We plan missions, which describe the locations that the agents must visit and in what order. Novel algorithms provide us with generated missions, guaranteeing that two sensors are at the right locations to perform a measurement. The algorithms avoid conflicts between the routes and provide an optimized coverage of the network.

The measurements are passed to the reconstruction algorithms to create a visualization of the area of interest that corresponds to the patterns in the data as best as possible. Regularization methods suppress noise in the measurements and increase the smoothness of the resulting image. We introduce a new Gaussian weighting model and apply maximum entropy minimization to the problem of radio tomographic imaging. Preliminary experiments show that the mobile radio tomography approach is effective, i.e., it is able to provide smooth reconstructed images in a relatively short time frame using algorithmically planned missions.

There is much potential for further research. One interesting topic is to replace the agents, that currently operate on the ground using small-scale robotic rover cars, with drones that fly at different altitudes. This leads to 3D reconstruction, e.g., by performing a reconstruction at different altitudes and combining the images, which are slices of the 3D model. The reconstruction algorithms could be modified to allow performing measurements anywhere in the 3D space, although this makes the problem more difficult to solve in real time.

Finally, improvements could be made to the algorithms related to planning and waypoint assignment tasks. This includes altering the objectives of the evolutionary multiobjective algorithm and using predetermined patterns that we encode in the variables. It is also not entirely clear yet how the network coverage, or the lack thereof, influences the quality of the reconstruction. The waypoint algorithm could be rebalanced to take less greedy steps or to factor in the time that certain actions take, such as turning around. Altering missions dynamically helps making adaptive scanning a viable approach.