Simulation of Human Induced Vibration of a Lively Footbridge

Abstract

In the last years, the need for structures able to link the functional and aesthetic role has led to the design of new flexible footbridges. The low ratio between permanent and variable loads makes them more sensitive to dynamic loads, such as the forces transmitted by pedestrians.

During the human walking, the pedestrian moves on a flexible structure adapting his gait to the bridge motion. The interaction between pedestrian and footbridge takes place at contact points, where the pedestrian transmits contact forces to the bridge that, in turn, imposes a set of displacements and velocities to the pedestrian’s feet. The description of the human being as a mechanical system allows for the derivation of the equation of motion of the bridge-pedestrian coupled system. In this work a previously developed bipedal pedestrian mass-spring-damper (MSD) model is adopted. The analytical formulation of the human-structure interaction, involving the derivation of the bridge-pedestrian coupled equations of motion, has been implemented in a numerical code, named INTER2.0. The bridge is modelled using a commercial FE code and its geometry is fully described. The code reads in input both the bridge structural matrices and the pedestrian dynamic properties needed to assembly the MSD matrices or the feet forces.

The present contribution investigates the effect, on a lively footbridge response, of a few parameters: distance between pedestrians and pedestrians’ trajectory. The results due to groups of pedestrians walking along different eccentric trajectories have highlighted the relation between the bridge mode excited and the pedestrians’ position. As it was expected, the eccentric transit induces a torsional behavior. In addition, the spatial distribution affects the bridge response: the vertical accelerations rise if the longitudinal distance among pedestrians increases, although this trend is not linear with the distance.

1 Introduction

In the last years the new footbridge design, moved by aesthetics requirements, has sprouted challenging bridges characterized by greater slenderness, longer spans, low damping and light materials [1]. As a consequence, their structural systems, with a low ratio between permanent and live loads, exhibit natural frequencies very close to the range of frequencies of human walking [2]. When the bridge accelerations exceed the limit perceived as comfortable and safe by humans, the utilization of the structure can be highly impaired. Thus, the design requires a greater care regarding vibration phenomena and the vibrations produced by human-induced loads are to be assessed within the class of serviceability limit states [3]. The vibration serviceability under human-induced dynamic forces is the governing criterion for the design of these slender structures.

During footbridge vibrations, some form of human-structure interaction (HSI) occurs, playing an important role in the structural dynamic response. HSI (a complex and inter-disciplinary issue) can be subdivided into two key areas [4]. One concerns the influence of structural vibration on forces induced by human occupants; the other the effect of pedestrians on the dynamic properties of civil engineering structures. This paper focuses on the second aspect.

The correct modeling of pedestrians represents an important issue into the study of HSI. A large research effort in the last 15 years has led to the development of both analytical expressions for the walking force and procedures to determine the footbridge response. Following the first simplified models, the increasing sophistication of the proposed expressions did not lead to significant improvements in numerical estimates of the response under pedestrian flows [5]. A mechanical model considers the mass, stiffness and damping of the pedestrian, all of which can interact with the structure [6]. Furthermore, the bridge response accounting for the human-structure interaction depends on both reliable estimates of expected loading scenarios and the accuracy of the models representing pedestrian.

Aim of this work is the study of the dynamic response of a footbridge accounting for the human-structure interaction (HSI) in the vertical direction. A mass-spring-damper (MSD) pedestrian model, developed in a previous work [7], has been adopted. The mechanical model is able to reproduce the correct human gait. Numerical analyses have been carried out with an ad-hoc numerical code, based on an uncoupled analytical formulation recently proposed [7]. The modeling and analysis approach is inherently uncoupled when forces are considered. Due to the pedestrian motion, the structural matrices of the coupled system are time-dependent and should be modified whenever the pedestrian’s foot position on the bridge changes. The proposed alternative solution strategy is based on the forced uncoupling of the system, based on the key assumption that the contact points between pedestrian and bridge deck are massless. The uncoupled formulation considers the footbridge and the pedestrian as two separate sub-systems (the former subjected to contact forces transmitted by the pedestrian, the latter excited by the bridge motion), reducing the computational burden associated to the time-varying properties of the matrices of the coupled system.

Numerical analyses are computed with the objective of evaluating the effect, on the bridge response, of a few parameters: pedestrians’ trajectory and distance between pedestrians. First, analyses with six pedestrians, walking in a single line, are carried out to study how transits, with the same spatial distribution but different eccentricity, affect the bridge response, highlighting the relation between the bridge mode excited and the pedestrians’ position. Secondly, analyses with nine pedestrians, placed on a uniform grid, investigate the variation of maximum accelerations when the mutual distance among pedestrians increases. Eight spatial distributions are considered, with an increasing value of the longitudinal distance among two subsequent pedestrians’ rows, in a range between a lower value of 1 m and an upper one of 4.5 m.

2 Seriate Footbridge

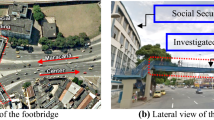
The Seriate footbridge in Fig. 1a, 63.75 m long, connects two cycle routes in the Serio Park (near to Milan, Italy). The width of the timber deck on a steel grid (Fig. 1b) ranges between 2.5 m at the entrance and 5 m at mid-span. The slightly curved longitudinal steel girders have a rise of 1.3 m. The transverse beams of the steel grid (Fig. 1b) are spaced 1 m apart and are subdivided in main and secondary elements. Main girders have a tapered section and are connected to the hangers. Secondary beams have an IPE 120 cross-section. The stringers are a pair of IPE 330 beams at the edges, and a central beam with a circular section (ϕ = 298.5 mm), deemed to stabilize the deck on the horizontal plane.

Fig. 1.

Seriate footbridge: (a) overall view; (b) footbridge deck, detail of longitudinal and transverse beam.

A series of X-braces (Fig. 1b) connects the main transverse girders providing stiffness in the horizontal plane. The timber deck (Fig. 1b) has only a minor structural role, providing the walking surface. The ends of the transverse main girders are crossed by stabilizing cables, whose sliding in the longitudinal direction is allowed by the interposition of a polymeric layer between the two contact surfaces.

The suspension system is composed of: (a) steel main pylons, slightly inclined with respect to the vertical plane, supporting the suspension system and the backstays cables as shown in Fig. 1a; (b) 2 main suspension cables (ϕ = 60 mm), supporting the longitudinal girders through 42 vertical hangers (ϕ = 16 mm); (c) backstays cables (ϕ = 60 mm), connecting the pylons top to the ground; (d) two stabilizing cables of opposed curvatures ϕ = 40 mm.

The suspension system is symmetric neither about the vertical plane crossing the longitudinal bridge axis nor about the vertical plane crossing the mid-span. All the cables were pre-tensioned during construction.

The dynamic behavior of the footbridge was investigated through a dynamic test. The bridge response under ambient excitation was recorded with conventional accelerograms. With output-only techniques typical of the operational modal analysis, 14 vibration modes were identified in the frequency range 0–10 Hz. The frequency of the fundamental mode was 1.03 Hz. Figure 2 depicts four mode shapes, whose natural frequency is into the walking load critical range, identified using the FDD method.

Fig. 2.

Mode shapes identified: (a) mode 2; (b) mode 3; (c) mode 4; (d) mode 5

A finite element model of the bridge, based on the original drawings, was set up within the ANSYS framework and a modal analysis was carried out in order to obtain the numerical dynamic properties. The agreement between experimental and numerical values is fully satisfactory. Further details on the derivation of the FE model are found in [8].

3 Pedestrian Mechanical Model

A mechanical system is the most accurate pedestrian modelling in the analytical study of human-structure interaction. In this work, reference is made to a bipedal mechanical model recently proposed [7], capable to simulate the human locomotion, characterized by the alternate sequence of single support phase (SSP) and double support phase (DSP) of the typical human gait cycle (Fig. 3a). SSP begins when the leading foot hits the ground and the trailing foot is off the ground, moving through the air towards the next position. DSP starts when the trailing foot hits the ground becoming the leading foot and both feet are in contact with the bridge deck.

Fig. 3.

Human gait cycle: (a) sequence of SSP and DSP; (b) single foot force model.

The pedestrian is modelled as a SDOF mass-spring-damper mechanical system. Its equation of motion takes into account the interaction with the bridge and the biomechanical force acting on it. The MSD system has two spring-damper legs (Fig. 4), capable to reproduce the correct human gait (SSP and DSP in a sequence). The legs parameters follow the data provided by Kim & Park [9]. The mass, lumped at the centre of gravity of the body, oscillates in the vertical direction only. A fictitious bio-mechanical force F_b excites the MSD system. By solving an inverse problem, in this work F_b has been derived as the force that, applied on the system moving on a rigid surface, produces a ground reaction force (transmitted by each leg) matching the single foot force model in Fig. 3b.

Fig. 4.

MSD model: left, only one leg is in contact, right, both legs are in contact.

4 Equations of Motion for the Coupled System

The coupled equations of motion governing the HSI are written for the overall system composed of the bridge and the pedestrian mechanical system, where the bridge is discretized with the FE method. Hence, the problem has a finite number of coordinates. The two systems interact at contact points exchanging a vertical contact force: the bridge, due to its flexibility, oscillates and applies a motion at the base of pedestrian’s feet. The walking pedestrian, excited by the biomechanical force and the motion applied by the bridge, transmits to the bridge deck a set of contact forces (leg internal forces). The coupled equations are first forcibly uncoupled and then solved via an iterative procedure [7, 10]. The pedestrian model and the uncoupled algorithm are implemented in a research code named INTER 2.0 [7].

4.1 Pedestrian Traffic and Spatial Configuration in INTER 2.0

Inter 2.0 can consider either a single pedestrian or a group of pedestrians. In both cases the pedestrian’s trajectory is a straight line parallel to the bridge axis, not necessarily coinciding with a line of nodes. The groups of pedestrians can be distributed according to three different spatial configurations: uniform grid (Fig. 5a), “chessboard” (Fig. 5b) and “random-like” distribution (Fig. 5c). Pedestrians move with the same step velocity and their mutual (deterministic) distance do not change during the analysis.

Fig. 5.

Pedestrians’ spatial configuration: (a) uniform grid; (b) “chessboard” grid; (c) “random-like” grid.

Three types of synchronization have been considered: full, partial and no synchronization, the only compatible with the probabilistic approach. A total synchronization takes place if n identical pedestrians walk perfectly in phase. Partial synchronization means in-phase walking along rows and uncorrelated phases among rows. No synchronization means that a group of n pedestrians walks with completely uncorrelated phases. The degree of synchronization is independent of the spatial configuration.

5 Numerical Results

The relevant response parameters adopted in this work are the maximum vertical accelerations and the time histories of vertical displacements. Both accelerations and displacements are evaluated in seven transverse sections of the deck for three points: two are placed at the base of handrails and the third one is on the longitudinal axis of the footbridge deck (Fig. 6).

Fig. 6.

(a) Bridge cross sections, (b) corresponding points nodes considered in the analysis.

The analyses have been performed with a staggered approach, without introducing the iteration process since, as the time step decreases, the solutions are convergent. The integration time step ∆t is 0.005 s, quite smaller than 1/10 of the period of the 14th mode, and sufficient to discretize accurately the forcing term. The Rayleigh damping matrix is computed for a 1% damping, a value experimentally identified, on the first and fourth mode, and the Newmark’s coefficient β and γ are respectively 0.25 and 0.5 (constant acceleration method). Finally, a velocity of 1.3 m/s, normal distribution mean value [11], is considered for each pedestrian.

Numerical analyses are computed with the objective of evaluating the effect, on the bridge response, of a few parameters: distance between pedestrians, degree of synchronization, correlation in terms of step frequency and spatial distribution.

5.1 Six Pedestrians with Different Trajectories

The six people are placed in a single line, parallel to the bridge axis, with a mutual distance of 2 m. Each of the three analyses is characterized by a different value of the eccentricity of the rectilinear trajectory from the longitudinal axis. In the first one, the pedestrians are walking on the left side of the deck, with an eccentricity of 1 m. In the second one, the eccentricity is the same, but the pedestrians are walking on the right side. Finally, the last configuration provides six pedestrians walking along the bridge longitudinal axis.

The six MSD pedestrians are considered uncorrelated and unrestricted. They have their own step frequency (f₁ = 1.843 Hz, f₂ = 2.057 Hz, f₃ = 1.675 Hz, f₄ = 1.776 Hz, f₅ = 1.634 Hz, f₆ = 1.799 Hz) drawn from a normal distribution, and no synchronization has been taken into account. The pedestrians have a common weight and height of 700 N and 1.70 m, respectively. Each pedestrian crosses the bridge about in 49 s and the last pedestrian exits the bridge about 8 s after the first.

Figure 7a–c show, respectively, the comparison between the displacement time-histories of nodes 16, 17 and 18 (at section #6, at ¾ of the span), for the cases of people walking along the left, right and central side, respectively. The comparison highlights that eccentric transits induce a torsional behavior, which could be amplified by the configuration of the bridge suspension system, which is not-symmetric respect to both the bridge longitudinal axis and the mid-span.

Fig. 7.

Displacement time-history of nodes at Sect. 6 for the pedestrians with: (a) left; (b) right and (c) no eccentricity. (d) Maximum vertical accelerations with six pedestrians having different eccentricity, for all nodes (s# identifies the section).

The analysis of plots in Fig. 7a and b highlights that the torsional behavior becomes larger when the pedestrians cross the section at study. Obviously, nodes closer to the pedestrians’ trajectory, i.e. node 16 for a left eccentricity and node 18 for a right one, experience displacements larger than those of the node on the opposite side. On the other hand, the pedestrians walking along the longitudinal axis do not induce a torsional effect. In fact, in Fig. 7c (same nodes of Fig. 7a, b), the displacement histories are overlapped during the whole time interval.

Figure 7d shows the maximum vertical acceleration attained at each of the nodes in Fig. 6b for the three analyses at study. As a general trend, at each section the eccentric transits produce larger accelerations than a centered load, with the exception of nodes at Sections 4 and 7, where the results are similar for the three load configurations. In addition, it can be noticed that, as for the displacement response, the lateral nodes of each section experience the largest acceleration with the first two load configurations, while a central trajectory does not produce a considerable difference on the nodes belonging to the same section. This finding can be explained with the modal shape of the third mode, a torsional mode with a node around midspan.

The vertical accelerations, produced by different transits, have been further analyzed by comparing, at each node, the corresponding Fourier spectra. From the analysis of the results, the following statements can be inferred:

• Fourier spectra due to eccentric transits, computed for lateral nodes, both on the left and right side, have a common pattern, different from that induced by pedestrians walking along the longitudinal axis (Fig. 8). However, the lateral nodes at mid-span show the same trend and frequency content (results not reported here for the sake of brevity);

  Fig. 8.

  

  Fourier spectrum of vertical acceleration at node 9 (Sect. 3): (a) left eccentricity, (b)right eccentricity, (c) no eccentricity.

• central nodes, along the longitudinal axis, are not influenced by the pedestrians’ position. In fact, at each node, the comparison among the three Fourier spectra shows a common pattern (Fig. 9). This behavior is coherent with the shape of the 8th mode, a torsional one, which has nodes close to the bridge axis [8].

  Fig. 9.

  

  Fourier spectrum of vertical acceleration at node 11 (Sect. 4): (a) left eccentricity, (b) right eccentricity, (c) no eccentricity.

5.2 Nine Pedestrian with Different Spatial Distributions

This section investigates the effect of pedestrians’ spatial distribution on the bridge response. The goal has been pursued by modifying the longitudinal distance among pedestrians, while the transverse one, equal to 0.75 m, remains constant. Analyses have been carried out by adopting nine pedestrians with a uniform distribution on three rows. The center of gravity of the group is on the longitudinal bridge axis. Eight spatial distributions have been considered, characterized by an increasing value of the longitudinal distance d among two subsequent pedestrians’ rows, equally spaced in a range between a lower value of 1 m and an upper one of 4.5 m. The pedestrians have a common step frequency, a common weight and a common height of 1.7 Hz, 700 N, and 1.70 m, respectively. Each pedestrian walks with a step velocity of 1.3 m/s. Pedestrians are not synchronized.

As a general trend, the comparison among the results of the eight analyses shows that the maximum accelerations tend to increase with the distance. However, the increment is more pronounced in the interval between 1.0 m and 2.5 m, becoming null or negligible when d exceeds 2.5 m. A few nodes, i.e. node 11, experience a slight decrease after 3 m. On the contrary, the accelerations at Sects. 3 and 5 increase when d varies from 1 m to 1.5 m and then tend to decrease. These two opposite behaviors are shown in Fig. 10a and b, respectively.

Fig. 10.

Plot of maximum accelerations as a function of distance d: (a) nodes 2, 11 and 20, (b) nodes 7, 8 and 9.

This behavior (larger accelerations associated to a larger distance) could be explained with the fact that pedestrians with a larger mutual distance excite the footbridge for a longer time than pedestrians close to each other. Also an effect of the mode shapes could have played a role.

On the other hand, the different pattern (some nodal accelerations increase while others decrease) could be related to the modal damping. In fact, by analyzing the Fourier spectra of acceleration of each node, it can be noticed that the maximum peak is not always in the same frequency range. Thus, the response of the seven sections at study could be affected by different modes, having different modal damping.

In this case, the Fourier spectra of nodes at Sects. 1, 2, 4, 6 and 7 have a maximum peak about the frequency describing the 2nd harmonic of the load (3.4 Hz), while the nodes at Sects. 3 and 5 experience accelerations whose Fourier spectrum has a maximum peak about the step frequency (1.7 Hz). Nodes on the same section are characterized by the same Fourier spectra. This pattern is common for the eight analyses.

Figure 11a and b show the Fourier spectrum of acceleration at node 8 and 11, respectively, while Fig. 11c and d show the time-history of vertical acceleration at node 20 (Sect. 7). The pattern of Fourier spectrum is common for the eight analyses highlighting that, whatever the longitudinal distance, the modes that are excited are always the same. As for the Fourier spectra, the eight acceleration histories, even though with different amplitudes, have a common pattern characterized by a beat phenomenon. Thus, it can be stated that the increase of distance induces only a variation in the acceleration amplitude, without modifying the trend of the time-history or the frequency content of Fourier spectrum.

Fig. 11.

Fourier spectrum of vertical acceleration at node 8 (Sect. 3): (a) d = 1.5 m, (b) d = 3.5 m. Acceleration time history at node 20 (Sect. 7): (c) d = 1.5 m, (d) d = 3.5 m.

6 Conclusions

In this paper the response of a lively footbridge to walking pedestrians is computed with an uncoupled approach. The bridge is modeled with the Finite Element Method. The pedestrian is represented by a mechanical bipedal model, simulating the sequence of SSP and DSP, typical of the human gait. The two systems interacts at contact points that are not necessarily coincident with bridge mesh nodes.

The case study is a lively footbridge, whose dynamic behavior has been extensively analyzed both experimentally and numerically. The results of the numerical analyses, computed with the objective of evaluating the effect on the bridge response of a few parameters (distance between pedestrians and spatial distribution) can be summarized as it follows:

• The numerical response is coherent with (and determined by) the dynamic properties of the bridge. In fact, the pattern of maximum acceleration follows the bridge modes excited by pedestrians’ walking.

• Acceleration time histories show a beat phenomenon. This fact can be explained by observing that the bridge has nine frequencies within the walking frequency range 1–4 Hz (considering also the second harmonic of the load).

• The effect of the second harmonic of the load (biomechanical force with a MSD model) on the response of the bridge at study is not negligible.

• Eccentric transits produce larger accelerations than those induced by a group of pedestrian walking without eccentricity. Moreover, as it was expected, the eccentric transit induces a torsional behavior in the bridge response.

• In general, the vertical accelerations increase with the longitudinal distance among pedestrians, although this is not a linear trend. In fact, the acceleration increment tends to become negligible or null for distances exceeding 3 m.

It is important to note that the analytical formulation and its numerical implementation are not restricted to the footbridge at study or to the mechanical model proposed. In fact, the generality of the uncoupled approach allows taking into account both different footbridges and different mechanical systems.