Accurate Dynamics Modeling and Feedback Control for Maneuverable-Net Space Robot

Abstract

Tethered Space Net (TSN) has been proposed since there is an increasing threat of space debris to spacecraft and astronauts in recent years. In this paper, we propose an improved TSN, named Maneuverable-Net Space Robot (MNSR), which has four maneuvering units in its four corners (square net). The four maneuverable units make the MNSR controllable. Because of autonomous maneuverability, the attitude dynamics of the platform, master tether and flexible net are strongly coupled. In order to design an effective controller to maintain the configuration of the maneuverable net, an accurate dynamics model of MNSR based on the Lagrangian method is derived. In our model, we consider the three-dimensional attitude of the platform, master tether and maneuvering-net as well. Due to the vibration of the in-plane and out-of-plane angles of the net tethers, feedback control is employed for MNSR. The simulation results demonstrate that the proposed control is efficient and suitable for the MNSR system.

1 Introduction

There is an increasing threat of space debris to spacecraft and astronauts since the first satellite was launched in October 4th, 1957 [1]. Some researchers proposed Tethered Space Capturing System to complete the capturing task which aimed at space debris removal [2]. Tethered Space Capturing System contains Tethered Space Robot (TSR) [3] (shown in Fig. 1), Tethered Space Harpoon (TSH) [4] (shown in Fig. 2) and Tethered Space Net (TSN) [5] (shown in Fig. 3). Nowadays, Tethered Space Net (TSN) has attracted much attention [5, 6]. TSN consists of platform satellite, tether, space net and four flying weights in each corner of the net, which is shown in Fig. 3. TSN is a flexible system and it converts traditional point-to-point capture into surface-to-point capture, which lowers the requirement on capture precision. Besides, it can be used for uncooperative target capture and long distance capture. So Tethered Space Net (TSN) is one of the most promising solutions for active space debris removal.

Fig. 1.

Tethered Space Robot (TSR)

Fig. 2.

Tethered Space Harpoon (TSH)

Fig. 3.

Tethered Space Net (TSN)

Fig. 4.

Maneuverable-Net Space Robot (MNSR)

A lot of studies have been focused on the TSN. Based on the previous studies of space webs, various dynamics model of TSN have been derived, such as rigid model [7], mass-spring model [8], absolute nodal coordinate formulation (ANCF) model [9]. Rigid model is most commonly used in tethered space system. It can be better used for analyzing in-plane and out-of-plane angles of the tether. Mass-spring model is always used for establishing a quadrangular mesh net, while absolute nodal coordinate formulation (ANCF) model can better describe the flexibility between two nodes on the net and reflect the dynamics of TSN. However, rigid model always treats the platform satellite as point mass, while the literatures about ANCF model only demonstrate the dynamics of the net and neglect the dynamics of platform. Thus, an accurate model for TSN, which considered the dynamics of platform, is necessary.

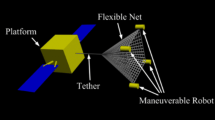
Based on the TSN, an improved TSN is proposed, named Maneuverable Net Space Robot (MNSR), which is shown in Fig. 4. The big difference between TSN and MNSR is that the MNSR has four maneuvering units in four corners (square net) instead of the four flying weights located at the four corners of traditional TSN. The four maneuvering units make the MNSR controllable. So the MNSR is more preferable for orbital capture. Huang et al. have already studied the dynamics and configuration control of MNSR in [10, 11].

In this paper, an accurate dynamic model of MNSR is derived in Sect. 2. Then in Sect. 3, a feedback control scheme is proposed for maintaining the configuration of maneuverable net. Some numerical simulations are shown to verify the control scheme in Sect. 4. Finally, the contribution of this paper is briefly summarized in Conclusion Sect. 5.

2 Dynamics Model

2.1 Description of the System

The schematic figure of the MNSR and generalized coordinates used to describe the motion are shown in Fig. 5. The position of the centre of the mass of the system C in its orbit around the Earth is defined by the true anomaly $\gamma$ and the orbit radius $R_c$. The coordinate system $C - {x_o}{y_o}{z_o}$ has ${z_o}$ axis along the orbit normal, ${y_o}$ axis radially outward away from the Earth along the local vertical and ${x_o}$ axis along the local horizontal completing the right hand triad. The six rotating coordinate system $({C_p} - {x_p}{y_p}{z_p}, {C_t} - {x_t}{y_t}{z_t},{C_k} - {x_k}{y_k}{z_k}, k=1,2,3,4)$ for platform, master tether and net tether are used with their origins at the center of mass of each of them respectively. The coordinate ${C_p} - {x_p}{y_p}{z_p}$ is obtained by the rotation $\theta$ (pitch angle of the platform satellite) about ${z_o}$ axis, and $\psi$ (roll angle of the platform satellite) about ${y_o}$ axis. The coordinate system ${C_t} - {x_t}{y_t}{z_t}$ is obtained via the rotation ${\alpha }$ (the in-plane angle of master tether) about ${z_o}$ axis, and ${\beta }$ (the out-of-plane angle of master tether) about ${y_o}$ axis. The coordinate ${C_k} - {x_k}{y_k}{z_k}$ is obtained via the rotation ${\alpha _k}$ (the in-plane angle of net tether) about ${z_o}$ axis, and ${\beta _k}$ (the out-of-plane angle of net tether) about ${y_o}$ axis. ${m_0},{m_t},m$ are the masses of the platform, master tether and maneuverable net tether respectively. l, lw are the length of master tether and tether net respectively.

Fig. 5.

Generalized coordinates for MNSR

2.2 Motion Equations of the System

The following assumptions are made for the dynamic model of MNSR.

• 1. Four maneuvering units are considered as mass points. Thus, the maneuverable net can be considered as four tethers (net tether) and four mass points (maneuvering unit) (shown in Fig. 5). The effect of the variation of maneuvering unit’s attitude and material damping of the net are ignored. The platform is considered as rigid body, and tethers are considered as rigid, inextensible and remaining straight.

• 2. Gravity is treated to be the only external force acting on the system.

• 3. The center of mass of the system is assumed to follow a circular Keplerian orbit.

The position vectors of platform, an elemental mass of master tether and net tether with respect to the center of the Earth, are respectively

$$\begin{aligned} \left\{ \begin{array}{l} {{\varvec{R}_t}} = {{\varvec{R}_0}} + {{\varvec{b}_0}} + {\textstyle {1 \over 2}}{{\varvec{r}_t}}\\ {{\varvec{R}_1}} = {{\varvec{R}_0}} + {{\varvec{b}_0}} + {{\varvec{r}_t}} + {{\varvec{r}_1}}\\ {{\varvec{R}_2}} = {{\varvec{R}_0}} + {{\varvec{b}_0}} + {{\varvec{r}_t}} + {{\varvec{r}_2}}\\ {{\varvec{R}_3}} = {{\varvec{R}_0}} + {{\varvec{b}_0}} + {{\varvec{r}_t}} + {{\varvec{r}_3}}\\ {{\varvec{R}_4}} = {{\varvec{R}_0}} + {{\varvec{b}_0}} + {{\varvec{r}_t}} + {{r_4}} \end{array} \right. \end{aligned}$$

(1)

where, ${\varvec{R}_0},{\varvec{R}_t},{\varvec{R}_k}(k = 1,2,3,4)$ are the position vectors of the mass of platform, master tether and net tethers respectively. ${\varvec{b}_0}$ is the offset from center of mass of platform to the attachment points on it. ${\varvec{r}_t},{\varvec{r}_k}(k = 1,2,3,4)$ denote the position vectors of an elemental mass of master tether and net tether with respect to the center of mass of the system.

The kinetic energy due to translation of the whole system is derived as

$$\begin{aligned} {T_{rans}} = {\textstyle {1 \over 2}}{m_0}{{ \varvec{{\dot{R}}}}_0}{{\varvec{{\dot{R}}}}_0} + {\textstyle {1 \over 2}}{m_t}{{\varvec{{\dot{R}}}}_t}{{\varvec{{\dot{R}}}}_t} + {\textstyle {1 \over 2}}m\sum \limits _{k = 1}^{n = 4} {({{{\varvec{{\dot{R}}}}}_k}{{{\varvec{{\dot{R}}}}_k})}} \end{aligned}$$

(2)

where

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{{\dot{R}}}_0} = {\varvec{{\dot{R}}}_c} - {\textstyle {{{m_t} + 4m} \over M}}{\varvec{{\dot{b}}}_o} - {\textstyle {{{\textstyle {1 \over 2}}{m_t} + 4m} \over M}}{\varvec{{\dot{r}}}_t} - {\textstyle {m \over M}}\sum \limits _{k = 1}^{n = 4} {{\varvec{{\dot{r}}}_k}} \\ {\varvec{{\dot{R}}}_t} = {\varvec{{\dot{R}}}_c} + {\textstyle {{{m_0}} \over M}}{\varvec{{\dot{b}}}_o} + {\textstyle {{{\textstyle {1 \over 2}}({m_0} - 4m)} \over M}}{\varvec{{\dot{r}}}_t} - {\textstyle {m \over M}}\sum \limits _{k = 1}^{n = 4} {{\varvec{{\dot{r}}}_k}} \\ {\varvec{{\dot{R}}}_k} = {\varvec{{\dot{R}}}_c} + {\textstyle {{{m_0}} \over M}}{\varvec{{\dot{b}}}_0} + {\textstyle {{{m_0} + {\textstyle {1 \over 2}}{m_t}} \over M}}{\varvec{{\dot{r}}}_t} - {\textstyle {{m - M} \over M}}{\varvec{{\dot{r}}}_k} - {\textstyle {m \over M}}\sum \limits _{q \ne k}^{1,2,3,4} {{\varvec{{\dot{r}}}_q}} \end{array} \right. \end{aligned}$$

(3)

and $M = {m_0} + {m_t} + 4m$.

The rotational kinetic energy of the whole system is determined via

$$\begin{aligned} \ {T_{rot}} = {\textstyle {1 \over 2}}{{\varvec{{\omega }}}_0}^{{T}}{{\varvec{{I}}}_0}{{\varvec{{\omega }}}_0} \end{aligned}$$

(4)

where ${{\varvec{{I}}}_0}$ is the moments inertia of platform, ${{\varvec{{I}}}_0} = diag({I_{oxx}},{I_{oyy}},{I_{ozz}})$

The potential energy of the system is given by

$$\begin{aligned} \ V = - \mu {m_0}{\textstyle {1 \over {\left| {\varvec{{R_0}}} \right| }}} - \mu {m_t}{\textstyle {1 \over {\left| {{{\varvec{{R}}}_t}} \right| }}} - \mu m\sum \limits _{k = 1}^{n = 4} {{\textstyle {1 \over {\left| {{{\varvec{{R}}}_k}} \right| }}}} \end{aligned}$$

(5)

where $\mu$ is the gravitational constant of the Earth.

The Lagrangian equation is used to obtain the equations of motion of the system from the kinetic and potential energy expressions

$$\begin{aligned} \frac{{d}}{{{dt}}}\left( {\frac{{\partial {T}}}{{\partial {\varvec{{\dot{q}}}_{i}}}}} \right) - \frac{{\partial {T}}}{{\partial {\varvec{{\dot{q}}}_{i}}}} + \frac{{\partial {V}}}{{\partial {\varvec{{\dot{q}}}_{i}}}} = {\varvec{Q}_{i}} \end{aligned}$$

(6)

where T and V are the total kinetic and potential energies of the system; ${\varvec{q}_{i}}$ are the generalized coordinates, which are chosen to be ${\varvec{q}_{i}} = {\{ \theta \;\;\psi \;\;\alpha \;\;\beta \;\;l\;\;{\alpha _k}\;\;{\beta _k}\} ^T}, (k=1,2,3,4)$. Consequently, generalized forces vector is ${\varvec{Q}_{i}}$, which is also the control force and chosen to be ${\varvec{Q}_{i}} = {\{ {{Q}_\theta }\;\;{{Q}_\psi }\;\;{{Q}_\alpha }\;\;{{Q}_\beta }\;\;{{Q}_l}\;\;{{Q}_{{\alpha _k}}}\;\;{{Q}_{{\beta _k}}}\} ^{T}}$.

A set of dimensionless quantities are defined as follows

$$\begin{aligned} \varLambda = {l / {Lr,}} \;\;\tau = \dot{\gamma }t,\;\; {\left( {} \right) ^\prime } = {{\mathrm{{d}}\left( {} \right) } / {\mathrm{{d}}\tau }} \end{aligned}$$

(7)

where Lr is the reference length of tether, $\varLambda$ is the nondimensional tether length, and $\tau$ is the non-dimensional time.

The non-dimensional equations of MNSR are then given by

$$\begin{aligned} \begin{array}{l} \theta ''[{M_A}{\cos ^2}\psi + Ioxx \cdot {\sin ^2}\psi + Iozz \cdot {\cos ^2}\psi ] + \alpha ''{M_D}\varLambda Lr\cos \psi \cos \beta \\ + \sum \limits _{k = 1}^{n = 4} {[{\alpha _k^{\prime \prime }}{M_E}lw\cos \psi \cos {\beta _k}} ]\\ - \psi '\left[ \begin{array}{l} 2{M_A}(1 + \theta ')\cos \psi \sin \psi + {M_D}\varLambda Lr(1 + \alpha ')\sin \psi \cos \beta \\ + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_E}lw(1 + {\alpha _k^\prime } )\sin \psi \cos {\beta _k}} \right] + 2Ioxx(1 + \theta ')\sin \psi \cos \psi } \\ {- 2Iozz(1 + \theta ')\sin \psi \cos \psi } \end{array} \right] \\ - \beta '{M_D}\varLambda Lr(1 + \alpha ')\cos \psi \sin \beta - \sum \limits _{k = 1}^{n = 4} {\left[ {{\beta _k^\prime } {M_E}lw(1 + {\alpha _k^\prime } )\cos \psi \sin {\beta _k}} \right] } \\ + \varLambda '{M_D}Lr(1 + \alpha ')\cos \psi \sin \beta + 3{M_A}{\cos ^2}\psi \cos \theta \sin \theta \\ + {M_D}\varLambda Lr\left( {2\sin \theta \cos \psi \cos \alpha \cos \beta + \cos \theta \cos \psi \sin \alpha \cos \beta } \right) \\ + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_E}lw\left( {2\sin \theta \cos \psi \cos {\alpha _k}cos{\beta _k} + \cos \theta \cos \psi \sin {\alpha _k}\cos {\beta _k}} \right) } \right] } \\ - {Q_\theta }/{\varOmega ^2} = 0 \end{array} \end{aligned}$$

(8)

$$\begin{aligned} \begin{array}{l} \psi ''\left[ {{M_A} + {I_{oyy}}} \right] + \beta ''{M_D}\varLambda Lr + \sum \limits _{k = 1}^{n = 4} {\left[ {{{\beta ''}_k}{M_E}lw} \right] } + {M_D}Lr\varLambda '\beta ' + {M_A}{(1 + \theta ')^2}\cos \psi \sin \psi \\ + {M_D}\varLambda Lr(1 + \theta ')(1 + \alpha ')\cos \beta \sin \psi + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_E}lw(1 + \theta ')(1 + {{\alpha '}_k})\cos {\beta _k}\sin \psi } \right] } \\ + 3{M_A}{\cos ^2}\theta \cos \psi \sin \psi + {M_D}\varLambda Lr(2\sin \psi \cos \theta \cos \alpha \cos \beta \\ - \sin \psi \sin \theta \sin \alpha \cos \beta + \cos \psi \sin \beta )\\ + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_E}lw(2\sin \psi \cos \theta \cos {\alpha _k}\cos {\beta _k} - \sin \psi \sin \theta \sin {\alpha _k}\cos {\beta _k} + \cos \psi \sin {\beta _k})} \right] } \\ - {I_{oxx}}{(1 + \theta ')^2}\sin \psi \cos \psi + {I_{ozz}}{(1 + \theta ')^2}\sin \psi \cos \psi \\ - {Q_\psi }/{\varOmega ^2} = 0 \end{array} \end{aligned}$$

(9)

$$\begin{aligned} \begin{array}{l} \alpha ''{M_B}{\cos ^2}\beta {\varLambda ^2}L{r^2} + \theta ''{M_D}\varLambda Lr\cos \psi \cos \beta + \sum \limits _{k = 1}^{n = 4} {\left[ {{\alpha _k^{\prime \prime }}{M_F}lw\varLambda Lr\cos \beta \cos {\beta _k}} \right] } \\ - \beta '\Big [ {2{M_B}{\varLambda ^2}L{r^2}\cos \beta \sin \beta \cdot (1 + \alpha ') + {M_D}\varLambda Lr(1 + \theta ')\cos \psi \sin \beta } \\ {\left. {}+ \sum \limits _{k = 1}^{n = 4} {\left[ {{M_F}lw\varLambda Lr(1 + {\alpha _k^\prime } )\sin \beta \cos {\beta _k}} \right] } \right] }\\ - \psi '{M_D}\varLambda Lr(1 + \theta ')\sin \psi \cos \beta - \sum \limits _{k = 1}^{n = 4} {\left[ {{\beta _k^\prime } {M_F}lw\varLambda Lr(1 + {\alpha _k^\prime } )\cos \beta \sin {\beta _k}} \right] } \\ + Lr\varLambda '\left[ 2{M_B}\varLambda Lr(1 + \alpha '){{\cos }^2}\beta + {M_D}(1 + \theta ')\cos \psi \cos \beta \right. \\ \left. + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_F}lw(1 + {\alpha _k^\prime } )\cos \beta \cos {\beta _k}} \right] } \right] \\ + 3{M_B}{\varLambda ^2}L{r^2}{\cos ^2}\beta \cos \alpha \sin \alpha + {M_D}\varLambda Lr(2\sin \alpha \cos \theta \cos \psi \cos \beta + \cos \alpha \sin \theta \cos \psi \cos \beta )\\ + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_F}lw\varLambda Lr(2\sin \alpha \cos \beta \cos {\alpha _k}\cos {\beta _k} + \cos \alpha \cos \beta \sin {\alpha _k}\cos {\beta _k})} \right] } \\ - {Q_\alpha }/{\varOmega ^2} = 0 \end{array} \end{aligned}$$

(10)

$$\begin{aligned} \begin{array}{l} \beta ''{M_B}{\varLambda ^2}L{r^2} + \psi ''{M_D}\varLambda Lr + \sum \limits _{k = 1}^{n = 4} {\left[ {{\beta _k^{\prime \prime }}{M_F}lw\varLambda Lr} \right] } \\ + \varLambda 'Lr\left[ {{M_D}\psi ' + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_F}lw{\beta _k^\prime }} \right] + 2{M_B}\beta '\varLambda Lr} } \right] \\ + {M_B}{\varLambda ^2}L{r^2}{(1 + \alpha ')^2}\cos \beta \sin \beta + {M_D}\varLambda Lr(1 + \theta ')(1 + \alpha ')\cos \psi \sin \beta \\ + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_F}lw\varLambda Lr(1 + \alpha ')(1 + {\alpha _k^\prime } )\cos {\beta _k}\sin \beta } \right] } + 3{M_B}{\varLambda ^2}L{r^2}{\cos ^2}\alpha \cos \beta \sin \beta \\ + {M_D}\varLambda Lr(2\sin \beta \cos \theta \cos \psi \cos \alpha - \sin \beta \sin \theta \cos \psi \sin \alpha + \sin \psi \cos \beta )\\ + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_F}lw\varLambda Lr(2\sin \beta \cos \alpha \cos {\alpha _k}\cos {\beta _k} - \sin \beta \sin \alpha \sin {\alpha _k}\cos {\beta _k} + \cos \beta \sin {\beta _k})} \right] } \\ - {Q_\beta }/{\varOmega ^2} = 0 \end{array} \end{aligned}$$

(11)

$$\begin{aligned} \begin{array}{l} \varLambda ''Lr{M_B} - {M_B}\varLambda Lr\left[ {{{(1 + \alpha ')}^2}{{\cos }^2}\beta + \beta ''} \right] - {M_D}\left[ {(1 + \theta ')(1 + \alpha ')\cos \psi \cos \beta + \psi '\beta '} \right] \\ - \sum \limits _{k = 1}^{n = 4} {\left[ {{M_F}lw\left[ {(1 + \alpha ')(1 + {\alpha _k^\prime } )\cos \beta \cos {\beta _k} + \beta '{\beta _k^\prime } } \right] } \right] } - 3{M_B}\varLambda Lr{\cos ^2}\beta {\cos ^2}\alpha \\ + {M_D}\left[ { - 2\cos \theta \cos \psi \cos \alpha \cos \beta + \sin \theta \cos \psi \sin \alpha \cos \beta + \sin \psi \sin \beta } \right] \\ + \sum \limits _{k = 1}^{n = 4} {\left[ {{M_F}lw\left[ { - 2\cos \alpha \cos \beta \cos {\alpha _k}\cos {\beta _k} + \sin \alpha \cos \beta \sin {\alpha _k}\cos {\beta _k} + \sin \beta \sin {\beta _k}} \right] } \right] } \\ - {Q_\varLambda }/{\varOmega ^2} = 0 \end{array} \end{aligned}$$

(12)

$$\begin{aligned} \begin{array}{l} {\alpha _k^{\prime \prime } }{M_C}l{w^2}{\cos ^2}{\beta _k} + \theta ''{M_E}lw\cos \psi \cos {\beta _k} + \alpha ''{M_F}lw\varLambda Lr\cos \beta \cos {\beta _k}\\ + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}\cos {\beta _k}\cos {\beta _q} \cdot {\alpha _q^{\prime \prime } }} \right] } \\ + {\beta _k^\prime } \left[ \begin{array}{l} {M_C}l{w^2}(1 + {\alpha _k^\prime } )2\cos {\beta _k}( - \sin {\beta _k}) + {M_E} \cdot lw(1 + \theta ')\cos \psi ( - \sin {\beta _k})\\ + {M_F}lw\varLambda Lr(1 + \alpha ')\cos \beta ( - \sin {\beta _k}) + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(1 + {\alpha _q^\prime } )( - \sin {\beta _k})\cos {\beta _q}} \right] } \end{array} \right] \\ \mathrm{{ + }}\psi '{M_E}lw(1 + \theta ')( - \sin \psi )\cos {\beta _k} + \varLambda 'Lr{M_F}lw(1 + \alpha ')\cos \beta \cos {\beta _k}\\ + \beta '{M_F}lw\varLambda Lr(1 + \alpha ')( - \sin \beta )\cos {\beta _k} + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(1 + {\alpha _q^\prime } )\cos {\beta _k}( - \sin {\beta _q}){\beta _q^\prime } } \right] } \\ + 3{M_C}l{w^2}{\cos ^2}{\beta _k}\cos {\alpha _k}\sin {\alpha _k} + {M_E}lw(2\sin {\alpha _k}\cos \theta \cos \psi \cos {\beta _k} + \cos {\alpha _k}\sin \theta \cos \psi \cos {\beta _k})\\ + {M_F}lw\varLambda Lr(2\sin {\alpha _k}\cos \alpha \cos \beta \cos {\beta _k} + \cos {\alpha _k}\sin \alpha \cos \beta \cos {\beta _k})\\ + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(2\sin {\alpha _k}\cos {\beta _k}\cos {\alpha _q}\cos {\beta _q} + \cos {\alpha _k}\cos {\beta _k}\sin {\alpha _q}\cos {\beta _q})} \right] } \\ - {Q_{{\alpha _k}}}/{\varOmega ^2} = 0 \end{array} \end{aligned}$$

(13)

$$\begin{aligned} \begin{array}{l} {\beta _k^{\prime \prime }}{M_C}l{w^2} + \psi ''{M_E}lw + \beta ''{M_F}lw\varLambda Lr \\ + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}{\beta _q^{\prime \prime } }} \right] } + {M_C}l{w^2}{(1 + {\alpha _k^\prime } )^2}\cos {\beta _k}\sin {\beta _k}\\ + {M_E}lw(1 + \theta ')(1 + {\alpha _k^\prime } )\cos \psi \sin {\beta _k} + {M_F}lw\varLambda 'Lr\beta ' \\ + {M_F}lw\varLambda Lr(1 + \alpha ')(1 + {\alpha _k^\prime } )\cos \beta \sin {\beta _k}\\ + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(1 + {\alpha _k^\prime } )(1 + {\alpha _q^\prime } )\cos {\beta _q}\sin {\beta _k}} \right] } + 3{M_C}l{w^2}{\cos ^2}{\alpha _k}\cos {\beta _k}\sin {\beta _k}\\ + {M_E}lw(2\sin {\beta _k}\cos \theta \cos \psi \cos {\alpha _k} - \sin {\beta _k}\sin \theta \cos \psi \sin {\alpha _k} + \sin \psi \cos {\beta _k})\\ + {M_F}lw\varLambda Lr(2\sin {\beta _k}\cos \alpha \cos \beta \cos {\alpha _k} - \sin {\beta _k}\sin \alpha \cos \beta \sin {\alpha _k} + \sin \beta \cos {\beta _k})\\ + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(2\sin {\beta _k}\cos {\alpha _k}\cos {\alpha _q}\cos {\beta _q} - \sin {\beta _k}\sin {\alpha _k}\sin {\alpha _q}\cos {\beta _q} + \cos {\beta _k}\sin {\beta _q})} \right] } \\ - {Q_{{\beta _k}}}/{\varOmega ^2} = 0 \end{array} \end{aligned}$$

(14)

where ${M_A} = {\textstyle {{{m_0}({m_t} + 4m)} \over M}}, {M_B} = {\textstyle {{{m_0}{{(\frac{1}{2}{m_t} + 4m)}^2} + \frac{1}{4}{m_t}{{({m_0} - 4m)}^2} + 4m{{({m_0} + \frac{1}{2}{m_t})}^2}} \over {{M^2}}}},$ ${M_C} = {\textstyle {{m(M - m)} \over M}}, {M_D} = {\textstyle {{{m_0}(\frac{1}{2}{m_t} + 4m)} \over M}},{M_E} = {\textstyle {{m{m_0}} \over M}}, {M_F} = {\textstyle {{m({m_0} + \frac{1}{2}{m_t})} \over M}}, {M_G} = - {\textstyle {{{m^2}} \over M}}$.

3 Control Scheme

In many studies about the dynamics analysis of tethered space system, we can see that the in-plane and out-of-plane angles of the tether vibrate with the frequencies of $\sqrt{3}$ and 2 times the orbital frequency respectively [12], which may lead to tangle of the master tether with platform and the chaos of the four net tethers, and lead to the failure of the mission. An appropriate controller for maintaining the configuration of the net is necessary.

It is clear that the dynamics of MNSR is complex and the state variables are strongly coupled. Some simplifications are made for the dynamic equations for the convenience of controller design. Assume that the length of master tether keeps constant during the station-keeping phase, that is, $\varLambda = 1$ and $\varLambda '' = \varLambda ' = 0$. And the platform is controllable and keeps constant, and the in-plane and out-of-plane angles of master tether can be kept in the desired values. Then, we only need to control the in-plane and out-of-plane angles of net tether, namely, the configuration of the maneuverable net.

The feedback control laws for MNSR are designed as

$$\begin{aligned} \begin{array}{l} {Q_{c{\alpha _k}}} = k{p_{\alpha k}} \cdot ({\alpha _{kd}} - {\alpha _k}) + k{d_{\alpha k}} \cdot ({{\alpha '_{kd}}} - {\alpha '_k})\\ {Q_{c{\beta _k}}} = k{p_{\beta k}} \cdot ({\beta _{kd}} - {\beta _k}) + k{d_{\beta k}} \cdot ({\beta '_{kd}} - {\beta '_k}) \end{array} \end{aligned}$$

(15)

where ${\alpha _{kd}}$, ${\beta _{kd}}$ and ${\alpha '_{kd}}$, ${\beta '_{kd}}$ are the desired values of in-plane and out-of-plane angles and derivative of in-plane and out-of-plane angles respectively. Thus, ${\alpha _{kd}} - {\alpha _k}$, ${\beta _{kd}} - {\beta _k}$ and ${\alpha '_{kd}} - \alpha '$, ${\beta '_{kd}} - {\beta '_k}$ are the error of angles and derivative of error of angles respectively. $k{p_{\alpha k}}$, $k{p_{\beta k}}$ and $k{d_{\alpha k}}$, $k{d_{\beta k}}$ are the parameters of error and derivative of error.

Then the control inputs ${Q_{\alpha k}},{Q_{\beta k}}(k = 1,2,3,4)$ can be derived as

$$\begin{aligned} \begin{array}{l} {Q_{{\alpha _k}}} = ( {M_C}l{w^2}{\cos ^2}{\beta _k} \cdot {Q_{c\alpha k}} + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}\cos {\beta _k}\cos {\beta _q} \cdot {Q_{c\alpha q}}} \right] } \\ + {\beta _k^\prime } \left[ \begin{array}{l} {M_C}l{w^2}(1 + {\alpha _k^\prime } )2\cos {\beta _k}( - \sin {\beta _k}) + {M_E} \cdot lw( - \sin {\beta _k})\\ + {M_F}lwLr( - \sin {\beta _k}) + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(1 + {\alpha _q^\prime } )( - \sin {\beta _k})\cos {\beta _q}} \right] } \end{array} \right] \\ + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(1 + {\alpha _q^\prime } )\cos {\beta _k}( - \sin {\beta _q}){\beta _q^\prime } } \right] } + 3{M_C}l{w^2}{\cos ^2}{\beta _k}\cos {\alpha _k}\sin {\alpha _k}\\ + {M_E}lw(2\sin {\alpha _k}\cos {\beta _k}) + {M_F}lwLr(2\sin {\alpha _k}\cos {\beta _k})\\ + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(2\sin {\alpha _k}\cos {\beta _k}\cos {\alpha _q}\cos {\beta _q} + \cos {\alpha _k}\cos {\beta _k}\sin {\alpha _q}\cos {\beta _q})} \right] } ) \cdot {\varOmega ^2} \end{array} \end{aligned}$$

(16)

$$\begin{aligned} \begin{array}{l} {Q_{{\beta _k}}}= ( {M_C}l{w^2} \cdot {Q_{c\beta k}} + \sum \limits _{q \ne k}^{1,2,3,4} {{M_G}l{w^2} \cdot {Q_{c\beta q}}} + {M_C}l{w^2}{(1 + {\alpha _k^\prime } )^2}\cos {\beta _k}\sin {\beta _k}\\ + {M_E}lw(1 + {\alpha _k^\prime } )\sin {\beta _k} + {M_F}lwLr(1 + {\alpha _k^\prime } )\sin {\beta _k} \\ + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(1 + {\alpha _k^\prime } )(1 + {\alpha _q^\prime } )\cos {\beta _q}\sin {\beta _k}} \right] } \\ + 3{M_C}l{w^2}{\cos ^2}{\alpha _k}\cos {\beta _k}\sin {\beta _k} + {M_E}lw(2\sin {\beta _k}\cos {\alpha _k}) + {M_F}lwLr(2\sin {\beta _k}\cos {\alpha _k})\\ + \sum \limits _{q \ne k}^{1,2,3,4} {\left[ {{M_G}l{w^2}(2\sin {\beta _k}\cos {\alpha _k}\cos {\alpha _q}\cos {\beta _q} - \sin {\beta _k}\sin {\alpha _k}\sin {\alpha _q}\cos {\beta _q} + \cos {\beta _k}\sin {\beta _q})} \right] } ) \cdot {\varOmega ^2} \end{array} \end{aligned}$$

(17)

4 Simulations

4.1 Simulation Environment

The simulations about controlled MNSR are demonstrated as follows and the simulation parameters are shown in Table 1.

Table 1. Simulation parameters

The initial values of in-plane and out-of-plane angles of net tethers are ${\alpha _k} = {\pi / {18}},\;\;{\pi / {18}},\;\; - {\pi / {18}},\;\;{{ - \pi } / {18}}$ and ${\beta _k} = {\pi / {18,\;\;{{ - \pi } / {18}},\;\; - {\pi / {18}},\;\;{\pi / {18}}}}$, and the desired values of in-plane and out-of-plane angles of net tethers are ${\alpha _{kd}} = {\pi / 6},\;\;{\pi / 6},\;\; - {\pi / 6},\;\;{{ - \pi } / 6}$ and ${\beta _{kd}} = {\pi / {6,\;\;{\pi / 6},\;\; - {\pi / 6},\;\;{\pi / 6}}}$ respectively.

4.2 Simulation Results

All the simulation results are shown in Figs. 6 and 7. Figure 6 shows that the in-plane and out-of-plane angles can be controlled in the desired values and the configuration of maneuverable net can be maintained in the desired state. Figure 7 demonstrates that control inputs of maneuvering units. The values of the control forces are in the acceptable range for spacecraft.

Fig. 6.

Variation of in-plane and out-of-plane angles of net tethers

Fig. 7.

Variation of control forces of MNSR

5 Conclusions

In this paper, an improved Tethered Space Net (TSN) System, named Maneuverable-Net Space Robot (MNSR), have been proposed for active space debris removal. In order to maintain the configuration of maneuverable net, it is necessary to employ a control strategy for MNSR. First, the 3-D dynamics model of MNSR is derived. Then, a feedback control is employed for maintaining the in-plane and out-of-plane angles of the net tethers in the desired angles. The simulation results show that the proposed control scheme is appropriate for the MNSR to maintain the configuration of maneuverable net.