Numerical Methods for Cooperative Control of Double Mobile Manipulators

Abstract

In this paper proposes a numerical methods based control algorithm for tracking trajectories applied in two anthropomorphic robotic arms mounted on an omnidirectional platform, which allows the transport of an object in common. For this, the kinematic modelation of the entire coupled system is performed, considering as the position of interest the midpoint of the operative ends of each manipulator and its formation characteristics. The stability of the proposed controller for tracking trajectories using numerical methods is demonstrated analytically, obtaining that the control is asymptotically stable. Finally the results obtained are evaluated in a virtual reality simulation environment.

1 Introduction

Robots nowadays are considered as a precision tool well they perform productive tasks in modern industry with a high level of complexity [1]; this reality has given rise to the programming and implementation of advanced control algorithms using different tools and simulation techniques the same serve as a fundamental basis for their real implementation [2].

A mobile manipulator robot refers to robots that are made up of a robotic arm mounted in a movable platform with legs or wheels [3]. This type of system has the ability to combine the skills and dexterities of manipulation of a fixed base manipulator with the locomotion of a mobile platform, granting the robot manipulator a larger workspace [4, 5], thus allowing the more usual missions of robotic systems that require locomotion and manipulation skills, increasing accuracy and getting better the quality of tasks [5, 6]. They offer multiple applications in different industrial and productive areas such as mining and construction or for the assistance of people [5].

There are areas where individual robots are limited in terms of manipulability, flexibility, accessibility and maneuverability, so that cooperative robots are implemented to execute the work, giving greater efficiency in industrial processes [7]. Transportation and handling are typical assignments in the industry, where large-scale use of autonomous robotic arms is being introduced [8, 9]. On the other hand, multiple robots that simultaneously manipulate a single object, called cooperative manipulation of the robot, have been an increasingly popular focus of research during recent decades, since it is recognized that many tasks can not be Performed by a single robot arm [10]. The most obvious case is that the load is too large for the robot to handle alone, so it is important to control both the absolute movement of the object and the internal stresses [11].

There are different works in the literature in which different control techniques, e.g., sliding mode based on PSO (particle optimization in-jambre) and ANFIS (adaptive system of neuro-fuzzy inference) for trajectory follow-up, PSO serves for to obtain discrete articulation angles and ANFIS to convert the angles of discrete joints into angles of continuous joints [12]. In [13], they present a system of N robots of a manipulator arm and a mobile platform that carry an object to follow a desired trajectory, position and orientation, they develop a control algorithm of commutation for the manipulation of distributed cooperation of rigid bodies in a flat environment and test the stability of control by Lyapunov. Multiple mobile manipulators are considered, which hold a common object in a cooperative way to follow a desired trajectory, the control of coordinated systems allows control of the object in non limited directions [14, 15]. In [16, 17], they present the transport of an object in cooperative form of multiple omnidirectional mobile manipulators through a centralized and decentralized architecture for tracking of trajectory with out collisions in order to capture the object and place it In the destination position.

In this work, it is considered two anthropomorphic robotic arms of omnidirectional type mounted on a mobile platform, for which the kinematic modeling is performed, considering as the point of interest the midpoint of the two operative ends. The design of the coordinated cooperative controller for tracking trajectories allows the transport of a common object, for this system the control is developed by the numerical methods, which eliminates the inherent errors of kinematics. The experiments through a virtual structure allow to demonstrate that the controller is appropriate for the solution of movement problems.

The article is organized in 5 Sections including the Introduction. Section 2 presents the kinematic modeling of the anthropomorphic arms mounted on an omnidirectional platform. The design and stability analysis of the control algorithm are presented in Sect. 3. The results and discussion are shown in Sect. 4. Finally, the conclusions are presented in Sect. 5.

2 Kinematic Models

The particular case of a omnidirectional mobile manipulator with 11DOF, composed by two robotic arms –of 4DOF each arm- mounted on a omnidirectional mobile platform. The mobile platform has four driven wheels which are controlled independently by four DC motors. The robotic arms are placed at a distance a of the center of mass G of the mobile platform and at a height $h_{alt}$ in relation to the absolute coordinate system ${<}{\mathsf{R}}{>}$. Each of the arms links is driven by independent DC motors.

For a mobile platform of omnidirectional wheels with location ${\mathbf{q}}_{\text{p}} = \left[ {\begin{array}{*{20}c} x & y & \psi \\ \end{array} } \right]^{T}$ in which two robotic arms are mounted with generalized coordinates ${\mathbf{q}}_{\text{a1}}$, ${\mathbf{q}}_{\text{a2}}$, and with positions of the operative end ${\mathbf{h}}_{1}$ and ${\mathbf{h}}_{2}$ corresponding to each one of the robotic arms, is given by

$$ \left\{ {\begin{array}{*{20}l} {h_{xi} = x \pm aC_{\varPsi } + l_{2i} C_{q2i} C_{q1i,\psi } + l_{3i} C_{q2i,q3i} C_{q1i,\psi } + l_{4i} C_{q2i,q3i,q4i} C_{q1i,\psi } } \hfill \\ {h_{yi} = y \pm aS_{\varPsi } + l_{2i} C_{q2i} S_{q1i,\psi } + l_{3i} C_{q2i,q3i} S_{q1i,\psi } + l_{4i} C_{q2i,q3i,q4i} S_{q1i,\psi } } \hfill \\ {h_{zi} = h_{alt} + l_{1i} + l_{2i} S_{q2i} + l_{3i} S_{q2i,q3i} + l_{4i} S_{q2i,q3i,q4i} } \hfill \\ \end{array} } \right. $$

(1)

where, $i = 1,2$ represents each robotic arm mounted on the omnidirectional mobile platform; $\psi$ is the orientation of the mobile platform; $q_{j}$ $j = 1,2,..,n_{a}$ ($n_{a} = 4$) are the joint positions of the robotic arm; $C_{q2i,q3i} =$ $\cos \left( {q_{2i} + q_{3i} } \right)$; $S_{q2i,q3i} = \sin \left( {q_{2i} + q_{3i} } \right)$; $C_{q1i,\psi } = \cos \left( {q_{1i} + \psi } \right)$; $S_{q1i,\psi } = \sin \left( {q_{1i} + \psi } \right)$; $C_{q2i,q3i,q4i} = \cos \left( {q_{2i} + q_{3i} + q_{4i} } \right)$; and $S_{q2i,q3i,q4i} =$ $\sin \left( {q_{2i} + q_{3i} + q_{4i} } \right)$.

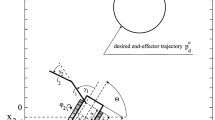
To determine the system modeling of a two-arm mobile platform, the virtual point in the X-Y-Z plane between the midpoint of each end effector of the robotic arms is fixed; The virtual point is defined by ${\mathbf{P}}_{F} = \left[ {\begin{array}{*{20}c} {h_{x} } & {h_{y} } & {h_{z} } \\ \end{array} } \right]$ that represents the position of its centroid on the inertial frame ${<}{\mathsf{R}}{>}$,

$$ \left\{ \begin{aligned} h_{x} = \frac{{h_{x1} + h_{x2} }}{2} \hfill \\ h_{y} = \frac{{h_{y1} + h_{y2} }}{2} \hfill \\ h_{z} = \frac{{h_{z1} + h_{z2} }}{2} \hfill \\ \end{aligned} \right. $$

(2)

While, the vector structure of the virtual shape is defined by ${\mathbf{S}}_{F} = \left[ {\begin{array}{*{20}c} {d_{F} } & {\theta_{F} } & {\phi_{F} } \\ \end{array} } \right]$, where, $d$ represents the distance between the position of the end-effector ${\mathbf{h}}_{1}$ and ${\mathbf{h}}_{2}$, $\theta$ and $\phi$ represents its orientation with respect to the global Y-axis and X-axis, respectability on the inertial frame ${<}{\mathsf{R}}{>}$, Fig. 1.

Fig. 1.

Mobile manipulator with two robotic arms of 4 DOF for the experiment

$$ \left\{ {\begin{array}{*{20}l} {d_{F} = \sqrt {\left( {h_{x2} - h_{x1} } \right)^{2} + \left( {h_{y2} - h_{y1} } \right)^{2} + \left( {h_{z2} - h_{z1} } \right)^{2} } } \hfill \\ {\theta_{F} = \arctan \left( {\frac{{h_{z} }}{{h_{x} }}} \right)} \hfill \\ {\phi_{F} = \arctan \left( {\frac{{h_{y} }}{{h_{x} }}} \right)} \hfill \\ \end{array} } \right. $$

(3)

The point of interest of the system is represented in a simplified way as ${\mathbf{h}} = [\begin{array}{*{20}c} {{\mathbf{P}}_{F} } & {\mathbf{S}} \\ \end{array}_{F} ]$, i.e.,

$$ {\mathbf{h}} = \left[ {\begin{array}{*{20}c} {hx} & {hy} & {hz} & d & \theta & \phi \\ \end{array} } \right]^{T} . $$

(4)

The other hand, the kinematic model of the omnidirectional mobile platform is represented as,

$$ \left[ {\begin{array}{*{20}c} {\dot{x}} \\ \begin{aligned} {\dot{y}} \hfill \\ {\dot{\psi }} \hfill \\ \end{aligned} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \psi } & { - \sin \psi } & 0 \\ {\sin \psi } & {\cos \psi } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{l} } \\ {u_{m} } \\ \omega \\ \end{array} } \right] $$

(5)

where, each linear velocity is directed as one of the axes of the frame ${<}P{>}$ attached to the center of gravity of the mobile platform: $u_{l}$ points to the frontal direction; $u_{m}$ points to the left-lateral direction¸ and the angular velocity $\omega_{{}}$ rotates the referential system ${<}P{>}$ counterclockwise, around the axis $P_{Z}$ (considering the top view).

Now, substituting (1), (2), (3) in (4) and deriving (4), we obtain the kinematic model of the point of interest of the mobile manipulators. Also the kinematic model can be written in compact form as ${\dot{\mathbf{h}}} = f\left( {{\mathbf{q}}_{{\mathbf{p}}} ,{\mathbf{q}}_{{\mathbf{a}}} } \right){\mathbf{v}}$, i.e.,

$$ {\dot{\mathbf{h}}}\left( t \right) = {\mathbf{J}}\left( {{\mathbf{q}}_{{\mathbf{p}}} ,{\mathbf{q}}_{{{\mathbf{a}}i}} } \right){\mathbf{v}}\left( t \right) $$

(6)

where, ${\dot{\mathbf{h}}}\left( t \right) = \left[ {\begin{array}{*{20}c} {\dot{h}_{x} } & {\dot{h}_{y} } & {\dot{h}_{z} } & {\dot{d}_{F} } & {\dot{\theta }_{F} } & {\dot{\phi }} \\ \end{array}_{F} } \right]^{T}$ is the velocity vector of the interest point; ${\mathbf{J}}\left( {\mathbf{q}} \right)$ represents the Jacobian matrix, ${\mathbf{v}}\left( t \right) = \left[ {\begin{array}{*{20}c} {u_{l} } & {u_{m} } & \omega & {\dot{q}_{11} } & \ldots \\ \end{array} } \right.$ $\left. {\begin{array}{*{20}c} {\dot{q}_{na1} } & {\dot{q}_{12} } & \ldots & {\dot{q}_{na2} } \\ \end{array} } \right]^{T}$ is the control vector of mobility of the interest point.

3 Control

Is proposed a control system based on the system kinematics (platform, arms and object), as shown in Fig. 2.

Fig. 2.

Trajectory tracking control

Considering the differential equation

$$ \dot{y} = f(y,u,t)\;\text{con}\;y(0) = y_{0} $$

where, $y$ represents the output of the system to be controlled, $\dot{y}$ first derivative $u$ the control action and $t$, the time. The values of $y(t)$ in the discret time $t = kT_{0}$, are called, $y(k)$ where $T_{0}$ represents the sampling period, and $k \in \left\{ {0,1,2,3,4,5 \ldots } \right\}$.

The use of numerical methods for the calculus of the system evolution is based mainly on the possibility to approximation the sistema state on the instant time $k + 1$, if the state and the control action on the time instant $k$ are known, this approximation is called the Euler method.

$$ y(k + 1) = y(k) + T_{0} f(y,u,t) $$

(7)

On this way the discrete model for the robot could be expressed by

$$ {\mathbf{h}}(k + 1) = {\mathbf{h}}(k) + T_{0} {\mathbf{J}}({\mathbf{q}}(k)){\mathbf{v}}(k) $$

(8)

In order that the tracking error tends to zero the following expresition is used

$$ {\mathbf{h}}(k + 1) = {\mathbf{hd}}(k + 1) - {\mathbf{W}}({\mathbf{hd}}(k) - {\mathbf{h}}(k)) $$

(9)

where, ${\mathbf{W}}$ is a diagonal matrix $0 {< }{\mathbf{diag}}\left( {w_{x} ,w_{y} ,w_{z} } \right){< }1$ and ${\mathbf{hd}}$ is the desired trajectory. From (7) and (8) is possible to get (9) using ${\mathbf{Au}} = {\mathbf{b}}$.

$$ \underbrace {{{\mathbf{J}}(\begin{array}{*{20}c} {{\mathbf{q}}(k)} \\ \end{array} )}}_{{\mathbf{A}}}\underbrace {{{\mathbf{v}}(k)}}_{{\mathbf{u}}} = \underbrace {{\frac{{{\mathbf{hd}}(k + 1) - {\mathbf{W}}\left( {{\mathbf{hd}}(k) - {\mathbf{h}}(k)} \right) - {\mathbf{h}}(k)}}{{T_{0} }}}}_{{\mathbf{b}}} $$

(10)

Hence, viable solution method is to formulate the problem as a constrained linear optimization problem.

$$ \tfrac{1}{2}\left\| {\mathbf{v}} \right\|_{2}^{2} \; = \hbox{min} . $$

Then yields the particular solution.

$$ {\mathbf{v}}\left( t \right) = {\mathbf{J}}^{T} ({\mathbf{JJ}}^{T} )^{ - 1} \frac{{{\mathbf{hd}}(k + 1) - {\mathbf{W}}\left( {{\mathbf{hd}}(k) - {\mathbf{h}}(k)} \right) - {\mathbf{h}}(k)}}{{T_{0} }} $$

(11)

Stability Analysis

In kinematics is fulfilled ${\mathbf{v}}_{\text{ref}} \text{ = }{\mathbf{v}}$, therefore the closed-loop equation is given by,

$$ {\mathbf{h}}(k + 1) - {\mathbf{h}}(k) = T_{0} {\mathbf{J}}\left( {{\mathbf{J}}^{T} ({\mathbf{JJ}}^{T} )^{ - 1} {\mathbf{b}}} \right) $$

(12)

where ${\mathbf{JJ}}^{T} ({\mathbf{JJ}}^{T} )^{ - 1} = {\mathbf{I}}_{m}$ the Eq. (11) is reduced to,

$$ {\mathbf{h}}(k + 1) - {\mathbf{h}}(k) = T_{0} {\mathbf{I}}_{m} {\mathbf{b}} $$

(13)

Through the properties of the identity matrix have

$$ {\mathbf{h}}(k + 1) - {\mathbf{h}}(k) = T_{0} \left( {\frac{{{\mathbf{hd}}(k + 1) - {\mathbf{W}}\left( {{\mathbf{hd}}(k) - {\mathbf{h}}(k)} \right) - {\mathbf{h}}(k)}}{{T_{0} }}} \right) $$

(14)

Reducing terms and grouping them you have that the error in the following state ${\mathbf{h}}_{d} (k + 1) - {\mathbf{h}}(k + 1)$ depends only on the previous error by a gain ${\mathbf{W}}\left( {{\mathbf{hd}}(k) - {\mathbf{h}}(k)} \right)$

$$ \left[ {\begin{array}{*{20}c} {h_{x} (k + 1)} \\ {h_{y} (k + 1)} \\ {h_{z} (k + 1)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {h_{xd} (k + 1) - w_{x} (e_{x} )} \\ {h_{yd} (k + 1) - w_{y} (e_{y} )} \\ {h_{zd} (k + 1) - w_{z} (e_{z} )} \\ \end{array} } \right] $$

$$ \left[ {\begin{array}{*{20}c} {e_{x} (k + 1)} \\ {e_{y} (k + 1)} \\ {e_{z} (k + 1)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {w_{x} (e_{x} (k))} \\ {w_{y} (e_{y} (k))} \\ {w_{z} (e_{z} (k))} \\ \end{array} } \right] $$

The error on the following states comes by

$$ \begin{array}{*{20}c} {e_{i} (k + 1) = w_{i} e_{i} (k)} \\ {e_{i} (k + 2) = w_{i} e_{i} (k + 1) = w_{i}^{2} e(k)} \\ {e_{i} (k + 3) = w_{i} e_{i} (k + 2) = w_{i}^{3} e(k)} \\ \vdots \\ {e_{i} (k + n) = w_{i} e_{i} (k + n - 1) = w_{i}^{n} e(k)} \\ \end{array} $$

Them the error approaches asymptotically to cero when $0 {\text{< w}}_{\text{i}} {< 1}$ y $n \to \infty$. This implies that the equilibrium point of the closed loop is asymptotically stable, so that the position error of the i-th final effector verifies ${\tilde{\mathbf{h}}}_{i} \left( t \right) \to 0$ asymptotically with $t \to \infty$.

4 Results

In order to evaluate the performance of the proposed controller, was developed in Matlab a 3D simulator in which the KUKA Youtbot robot is considered, which is made up of an omnidirectional mobile platform with mecanum wheels and two anthropomorphic robotic arms [18].

The simulation experiments implemented recreate an application of cooperation and coordination between two robotic arms and a mobile platform in order to perform tasks of handling a load. Figure 3 shows the stroboscopic movement in the X-Y-Z space of the reference system ${<}{\mathsf{R}}{>}$, which allows to verify that the proposed controller works correctly in cooperation tasks when moving an object in common. The Fig. 4 shows the trajectories described by the operative ends of the robotic arms when performing the task; In the graph you can see the trajectories described by the robot.

Fig. 3.

Stroboscopic movement of the mobile manipulator

Fig. 4.

Path followed by the point of interest.

Figure 5 show that the control errors of the position of the point of interest formed by the ends of the robotic arms; While Fig. 6 illustrates shape and orientation errors, I.e. the distance between the operative ends and the angles forming the object with the arms over the XY and YZ planes with respect to the reference system ${<}{\mathsf{R}}{>}$; in the two graphs it can be seen that control errors tend to zero asymptotically when $\text{t} \to \infty$.

Fig. 5.

Errors of position of the point of interest or midpoint of the operative ends.

Fig. 6.

Errors of shape of the object to be transported

Finally Figs. 7 and 8 its show the maneuverability commands applied to the omnidirectional platform and the anthropomorphic arms respectively in order to accomplish the task objective.

Fig. 7.

Omnidirectional platform speeds

Fig. 8.

Robotic arm speeds.

5 Conclusions

In this work the design of a coordinated cooperative controller for the trajectory tracking that allows to transport an object in common was presented. The design of the controller is based on a kinematic control that meets the purpose of movement, reference velocities were defined for the omnidirectional platform and the robotic arms. Stability and robustness are tested by the numerical methods. Experiments carried out trough a virtual reality structure confirm the scope of the controller to solve different problems of movement through a strong choice of control references.