Keywords

1 Introduction

As an automatic manufacturing device, industrial robots have been widely used and play an important role in many fields of industrial applications, thanks to their high repeatability accuracy and operational stability. Amongst the industrial applications, this type of serial manipulators are well adapted in welding industry [3], such as auto industry. Besides, the robots can also be used in shipbuilding industry, i.e., the large-scale hull welding, as displayed in Fig. 1. In this procedure, the welding trajectory is firstly detected by the vision system, where the data of the trajectory will be transferred to the control system for robot programming to accomplish the welding procedure. This means that the robot will conduct an off-line task.

The robots’ motions are usually generated via the robotic controllers by virtue of the inverse kinematic model to compute the input signals for actuators corresponding to the desired end-effector position, where the compliance errors are ignored. On the other hand, as depicted in Fig. 1(c), under certain external load, particularly, the arm gravity and dynamic inertial forces, the kinematic control becomes non-applicable due to the elastic compliance errors caused by the limited strength of the robot components [12], namely, the actual trajectory will shift away from the desired path, resulting in the decreased product quality wherefrom high precision is needed in the applications.

Fig. 1.
figure 1

The robot-based ship hull welding: (a) steel sheet on the supporter; (b) overall scheme; (c) reaction forces onto the welding gun.

Full size image

The compliance error, i.e., geometric changes of the robot end-effector, can be compensated through the calibration [7, 21], whereas, this technique is sometimes expensive. An economic way to handle the problem of error compensation is the modification of the robot control scheme [6, 10] that defines the prescribed trajectory in Cartesian space: based on the error model, the loaded input trajectory is regenerated to achieve the coincidence between the output trajectory and the desired one, while input trajectory differs from the target one. The modification of the input trajectory is to be based on the compliance error model that calls for the computation of the stiffness matrix [8]. The stiffness matrix for the serial robotics was first derived by Salisbury [15], where only the actuation compliance described by one-dimensional linear springs was considered. In this approach, the derivation of the stiffness is on the basis of the assumption that the manipulator is in an unloaded equilibrium configuration. In practice, the external loads directly influence on the manipulator equilibrium configuration and may modify the stiffness properties [2, 4]. As a consequence, the structural compliance and the robot geometry change due to external loads and gravity should be considered [11, 13, 14]. Thus, this work focuses on the compliance error modeling and compensation that is able to take into account the influence of the external and internal wenches and robot gravity onto the stiffness matrix and elastic deformations.

This paper deals with the stiffness modeling and compliance error compensation of an industrial robot in ship hull welding. The Cartesian stiffness matrix is computed in loaded configurations, where the actuation and structural stiffness is considered as well as the influence of the arm gravity and external loads. A method to modify the input trajectory is presented for error compensation. This method is numerically illustrated with the welding robot along a trajectory and the results show the effectiveness of the error compensation approach.

2 Industrial Welding Robot

Figure 2 shows the ABB IRB4600_60/205 robot [1] as the welding robot in this project. IRB 4600 series is ABB Robotics pioneer of the new sharp generation with enhanced and new capabilities, of which one industrial application is dedicated to welding.

Fig. 2.
figure 2

The ABB IRB4600_60/205 robot and its coordinate systems.

Full size image

2.1 Kinematics of the Industrial Robot

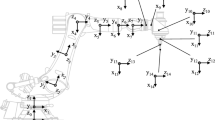
Following the Denavit–Hartenberg (D–H) convention [5], the Cartesian coordinate systems are established for each link of the robotic arm as shown in Fig. 2. Hereafter, let \(\mathbf {i}\), \(\mathbf {j}\) and \(\mathbf {k}\) be the unit vectors along x-, y- and z-axis, respectively. The transformation matrix in the forward kinematics of the end-effector in the reference frame \((x_0,\,y_0,\,z_0)\) is expressed as

$$\begin{aligned} ^0\mathbf {A}_6=\begin{bmatrix} \mathbf {R}&\mathbf {q} \\ \mathbf {0}&1 \\ \end{bmatrix}=\prod ^6_{i=1}{^{i-1}\mathbf {A}_i}\quad \mathrm {where} \quad ^{i-1}\mathbf {A}_i=\begin{bmatrix} ^{i-1}\mathbf {R}_i&^{i-1}\mathbf {q}_i \\ \mathbf {0}&1 \\ \end{bmatrix} \end{aligned}$$
(1)

with

$$\begin{aligned}&^{i-1}\mathbf {R}_i=\mathbf {R}_{z_{i-1}}(\theta _i)\mathbf {R}_{x_{i}}(\alpha _i) \end{aligned}$$
(2a)
$$\begin{aligned}&{^{i-1}\mathbf {q}_i}=\begin{bmatrix} a_i\cos \alpha _i&a_i\sin \alpha _i&d_i \\ \end{bmatrix}^T \end{aligned}$$
(2b)

where the D–H parameters are listed in Table 1. The inverse geometry problem of the six-axis robotics has been well documented in the literature [16].

Table 1. D-H parameters of the IRB4600_60/205 robot.
Full size table

2.2 Jacobian Matrix

The joint angular velocity can be calculated with the Jacobian matrix as below:

$$\begin{aligned} \dot{\varvec{\theta }}=\mathbf {J}^{-1}\dot{\mathbf {t}} \end{aligned}$$
(3)

where \(\dot{\varvec{\theta }}=\begin{bmatrix} \dot{\theta }_1&\dot{\theta }_2&\ldots&\dot{\theta }_6 \\ \end{bmatrix}^T\) denotes the vector of the joint angular velocities, and \(\dot{\mathbf {t}}=\begin{bmatrix}\varvec{\omega }^T&\dot{\mathbf {q}}^T \\ \end{bmatrix}^T\) stands for the end-effector twist, \(\varvec{\omega }\) being the angular velocities. Moreover, \(\mathbf {J}\) is the Jacobian matrix of the robotic arm [17], namely,

$$\begin{aligned} \mathbf {J}=\begin{bmatrix} \mathbf {j}_1&\mathbf {j}_2&\ldots&\mathbf {j}_6 \\ \end{bmatrix}\quad \mathrm {where} \quad \mathbf {j}_i=\begin{bmatrix} \mathbf {z}_{i-1} \\ \mathbf {p}_{i-1}\times \mathbf {z}_{i-1} \\ \end{bmatrix} \end{aligned}$$
(4)

with

$$\begin{aligned} \mathbf {z}_{i-1}=\mathbf {R}_{i-1}\mathbf {k};\quad \mathbf {p}_{i-1}=\mathbf {q}_{i-1}-\mathbf {q} \end{aligned}$$
(5)

where \(\mathbf {R}_{i-1}\) and \(\mathbf {q}_{i-1}\) denote the rotation matrix and position vector of the transformation matrix from the reference coordinate system to the \((i-1)\)th coordinate system, respectively, which can be extracted from \(\prod ^{i-1}_{i=0}{^{i-1}\mathbf {A}_i}\) in Eq. (1).

2.3 Robot Dynamics

The dynamic behavior of the robot under the load \(\mathbf {f}_{e}\) during the welding can be described as

$$\begin{aligned} \mathbf {M}\delta \ddot{\mathbf {t}} + \mathbf {C}\delta \dot{\mathbf {t}} + \mathbf {K}\delta \mathbf {t} = \mathbf {f}_{e} \end{aligned}$$
(6)

where \(\mathbf {M}\) is 6-dimensional mass matrix that represents the global behavior of the robot in terms of natural frequencies, \(\mathbf {C}\) is 6-dimensional damping matrix, and \(\mathbf {K}\) is 6-dimensional Cartesian stiffness matrix of the robot under the external loading \(\mathbf {f}_{e}\) [18]. Moreover, \(\delta \mathbf {t}\), \(\delta \dot{\mathbf {t}}\) and \(\delta \ddot{\mathbf {t}}\) are the instantaneous dynamic displacement, velocity and acceleration of the tool end-point, respectively.

The mass matrix \(\mathbf {M}\) in Eq. (6) can be solved based on the dynamic equation of motion (EOM) [9] of a serial robot as below:

$$\begin{aligned} \mathbf {M}(\varvec{\theta })\ddot{\varvec{\theta }} + \mathbf {v}(\varvec{\theta },\,\dot{\varvec{\theta }}) + \mathbf {g}(\varvec{\theta }) = \varvec{\tau }\end{aligned}$$
(7)

where \(\varvec{\theta }\), \(\dot{\varvec{\theta }}\), \(\ddot{\varvec{\theta }}\) are 6-dimensional vectors of generalized joint angles, angular velocities, and angular accelerations, respectively. \(\mathbf {M}(\varvec{\theta })\) is the \(6\times 6\) general inertial matrix, \(\mathbf {v}(\varvec{\theta },\,\dot{\varvec{\theta }})\) is a 6-dimensional vector representing the Coriolis and centrifugal forces, and \(\mathbf {g}(\varvec{\theta })\) is a 6-dimensional vectors accounting for the force due to gravity. Moreover, \(\varvec{\tau }\) is the vector of general external forces applied at joints.

3 Compliance Error Modeling and Compensation

In order to compensate the positioning errors of the robot end-effector for high-quality welding, the compliance errors caused by the external payloads and robot gravity should be calculated precisely, which calls for the computation of the stiffness matrix of the robot.

3.1 Elastostatic Modeling

In this work, the virtual spring approach [13] is adopted to derive the stiffness matrix, based on the screw coordinates [19, 20]. Figure 3 shows the VJM model of the robotic arm, where \(\mathbf {g}_j\), \(j=1,\,2,\,\ldots ,\,8\), stand for the gravity and \(\mathbf {f}_e\) denotes the external loads.

Fig. 3.
figure 3

Virtual-spring model of the industrial robot with auxiliary loads, where \(A_c\) and EE stand for the actuator and end-effector, respectively.

Full size image

Let \(\varvec{\theta }\), \(\varvec{\theta }'\) be the original and the deformed angular displacements of the joints, respectively, in accordance with the principle of virtual work, the work of the auxiliary loads is equal to the work of internal forces \(\varvec{\tau }_\theta \) [13], namely,

$$\begin{aligned} \sum (\mathbf {g}_j^T\delta \mathbf {t}_j)+\mathbf {f}_e^T\delta \mathbf {t}=\varvec{\tau }_\theta ^T(\varvec{\theta }'-\varvec{\theta }) \end{aligned}$$
(8)

where the virtual displacements \(\delta \mathbf {t}_j\) and \(\delta \mathbf {t}\) can be computed from the linearized geometrical model derived from \(\delta \mathbf {t}_j=\mathbf {J}_j(\varvec{\theta }'-\varvec{\theta })\) and \(\delta \mathbf {t}=\mathbf {J}_\theta (\varvec{\theta }'-\varvec{\theta })\), respectively, \(\mathbf {J}_j\) and \(\mathbf {J}_\theta \) being the Jacobians, namely,

$$\begin{aligned}&\mathbf {J}_\theta =\begin{bmatrix} \mathbf {j}_1&\mathbf {j}_2&\mathbf {J}_U&\mathbf {j}_3&\mathbf {j}_4&\mathbf {J}_F&\mathbf {j}_5&\mathbf {j}_6 \\ \end{bmatrix}\in \mathbb {R}^{6\times 18} \end{aligned}$$
(9)
$$\begin{aligned}&\mathbf {J}_j=\mathbf {J}_\theta (:,\,1{:}\,k) \end{aligned}$$
(10)

where \(\mathbf {J}_\theta (:,\,1{:}\,k)\) stands for the first k columns in \(\mathbf {J}_\theta \) and k stands for the number of the mobilities of the virtual springs from the base to \(\mathbf {g}_j\). Moreover, \(\mathbf {J}_U\) and \(\mathbf {J}_F\), respectively, relate the link deflections of the upper arm and forearm to the end-effector, expressed as

$$\begin{aligned}&\mathbf {J}_U=\begin{bmatrix} \mathbf {x}_1&\mathbf {y}_1&\mathbf {z}_1&\mathbf {0}&\mathbf {0}&\mathbf {0} \\ \mathbf {q}_2\times \mathbf {x}_1&\mathbf {q}_2\times \mathbf {y}_1&\mathbf {q}_2\times \mathbf {z}_1&\mathbf {x}_1&\mathbf {y}_1&\mathbf {z}_1 \\ \end{bmatrix} \end{aligned}$$
(11a)
$$\begin{aligned}&\mathbf {J}_F=\begin{bmatrix} \mathbf {z}_3&\mathbf {x}_3&\mathbf {y}_3&\mathbf {0}&\mathbf {0}&\mathbf {0} \\ \mathbf {q}_4\times \mathbf {z}_3&\mathbf {q}_4\times \mathbf {x}_3&\mathbf {q}_4\times \mathbf {y}_3&\mathbf {z}_3&\mathbf {x}_3&\mathbf {y}_3 \\ \end{bmatrix} \end{aligned}$$
(11b)

Equation (8) is rewritten as

$$\begin{aligned} \sum (\mathbf {g}_j^T\mathbf {J}_j(\varvec{\theta }'-\varvec{\theta }))+\mathbf {f}_e^T\mathbf {J}_\theta (\varvec{\theta }'-\varvec{\theta }) =\varvec{\tau }_\theta ^T(\varvec{\theta }'-\varvec{\theta }) \end{aligned}$$
(12)

sequentially, the force equilibrium equation for the robotic arm is derived as

$$\begin{aligned} \varvec{\tau }_\theta =\sum (\mathbf {J}_j^T\mathbf {g}_j)+\mathbf {J}_\theta ^T\mathbf {f}_e =\mathbf {J}_g^T\mathbf {G}+\mathbf {J}_\theta ^T\mathbf {F} \end{aligned}$$
(13)

with

$$\begin{aligned} \mathbf {J}^T_g=\begin{bmatrix} \mathbf {J}_1&\mathbf {J}_2&\ldots&\mathbf {J}_8 \\ \end{bmatrix}\in \mathbb {R}^{6\times 48};\quad \mathbf {G}=\begin{bmatrix} \mathbf {g}^T_1&\mathbf {g}^T_2&\ldots&\mathbf {g}^T_8 \\ \end{bmatrix}^T\in \mathbb {R}^{48} \end{aligned}$$
(14)

With the linear force-deflection relation, the equilibrium condition is written as

$$\begin{aligned} \mathbf {J}_g^T\mathbf {G}+\mathbf {J}_\theta ^T\mathbf {f}_e=\mathbf {K}_\theta (\varvec{\theta }'_i-\varvec{\theta }_i) \end{aligned}$$
(15)

with the stiffness matrix \(\mathbf {K}_\theta \) in the joint space expressed as

$$\begin{aligned} \mathbf {K}_\theta =\mathrm {diag} \begin{bmatrix} K_{\mathrm {act},1}&K_{\mathrm {act},2}&\mathbf {K}_U&K_{\mathrm {act},3}&K_{\mathrm {act},4}&\mathbf {K}_F&K_{\mathrm {act},5}&K_{\mathrm {act},6} \end{bmatrix} \end{aligned}$$
(16)

where \(K_{\mathrm {act},i}\) is the actuation stiffness, and \(\mathbf {K}_U\) and \(\mathbf {K}_F\), calculated by the Euler-Bernoulli beam model, represent the \(6\times 6\) stiffness matrices of the upper arm and forearm, respectively.

To compute the stiffness matrix of the loaded mode, let assume that a neighborhood of the loaded configuration, where the external loads and the joint displacement are supposed to be incremented by some small values \(\delta \mathbf {f}_e\) and \(\delta \varvec{\theta }\), also satisfies the equilibrium conditions, leading to

$$\begin{aligned} (\mathbf {J}_{g}+\delta \mathbf {J}_{g})^T\mathbf {G}+(\mathbf {J}_{\theta }+\delta \mathbf {J}_{\theta })^T(\mathbf {f}_e+\delta \mathbf {f}_e) =\mathbf {K}_\theta (\varvec{\theta }'-\varvec{\theta }+\delta \varvec{\theta }) \end{aligned}$$
(17)

with the linearized kinematic constraint:

$$\begin{aligned} \delta \mathbf {t}=\mathbf {J}_{\theta }\delta \varvec{\theta }\end{aligned}$$
(18)

Upon the removal of the unchanged equilibrium condition of Eq. (15) from Eq. (17), after linearization, one obtains

$$\begin{aligned} \mathbf {H}_{g}^T\otimes \mathbf {G}\delta \varvec{\theta }+\mathbf {J}_\theta ^T\delta \mathbf {f}_e +\mathbf {H}_{\theta }^T\otimes \mathbf {f}_e\delta \varvec{\theta }=\mathbf {K}_\theta \delta \varvec{\theta }\end{aligned}$$
(19)

where the symbol \(\otimes \) represents the Kronecker product between matrices, and \(\mathbf {H}_g=\partial \mathbf {J}_g/\partial \varvec{\theta }\), \(\mathbf {H}_{\theta }=\partial \mathbf {J}_{\theta }/\partial \varvec{\theta }\), namely, the Hessian matrices. Combing Eqs. (18) and (19), the kineto-static model of the industrial robot is reduced to

$$\begin{aligned} \begin{bmatrix} \mathbf {0}&\mathbf {J}_{\theta } \\ \mathbf {J}_{\theta }^T&\mathbf {K}_E-\mathbf {K}_\theta \\ \end{bmatrix} \begin{bmatrix} \delta \mathbf {f}_e \\ \delta \varvec{\theta }\\ \end{bmatrix}=\begin{bmatrix} \delta \mathbf {t} \\ \mathbf {0} \\ \end{bmatrix} \end{aligned}$$
(20)

with

$$\begin{aligned} \mathbf {K}_E=\mathbf {H}_{g}^T\otimes \mathbf {G}+\mathbf {H}_{\theta }^T\otimes \mathbf {F} \end{aligned}$$
(21)

From the force-deformation equation \(\delta \mathbf {f}_e=\mathbf {K}\delta \mathbf {t}\) of the end-efector, the Cartesian stiffness matrix \(\mathbf {K}\) of the robot is calculated as,

$$\begin{aligned} \mathbf {K}=\left( \mathbf {J}_{\theta }\left( \mathbf {K}_\theta -\mathbf {K}_E\right) ^{-1}\mathbf {J}_{\theta }^T\right) ^{-1} \end{aligned}$$
(22)
Fig. 4.
figure 4

Error compensation procedure for the welding robot.

Full size image

3.2 Error Compensation Procedure

The motions of the industrial robots are usually generated according to the inverse kinematics, from which the input signals of the actuators \(\varvec{\theta }\) corresponding to the desired end-effector position \(\mathbf {p}\) are computed. However, with the external loads \(\mathbf {f}_e\) exerted to the end-effector, the kinematic control becomes non-applicable due to the compliance error \(\delta \mathbf {t}\) of the end-effector, thus, the actual position is computed from the stiffness model

$$\begin{aligned} \mathbf {p}'=\mathbf {p}+\delta \mathbf {t}\quad \mathrm {where} \quad \delta \mathbf {t}=\mathbf {K}^{-1}(\mathbf {f}_e + \mathbf {J}^{-T}\varvec{\tau }) \end{aligned}$$
(23)

here, \(\mathbf {f}_e + \mathbf {J}^{-T}\varvec{\tau }\) stands for the combination of the force and inertial forces. In order to make the end-effector be located in the desired position \(\mathbf {p}\), the compliance error between \(\mathbf {p}\) and \(\mathbf {p}'\), under the loads \(\mathbf {f}_e\), should be compensated. Let suppose the modified end-effector position to be \(\mathbf {p}_f=\mathbf {p}-\delta \mathbf {t}\), under the same loads \(\mathbf {f}_e\), the actual position after compensation \(\mathbf {p}_c\) should be in the neighborhood of the desired position, namely,

$$\begin{aligned} \mathbf {p}_c=\mathbf {p}_f+\delta \mathbf {t}_f\approx \mathbf {p}\quad \mathrm {where} \quad \delta \mathbf {t}_f=\mathbf {K}_f^{-1}(\mathbf {f}_e + \mathbf {J}_f^{-T}\varvec{\tau }_f) \end{aligned}$$
(24)

where \(\mathbf {K}_f\) is the stiffness matrix evaluated at the deflected position, and \(\mathbf {J}_f\) and \(\varvec{\tau }_f\) are the Jacobian and joint torque at the actual positions, respectively. As a consequence, the modified end-effector location \(\mathbf {p}_f\) can be calculated from the following iterative procedure,

$$\begin{aligned} \mathbf {p}'_c=\mathbf {p}+\lambda (\mathbf {p}-\mathbf {p}_c) \end{aligned}$$
(25)

where the prime term corresponds to the next iteration, and \(\lambda =\varDelta _t/\Vert \mathbf {p}-\mathbf {p}_c\Vert \) is the scalar parameter to achieve the convergence, \(\varDelta _t\) being the maximum magnitude among the elements in \(\mathbf {p}-\mathbf {p}_c\). This iterative method, presented in Fig. 4, will stop until \(\Vert \mathbf {p}-\mathbf {p}_c\Vert \le \epsilon \), where \(\epsilon \) is an acceptable tolerance. Using this procedure to modify the reference trajectory in the robotic control, it is possible to compensate compliance errors to follow accurately the desired trajectory.

4 Case Study of Error Compensation

The previously presented stiffness modeling and error compensation procedure are illustrated with the welding robot under study, namely, the ABB IRB 4600 robot, along a trajectory as displayed in Fig. 5 together with the motion profiles of the end-effector. Based upon the FEA based evaluation, the upper arm and forearm can be treated as rigid links, compared to the actuation stiffness as listed in Table 2. Other detailed technical parameters and specifications of the robot can be found from the user manual [1], and the external wrench applied to the robot end-effector is supposed to be pure forces \(\mathbf {f}_e = \begin{bmatrix} 200&-200&-200 \\ \end{bmatrix}^T\), which is considered to be constant. Here, the requirement on the welding accuracy is higher than \(0.5\,\mathrm {mm}\).

Table 2. Joint stiffness values of the welding robot (unit: \([10^6\cdot \mathrm {Nm/rad}]\)).
Full size table
Fig. 5.
figure 5

The motion profiles of the welding robot: (a) desired and actual trajectories without error compensation; (b) end-effector velocities.

Full size image
Fig. 6.
figure 6

The positioning errors and trajectory after compensation: (a) positioning errors (dashed line–before compensation; solid line–after compensation); (b) comparison of target and actual trajectories.

Full size image

Figure 6 shows the comparison of the positioning errors and trajectories before and after compensation. It is seen that the maximum positioning error can be reduced to \(0.01\,\mathrm {mm}\) when the robot tracks the modified trajectory, meaning that the positioning error after compensation can be ignored as it is much smaller than the acceptable error. Compared to the positioning error without compensation, the robot accuracy improves around \(98\%\), which makes the actual trajectory after compensation coincident with the desired trajectory approximately, as shown in Fig. 6(b). The comparison reveals that the approach of error compensation can effectively improve the operational accuracy of the robot, also applicable to other industrial applications, such as milling.

5 Conclusions

This paper deals with the kinetostatic modeling and compliance error compensation for an industrial robot in the ship hull welding. Besides the actuation and structural stiffness, the Cartesian stiffness matrix of the robot is derived with the consideration of the arm gravity and the external loads in the welding process as well as the inertial forces. An iterative error compensation method is introduced and is numerically illustrated along a welding trajectory. The results show that the error compensation procedure can effectively improve the operational precision to make the manipulator track the desired trajectory within acceptable positioning errors. The proposed approach implies that the manipulator accuracy can be effectively improved when the control strategy is based on the combination of the kinematic, kinetostatic and dynamic models, which is applicable to other industrial applications, such as machining.