Multi-Class Error-Diffusion with Blue-Noise Property and Its Application

Abstract

Error-diffusion is commonly used as a sampling algorithm over a single channel of input signal in existing researches. But there are cases where multiple channels of signal need to be sampled simultaneously while keeping their blue-noise property for each individual channel as well as their superimposition. To solve this problem, we propose a novel discrete sampling algorithm called Multi-Class Error-Diffusion (MCED). The algorithm couples multiple processes of error-diffusion to maintain a sampling output with blue-noise distribution. The correlation among the classes are considered and a threshold displacement is introduced into each process of error-diffusion for solving the sampling conflicts. To minimize the destruction to the blue-noise property, an optimization method is used to find a set of optimal key threshold displacements. Experiments demonstrate that our MCED algorithm is able to generate satisfactory multi-class sampling output. Several application cases including color image halftoning and vectorization are also explored.

1 Introduction

Error-diffusion (ED) is originally a halftoning technique that quantizes a multi-level image to a binary one while preserving its visual appearance through diffusing the quantization error of one pixel to its neighborhood [7]. It is widely used in the industry of printing and displaying, and also an important sampling algorithm working on discrete domain. Moreover, some researchers extend its usage into digital geometry processing [1].

Previous research mainly focused on the behavior of error-diffusion sampling over a single channel of input signal [4, 14, 18, 22]. However, there are cases where multiple channels of input signal need to be sampled simultaneously, while certain ideal properties such as blue-noise are also required for all the sampling output of these channels.

Simply overlapping the output of blue-noise sampling for multiple individual channels can not guarantee the blue-noise property of their superimposition. Hence, we are aiming to propose a novel Multi-Class Error-diffusion (MCED) algorithm to solve this problem. Here, a class refers to the sampling process for a single channel of input signal as well as its sampling output. For an ideal multi-class error-diffusion with blue-noise property, the following requirements must be satisfied:

• 1. The sampling point distribution of each individual class should possess blue-noise property.

• 2. When the sampling output of all the classes are superimposed, no two sampling points from different classes can occupy the same position.

• 3. When all the sampling points from all the classes are superimposed and considered as a whole, their distribution should possess blue-noise property.

The first requirement is naturally guaranteed by the standard ED algorithm. For the second, we remain only one class with the highest priority and disable the others when conflict occurs. However, the selection of a certain class may disrupt the point distribution of other classes which violates the first requirement. To solve this problem, we introduce a threshold displacement into each process of ED and they are optimized to minimize the destruction to the blue-noise property. Since the frequency spectrum property of each class and the final output is considered during the threshold displacement optimization, the blue-noise property is promised after all classes are superimposed (the third requirement). After meeting these requirements, our MCED algorithm generates satisfactory multi-class sampling output.

The contributions of our work includes:

• 1. Proposing a multi-class error-diffusion framework, the validity of which can be explained by the commonly used Fourier transform [12];

• 2. Giving a parameter optimization method to ensure the blue-noise property of the output. Experiment results using these optimal parameters show the effectiveness of the method;

• 3. Several applications of the MCED are explored, showing that our algorithm is generic and applicable in many areas in computer graphics.

2 Related Work

The original ED is an algorithm invented for gray-scale image displaying and printing [7]. It is also frequently used in many other areas in computer graphics as a sampling algorithm [1, 3, 11]. There are a lot of research which aims at improving its behavior for sampling a single channel of input signal [4, 13, 23]. Ulichney first proposed the concept of blue-noise [18] and used it as a tool to measure the quality of ED output. Some of the work also aims at giving a solid mathematical analysis of the behavior of error diffusion algorithm. These analyses can explain or predict the results of many techniques originated from the original error diffusion algorithm [12, 21].

Using ED to sample multiple channels of input signals in a coordinated way is not a novel problem. It traditionally exists in the area of color printing, where a limited number of colorants are used to reproduce a continuous-tone color image [2]. Many studies focus on solving this problem using ED technique, which is called vector error-diffusion in some literature, because they quantized the input signals simultaneously by treating them as a vector [6, 9, 10]. For example, the vector ED algorithm proposed in [5] uses an optimum matrix-valued error filter to take into account the correlation among color planes. It can generate sampling output with blue-noise property for color images, but cannot guarantee this property for each individual color channel.

Wei extends the traditional Poisson disk sampling for a single channel of signal into a multi-class blue-noise sampling algorithm [19]. The algorithm is able to sample a set of input signals in a correlated way while keeping the blue-noise property of the whole output. It can also precisely control the number or density of the generated sampling points. Unlike the ED which works directly in a discrete domain, this algorithm is originally designed in a continuous domain. Hence it is not suitable to be applied in certain application areas that deal with discrete domain, such as color image halftoning [20].

3 Multi-Class Error-Diffusion

Our multi-class error diffusion algorithm is built using the state-of-art standard error diffusion. In this section, we first describe the standard error diffusion utilized in our algorithm and then give our MCED framework.

3.1 Standard Error Diffusion

The original error diffusion algorithm given by Floyd et al. in [7] is shown inside the dashed line of Fig. 1. In this algorithm, each pixel $p(x, y) \in [0, 1]$ in the input image p is parsed with a serpentine scan line order and quantized by a quantizer:

$$\begin{aligned} Q(p^,,u)={\left\{ \begin{array}{ll} 1,&{} p^, > u \\ 0,&{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(1)

Fig. 1.

The principle of the standard error-diffusion.

After that, the quantization error e(x, y) is calculated and distributed into multiple unparsed pixels by accumulating to an error buffer $b(\cdot , \cdot )$, which is used to compensate the error. Therefore, for pixel p(x, y), the actual input $p^{,}$ to the quantizer $Q(\cdot ,\cdot )$ is $p^, = p(x, y) + b(x, y)$. Here, the error filter $a_{jk}$ is a set of constant coefficients, and the quantization threshold u in $Q(\cdot ,\cdot )$ is also a fixed value, e.g. $u = 0.5$.

Some important improvements to the original ED algorithm include the introduction of a variable error filter [14] and a variable threshold value [22] to ensure the blue-noise property of the sampling output. In this paper, we use Zhou and Fang’s threshold modulated ED algorithm to build our MCED framework. Similar as in [4], we refer to that algorithm as the standard ED, and its diagram is given by Fig. 1 as a whole. Unlike the original ED, the threshold u and the error filter $a_{jk}$ here are not constant, but functions of the input pixel $p=p(x, y)$, that is, $u = 0.5 + r(p)$, and $a_{jk} = a_{jk}(p)$. Here, $r(p) = \delta (p)\cdot \lambda (x, y)$ is a modulated white noise. The modulation strength $\delta (p)$ for the white noise $\lambda (x, y)$, and the error filter $a_{jk}(p)$ are pre-optimized so that the output of the standard ED possesses blue-noise property.

3.2 MCED Framework

Our MCED algorithm mainly concerns about simultaneously sampling on multiple channels of input signals and maintaining the blue-noise property for all the classes as well as their superimposition. If simply performing the standard ED independently on each channel of input signal, there may be sampling points from different classes situated at the same sampling position when they are superimposed, which is called sampling conflict. Hence, the blue-noise property of the superimposed output cannot be guaranteed.

To solve this problem, we first perform the quantization on each channel of signal, and produce a set of initial sampling outputs with sampling conflicts. Then, the conflicts are removed by disabling the outputs of certain classes based on the inter-class correlation. In this way, the initial outputs are modified to generate the final sampling points. During the process of quantization and error-diffusion, a threshold displacement is introduced to decrease the occurrence of sampling conflict and maintain the blue-noise property.

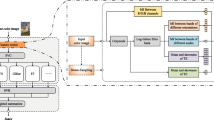
The framework of our MCED algorithm is illustrated in Fig. 2. It takes n channels of signals $\{p_i \vert i=1,\cdots ,n\}$ as input, where $p_i=p_i(x,y)$ is a 2-D discrete function that satisfies $p_i(x,y) \in [0,1]$ and $\sum _{i=1}^np_i(x,y) \le 1$. In fact, it defines the density of sampling points to be generated at the spatial position (x, y). Specially, when $p_i$ represents an image, element $p_i(x, y)$ is the intensity of the pixel at position (x, y).

Fig. 2.

The framework of our MCED algorithm, where $\{p_i \vert i=1,\cdots ,n\}$ are the input signals, and $p_0=\sum _{i=1}^n p_i$ is an internal reference signal. After two processing steps of modified standard ED, $Q_i$ and $E_i$, the framework generates blue-noise sampling outputs $\{c_i \vert i=0,\cdots ,n\}$. The pseudo code for the framework can be found in the Appendix A.

Fig. 3.

Two processing steps of modified ED: $Q_i$ (left) performs only the quantization and $E_i$ (right) complete the final error-diffusion ($i=0,\ldots ,n$).

Our framework concerns the processing of individual channels of signals as well as their correlations, and produces corresponding sampling point sets $\{c_i \vert i=1,\cdots ,n\}$, where $c_i(x,y)=1$ indicates a sampling point generated at (x, y) for signal $p_i$, while 0 means no point generated. Therefore, the sampling process from the input $p_i$ to the output $c_i$ is referred as a class $C_i$.

To facilitate the inter-class correlation, we define a special internal signal $p_0$, whose sampling density is $p_0(x,y)=\sum _{i=1}^np_i(x,y)$. Sampling to $p_0$ with the standard ED, we can also obtain a blue-noise output, which is used as a reference for the superimposition of the sampling output of all the classes. That means the corresponding output of $p_0$, denoted as $c_0$, will be identical to the superimposition of $\{c_i \vert i=1,\cdots ,n\}$. Hence, we name $C_0$ as a reference class.

Our framework parses the elements $\{p_i(x, y) \vert i=0,\cdots ,n\}$ in a serpentine scan line order. All $p_i(x, y)$ at the same position (x, y) are processed simultaneously, and then the processing moves to the next position. For each group of $\{p_i(x, y) \vert i=0,\cdots ,n\}$ at (x, y), the processing of each class includes two steps: $Q_i$ and $E_i$. $Q_i$ performs independent sampling and produces initial output $c_i^{0} (x, y)$ for each individual class $C_i$; while $E_i$ modifies the initial output according to the correlation between the sampling classes and generate the final output $c_i(x, y)$.

3.3 Quantization and Error-Diffusion

The work flow of the two processing steps, $Q_i$ and $E_i$, are shown in Fig. 3. Actually, $E_i$ is a modified version of the standard ED given in Fig. 1. It simply adds one more variable $m_i$ to the latter’s quantization threshold. This simple modification plays an important role in our framework, because $m_i$ will be used to introduce the inter-class correlation into the sampling, and that is the key to avoid sampling conflict and ensure the blue-noise property of $c_i$.

It is notable that $Q_i$ produces only the initial sampling output, hence it performs only the quantization part of $E_i$. Although $Q_i$ shares the error buffer $b_i(\cdot , \cdot )$ with $E_i$, it does not modify $b_i(\cdot , \cdot )$. This is because the output of $Q_i$ will be modified in $E_i$ and thus the quantization error made in the latter step is the one that is to be distributed for the further processing.

3.4 Removing Sampling Conflicts

In our framework, the input signal $p_i$, $i = 0, \cdots , n$, of each class is firstly processed by $Q_i$, and generates corresponding uncorrelated blue-noise output $c_i^{0}$. In order to eliminate the conflict after superimposition, the correlation between classes are introduced by the reference class $C_0$. Based on that, some classes with sampling conflicts will be disabled, i.e. they will be prohibited to produce a sampling point.

Fig. 4.

Eliminating sampling conflicts by disabling some of the classes.

As shown in Fig. 4, when $Q_0$ of class $C_0$ does not generate a sampling point at current position (x, y), the output of all $\{E_i \vert i \ne 0\}$ should be forced to be 0. In other words, all $E_i$ should be disabled from generating a sampling point at (x, y), for there is no correspondence in the final superimposition. Similarly, when $Q_0$ generates sampling point but none of $\{Q_i \vert i \ne 0\}$ does, $E_0$ should also be disabled because no $E_i$ will provide sampling point to form this superimposition. The third case, in which $\{Q_i \vert i \ne 0\}$ generate sampling points without conflicts, is the ideal case that we are expecting and no modification to $\{c_i^{0} \vert i \ne 0\}$ is needed. Finally, when sampling conflicts occur ($\sum _{j\ne 0} c_j^{0} > 1$), most of the conflicting classes must be disabled, and only one of them with the highest priority is allowed to remain. Here, we give the priority to the class $C_k$ with the highest average sampling density, i.e. $k={argmax}_{j}\sum _{(x,y)}{p_j(x,y)}$, for $j\ne 0$ and $c_j^{0}=1$. Then, a binary selecting signal $s_i$ ($i \ne 0$) is defined, where $s_i=0$ means $E_i$ should be disabled:

$$\begin{aligned} s_i = \left\{ \begin{array}{ll} 0, &{} \sum _{j\ne 0} c_j^{0}> 1 \, \text { and } \, i \ne k; \\ 1, &{} \sum _{j\ne 0} c_j^{0} > 1 \, \text { and } \, i = k; \\ 1, &{} \sum _{j\ne 0} c_j^{0} \le 1 . \end{array} \right. \end{aligned}$$

(2)

To disable a class, we utilize another disabling signal to modify the quantization threshold. It is based on an important fact about the ED: If the threshold u in the quantizer $Q(p^,, u)$ takes a value larger than any possible value of input p, the output of Q will be forced to be 0, and the corresponding class will be disabled. As shown in Fig. 2, the disabling signals are obtained based on the initial outputs $\{c_i^{0} \vert i = 0, \cdots , n\}$ by the Disable control, where $d_0= \lnot (c_1^{0} \vee c_2^{0} \cdots \vee c_n^{0})$ and $d_1= \lnot (c_0^{0})$. Then, combining with the selecting signal $s_i$, $d_1$ turns into a $d_{1i} = d_1 \wedge s_i$ for each $E_i$ ($i \ne 0$). Therefore, if $d_0/d_{1i}=1$, a large value ($+\infty$) will be added to the corresponding quantization threshold, and the class will be disabled.

In this way, $d_0$, $d_1$ and $s_i$ facilitate the correlation described in Fig. 4. For example, when $c_0^{0} = 1$ and $c_i^{0} = 1$ ($i \ne 0$), we have $d_0 = 0$ and $d_1 = 0$, and the output of $E_i$ will be decided by its priority: if $s_i = 0$, $E_i$ will be disabled. After the class disabling, sampling conflicts can be removed and no more than one sampling point will be generated at each position.

3.5 Maintaining Blue-Noise Property

Modifying the output of certain $Q_i$ to remove the sampling conflicts may cause the destruction of the blue-noise property of the initial outputs. To solve this problem, we make use of another important fact for ED: For a given input signal, a constant variation of the quantization threshold u will change the distribution of output sampling points, but will not affect the average sampling density, as long as u is not constantly $+\infty$. This fact can be proofed with the analysis tool provided in [12], which will be briefly described in Sect. 7. Therefore, adding a properly chosen threshold displacement $t_i$ to the threshold u will help to decrease the chance of the sampling conflict occurrence and restore the blue-noise distribution. The detail of $t_i$ will be discussed in the next section.

Hence, the disabling signals $d_0/d_{1i}$, along with the threshold displacement $t_i$, are finally added to the thresholds of $E_i$ via the modification term $m_i$ in the second step. Then, $E_i$ quantizes the input element $p_i(x,y)$ at current position (x, y), and the quantization error is distributed and accumulated to the error buffer b(j, k). The above processing is repeated during the parsing of the input elements. When all the elements $p_i(x,y)$ are parsed, the final blue-noise MCED output $c_i$ that satisfies all the requirements given in Sect. 1 can be generated.

4 Threshold Displacement

After the first step of the MCED, the output of some of the classes is disabled due to sampling conflicts. This may disrupt the blue-noise property that originally existed in the standard ED output. We solve this problem by adding a constant displacement value $t_i$ to the quantization threshold for the input $p_i$, since a shift of the threshold may change the distribution of sampling points and thus may decrease the chance of sampling conflicts. Therefore, it is possible to ensure a better blue-noise output with a properly chosen $t_i$.

4.1 Displacement Optimization

Our goal is to find a set of optimal threshold displacements $\{t_i \vert i=0,1,\cdots ,n\}$, to decrease the probability of sampling conflict occurrence. Since the sampling conflict is a interference among all the classes, the value of the displacement $t_i$ is related to all the input signals $\{p_i \vert i=1,\cdots ,n\}$. For each class $C_i,i=0,\cdots ,n$, in a n-class MCED, we treat the influence from all other sampling classes as a noise, which is characterized by its strength $\sigma _i= \sum _{j \not = 0 \wedge j\not = i}p_j$. We assume that the same amount of $\sigma _i$ for a given $p_i$ will result in similar output. Since $\sigma _i$ can be derived from $\sigma _i=p_0-p_i$, then $t_i$ can be simplified as a function of $p_i$ and $p_0$. As class $C_0$ is designed as a reference for the superimposition of other n classes, $t_0$ is related with only the sum of other classes inputs, i.e. $p_0=\sum _{i=1}^n p_i$.

Therefore, given an input combination $(p_0,p_i), i=1,\cdots ,n$, in a n-class MCED, we have:

$$\begin{aligned} {\left\{ \begin{array}{ll} t_i=g(p_0, p_i), i=1,\cdots ,n, \\ t_0=f(p_0). \end{array}\right. } \end{aligned}$$

(3)

Then, optimal $t_i$ are calculated by solving an optimization problem. The optimization target function is defined according to the Fourier power spectrum of the sampling output. Based on the existing research [18, 22], the blue-noise property of a sampling set can be measured by the anisotropy and the lower frequency ratio of its spectrum. In this paper, the sampling output of ED are affected by both the input signal $p_i$ and the threshold displacement $t_i$. Therefore, the anisotropy $\alpha (p_i, t_i)$ and lower frequency ratio $\beta (p_i, t_i)$ for the final output $c_i$ can be modified from their original formulations in [22]:

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha (p_i, t_i) = Corre(P_0(p_i, t_i), P_{45}(p_i, t_i), P_{90}(p_i, t_i)), \\ \beta (p_i, t_i) = L(p_i, t_i), \end{array}\right. } \end{aligned}$$

(4)

where $Corre(\cdot )$ is a cross-correlation function; $P_0(\cdot )$, $P_{45}(\cdot )$ and $P_{90}(\cdot )$ are segmented radially averaged power spectrums; $L(\cdot )$ is the lower frequency ratio.

Therefore, our target function T to be minimized in the searching of optimal threshold displacements $t_i$ is defined as:

$$\begin{aligned} {\begin{matrix} T=\omega _1 \cdot \left( \omega _0 \cdot \sum _{i=1}^N\alpha (p_i, t_i)+(1-\omega _0) \cdot \sum _{i=1}^N\beta (p_i, t_i) \right) \\ +\,(1-\omega _1) \cdot \left( \omega _0 \cdot \alpha (p_0, t_0)+(1-\omega _0) \cdot \beta (p_0, t_0) \right) , \end{matrix}} \end{aligned}$$

(5)

where the weights $\omega _0=0.5$ and $\omega _1=0.7$ are taken in our implementation. A simplex method [15] is adopted to automatically search for the optimal displacement $\{t_i \vert i=0,1,\cdots ,n\}$.

Figure 5 ¹ demonstrates an example of the displacement optimization. Given $p_1=\frac{32}{255}$, $p_2=\frac{21}{255}$, $p_3=\frac{16}{255}$, $p_4=\frac{12}{255}$, $p_5=\frac{8}{255}$, $p_6=\frac{6}{255}$, $p_7=\frac{5}{255}$, and $p_0=\sum _{i\ne 0} p_i=\frac{100}{255}$, the optimized threshold displacements are: $t_1=\frac{34}{255}$, $t_2=\frac{18}{255}$, $t_3=\frac{52}{255}$, $t_4=\frac{23}{255}$, $t_5=\frac{80}{255}$, $t_6=\frac{46}{255}$, $t_7=\frac{17}{255}$, and $t_0=-\frac{9}{255}$. The sampling outputs of classes $\{C_i \vert i=0,\cdots ,7\}$, and their corresponding Fourier power spectra are given in the figure. Figure 5(h) is the superimposition of the dots from the 7 classes, which are colored in red, green, blue, yellow, magenta, cyan and white, respectively. The optimization is performed on $256\times 256$ patches.

Fig. 5.

Optimization result for a 7-class ED. (a)–(h) Sampling outputs of each classes $C_i$. (i)–(p) Corresponding Fourier power spectra. (Image best viewed at 306 DPI). (Color figure online)

4.2 Displacement Interpolation

To decrease computational costs, we perform displacement optimization only on a set of selected key input combinations, by minimizing the target function T in Eq. 5. Then, the optimal threshold displacements for other input combinations can be calculated by interpolation, where $t_i=g(p_0, p_i)$, $i=1,\cdots ,n$, is implemented with a bilinear interpolation, and $t_0=f(p_0)$ with a 1-D linear interpolation.

The key input combinations and their corresponding optimal threshold displacement values are shown in the tables contained in Fig. 6. The key levels are selected by an interval of $\frac{16}{255}$. For convenience, all the numbers filled into the table are 255 times of their real values. The right table gives the correspondence between the threshold displacement $t_0$ and the input $p_0$ of the reference class $C_0$, as $t_0 = f(p_0)$. The left table is composed of two parts:

• The values of the threshold displacement $t_i = g(p_0, p_i)$ for the given key input combinations are enumerated in the lower-left triangle area. They are obtained by solving the optimization problem of Eq. 5. The indices of $p_0$ and $p_i$ are given in the bottom row and the leftmost column, respectively.

• The corresponding power spectra of the sampling outputs for $p_i$ and $p_0$ can be found in the upper-right triangle area, where the left image is for $p_i$ and the right for $p_0$. The indices of $p_0$ and $p_i$ are given in the top row and the rightmost column. The power spectra show that, for the given input combinations, our optimization successfully converges to threshold displacements that can produce outputs with ideal blue-noise property.

Hence, the threshold displacement of a key input combination can be read directly from the table. For example: given $p_0=\frac{112}{255}$ and $p_i=\frac{16}{255}$, the displacement value $t_i=g(\frac{112}{255}, \frac{16}{255})=\frac{49}{255}$ can be found in the cell at the 8th row and the 2nd column of the left table, and the corresponding power spectra are in the cell at the 2nd row and 8th column.

Then, for arbitrary combination $(p_0, p_i)$ that is not included in Fig. 6, we use a bilinear interpolation to obtain their $t_0$ and $t_i$. For example, for an input $(p_0, p_i)=(\frac{122}{255}, \frac{21}{255})$, its $t_i$ is interpolated between four key values $g(\frac{112}{255}, \frac{16}{255})$, $g(\frac{112}{255}, \frac{32}{255})$, $g(\frac{128}{255}, \frac{16}{255})$ and $g(\frac{128}{255}, \frac{32}{255})$ that exist in the table. The value of $t_0$ is interpolated in a similar way, but using a 1-d linear interpolation between the values in the right table. Figures 7 and 8 are two groups of experiment results of a two-class MCED using our key values and interpolation mechanism. It can be seen that the sampling results meet the requirement of MCED given in Sect. 1.

Fig. 6.

Threshold displacement $t_0$ and $t_i$ with their Fourier analysis results for different key input combinations $(p_0, p_i)$. For convenience, the numbers in this table are all 255 times of the value by their definition.

Fig. 7.

Two-class ED with density changing horizontally from $\frac{255}{255}$ to 0 in opposite directions, $p_0=\frac{255}{255}$. (a) is the superimposition, (b) and (c) are the sampling points for the two classes, shown in red and green respectively. The image is best viewed in PDF reader with 100% scaling ratio at 150 DPI. (Color figure online)

Fig. 8.

Two-class ED with density changing horizontally from $\frac{51}{255}$ to 0 in opposite directions, $p_0=\frac{51}{255}$. (a) is the superimposition, (b) and (c) are the sampling points for the two classes, shown in red and blue respectively. The image is best viewed in PDF reader with 100% scaling ratio at 150 DPI. (Color figure online)

5 Experimental Results

We proposed a multi-class ED algorithm that is able to produce blue-noise sampling points on multiple input signals as well as their superimposition. Given k channel of signals, each with n elements, the time complexity of our algorithm (Algorithm 1) is $\mathcal {O}(kn)$. Some experimental results have been shown in Sect. 4.

In this section, we compare our Multi-class ED with the per-channel standard ED [22], and our method achieves results significantly better than the latter. As illustrated in Fig. 9(b)–(g), applying our MCED to three channels of input signal, three sampling point sets with blue-noise distribution can be produced (Fig. 9(b)(d)(f), colored with red, green and blue for distinction). The corresponding Fourier power spectra in Fig. 9(c)(e)(g) demonstrate the perfect blue-noise property of each class. Figure 9(a) is a colored superimposition of the three classes. Since no sampling conflicts exist, i.e., none of the sampling point overlaps with others, there are no color other then red, green and blue in the image. Figure 9(h)–(i) show that the superimposed point sets also possesses blue-noise property.

Fig. 9.

A 3-class MCED sampling result. Each individual class (b–g) and their superimposition (h–i) possess perfect blue-noise property. (Best viewed at 150 DPI.) (Color figure online)

Fig. 10.

A 3-class sampling using standard ED. Large number of conflicting sampling points exists (e–h), and the superimposition does not possess blue-noise property (i–j). (Best viewed at 150 DPI). (Color figure online)

On the contrary, if applying the standard ED to each channel of signal separately, though each set of sampling points has blue-noise distribution, a large number of sampling conflicts will occur when the three point sets are superimposed. Figure 10(a) is also a colored superimposition of the sampling point sets, where each color channel correspond to a class. Then, in Fig. 10(b)–(d) are the sampling points that do not overlap with others, and Fig. 10(e)–(h) show the conflicting sampling points, generated by the overlapping of points from different classes (The colors indicate the combination). Consequently, the superimposition set can not maintain blue-noise property (Fig. 10(i)–(j)).

The sampling conflicts are harmful in certain application areas, such as color printing. For the per-channel ED, uncontrollable overlapping of sampling points will affect the controlling of the maximum ink amount at each position, and the final printing quality. Our MCED method can help to solve this problem and hence brings an important improvement.

6 Applications

6.1 MCED for Color Image Halftoning

ED algorithm is widely used in grayscale image halftoning due to its ideal blue-noise property [14, 22]. For color image halftoning, a commonly used way is to perform standard ED independently on each color plane, and then superimpose the results to create a color halftoning. Since halftoning dots for each color plane are generated independently, the blue-noise property for their superimposition can not be guaranteed. This may result in uncontrolled color appearance in the generated halftone image (Fig. 11(p)).

In this section, we utilize our MCED to generate color halftone images that meet the requirements: The distribution of the halftone dots with the same color should possess blue-noise property; The distribution of all the dots contained in the halftone image as a whole should also possess blue-noise property.

15-Class ED for CMYK Color Halftoning

CMYK Color Images. In the state-of-the-art color printing systems, the device-independent colors are converted to the densities of the ink dots in four primary colors: Cyan, Magenta, Yellow and Black. We denote them as well as their densities as $\mathcal {D}_1$, $\mathcal {D}_2$, $\mathcal {D}_3$, $\mathcal {D}_4$, respectively, and they are the input of the halftoning algorithms. When the output halftoning image is printed using the four color inks, the dots generated on paper will appear in totally 15 colors, corresponding to all possible ink overprints.

If $\sum _{i=1}^4\mathcal {D}_i>1$ within a local area in a CMYK halftone image, there must be dots with different primary colors placed at the same position, and new colors will be created. The colors generated by 2 primary colors, namely the 2nd order colors, are denoted as $\mathcal {C}_{12}$, $\mathcal {C}_{13}$, $\mathcal {C}_{14}$, $\mathcal {C}_{23}$, $\mathcal {C}_{24}$, $\mathcal {C}_{34}$. The subscript indicate the overprinted primary colors, e.g., $\mathcal {C}_{12}$ is an overprinting of $\mathcal {D}_1$ and $\mathcal {D}_2$. In the six colors, $\mathcal {C}_{12}$, $\mathcal {C}_{13}$ and $\mathcal {C}_{23}$ correspond to blue, green and red respectively, and the remaining are very dark colors because they contain black. Similarly, the 3rd and the 4th order colors generated by 3 or 4 primary colors are denoted as $\mathcal {C}_{123}$, $\mathcal {C}_{124}$, $\mathcal {C}_{134}$, $\mathcal {C}_{234}$, $\mathcal {C}_{1234}$. Specially, the subsets of halftone dots generated by only one primary color are denote as $\mathcal {C}_1$, $\mathcal {C}_2$, $\mathcal {C}_3$, $\mathcal {C}_4$.

Without ambiguity, we use the same notations for the dot density and the sampling class for each color. Hence, there is a total of 15 classes to be sampled in MCED. Before applying our MCED in CMYK color halftoning, the densities of the 15 classes need to decided.

Linear Programming for Dot Densities. For a color image pixel with $\sum _{i=1}^4\mathcal {D}_i \le 1$, the dot densities are simply $\mathcal {C}_1 = \mathcal {D}_1$, $\mathcal {C}_2 = \mathcal {D}_2$, $\mathcal {C}_3 = \mathcal {D}_3$, $\mathcal {C}_4 = \mathcal {D}_4$, and the densities for higher order colors are 0. While for a pixel with $\sum _{i=1}^4\mathcal {D}_i>1$, the dot densities must satisfy:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {C}_1+\mathcal {C}_2+\mathcal {C}_3+\mathcal {C}_4 \\ + \mathcal {C}_{12}+ \mathcal {C}_{13}+ \mathcal {C}_{14}+ \mathcal {C}_{23} + \mathcal {C}_{24}+ \mathcal {C}_{34} \\ + \mathcal {C}_{123}+ \mathcal {C}_{124}+ \mathcal {C}_{134}+ \mathcal {C}_{234}+ \mathcal {C}_{1234} = 1, \\ \mathcal {C}_1 + \mathcal {C}_{12} + \mathcal {C}_{13} + \mathcal {C}_{14} + \mathcal {C}_{123} + \mathcal {C}_{124} + \mathcal {C}_{134} + \mathcal {C}_{1234} = \mathcal {D}_1,\\ \mathcal {C}_2 + \mathcal {C}_{12} + \mathcal {C}_{23} + \mathcal {C}_{24} + \mathcal {C}_{123} + \mathcal {C}_{124} + \mathcal {C}_{234} + \mathcal {C}_{1234} = \mathcal {D}_2,\\ \mathcal {C}_3 + \mathcal {C}_{13} + \mathcal {C}_{23} + \mathcal {C}_{34} + \mathcal {C}_{123} + \mathcal {C}_{134} + \mathcal {C}_{234} + \mathcal {C}_{1234} = \mathcal {D}_3,\\ \mathcal {C}_4 + \mathcal {C}_{14} + \mathcal {C}_{24} + \mathcal {C}_{34} + \mathcal {C}_{124} + \mathcal {C}_{134} + \mathcal {C}_{234} + \mathcal {C}_{1234} = \mathcal {D}_4. \end{array}\right. } \end{aligned}$$

(6)

Eq. 6 is a linear programming problem, which can be solved by specifying one or more optimization target to be maximized [15]. In our experiments, we define the optimization target h as:

$$\begin{aligned} h =\mathcal {C}_1+\mathcal {C}_2+\mathcal {C}_3+ \mathcal {C}_{12} + \mathcal {C}_{13} + \mathcal {C}_{23} + \mathcal {C}_{123}. \end{aligned}$$

(7)

This target function maximizes the colors created by C, M and Y, and minimizes those mixed with black, because black always tends to cover the appearance of other colors. When the densities of each class at each pixel are obtained, they are sent into our 15-class ED and produce an output halftone image.

Fig. 11.

CMYK color image halftoning using our 15-class MCED. Blue-noise dot distributions are generated for all classes (a)–(m), as well as their superimposition (n). (o): Colored superimposition. (p): Halftoning result by the standard ED. (Best viewed at 100% scaling ratio, 600 DPI). (Color figure online)

Fig. 12.

More CMYK color image halftoning results using MCED. (Best viewed at 100% scaling ratio, 300DPI). (Color figure online)

Figure 11 shows an example of our 15-class ED color halftoning. It is able to create blue-noise dot distributions for all of the classes (Fig. 11(a)–(m), some empty classes are omitted), as well as their superimposition (Fig. 11(n)). Comparing our result (Fig. 11(o)) with that of the standard ED (Fig. 11(p)), it can be seen that our result demonstrates better blue-noise property. More CMYK image halftoning results using our MCED are given in Fig. 12.

Comparison with Vector Error-Diffusion. We also compared the performance of our MCED with the vector error diffusion (VED) [5] on color image halftoning. Both algorithms process multiple channels of signals using ED in a coordinated way. The VED treats the signals as a vector, and uses an optimum matrix-valued error filter to introduce the correlation among the color planes, hence it can generate good color halftoning results. However, it does not evaluate the dot distribution on each color planes and the conflict between them. Thus, the blue-noise property on each individual color plane cannot be promised. On the contrary, our MCED can generate blue-noise outputs on each individual channel of input signal, as well as their superimposition. Figure 13 demonstrates a per-channel comparison of the two algorithms on RGB color image halftoning. It can be seen that our MCED produce obviously better sampling results with smoother distribution and less artificial textures.

Fig. 13.

Color image halftoning using our MCED method and the Vector ED [5]. (a) The superimposed color halftoning image; (b) Zoom-in viewing of the dot distribution in the red box in (a); (c)–(h) The halftoning output of the corresponding color plane. (Images best viewed at 100% scaling ratio, 600 DPI). (Color figure online)

Fig. 14.

An example of 7-tone ED. For an image with intensity ranges from 1 to 0 (from center to border), a multi-tone rendering of the image (h) is generated by our MCED using 7 intensities (tones) given in the figure. (a)–(g) show the distribution of the pixels with these intensities respectively. (Images best viewed at 300 DPI). (Color figure online)

6.2 Multi-tone Error-Diffusion

Multi-toning, also known as multi-level halftoning [10, 16], aims to reproduce a continuous tone image with dots of a limited number of intensities $\{k_i \vert i=1,\cdots ,n\}$ ($k_i<k_j, \text { if } i<j$). It is useful in printing with multiple types of inks or dot sizes. Blue-noise property is also required in multi-tone images for visually pleasant result, hence our MCED method is also a solution for multi-tone image generation.

Given a pixel (x, y) in a continuous tone image with intensity p(x, y), if $k_i< p(x, y) < k_{i+1}$, then p(x, y) can be simulated with a linear combination of the halftone patterns with intensity $k_i$ and $k_{i+1}$:

$$\begin{aligned} p(x, y) = p_i(x, y) \cdot k_i + p_{i+1}(x, y) \cdot k_{i+1}, \end{aligned}$$

(8)

where $p_i(x, y)$ and $p_{i+1}(x, y)$ are respectively the densities of the halftone pattern of pixels with intensity $k_i$ and $k_{i+1}$ at (x, y), and $p_i(x, y)+p_{i+1}(x, y)=1$. For $j\ne i$ and $j\ne i+1$, we let $p_j(x, y)=0$.

Therefore, considering $p_i(x, y)$ as the input of class $C_i$ in a n-class ED, a n-tone image can be generated by our MCED algorithm. Figure 14 shows an example of 7-tone image generated with our method. The halftone patterns for the given intensities $\{k_i \vert i=1, \ldots ,7\}$ can be found in Fig. 14(a)–(g), and all of them possess ideal blue-noise property.

6.3 Color Image Vectorization

A typical catalog of color image vectorization methods [17] build polygon meshes on the image plane based on a set of sampling points. Then, by assigning each polygon node the image color at the same position, the original image can be converted to a vector form. The colors inside a polygon is calculated by interpolating between the colors of its nodes. Hence, the quality of the sampling point distribution is crucial for the quality of final vectorization results.

Our MCED method can provide ideal sampling point distribution for such a vectorization task. Here, the input image is in RGB, and the sampling points can be generated in the three color planes using our MCED in a similar way as in Sect. 6.1. After superimposing the sampling points, a planar triangle mesh is obtained by Delaunay triangulation, which can be used as the foundation of the vector image.

To preserve the image features during vectorization, we extract a salience map from the gradient of the original color image. At each pixel, the salience is defined as the sum of the absolute value of the gradient components, which is calculated by a Sobel operator. The salience is separately computed in the three color planes, and the resulting salience map is also a RGB image. Hence, sampling on the salience map instead of the original image, we can obtain a sampling point set that better preserves the features.

7 Analysis and Conclusion

This paper gives an algorithm for multi-class ED. The key technique of this algorithm is to use the optimized threshold displacement to minimize the distortion to the blue-noise property caused by inter-class correlation in multi-class error-diffusion. Our experiment shows that this technique can effectively maintain the blue-noise property that the standard error-diffusion possesses. The reason for this can be explained by Fourier transform-based analysis [8, 12].

7.1 Analysis

According to [12], for the original ED, the power spectrum B(u, v) of the Fourier transform of the output image can be written as:

$$\begin{aligned} B(u, v) = I(u, v) + F(u, v)E(u, v), \end{aligned}$$

(9)

where $I(\cdot )$ and $E(\cdot )$ are the Fourier transform of the input image and the error map e(x, y) generated during error-diffusion; $F(\cdot )$ is a high-pass filter defined solely by the diffusion filter.

For each class $C_i$, our algorithm is based on [22] by adding an extra modulation $m_i$ to its threshold, and $m_i$ includes the displacement $t_i$, which is in nature a noise from other ED classes. Also according to [12], threshold modulation is equivalent to sending to the original ED an equivalent image that is the sum of the original image and a filtered modulation, where the filter $F(\cdot )$ is exactly the one in Eq. 9. Therefore we have:

$$\begin{aligned} B(u,v) = I(u,v) +F(u,v) (D_ i(u,v)+M(u,v)) + F(u,v) E^{\prime }(u,v), \end{aligned}$$

(10)

where $D_i(u,v)$ is the Fourier transform of $d_{1i}$, M(u, v) is the Fourier transform of the threshold modulation r(p) defined in Fig. 1, $E^{\prime }(u,v)$ is the Fourier transform of the error map e(x, y) for the equivalent image. Note that $t_i$ does not appear in Eq. 10 because it is a DC component and is filtered out by $F(\cdot )$. Hence, threshold displacements do not have influence on the average density of the output image of any class.

It is also noted that in Eq. 10, only $D_i(\cdot )$ and $E^{\prime }(\cdot )$ are decided by the threshold displacement $\{t_i\}$. Considering the fact that $t_i$ actually has the effect of decreasing or increasing the amount of slow response phenomenon at the beginning of the ED, so properly chosen $\{t_i\}$ are able to minimize the amount of sampling conflict, which in turn can improve the anisotropy and lower frequency ratio defined in Eq. 4.

7.2 Limitation and Future Work

In the experiment results of our paper, smear artifacts may appear in the sampling classes with low average sampling density (Fig. 14(g)). This is because we use $s_i$ to choose the class with the highest average intensity when sampling conflict occurs and this may cause classes with less average intensity to generate output with lower quality. Hence, the selection of $s_i$ is a topic to be investigated.

The optimal threshold displacement $t_i=g(p_0, p_i)$ has the effect of reducing slow response [9], which is also called transient effect in some literature [22]. That effect in our MCED is shown obliviously in Fig. 15. At the top of the image, our sampling result (Fig. 15(d)) has very weak slow response than that generated by the standard ED (Fig. 15(a)). In fact, the amount of slow response directly affects the lower frequency ratio $\beta (p_i,t_i)$ in Eq. 4. Our displacement optimization automatically guides $t_i$ to a proper value to decrease the anisotropy and lower frequency ratio, and consequently, reduces the slow response. Hence, introducing threshold displacement into the single-class standard ED to further reduce its slow response is also a future research topic to be explored.

Fig. 15.

Color image vectorization using our MCED vs. the standard ED. (a) and (d) are triangulation on points sampled by Standard ED and MCED, (b) and (c) are corresponding rendering result. The input image is in RGB. (Color figure online)

A Pseudo Code of MCED

Algorithm 1 is the pseudo-code for the framework of MCED, and the main functions are explained as follows:

GetDisplacement() evaluates $t_i$ by accessing the lookup table (Fig. 6) we described in Sect. 4.2.

GetCoefficient() and GetStandardThreshold() are functions for finding appropriate diffusion coefficients and threshold for the standard ED.

Quantize() compares pixel value to the threshold and returns 0 if below, 1 otherwise (Eq. 1).

HaveConflict() returns TRUE if more than one sampling points from different classes situate at the current position, and NoConflict() indicates only one class sampled at the position.

FindMaxClass() finds the class whose sum of densities at all the spatial positions is the maximum.

DistributeError() distributes the quantization errors to neighboring pixels according to the error filter.