Relative Pose Estimation from Straight Lines Using Optical Flow-Based Line Matching and Parallel Line Clustering

Abstract

This paper tackles the problem of relative pose estimation between two monocular camera images in textureless scenes. Due to a lack of point matches, point-based approaches such as the 5-point algorithm often fail when used in these scenarios. Therefore we investigate relative pose estimation from line observations. We propose a new algorithm in which the relative pose estimation from lines is extended by a 3D line direction estimation step. Using the estimated line directions, the robustness and computational efficiency of the relative pose calculation is greatly improved. Furthermore, we investigate line matching techniques as the quality of the matches influences directly the outcome of the relative pose estimation. We develop a novel line matching strategy for small baseline matching based on optical flow which outperforms current state-of-the-art descriptor-based line matchers. First, we describe in detail the proposed line matching approach. Second, we introduce our relative pose estimation based on 3D line directions. We evaluate the different algorithms on synthetic and real sequences and demonstrate that in the targeted scenarios we outperform the state-of-the-art in both accuracy and computation time.

1 Introduction

Relative pose estimation is the problem of calculating the relative motion between two or more images. It is a fundamental component for many computer vision algorithms such as visual odometry, simultaneous localization and mapping (SLAM) or structure from motion (SfM). In robotics, these computer vision algorithms are heavily used for visual navigation.

The classical approach to estimate the relative pose between two images combines point feature matches (e.g. SIFT [1]) and a robust (e.g. RANSAC [2]) version of the 5-point-algorithm [3]. This works well under the assumption that enough point matches are available, which is usually the case in structured and textured surroundings.

As our target application is visual odometry and SLAM in indoor environments (e.g. office buildings) where only little texture is present, point-based approaches do not work. But lots of lines are present in those scenes (cf. Fig. 1), hence, we investigate lines for relative pose estimation.

Fig. 1.

A typical indoor scene with few texture in which a lot of lines are detected.

This paper recaps our previous work on relative pose estimation [4] and extends it by a novel line matching scheme which is based on optical flow calculation. We will present more details on the robust relative pose estimation framework and show in a thorough evaluation of the line matching and the relative pose estimation that we reach state-of-the-art results.

Our contributions are:

• a new line matching scheme in which optical flow estimation is used to find the correspondences

• a robust and fast framework combining all necessary steps for relative pose estimation using lines.

2 Related Work

The trifocal tensor is the standard method for relative pose estimation using lines. Its calculation requires at least 13 line correspondences across three views [5, 6]. It is in general not possible to estimate the camera motion from two views as shown by Weng et al. [7] unless further knowledge of the observed lines is exploited. If for example different pairs of parallel or perpendicular lines are given, as it is always the case in the “Manhattan world”¹, the number of required views can be reduced to two.

As the number of views is reduced, the number of required line correspondences declines as well, because only five degrees of freedom have to be estimated (three for the rotation and two for the translation up to scale) compared to 26 for the trifocal tensor. Problems with small degrees of freedom are beneficial for robust methods like RANSAC as the number of required iterations can be lowered. As for the method proposed in this paper, only two views are required where the rotation is estimated from a minimal of two 3D line direction correspondences and the translation from at least two intersection points.

In their work, Elqursh and Elgammal [8] employ the “Manhattan world” assumption and require only two views as well. They try to find “triplets” of lines, where two of the lines are parallel and the third is perpendicular to the others. The relative pose can then be estimated from one triplet. The pose estimation process is split up into two steps: first, the vanishing point information of the triplet is used to calculate the relative rotation. Then, the relative translation is estimated using the already calculated rotation and intersection points between lines. The detection of valid triplets for rotation estimation is left over to a “brute force” approach, in which all possible triplet combinations are tested through RANSAC. As the number of possible triplets is in $O(n^3)$ for n lines, this computation is very expensive. Contrarily, our rotation estimation method is more efficient as we calculate it from 3D line directions and the number m of different 3D line directions per image is much smaller than the number of lines (in our cases $m < 10$ whereas $n > 100$). In addition, we do not need the restricting “Manhattan world” assumption which would require orthogonal dominant directions but a less stricter form where we allow arbitrary directions.

Similar approaches requiring two views were presented by Wang et al. [9] and Bazin et al. [10]. In both works, the pose estimation is split up into rotation and translation estimation as well, where the rotation calculation relies on parallel lines. Bazin et al. estimate the translation from SIFT feature point matches. Their approach is also optimized for omnidirectional cameras. Our method requires only lines and no additional point feature detection as we calculate the translation from intersection points.

There exists already several approaches to match lines across images: Prominent descriptor-based approaches are “Mean Standard Deviation Line Descriptor” (MSLD) [11], “Line-based Eight-directional Histogram Feature” (LEHF) [12] and “Line Band Descriptor” (LBD) [13, 14]. These approaches follow the idea of describing the local neighborhood of a line-segment by analyzing its gradients and condensing their information into a descriptor vector. In the matching process, the descriptors are compared and the most similar descriptor decides the match. Often, techniques like thresholding the descriptor distance, “Left/Right Checking” (LRC) or “Nearest Neighbor Distance Ratio” (NNDR) are employed to robustify the matching. LRC ensures that the matching is symmetrical by only accepting matches where matching from “left” image to “right” image gives the same result as matching from “right” to “left”. LRC handles therefore occlusions. NNDR is known from SIFT feature matching [1] and follows the idea that the descriptor distance for a correct match should be significantly smaller than the distance to the closest incorrect match.

As local neighborhoods of different lines are often not distinguishable, the resulting descriptors are similar and therefore not feasible for matching under severe viewpoint changes. Explicitly designed for the tracking of lines in sequences are the approaches from Deriche and Faugeras [15] and Chiba and Kanade [16]. Deriche and Faugeras propose a Kalman filter for predicting the line-segment’s geometry in the next image, whereas Chiba and Kanade use optical flow for the prediction. Both approaches define a similarity function using only the geometry of the line to associate the predicted line with an observed one. As the changes between consecutive image frames are small, geometry is sufficient for the matching.

We present a novel matching technique which is also designed for the tracking of lines. Our algorithm is based on optical flow. We do not need to calculate descriptors as the optical flow vectors serve to associate line-segments in the images which saves valuable execution time. We can show that our approach shows better matching performance while requiering less computation time than state-of-the-art descriptor-based approaches in small baseline cases.

Computer vision systems requiring relative pose estimation are e.g. visual odometry, SLAM and SfM. Several line-based SfM methods exist like [6, 7, 17, 18] which formulate the SfM problem as a nonlinear optimization. The initial configuration is calculated using the trifocal tensor or is derived from other input data. The approach from Schindler et al. [18] takes “Manhattan World” assumptions into account and includes a vanishing point clustering on pixel level. Our method could be used in these SfM algorithms as an alternative for initialization requiring only two views. An EKF-based SLAM method called “StructSLAM” [19] has recently been published which extends a standard visual SLAM method with “structure lines” which are lines aligned with the dominant directions. Witt and Weltin [20] presented a line-based visual odometry algorithm using a stereo camera setup. The relative pose is estimated using a nonlinear optimization of the 3D line reconstruction similar to ICP. Holzmann et al. [21] proposed a line-based visual odometry using a stereo camera, too. They present a direct approach and calculate the displacement between two camera poses by minimizing the photometric error of image patches around vertical lines.

The paper is structured as follows: in Sect. 3 we present our novel line matching algorithm based on optical flow. The line correspondences are then used in our relative pose estimation which is explained in Sect. 4. The paper is concluded with an extensive evaluation of the optical flow-based line matching (Sect. 5.1) and the relative pose estimation algorithm (Sect. 5.2) where we show that we outperform the current state-of-the-art.

3 Optical Flow-Based Line Matching

The proposed matching algorithm is explicitly designed for the matching of lines under small viewpoint changes such as consecutive frames in image sequences. It follows the idea of Chiba and Kanade [16] in the point that optical flow calculation is exploited to generate the matches.

The algorithm consists of three main stages: first, the optical flow is calculated for points along the line-segments. Second, the flow vectors originating from the same line are checked for consistency. In the third step the flow vectors are used in a histogram-based approach to generate the matches. Every step is discussed in detail in the following sections.

3.1 Optical Flow Calculation

In the first step the optical flow is calculated using the method from Lucas and Kanade [22]. We name the point in the original image $\mathbf {p}$ and the point in the image after the motion $\mathbf {p}' = \mathbf {p} + \mathbf {v}$ where $\mathbf {v}$ is the optical flow vector.

In contrast to the matching procedure from Chiba and Kanade [16], we do not calculate the optical flow over a static grid on the whole image but consider only the image regions which are interesting for the matching of lines: the pixels belonging to the extracted line-segments. The question is now if all pixels belonging to line-segments should be used or if certain pixels are more appropriate for optical flow calculation then others?

Shi and Tomasi [23] tackled this question and analyzed which image regions are well suited for the Lucas-Kanade optical flow method. They found that the eigenvalues of the gradient matrix $\MakeUppercase {\mathbf {G}}$ of a pixel $\mathbf {p}$ are good indicators for the eligibility with

$$\begin{aligned} \MakeUppercase {\mathbf {G}} = \begin{pmatrix} g_{x}^{2} &{} g_{x} g_{y} \\ g_{x} g_{y} &{} g_{y}^{2} \end{pmatrix} \quad \text { and } \quad \mathbf {g} = \begin{pmatrix} g_{x} \\ g_{y} \end{pmatrix} \text { the gradient at point } \mathbf {p}. \end{aligned}$$

(1)

If both eigenvalues are small, the pixel belongs to an uniform region which is uneligible for flow calculation. If one eigenvalue is small and the other large, the image region contains an edge. Edges are prone to the aperture problem so they are also unfit for flow estimation. Unfortunately, this is the most common case in our scenario as the lines are extracted from such image regions. It is best when both eigenvalues are large. Here, the image region is structured (e.g. contains a corner) and is therefore good for flow calculation. Shi and Tomasi propose to threshold the minimal eigenvalue to detect these suitable regions. We follow this idea and calculate the minimal eigenvalue for pixels belonging to lines. For each line, non-maximum suppression is applied on the minimal eigenvalues to keep only pixels which are local maximums. These pixels are then sorted by their eigenvalue and only the best 50% per line are kept. Figure 2(a) shows which “corner-like” points are selected for the optical flow calculation and Fig. 2(b) visualizes the result of the optical flow estimation on these points.

3.2 Consistency Check

The optical flow calculation is not error-free due to occlusion, noise etc. (cf. Fig. 2(b)). To mitigate the influence of these errors on the matching result, we introduce a filtering step where flow vectors which violate the “consistency” are discarded.

We define the consistency in two ways: first, the appearance of a point before and after the motion must stay the same - we call this the “appearance consistency”. Second, we define the “consistent motion constraint” which states that points belonging to the same line must move in a consistent way.

We calculate the L1-norm between the image patch around the original point $\mathbf {p}$ in image I and the patch around the moved point $\mathbf {p'}$ in image $I'$ and use this value as measure for the “appearance consistency”. We discard the 5% of flow vectors with the highest norm. For the second rule, we check if the points $\mathbf {p'}$ originating from the same line $\mathbf {l}$ also form a line. We use a line fitting algorithm in RANSAC scheme to calculate the line which agrees best with the points $\mathbf {p'}$. Then, all points are discarded which do not fit to this line. A point fits to this line if its point-line distance is less or equal to 1 px.

Figure 2(c) depicts which flow vectors are discarded by the “appearance consistency” and the “consistent motion constraint” and which are used for further processing.

Fig. 2.

(a) “Corner-like” points on the line segments for which the optical flow is estimated. (b) Resulting optical flow vectors. (c) Flow vectors in red are discarded due to the “appearance consistency”, flow vectors in blue due to the violation of the “consistent motion constraint”. Just the flow vectors drawn in green are considered for further processing. (Color figure online)

3.3 Histogram-Based Line Matching Using Optical Flow Vectors

After the optical flow result is filtered, the lines of image I and $I'$ are finally associated. Due to noise and different line segmentation, the endpoints $\mathbf {p'}$ of the flow vectors will not lie directly on the lines in image $I'$. To associate the endpoints $\mathbf {p}'$ with lines $\mathbf {l}'$ and then the lines $\mathbf {l}'$ with lines $\mathbf {l}$ from image I, we designed an histogram-based approach where every optical flow endpoint $\mathbf {p}'$ votes for its nearby lines $\mathbf {l}'$. The votes are then accumulated over all points originating from the same line $\mathbf {l}$. The line $\mathbf {l}'$ with the most votes is then the match of $\mathbf {l}$. Algorithm 1 depicts this histogram-based matching process in detail.

The only adjustable parameter in this histogram-based matching process is $\delta$ which defines the search region for nearby lines around point $\mathbf {p}'$. We found experimentally that $\delta = 2\,\text {px}$ is a good value.

In Fig. 3 the resulting line matches are shown.

Fig. 3.

Line matches generated with the optical-flow line matching algorithm. Corresponding lines share the same color in left and right image. (Color figure online)

4 Relative Pose Estimation from Lines

In the following, we recap our previously presented relative pose estimation [4]. First, we detail how to calculate the rotation from 3D line directions (Sect. 4.2). Once the rotation between the two views is estimated, the translation is calculated using intersection points which is illustrated in Sect. 4.3. In Sect. 4.4 the robust relative pose estimation framework is presented which combines the rotation and translation estimation.

4.1 Notation

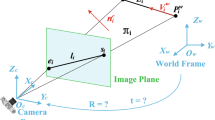
In relative pose estimation, we deal with entities in different coordinate systems: there are objects in the image (denoted by subscript i, like the line $\mathbf {l}_i$ or point $\mathbf {p}_i$) and in the camera frame (denoted by subscript c, like the 3D line direction vector $\mathbf {d}_c$).

A projective mapping is used to project a point $\mathbf {X}_c$ from the camera frame onto the image plane. $\MakeUppercase {\mathbf {K}}$ is the known $3 \times 3$ calibration matrix of the camera.

$$\begin{aligned} \mathbf {x}_i&= \MakeUppercase {\mathbf {K}} \mathbf {X}_c \end{aligned}$$

(2)

The transformation between two coordinate systems is defined by the matrix ${\MakeUppercase {\mathbf {T}}}_{to \leftarrow from} = \left[ {\MakeUppercase {\mathbf {R}}}_{to \leftarrow from}, {\mathbf {t}}_{to \leftarrow from} \right]$ with ${\MakeUppercase {\mathbf {R}}}_{to \leftarrow from} \in \mathbb {SO}(3)$ the rotation and ${\mathbf {t}}_{to \leftarrow from} \in \mathbb {R}^3$ the translation. The transformation from a point $\mathbf {X}_{c_a}$ in camera a into the coordinate system of the camera b is done with

$$\begin{aligned} \mathbf {X}_{c_b}&= {\MakeUppercase {\mathbf {R}}}_{c_b \leftarrow c_a} \mathbf {X}_{c_a} + {\mathbf {t}}_{c_b \leftarrow c_a}. \end{aligned}$$

(3)

4.2 Rotation Estimation from 3D Line Directions

The transformation of a 3D line direction depends only on the rotation:

$$\begin{aligned} \mathbf {d}_{c_2}&= {\MakeUppercase {\mathbf {R}}}_{c_2 \leftarrow c_1} \mathbf {d}_{c_1} \end{aligned}$$

(4)

Given m corresponding (and possible noisy) directions, we want to find the rotation ${\MakeUppercase {\mathbf {R}}}_{c_2 \leftarrow c_1}$ between two cameras $c_1$ and $c_2$ which minimizes

(5)

where $\MakeUppercase {\mathbf {D}}_{c_1}$ and $\MakeUppercase {\mathbf {D}}_{c_2}$ are $3 \times m$ matrices which contain in each column the corresponding directions. This problem is an instance of the “Orthogonal Procrustes Problem” [24]. We employ the solution presented by Umeyama [25] which returns a valid rotation matrix as result by enforcing $\det ( {\MakeUppercase {\mathbf {R}}}_{c_2 \leftarrow c_1}) = 1$:

$$\begin{aligned} {\MakeUppercase {\mathbf {R}}}_{c_2 \leftarrow c_1}&= \MakeUppercase {\mathbf {U}}\MakeUppercase {\mathbf {S}}{\MakeUppercase {\mathbf {V}}}^\mathrm {T} \end{aligned}$$

(6)

with

(7)

(8)

At least two non-collinear directions are required to calculate a solution.

The challenging task is now to extract 3D line directions from line observations in the two images and to bring these extracted directions in correspondence. We solve the direction estimation using a parallel line clustering approach which is explained now. Afterwards, we describe the matching of 3D line directions.

3D Line Direction Estimation by Parallel Line Clustering. The goal of this phase is to cluster lines of an image which are parallel in the world and to extract the shared 3D line direction for each cluster. This problem is closely related to the vanishing point detection, as the vanishing point $\mathbf {v}_i$ of parallel lines is the projection of the 3D line direction $\mathbf {d}_C$ [6]:

$$\begin{aligned} \mathbf {v}_i&= \MakeUppercase {\mathbf {K}} \mathbf {d}_c \end{aligned}$$

(9)

We suggest to work directly with 3D line directions $\mathbf {d}_c$ and not with the 2D vanishing points. Working in 3D space is beneficial, because it is independent from the actual camera (perspective, fisheye etc.) and allows an intuitive initialization of the clustering. In (9), we introduced how the vanishing point and the 3D line direction are related. Now, we have to transfer the line $\mathbf {l}_i$ into its corresponding 3D expression – its back-projection. The back-projection of an image line is the plane $\mathbf {\Pi }_c$ whose plane normal vector is given by (cf. [6]):

$$\begin{aligned} \mathbf {n}_c&= {\MakeUppercase {\mathbf {K}}}^\mathrm {T} \mathbf {l}_i \end{aligned}$$

(10)

Expectation-Maximization Clustering. Many of the vanishing point detection algorithms employ the Expectation-Maximization (EM) clustering method [26] to group image lines with the same vanishing point [27, 28]. We got inspired by the work of Košecká and Zhang [28] and we adapt their algorithm so that it directly uses 3D line directions instead of vanishing points. This enables us to introduce a new and much simpler cluster initialization in which we directly set initial directions derived from the target environment.

The EM-algorithm iterates the expectation and the maximization step. In the expectation phase, the posterior probabilities $p({\mathbf {d}_{c}^{(k)}} | {\mathbf {n}_{c}^{(j)}})$ are calculated. The posterior mirrors how likely a line $\mathbf {l}_{i}^{(j)}$ (with plane normal $\mathbf {n}_{c}^{(j)}$) belongs to a certain cluster k represented by direction $\mathbf {d}_{c}^{(k)}$. Bayes’s theorem is applied to calculate the posterior:

$$\begin{aligned} p\left( \mathbf {d}_{c}^{(k)} | \mathbf {n}_{c}^{(j)} \right)&= \frac{ p\left( \mathbf {n}_{c}^{(j)} | \mathbf {d}_{c}^{(k)}\right) p\left( \mathbf {d}_{c}^{(k)} \right) }{ p\left( \mathbf {n}_{c}^{(j)}\right) } \end{aligned}$$

(11)

We define the likelihood as

$$\begin{aligned} p\left( \mathbf {n}_{c}^{(j)} | \mathbf {d}_{c}^{(k)}\right)&= \frac{1}{\sqrt{2\pi \sigma _k^2}} \exp \left( \frac{ -\left( { \left. \mathbf {n}_{c}^{(j)} \right. }^\mathrm {T} \mathbf {d}_{c}^{(k)} \right) ^2}{ 2\sigma _k^2 } \right) \end{aligned}$$

(12)

The likelihood reflects that a 3D line in the camera frame (and its direction $\mathbf {d}_{c}^{(j)}$) should lie in $\mathbf {\Pi }_{c}^{(j)}$ and is therefore perpendicular to the plane normal $\mathbf {n}_{c}^{(j)}$. If we substitute $\mathbf {n}_{c}^{(j)}$ and $\mathbf {d}_{c}^{(k)}$ with (9) and (10), we come to a likelihood term in the 2D image space which is the same as in the work of Košecká and Zhang [28].

In the maximization step, the probabilities from the expectation step stay fixed. The direction vectors are in this phase re-estimated by maximizing the objective function:

(13)

with

$$\begin{aligned} p\left( \mathbf {n}_{c}^{(j)}\right)&= \sum _{k} p\left( \mathbf {d}_{c}^{(k)}\right) p\left( \mathbf {n}_{c}^{(j)} | \mathbf {d}_{c}^{(k)} \right) \end{aligned}$$

(14)

As pointed out in [28], in the case of a Gaussian log-likelihood term, which is here the case, the objective function is equivalent to a weighted least squares problem for each $\mathbf {d}_{c}^{(k)}$:

(15)

After each EM-iteration, we delete clusters with less than two assignments to gain robustness.

Cluster Initialization. For initialization, we define a set of 3D directions which are derived from the targeted environment as follows: We apply our method in indoor scenes, hence we find the three dominant directions of the “Manhattan world”. In addition, the camera is mounted pointing forward with no notable tilt or rotation against the scene, therefore we use the three main directions ${(1~0~0)}^\mathrm {T}$, ${(0~1~0)}^\mathrm {T}$, ${(0~0~1)}^\mathrm {T}$ for initialization. For robustness, we add all possible diagonals like ${(1~1~0)}^\mathrm {T}$, ${(1~-1~0)}^\mathrm {T}, \ldots , {(1~1~1)}^\mathrm {T}$ (e.g. to capture the staircase in Fig. 4b)) and end up with overall 13 line directions. All line directions are normalized to unit length and have initially the same probability. The variance of each cluster is initially set to $\sigma _k^2 = \sin ^2( 1.5^{\circ })$ which reflects that the plane normal and the direction vector should be perpendicular up to a variation of $1.5^{\circ }$.

Note that this derivation of initial directions is easily adoptable for other scenes or camera mountings. If the camera is for example mounted in a rotated way, we can simply rotate the directions accordingly. If such a derivation is not possible, we suggest to use the initialization technique proposed in [28] where the initial vanishing points are calculated directly from the lines in the image.

If an image sequence is processed, we propose to additionally use the directions estimated from the previous image in the initialization as “direction priors”. In this case, we assign these priors a higher probability. We argue that the change between two consecutive images is rather small so the estimated directions from the previous image seem to be an valid initial assumption.

Results from the clustering step are visualized in Fig. 4.

Fig. 4.

Results of the parallel line clustering. Lines with the same color belong to the same cluster and are parallel in 3D. Each cluster has a 3D direction vector $\mathbf {d}_c$ assigned which represents the line direction viewed from this image. (Color figure online)

3D Line Direction Matching. We need to establish correspondences between the 3D line directions (the clusters) of the two images in order to calculate the relative rotation. This is done using RANSAC.

The mathematical basis for the algorithm is that – as previously stated – the transformation of a direction $\mathbf {d}_{c_1}$ from the first camera to the direction $\mathbf {d}_{c_2}$ in the second camera depends only on the rotation ${\MakeUppercase {\mathbf {R}}}_{c_2 \leftarrow c_1}$ (cf. Eq. (4)). In the presence of noise, this equation does not hold, so we use the angular error $\varepsilon$ between the directions:

$$\begin{aligned} \varepsilon&= \arccos \left( \frac{ {\mathbf {d}_{c_2}}^\mathrm {T} {\MakeUppercase {\mathbf {R}}}_{c_2 \leftarrow c_1} \mathbf {d}_{c_1} }{ \Vert \mathbf {d}_{c_1} \Vert \Vert \mathbf {d}_{c_2} \Vert } \right) \end{aligned}$$

(16)

The RANSAC process tries to hypothesize a rotation which has a low angular error $\varepsilon$ over a maximized subset of all possible correspondences. A rotation can be hypothesized from two randomly selected direction correspondences as described earlier. The idea behind this procedure is that only the correct set of correspondences yields a rotation matrix with small angular errors. Therefore, the correct rotation matrix only selects the correct correspondences into the consensus set.

The method has one drawback: it happens that different rotation hypotheses with different sets of correspondences result in the same angular error. This happens especially in an “Manhattan world” environment. This ambiguity is illustrated in Fig. 5.

Fig. 5.

Ambiguity in the direction matching. Which is the correct correspondence assignment for the directions from the left to the right? We could either rotate 45$^{\circ }$ clockwise in the plane ($\MakeUppercase {\mathbf {R}}_1$) or 45$^{\circ }$ counter-clockwise and then rotate around the green direction vector ($\MakeUppercase {\mathbf {R}}_2$). In this setting, the angular errors for $\MakeUppercase {\mathbf {R}}_1$ and $\MakeUppercase {\mathbf {R}}_2$ are the same. (Color figure online)

As we have no other sensors in our system to resolve these ambiguities, we assume small displacements between the images and therefore restrict the allowed rotation to less than 45$^{\circ }$. As we target visual odometry and SLAM systems, this is a valid assumption. Alternatively, if e.g. an IMU is present, its input could also be used.

4.3 Translation Estimation from Intersection Points

The translation is estimated in the same way as proposed by Elqursh and Elgammal [8]. Intersection points of coplanar 3D-lines are invariant under projective transformation and therefore fulfill the epipolar constraint [6]:

$$\begin{aligned} {\mathbf {p}_{i_2}}^\mathrm {T} {\MakeUppercase {\mathbf {K}}}^{-\mathrm {T}} \left[ {\mathbf {t}}_{c_2 \leftarrow c_1} \right] _{\times } {\MakeUppercase {\mathbf {R}}}_{c_2 \leftarrow c_1} \MakeUppercase {\mathbf {K}}^{-1} \mathbf {p}_{i_1}&= 0 \end{aligned}$$

(17)

If two intersection point correspondences and the relative rotation are given, the epipolar constraint equation can be used to solve ${\mathbf {t}}_{c_2 \leftarrow c_1}$ up to scale.

As we have no knowledge which intersection points from all $\frac{n(n-1)}{2}$ possibilities (with n the number of line correspondences) belong to coplanar lines, we follow the idea from [8] and use RANSAC to select the correct correspondences from all possible combinations while minimizing the Sampson distance defined in [6]. In contrast to [8], we can reduce the initial correspondence candidates as we take the clusters into account and only calculate intersection points between lines of different clusters.

4.4 Robust Relative Pose Estimation Framework

In this section, the explained algorithms are combined to an robust framework for relative pose estimation. The overall structure of the framework is depicted in Fig. 6.

Fig. 6.

The relative pose estimation framework.

The image line correspondences between the two images for which the relative pose is searched define the input of the framework. At first, the parallel line clustering is executed to estimate the 3D directions of the observed lines in both images. Each 3D line direction $\mathbf {d}_c$ is associated with a probability $p(\mathbf {d}_c)$ which reflects the size of the corresponding cluster. The more lines share the same direction, the higher the probability. We use this probability to guide the direction matching process: at the start, we select only 3D line directions from both images whose probability exceeds 0.1 and compute for them the direction matching with the RANSAC procedure as described. If the RANSAC process fails, the probability threshold is halved so more directions are selected and the RANSAC process is started again. This procedure in continued until a matching is found or all 3D line directions are selected and still no solution is obtained. In this case, the whole relative pose estimation process stops with an error. On success, the matched 3D directions and the corresponding rotation matrix is outputted. This rotation matrix is the rotation ${\MakeUppercase {\mathbf {R}}}_{c_2 \leftarrow c_1}$ between the two cameras.

Once the rotation is estimated, the translation is calculated from intersection points. Translation ${\mathbf {t}}_{c_2 \leftarrow c_1}$ and rotation ${\MakeUppercase {\mathbf {R}}}_{c_2 \leftarrow c_1}$ combined form the overall transformation ${\MakeUppercase {\mathbf {T}}}_{c_2 \leftarrow c_1}$ between the two cameras. As errors of the rotation directly influence the translation estimation, we use the inlier intersection points from the RANSAC step for a nonlinear optimization of the overall pose.

The optimized pose has still an ambiguity in the sign of the translation which needs to be resolved. We triangulate all line matches with respect to $c_1$. For every triangulated line $\mathbf {L}_{c_1}$ with endpoints $\mathbf {p}_{L}^{(i)}$, we measure the parallax $\rho$ between its observations (this is the angle between the two back-projected planes $\mathbf {\Pi }_{c_1}$ and $\mathbf {\Pi }_{c_2}$ which intersect in the triangulated line) and check if the triangulation result is in front of the camera by calculating a visibility score $\nu$:

(18)

with $\mathbf {r}_{c_1}^{(i)}$ are the back-projected rays of the endpoints of the line-segment seen in $c_1$. This value is weighted by the parallax angle and summed over all triangulated lines to form the ambiguity score A. To mitigate the influence of large parallax angles, we cut $\rho$ if it becomes bigger than a certain threshold $\rho _{t}$:

$$\begin{aligned} \rho _c&= {\left\{ \begin{array}{ll} \rho &{} \text {if } \rho \le \rho _t \\ \rho _t &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(19)

The overall ambiguity score is then

(20)

If $A < 0$, the sign of the translation is changed, otherwise the translation stays as it is.

Once the ambiguity is resolved, the relative pose estimation is completed.

5 Experiments and Evaluation

In the following, we evaluate the presented optical flow-based line matching algorithm and the robust relative pose estimation approach. All experiments were conducted on a Intel® Xeon™ CPU with 3.2 GHz and 32 GB RAM.

5.1 Evaluation of Line Matching

Now, we analyze the matching performance of the proposed matching algorithm and compare it to other state-of-the-art line matching approaches.

In detail, we use LEHF² from Hirose and Saito [12], MSLD³ from Wang et al. [11] and LBD⁴ from Zhang and Koch [13, 14] for comparison. All three methods are combined with the LRC matching strategy and a global threshold on the descriptor distance. The threshold for LEHF and MSLD is set to 0.6 whereas LBD has a threshold of 52.

We use two common measures known from binary classification tasks to evaluate the matching performance: precision and recall:

$$\begin{aligned} \text {precision}&= \frac{\text {correct matches}}{\text {all matches}} \end{aligned}$$

(21)

$$\begin{aligned} \text {recall}&= \frac{\text {correct matches}}{\text {all labeled matches}} \end{aligned}$$

(22)

The execution time of the algorithms is also measured.

Figure 7 shows the matching precision and recall of the different matching algorithms on the matching test set which is shown in the Appendix A.

Fig. 7.

Comparison of precision and recall of different matching approaches on the evaluation test set.

First of all, we observe that our proposed matching algorithm gives poor results on the “Facade01” and “Facade02” image pairs. These two image pairs clearly mark the limit of our approach as the images change a lot due to huge variation in viewpoint (“Facade01”) or camera rotation (in “Facade02”). As consequence, the optical flow method does not succeed in calculating a correct flow which explains the low precision and recall values for our method. Besides that, the matching precision of our algorithm is comparable to the other approaches, in the case of the “Office03” image pair it is even $5\%$ better then the next best (1.000 compared to 0.949 for MSLD). The recall increases in most cases between $4\%$ for the “Warehouse01” image pair (from 0.925 for LEHF to 0.963) and $19\%$ for the “Office03” image pair (from 0.804 for LEHF to 0.957). We conclude that our method is preferable to the other methods under small motion as we succeed in retrieving more correct matches with the same precision.

In Fig. 8 the average time over 50 executions of matching is plotted. As LEHF, MSLD, and LBD are descriptor-based, we additionally visualize the computation time to build the descriptors in both images.

Fig. 8.

Comparison of the execution time of different matching approaches on the evaluation test set. The plotted values are the mean over 50 executions. The time for descriptor calculation is additionally visualized for the descriptor-based approaches LEHF, MSLD and LBD.

We observe that the matching process itself of MSLD and LEHF is very fast compared to our optical-flow based method. But the construction of the descriptors consumes most of the time. Especially the MSLD descriptor is expensive to compute which results in an accumulated matching and description time between 143 ms and 1064 ms. The LEHF descriptor is much more efficient and has accumulated runtimes between 9 ms and 59 ms which makes it comparable to the runtime of our optical flow-based matching with runtimes between 13 ms and 79 ms. The matching time of LBD is comparable to our algorithm but with the descriptor calculation the runtime increases and results in overall runtime between 26 ms to 140 ms.

From the evaluation of matching performance and runtime we conclude that our proposed optical flow-based matching technique outperforms the state-of-the-art methods in matching under small baseline. We achieve the same precision as the state-of-the-art while attaining a higher recall. The runtime is on the same level as the fastest state-of-the-art approach - LEHF - and clearly better than the other evaluated methods.

5.2 Evaluation of Relative Pose Estimation

Now, we evaluate our proposed robust algorithm for relative pose estimation. First, we introduce the datasets which we use for evaluation. Afterwards, we conduct our experiments and compare our algorithm to the state-of-the-art.

Datasets. For our experiments, we use synthetic and real image sequences. For the synthetic data, we created a typical indoor scene with a 3D wireframe model and generated images from it by projecting the line-segments from the model into a virtual pinhole camera. The generated sequence consists of 1547 images. Example images are shown in Fig. 9.

Fig. 9.

A synthetic images showing a typical indoor scenario.

To see how image noise affects the processing, we add Gaussian noise on the image lines. We do not add noise on the endpoints of the line-segments, because this effects segments of various length differently. We rather rotate the segments around their center point, where $\sigma$ is the standard deviation of the rotation in degree.

For the experiments on real data, we use publicly available datasets with ground truth information of the camera poses. We select indoor sequences from robotics context as this is our targeted scenario but also evaluate on outdoor sequences from the automotive sector to test our algorithms in a variety of scenes. Robotic indoor scenes are represented by sequences from the “RGB-D SLAM benchmark” from TU Munich [29] and by the “Corridor” sequence from Oxford⁵. For outdoor scenes we use the “Stereo Ground Truth With Error Bars benchmark” from HCI [30] and the “KITTI Vision Benchmark Suite” from KIT [31]. The detailed overview of the used sequences is given in Table 1.

Table 1. List of sequences.

As the datasets are now defined, we evaluate the accuracy of the resulting relative pose and compare it to the state-of-the-art algorithms using points or lines.

Comparison with State-of-the-Art. In this experiment, we compare the accuracy of our relative pose computation with the “Triplet” approach [8] – the state-of-the-art using lines – and with the “5-point” algorithm [3] as state-of-the-art representative for relative pose estimation using points.

The experimental setup is as follows: The line matching algorithm described in Sect. 3 is executed for each pair of consecutive images. For the 5-point algorithm, we detect and match SIFT features [1]. The detected image lines (or points) along with their correspondences define the input for the relative pose estimation. The estimation algorithms are executed and the resulting relative poses $\left( \MakeUppercase {\mathbf {R}}_{est}, \mathbf {t}_{est} \right)$ compared to the ground truth poses $\left( \MakeUppercase {\mathbf {R}}_{gt}, \mathbf {t}_{gt} \right)$ of the test sequences. We evaluate the error in rotation and translation where the rotation error is the rotation angle of the axis-angle representation of $\MakeUppercase {\mathbf {R}}_{est} {\MakeUppercase {\mathbf {R}}_{gt}}^\mathrm {T}$. The translation error is expressed as angle between the ground truth translation and the estimated translation. We average the rotation and translation error angles $\alpha$ over each sequence using the following formula:

(23)

Fig. 10.

Accuracy of the relative pose computation on the synthetic sequence.

Fig. 11.

Runtime analysis of the relative pose computation on the synthetic sequence.

Additionally, we measure the execution time of each relative pose estimation algorithm.

We start the evaluation on the synthetic dataset using different noise levels $\sigma$. Since the synthetic dataset contains only lines, we just compare against the Triplet algorithm. The accuracy of the algorithms in term of rotation and translation error is shown in Fig. 10. The runtime behavior is presented in Fig. 11.

As expected, the accuracy of the relative pose estimation decreases while adding more and more noise to the date. Focusing on the rotation accuracy, our proposed algorithm seems to be more robust since the increase of the error is less compared to the Triplet approach. In the noise-free scenario, both approaches give similar results. Looking on the translation accuracy, the discrepancy between the results of both algorithms is much more severe (angle difference $>15^{\circ }$). On the first glance, this is surprising as both methods use intersection points to determine the translation. We give two explanations for this: first of all, the translation estimation is relying on the previously found rotation. As shown, the rotation estimated with our algorithms is more accurate so the translation estimation starts of better. Second, we only calculate intersection points for lines with different 3D direction which excludes vanishing points and favors real intersections. Even if vanishing points are theoretically inliers to the translation estimation, they are often far outside the image (e.g. the vanishing point of two parallel lines in the image) and affected by numerical errors. Also, slight measurement errors can lead to a huge error on the vanishing point’s position so we decided to filter them out using the described procedure.

The execution time of the relative pose algorithm is depending on the number of input feature matches. The Triplet algorithm and our proposed method uses the same line matching input; for the synthetic dataset we have on average 31.10 matches per image pair. Despite the same input, our proposed algorithm needs only between 20% and 35% of the runtime. This is due to the fact that in the Triplet approach all possible $O(n^3)$ triplet combinations (n is the number of line matches) are generated and then tested in a RANSAC scheme to calculate the rotation which is very time consuming. Contrary to that, our estimation is based on the line directions calculated in the clustering step. In this sequence, we extract only around 3 different line directions per image, hence the rotation calculation is very fast. The number of generated intersection points is also lower as mentioned above which speeds up the translation estimation.

Now, we evaluate our algorithm on real data sequences and compare its accuracy against the Triplet approach as before and additionally against the 5-point approach. The accuracy on the real image datasets is visualized in Fig. 12, the runtime performance shown in Fig. 13.

Fig. 12.

Accuracy of the relative pose computation on the real sequence.

Fig. 13.

Runtime analysis of the relative pose computation on the real image sequence.

This experiment confirms the previous results. Our proposed algorithm gives better results than the Triplet method on all sequences. On the four indoor sequences (“OxfordCorridor” and “TUMPioneer”) our line based algorithm can compete with the 5-point algorithm. Both, rotation and translation accuracy are in a similar range, for the “TUMPioneerSLAM3” the translation error is even 8% better. But for the outdoor sequences (“HeiSt” and “KITTI”), the point-based method seems to be superior. Whereas for “HeiSt01” and “HeiSt02” our algorithm can correctly calculate the rotation, it cannot handle the “KITTI05” sequence and shows much more rotation error than the point-based approach. Also the translation error is much higher. One reason for the dominance of the 5-point algorithm on the outdoor sequences is that this setting is much more suited for the SIFT feature as a lot of texture is present in the images. This is not the case for the indoor sequences, especially the TUM dataset, where white walls and room structure are dominating.

Regarding the execution time, we clearly see that the more matches we have, the slower the algorithms. The triplet approach is in the order of one magnitude slower than our approach which is explained by their expensive triplet calculation as explained earlier. But our approach is still around two magnitudes slower that the 5-point algorithm. One reason is that the 5-point algorithm estimates rotation and translation in one step so only one RANSAC iteration is executed. The Triplet algorithm and our approach need two: one for the rotation estimation and one for the translation. Another important factor is the need of intersection points for translation estimation. The number of intersection points is in $O(n^2)$ for n matches. Even as we have less line matches then point matches (around 100 line matches compared to 200 point matches), the number of intersection points is much bigger.

Overall, this experiment shows that our presented algorithm is feasible for relative pose estimation. It is clearly superior to the Triplet method as average rotation and translation errors are smaller – and that with significantly lower computation time. In some scenarios it can compete with point-based approaches in terms of accuracy but the computation time is a limiting factor here.

6 Conclusion

In this paper, we presented a innovative relative pose estimation scheme using lines.

First, we introduced a novel line matching algorithm for small baseline displacement based on optical flow. We investigated line matching since relative pose estimation is directly influenced by the correspondences found. In a comparison to other state-of-the-art descriptor-based line matching approaches we could demonstrate that our proposal shows better recall by same precision with same or smaller computation time.

Second, we explained our proposed relative pose estimation framework. In our approach, we estimate the 3D line directions through a clustering step of parallel lines in the world and use this information throughout the whole processing pipeline. The direction information is used to calculate the relative rotation and to limit the intersection point calculation. Rotation and translation estimation are embedded into a robust relative pose estimation framework.

Finally, we compared our relative pose estimation to the state-of-the-art approach using lines from Elqursh and Elgammal [8] and against Nister’s point-based algorithm [3]. We evaluated on publicly available indoor and outdoor datasets and showed that our method outperforms the line-based approach in terms of accuracy and runtime. Especially the runtime can be reduced from seconds to milliseconds. The point-based approach performs better as expected in highly textured outdoor scenes but our method can compete in textureless indoor scenarios.

In the future, we want to extend our approach to a complete SLAM system. To reach this goal, we need to relax the restriction to small motions in the direction matching. Also, line matching strategies supporting wide-baselines should be investigated.

A Matching Test Set

The test set consists of 8 image pairs with small baseline displacement showing different indoor and outdoor scenes. For each image in the test set, we detect line-segments using the LSD algorithm⁶ [32]. Then, we manually label corresponding lines in the image pairs and save them as ground truth matches. Note that a line-segment can correspond to multiple line-segments in the other image as the line segmentation may vary.

The complete test set is shown in Fig. 14. The image pairs “Facade01” and “Facade02” are taken from the matching evaluation from Zhang et al. [13, 14], “HeiSt02” from the Heidelberger Stereo benchmark [30], “Kitti02” from the KITTI odometry benchmark [31] and“Oxford02” from the Oxford multiview dataset⁷.

Fig. 14.

Image pairs of the test set.