1 Introduction

Determination of active earth pressure exerted by a backfill soil mass is of considerable importance in the safe design of any retaining structures and helpful partly also for the problems related to sheet piles, braced cuts and foundations etc. Most of the earlier studies deal with this problem assuming the backfill soil mass as either in a state of fully saturated or dry condition. In practice, very often, the backfill soil mass is in unsaturated state. Analysis based on total stress concept for unsaturated soil zone that exist normally above the water table can lead to catastrophic failure of earth structures (Yoo and Jung 2006; Godt et al. 2009; Kim and Borden 2013; Koerner and Koerner 2013). Therefore, the variation of effective stress in the unsaturated soil zone above the water table is required to be established more accurately in order to analyze the stability of retaining structures against different possible failures in various stages of its construction. However, the establishment of the variation of effective stress in the unsaturated soil may become difficult owing to the presence of many environmental factors. For instance, flow conditions such as rainfall infiltration or evaporation largely changes the profiles of matric suction and thus, the profiles of effective stress in the unsaturated soil zone are changed. Pufahl et al. (1983) have used two different types of assumptions for defining the nature of matric suction profiles namely, (i) a constant with depth, and (ii) linearly varying with depth in the analysis of earth pressure behind retaining wall with unsaturated backfill. The extended Mohr-Coulomb failure criterion given by Fredlund et al. (1978) was used for describing the maximum shearing resistance offered by unsaturated soil mass; however, this criterion does not consider the nonlinear variation in shear strength due to changes in matric suction beyond air entry value. Also, the effect of change of flux at the ground surface on the shear strength of soil was not taken into account. Nevertheless, the extended Mohr-Coulomb failure criterion given by Fredlund et al. (1978) is still being widely used due to its simplicity for circumstances in which the above mentioned factors are of least important in design. On the other hand, Lu and Likos (2004) have presented modified Mohr-Coulomb failure criterion for describing the shear strength of unsaturated soil; in this failure criterion, both Bishop’s effective stress and the suction stress concept were incorporated to define a unified effective stress for saturated as well as unsaturated soil. Therefore, it captures the nonlinear variation in shear strength of unsaturated soils owing to change in matric suction with respect to flow conditions and location of ground water table. As a consequence, this approach enables the realistic nonlinear distribution of active pressure along the length of wall to be predicted. Further, this approach is simple and realistic, satisfying also the flux boundary conditions at the ground surface. The well-known Rankine’s earth pressure theory has been extended to unsaturated soils in all the studies mentioned above. Using the definitions of Coulomb earth pressure and applying the unified shear strength theory, Liang et al. (2012) obtained solutions for determining the active earth pressures of unsaturated soils without considering the effect of location of water table and backfill flow conditions. Very recently, Vahedifard et al. (2015) have computed the magnitude of active earth pressure coefficients by employing a log-spiral mechanism with the application of modified Mohr-Coulomb failure criterion.

The above cited studies have clearly demonstrated the importance of explicit consideration of effective stresses in the analysis of retaining walls with unsaturated soil backfill. Although extended Rankine’s solution for retaining walls with unsaturated soil backfill has been available for determining active earth pressure distributions, its applicability is only limited to smooth vertical walls. Further, it does not account the effect of ground surcharge pressure. In the present research, by using Coulomb failure mechanism in combination with modified Mohr-Coulomb failure criterion, the active earth pressure coefficients and its distribution against retaining wall with inclined back surface retaining unsaturated soil backfill has been established. The variation of soil suction stress within the vadose zone of the backfill soil mass under various unsaturated flow conditions has been explicitly considered in the analysis. The influence of different unsaturated flow conditions (i.e., infiltration, no-flow and evaporation conditions) and location of water table below base of wall on the magnitude of active earth pressure coefficients and its distribution for varying parameters such as inclination of wall, roughness and adhesion of soil-wall interface, ground surcharge pressure, properties of backfill soil has been examined thoroughly. Finally, the solutions obtained from the present theory have been compared with analytical solutions obtained by Lu and Likos (2004), Vahedifard et al. (2015). It should be noted that (i) extended Rankine’s solution presented by Lu and Likos (2004) allows computing only the distribution of active earth pressure against the smooth vertical walls, and (ii) the method suggested by Vahedifard et al. (2015) allows only the magnitude of active earth pressure coefficients to be computed.

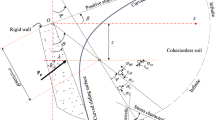
2 Problem Statement and Assumptions

A rigid retaining wall of height H with back surface OA is shown in Fig. 1. The back surface of the wall makes an angle of i with the vertical plane. The backfill soil mass is in unsaturated state, and is subjected to a uniform and continuous ground surcharge pressure of magnitude χ. Soil mass is assumed to obey modified Mohr-Coulomb failure criterion. The effective values of internal friction angle and cohesion are ϕ′ and c′, respectively. The water table is assumed to be located at a depth H 0 with respect to the base of wall. During the event of rainfall infiltration and evaporation, vertical one-dimensional unsaturated flow condition is assumed to prevail. Therefore, a constant magnitude of flow rate q at the backfill ground surface is considered with (i) negative sign for steady state infiltration case, and (ii) positive sign for steady state evaporation case. Under no flow condition, the value of q obviously becomes equal to zero. For the case of rough walls, the active earth resistance P a exerted by backfill soil mass is inclined an angle δ with the normal to the wall surface as shown in Fig. 1. A total tangential adhesive force C w is assumed to be acting at the soil-wall interface due to the wall adhesion component along the length of wall OA. It is aimed to determine the magnitude of total active earth resistance P a exerted by unsaturated soil backfill on the inclined surface of rigid wall. When the stresses in the backfill soil gets relaxed enough to reach the limiting active state, soil mass is assumed to fail in the shape a triangular wedge OAB with the rupture surface OB making an angle β with the horizontal plane. This simple mechanism is exactly the same as that considered earlier by Coulomb. In order to satisfy the modified Mohr-Coulomb failure criterion, the direction of inward reaction force R f must make an angle ϕ′ with the normal to the planar failure surface. The magnitude of total tangential cohesive force C f acts along the failure surface is simply equal to c′ × L OB ; where L OB is the length of surface OB. The normal force resulting from suction stress \( P_{{\sigma_{s} }} \) acts outwards on the failure surface OB.

Fig. 1.
figure 1

Details of forces acting on the triangular soil wedge

Full size image

3 Method of Analysis

3.1 Shear Strength Based on Modified Mohr-Coulomb Failure Criterion

Following Lu and Likos (2004), on the basis of unified effective stress principle with modified Mohr-Coulomb failure criterion, the shear strength τ f of saturated or unsaturated soil mass can be written as follows,

$$ \tau_{f} = c^{{\prime }} + \sigma^{{\prime }} \tan \phi^{{\prime }} $$
(1)
$$ \sigma^{{\prime }} = \sigma - u_{a} + \sigma_{s} $$
(2)

where τ f defines shear stress at failure, c′ and ϕ′ are the effective cohesion intercept and effective internal friction angle of soil; σ′ represents the effective stress; σ refers to the total stress on the failure plane; u a is the pore air pressure or is generally considered as atmospheric pressure if not specified which has been taken equal to zero in the present analysis; σ s represents the suction stress. Considering explicitly the influence of depth of water table H 0 and the properties of soil mass, the suction stress σ s at any distance measured from the base of the wall in the unsaturated soil backfill under various unsaturated flow conditions can be represented by the following expression (Lu and Likos 2004),

$$ \sigma_{s} = - \frac{1}{\alpha }\frac{{\ln \left[ {\left( {1 + \frac{q}{{k_{s} }}} \right)e^{{ - \alpha \gamma_{w} \left( {H_{0} + y} \right)}} - \frac{q}{{k_{s} }}} \right]}}{{\left[ {1 + \left\{ { - \ln \left[ {\left( {1 + \frac{q}{{k_{s} }}} \right)e^{{ - \alpha \gamma_{w} \left( {H_{0} + y} \right)}} - \frac{q}{{k_{s} }}} \right]} \right\}^{n} } \right]^{{\frac{n - 1}{n}}} }} $$
(3)

where, k s is the saturated hydraulic conductivity; γ w is the unit weight of water; y is the vertical distance from the base of the wall as shown in Fig. 1. α and n are the fitting parameters; α approximates the inverse of the air-entry pressure, and n is directly related to the distribution of the soil’s pore size. The possible ranges of α and n for a given soil type can be found in Lu and Likos (2004), Vahedifard et al. (2015). The active earth pressure on retaining walls is affected by the existence of apparent cohesion in the backfill soil mass. The apparent cohesion is defined as the shear strength mobilized by suction stress through the internal angle of friction in the unified effective stress theory, which is expressed as

$$ c_{a} = \sigma_{s} \tan \phi^{{\prime }} $$
(4)

where c a  = apparent cohesion; and ϕ′ = internal angle of friction.

3.2 Active Earth Pressure in Unsaturated Soil

Under limiting equilibrium condition, by considering horizontal and vertical equilibrium of various forces acting on the failure wedge OAB as illustrated in Fig. 1, the magnitude of active force P a per unit length of wall, for the case where there is no tensile crack appears in the backfill can be written as,

$$ P_{a} = \frac{{(W_{\gamma } + Q_{\chi } )\,\sin \,(\beta - \phi^{{\prime }} ) - C_{w} \sin \,(\beta - \phi^{{\prime }} - i) - C_{f} \cos \,\phi^{{\prime }} - P_{{\sigma_{s} }} \sin \phi^{{\prime }} }}{{\cos \,(\beta - \phi^{{\prime }} - \delta - i)}} $$
(5)
$$ C_{w} = \frac{{kc^{{\prime }} H}}{\cos \,i}\frac{\tan \delta }{{\tan \phi^{{\prime }} }} $$
(6)

here, W γ denotes the weight of soil block OAB and Q χ is the vertical downward force due to surcharge χ placed on the backfill; k denotes the adhesion factor; k = 0 if no wall adhesion is present, i.e., C w  = 0 and k = 1 when C w  > 0. The magnitude of the outward normal force \( P_{{\sigma_{s} }} \) due to suction stress can be computed by the following expression,

$$ P_{{\sigma_{s} }} = \frac{1}{\sin \,\beta }\int\limits_{0}^{H} {\sigma_{s} } dy $$
(7)

The magnitude of total active earth thrust corresponding to critical failure wedge can be found out by maximizing the function given in Eq. (5) with respect to the angle.

Finally, a unique active earth pressure coefficient in unsaturated soil is defined in the following fashion,

$$ K_{a} = \frac{2}{{\gamma H^{2} }}\left. {\hbox{max} \left( {P_{a} } \right)\,} \right|\,_{\beta > 0} $$
(8)

It is worth mentioning that the magnitudes of neither \( P_{a} \) nor \( K_{a} \) has been corrected for the effect of tension crack zone which would be commonly encountered in the field. The procedure for considering such effects will be discussed in the following section.

3.3 Distribution of Active Earth Pressure

The distribution of earth pressure can be obtained by performing differentiation of the Eq. (5) with respect to the y. In the other words, to obtain the magnitude of active earth pressure p a exerted by unsaturated soil backfill at any distance y from the base of the retaining wall, the expression for active force P a given in the Eq. (5) is differentiated with respect to y, which provides,

$$ p_{a} (y) = \left[ {\gamma \left( {H - y} \right) + \chi } \right]F_{1} - kc^{{\prime }} F_{2} - c^{{\prime }} F_{3} - \sigma_{s} F_{4} $$
(9)

Where,

$$ F_{1} = \frac{{\cos (\beta - i)\sin (\beta - \phi^{\prime})}}{{\cos i\,\sin \beta \,\cos (\beta - \phi^{\prime}\delta - i)}} $$
$$ F_{2} = \frac{\tan \delta }{{\tan \phi^{{\prime }} }}\frac{{\sin (\beta - \phi^{{\prime }} - i)}}{{\cos i\,\cos (\beta - \phi^{{\prime }} - \delta - i)}} $$
$$ F_{3} = \frac{{\cos \phi^{{\prime }} }}{{\sin \beta \,\cos (\beta - \phi^{{\prime }} - \delta - i)}} $$
$$ F_{4} = \frac{{\sin \phi^{{\prime }} }}{{\sin \beta \,\cos (\beta - \phi^{{\prime }} - \delta - i)}} $$

3.4 Depth of Tensile Crack

Because of the negligible or no strength of soils in resisting any tensile stresses, the development of tension crack in the backfill could normally be an unavoidable phenomenon. The maximum possible value of the tensile crack depth H t (= H − y 0) could be developed in the unsaturated soil backfill under active state, can be obtained by satisfying the condition, y = y 0 when \( p_{a} (y) = 0 \). Therefore, with the usage of Eq. (9) and satisfaction of zero active earth pressure at a distance y 0 from the wall base, the depth of tensile crack H t can be expressed as follows,

$$ H_{t} = \frac{{\left( {kF_{2} + F_{3} } \right)\,c^{{\prime }} + \left. {\sigma_{s} \,} \right|\,_{y = y0} F_{4} }}{{\gamma F_{1} }} - \frac{\chi }{\gamma } $$
(10)

where,

$$ \left. {\sigma_{s} } \right|\,_{y = y0} = - \frac{1}{\alpha }\frac{{\ln \left[ {\left( {1 + \frac{q}{{k_{s} }}} \right)e^{{ - \alpha \gamma_{w} \left( {H_{0} + H - H_{t} } \right)}} - \frac{q}{{k_{s} }}} \right]}}{{\left[ {1 + \left\{ { - \ln \left[ {\left( {1 + \frac{q}{{k_{s} }}} \right)e^{{ - \alpha \gamma_{w} \left( {H_{0} + H - H_{t} } \right)}} - \frac{q}{{k_{s} }}} \right]} \right\}^{n} } \right]^{{\frac{n - 1}{n}}} }} $$

The above equation is implicit and hence, the value of H t from Eq. (10) is obtained herein efficiently by using an iterative process for different parameters such as vertical unsaturated steady state flow rate, depth of water table, properties of soil and wall geometry. The correct solution for H t is assumed to be obtained when the difference between solutions of two consecutive computations shows negligible value in the order of 10−6.

3.5 Magnitude of Active Earth Pressure with Tensile Crack

Considering the possible occurrence of tensile crack in the backfill under active limiting state, the magnitude of total active resistance P′ a per unit length of wall, can be obtained as follows,

$$ P_{a}^{{\prime }} = \int\limits_{0}^{{H - H_{t} }} {p_{a} } (y)dy $$
(11)

On solving and simplifying Eq. (11),

$$ P_{a}^{{\prime }} = \frac{{H - H_{t} }}{2} \times \left[ {(2\chi + \gamma (H + H_{t} ))F_{1} - 2c^{{\prime }} kF_{2} - 2c^{{\prime }} F_{3} - 2P_{{\sigma_{s} }}^{{\prime }} F_{4} } \right] $$
(12)

where,

$$ P_{{\sigma_{s} }}^{{\prime }} = \frac{1}{{H - H_{t} }}\int\limits_{0}^{{H - H_{t} }} {\sigma_{s} } dy $$
(13)

A unique active earth pressure coefficient for the occurrence of tensile crack in the backfill is defined as follows,

$$ K_{a}^{{\prime }} = \frac{{2P_{a}^{{\prime }} }}{{\gamma H^{2} }} $$
(14)

Thus, the established expressions from the proposed approach allows estimating (i) the magnitude of active earth pressure before and after the formation of tensile crack in the backfill; (ii) the distribution of active earth pressure, and (iii) the maximum possible depth of tensile crack that would occur under active state.

4 Results and Discussion

All the computations required for obtaining the solutions were performed by generating the necessary computer codes. In order to examine the influence of vertical unsaturated steady state flow conditions on the magnitude of active resistance exerted by different types of backfill soils such as sand and clay, the rate of flow q under infiltration, no-flow and evaporation conditions equal to −3.14×10−8 m/s, 0 m/s and 1.15×10−8 m/s, respectively have been considered on the basis of steady-state infiltration and evaporation rates commonly encountered in the field under natural environmental conditions (Lu and Likos 2004). Different properties of clay and sand used in this analysis are given in Table 1. The typical values of α, n and k s given in Table 1 are collected from the literature (Lu and Likos 2004; Vahedifard et al. 2015) for the chosen soil types. In order to carry out the parametric study, (i) the cohesion and backfill surcharge pressure have been normalized as c′/γH and χ/γH, respectively, and (ii) the unit weight of chosen soils were kept equal to 20 kN/m3 irrespective of the soil types. Using Eq. (3) and the properties of soil (Table 1) taken to consideration for performing the analysis, the profile of suction stress has been plotted in Fig. 2(a–b) in terms of normalized suction stress (\( \sigma_{s}/{\gamma}{H} \)) vs. normalized distance above water (y + H 0 )/H for different wall heights and flow conditions with backfill as clay and sand. It has been found that the suction stress σ s profiles in unsaturated clay is almost linear and independent of wall height whose magnitude drastically reduces when flow changes from infiltration to evaporation and for all flow conditions, the value of suction stress is always zero at the level of water table and attains its maximum value at the ground surface. The suction stress σ s profiles in unsaturated sand is highly nonlinear, reduces with a decrease in the height of wall and independent of backfill flow conditions, that is, the stress profiles merge to a single line for all types of flow for a given height of wall. Further, in sand, the value of suction stress increases gradually when the distance from the water table (y + H 0) increases before attaining a peak value after which the value drops continuously and may even get diminishes when the distance (y + H 0) approaches to the ground surface. Similarly using Eqs. (3) and (4), the profile of apparent cohesion for soils under unsaturated steady flow can be obtained, and the profile of both suction stress and apparent cohesion are found to be almost the same with changes only on the magnitudes.

Table 1. Properties of unsaturated clay and sand under consideration
Full size table
Fig. 2.
figure 2

Variation of normalized suction stress with normalized distance above water for different wall heights and flow conditions with backfill as (a) clay; and (b) sand.

Full size image

Figures 3 shows the variation of the active earth pressure coefficients, K a and \( K_{a}^{\prime } \) with height of wall H under the influence of different backfill flow conditions (infiltration, no-flow and evaporation) for wall inclinations i = 0° with k = 0, H 0 = 0, δ = 1/2ϕ′ and \( \chi /\gamma H = 0. 1 \). It can be seen that the magnitude of K a and \( K_{a}^{\prime } \) are found to be continuously increasing with an increase in the height of wall H for unsaturated sand backfill. The values of K a and \( K_{a}^{\prime } \) corresponding to different unsaturated flow conditions such as infiltration, no-flow and evaporation has been found to be almost the same for unsaturated sand at all the heights of the wall as a result of which the curves for K a and \( K_{a}^{\prime } \) corresponding to different backfill flow in unsaturated sand merged to a single curve. On the other hand, in the case of clay backfill, hardly any change in the values of K a and \( K_{a}^{\prime } \) is found to occur with change in the values of H indicating that the pressure coefficients are independent of the wall height. Moreover, the values of \( K_{a}^{\prime } \) have been found to be greater than K a for all the flow conditions and the difference between \( K_{a}^{\prime } \) and K a increases when the flow changes from evaporation to no flow to infiltration condition. In unsaturated sand, significant difference between the magnitudes of K a and \( K_{a}^{\prime } \) is observed for wall height less than 2 m.

Fig. 3.
figure 3

Variation of active earth pressure coefficients, K a and \( K_{a}^{\prime } \) with H for different flow conditions with i = 0°, k = 0, H 0 = 0, δ = 1/2ϕʹ and χ/γH = 0.1.

Full size image

For H 0 = 0, δ = 0 and χ/γH = 0, the variation of K a and \( K_{a}^{\prime } \) in sand backfill with ϕ′ (i) for different heights of wall is presented in Figs. 4(a) for i = −10°, and (ii) for different inclinations of wall with vertical for H = 3 m is illustrated in Figs. 4(b). The magnitudes of K a and \( K_{a}^{\prime } \) decrease continuously with increasing soil friction angle and decreasing height of wall. As aforementioned, it can also be seen from the Fig. 4(a) that the magnitudes of pressure on the retaining wall before and after the crack formation in the backfill mass is exactly the same for wall heights greater than 2 m. For lower heights of wall, the active earth pressure coefficients K a may even become zero when ϕ′ is less than 30°; in such cases the soil backfill has the capability to remain stable without exerting any pressure on the retaining wall. However, the wall may be unstable as active pressure is exerted in the presence of tensile crack. Figures 4(b) shows that the values of K a and \( K_{a}^{\prime } \) in sand backfill changes significantly with the inclination of wall. For positive inclination of wall, the magnitude of active pressure on the wall is higher than the negative inclination. This clearly shows that the wall inclination angles have larger impact on the magnitudes of active earth pressure.

Fig. 4.
figure 4

Variation of active earth pressure coefficients, K a and \( K_{a}^{\prime } \) in sand backfill with ϕ′ and H 0 = 0, δ = 0 and χ/γH = 0 for (a) i = −10° for different flow wall heights; and (b) H = 3 m for different vertical inclinations of wall

Full size image

The distribution of normalized active earth pressure p a /γH along the normalized depth of wall y/H for two different surcharges (χ/γH = 0 and 0.1) and for different flow conditions is shown in Figs. 5(a–b) for H = 3 m with k = 0, i = 0°, H 0 = 0 and δ = 0. The pressure distribution curves for the case of unsaturated sand are found to be nonlinear and not changing with the variation in unsaturated flow conditions. For the case of unsaturated clay backfill, the distribution of p a /γH along the normalized depth of wall y/H is almost linear in nature. The pressure distribution curves for unsaturated clay backfill tend towards steeper with the flow conditions changing from evaporation to infiltration. It can be noted that the active earth pressure becomes negative in the upper half of the retaining wall for all the flow conditions and the depth of tensile crack zone (equal to the depth at which the pressure curves changes its sign) is found to increase when the backfill flow changes from infiltration to evaporation. Therefore, the magnitudes of \( K_{a}^{\prime } \) are noticed to be maximum and minimum for the case of infiltration and evaporation, respectively. The increase in the magnitude of backfill surcharge pressure causes the pressure distribution curves to shift towards the positive axis resulting an increase in the values of K a and \( K_{a}^{\prime } \).

Fig. 5.
figure 5

Distribution of active earth pressure along height of wall for different flow conditions with k = 0, H = 3 m; H 0 = 0, δ = 0 and i = 0° for (a) χ/γH = 0; and (b) χ/γH = 0.1

Full size image

For studying the effect of soil-wall interface characteristics on the active earth pressure distribution, Figs. 6 and 7 are plotted for χ/γH = 0, H = 3 m, i = 0° and H 0 = 0 corresponding to different backfill flow conditions. It can be seen from the Fig. 6 that the increase in the wall adhesion from its possible minimum (k = 0) to maximum (k = 1) values tend to shift the pressure distribution curves slightly towards the negative pressure axis, which indicates a marginal decrease in the pressure coefficients corresponding to different flow conditions. The increase in the soil-wall interface friction angle (δ) reduces the magnitude of active earth pressure. It is worth mentioning that the change of flow conditions and soil-wall interface friction angle does not seem to alter the pressure distribution curves near the top of wall in the unsaturated sand backfill.

Fig. 6.
figure 6

Distribution of active earth pressure in clay backfill for different flow conditions, and soil-wall adhesion with χ/γH = 0; H = 3 m; H 0 = 0, δ = 1/2ϕ′ and i = 0°

Full size image
Fig. 7.
figure 7

Distribution of active earth pressure in sand backfill along height of wall for different flow conditions, and soil-wall interface friction angles with χ/γH = 0; H = 3 m; H 0 = 0 and i = 0°

Full size image

In order to examine the effect of location of water table (H 0) on the active pressure distribution, for different normalized values of location of water table \( H_{0}/{H} \) by taking the values of parameters χ/γH = 0, H = 3 m, δ = 0 and i = 0°, the variation of p a /γH along the normalized depth of wall y/H is shown in Figs. 8 and 9 for unsaturated sand and clay as backfill, respectively. For a given orientation, heights of wall and backfill properties of sand, the pressure distribution curves in the sand backfill (Fig. 8) are highly non-linear for lower values of \( H_{0}/{H} \) < 1/3, and nearly linearly active earth pressure profiles were observed for larger values of \( H_{0}/{H} \). As aforementioned and referring to Fig. 2, the suction stress reaches peak value at a relatively lower height above the water table which in turn causes the active earth pressure profile to attain a nearly linear trend either with increasing the height of wall or lowering of water table. The magnitudes of active earth pressure gradually increases with an increase in the values of \( H_{0}/{H} \). Thus, in practical situations, it may be expected that the height and location of water table has significant effect either on reducing or on increasing the values of active earth pressure depending the geometry of wall and properties of sand backfill. Figures 9 shows in the case of clay backfill, the pressure distribution curves are shifted towards the negative pressure axis with increasing in \( H_{0}/{H} \) for all flow conditions. Unlike sand backfill, a greater dependency of flow type on changing the profiles of active earth pressure in clay backfill is observed and the reduction in the magnitude of earth pressure is found to increase with changing flow condition from infiltration to evaporation. As the variation of suction stress profiles between the water table and the top surface of retained soil mass at a given flow rate is almost linear in unsaturated clay, any increase in the value of \( H_{0}/{H} \) will obviously lead to reduction in the magnitude of earth pressure.

Fig. 8.
figure 8

Distribution of active earth pressure in sand backfill along height of wall for different flow conditions, and water table positions from the wall base with χ/γH = 0; H = 3 m; δ = 0 and i = 0°

Full size image
Fig. 9.
figure 9

Distribution of active earth pressure in clay backfill along height of wall for different flow conditions, and water table positions from the wall base with χ/γH = 0; H = 3 m; δ = 0; k = 0 and i = 0°

Full size image

5 Comparison with Available Solutions

The active earth pressure coefficients obtained from the present analysis has been compared with the solutions reported by Vahedifard et al. (2015) for an inclined wall (i = −10°) with H = 4 m, H 0 = 0, χ/γH = 0, δ = 0 for two different backfill soils. The associated comparisons are presented in Fig. 10(a–b). It can be noticed from Fig. 10(a) that the magnitudes of active earth pressure coefficients obtained (K a ) for unsaturated sand backfill are slightly higher (critical) than that reported by Vahedifard et al. (2015) using log spiral slip surface. It is noteworthy that no tensile crack could be developed in the backfill soil mass under limiting active state based on Eq. (10). For clay backfill as shown in Fig. 10(b), the present solutions for active earth pressure coefficients K a and \( K_{a}^{\prime } \) obtained with and without considering the effects of tensile crack has been compared with K a values reported by Vahedifard et al. (2015). It is found that the values of K a provided by Vahedifard et al. (2015) lies in between the K a and \( K_{a}^{\prime } \) values obtained in the present analysis. The difference in two solutions may be expected due to the assumption followed by Vahedifard et al. (2015) in defining the point of application of active pressure.

Fig. 10.
figure 10

Comparison of active earth pressure coefficients from the present study with that reported by Vahedifard et al. (2015) for (a) sand backfill; (b) clay backfill

Full size image

In Fig. 11(a–b), the active earth pressure profiles established from the present analysis are compared with solutions of Lu and Likos (2004) for two different unsaturated backfill soils retaining by a smooth vertical wall with H 0 = 10 m, H 0 = 0, χ/γH = 0, k = 0 and δ = 0. It can be clearly seen that the present solution are exactly the same to that reported by Lu and Likos (2004) based on extended Rankine’s theory. In case of a smooth vertical wall with k = 0, the value of critical failure plane corresponding to maximum active pressure is found to be 45 + ϕ′/2. Thus, the solutions from the present method for a vertical smooth wall with k = 0 and the extended solutions provided by Lu and Likos (2004) remains exactly the same.

Fig. 11.
figure 11

Comparison of active earth pressure distribution against vertical smooth walls for (a) sand backfill, and (b) clay backfill under different backfill flow conditions from the present study with that reported by Lu and Likos (2004)

Full size image

6 Conclusions

With the consideration of simple Coulomb failure mechanism based on modified Mohr-Coulomb yield criterion, the active earth pressure coefficient and its distribution against retaining walls with unsaturated backfill soils has been presented in the framework of limit equilibrium analysis. The effect of different vertical flow conditions and the location of water table with respect to base of wall on the active earth pressure exerted by unsaturated clay and sand backfill have been studied by varying different parameters such as inclination of wall, roughness and adhesion of soil-wall interface. The present approach allows computing the active pressure developed due to unsaturated backfill before and after the occurrence of tensile crack. For a given internal friction angle of soil, wall orientation and soil-wall interface property, the active earth pressure in unsaturated sand is found to be largely dependent on the height of wall and also the location of water table; whereas, in unsaturated clay, it is dependent on the location of ground water table. The variation in flow conditions alters more significantly the magnitude of resultant active earth thrust against the wall with unsaturated clay backfill; however, for unsaturated sand backfill, the magnitude of resultant active force remains unaffected with changes in the backfill flow conditions. The present study could be helpful to understand the causes of failure of retaining structures under different flow conditions in the presence of unsaturated backfill.