Abstract
This paper investigates the thermomechanical behavior of Al-Mg alloys submitted to biaxial loading until fracture. The study aims to characterize calorimetric signature accompanying the formation and propagation of Portevin-Le Chatelier (PLC) bands induced by such a loading condition. Full kinematic and thermal fields on the specimen surface were characterized by using Digital Image Correlation (DIC) and infrared thermography (IRT). Heat source field was reconstructed from the temperature field and the heat diffusion equation. The heat source map enables us to visualize spatio-temporal gradients in the calorimetric response of the material and to investigate the kinematics of PLC bands induced by equibiaxial tensile loading. Under certain conditions, heat source maps can be seen as mechanical dissipation maps. At the specimen centre, the heat source exhibits jumps that fit with jumps of temperature and equivalent deformation rate.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
- Portevin-Le Chatelier effect
- Aluminum alloy
- Equibiaxial tension test
- Infrared thermography
- Heat source reconstruction
5.1 Introduction
Plastic instabilities take place in numerous materials, reduce material ductility and induce surface roughness, which are parameters of crucial significance in the field of sheet metal forming. The Portevin-Le Chatelier (PLC) effect is such a plastic instability and is one of the macroscopic manifestations of dynamic strain aging (DSA) [1, 2]. From a mechanical point of view, it corresponds to an irregular plastic flow and propagation of high-strain bands in the material [3, 4]. Generally, PLC effects are investigated under uniaxial tension. Very few studies focus on the occurrence of PLC under another monotonic strain path (compression [5] or simple shear [6]). Concerning the type of material used, Al-Mg alloys are some of the most studied systems [7,8,9,10,11], typically the AA5000 series. To our knowledge, no study has been reported in the literature on PLC effects in Al-Mg alloys under equibiaxial tension, while most metal forming operations are carried out under these loading conditions. Furthermore, plastic deformation in metals leads to the dissipation of the main part of the mechanical energy into heat. This intrinsic dissipation results in an increase of the material temperature. It is therefore relevant to investigate PLC effects in a complementary manner by measuring temperature variation at the surface of the material. Several studies in this field have been reported in the literature [6, 12,13,14,15]. In most studies, infrared cameras are used to measure the temperature field at the surface of the specimen. Nevertheless, numerous studies previously carried out by Chrysochoos et al. have shown that heat sources produced by the material itself are more relevant than temperatures for analyzing such phenomena [16,17,18,19]. The main reason is that the temperature field is influenced by heat conduction as well as heat exchanges with the ambient air and the grips of the testing machine. To our best knowledge, only studies [20, 21] provide heat source distributions induced by PLC effects in a metallic material, but under uniaxial tensile loading conditions.
The present paper investigates the PLC effects in Al-Mg alloy sheet under equibiaxial loading conditions by means of IR thermography measurements. Heat sources produced or absorbed by the material itself during deformation are deducted from temperature field measurements by using the heat diffusion equation. The heat source map enables us to visualize spatio-temporal gradients in the calorimetric response and to investigate the kinematics of PLC bands induced by equibiaxial tensile loading. In certain cases precisely detailed in the paper, the heat source map gives the mechanical dissipation field.
5.2 Specimen Preparation and Testing Conditions
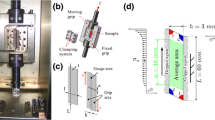
The material reviewed here is the aluminium alloy AA5086-H111. It is an Al-Mg alloy with an average magnesium weight ratio of 4 %. In order to reach high strain levels in the central zone of the specimen, a dedicated cruciform shape has been designed from finite element simulations (see Fig. 5.1a) and submitted by the present authors [22]. A progressive thickness reduction in the central zone is adopted. The central region of the specimen is manufactured by using a computer numerical control (CNC) lathe. The experimental device is a servo-hydraulic testing machine provided with four independent dynamic actuators, permitting biaxial tensile tests on cruciform specimens along two perpendicular axes. The overview of the experimental set-up is given in Fig. 5.1b. The strain path during the test can be directly controlled by the actuator motion. The results presented in this work are obtained under an equibiaxial strain state, with the same velocity of 1 mm/s for both axes.
5.3 Full Field Measurements
5.3.1 Kinematic Field Measurement
Images of the gauge area of the cruciform specimen were recorded with a Fastcam Ultima APX-RS digital camera. As shown in Fig. 5.1b, the camera is placed perpendicularly to the surface observed. Images are obtained by using an optical mirror. The acquisition frequency is set at 250 frames per second. The spatial resolution is 0.054 mm/pixel. The DIC software CORRELA 2D was used to compute the in-plane strain field. Major and minor strains are calculated on a square area (approximately 16 × 16 mm). Equivalent strain is calculated as follows:
where ε ij are the components of the strain tensor.
5.3.2 Temperature Field Measurement
Temperature field measurements were performed using a FLIR X6540sc infrared camera, which features a focal plane array of 640 × 512 pixels and detectors with a wavelength range of 1.5–5.1 μm. Integration time was equal to 1,000 μs. The acquisition frequency was set at 250 frames per second. The NETD was equal to 20 mK at 25 °C. The camera detector calibration was performed with a black body using a Non-Uniformity Correction (NUC) procedure. Temperature variation fields were obtained by subtracting the initial temperature field (before applying mechanical loading) from the current one. The spatial resolution, corresponding to the pixel size on the measurement plane, was equal to 0.206 mm/pixel. A thin, opaque and uniform black paint was sprayed on the specimen surface to obtain a thermal emissivity close to one.
5.4 Bi-Dimensional Heat Source Reconstruction from Temperature Field Measurement
Considering the first and second principles of thermodynamics, assuming that Fourier’s law is used to model heat conduction and that the heat conduction is isotropic, the 2D formulation of the heat diffusion equation writes [23]:
where ∆2D is the two-dimensional Laplace operator in the (x, y) plane. τ is the time constant, which is considered as a time constant characterizing the heat exchange with ambient air. ρ is the density, \( {C}_{E,{V}_K} \) is the specific heat at constant strain E and internal variables V K and θ is the temperature variation.
5.5 Typical Results and Discussion
5.5.1 Mechanical Response
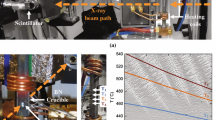
Figure 5.2a shows the evolution of forces during the test, along the two perpendicular directions. The first part of the curves (t ∈ [1.75; 2.2]) corresponds to the elastic deformation of the cruciform specimen and the two curves are quasi-superimposed. This means that the test was conducted under quasi-perfect equibiaxial loading conditions. In the second part of the curve (t > 2.2 s), plastic deformation starts at a corresponding force approximately equal to 2,400 N. In the plastic domain, the zoom in on the curves shows that force profiles exhibit slight fluctuations. Under tensile loading conditions, such fluctuations are the signature of type A PLC bands [4]. The gap between the values of the two forces is due to anisotropy.
5.5.2 Thermal Response at the Specimen Centre
Figure 5.2b gives the temperature variations and equivalent strain at the centre of the cruciform specimen versus time. At the very beginning of the test, strain increase leads to temperature decrease. This is typically observed in purely thermoelastic response of materials such as metallic ones. From t = 2.3 s on, temperature increases. Mechanical dissipation due to plasticity is produced and is of a first order compared to the thermoelastic coupling. In Fig. 5.3, equivalent strain rate alternates between low (but always positive) and high values, which forms steps in the plastic domain for the equivalent strain. When equivalent strain rate value is high, temperature strongly increases. This is the signature of PLC bands formation and propagation.
5.5.3 Calorimetric Response at the Specimen Centre
At the very beginning of the test, the material absorbs heat (heat source is negative). From t = 2.2 s on, the material continues absorbing heat but at a lower rate, since mechanical dissipation due to plasticity occurs. From t = 2.3 s on, heat produced due to plasticity is superior to heat absorbed due to thermoelasticity, and the heat source becomes positive. As a consequence, the temperature starts to increase. Subsequently, each jump in the equivalent strain induces a strong heat production and a jump in temperature. In terms of heat sources, the maximum value reached during the jumps increases monotonically from 5.106 to 3.107W/m3 and more before failure. Between two strain jumps, equivalent strain rate is lower (but always positive) and corresponding average heat sources mostly negative. This proves that after PLC band passage, the material mainly deforms elastically, which mainly explains why temperature decrease after each jump. Heat diffusion also occurs but its contribution to the temperature decrease is less than 1 % of the total heat source. These results prove that temperature drops after PLC band passage are mainly due to thermoelasticity.
5.5.4 Bidimensional Heat Source Reconstruction
The kinematics of PLC bands is usually investigated under uniaxial loading conditions by using full field kinematic measurements. It is also investigated using quantitative calorimetry obtained by temperature field measurement, since these bands have a specific calorimetric signature [21]. To our knowledge, this is the first study of PLC band kinematics under equibiaxial loading condition by means of quantitative calorimetry.
Figure 5.4 presents heat source maps obtained for different jumps in terms of heat source, which corresponds to the formation and propagation of PLC bands. For each jump considered, a set of three heat source maps is given. The three maps correspond, from the bottom to the top, to the beginning, the middle and maximum value of heat source during the jump. In order to distinguish the calorimetric signature of PLC bands, the maps given are anamorphosed, i.e. the scale is given in maximum and minimum values in the considered image. Here, PLC band kinematics is studied qualitatively, this is why no bar scale is shown. Several results can be derived from these maps:
-
PLC bands are highly dissipative: they clearly appear in red color in the heat source field.
-
PLC bands form a cross that propagates from the specimen centre to the borders of the square zone. The cross is formed in a zone under equibiaxial loading, and branches propagate in zones of different loading condition, i.e. from equibiaxial to quasi-uniaxial strain states. Further investigations of the effects of strain path on PLC kinematics are currently carried out in our laboratory.
-
PLC band kinematics is highly repeatable from one heat source jump to another: the same shape of PLC bands and the same angles of the formed cross are observed.
-
As thermoelasticity leads to low heat absorption compared to the heat produced by PLC bands, these maps can be assumed to give mechanical dissipation field. This assumption is classically used to neglect the effect of thermoelastic coupling [16, 21]. Therefore, heat source maps can be considered as mechanical dissipation maps.
Further analyses on the PLC band kinematics have been carried out and four steps have been identified. They are precisely presented and detailed in [24].
5.6 Conclusion
This paper provides the first study on spatio-temporal distribution of heat produced by PLC bands formed under equibiaxial tensile loading. Equibiaxial tensile testing has been carried out at an ambient temperature with an Al-Mg alloy. The temperature field was measured during the test and corresponding heat sources were reconstructed by means of the bidimensional formulation of the heat diffusion equation. The heat source map enables us to visualize spatio-temporal gradients in the calorific response of the material and to investigate the kinematics of PLC bands induced by equibiaxial tensile loading, which forms dissipative waves. At the specimen centre, the heat source exhibits jumps that fit well with jumps in the equivalent deformation rate and the temperature. The results are a promising alternative of inquiry into the effects of complex loading conditions as those encountered during sheet metal forming processes on occurrence and kinematics of PLC bands. Additionally, the present study provides additional data for the development and validation of PLC band kinematic models.
References
Van Den Beukel, A.: Theory of the effect of dynamic strain aging on mechanical properties. Phys. Status Solidi. 30, 197 (1975)
Kubin, L.P., Estrin, Y.: Acta Metall. 33, 397 (1985)
Estrin, Y., Kubin, L.P., Aifantis, E.C.: Introductory remarks to the viewpoint set on propagative plastic instabilities. Scr. Metall. Mater. 29(9), 1147–1150 (1993)
Jiang, H., Zhang, Q., Chen, X., Chen, Z., Jiang, Z., Wu, X., Fan, J.: Three types of Portevin-Le Chatelier effects: experiment and modelling. Acta Mater. 55(7), 2219–2228 (2007)
Lebedkina, T.A., Lebyodkin, M.A.: Effect of deformation geometry on the intermittent plastic flow associated with the Portevin-Le Chatelier effect. Acta Mater. 56(19), 5567–5574 (2008)
Coër, J., Manach, P.Y., Laurent, H., Oliveira, M.C., Menezes, L.F.: Piobert-Lüders plateau and Portevin-Le Chatelier effect in an al-mg alloy in simple shear. Mech. Res. Commun. 48, 1–7 (2013)
Balik, J., Lukac, P.: Portevin-Le Chatelier instabilities in Al-3 Mg conditioned by strain rate and strain. Acta Metall. Mater. 41(5), 1447–1454 (1993)
Fujita, H., Tabata, T.: The effect of grain size and deformation sub-structure on mechanical properties of polycrystalline aluminum. Acta Metall. 21(4), 355–365 (1973)
Korbel, A., Dybiec, H.: The problem of the negative strain-rate sensitivity of metals under the Portevin-Le Chatelier deformation conditions. Acta Metall. 29(1), 89–93 (1981)
Thomas, A.T.: The tensile deformation behaviour of an aluminium-magnesium alloy. Acta Metall. 14(10), 1363–1374 (1966)
Li, M., Lege, D.J.: Serrated flow and surface markings in aluminum alloys. J. Eng. Mater. Technol. 120, 48–56 (1998)
Coër, J., Bernard, C., Laurent, H., Andrade-Campos, A., Thuillier, S.: The effect of temperature on anisotropy properties of an aluminium alloy. Exp. Mech. 51(7), 1185–1195 (2010)
Hu, Q., Zhang, Q., Cao, P., Fu, S.: Thermal analyses and simulations of the type a and type b Portevin-Le Chatelier effects in an al-mg alloy. Acta Mater. 60(4), 1647–1657 (2012)
Ait-Amokhtar, H., Fressengeas, C., Boudrahem, S.: The dynamics of Portevin-Le Chatelier bands in an al-mg alloy from infrared thermography. Mater. Sci. Eng. A. 488, 540–546 (2008)
Bernard, C., Coër, J., Laurent, H., Chauvelon, P., Manach, P.Y.: Relationship between local strain jumps and temperature bursts due to the Portevin-Le Chatelier effect in an al-mg alloy. Exp. Mech. 53(6), 1025–1032 (2013)
Chrysochoos, A., Louche, H.: Thermal and dissipative effects accompanying luders band propagation. Mat. Sci. Eng. A Struct. 307, 15–22 (2001)
Berthel, B., Wattrisse, B., Chrysochoos, A., Galtier, A.: Thermographic analysis of fatigue dissipation properties of steel sheets. Strain. 43, 273–279 (2007)
Wattrisse, B., Chrysochoos, A., Muracciole, J.-M., Némoz-Gaillard, M.: Analysis of strain localization during tensile tests by digital image correlation. Exp. Mech. 41, 29–39 (2001)
Chrysochoos, A., Huon, V., Jourdan, F., Muracciole, J.-M., Peyroux, R., Wattrisse, B.: Use of full-field digital image correlation and infrared thermography measurements for the thermomechanical analysis of material behaviour. Strain. 46, 117–130 (2010)
Louche, H., Vacher, P., Arrieux, R.: Thermal observations associated with the Portevin-Le Chatelier effect in an al-mg alloy. Mater. Sci. Eng. A. 404, 188–196 (2005)
Delpueyo, D., Balandraud, X., Grediac, M.: Calorimetric signature of the Portevin-Le Chatelier effect in an aluminum alloy from infrared thermography measurements and heat source reconstruction. Mater. Sci. Eng. A. 651, 135–145 (2016)
Zidane, I., Guines, D., Leotoing, L., Ragneau, E.: Development of an in-plane biaxial test for forming limit curve (FLC) characterization of metallic sheets. Meas. Sci. Technol. 21(5), 055701 (2010)
Chrysochoos, A., Louche, H.: An infrared image processing to analyse the calorific effects accompanying strain localisation. Int. J. Eng. Sci. 38, 1759–1788 (2000)
Le Cam, J.-B., Robin, E., Leotoing, L., Guines, D.: Calorimetric analysis of Portevin-Le Chatelier bands under equibiaxial loading conditions in Al–Mg alloys: Kinematics and mechanical dissipation. Mech. Mater. 105, 80–88 (2017)
Funding Information
This work has received the financial support of the AIS Scientific Grant from Rennes Métropole (2012), the Mission of Resources and Skills Technology (MRCT) Grant from the French National Center for Scientific Research (2012), the Interdisciplinary Mission (MI) Grant from the French National Center for Scientific Research (2013).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 The Society for Experimental Mechanics, Inc.
About this paper
Cite this paper
Le Cam, JB., Robin, E., Leotoing, L., Guines, D. (2018). Calorific Signature of PLC Bands Under Biaxial Loading Conditions in Al-Mg Alloys. In: Baldi, A., Considine, J., Quinn, S., Balandraud, X. (eds) Residual Stress, Thermomechanics & Infrared Imaging, Hybrid Techniques and Inverse Problems, Volume 8. Conference Proceedings of the Society for Experimental Mechanics Series. Springer, Cham. https://doi.org/10.1007/978-3-319-62899-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-62899-8_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-62898-1
Online ISBN: 978-3-319-62899-8
eBook Packages: EngineeringEngineering (R0)